Open Access Article
Open Access ArticleProbing a variation of the inverse-trans-influence in americium and lanthanide tribromide tris(tricyclohexylphosphine oxide) complexes†
Cory J.
Windorff
 ,
Cristian
Celis-Barros
,
Cristian
Celis-Barros
 ,
Joseph M.
Sperling
,
Joseph M.
Sperling
 ,
Noah C.
McKinnon
and
Thomas E.
Albrecht-Schmitt
,
Noah C.
McKinnon
and
Thomas E.
Albrecht-Schmitt
 *
*
Department of Chemistry and Biochemistry, Florida State University, 95 Chieftan Way, RM. 118 DLC, Tallahassee, Florida 32306, USA. E-mail: talbrechtschmitt@fsu.edu
First published on 5th February 2020
Abstract
The synthesis, characterization, and theoretical analysis of meridional americium tribromide tris(tricyclohexylphosphine oxide), mer-AmBr3(OPcy3)3, has been achieved and is compared with its early lanthanide (La to Nd) analogs. The data show that homo trans ligands display significantly shorter bonds than the cis or hetero trans ligands. This is particularly pronounced in the americium compound. DFT along with multiconfigurational CASSCF calculations show that the contraction of the bonds relates qualitatively with overall covalency, i.e. americium shows the most covalent interactions compared to lanthanides. However, the involvement of the 5p and 6p shells in bonding follows a different order, namely cerium > neodymium ∼ americium. This study provides further insight into the mechanisms by which ITI operates in low-valent f-block complexes.
Introduction
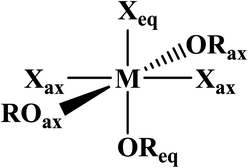
Phosphine oxides are highly stable ligands that have been utilized primarily for catalysis on elements across the periodic table.1 The study of phosphine oxides with f-elements has primarily focused on their use in extraction processes2–5 and in (pseudo)halide/nitrate f-element starting materials.6–9 The effect of two ligands trans to one another is most prototypically examined in the actinyls, AnO2n+, where the trans-oxygens display unusually short bond distances and high bond strength, best described as bond order of three.10 This effect, termed the inverse-trans-influence (ITI) as a general concept has become the focus of several experimental and theoretical investigations and has evolved to be primarily applied to ligands trans to multiply bonded ligands.11–17 This has also been studied in the [AnOX5]n− complexes (An = PaV, UVI, X = F, Cl, Br),18,19 where reaction of HBr with [UOCl5]1− yields [UO(Cl)Br4]1− where all of the equatorial Cl's have been replaced by Br's, but the trans-Cl is retained, which also possess the shortest M–Cl bond in the molecule.19 These seminal studies helped to show that something was unusual with high valent actinides where a ligand was trans to an oxo ligand, though these studies have not been revisited with modern instrumentation and methods. A prototypical examination on the effect of ITI is through the use of meridional octahedral compounds, e.g. mer-MX3L3, Fig. 1, which has been thoroughly studied in the transition metal series, but is significantly less studied in the f-block.20 However, the primary focus of structural and theoretical studies on actinide molecules displaying the ITI effect have been focused on high valent, +4 to +6, oxidation states.13,21–25 Lanthanides have only been subjected to structural studies in the +3 oxidation state,12,26 with some analysis of Ce(IV) and hypothetical Pr(IV) and Tb(IV) molecules.15,17 In this study on a variation of the ITI we are relying on a hole being created in 5/6p-orbitals of a low valent f-element complex without substantive multiple bond character in the trans ligand. The amount of ITI can be quantified as a percentage that implies that the lower the percentage value the larger the ITI effect, eqn (1), where r = bond distance, M = metal, X = neutral or anionic ligand.27 Herein, we base our discussion from the most basic and general definition given in the literature by Denning as the polarization of the core electrons towards the f shell driven by a tightly bound ligand. Because these orbitals are lower in energy in the valence region.28 This effect produces an electron deficiency in the position trans to the polarizing ligand that is compensated by a secondary ligand. This broad and perhaps oversimplified definition of ITI represents a solid basis without the need to assume any oxidations state or ligands.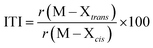 | (1) |
The minor actinides, Am and Cm, contribute high levels of radiation and heat in spent nuclear fuel. Long-lived isotopes of Am [241Am (t1/2 = 432 years), 243Am (t1/2 = 7370 years)] can be transmuted into radionuclides with a much shorter-half life, which is important for the end of the nuclear fuel cycle. However, the separation of these minor actinides from other fission products, such as lanthanides, remains a difficult problem. The additional separation of AmIII/CmIII is a great challenge due to their similar chemical properties and ionic radii. Phosphine oxide ligands have recently demonstrated relatively high selectivity for the Am–Cm pair in the form of (Ph2PyPO)2M(NO3)3.29 Although phosphine oxides are heavily utilized in separation of f-elements relevant to the nuclear fuel cycle, there have been few crystallographic studies for trans-uranium elements, and indeed only the mono and bis[Opy-2,6-CH2(Ph)2PO], NOPOPO, adducts have been reported.30 Herein we examine the synthesis and structure in saturated tri-cyclohexylphosphine oxide adducts of f-element tribromides, and the effects of the ITI on trivalent f-elements.
Experimental details
General considerations
Caution! 243Am (t1/2 = 7364 years) and its daughters have high specific activity α-particle and, γ emitting radionuclides, and its use presents extreme hazards to human health. This research was conducted in radiological and nuclear facilities with appropriate analyses of these hazards and implementation of controls for the safe handling and manipulation of these toxic and radioactive materials.Materials
All experiments were conducted in air with no attempt to exclude air or water. Reagents and solvents, OPcy3 (cy = cyclohexyl, C6H11, Alfa Aesar), CDCl3, CD2Cl2, CD3OD, (Cambridge), iPrOH, MeOH, DCM (Sigma) NH3(aq) (Baker) were purchased from commercial sources and used as received. LnBr3·6H2O (Ln = La–Nd) were synthesized by dissolution of Ln2O3 in concentrated HBr(aq) and heated at 150 °C in a box furnace until viscous, then agitated, stirred until cooled to room temperature, dissolved in water and evaporated to a residue. This process was repeated twice. The product was washed with ether, to remove residual acid and Br2, until washings were colorless, dried under house vacuum for 10–15 min and stored in a desiccator and used with the assumed hydration number of six. All 243Am synthetic manipulations were performed in a certified chemical fume hood, and a known concentration stock solution was prepared as previously described.31 Aqueous manipulations were performed with >18 Ω water from a Millipore purification system.Instrumentation
1H, 13C{1H} and 31P{1H} NMR spectra were recorded at 298(2) K on a Bruker 600 MHz NMR spectrometer operating at 600.13, 150.90, and 242.94 MHz, respectively, low temperature 1H and 31P{1H} spectra were recorded on a Varian Inova 500 MHz spectrometer at 187 K operating at 499.80, 202.34 MHz, respectively, for all lanthanide samples. The sample of 243AmBr3(OPcy3)3 was recorded at 295(2) K on a Bruker 400 MHz NMR spectrometer operating at 400.17, 100.62, and 161.99 MHz, respectively. 1H and 13C{1H} were referenced to internal solvent resonances, 31P{1H} spectra were referenced externally to 85% H3PO4. For radiologic containment, 243AmBr3(OPcy3)3 was dissolved in minimal CDCl3, transferred to a PTFE NMR tube liner, sealed, checked for contamination, placed inside a high quality borosilicate NMR tube, and checked again for contamination before being transported to the spectrometer. Due to the paramagnetism of Am3+, Ce3+, Pr3+ and Nd3+, and in particular the small sample size of 243AmBr3(OPcy3)3, only unambiguously identifiable peaks are assigned. For clarity all paramagnetic 13C{1H} and 31P{1H} spectra were processed with a 5 and 10 Hz line broadening, respectively. High resolution mass-spectra were recorded on an Agilent 6200 Q-TOF-MS coupled to a DART SVP (IonSense) ambient ionization source. All analyses were conducted in positive mode with a DART helium gas at 350 °C, Q-TOF heater gas (He) at 300 °C, drying gas flow at 0.2 L min−1, fragmentor voltage 175 V, skimmer voltage 65 V, and a mass range of 100–1700 amu with high resolution. Solution phase UV/vis/NIR measurements were made on an Agilent Technologies Cary 6000i UV/vis/NIR spectrophotometer in 1.0 cm small volume quartz cells between 200 to 1400 nm (methanol) or 235 to 1000 nm (DCM), at a resolution of 0.1 nm. Single crystal UV/vis/NIR measurements were recorded on crystals in immersion oil® placed on a glass slide and recorded using a CRAIC microphotospectrometer from 320 to 1700 nm. Single crystals of the lanthanide complexes were mounted on nylon cryoloops with Paratone-N oil. Crystals of 243AmBr3(OPcy3)3 was mounted with appropriate layers of containment. Crystallographic data from all single crystals were collected on a Bruker D8 Quest diffractometer with a Photon 100 complementary metal-oxide-semiconductor (CMOS) detector, and cooled to 120(2) or 130(2) K using an Oxford Cryostream or CRYO Industries low-temperature device. The instrument was equipped with graphite monochromatized Mo Kα X-ray source (λ = 0.71073 Å). The APEX3 (ref. 32) program package was used to determine the unit-cell parameters and for data collection. The raw frame data was processed using SAINT33 and SADABS34 to yield the reflection data file. Subsequent calculations were carried out using the SHELXTL35,36 or OLEX2 (ref. 37) programs.Theoretical methods
The coordinates of MBr3(OPcy3)3 (M = Am, Ce, Nd) for the calculations were obtained directly from the crystal structure to keep the constraints imposed by the solid-state packing. To utilize multiconfigurational calculations, the complete active space self-consistent field (CASSCF) approximation38 was used as implemented in the ORCA 4.1.1 program.39 Wave functions were obtained utilizing the SARC-TZVP basis set for the metal centers and the Def2-TZVP basis functions for the rest of the atoms. The active space considered were n electrons (n = 1, 3, 6 for Ce, Nd, and Am) in the seven f orbitals giving rise to a CAS(n,7). Scalar relativistic effects were included by the second-order Douglas–Kroll–Hess (DKH2) Hamiltonian. State interactions via quasi-degenerate perturbation theory (QDPT) were used to correct the wave function for spin–orbit coupling (SOC). The resulting wave functions (SO-CAS) were used to analyze the nature of the ground and low-lying excited states, whereas the scalar relativistic wave functions (SR-CAS) were used for further bonding analysis.The nature of the chemical bonds was addressed performing a topological analysis of the electron density using Bader's quantum theory of atoms in molecules (QTAIM) analysis. Key elements within QTAIM were extracted such as the electron density, delocalization indices, and energy densities at the interatomic region (bond critical point, BCP) which have been employed previously for this aim.40–48 The covalency was analyzed, on one hand, by changes in the concentration of the electron density at the BCP along with changes in the delocalization indices. On the other hand, energy densities show the polarization of the covalent bond by looking at the ratios between potential [V(r)] and kinetic [G(r)] energy densities, which for partial covalent bonds lie in between values of 1 and 2. The total energy density shows the degree of covalency that is represented by the level of predominance of the potential over the kinetic energy density.49
A model system was also investigated where the cyclohexyl groups were replaced by methyl groups to simplify the molecular orbital energy diagram picture and allow the observations between the Am, Ce and Nd complexes to be made. The methyl groups were re-optimized while the rest of the molecule was kept frozen to conserve the crystallographic geometry surrounding the metal atom. These calculations were performed in the ADF2019 suite50,51 using the PBE functional along with the TZP basis set. Frozen-core and all-electron calculations were performed for the full structure to prove the role of 5/6p orbitals in the stabilization of the complexes at the same level of theory. For the frozen-core calculations only core orbitals of metal centers were frozen, i.e. up to 5p for lanthanides and 6p for americium. In the particular case of Am, the frozen-core basis set was manually created with support from the ADF developers because it is not available in ADF2019. Furthermore, all-electron geometry optimizations were performed in the model system to confirm that geometries observed experimentally are not imposed by either crystal packing or steric hindrance, see Table S2†. Additionally, ligand-field DFT52,53 was used to examine the reduction of the inter-electronic repulsion within the 5/6p shell due to central-field and symmetry-restricted covalency. The procedure used herein has been previously described for Cs2KYF6:Pr3+,52 where occupation numbers in the f-shell were allowed to be fractional. The reductions were obtained not only with respect to the free ions but also compared to the nona-aquo complexes, [M(H2O)9]3+, where the geometries were taken from the crystallographic data in the literature.54–56
Synthesis of 243AmBr3(OPcy3)3
An aliquot of 243Am (3.0 mg, 12 μmol) was drawn from a 2 M HCl stock solution and precipitated with excess NH3(aq) to give a pale yellow solid naïvely formulated as “243Am(OH)3”, washed with water (2 × 2 mL), suspended in water (∼1 mL) and dissolved with HBr(aq) (concentrated, ∼0.5 mL) to give a yellow solution. The yellow solution was transferred to a 20 mL scintillation vial, placed under a heat lamp and gently evaporated to a yellow residue formulated as 243AmBr3·nH2O. The residue was dissolved in iPrOH (1.50 mL) to give a dark yellow solution. A colorless solution of OPcy3 (11 mg, 38 μmol) in iPrOH (1.00 mL) was added to the 243Am solution, which quickly became turbid and clear again. The solution was capped and left to stand undisturbed. Over 3 h amber colored X-ray quality crystals were deposited. A small sample was withdrawn for spectroscopy (single crystal X-ray diffraction and solid state UV/vis/NIR). The solution was capped and left to stand for 3 days to allow further crystallization. The mother liquor was decanted, washed with Et2O (3 × 0.5 mL), dried in air and transferred to a glovebox dedicated to actinide chemistry to give 243AmBr3(OPcy3)3 as a yellow/brown crystalline solid, 9.0 mg, 54%. 1H NMR (CDCl3; 400 MHz, 295 K) δ: 1.80 (br, s, cy), 1.67 (br, s, cy), 1.39 (br, s, cy), 1.14 (br, s, cy); 13C{1H} NMR (CDCl3; 101 MHz, 295 K) δ: 27.08 (2JPC = 27 Hz, cy), 26.15 (cy) 25.90 (cy); 31P{1H} NMR (CDCl3; 162 MHz, 295 K) δ: 108.89 (s, ν1/2 = 141 Hz). Due to the weak paramagnetism and small sample size 1H integration is ambiguous and 1H and 13C{1H} peak assignments are tentative, see ESI.† UV/vis/NIR [λmax, nm [cm−1], single crystal]: 340.0 nm [29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 411] charge transfer, 368.4 [27
411] charge transfer, 368.4 [27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 148] 5G2′, 380.9 [26
148] 5G2′, 380.9 [26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 252] 5G4′, 433.4 [23
252] 5G4′, 433.4 [23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 074] 5H4′, 457.5 [21
074] 5H4′, 457.5 [21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 856] 5G2′, 477.0 [20
856] 5G2′, 477.0 [20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 695] 5D2′, 508.0 [19
695] 5D2′, 508.0 [19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 685] 5L6′, 524.2 [19
685] 5L6′, 524.2 [19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 075] 5L6′, 777.4 [12
075] 5L6′, 777.4 [12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 863] 7F6′, 805.8 [12
863] 7F6′, 805.8 [12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 422] 7F6′, 823.2 [12
422] 7F6′, 823.2 [12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 147] 7F6′, 1042.6 [9591] 7F4′.
147] 7F6′, 1042.6 [9591] 7F4′.
General synthesis of LnBr3(OPcy3)3, (Ln = La, Ce, Pr, Nd)
As an alternative to the literature57 a colorless solution of OPcy3 (18 mg, 61 μmol) in iPrOH (1.0 mL) was added to a yellow solution of LnBr3·6H2O (∼10 mg, ∼20 μmol) in iPrOH (1.5 mL) causing the solution to become turbid and then clear. The vial was capped and left to stand overnight during which colorless (La, Pr, Nd) or orange (Ce) X-ray quality crystals were deposited. A small sample was withdrawn for spectroscopy (single crystal X-ray diffraction and solid state UV/vis/NIR). The mother liquor was decanted, washed with Et2O (3 × 0.5 mL), dried in air and briefly dried under reduced pressure (house vacuum) to give LnBr3(OPcy3)3 as a crystalline solid.LaBr3(OPcy3)3
Colorless LaBr3(OPcy3)3 20 mg, 80%. 1H NMR (CDCl3; 600 MHz, 298 K) δ: 2.068 (m, 8H, cy), 1.991 (m, 18H, cy), 1.842 (m, 18H, cy), 1.700 (m, 9H, cy), 1.600 (m, 18H, cy), 1.352–1.261 (m, 28H, cy); 1H NMR (CD2Cl2; 600 MHz, 298 K) δ: 2.095 (m, 9H, cy), 1.989 (s, 18H, cy), 1.853 (m, 18H, cy), 1.714 (m, 9H, cy), 1.661 (m, 18H, cy), 1.386–1.282 (m, 28H, cy); 1H NMR (CD2Cl2; 500 MHz, 187 K) δ: 1.999 (s, 6H, cy), 1.849 (s, 15H, cy), 1.750 (s 26H, cy), 1.563 (m, 24H, cy), 1.199 (m, 33H, cy); 1H NMR (MeOD-d4; 600 MHz, 298 K) δ: 2.021 (m, 9H, cy), 1.941 (m, 18H, cy), 1.861 (m, 18H, cy), 1.760 (s, 9H, cy), 1.475 (m, 18H, cy), 1.372–1.295 (m, 28H, cy); 1H NMR (MeOD-d4; 500 MHz, 187 K) δ: 2.050 (m, 9H, cy), 1.871 (m, 36H, cy), 1.861 (m, 18H, cy), 1.753 (m, 9H, cy), 1.428–1.304 (m, 46H, cy); 13C{1H} NMR (CDCl3; 151 MHz, 298 K) δ: 34.772 (1JCP = 34.8 Hz, i-cy), 26.893 (2JCP = 26.94 Hz, cy), 25.996 (cy), 25.901 (cy); 13C{1H} NMR (CD2Cl2; 151 MHz, 298 K) δ: 36.893 (1JCP = 37.0 Hz, i-cy), 29.243 (2JCP = 29.2 Hz, cy), 28.161 (cy); 13C{1H} NMR (MeOD-d4; 151 MHz, 298 K) δ: 31.061 (1JCP = 36.1 Hz, i-cy), 27.736 (2JCP = 27.74 Hz, cy), 27.170 (cy), 27.055 (cy); 31P{1H} NMR (CDCl3; 243 MHz, 298 K) δ: 60.314 (s, OP); 31P{1H} NMR (CD2Cl2; 243 MHz, 298 K) δ: 60.483 (s, OP), 31P{1H} NMR (CD2Cl2; 202 MHz, 187 K) δ: 62.216 (s, 4P, OP), 61.770 (s, 4P, OP), 61.280 (s, 2P, OP), 60.865 (s, br, 9P, OP); 31P{1H} NMR (MeOD-d4; 243 MHz, 298 K) δ: 57.209 (s, OP), 31P{1H} NMR (MeOD-d4; 202 MHz, 187 K) δ: 57.192 (s, OP). UV/vis/NIR [MeOH, λmax, nm (ε, M−1 cm−1)]: 209.6 (870), 268.5 (170).CeBr3(OPcy3)3
Orange CeBr3(OPcy3)3 20 mg, 75%. 1H NMR (CDCl3; 600 MHz, 298 K) δ: 5.29 (br, s, 9H, cy), 3.64 (br, s, 18H, cy), 2.68 (br, s, 18H, cy), 2.01 (s, 18H, cy), 1.82 (s, 25H, cy), 1.22 (br, s, 10H, cy); 1H NMR (CD2Cl2; 600 MHz, 298 K) δ: 4.94 (br, s, 9H, cy), 3.45 (br, s, 18H, cy), 2.53 (br, s, 18H, cy), 1.96 (s, 20H, cy), 1.77 (s, 26H, cy), 1.22 (br, s, 9H, cy); (CD2Cl2; 500 MHz, 187 K)58δ: 12.74, 9.93, 6.94, 4.70, 3.71, 3.39, 2.76, 2.12, 1.90, 1.28, 0.17, −0.48, −1.32, −2.02, −5.20; 1H NMR (MeOD-d4; 600 MHz, 298 K) δ: 1.37 (br, s, 9H, cy), 0.86 (br, s, 18H, cy), 0.39, 0.34, 0.33 (br, m, 36H, cy), 0.20 (m, 10H, cy), 0.11 (m, 26H, cy), −0.24 (br, m, 10H, cy); 1H (MeOD-d4; 500 MHz, 187 K) δ: 2.04 (br, s, 9H, cy), 1.87 (br, s, 32H, cy), 2.68 (br, s, 18H, cy), 2.01 (s, 18H, cy), 1.82 (s, 25H, cy), 1.22 (br, s, 10H, cy); 13C{1H} NMR (CDCl3; 151 MHz) δ: 38.76 (1JCP = 38.8 Hz, i-cy), 27.51 (cy), 26.06 (cy); 13C{1H} NMR (CD2Cl2; 151 MHz, 298 K) δ: 40.77 (1JCP = 40.8 Hz, i-cy), 29.75 (2JCP = 29.7 Hz, cy), 29.52 (cy), 28.33 (cy); 13C{1H} NMR (MeOD-d4; 151 MHz, 298 K) δ: 39.42 (1JCP = 37.6 Hz, i-cy), 28.00 (2JCP = 28.0 Hz, cy), 27.85 (cy), 27.20 (cy); 31P{1H} NMR (CDCl3; 243 MHz) δ: 109.48 (s, OP); 31P{1H} NMR (CD2Cl2; 243 MHz, 298 K) δ: 107.70 (s, OP), 31P{1H} NMR (CD2Cl2; 202 MHz, 187 K) δ: 134.28 (s, 1P, OP), 118.82 (s, 3P, OP), 113.90 (s, 2P, OP); 31P{1H} NMR (MeOD-d4; 243 MHz, 298 K) δ: 69.36 (s, OP), 31P{1H} NMR (MeOD-d4; 202 MHz, 187 K) δ: 57.16 (s, OP). UV/vis/NIR [λmax, nm, single crystal]: 339; [DCM, λmax, nm (ε, M−1 cm−1)]: 326.6 (1160); [MeOH, λmax, nm (ε, M−1 cm−1)]: 209.1 (1020), 231.6 (250), 252.7 (340), 314.9 (620). DART-MS (m/z, relative abundance, %) = 1188.34 (100), 1190.34 (61), 1189.34 (58), 1186.34 (52), 1191.34 (31), 1187.345 (29) [CeBr2(OPcy3)3]+.PrBr3(OPcy3)3
Colorless PrBr3(OPcy3)3 22 mg, 83%. 1H NMR (CDCl3; 600 MHz, 298 K) δ: 20.85 (br, s, ν1/2 = 1470 Hz, 5H, cy), 13.55 (br, s, ν1/2 = 860 Hz, 16H, cy), 10.52 (br, s, ν1/2 = 930 Hz, 14H, cy), 4.8 (br, s, 20H, cy), 3.40 (br, s, 21H, cy), 2.72 (br, s, 12H, cy), 1.44 (br, s, 11H, cy); 1H NMR (CD2Cl2; 600 MHz, 298 K) δ: 20.31 (br, s, ν1/2 = 2000 Hz, 9H, cy), 13.04 (br, s, ν1/2 = 1600 Hz, 18H, cy), 10.06 (br, s, ν1/2 = 1800 Hz, 18H, cy), 4.71 (s, 20H, cy, overlapping with solvent), 3.31 (s, 20H, cy), 2.55 (s, 12H, cy), 1.18 (s, 10H, cy); 1H NMR (CD2Cl2; 500 MHz, 187 K)59δ: 68.23 (br, s, 3H, cy), 46.78 (br, s, 9H, cy), 41.45 (br, s 10H, cy), 14.55 (br, s, 9H, cy), 8.73 (s, 10H, cy), 6.64 (s, 11H, cy), 2.15 (s, 4H, cy) −1.54 (s, 5H, cy), −2.06 (s, 6H, cy), −11.41 (s, 1H, cy), −14.38 (m, 6H, cy), −25.25 (br, s, 2H, cy); 1H NMR (MeOD-d4; 600 MHz, 298 K)60δ: 4.26, 3.62 (br, s, 27H, cy, overlapping with each other and solvent), 2.22 (s, 23H, cy), 2.01 (br, s, 31H, cy), 1.54 (br, s, 12H, cy); 1H NMR (MeOD-d4; 500 MHz, 187 K) δ: 2.04 (br, m, 9H, cy), 1.87 (br, s, 33H, cy), 1.76 (br, s, 9H, cy), 1.34 (br, m, 42H, cy); 13C{1H} NMR (CD2Cl2; 151 MHz, 298 K) δ: 58.38 (br, i-cy), 38.96 (cy), 32.81 (cy), 29.95 (cy); 13C{1H} NMR (MeOD-d4; 151 MHz, 298 K) δ: 42.09 (1JCP = 42.1 Hz, i-cy), 30.31 (cy), 28.84 (cy), 27.76 (cy); 31P{1H} NMR (CD2Cl2; 243 MHz, 298 K) δ: 204.14 (br, s, ν1/2 = 5700 Hz, OP), 31P{1H} NMR (CD2Cl2; 202 MHz, 187 K) δ: 467.96 (s, 2P, OP), 80.92 (s, 1P, OP); 31P{1H} NMR (MeOD-d4; 243 MHz, 298 K) δ: 75.54 (br, s, ν1/2 = 8000 Hz, OP), 31P{1H} NMR (MeOD-d4; 202 MHz, 187 K) δ: 57.14 (s, OP). UV/vis/NIR [DCM, λmax, nm (ε, M−1 cm−1)]: 245.0 (390); [MeOH, λmax, nm (ε, M−1 cm−1)]: 232.9 (270), 268.5 (30), 446.2 (8) 3P2, 470.8 (5) 3P1, 483.0 (6) 3P0, 595.7 (3) 1D2.NdBr3(OPcy3)3
Pale green NdBr3(OPcy3)3 19 mg, 82%. 1H NMR (CDCl3; 600 MHz, 298 K) δ: 11.77 (br, s, ν1/2 = 590 Hz, 8H, cy), 7.39 (br, s, ν1/2 = 320 Hz, 17H, cy, overlapping with solvent), 5.53 (br, s, ν1/2 = 400 Hz, 17H, cy), 3.05 (br, s, 18H, cy), 2.53 (br, s, 19H, cy), 2.14 (br, s, ν1/2 = 11H, cy), 1.21 (br, s, 11H, cy); 1H NMR (CD2Cl2; 600 MHz, 298 K) δ: 11.41 (br, s, ν1/2 = 890 Hz, 9H, cy), 7.07 (br, s, ν1/2 = 450 Hz, 18H, cy), 5.32 (br, s, ν1/2 = 520 Hz, 18H, cy, overlapping with solvent), 3.01 (br, s, 18H, cy), 2.44 (br, s, 18H, cy), 2.07 (br, s, 9H, cy), 1.10 (br, m, 9H, cy); 1H NMR (CD2Cl2; 500 MHz, 187 K) δ: 43.33 (br, s, 6H, cy), 28.35 (br, s, 10H, cy), 24.11 (br, s, 10H, cy), 9.40 (br, s, 10H, cy), 5.76, 4.47, 3.64, 2.10, 1.41, 0.55, −0.53 (s, 51H, cy, overlapping resonances) −2.76 (br, s, 4H, cy), −4.73 (br, s, 6H, cy), −6.28 (br, s, 3H, cy), −12.34 (br, s, 4H, cy); 1H NMR (MeOD-d4; 600 MHz, 298 K) δ: 2.88 (br, s, ν1/2 = 300 Hz, 18H, cy), 2.26 (br, s, ν1/2 = 180 Hz, 18H, cy), 1.98 (m, 20H, cy), 1.83 (m, 12H, cy), 1.63 (br, s, 18H, cy), 1.34 (m, 11H, cy); 1H NMR (MeOD-d4; 500 MHz, 187 K) δ: 2.04 (br, m, 9H, cy), 1.87 (br, m, 32H, cy), 1.75 (br, s, 9H, cy), 1.34 (br, m, 41H, cy); 13C{1H} NMR (CD2Cl2; 151 MHz, 298 K) δ: 44.37 (br, i-cy), 33.00 (br, cy), 30.81 (cy), 28.93 (cy); 31P{1H} NMR (CD2Cl2; 243 MHz, 298 K) δ: 184.78 (br, s, ν1/2 = 2400 Hz, OP), 31P{1H} NMR (CD2Cl2; 202 MHz, 187 K) δ: 426.65 (s, 2P, OP), 174.66 (s, 1P, OP); 31P{1H} NMR (MeOD-d4; 243 MHz, 298 K) δ: 70.41 (br, s, ν1/2 = 5200 Hz, OP), 31P{1H} NMR (MeOD-d4; 202 MHz, 187 K) δ: 57.12 (s, OP). UV/vis/NIR [λmax, nm, single crystal]: 532, 573, 576, 584, 588, 592, 595, 600, 607 – all excitations are 4G7/2 or 4G5/2, 738 4F7/2, 746(sh) 4S3/2, 806 2H9/2; [DCM, λmax, nm (ε, M−1 cm−1)]: 531.9 (5), 573.7 (9), 576.3 (sh, 8), 584.6 (8), 587.6 (sh, 7), 606.9 (5) – all excitations are 4G7/2 or 4G5/2, 738.2 (4) 4F7/2, 747.8 (sh, 4) 4S3/2, 806.7 (3) 2H9/2; [MeOH, λmax, nm (ε, M−1 cm−1)]: 217.4 (300), 329.3 (sh, 7) 2I15/2 or 4D7/2, 349.7 (7) 2I11/2, 351.5 (7) 4D1/2, 356.5 (7) 4D5/2, 429.0 (2) 2P1/2, 433.4 (2) 2P1/2, 462.4 (sh, 2) 2K15/2 or 4G11/2, 469.8 (2) 2D3/2, 477.3 (2) 2G9/2, 512.5 (3) 4G9/2 or 2K13/2, 524.9 (4) 4G7/2, 572.3 (sh, 5) 4G5/2 or 4G7/2, 583.0 (11) 4G5/2 or 4G7/2, 626.7 (1) 2H11/2, 675.8 (sh, 1) 4F9/2, 684.8 (1) 4F9/2, 736.1 (5) 4F7/2 or 4S3/2, 738.7 (5) 4F7/2 or 4S3/2, 749.1 (9) 4F7/2 or 4S3/2, 801.0 (14) 2H9/2, 866.8 (4) 4F3/2, 872.3 (sh, 3) 4F3/2, 887.2 (sh, 1) 4F3/2.Results and discussion
Synthesis
Previously published literature on LnCl3(OPR3)x show that the products have poor solubility or are prone to speciation.61–63 The more solubilizing bromide anion was studied instead. The known mer-LnBr3(OPcy3)3 (mer = meridional; cy = cyclohexyl, C6H11) have been recently reported and give opportunity for extension to the trivalent actinides, though small lanthanides can speciate.57,64–66 There has been just one report of a single crystal Am–Br compound, AmBr3(THF)4.67The previously reported syntheses of mer-LnBr3(OPcy)3, (cy = cyclohexyl, C6H11) utilized boiling ethanol and describe the complexes as having low solubility.57 By changing the alcohol to iso-propyl alcohol (iPrOH) and working on a scale relevant to actinides, i.e. ≤0.02 mmol of metal content, a smooth synthesis is obtained. This was extended to americium by starting from a stock solution of AmCl3·nH2O in HCl, precipitating the hydroxide, dissolving the product in HBr(aq) and evaporating to dryness, forming a putative AmBr3·nH2O solid. Combining the components in iPrOH initially forms a turbid solution which clarified within minutes and upon standing at room temperature, amber colored X-ray quality crystals formed within 2 h, eqn (2). A small sample was removed for spectroscopy and the solution was left to stand several days to increase the crystalline yield before work up, Fig. 2.
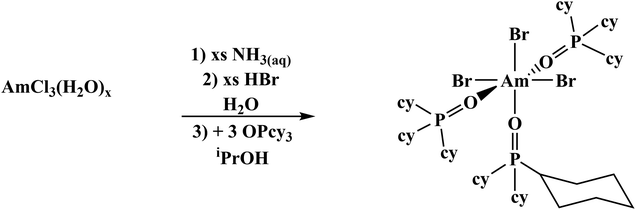 | (2) |
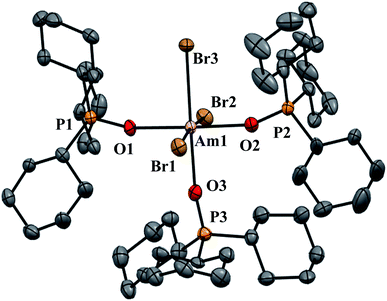 | ||
| Fig. 2 Thermal ellipsoid plot of AmBr3(OPcy3)3 drawn at the 50% probability level with hydrogen atoms omitted for clarity. | ||
Crystallography
AmBr3(OPcy3)3 crystallizes as the meridional isomer, mer-AmBr3(OPcy3)3, in the orthorhombic Pca21 space group and is isomorphous with its lanthanide analogs.25 Based on the Flack parameter, a small (≤3%) enantiomorphic twin was dealt with using a TWIN/BASF refinement, see ESI.†68 The Am–Br bond lengths fall into two classes, that of axial (ax) and equatorial (eq) ligands, where axial ligands consist of a homo-ligand trans to the ligand of interest, and equatorial ligands where a hetero ligand is trans to the ligand of interest, Fig. 1. The Am–Oax bond lengths are 2.302(7), and 2.312(7) Å while the Am–Oeq bond is 2.349(6) Å, a separation of 3σ. The Am–Brax atoms display a bond distance of 2.870(1), and 2.882(1) Å and the Breq atom displays a significantly longer distance of 2.912(1) Å. These values are all significantly longer than the 2.8222(6), 2.8445(6), and 2.8610(6) Å bond lengths reported in AmBr3(THF)4.67 However, all of the 2.466(4)–2.533(4) Å Am–OTHF bond lengths in AmBr3(THF)4 are significantly longer than Am–O bond lengths in AmBr3(OPcy3)3. The 2.34(1)–2.51(1) Å Am–O bond lengths reported for the NOPOPO ligand in Am(NOPOPO)(NO3)3 and [Am(NOPOPO)2(NO3)][NO3]2 {NOPOPO = Bis[(phosphino)methyl]pyridine-1-oxide, Opy-2,6-CH2(Ph)2PO} are only comparable to 2.349(6) Å Am–Oeq bond since the Am–Oax bond lengths are all significantly shorter, Table 1.30 All of the X–Am–Y bond angles are between 85.2(2)–95.60(5)° for cis ligands and 172.74(3)–178.1(2)° for trans ligands, see ESI.†In the course of preparing the synthesis of mer-AmBr3(OPcy3)3, the analogous lanthanides, La–Nd, were examined using the modified synthesis stated above, since the 6-coordinate radius of Am3+, 0.975 Å, is most closely related to Nd3+, 0.983 Å.69 It was found that the Nd and Pr analogs, mer-LnBr3(OPcy3)3, are isomorphous with the previously reported structures, except the half occupied lattice water was not located in our structures, see ESI.†57 The Ce analog, mer-CeBr3(OPcy3)3 is not yet reported and the structure was collected. The La analog was reported in the P21 space group with a lattice ethanol molecule, mer-LaBr3(OPcy3)3·EtOH, however upon synthesis in iPrOH, the isomorphous Pca21 unit cell was obtained and is reported here, see ESI.† Crystals of CeBr3(OPcy3)3 are orange, while crystals of the La, Pr and Nd analogs are all colorless. Bulk samples of PrBr3(OPcy3)3 and NdBr3(OPcy3)3 are pale yellow and pale green, respectively. The bond metrics of the lanthanides examined here all display the same axial/equatorial bonding patterns, that being axial ligands display much shorter bond lengths than equatorial ligands, with distorted octahedral geometries, see ESI.† Additionally, we examined the length of the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P bond, finding that all of the O
P bond, finding that all of the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P bond lengths significantly increase from the 1.490(2) Å length reported in the free ligand,70 The O
P bond lengths significantly increase from the 1.490(2) Å length reported in the free ligand,70 The O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P bond length increase in the Am and Ce complexes exhibited an average 0.030 and 0.028 Å, increase, respectively, while the La, Pr and Nd complexes only exhibited a 0.022, 0.023 and 0.022 Å, average bond length increase from the free ligand, respectively.
P bond length increase in the Am and Ce complexes exhibited an average 0.030 and 0.028 Å, increase, respectively, while the La, Pr and Nd complexes only exhibited a 0.022, 0.023 and 0.022 Å, average bond length increase from the free ligand, respectively.
For the sake of comparison we turned to the d-block to see if the same trend is also observed in transition metals. Two examples, mer-MoCl3(OPMe3)371 and mer-VCl3(OPEt3)372 have been reported. The Mo complex exhibits consistent bond lengths for both the Mo–Cl bonds and the Mo–O bonds. While the V complex shows some evidence of this lengthening of hetero-trans ligands where two of the V–Cl bonds are significantly different and two are slightly less than 3σ in separation. The V–O bonds show two bonds that are significantly different and two slightly more than 3σ in separation. We also compared the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P bond lengths of CoX2(OPcy3)2 (X = Cl, Br, I, NCS) where a regular increase in bond length is observed based on the identity of X, 0.021, 0.018, 0.15 and 0.025 Å, respectively.73
P bond lengths of CoX2(OPcy3)2 (X = Cl, Br, I, NCS) where a regular increase in bond length is observed based on the identity of X, 0.021, 0.018, 0.15 and 0.025 Å, respectively.73
With this f-element data in hand, the calculations of ITI effect from eqn (1) were carried out on the MBr3(OPcy3)3 (M = Am, La, Ce, Pr, Nd) complexes examined here. The data show that a subtle increase in ITI effect is seen with decreasing ionic radius, Table 2, all of the data are within the error of one another. When the ITI calculations were repeated using the crystallographic data for the previously published LnBr3(OPcy3)3 compounds (Ln = La, Pr, Nd, Gd, Ho), as well as LnI3(Et2O)3,26LnCl3(HMPA)3,74–76 and the series YbX3(THF)3 (X = Cl, Br, I),11,77,78 the data shows no clear trends or patterns with respect to lanthanide or halide identity, where the halide ligands usually show no ITI. The oxygen donors follow the pattern in terms of ITI values where: Et2O > THF > HMPA, which appears counter intuitive since HMPA is regarded as a strong donor, while Et2O is regarded as a weak donor, see Tables S11–S14.† Without more sophisticated investigations and based on these small data sets, it is not clear what ligands affect the values for ITI calculations in terms of donor strength, steric bulk and crystallization effects. No analogous actinide compounds were located, likely due to the prevalence of the +4 oxidation state in the early actinides and the scarcity of trans-plutonium crystallographic data.
Electronic absorption spectroscopy
The electronic absorption spectroscopy for AmBr3(OPcy3)3 shows an intense charge transfer band centered at λmax 340 nm (29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 411 cm−1) in addition to the Laporte forbidden 5f → 5f transitions characteristic of AmIII.79,80 With few exceptions, the energies of the absorptions are similar to those reported in the low temperature spectrum of AmBr3 and the recently reported spectrum of (PPh4)3AmCl6.80,81 The characteristic 5L6′ excitation reported at 510 nm (19
411 cm−1) in addition to the Laporte forbidden 5f → 5f transitions characteristic of AmIII.79,80 With few exceptions, the energies of the absorptions are similar to those reported in the low temperature spectrum of AmBr3 and the recently reported spectrum of (PPh4)3AmCl6.80,81 The characteristic 5L6′ excitation reported at 510 nm (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 588 cm−1) has shifted to 508 nm (19
588 cm−1) has shifted to 508 nm (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 685 cm−1), Fig. 3.79,80 All of the transitions were assigned using the reported values for AmBr3 and were confirmed through theoretical analysis.79,80AmBr3(OPcy3)3 is not fluorescent at room temperature even with long integration times (≥2000 ms) at an excitation wavelength of 365 or 420 nm.
685 cm−1), Fig. 3.79,80 All of the transitions were assigned using the reported values for AmBr3 and were confirmed through theoretical analysis.79,80AmBr3(OPcy3)3 is not fluorescent at room temperature even with long integration times (≥2000 ms) at an excitation wavelength of 365 or 420 nm.
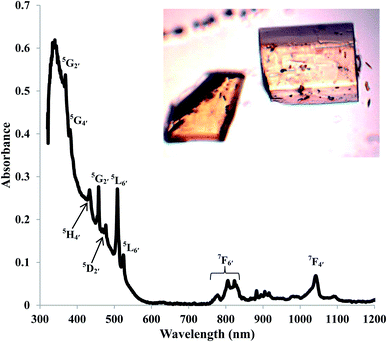 | ||
| Fig. 3 Solid state UV/vis/NIR of AmBr3(OPcy3)3 at room temperature, with excitation assignments and photograph of crystals. | ||
The solid state absorption spectrum of CeBr3(OPcy3)3 displays an intense charge transfer band with λmax of 339 nm (29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 479 cm−1). NdBr3(OPcy3)3 reveals, sharp hypersensitive transitions of low intensity between 500–607 nm consistent with the 4G7/2 and 4G5/2 excitations, similar to the values reported for NdBr3(g) at 1195 °C, while several of the typical 4f → 4f transitions reported for Nd(ClO4)3(aq) were not observed.82–84LaBr3(OPcy3)3 and PrBr3(OPcy3)3 gave no UV/vis/NIR peaks between 320–1700 nm. The former is typical of the 5d04f0 La3+ ion, while the latter is unusual for the 4f2 Pr3+ ion,84 this may be due to the pseudo inversion center present in MBr3(OPcy3)3. Though the Pr3+ ion possesses hypersensitive 3P2 and 1D2 transitions at 444.4 nm (22
479 cm−1). NdBr3(OPcy3)3 reveals, sharp hypersensitive transitions of low intensity between 500–607 nm consistent with the 4G7/2 and 4G5/2 excitations, similar to the values reported for NdBr3(g) at 1195 °C, while several of the typical 4f → 4f transitions reported for Nd(ClO4)3(aq) were not observed.82–84LaBr3(OPcy3)3 and PrBr3(OPcy3)3 gave no UV/vis/NIR peaks between 320–1700 nm. The former is typical of the 5d04f0 La3+ ion, while the latter is unusual for the 4f2 Pr3+ ion,84 this may be due to the pseudo inversion center present in MBr3(OPcy3)3. Though the Pr3+ ion possesses hypersensitive 3P2 and 1D2 transitions at 444.4 nm (22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1) and 588.2 nm (17
500 cm−1) and 588.2 nm (17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1), respectively, but were not observed through repeated collections, see Fig. S3–S7† for spectra.83,84
000 cm−1), respectively, but were not observed through repeated collections, see Fig. S3–S7† for spectra.83,84
To further explore the unusual observations of PrBr3(OPcy3)3, solution phase electronic absorption spectra of all four LnBr3(OPcy3)3 compounds were recorded in a non-coordinating (DCM) and a coordinating (MeOH) solvent. The spectra recorded in DCM reproduce the solid state spectra for all LnBr3(OPcy3)3, with a large charge transfer band observed for CeBr3(OPcy3)3 and the hypersensitive 4G7/2 and 4G5/2 excitations in Nd being observed. Spectra of PrBr3(OPcy3)3 recorded in DCM display a charge transfer band at λmax 245.0 nm (40 816 cm−1), the edge of which is observed in the other compounds, including the free ligand, see ESI.† The spectra recorded in MeOH told a different story where the NdBr3(OPcy3)3 and PrBr3(OPcy3)3 gave the f → f transitions observed in the respective aquo-ions Ln(ClO4)3(aq).84 With the larger window afforded by MeOH, a large charge transfer band for all the metals in a range of 209–234 nm (47 847–42 735 cm−1), this is also observed in the free ligand and has been characterized as an O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P π → σ* P–C intraligand charge transfer excitation by theoretical analysis. Additionally, LaBr3(OPcy3)3 and PrBr3(OPcy3)3 both display a second, smaller charger transfer peak at 285.5 nm (35 026 cm−1) and 268.5 nm (37 244 cm−1), respectively, which theoretical analysis has characterized as a Br → Ln LMCT excitation. While CeBr3(OPcy3)3 shows several charge transfer peaks 209–315 nm (47 847–31 746 cm−1), see ESI.† None of the lanthanide compounds were fluorescent in the solid state.
P π → σ* P–C intraligand charge transfer excitation by theoretical analysis. Additionally, LaBr3(OPcy3)3 and PrBr3(OPcy3)3 both display a second, smaller charger transfer peak at 285.5 nm (35 026 cm−1) and 268.5 nm (37 244 cm−1), respectively, which theoretical analysis has characterized as a Br → Ln LMCT excitation. While CeBr3(OPcy3)3 shows several charge transfer peaks 209–315 nm (47 847–31 746 cm−1), see ESI.† None of the lanthanide compounds were fluorescent in the solid state.
Multi-nuclear NMR spectroscopy
In order to gain more insight into the system, and due to the convenient spectroscopic handle provided by the 31P nucleus, 1H, 13C{1H} and 31P{1H} multi nuclear NMR spectra were recorded, in a non-coordinating (DCM-d2) and in a coordinating (MeOD-d4) solvent, the compounds display limited solubility in alcohols and chloroform, but good solubility in DCM. Due to radiological constraints and small sample sizes obtaining NMR spectra on americium samples can be difficult. Exceptions have included Evans' method studies,85 a notable solid state MAS study of AmO286 and the recent report of Am(C5Me4H)3.87 Some 31P{1H} data has been reported previously for other LnBr3(OPcy3)3 complexes,57 here we seek to add to this data and compare it with its americium analog. Because of the weak paramagnetism of the 5f6 Am3+ ion, 1.64 μB,85 a shorter relaxation time (d1 = 1 s) was utilized along with several extra scans to obtain a good signal for AmBr3(OPcy3)3 at a shift of δ 108.89 ppm, Fig. 4. To the best of our knowledge this is the first report of a 31P NMR signal in an americium complex, however we only able to study the complex in one solvent (CDCl3) due to sample integrity as well as radiological constraints.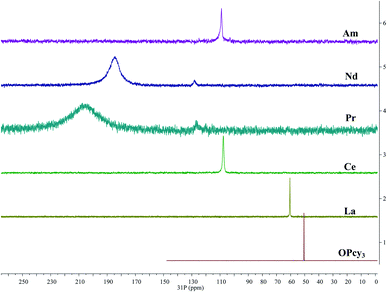 | ||
| Fig. 4 Stacked 31P{1H} NMR spectra of MBr3(OPcy3)3 (M = Am, Nd, Pr, Ce, La) including OPcy3 in CDCl3 or CD2Cl2 at 298 K. | ||
The signal of AmBr3(OPcy3)3 is similar in chemical shift to the 4f1CeBr3(OPcy3)3 at δ 109.48 and 107.70 ppm in CDCl3 and CD2Cl2, respectively. Both signals are shifted down field from the diamagnetic LaBr3(OPcy3)3 (δ 60.314 and 60.483 ppm in CDCl3 and CD2Cl2, respectively) and the free ligand OPcy3 (δ 50.574 ppm, CDCl3) which was recorded for comparison. The more paramagnetic 4f2 and 4f3PrBr3(OPcy3)3 and NdBr3(OPcy3)3 are significantly shifted further down field (δ 204.1 and 184.8 ppm, respectively, in CD2Cl2) and are significantly broadened (ν1/2 = 5700 and 2400 Hz, respectively), Fig. 4. In the original report of LnBr3(OPcy3)3 it was stated that Nd displays two resonances at δ 187.4 and 167.6 (CDCl3) at room temperature,57 in our hands both the Pr and Nd gave two signals, however, one is significantly larger than the second and required more than 400 scans to observe, with 800 scans needed for satisfactory signal:noise, see ESI.† We suspect the second resonance is a small phosphorous containing impurity, which was more evident in the variable temperature studies, see below. Due to the high fluxionality of the cyclohexyl rings the 1H NMR spectra are complicated and provide limited information. In particular the paramagnetism in PrBr3(OPcy3)3 and NdBr3(OPcy3)3 give rise to several broad peaks over a range of about 20 ppm, some with widths up to 2000 Hz, see experimental and ESI† for spectra. The 13C{1H} NMR spectra of MBr3(OPcy3)3 show several signals and are consistent with a single chemical environment for the carbons. Due to the small sample size of AmBr3(OPcy3)3 only three of the expected four signals were observed, with the ipso-carbon likely being too broad and weak to be observed in this experiment, though a doublet at δ 27.08 ppm with JCP coupling constant of 27 Hz is consistent with the carbon α to the ipso-carbon. For the diamagnetic free ligand and LaBr3(OPcy3)3 both 1-bond and 2-bond C–P coupling was observed with constants of ca. 35 and 27 Hz in CDCl3, respectively, see ESI† for spectra. When the same lanthanide complexes were recorded in a coordinating solvent, MeOD-d4, all of the paramagnetic spectra display smaller paramagnetic shifts for all the observed nuclei relative to their analogous spectra in CD2Cl2, see ESI.†
The room temperature 31P{1H} spectra all display a single resonance at room temperature which contrasts the solid state structures which contain two distinct environments, the short homo-trans and the long hetero-trans environments, this suggests that the system is highly dynamic at room temperature. To investigate this we recorded low temperature, −86 °C, spectra of all of the lanthanide samples in both MeOD-d4 and CD2Cl2, to ensure all of the 31P{1H} spectra were quantitative all spectra were recorded with d1 ≫ T1. The spectra of all of the lanthanides in MeOD-d4 at low temperature all display a single, sharp resonance at δ 57.19 ppm, similar to what would be expected for free OPcy3, see ESI.† It is likely that at low temperature the lanthanide ions shed their phosphine oxide ligands to form the lanthanide bromide solvento complexes.88 This offers valuable insight into the control of the coordination sphere about the metal atom as different syntheses have shown that product identity is sensitive to the identity of the solvent.57,89
It was previously reported that when LaBr3(OPcy3)3 is cooled to −80 °C in CD2Cl2 two resonances are observed at δ 62.8 and 62.4 ppm. In our hands when the spectra of LnBr3(OPcy3)3 in CD2Cl2 were recorded at −86 °C the La complex gave four signals between δ 62.22 to 60.86 ppm in a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 : 2
4 : 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 ratio. The Ce complex also gave three major resonances between δ 134.28 to 113.90 ppm in a 1
9 ratio. The Ce complex also gave three major resonances between δ 134.28 to 113.90 ppm in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio, with multiple smaller peaks present, likely due to some decomposition. However the Pr and Nd complexes gave two, well resolved resonances in 2
2 ratio, with multiple smaller peaks present, likely due to some decomposition. However the Pr and Nd complexes gave two, well resolved resonances in 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio at δ 468.0, 80.9 and 426.7, 174.7 ppm, respectively, with a small (<10%) phosphorous containing impurity present that also presents a paramagnetic shift, see ESI.† While not ideal, these results, particularly in CD2Cl2 show that at low temperature a static mer-octahedral environment is present, similar to the crystal structure, and corroborating earlier studies with these LnBr3(OPcy3)3 complexes.57,90–92
1 ratio at δ 468.0, 80.9 and 426.7, 174.7 ppm, respectively, with a small (<10%) phosphorous containing impurity present that also presents a paramagnetic shift, see ESI.† While not ideal, these results, particularly in CD2Cl2 show that at low temperature a static mer-octahedral environment is present, similar to the crystal structure, and corroborating earlier studies with these LnBr3(OPcy3)3 complexes.57,90–92
Theoretical analysis
Bonding analysis
To obtain a deeper understanding of the bonding in MBr3(OPcy3)3, a Quantum Theory of Atoms In Molecules (QTAIM) analysis was performed to calculate the concentration of electron density ρ(r), delocalization indices δ(r), and energy densities [potential, V(r), kinetic, G(r), and total energy densities, H(r)]. All of these metrics are utilized to determine the degree of covalency exhibited in the bonding interactions. Based on previous studies where the nature of bonding interactions of f-block complexes has been shown that bonds are not formally covalent, but rather partially covalent.46,47,93 A partial covalent bond implies positive values for the Laplacian of the electron density, ∇ρ(r), and negative values for total energy densities, H(r). Here, the term “covalency” refers to the metal–ligand interaction needed to experience orbital overlap, which is reflected by the buildup of electron density [ρ(r)] in the interatomic region. Furthermore, covalency can be enhanced by a better energy match between the atomic orbital involved, which is reflected by the delocalization of the electrons in the interatomic region.From a general perspective the results herein show that the M–Br bonds displays a low concentration of electron density in the interatomic region compared to the M–O bonds, Fig. 5a, though similar delocalization indices, Fig. 5b, implying that the covalency in the M–O bonds occur due to increased orbital overlap, whereas the better energy match between parent metal–ligand orbitals for the M–Br bonds compensate for the lack of electron density concentration. A more subtle difference is observed in the energy density of the M–O bonds, particularly the M–O(3) bond where CeBr3(OPcy3)3 most resembles AmBr3(OPcy3)3. Whereas the M–Br bonds of CeBr3(OPcy3)3 and NdBr3(OPcy3)3 are closer to each other, Fig. 6a. The origin of these subtleties resides in the balance between kinetic, G(r), and potential energy, V(r), densities with respect to the Laplacian of the electron density, ∇2ρ(r), where a more careful treatment can be performed, when the total electron densities, H(r), is normalized by the electron density at the Bond Critical Point (BCP). This allows the role of the kinetic, G(r), and potential energies, V(r), to be isolated from the concentration of electron density, ρ(r), Fig. 6b. When the data are compared, the same trends are observed. It appears that CeBr3(OPcy3)3 and NdBr3(OPcy3)3 differ from each other in that: the bonding patterns are independent of the concentration of electron density, ρ(r), i.e. Ce stabilizes the electrons in the interatomic region similarly to Nd when a more polarizable ligand is present like Br, while Ce resembles Am when a harder–donor ligand is present, like OPR3. Moreover, the dominance of potential energy, V(r), over kinetic energy, G(r) is independent of the electron density, which shows that the covalent contribution in Nd–O(3) bond is almost negligible, Fig. 6b.
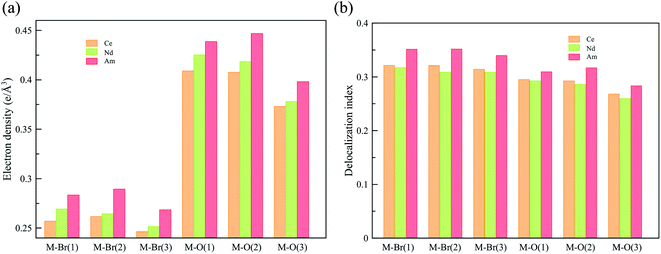 | ||
| Fig. 5 QTAIM metrics of the Bond Critical Points (BCPs) derived from the SR-CAS(n,7) wave functions, (a) concentration of the electron density, (b) delocalization indices. See ESI† for exact numbers. | ||
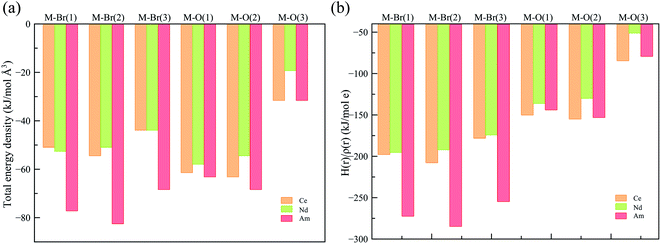 | ||
| Fig. 6 (a) Total energy density over the electron density (b) total energy density over concentration of electron density at the BCP derived from a SR-CAS(7,7) wave function. See ESI† for exact numbers. | ||
Further characterization of the bonds is provided by the ratio between potential, V(r), and kinetic, G(r), energy densities, that shows the extent of the polarization of the bond, again the M–Br bonds are less polarized than the M–O bonds, where Am shows the least polarized bonds (down to 86% of polarization), Table 3. This agrees with the better energy match provided by Br− with the lanthanides and actinides, but is most pronounced in the Am complex.
| |V(r)|/G(r) (kJ mol−1 Å−3) | |||
|---|---|---|---|
| Ce | Nd | Am | |
| M(1)–Br(1) | 1.10 | 1.10 | 1.13 |
| M(1)–Br(2) | 1.11 | 1.10 | 1.14 |
| M(1)–Br(3) | 1.09 | 1.09 | 1.12 |
| M(1)–O(1) | 1.05 | 1.04 | 1.04 |
| M(1)–O(2) | 1.05 | 1.04 | 1.04 |
| M(1)–O(3) | 1.03 | 1.02 | 1.02 |
Qualitatively, the ITI correlates with the previous bonding analysis.27 However, quantitatively, this does not appear to be the case due to the simple shortening of the bond, which could imply different effects operating simultaneously in the complex. Another way to corroborate the presence of the ITI is by the inclusion of the 5/6p orbitals in an all-electron versus a frozen-core calculation.27 Our results show that CeBr3(OPcy3)3 exhibits the highest amount of stabilization (57.9 kJ mol−1), then AmBr3(OPcy3)3 (16.6 kJ mol−1), and NdBr3(OPcy3)3 (11.9 kJ mol−1) shows the least amount of stabilization by the inclusion of the 5/6p shell, which confirms the presence of an ITI-like mechanism in these systems. However, the energies of stabilization do not correlate with the trend observed for the ITI percentages coming directly from the contraction of the bonds in the trans positions. This is not necessarily true for a system presenting more than one ITI mechanism because they compete within the same molecule, and therefore become more complicated to analyze. For clarity in the construction of an MO energy level diagram, the cyclohexyl rings were truncated to methyl groups, e.g.MBr3(OPMe3)3, Fig. 7.94 This mixing is produced with the O 2p and P 3s orbitals, providing a more delocalized character of the bond and the stronger mixing between 5p orbitals in Ce is observed, Fig. 7.
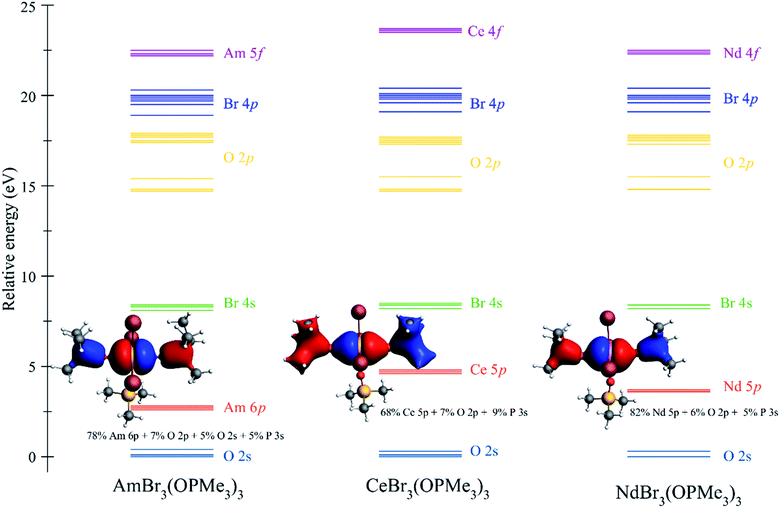 | ||
| Fig. 7 Molecular orbital (MO) energy level diagram for MBr3(OPMe3)3 (M = Am, Ce, Nd) from a scalar relativistic PBE/TZVP calculation. MO labels correspond to the predominant shell in the MO, for the MO composition see Tables S3–S5.† MO depictions correspond to the involvement of the semi-core 5/6p orbitals in orbital mixing. | ||
Another way to show the role of the Ln/An 5/6p orbitals in an ITI-like mechanism is to assess the reduction of the electron repulsion of these semi-core electrons in the complex with respect to the free-ion. Within ligand field theory (LFT) the one-electron inter-electronic repulsion integrals are described by the Slater–Condon parameters Fk(nl,nl) and the spin–orbit coupling parameter ζnl (n = shell, l = s, p, d, f).95,96 Previous studies have successfully applied a non-empirical method to obtain these parameters using a ligand-field DFT (LFDFT) capable of predicting the electronic structure of lanthanide complexes.52,97–100 Since the reductions of the Slater–Condon parameters with respect to the free-ion are related to the central-field and symmetry-restricted covalency, their evaluation will provide further insight into the nature of an ITI-like mechanism in these complexes.
The reduction of the LF parameters is considerably larger in CeBr3(OPcy3)3 compared to NdBr3(OPcy3)3 and AmBr3(OPcy3)3, whose reductions are similar, Table 4. These results agree with the stabilization energies obtained between frozen-core to all-electron calculations, confirming the presence of an ITI-like mechanism. This also shows that the sizable reductions indicate an important covalent component related to the 5/6p orbital involvement in the interaction between the metal ions and the Br− and phosphine oxide ligands.
| F 2(p,p) (eV) | ζ 5/6p (eV) | |||||
|---|---|---|---|---|---|---|
| [M(H2O)9]3+ | MBr3(OPcy)3 | Δ red | [M(H2O)9]3+ | MBr3(OPcy)3 | Δ red | |
| a See ESI for Slater–Condon parameters. b Δ red refers to the difference between the aquo and MBr3(OPcy)3 (M = Ce, Nd, Am) complexes. | ||||||
| CeIII | 28% | 70% | 42% | 18% | 47% | 29% |
| NdIII | 21% | 43% | 22% | 15% | 28% | 13% |
| AmIII | 19% | 45% | 25% | 14% | 27% | 12% |
The differences in bonding observed between lanthanides and actinides make the comparison more complicated due to the involvement of the 5f electrons in the case of americium, which significantly increases the covalent character of the bond. In this context, only Ce and Nd could be compared with QTAIM metrics, where delocalization and total energy densities predict the trend observed in the stabilization energies from the involvement of the 5p electrons.
Further insight into the nature of metal–ligand bonding and the role of pseudo-core orbitals can be obtained by localizing the electron density through natural localized molecular orbitals (NLMOs). Assuming these systems behave as Lewis structures, NLMOs provide a good alternative to understand the nature of the bonds.
In order to confirm the involvement of pseudo-core electrons in this ITI-like mechanism, the uranyl unit [UO2]2+ was calculated as a reference sample, as it corresponds to the strongest known example of the ITI.10 Within the NLMO framework, the 6s and 6p pseudo-core electrons deviate from the core behavior, especially one p orbital that by symmetry can mix with the oxo 2p orbitals. This NLMO is dominated by a uranium pf natural hybrid orbital (NHO) (76% 6p + 24% 5f) with polarization towards the oxo ligands, Table S7.† A similar picture is seen in the theoretical models MBr3(OPMe3)3 (M = Am, Nd), where the pseudo-core electrons are delocalized with 4f/5f orbitals and display some polarization towards the O and P atoms of the phosphine oxide ligands, with the Am analog the most similar to U in terms of hybridization. The Ce analog shows a slightly different pattern, where pf hybridization is rather small and orbital mixing is produced directly between pseudo-core electrons and the phosphine oxide ligands, NLMOs 4–5, Table S7.† This implies that the bonds in Ce should be more directional than in the Am and Nd analogs.
Moving strictly to the nature of the bond, all three have similar bonding patterns, although Am shows a more balanced 5f/6d ratio in the formation of NLMOs, see Tables S8–S10.† This is somewhat expected in that bond formation in trivalent lanthanide complexes is primarily through 5d orbitals. The M–OPcy3 bonds are formed by involvement of orbitals from the phosphine oxide moiety giving rise to highly polarized covalent bonds. On the other hand, the M–Br bonds are less polar because of the better energy match between the 4p orbitals and the 4f/5f metal orbitals. This could also be related to what is observed in the QTAIM results, where the M–Br bonds are as delocalized as the M–OPcy3 bonds but with a lower concentration of electron density, see ESI.†
Based on the above results, we can describe the bonding in these LnBr3(OPcy3)3 molecules as displaying an ITI effect because the pseudo-core electrons are delocalized only towards the f orbitals in the same way as for the uranyl unit. The involvement of the f and d orbitals remains very close to what is expected for trivalent complexes.
Conclusions
The synthesis and characterization of AmBr3(OPcy3)3 has been achieved and shows the same meridional coordination geometry as the larger lanthanides. Spectroscopic analysis by single crystal X-ray diffraction shows that the homo-trans ligands display significantly shorter bonds than the hetero-trans ligands. Single crystal UV/vis/NIR spectra show large charge transfer bands for the Ce and Am complexes. Analysis by 31P NMR spectroscopy illustrates the weak paramagnetism of the 5f6 Am3+ center. Bonding analyses show that the complex displays a significant inverse-trans-influence (ITI) with the bonding ligands, though its mechanism is not directly related to the involvement of the 5/6p electrons. This suggests that there is interplay between the involvement of valence electrons that significantly separates the lanthanides from the actinides. CeBr3(OPcy3)3 shows the highest amount of 5p electron involvement in covalency. This is observed by the reduction of the electron–electron repulsion of the 5p shell compared to the aquo-complex, [Ce(H2O)9]3+. This study provides further evidence of an ITI-like mechanism in low-valent f-block complexes, and their potential occurrence in heavier actinides, whose chemistry is dominated by the trivalent oxidation state. Furthermore, it constitutes a new feature that can be exploited for rational ligand design in order to achieve selective ligands for separations in nuclear waste treatment.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
We thank the support of the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Heavy Element Chemistry program under Award Number DE-FG02-13ER16414. The 243Am used in this research were supplied by the U.S. Department of Energy Isotope Program, managed by the Office of Science for Nuclear Physics. We thank Dr Benjamin W. Stein and Dr Conrad A. P. Goodwin of Los Alamos National Laboratory for helpful discussions. We are grateful to Dr Ion Ghiviriga, Prof. Adam Veige, and Dr Banghao Chen for their assistance with the NMR experiments as well as Dr Xinsong Lin for his assistance with the DART-MS. We thank Mr Jason Johnson and Ms Ashley Gray of Florida State University for radiological assistance.Notes and references
- V. V. Grushin, Chem. Rev., 2004, 104, 1629–1662 CrossRef CAS PubMed.
- E. K. Watson and W. A. Rickelton, Solvent Extr. Ion Exch., 1992, 10, 879–889 CrossRef CAS.
- F. Arnaud-Neu, J. K. Browne, D. Byrne, D. J. Marrs, M. A. McKervey, P. O'Hagan, M. J. Schwing-Weill and A. Walker, Chem.–Eur. J., 1999, 5, 175–186 CrossRef CAS.
- M. Gilmore, É. N. McCourt, F. Connolly, P. Nockemann, M. Swadźba-Kwaśny and J. D. Holbrey, ACS Sustainable Chem. Eng., 2018, 6, 17323–17332 CrossRef CAS.
- L. R. Morss, N. M. Edelstein and J. Fuger, The Chemistry of the Actinide and Transactinide Elements, Springer, Dordrecht, The Netherlands, 4th edn, 2010 Search PubMed.
- S. Mishra, Coord. Chem. Rev., 2008, 252, 1996–2025 CrossRef CAS.
- C. Berthon, N. Boubals, I. A. Charushnikova, D. Collison, S. M. Cornet, C. Den Auwer, A. J. Gaunt, N. Kaltsoyannis, I. May, S. Petit, M. P. Redmond, S. D. Reilly and B. L. Scott, Inorg. Chem., 2010, 49, 9554–9562 CrossRef CAS PubMed.
- M. B. Jones and A. J. Gaunt, Chem. Rev., 2013, 113, 1137–1198 CrossRef CAS.
- A. W. G. Platt, Coord. Chem. Rev., 2017, 340, 62–78 CrossRef CAS.
- R. G. Denning, J. Phys. Chem. A, 2007, 111, 4125–4143 CrossRef CAS PubMed.
- T. J. Emge, A. Kornienko and J. G. Brennan, Acta Crystallogr., Sect. C: Struct. Chem., 2009, 65, m422–m425 CrossRef CAS PubMed.
- K. Krogh-Jespersen, M. D. Romanelli, J. H. Melman, T. J. Emge and J. G. Brennan, Inorg. Chem., 2010, 49, 552–560 CrossRef CAS PubMed.
- A. J. Lewis, K. C. Mullane, E. Nakamaru-Ogiso, P. J. Carroll and E. J. Schelter, Inorg. Chem., 2014, 53, 6944–6953 CrossRef CAS PubMed.
- H. S. La Pierre, M. Rosenzweig, B. Kosog, C. Hauser, F. W. Heinemann, S. T. Liddle and K. Meyer, Chem. Commun., 2015, 51, 16671–16674 RSC.
- M. Gregson, E. Lu, D. P. Mills, F. Tuna, E. J. McInnes, C. Hennig, A. C. Scheinost, J. McMaster, W. Lewis, A. J. Blake, A. Kerridge and S. T. Liddle, Nat. Commun., 2017, 8, 14137 CrossRef CAS PubMed.
- I. Fryer-Kanssen and A. Kerridge, Chem. Commun., 2018, 54, 9761–9764 RSC.
- E. Lu, S. Sajjad, V. E. J. Berryman, A. J. Wooles, N. Kaltsoyannis and S. T. Liddle, Nat. Commun., 2019, 10, 634 CrossRef PubMed.
- D. Brown and C. E. F. Rickard, J. Chem. Soc. A, 1971, 81–87 RSC.
- K. W. Bagnall, J. G. H. du Preez, B. J. Gellatly and J. H. Holloway, Dalton Trans., 1975, 1963–1968 RSC.
- B. J. Coe and S. J. Glenwright, Coord. Chem. Rev., 2000, 203, 5–80 CrossRef CAS.
- A. J. Lewis, P. J. Carroll and E. J. Schelter, J. Am. Chem. Soc., 2013, 135, 13185–13192 CrossRef CAS PubMed.
- B. Kosog, H. S. La Pierre, F. W. Heinemann, S. T. Liddle and K. Meyer, J. Am. Chem. Soc., 2012, 134, 5284–5289 CrossRef CAS.
- S. G. Minasian, J. M. Keith, E. R. Batista, K. S. Boland, D. L. Clark, S. D. Conradson, S. A. Kozimor, R. L. Martin, D. E. Schwarz, D. K. Shuh, G. L. Wagner, M. P. Wilkerson, L. E. Wolfsberg and P. Yang, J. Am. Chem. Soc., 2012, 134, 5586–5597 CrossRef CAS PubMed.
- H. S. La Pierre and K. Meyer, Inorg. Chem., 2013, 52, 529–539 CrossRef CAS PubMed.
- L. P. Spencer, P. Yang, S. G. Minasian, R. E. Jilek, E. R. Batista, K. S. Boland, J. M. Boncella, S. D. Conradson, D. L. Clark, T. W. Hayton, S. A. Kozimor, R. L. Martin, M. M. MacInnes, A. C. Olson, B. L. Scott, D. K. Shuh and M. P. Wilkerson, J. Am. Chem. Soc., 2013, 135, 2279–2290 CrossRef CAS PubMed.
- T. P. Gompa, N. T. Rice, D. R. Russo, L. M. Aguirre Quintana, B. J. Yik, J. Bacsa and H. S. La Pierre, Dalton Trans., 2019, 48, 8030–8033 RSC.
- E. O'Grady and N. Kaltsoyannis, Dalton Trans., 2002, 1233–1239 RSC.
- R. G. Denning, in Complexes, Clusters and Crystal Chemistry, Springer Berlin Heidelberg, Berlin, Heidelberg, 1992, pp. 215–276 Search PubMed.
- P. I. Matveev, N. E. Borisova, N. G. Andreadi, G. G. Zakirova, V. G. Petrov, E. V. Belova, S. N. Kalmykov and B. F. Myasoedov, Dalton Trans., 2019, 48, 2554–2559 RSC.
- J. F. Corbey, B. M. Rapko, Z. Wang, B. K. McNamara, R. G. Surbella III, K. L. Pellegrini and J. M. Schwantes, Inorg. Chem., 2018, 57, 2278–2287 CrossRef CAS PubMed.
- J. N. Cross, J. A. Macor, J. A. Bertke, M. G. Ferrier, G. S. Girolami, S. A. Kozimor, J. R. Maassen, B. L. Scott, D. K. Shuh, B. W. Stein and S. C. Stieber, Angew. Chem., Int. Ed., 2016, 55, 12755–12759 CrossRef CAS PubMed.
- APEX3, 2017, 3–0, Bruker AXS, Inc., Madison, WI, 2017 Search PubMed.
- SAINT, 8.34a, Bruker AXS, Inc, Madison, WI, 2013 Search PubMed.
- G. M. Sheldrick, SADABS, 2012/1, Bruker AXS, Inc, Madison, WI, 2012 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- P.-Å. Malmqvist and B. O. Roos, Chem. Phys. Lett., 1989, 155, 189–194 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- N. Kaltsoyannis, Inorg. Chem., 2013, 52, 3407–3413 CrossRef CAS.
- Q. R. Huang, J. R. Kingham and N. Kaltsoyannis, Dalton Trans., 2015, 44, 2554–2566 RSC.
- I. Fryer-Kanssen, J. Austin and A. Kerridge, Inorg. Chem., 2016, 55, 10034–10042 CrossRef CAS.
- A. Kerridge, Chem. Commun., 2017, 53, 6685–6695 RSC.
- F. D. White, A. N. Gaiser, E. J. Warzecha, J. M. Sperling, C. Celis-Barros, S. R. Salpage, Y. Zhou, T. Dilbeck, A. J. Bretton, D. S. Meeker, K. G. Hanson and T. E. Albrecht-Schmitt, Inorg. Chem., 2018, 57, 12969–12975 CrossRef CAS PubMed.
- B. E. Klamm, C. J. Windorff, C. Celis-Barros, M. L. Marsh, D. S. Meeker and T. E. Albrecht-Schmitt, Inorg. Chem., 2018, 57, 15389–15398 CrossRef CAS PubMed.
- E. Warzecha, C. Celis-Barros, T. Dilbeck, K. Hanson and T. E. Albrecht-Schmitt, Inorg. Chem., 2019, 58, 228–233 CrossRef CAS PubMed.
- A. T. Chemey, C. Celis-Barros, K. Huang, J. M. Sperling, C. J. Windorff, R. E. Baumbach, D. E. Graf, D. Páez-Hernández, M. Ruf, D. E. Hobart and T. E. Albrecht-Schmitt, Inorg. Chem., 2019, 58, 637–647 CrossRef CAS.
- D. Dan, C. Celis-Barros, F. D. White, J. M. Sperling and T. E. Albrecht-Schmitt, Chem.–Eur. J., 2019, 25, 3248–3252 CAS.
- E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529–5542 CrossRef CAS.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403 Search PubMed.
- H. Ramanantoanina, W. Urland, F. Cimpoesu and C. Daul, Phys. Chem. Chem. Phys., 2013, 15, 13902–13910 RSC.
- M. Atanasov, C. A. Daul and C. Rauzy, in Optical Spectra and Chemical Bonding in Inorganic Compounds: Special Volume dedicated to Professor Jørgensen I, ed. D. M. P. Mingos and T. Schönherr, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004, pp. 97–125 Search PubMed.
- P. Lindqvist-Reis, C. Apostolidis, J. Rebizant, A. Morgenstern, R. Klenze, O. Walter, T. Fanghänel and R. G. Haire, Angew. Chem., Int. Ed., 2007, 46, 919–922 CrossRef CAS.
- R. E. Gerkin and W. J. Reppart, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1984, 40, 781–786 CrossRef.
- Y. V. Nelyubina, L. N. Puntus and K. A. Lyssenko, Chem.–Eur. J., 2014, 2860–2865 CrossRef CAS PubMed.
- A. Bowden, A. M. J. Lees and A. W. G. Platt, Polyhedron, 2015, 91, 110–119 CrossRef CAS.
- Because all of the signals are overlapping no meaningful integration can be obtained, therefore only peaks are listed, see ESI† for spectrum.
- Due to the numerous peaks only relative integrations are given.
- Due to the breadth of the peaks only tentative integrations are given.
- J. V. Kingston, E. M. Krankovits and R. J. Magee, Inorg. Nucl. Chem. Lett., 1969, 5, 485–489 CrossRef CAS.
- M. J. Glazier, W. Levason, M. L. Matthews, P. L. Thornton and M. Webster, Inorg. Chim. Acta, 2004, 357, 1083–1091 CrossRef CAS.
- N. J. Hill, W. Levason, M. C. Popham, G. Reid and M. Webster, Polyhedron, 2002, 21, 445–455 CrossRef CAS.
- A. M. J. Lees and A. W. G. Platt, Polyhedron, 2014, 67, 368–372 CrossRef CAS.
- Y. C. Chen, J. L. Liu, L. Ungur, J. Liu, Q. W. Li, L. F. Wang, Z. P. Ni, L. F. Chibotaru, X. M. Chen and M. L. Tong, J. Am. Chem. Soc., 2016, 138, 2829–2837 CrossRef CAS PubMed.
- Y. X. Wang, Y. Ma, Y. Chai, W. Shi, Y. Sun and P. Cheng, J. Am. Chem. Soc., 2018, 140, 7795–7798 CrossRef CAS PubMed.
- S. S. Galley, J. M. Sperling, C. J. Windorff, M. Zeller, T. E. Albrecht-Schmitt and S. C. Bart, Organometallics, 2019, 38, 606–609 CrossRef CAS.
- H. Flack, Acta Crystallogr., Sect. A: Found. Crystallogr., 1983, 39, 876–881 CrossRef.
- R. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- J. A. Davies, S. Dutremez and A. A. Pinkerton, Inorg. Chem., 1991, 30, 2380–2387 CrossRef CAS.
- F. A. Cotton and R. L. Luck, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1991, 47, 1069–1072 CrossRef.
- F. A. Cotton, J. Lu and T. Ren, Inorg. Chim. Acta, 1994, 215, 47–54 CrossRef CAS.
- R. Bou-Moreno, S. A. Cotton, V. Hunter, K. Leonard, A. W. G. Platt, P. R. Raithby and S. Schiffers, Polyhedron, 2011, 30, 2832–2836 CrossRef CAS.
- L. J. Radonovich and M. D. Glick, J. Inorg. Nucl. Chem., 1973, 35, 2745–2752 CrossRef CAS.
- X.-W. Zhang, X.-F. Li, F. Benetollo and G. Bombieri, Inorg. Chim. Acta, 1987, 139, 103–104 CrossRef CAS.
- Z. Hou, K. Kobayashi and H. Yamazaki, Chem. Lett., 1991, 20, 265–268 CrossRef.
- G. B. Deacon, T. Feng, P. C. Junk, B. W. Skelton, A. N. Sobolev and A. H. White, Aust. J. Chem., 1998, 51, 75–89 CrossRef CAS.
- G. B. Deacon, T. Feng, P. C. Junk, G. Meyer, N. M. Scott, B. W. Skelton and A. H. White, Aust. J. Chem., 2000, 53, 853–865 CrossRef CAS.
- W. T. Carnall and B. G. Wybourne, J. Chem. Phys., 1964, 40, 3428–3433 CrossRef CAS.
- R. G. Pappalardo, W. T. Carnall and P. R. Fields, J. Chem. Phys., 1969, 51, 1182–1200 CrossRef CAS.
- J. N. Cross, J. Su, E. R. Batista, S. K. Cary, W. J. Evans, S. A. Kozimor, V. Mocko, B. L. Scott, B. W. Stein, C. J. Windorff and P. Yang, J. Am. Chem. Soc., 2017, 139, 8667–8677 CrossRef CAS PubMed.
- B. R. Judd, J. Chem. Phys., 1966, 44, 839–840 CrossRef CAS.
- D. E. Henrie, R. L. Fellows and G. R. Choppin, Coord. Chem. Rev., 1976, 18, 199–224 CrossRef CAS.
- K. Binnemans and C. Görller-Walrand, Chem. Phys. Lett., 1995, 235, 163–174 CrossRef CAS.
- T. F. Wall, S. Jan, M. Autillo, K. L. Nash, L. Guerin, C. L. Naour, P. Moisy and C. Berthon, Inorg. Chem., 2014, 53, 2450–2459 CrossRef CAS PubMed.
- L. Martel, N. Magnani, J. F. Vigier, J. Boshoven, C. Selfslag, I. Farnan, J. C. Griveau, J. Somers and T. Fanghänel, Inorg. Chem., 2014, 53, 6928–6933 CrossRef CAS PubMed.
- C. A. P. Goodwin, J. Su, T. E. Albrecht-Schmitt, A. V. Blake, E. R. Batista, S. R. Daly, S. Dehnen, W. J. Evans, A. J. Gaunt, S. A. Kozimor, N. Lichtenberger, B. L. Scott and P. Yang, Angew. Chem., Int. Ed., 2019, 58, 11695–11699 CrossRef CAS PubMed.
- Since the MeOD-d4 was not rigorously dried, there is water present in all of the spectra leaving the possibility to form complex Ln(H2O)x(MeOD)yBr3 compounds where Br can be inner or outer sphere.
- A. Bowden, A. W. G. Platt, K. Singh and R. Townsend, Inorg. Chim. Acta, 2010, 363, 243–249 CrossRef CAS.
- A. Bowden, S. J. Coles, M. B. Pitak and A. W. Platt, Inorg. Chem., 2012, 51, 4379–4389 CrossRef CAS PubMed.
- A. Bowden, S. J. Coles, M. B. Pitak and A. W. G. Platt, Polyhedron, 2014, 68, 258–264 CrossRef CAS.
- S. J. Coles, M. B. Pitak and A. W. G. Platt, Eur. J. Inorg. Chem., 2017, 2017, 1464–1471 CrossRef CAS.
- C. Celis-Barros, D. Páez-Hernández, M. J. Beltrán-Leiva and R. Arratia-Perez, Phys. Chem. Chem. Phys., 2018, 20, 4038–4049 RSC.
- The truncated molecules were utilized to remove C–C and C–H interactions of similar energy from the MO calculations, calculations on the metal–ligand interactions were shown to be the same on the full and truncated molecules, see theoretical details in the experimental section and the ESI for further details.†.
- A. B. P. Lever, Inorganic electronic spectroscopy, Elsevier Pub. Co, Amsterdam, New York, 1968 Search PubMed.
- E. U. Condon and G. Shortley, The theory of atomic spectra, Cambridge University Press, Cambridge, 1951 Search PubMed.
- H. Ramanantoanina, W. Urland, B. Herden, F. Cimpoesu and C. Daul, Phys. Chem. Chem. Phys., 2015, 17, 9116–9125 RSC.
- H. Ramanantoanina, M. Sahnoun, A. Barbiero, M. Ferbinteanu and F. Cimpoesu, Phys. Chem. Chem. Phys., 2015, 17, 18547–18557 RSC.
- H. Ramanantoanina, W. Urland, A. García-Fuente, F. Cimpoesu and C. Daul, Chem. Phys. Lett., 2013, 588, 260–266 CrossRef CAS.
- H. Ramanantoanina, F. Cimpoesu, C. Göttel, M. Sahnoun, B. Herden, M. Suta, C. Wickleder, W. Urland and C. Daul, Inorg. Chem., 2015, 54, 8319–8326 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Photographs of compounds, NMR spectra, electronic absorption spectra, additional theoretical calculation. CCDC 1959746–1959750. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9sc05268b |
| This journal is © The Royal Society of Chemistry 2020 |