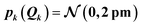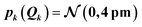Open Access Article
Open Access ArticleTowards theoretical spectroscopy with error bars: systematic quantification of the structural sensitivity of calculated spectra†
Tobias G.
Bergmann
 ,
Michael O.
Welzel
,
Michael O.
Welzel
 and
Christoph R.
Jacob
and
Christoph R.
Jacob
 *
*
Technische Universität Braunschweig, Institute of Physical and Theoretical Chemistry, Gaußstraße 17, 38106 Braunschweig, Germany. E-mail: c.jacob@tu-braunschweig.de
First published on 27th December 2019
Abstract
Molecular spectra calculated with quantum-chemical methods are subject to a number of uncertainties (e.g., errors introduced by the computational methodology) that hamper the direct comparison of experiment and computation. Judging these uncertainties is crucial for drawing reliable conclusions from the interplay of experimental and theoretical spectroscopy, but largely relies on subjective judgment. Here, we explore the application of methods from uncertainty quantification to theoretical spectroscopy, with the ultimate goal of providing systematic error bars for calculated spectra. As a first target, we consider distortions of the underlying molecular structure as one important source of uncertainty. We show that by performing a principal component analysis, the most influential collective distortions can be identified, which allows for the construction of surrogate models that are amenable to a statistical analysis of the propagation of uncertainties in the molecular structure to uncertainties in the calculated spectrum. This is applied to the calculation of X-ray emission spectra of iron carbonyl complexes, of the electronic excitation spectrum of a coumarin dye, and of the infrared spectrum of alanine. We show that with our approach it becomes possible to obtain error bars for calculated spectra that account for uncertainties in the molecular structure. This is an important first step towards systematically quantifying other relevant sources of uncertainty in theoretical spectroscopy.
1 Introduction
The quantum-chemical calculation of molecular spectra has nowadays become an essential tool for determining the structure of molecules.1 In many cases, structural information can only be extracted from experimental spectra by combining them with computations.2 Examples include the elucidation of the gas-phase structure of polypeptides with vibrational spectroscopy,3–7 the assignment of the absolute configuration of chiral molecules with chiroptical spectroscopic techniques,8–11 and the identification of active species and catalytic intermediates with X-ray spectroscopy.12–15While in some cases, high-resolution spectroscopic experiments can resolve the individual spectroscopic transition, this is usually not the case for most common applications that aim at obtaining structural information from spectroscopic experiments, such as those mentioned above. Instead, the quantity of interest is the spectral intensity as a function of the radiation energy, σ(E), in a relevant energy range, which is usually calculated as,
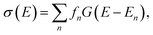 | (1) |
However, quantum-chemical calculations are affected by numerous uncertainties and in general the agreement between experiment and computation cannot be expected to be perfect. Sources of uncertainties include the structure of the molecular model, the description of environment effects, and errors of the quantum-chemical methods used for calculating spectra. The comparison of measured and calculated spectra thus requires carefully judging these uncertainties. To this end, one generally relies on the often rather subjective judgement of computational chemists.
Methods for the systematic assessment of uncertainties in computer simulations are developed in the field of uncertainty quantification, which is a subfield of applied mathematics that has developed in the past decades (for textbooks, see, e.g., ref. 16 and 17). It provides tools that are widely used in simulation science.18,19 However, their application in quantum chemistry is only just emerging (for a recent review, see ref. 20). For quantifying uncertainties in reaction energies that are due to errors of approximate density-functional theory (DFT), Nørskov, Sethna, Jacobsen, and coworkers have developed the Bayesian error estimation exchange–correlation functional (BEEF),21–24 while Reiher and coworkers extended this approach by parametrizing problem-specific exchange–correlation functionals with built-in error estimation.25,26 Recently, the BEEF family of xc functionals has been applied to quantify uncertainties in calculated vibrational frequencies.27 Several groups have addressed the assignment of uncertainties to the parameters of calibration models,28 such as scaling factors for harmonic vibrational frequencies,29,30 or linear regression models for the quantum-chemical calculation of Mössbauer isomer shifts.31 Similarly, uncertainties in the parameters of the semi-empirical PM7 method,32 of Grimme's D3 dispersion correction,33 and of neural networks for the exploration of chemical space34 have been assessed.
Here, our objective is to further explore the application of methods of uncertainty quantification to the quantum-chemical calculation of molecular spectra. Within a chosen quantum-chemical model, the calculated spectral intensity will depend on the input molecular structure R that is used in the quantum-chemical calculation, i.e.,
Previously, some authors have addressed the quantification of uncertainties introduced by approximations in the quantum-chemical model on spectroscopic properties.27,29–31 Here, we aim at systematically quantifying a further source of uncertainty, namely the dependence of σ(E; R) on the input molecular structure.35 The structural sensitivity presents a challenging case because the calculated spectrum depends on a rather large number of independent parameters (i.e., the nuclear coordinates R). In this respect, it fundamentally differs from, e.g., uncertainties due to approximation in the quantum-chemical model, which are usually related to only a few parameters. Thus, while the structural sensitivity is only one of many relevant sources of uncertainty, it serves as a first step towards establishing a methodological framework that can be extended to other sources of uncertainty.
Specifically, we set out to establish “error bars” that account for the structural sensitivity of a calculated spectrum. In this paper, we present a methodology that allows us to answer the following two questions: (1) Given distortions ΔR of a reference structure R0 with |ΔR| ≤ dmax, what is the range of calculated spectra σ(E; R0 + ΔR)? (2) Given a probability distribution for distortions of a reference structure R0, how can we characterize the resulting probability distribution for the calculated spectra? This can then be employed to obtain error bars for the calculated spectrum of the reference structure that either represent bounds on the calculated spectra of distorted structures or that quantify the uncertainty due to structural distortions in a statistical fashion.
We aim at developing a methodology that is generally applicable for any type of computational spectroscopy providing a spectral intensity σ(E) that can be compared to an experimental spectrum. To this end, we will consider typical applications in which structural information in extracted from the comparison of experimental and calculated spectra, such as X-ray emission spectroscopy (XES) of transition metal complexes, vibrational spectroscopy, and UV/Vis spectroscopy.
This work is organized as follows. In Section 2, we show how the structural distortions that are most influential for the calculated spectrum can be identified. This is then used in Section 3 to construct nonlinear surrogate models of the dependence of the calculated spectrum on the input molecular structure, and we use this model for analyzing the propagation of uncertainties in the molecular structure to the calculated spectrum in Section 4. In Sections 2–4, we illustrate our methodology for the calculated XES spectrum of iron pentacarbonyl Fe(CO)5 as a test case. Results for further test cases covering XES, UV/Vis spectroscopy, and infrared spectroscopy are presented in Section 5. Finally, in Section 6 we present our conclusions as well as perspectives for future work. The computational details are given in the Appendix.
2 Identification of influential structural distortions
As the space of possible molecular structures R for a given atomic composition is intractably vast and because large parts of this space are chemically irrelevant, we only aim at analyzing the structural sensitivity of calculated molecular spectra around a chosen reference structure R0, i.e., R = R0 + ΔR. Usually, this will be the structure obtained as a minimum on the potential energy surface, but other choices are also possible. In the following, we will consider distortions of this reference structure,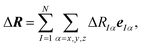 | (2) |
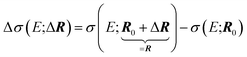 | (3) |
The dependence of the calculated spectrum on the molecular structure around R can the be subjected to a local sensitivity analysis,36 which considers the linearized model
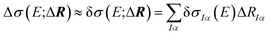 | (4) |
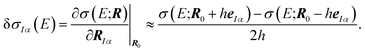 | (5) |
This linear structural sensitivity can be calculated by numerical differentiation, i.e., by calculating the spectrum for displaced molecular structures.35 Here, we employ a symmetric two-point formula [see eqn (5)] and a displacement of h = 0.5 pm. Tests included in our earlier work showed that this numerical derivative is rather insensitive with respect to the magnitude of the displacement and found that h = 0.5 pm should be a reasonable choice.35 Overall, the calculation of the linear structural sensitivity for all 3N Cartesian displacements requires 6N calculations of spectra for displaced structures.
To identify the linear combinations of structural distortions that are most influential on the calculated spectrum, a principal component analysis37 can be performed. After discretizing the energy axis of the calculated spectrum E = {Ej} (with j = 1, …, M, where M ≫ 3N), the linear structural sensitivities can be collected in a (3N × M)-matrix X with
| XIα,j = δσIα(Ej), | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 evenly spaced points in the relevant energy range. With the singular value decomposition of X = U·S·VT, we obtain
000 evenly spaced points in the relevant energy range. With the singular value decomposition of X = U·S·VT, we obtain| UT·X = S·VT, | (7) |
Here, the columns of U define principal component distortions,
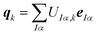 | (8) |
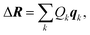 | (9) |
The linear structural sensitivities can now also be expressed with respect to the principal component distortions as
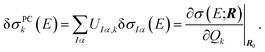 | (10) |
By comparing with eqn (7), we find
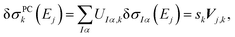 | (11) |
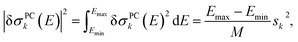 | (12) |
Altogether, the linearized model of eqn (4) can now be expressed as
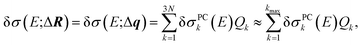 | (13) |
As an example, we consider the structural sensitivity of the calculated XES spectrum of Fe(CO)5. XES is widely used to obtain insights into the geometrical and electronic structure at transition metal centers from the combination of experimental and theoretical spectroscopy.12–15 Fe(CO)5 is a prototypical transition metal complex, and its XES spectrum has been previously studied both experimentally and computationally. As the calculation of XES spectra within a ΔDFT approximation38 only requires a ground-state calculation, it constitutes an ideal first test case. For this example, we already explored the dependence on manually selected structural distortions in our previous work.35 An in-depth experimental and computational study of the XES spectrum of Fe(CO)5 can be found in ref. 39.
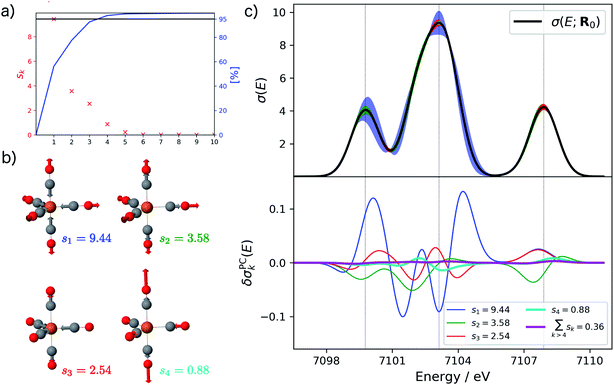
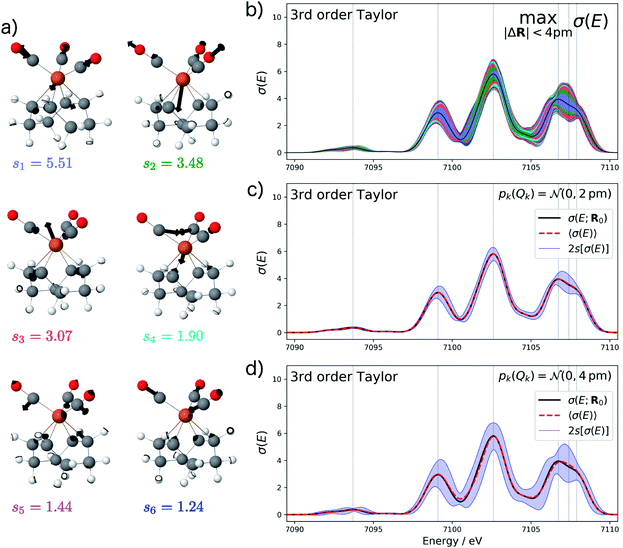
Starting from the minimum energy structure of Fe(CO)5, we calculated the linear structural sensitivity δσIα(E) with respect to all 33 Cartesian displacements by numerical differentiation and performed the principal component analysis outlined above. The resulting singular values are plotted in Fig. 1a. We find that the four largest singular values (s1 = 9.44, s2 = 3.58, s3 = 2.54, s4 = 0.88) account for over 95% of the sum of all singular values. The sum of the remaining 29 singular values amounts to only 0.36. The corresponding sensitivity modes qk are visualized in Fig. 1b and the corresponding principal component structural sensitivities δσPCk are shown in Fig. 1c.
For the largest singular value s1, the sensitivity mode q1 is given by a collective symmetric C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching coordinate. Distorting the molecular structure along this mode will mainly affect the position and intensity of the first peak as well as the intensity of the second peak in the calculated XES spectrum, while it leaves the third peak mostly unchanged (see blue graphs in Fig. 1c). The second sensitivity mode q2 corresponds to a symmetric Fe–C stretching coordinate. A distortion along this mode will affect all three peaks, but to a much smaller extent than for the first sensitivity mode (see green graphs in Fig. 1c). The third and forth sensitivity modes q3 and q4 are asymmetric Fe–C and C
O stretching coordinate. Distorting the molecular structure along this mode will mainly affect the position and intensity of the first peak as well as the intensity of the second peak in the calculated XES spectrum, while it leaves the third peak mostly unchanged (see blue graphs in Fig. 1c). The second sensitivity mode q2 corresponds to a symmetric Fe–C stretching coordinate. A distortion along this mode will affect all three peaks, but to a much smaller extent than for the first sensitivity mode (see green graphs in Fig. 1c). The third and forth sensitivity modes q3 and q4 are asymmetric Fe–C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching coordinates, respectively, in which the distortions of the axial and equatorial ligands form an out-of-phase combination. Again, it is obvious form Fig. 1c (see red and cyan graphs) that the effect of a distortion along q3 and q4 further decreases, and is already almost negligible for q4.
O stretching coordinates, respectively, in which the distortions of the axial and equatorial ligands form an out-of-phase combination. Again, it is obvious form Fig. 1c (see red and cyan graphs) that the effect of a distortion along q3 and q4 further decreases, and is already almost negligible for q4.
Finally, the lower panel of Fig. 1c also includes the sum of the principal component structural sensitivities corresponding to all remaining singular values (magenta line), which turns out to be negligible. Thus, a principal component analysis allows for a significant reduction of the dimensionality of the linearized change in the calculated spectrum,
| δσ(E;ΔR) = δσ(E;Δq) ≈ δσ(E;Q1, …, Qkmax). | (14) |
3 Construction of nonlinear surrogate models
Based on a principal component analysis, the dimensionality of a linearized model can be significantly reduced by only considering the most influential principal component distortions and neglecting non-influential distortions. This can now be used as starting point for constructing nonlinear surrogate models of the structural sensitivity of calculated spectra within this reduced space, i.e.,| Δσ(E;ΔR) ≈ Δσ(E;Q1, …, Qkmax). | (15) |
A general ansatz for a nonlinear surrogate model within the reduced space of the displacements that are most influential in the linearized model is given by
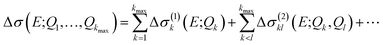 | (16) |
| Δσ(1)k(E;Qk) = Δσ(E;0, …,Qk, …, 0), | (17) |
| Δσ(2)kl(E;Qk, Ql) = Δσ(E;0, …, Qk, …, Ql, …, 0) − Δσ(1)k(E;Qk) − Δσ(1)l(E;Ql), | (18) |
In the linearized model of eqn (13), two-mode and higher-order contributions are neglected while the one-mode contributions are approximated as
| Δσ(1)k(E;Qk) ≈ δσPCk(E)Qk. | (19) |
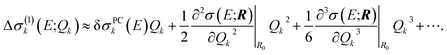 | (20) |
Similarly, instead of neglecting the two-mode contributions, these could be approximated via a Taylor expansion,
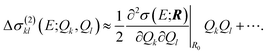 | (21) |
As an alternative to a Taylor expansion, the one-mode, two-mode, higher-order contributions could also be approximated by a discretized representation on a suitable grid of distortions in the relevant range. Note that the fact that the surrogate model is only constructed in the reduced space of the most influential sensitivity modes significantly reduces the number of additional quantum-chemical calculations of the spectrum for distorted structures that are required for its construction.
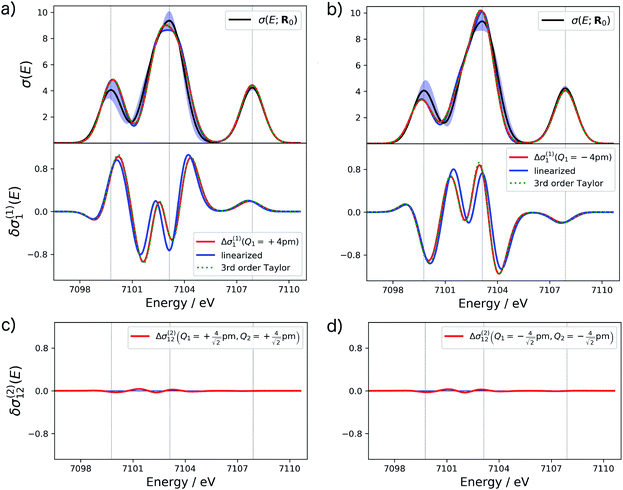
The accuracy of different approximations within a surrogate model can be assessed by comparing the change in the spectrum predicted by the model to the one obtained from a calculation of the spectrum for a distorted structure. For the example of the XES spectrum of Fe(CO)5, such a comparison is shown for selected terms in Fig. 2.
For the one-mode contributions, we consider a distortion of ±4 pm along the most influential sensitivity mode in Fig. 2a and b. The exact one-mode contribution obtained from a calculations of the spectrum for distorted structures (red line) is in good agreement with the linearized model (blue line), but some differences appear in the region of the first and second peak. When going to a 3rd order Taylor expansion (dashed green line), these differences disappear and an almost perfect agreement with the exact one-mode contribution is found on the scale of the figure. Fig. 2c and d shows the exact two-mode contribution obtained from calculating the spectrum for structures that were simultaneously distorted by |Δq| = 4 pm along the two most influential sensitivity modes. The plots show that these two-mode contributions are almost negligible.
Based on these tests, in the following we use a 3rd order Taylor expansion for the one-mode contributions and neglect all two-mode contributions. Of course, such a choice will have to be reassessed for different test cases. More systematic schemes for the construction of non-linear surrogate models that include additional terms on-the-fly as needed can also be envisioned.
4 Analysis of uncertainty propagation
A surrogate model of the change in the calculated spectrum Δσ(E;ΔR) can be evaluated for arbitrary structural distortions without significant computational effort. This now makes it possible to analyze the propagation of uncertainties in the molecular structure to uncertainties in the calculated spectrum.First, we consider the molecular structures that can be obtained from the reference structure by distortions up to a given magnitude dmax, i.e., with |ΔR| ≤ dmax. As the transformation from Cartesian distortions to sensitivity modes is orthogonal, this is equivalent to |Δq| ≤ dmax. Such distortions will result in changes in the calculated spectrum, for which we want to determine upper and lower bounds. For a surrogate model expressed as HDMR expansion up to two-mode contributions we find,
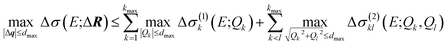 | (22) |
The calculation of the maximum and minimum of the change in the spectrum is thus reduced to determining the maximum and minimum for the one-mode and two-mode contributions, i.e., for simple one- or two-dimensional functions. For the linearized model, only the one-mode contributions at the maximum displacements Qk = ±dmax need to be considered. In the general case, the maximum and minimum can be found by sampling the one-mode and two-mode contributions in the relevant interval (e.g., using 100 evenly spaced points between −dmax and +dmax for the one-mode contributions).
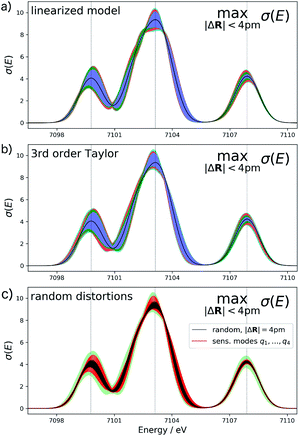
For the test case of the XES spectrum of Fe(CO)5, the error bars for distortions of up to 4 pm calculated according to eqn (22) are shown in Fig. 3a for the linearized model and in Fig. 3b for a non-linear surrogate model based on a 3rd-order Taylor expansion for the one-mode contributions.
For the linearized model, some artifacts are observed for the error bars. In particular, there are points at which the error almost vanishes between the first two peaks at ca. 7101 eV and close to the maximum of the second peak. Moreover, for the second peak the error bars appear rather bumpy. These features disappear for the nonlinear surrogate model, for which smooth error bars are obtained that seem overall reasonable.
To verify the accuracy of the obtained error bars, we have explicitly calculated the spectra for 100 distorted molecular structures with |ΔR|. These are shown as black lines in Fig. 3c. We notice that for these random distortions, the effect on the calculated spectra is significantly below the maximum indicated by the error bars, but their spread follows the same patterns. However, with only 100 distorted structures in the 33-dimensional space of possible distortions, it is not surprising that the distortions that have the largest effect on the calculated spectra are not sampled. Therefore, Fig. 3c also includes the spectra calculated for structures distorted along the four most influential sensitivity modes as red lines. For these distortions, we see a significantly larger effect than for random distortions. The spread of the calculated spectra now approaches the error bars, while all spectra calculated for distorted structures remain within the calculated error bars.
The error bars in Fig. 3b indicate that the uncertainty in the position and intensity of the first peak is larger than for the third peak. For the second peak, the uncertainty is rather small for the position of the peak while there is a larger effect of structural distortions for its intensity. Eqn (22) allows for a decomposition into contributions of the different sensitivity modes that is also included in Fig. 3 and allows for a further analysis. For instance, the uncertainty for the first and second peak is mostly due to the first sensitivity mode, while for the third peak the first three sensitivity modes contribute roughly equally to the uncertainty.
Second, we turn to a probabilistic picture and set out to determine the propagation of statistical uncertainties in the underlying molecular structure to the calculated spectrum. To this end, we consider the distortions in the molecular structure as a random variable with the probability density p(Δq). Here, we assume that distortions along the different sensitivity modes are uncorrelated, i.e.,
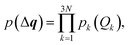 | (23) |
The calculated spectrum will thus also become a random variable with an associated probability density,
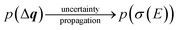 | (24) |
The probability distribution for the calculated spectrum can be characterized by calculating its moments,
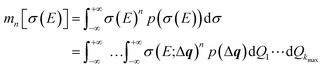 | (25) |
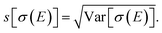
For our surrogate model with up to two-mode contributions, the mean value of the probability distribution for the calculated spectrum can be calculated as,
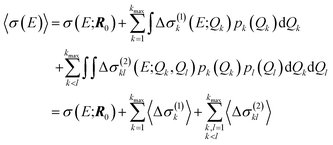 | (26) |
Note that this mean value does not necessarily agree with the spectrum calculated for the undistorted structure, even tough the mean of the distribution of the distortions equals the reference structure.
If only one-mode contributions are included, the variance can be calculated as,
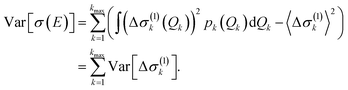 | (27) |
For the test case of the XES spectrum of Fe(CO)5, we assume a normal distribution with a mean of zero and with standard deviation sQ for distortions along all sensitivity modes,
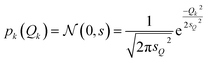 | (28) |
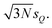 Thus, the considered distortions are much larger than those considered above, but their largest part will always be along non-influential sensitivity modes.
Thus, the considered distortions are much larger than those considered above, but their largest part will always be along non-influential sensitivity modes.
The calculation of the error bars requires calculating the integrals in eqn (26) and (27). With our surrogate model based on a Taylor expansion of the one-mode contributions and normally distributed distortions these could be obtained analytically, but using a numerical integration scheme such as Gauss–Hermite quadrature or Monte–Carlo sampling is more general. For simplicity, here we apply numerical integration with a grid of 1000 evenly spaced points between −4sQ and +4sQ.
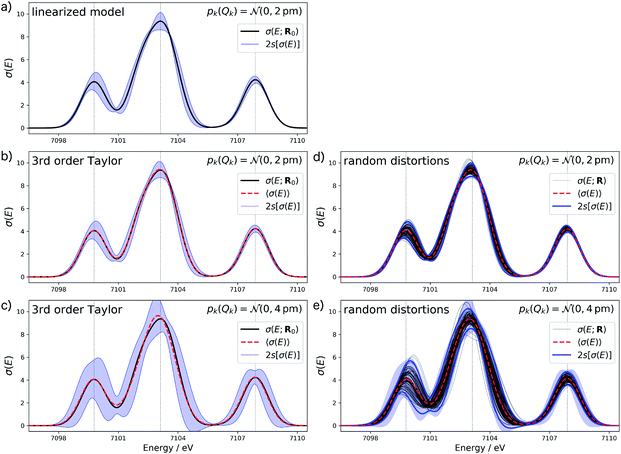
Fig. 4a shows the calculated XES spectrum of Fe(CO)5 with 2s error bars assuming a normal distribution with 2sQ = 4 pm for the structural distortions within the linearized surrogate model. In this case, the mean of the calculated spectrum coincides with the spectrum of the undistorted structure. Again, the error bars obtained with the linearized surrogate model show some unphysical features at the minimum at ca. 7101 eV and close to the maximum of the second peak at ca. 7103 eV. With the surrogate model employing a 3rd order Taylor expansion (see Fig. 4b) these mostly disappear and the error bars become overall smooth.
When increasing the standard deviation of the normal distribution assumed for the structural distortions to 2sQ = 8 pm, the error bars increase (see Fig. 4c). However, this increase is not proportional and different new features are introduced for the individual peaks in the spectrum. For instance, the error bars for the second peak are larger for an increase in the intensity than for a decrease and also show a larger probability for a shift of this peak to lower energies. This also results in a shift of the mean of the calculated spectrum compared to the spectrum of the undistorted structure.
To verify the accuracy of the obtained error bars, we re-calculated the XES spectrum for 100 random distortions sampled from independent normal distributions for each Cartesian coordinate. These randomly sampled calculated spectra are shown in Fig. 4d and e for 2sQ = 4 pm and 2sQ = 8 pm, respectively, together with the corresponding error bars, obtained as two standard deviations of the calculated spectra. For 2sQ = 4 pm (see Fig. 4d), we find an almost perfect agreement of the error bars obtained from random sampling with the error bars derived from our non-linear surrogate model. On the other hand, for 2sQ = 8 pm (see Fig. 4e) larger deviations appear. For the first peak, the surrogate model predicts too large error bars at the low-energy shoulder of the peak, and for the third peak it overestimates the uncertainty for a shift of the peak position. These differences points to a breakdown of the 3rd order Taylor expansion for larger distortions. In addition, for larger distortions it is also not clear whether with only 100 random distortions, all relevant distortions are sampled sufficiently.
The main features of the error bars in Fig. 4 are overall similar to those already observed in Fig. 3. The largest error bars is found for the first and second peak, whereas the uncertainty is smaller for the third peak. To allow for a further analysis, Table 1 collects quantitative statistical metrics for the intensity at the positions of the three peaks. At the first and third peak, the mean on the calculated intensity 〈σ(Ej)〉 coincides with the intensity that is calculated for the undistorted structure σ(Ej;R0), while for the second peak the mean intensity slightly deviates from the intensity for the reference structure. This deviation increases when increasing the standard deviation of the normal distribution that is assumed for the structural distortions.
Table 1 further includes the variance of the intensity at the peak maxima Var[σ(Ej)], its standard deviation 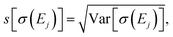 and the coefficient of variance (COV), s[σ(Ej)]/〈σ(Ej)〉. As it is normalized to the mean intensity, the latter gives a measure of the relative uncertainty. These quantitative metrics confirm the observations already made in Fig. 4, i.e., the absolute uncertainty, as measured by the variance or the standard deviation, is largest for the first and the second peak, while it is considerably lower for the third peak.
and the coefficient of variance (COV), s[σ(Ej)]/〈σ(Ej)〉. As it is normalized to the mean intensity, the latter gives a measure of the relative uncertainty. These quantitative metrics confirm the observations already made in Fig. 4, i.e., the absolute uncertainty, as measured by the variance or the standard deviation, is largest for the first and the second peak, while it is considerably lower for the third peak.
The COV shows that the relative uncertainty is the largest for the first peak, while it is considerably smaller for the second and third peak. When increasing the uncertainty that is assumed for the structural distortions by a factor of two, the standard deviation and COV approximately double for all three peaks. Note, however, that the considered metrics only account for the intensity at the position of the peak, and thus only partly capture differences in the uncertainty of the peak position.
5 Further test cases: XES, UV/Vis, and IR
The methodology for quantifying the structural sensitivity of calculated spectra developed in the previous sections is not restricted to the test case of the XES spectrum of Fe(CO)5 considered so far, but should be generally applicable to different spectroscopies. To demonstrate this and to explore the limitations of the current approach, in this section we investigate additional test cases from XES, ultraviolet/visible (UV/Vis), and infrared (IR) spectroscopy. These test cases cover a divers set of computational spectroscopies treated with different computational approaches (ground-state ΔDFT, time-dependent DFT, and harmonic vibrational analysis).First, we consider the XES spectrum of another iron complex, Fe(CO)3(cod) (cod = cyclooctadienyl, C8H12).39,49 This is another typical transition metal complex, but features a more complex coordination environment compared to Fe(CO)5. The sensitivity of the calculated XES spectrum with respect to selected distortions has been explored previously in ref. 35. Here, we now consider distortions with respect to all possible distortions as described above.
The sensitivity modes resulting from the principal component analysis are shown in Fig. 5a. We find that only 11 of the in total 81 sensitivity modes are required to account for 95% of the sum of all singular values. For these 11 sensitivity modes, we set up our surrogate model in the same fashion as for Fe(CO)5, i.e., a 3rd order Taylor expansion was used for the one-mode contributions while neglecting two-mode and higher-order contributions. The calculated spectrum together with error bars is shown in Fig. 5b–d. A comparison to the error bars obtained from randomly sampling 100 distortions, which shows an excellent agreement with our non-linear surrogate model for both sQ = 2 pm and sQ = 4 pm, is given in Fig. S2 in the ESI.†
As for Fe(CO)5, the two most influential sensitivity modes correspond to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching and Fe–C stretching vibrations. The third sensitivity mode can be interpreted as a Fe–cod stretching mode, whereas the fourth and fifth sensitivity mode describe deformations of the CO ligand sphere. Note that the most influential sensitivity modes do not include any changes of the structure of the cod ligand, which indicates that such distortions do not alter the calculated XES spectrum significantly.
O stretching and Fe–C stretching vibrations. The third sensitivity mode can be interpreted as a Fe–cod stretching mode, whereas the fourth and fifth sensitivity mode describe deformations of the CO ligand sphere. Note that the most influential sensitivity modes do not include any changes of the structure of the cod ligand, which indicates that such distortions do not alter the calculated XES spectrum significantly.
The calculated error bars are similar to those found for Fe(CO)5 for the three most intense peaks (see also Section S5 in the ESI† for a discussion of quantitative metrics). For the weak features between ca. 7092 and 7095 eV, the error bars are very small, i.e., even though it is only weak this region appears to be rather insensitive to structural distortions. Noteworthy are also the error bars for the third peak at ca. 7106–7109 eV. Within the error bars, this peak could show only one maximum (as for the reference structure) or two maxima. Such insights provided by the error bars for calculated spectra will potentially be crucial for the comparison of calculated and measured spectra.
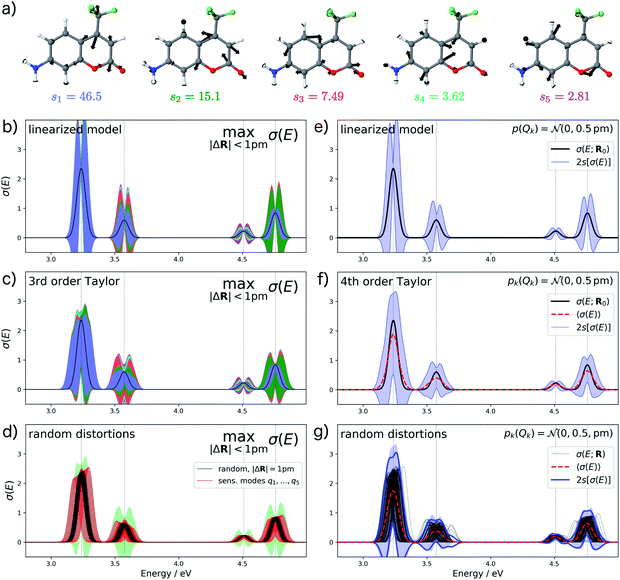
As a second test case, we consider the electronic excitation (UV/Vis) spectrum of the dye molecule aminocoumarin C151. Such coumarin dyes are widely used for studying photochemistry and thus provide a typical test case. We have previously investigated aminocoumarin C151 as a model system for simulating solvent effects on electronic excitations.50 Besides the effect of the solvent environment, a further contribution to such solvent effects are fluctuations of the molecular structure which have distinct effects on the calculated UV/Vis spectrum.
For analyzing the structural sensitivity of the calculated UV/Vis spectrum of aminocoumarin C151 we considered the region between 2.5 and 5.0 eV, in which four allowed electronic transitions are found. We performed a principal component analysis of the linear structural sensitivities as described above. Here, only five sensitivity modes, which are shown in Fig. 6a, are required to account for 95% of the sum of all 66 singular values. These all correspond to different ring breathing modes of the conjugated aromatic system. Note that the influence of the first sensitivity mode is already more than three times larger than for the second sensitivity mode.
For the calculation of error bars, we used both the linearized model and a 4th order Taylor expansion of the one-mode contributions, while neglecting two-mode and higher-order contributions. The resulting error bars are shown in Fig. 6b, c, e and f. First, we notice that the effect of structural distortions on the calculated spectra is much larger than for XES. Therefore, we only consider maximum distortions of up to 1 pm and assumed a normal distribution with a standard deviation of sQ = 0.5 pm, respectively. Even for these smaller distortions, the difference between the linearized model and the non-linear model using a 4th order Taylor expansion of the one-mode contributions is rather pronounced. With the linearized model, the error bars extend quite far to negative intensities, which is unphysical and indicates a breakdown of the linear approximation. This is to a large extent corrected when switching to a 4th order Taylor expansion.
Further inspection shows that for all peaks, the dominating effect of structural distortions is a shift of the peak position. Once this shift becomes large compared to the width of the peak, it is not well described by a linear expansion of the difference spectrum. This is most obvious in Fig. 6c for the first peak. Here, the 4th order Taylor expansion is mostly sufficient for recovering such a shift in the peak position (see Fig. 6d), but for larger shifts even a higher-order Taylor expansion might not be adequate. However, even though the 4th order Taylor expansion improves upon the linearized model, it still results in some unphysical extent of the calculated error bars to negative intensities. Note, that our form of the nonlinear surrogate model is also able to accommodate other approximations than a Taylor expansion for the one-mode (and possibly higher-order) contributions, which might be more suitable for describing larger shifts in peak positions.
To assess the accuracy of the error bars obtained with our nonlinear surrogate model, Fig. 6d and g show the spectra obtained for 100 randomly sampled distortions. For random distortions with |ΔR| = 1 pm (see Fig. 6d), all calculated spectra are within the boundaries for the maximum change in the calculated spectrum. However, the magnitude of the change is significantly smaller because the most influential distortions are not sampled sufficiently. When considering explicit distortions along the most influential sensitivity modes, the error bars are approached more closely. When sampling independent normally-distributed distortions (see Fig. 6g), we find that the error bars obtained from the standard deviation of the calculated spectra are in very good agreement with those obtained from the nonlinear surrogate model. Note that even though the spectra always remain positive, these error bars extend to negative intensities, which might appear unphysical. However, this is a consequence of the fact that the calculated spectrum do not follow a normal distribution anymore, which leads to a breakdown of the interpretation of the 2s error bars as 95% confidence intervals.
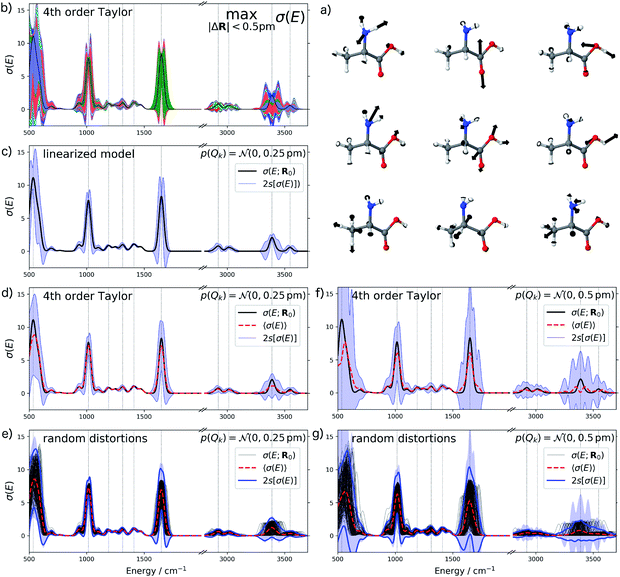
Finally, we consider the calculated harmonic IR spectrum of the amino acid alanine as a third test case. Vibrational spectroscopy is a prime example for a spectroscopic method that is used for making structural assignments based on the direct comparison of calculated and measured spectra (see, e.g., ref. 3–7). As many such studies concern polypeptides, alanine as one of the simplest amino acids is well suited as a first test case. Note that for vibrational spectra, the sensitivity of the calculated harmonic spectra with respect to structural distortions is related to the anharmonicity of the potential energy surface and the resulting error bars thus also give an indication for uncertainties resulting from the neglect of anharmonicities.
For the IR spectrum of alanine, we analyzed the structural sensitivity in the region between 500–4000 cm−1. Here, we find that 13 out of 39 sensitivity modes need to be included to account for 95% of the sum of all singular values. The nine most influential sensitivity modes are visualized in Fig. 7a. The comparison with the color-coded error bars for maximum distortions of up to 0.5 pm in Fig. 7b shows that different peaks are affected by the individual sensitivity modes. For instance, the amide I (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching) vibration at ca. 1650 cm−1 is almost exclusively influenced by the second sensitivity mode, which corresponds to a change of the C
O stretching) vibration at ca. 1650 cm−1 is almost exclusively influenced by the second sensitivity mode, which corresponds to a change of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond length.
O bond length.
As for UV/Vis spectroscopy, we find that also the calculated IR spectra are much more sensitive to structural distortions than the XES spectra. Therefore, we consider only normally distributed distortions with a standard deviation of sQ = 0.25 pm in Fig. 7c and d. Again, we find that going from a linearized model to a 4th order Taylor expansion of the one-mode contributions significantly reduces the extent of the error bars to negative intensities. We also note that when going to normally distributed distortions with a standard deviation of sQ = 0.5 pm (see Fig. 7f), the 4th order Taylor expansion breaks down, i.e., more sophisticated approximations for the one-mode contributions will be required for describing such larger distortions. This is confirmed by the comparison with the error bars obtained from randomly sampled distortions that is shown in Fig. 7e and g.
Inspecting the error bars in Fig. 7d as well as the corresponding quantitative statistical metrics listed in Table 2 reveals rather different uncertainties in different regions of the spectrum. While the fingerprint region below ca. 800 cm−1 is subject to large absolute uncertainties as well as for the amide I peak at ca. 1650 cm−1 (which mainly consists of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration), a rather small absolute uncertainty is found for the position of the peak at ca. 1016 cm−1 as well as for low-intensity peaks between ca. 1050 and 1500 cm−1 (which are due to the Cα–N stretching, Cα–H bending and the symmetric CH3 bending vibrations). In the high-wavenumber region, the C–H stretching vibrations in the region between ca. 2800–3150 cm−1 is affected by a significantly smaller absolute uncertainty that the O–H and N–H stretching vibrations in the region between ca. 3200–3700 cm−1.
O stretching vibration), a rather small absolute uncertainty is found for the position of the peak at ca. 1016 cm−1 as well as for low-intensity peaks between ca. 1050 and 1500 cm−1 (which are due to the Cα–N stretching, Cα–H bending and the symmetric CH3 bending vibrations). In the high-wavenumber region, the C–H stretching vibrations in the region between ca. 2800–3150 cm−1 is affected by a significantly smaller absolute uncertainty that the O–H and N–H stretching vibrations in the region between ca. 3200–3700 cm−1.
| E j /cm−1 | Assignment | σ(Ej;R0) | 〈σ(Ej)〉 | Var[σ(Ej)] | s[σ(Ej)] | COV[σ(Ej)] |
|---|---|---|---|---|---|---|
| 534.7 | Fingerprint | 11.12 | 8.66 | 8.77 | 2.96 | 0.34 |
| 1015.6 | X–H bend | 7.70 | 7.22 | 0.48 | 0.69 | 0.10 |
| 1191.3 | Cα–N stretch | 0.88 | 0.86 | 0.00 | 0.04 | 0.05 |
| 1313.1 | Cα–H bend | 0.99 | 0.96 | 0.02 | 0.15 | 0.16 |
| 1412.5 | Symm. CH3 bend | 1.08 | 1.07 | 0.00 | 0.06 | 0.06 |
| 1650.9 | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch O stretch |
8.31 | 7.18 | 3.52 | 1.88 | 0.26 |
| 2922.2 | C–H stretch | 0.79 | 0.66 | 0.05 | 0.22 | 0.34 |
| 3014.7 | C–H stretch | 0.59 | 0.54 | 0.02 | 0.13 | 0.24 |
| 3390.2 | O–H stretch | 2.07 | 1.10 | 0.88 | 0.94 | 0.85 |
| 3547.1 | N–H stretch | 0.58 | 0.37 | 0.05 | 0.23 | 0.62 |
Considering the COV, the latter stand out as the peaks with the highest relative uncertainty. For the C–H stretching, amide I (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching), and the fingerprint region, the COV is smaller by about a factor of two, but is still sizable. The intensities of the peaks in the region between ca. 1050 and 1500 cm−1 show not only the smallest absolute uncertainty, but also the smallest COV.
O stretching), and the fingerprint region, the COV is smaller by about a factor of two, but is still sizable. The intensities of the peaks in the region between ca. 1050 and 1500 cm−1 show not only the smallest absolute uncertainty, but also the smallest COV.
Such a systematic assessment of the uncertainties in the positions and intensities of different peaks in calculated vibrational spectra will potentially enable a much more reliable assignment of experimental spectra. Most importantly, it allows one to identify spectral features that are subject to high uncertainties. For these peaks, one can then selectively refine the computational methodology in order to reduce the uncertainty.
6 Conclusions and outlook
Altogether, we have presented a methodology for systematically quantifying the structural sensitivity of calculated molecular spectra. It allows for the inclusion of error bars indicating the uncertainties in a calculated spectrum that are due to uncertainties in the underlying molecular structure. It is thus a crucial first step towards theoretical spectroscopy with error bars and will enable a systematic assessment of the agreement between computational and experimental spectra. While we demonstrated its applicability to XES, UV/Vis, and IR spectroscopy, our methodology is not specific to certain spectroscopies but should be generally applicable to any type of computational spectroscopy providing a spectral intensity as function of excitation energy.Our starting point for quantifying the structural sensitivity is a principal component analysis of the linear structural sensitivity with respect to all possible Cartesian displacements. This leads to sensitivity modes, which correspond to collective distortions of the reference structure. We could show that only a small fraction of all sensitivity modes need to be included to describe the full linear structural sensitivity. Currently, our approach initially requires the calculation of 6N spectra for displaced structures, which can be a significant increase of the computational effort. However, different strategies for making this step more efficient could be explored in future work, e.g., the analytical calculation of the derivative of the spectra with respect to structural distortions (see, e.g., ref. 51), the determination of the most influential sensitivity modes at a lower level of theory, or an iterative calculation of the largest singular values and the corresponding singular vectors.52
Within the reduced space of the most influential sensitivity modes, one can subsequently set up a nonlinear surrogate model of the structural sensitivity, for which an HDMR expansion provides a convenient and general ansatz. Here, we employed a 3rd or 4th order Taylor expansion for the one-mode contributions and neglected two-mode and higher-order contributions. We found that such an approximation is sufficient as long as the shifts in peak positions remain small compared to their width. If this is no longer the case, more sophisticated approximations will be required, but can easily be accommodated within the general form of the surrogate model introduced here. For the systematic construction of surrogate models of the structural sensitivity, iterative schemes that include additional data points as needed could be devised in analogy to methods available for the construction of anharmonic potential energy surfaces.53,54
With a surrogate model of the structural sensitivity, it becomes possible to perform a statistical analysis of the propagation of uncertainties in the molecular structure to the calculated spectra, which ultimately provides error bars for the calculated spectra. In the present work, we assumed an ad hoc uncertainty for the molecular structure, either by specifying a maximum distortion or by assuming a normal distribution with a certain standard deviation. In future applications, these structural uncertainties could be obtained from more physical considerations, e.g., by assuming a thermal population of vibrational modes. Here, we characterized the uncertainty in the calculated spectrum either by giving upper and lower bounds or by calculating the standard deviation of the probability distribution for the calculated spectra. This could be extended by performing additional statistical analyses, e.g., by explicitly calculating confidence or credible intervals for the calculated spectrum.
The resulting error bars make it possible to identify which spectral features are associated with a large structural sensitivity and which spectral features are rather insensitive to distortions of the underlying molecular structure. For instance, our analysis of the structural sensitivity of the calculated IR spectrum of alanine reveals that peaks that are due to stretching modes show a significantly larger uncertainty than those due to bending modes. Moreover, the analysis of the sensitivity modes reveals the collective distortions that have the largest influence on the calculated spectrum. For alanine, we find that changes of the N–H, O–H, and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond lengths have the largest effect on the calculated IR spectrum. Altogether, the novel analysis tools developed here make it possible to assess the relationship between molecular structure and calculated spectra in a quantitative way and will ultimately make structural assignments based on the comparison of experimental and calculated spectra more reliable.
O bond lengths have the largest effect on the calculated IR spectrum. Altogether, the novel analysis tools developed here make it possible to assess the relationship between molecular structure and calculated spectra in a quantitative way and will ultimately make structural assignments based on the comparison of experimental and calculated spectra more reliable.
Here, we have considered distortions of the underlying molecular structure as the only source of uncertainty. Of course, calculated spectra are also subject to additional sources of uncertainty, most importantly errors of the approximate exchange–correlation functional in DFT. The methodology presented here can be combined with existing approaches for quantifying such uncertainties of quantum-chemical approximations (see e.g., ref. 23–27). Moreover, our general methodology can be extended to other sources of uncertainties that depend on a larger number of parameters, e.g., uncertainties introduced by an environment that is described by an embedding potential.55 Ultimately, we envision the quantification of all relevant sources of uncertainties in calculated spectra, and consider the present work an important step in this direction.
Appendix: computational details
All quantum-chemical calculations have been performed using the Amsterdam Density Functional (ADF) program package.56,57 The calculations were automated using the PyADF scripting framework,58 and the methodology for the analysis of the structural sensitivity of calculated spectra described here has been implemented as an add-on to PyADF. Normally-distributed random distortions (used in Fig. 4d, e, 6g, 7e and g) are obtained by drawing each component of the displacement vector ΔR from an independent normal distribution with the desired standard deviation. Random distortions with a given magnitude |ΔR| (used in Fig. 3c and 6d) are obtained from these normally-distributed random distortions by rescaling the displacement vector accordingly.The molecular structures of Fe(CO)5 and of Fe(CO)3(cod) were optimized employing the BP86 exchange–correlation (xc) functional59,60 in combination with a Slater-type TZ2P basis set.61 For aminocoumarin C151, the structure was optimized using BP86 and a TZP basis set. For alanine, BP86 and a DZ basis set were used in combination with a COSMO solvation model62 with default parameters.
For the calculation of XES spectra, we employed the ΔDFT approach of Lee et al.,38 in which excitation energies are calculated as occupied orbital energy differences. This ΔDFT approach is a rather simple approximation, but it has been shown to be reliable for valence-to-core XES spectra of diverse transition metal complexes,63–71 including the ones considered here.39 XES intensities are obtained from transition moments between occupied orbitals, including contributions beyond the electric dipole approximation.72,73 All calculations of XES spectra were performed with the BP86 xc functional and a QZ4P basis set in combination with the COSMO solvation model62 with default parameters. The calculated spectra were shifted by 180.62 eV (ref. 35 and 49) and a Gaussian line broadening with a full-width at half maximum of 1.5 eV was applied to each calculated transition. For Fe(CO)5, we considered the region between 7094.62 eV and 7110.62 eV as relevant energy range, whereas for Fe(CO)3(cod) the region between 7088.62 eV and 7110.62 eV was used.
The UV/Vis spectrum of aminocoumarin C151 was calculated using time-dependent DFT (TD-DFT) as implemented in ADF.74 In all TD-DFT calculations, the SAOP model potential75,76 was used in combination with a TZP basis set. The spectra were obtained by applying a Gaussian line broadening with a FWHM of 0.08 eV, and the broadened spectrum in the region between 2.5 eV and 5.0 eV was used as quantity of interest.
Harmonic infrared spectra of alanine were calculated with ADF using its analytical frequency module77 using BP86/DZ and a COSMO solvation model. A Gaussian line broadening with a FWHM of 50 cm−1 was employed. Here, the broadened spectrum was considered in the region between 500 cm−1 and 4000 cm−1.
Author contributions
CRJ designed the study and supervised the project. TGB and MOW developed the methodology and algorithms. TGB implemented the software, assisted by MOW. TGB performed all calculations and wrote a first draft of the manuscript. CRJ wrote the final version of the manuscript, which all authors critically revised and approved.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Prof. Ulrich Römer (TU Braunschweig, Institute for Dynamics and Vibrations) for inspiring discussions on uncertainty quantification.Notes and references
- J. Grunenberg, Computational spectroscopy: methods, experiments and applications, Wiley-VCH, Weinheim, 2010 Search PubMed.
- F. Neese, Angew. Chem., Int. Ed., 2017, 56, 11003–11010 CrossRef CAS PubMed.
- N. C. Polfer, J. Oomens, S. Suhai and B. Paizs, J. Am. Chem. Soc., 2007, 129, 5887–5897 CrossRef CAS PubMed.
- T. R. Rizzo, J. A. Stearns and O. V. Boyarkin, Int. Rev. Phys. Chem., 2009, 28, 481–515 Search PubMed.
- F. Schinle, C. R. Jacob, A. B. Wolk, J.-F. Greisch, M. Vonderach, P. Weis, O. Hampe, M. A. Johnson and M. M. Kappes, J. Phys. Chem. A, 2014, 118, 8453–8463 CrossRef CAS PubMed.
- N. L. Burke, A. F. DeBlase, J. G. Redwine, J. R. Hopkins, S. A. McLuckey and T. S. Zwier, J. Am. Chem. Soc., 2016, 138, 2849–2857 CrossRef CAS PubMed.
- K. N. Blodgett, J. L. Fischer, J. Lee, S. H. Choi and T. S. Zwier, J. Phys. Chem. A, 2018, 122, 8762–8775 CrossRef CAS PubMed.
- J. Haesler, I. Schindelholz, E. Riguet, C. G. Bochet and W. Hug, Nature, 2007, 446, 526–529 CrossRef CAS PubMed.
- C. R. Jacob, S. Luber and M. Reiher, ChemPhysChem, 2008, 9, 2177–2180 CrossRef CAS PubMed.
- K. H. Hopmann, J. Sebestik, J. Novotná, W. Stensen, M. Urbanova, J. Svenson, J. S. Svendsen, P. Bour and K. Ruud, J. Org. Chem., 2012, 77, 858–869 CrossRef CAS PubMed.
- C. Merten, T. P. Golub and N. M. Kreienborg, J. Org. Chem., 2019, 84, 8797–8814 CrossRef CAS PubMed.
- K. M. Lancaster, M. Roemelt, P. Ettenhuber, Y. Hu, M. W. Ribbe, F. Neese, U. Bergmann and S. DeBeer, Science, 2011, 334, 974–977 CrossRef CAS.
- A. Boubnov, H. W. P. Carvalho, D. E. Doronkin, T. Günter, E. Gallo, A. J. Atkins, C. R. Jacob and J.-D. Grunwaldt, J. Am. Chem. Soc., 2014, 136, 13006–13015 CrossRef CAS PubMed.
- T. Günter, H. W. P. Carvalho, D. E. Doronkin, T. Sheppard, P. Glatzel, A. J. Atkins, J. Rudolph, C. R. Jacob, M. Casapu and J.-D. Grunwaldt, Chem. Commun., 2015, 51, 9227–9230 RSC.
- L. Burkhardt, M. Holzwarth, B. Plietker and M. Bauer, Inorg. Chem., 2017, 56, 13300–13310 CrossRef CAS.
- R. Smith, Uncertainty Quantification: Theory, Implementation, and Applications, Society for Industrial and Applied Mathematics, Philadelphia, 2014 Search PubMed.
- T. J. Sullivan, Introduction to Uncertainty Quantification, Springer, New York, NY, 1st edn, 2015 Search PubMed.
- K. K. Irikura, R. D. Johnson III and R. N. Kacker, Metrologia, 2004, 41, 369 CrossRef CAS.
- S. C. Glotzer, S. Kim, P. T. Cummings, A. Deshmukh, M. Head-Gordon, G. Karniadakis, L. Petzold, C. Sagui and M. Shinozuka, WTEC Panel Report on International Assessment of Research and Development in Simulation-Based Engineering and Science, 2013, DOI:10.2172/1088842, http://www.osti.gov/servlets/purl/1088842/.
- G. N. Simm, J. Proppe and M. Reiher, Chimia, 2017, 71, 202–208 CrossRef CAS PubMed.
- J. J. Mortensen, K. Kaasbjerg, S. L. Frederiksen, J. K. Nørskov, J. P. Sethna and K. W. Jacobsen, Phys. Rev. Lett., 2005, 95, 216401 CrossRef CAS.
- J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149 CrossRef.
- J. Wellendorff, K. T. Lundgaard, K. W. Jacobsen and T. Bligaard, J. Chem. Phys., 2014, 140, 144107 CrossRef.
- A. J. Medford, J. Wellendorff, A. Vojvodic, F. Studt, F. Abild-Pedersen, K. W. Jacobsen, T. Bligaard and J. K. Nørskov, Science, 2014, 345, 197–200 CrossRef CAS PubMed.
- G. N. Simm and M. Reiher, J. Chem. Theory Comput., 2016, 12, 2762–2773 CrossRef CAS PubMed.
- J. Proppe, T. Husch, G. N. Simm and M. Reiher, Faraday Discuss., 2017, 195, 497–520 RSC.
- H. L. Parks, A. J. H. McGaughey and V. Viswanathan, J. Phys. Chem. C, 2019, 123, 4072–4084 CrossRef CAS.
- P. Pernot, J. Chem. Phys., 2017, 147, 104102 CrossRef PubMed.
- K. K. Irikura, R. D. Johnson, R. N. Kacker and R. Kessel, J. Chem. Phys., 2009, 130, 114102 CrossRef PubMed.
- R. D. Johnson, K. K. Irikura, R. N. Kacker and R. Kessel, J. Chem. Theory Comput., 2010, 6, 2822–2828 CrossRef CAS PubMed.
- J. Proppe and M. Reiher, J. Chem. Theory Comput., 2017, 13, 3297–3317 CrossRef CAS PubMed.
- J. Oreluk, Z. Liu, A. Hegde, W. Li, A. Packard, M. Frenklach and D. Zubarev, Sci. Rep., 2018, 8, 13248 CrossRef PubMed.
- T. Weymuth, J. Proppe and M. Reiher, J. Chem. Theory Comput., 2018, 14, 2480–2494 CrossRef CAS PubMed.
- J. P. Janet, C. Duan, T. Yang, A. Nandy and H. J. Kulik, Chem. Sci., 2019, 10, 7913–7922 RSC.
- S. W. Oung, J. Rudolph and C. R. Jacob, Int. J. Quantum Chem., 2018, 118, e25458 CrossRef.
- D. G. Cacuci, Sensitivity & Uncertainty Analysis, Volume 1: Theory, Chapman and Hall/CRC, Boca Raton, 1st edn, 2003 Search PubMed.
- H. Abdi and L. J. Williams, Wiley Interdiscip. Rev.: Comput. Stat., 2010, 2, 433–459 CrossRef.
- N. Lee, T. Petrenko, U. Bergmann, F. Neese and S. DeBeer, J. Am. Chem. Soc., 2010, 132, 9715–9727 CrossRef CAS PubMed.
- M. U. Delgado-Jaime, S. DeBeer and M. Bauer, Chem.–Eur. J., 2013, 19, 15888–15897 CrossRef CAS PubMed.
- G. Li, S.-W. Wang, H. Rabitz, S. Wang and P. Jaffé, Chem. Eng. Sci., 2002, 57, 4445–4460 CrossRef CAS.
- I. M. Sobol, Mathematical Modeling and Computational Experiment, 1995, 1, 407–414 Search PubMed.
- G. Li, C. Rosenthal and H. Rabitz, J. Phys. Chem. A, 2001, 105, 7765–7777 CrossRef CAS.
- J. O. Jung and R. B. Gerber, J. Chem. Phys., 1996, 105, 10332–10348 CrossRef CAS.
- O. Christiansen, Phys. Chem. Chem. Phys., 2012, 14, 6672–6687 RSC.
- H.-D. Meyer, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 351–374 CAS.
- P. T. Panek and C. R. Jacob, J. Chem. Phys., 2016, 144, 164111 CrossRef PubMed.
- K. Sepahvand, S. Marburg and H. J. Hardtke, Int. J. Appl. Mech., 2010, 02, 305–353 CrossRef.
- B. Iooss and P. Lemaître, Uncertainty Management in Simulation-Optimization of Complex Systems: Algorithms and Applications, Springer US, Boston, MA, 2015, pp. 101–122 Search PubMed.
- A. J. Atkins, M. Bauer and C. R. Jacob, Phys. Chem. Chem. Phys., 2015, 17, 13937–13948 RSC.
- J. Neugebauer, C. R. Jacob, T. A. Wesolowski and E. J. Baerends, J. Phys. Chem. A, 2005, 109, 7805–7814 CrossRef CAS PubMed.
- D. Rappoport and F. Furche, J. Chem. Phys., 2005, 122, 064105 CrossRef PubMed.
- N. Halko, P. G. Martinsson and J. A. Tropp, SIAM Rev., 2011, 53, 217–288 CrossRef.
- G. Rauhut, J. Chem. Phys., 2004, 121, 9313–9322 CrossRef CAS PubMed.
- M. Sparta, I.-M. Høyvik, D. Toffoli and O. Christiansen, J. Phys. Chem. A, 2009, 113, 8712–8723 CrossRef CAS PubMed.
- A. S. P. Gomes and C. R. Jacob, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2012, 108, 222 RSC.
- Software for Chemistry and Materials, ADF, Amsterdam density functional program, Amsterdam, 2019, http://www.scm.com Search PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- C. R. Jacob, S. M. Beyhan, R. E. Bulo, A. S. P. Gomes, A. W. Götz, K. Kiewisch, J. Sikkema and L. Visscher, J. Comput. Chem., 2011, 32, 2328–2338 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed.
- E. Van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156 CrossRef CAS PubMed.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- G. Smolentsev, A. V. Soldatov, J. Messinger, K. Merz, T. Weyhermüller, U. Bergmann, Y. Pushkar, J. Yano, V. K. Yachandra and P. Glatzel, J. Am. Chem. Soc., 2009, 131, 13161–13167 CrossRef CAS PubMed.
- K. M. Lancaster, K. D. Finkelstein and S. DeBeer, Inorg. Chem., 2011, 50, 6767–6774 CrossRef CAS PubMed.
- C. J. Pollock and S. DeBeer, J. Am. Chem. Soc., 2011, 133, 5594–5601 CrossRef CAS PubMed.
- M. A. Beckwith, M. Roemelt, M.-N. Collomb, C. DuBoc, T.-C. Weng, U. Bergmann, P. Glatzel, F. Neese and S. DeBeer, Inorg. Chem., 2011, 50, 8397–8409 CrossRef CAS PubMed.
- M. Roemelt, M. A. Beckwith, C. Duboc, M.-N. Collomb, F. Neese and S. DeBeer, Inorg. Chem., 2012, 51, 680–687 CrossRef CAS PubMed.
- S. N. MacMillan, R. C. Walroth, D. M. Perry, T. J. Morsing and K. M. Lancaster, Inorg. Chem., 2014, 54, 205–214 CrossRef.
- J. A. Rees, R. Bjornsson, J. Schlesier, D. Sippel, O. Einsle and S. DeBeer, Angew. Chem., 2015, 127, 13447–13450 CrossRef.
- J. K. Kowalska, A. W. Hahn, A. Albers, C. E. Schiewer, R. Bjornsson, F. A. Lima, F. Meyer and S. DeBeer, Inorg. Chem., 2016, 55, 4485–4497 CrossRef CAS PubMed.
- C. Kupper, J. A. Rees, S. Dechert, S. DeBeer and F. Meyer, J. Am. Chem. Soc., 2016, 138, 7888–7898 CrossRef CAS PubMed.
- S. Bernadotte, A. J. Atkins and C. R. Jacob, J. Chem. Phys., 2012, 137, 204106 CrossRef PubMed.
- A. J. Atkins, M. Bauer and C. R. Jacob, Phys. Chem. Chem. Phys., 2013, 15, 8095–8105 RSC.
- S. J. A. van Gisbergen, J. G. Snijders and E. J. Baerends, Comput. Phys. Commun., 1999, 118, 119–138 CrossRef CAS.
- P. R. T. Schipper, O. V. Gritsenko, S. J. A. van Gisbergen and E. J. Baerends, J. Chem. Phys., 2000, 112, 1344–1352 CrossRef CAS.
- O. V. Gritsenko, P. R. T. Schipper and E. J. Baerends, Chem. Phys. Lett., 1999, 302, 199–207 CrossRef CAS.
- S. K. Wolff, Int. J. Quantum Chem., 2005, 104, 645–659 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc05103a |
| This journal is © The Royal Society of Chemistry 2020 |