Open Access Article
Open Access ArticleIs silver a mere terminal oxidant in palladium catalyzed C–H bond activation reactions?†
Bangaru
Bhaskararao
a,
Sukriti
Singh
a,
Megha
Anand
b,
Pritha
Verma
a,
Prafull
Prakash
a,
Athira
C
a,
Santanu
Malakar
a,
Henry F.
Schaefer
 b and
Raghavan B.
Sunoj
b and
Raghavan B.
Sunoj
 *a
*a
aDepartment of Chemistry, Indian Institute of Technology Bombay, Powai, Mumbai 400076, India
bCenter for Computational Quantum Chemistry, University of Georgia, Athens, GA 30602, USA. E-mail: sunoj@chem.iitb.ac.in
First published on 13th November 2019
Abstract
In the contemporary practice of palladium catalysis, a molecular understanding of the role of vital additives used in such reactions continues to remain rather vague. Herein, we disclose an intriguing and a potentially general role for one of the most commonly used silver salt additives, discovered through rigorous computational investigations on four diverse Pd-catalyzed C–H bond activation reactions involving sp2 aryl C–H bonds. The catalytic pathways of different reactions such as phosphorylation, arylation, alkynylation, and oxidative cycloaddition are analyzed, with and without the explicit inclusion of the silver additive in the respective transition states and intermediates. Our results indicate that the pivotal role of silver salts is likely to manifest in the form of a Pd–Ag heterobimetallic species that facilitates intermetallic electronic communication. The Pd–Ag interaction is found to provide a consistently lower energetic span as compared to an analogous pathway devoid of such interaction. Identification of a lower energy pathway as well as enhanced catalytic efficiency due to Pd–Ag interaction could have broad practical implications in the mechanism of transition metal catalysis and the current perceptions on the same.
Introduction
There have been many endeavours toward activating relatively inert C–H bonds in an aryl or an alkyl group of organic molecules by using transition metal catalysts.1,2 This domain, popularly known as C–H activation, has witnessed unprecedented growth in the last two decades.3,4 Although converting inert hydrocarbons, aromatic or aliphatic, into more useful compounds through transition metal catalyzed C–H functionalization was a distant goal in the early days, it has become increasingly more amenable in recent times.5–7 Today, transition metal catalysis is accepted by both academia and industry and is capable of providing difficult-to-access compounds as well as improved catalytic efficiency.8–10 One of the most widely used transition metals in catalysis is palladium,11,12 which offers significant versatility in its catalytic attributes.Irrespective of the mechanistic nuances in homogeneous transition metal catalysis terminal oxidants are typically employed to regenerate the catalyst or its active species. While a whole range of oxidants such as copper acetate, molecular oxygen, benzoquinone, etc., are in use,13–15 silver salts like silver acetate or silver triflate seem to remain one of the most prominent choices.16–19 It is inherently interesting to inquire whether the customary choice of silver salts in a gamut of different palladium-catalyzed reactions has more to do with practice or whether it could have an underlying molecular origin. A recent effort involving multiple roles of silver salt additives in the mechanism of a palladium-catalyzed meta C–H activation reaction is particularly impressive toward this end.20
With the silver salts as one of the most widely used additives in conjunction with palladium catalysts, an important question that continues to remain unanswered is the effect of the timing and mode of action of these silver salts in the catalytic cycle, especially on the catalyst itself. In a typical scenario wherein a Pd(0)/Pd(II) catalytic cycle is involved, the action of an oxidant is suggested to occur in the catalyst regeneration step.2 This premise would naturally imply a rather passive, or even no, role for such additives until the end of a given catalytic cycle, when the catalyst acquires a lower oxidation state through the reductive elimination step. Motivated by these lacunae, the fundamental question we wish to address through this study is whether the silver salts can be envisaged to play a more active role in the catalytic cycle than merely acting as a terminal oxidant. If so, how does it differ from the earlier or conventional mechanistic pathways in palladium catalysis?
In order to examine the molecular origin of how silver salt additives influence the vital steps in palladium catalysis, we have chosen a rich and diverse set of reactions, as shown in Scheme 1. These reactions provide a representative class of contemporary examples of palladium catalyzed C–H activation reactions that employ silver salts. In addition, energetic or mechanistic insights into all these reactions have not yet been reported. Over the last couple of decades, computational studies have become an integral part of mechanistic investigations of transition metal catalysis.21,22 The key objective here is to examine whether or not a generalizable role for silver salts in palladium catalysis exists. We use modern computational tools to probe the role of silver in a comprehensive manner by establishing the associated energetics of the catalytic transformations. Gibbs free energies obtained in a suitable continuum solvent by using the DFT(M06) functional are employed for our discussion.23
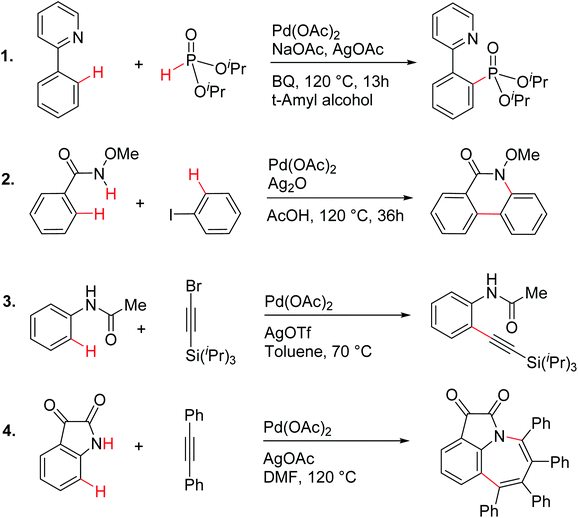 | ||
| Scheme 1 Palladium acetate catalyzed reactions involving C–H activation and reductive elimination in the presence of various silver salt additives.24 | ||
Results and discussion
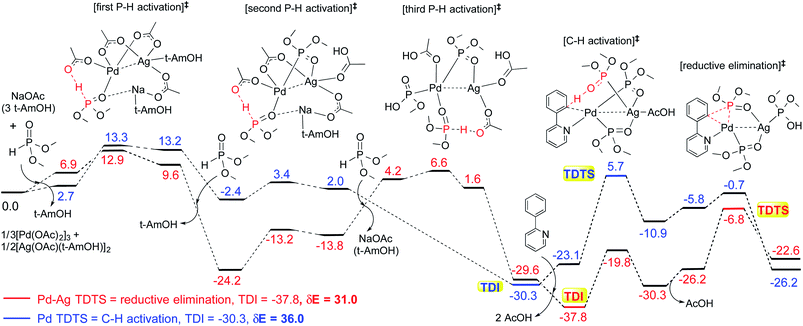
These reactions can broadly be classified as belonging to directed C–H activation, wherein the directing group helps bring the transition metal closer to the site of the reaction. The choice of reactions 1–4, as listed in Scheme 1, is guided by certain vital similarities, such as the use of palladium acetate and silver salt additives, and some desirable diversity in the reaction type. The prototypical directing groups such as pyridine, amide, and anilide are present in the substrates in reactions 1–4 and involve aryl C(sp2)–H activations. Dual aryl C–H activations in 2 and cyclization in 4 are other notable features. These reactions can be chemically classified as phosphorylation (1), arylation (2), alkynylation (3), and oxidative cycloaddition (4). Most of the final products or their variants have their own practical significance, either due to their potential biological activity or other important aspects, thus providing additional significance to the reactions examined in this study.25While the mechanisms of these reactions are of inherent interest and could present different levels of complexities, herein we focus on the most important steps, namely, (a) the turnover determining step, (b) concerted metalation–deprotonation (CMD), and (c) reductive elimination (RE).26,27 The catalytic efficiency depends on the energetic span, calculated as the difference in energy between the turnover determining transition state (TDTS) and turnover determining intermediate (TDI). Through this comprehensive investigation we wish to enunciate the details of energetic span (δE) and how the inclusion of silver salt impacts the same. While we have carefully examined the role of silver salts in all the catalytic steps, such as oxidative addition, migratory insertion, etc., as applicable,20,28Scheme 2 presents only a succinct and generalized representation of the mechanism by using a monometallic Pd-species for reactions 1–4. Among the reactions considered here, the most likely mechanism for 1 and 4 involve a Pd(0)/Pd(II) catalytic cycle while a Pd(II)/Pd(IV) pathway is likely for 2 and 3. In reactions 2 and 3, oxidative addition to the second substrate is additionally involved.24 First, we have examined the catalytic activity of palladium acetate by locating the corresponding transition states, all in the absence of the silver additive (conventional pathway). Then, silver acetate or silver triflate is explicitly included in the respective transition states to see whether or not the additives impart any noticeable effect on the energetic course of the reaction.
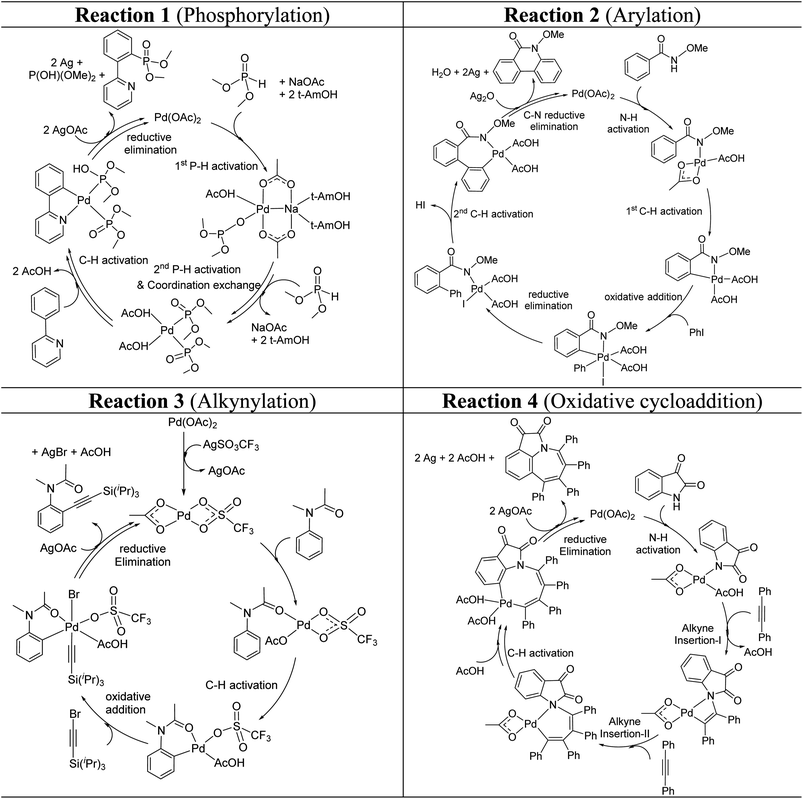 | ||
| Scheme 2 Key steps involved in the catalytic cycles for reactions 1–4, shown using a monometallic Pd species. | ||
As the silver salt can interact with different binding sites of the substrate, a rigorous sampling of different likely configurations in the transition states is performed so as to identify the most preferred pathway. The discussion in this manuscript thus employs only the lowest energy transition states and the corresponding intermediates. During the course of geometry optimization, performed as part of the configuration sampling, we noticed a systematic tendency of the silver atom to remain closer to palladium across all these reaction types (1–4). Further sampling of the lower energy transition states helped us identify an interesting Pd–Ag heterobimetallic interaction, as shown using a generalized representation in Fig. 1. Although the catalytic attributes of d8–d10 heterobimetallic complexes have only been rarely documented,29 the crystal structures of related compounds have been reported earlier.30,31 Interestingly, the number of attempts on the use of pre-designed heterobimetallic homogeneous catalysts has been on a steady increase in recent years.32–35 In such heterobimetallic systems, the intermetallic interaction is generally exploited for fine-tuning the catalytic attributes. However, the influence of metal salt additives in the catalytic cycle through intermetallic interaction is seldom documented. The energetic comparison between the conventional and the refined transition states with Pd–Ag heterobimetallic interaction is presented in the following sections.
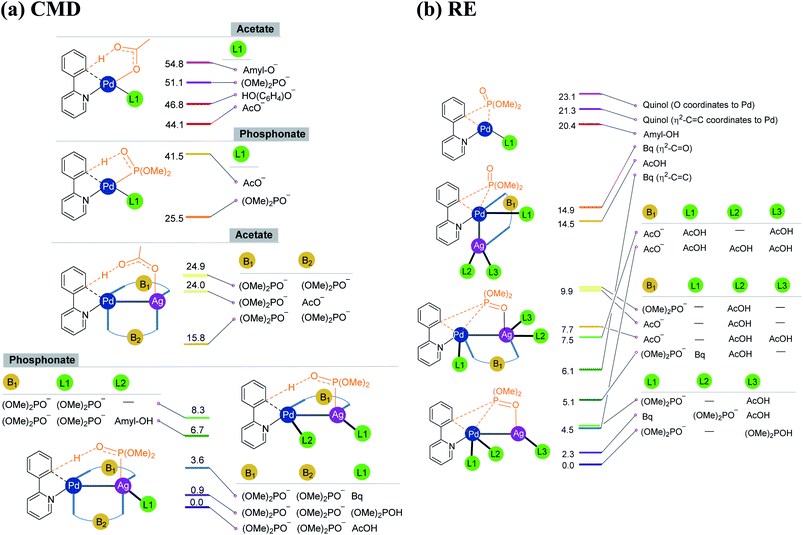 | ||
| Fig. 1 Important ligand combinations considered in the (a) CMD and (b) RE transition states in the case of the phosphorylation reaction (1). The relative energies of transition states shown in the stacking are in kcal mol−1. The CMD TSs with free energies of 24.9 and 15.8 kcal mol−1 differ in the mode of coordination of the phosphonate bridge that connects Pd and Ag (see Fig. S6.2 in the ESI†). | ||
As our study aims to shed light on the energetic details of catalytic pathways, it is prudent that such conclusions are derived on the basis of the lowest energy pathways. The details on how the most preferred transition states are identified in this study are therefore vital at this juncture. Under the reactions conditions, several ligand combinations as well as differences in the type of Pd–Ag heterobimetallic bridging ligand are likely.36 In Fig. 1, we provide a subset of such ligand combinations around the metal, chosen from a larger set of such possibilities for the phosphorylation reaction (1) as an illustrative example.37 As can be gathered from Scheme 1, the phosphorylation of 2-phenylpyridine involves the use of dialkylhydrogen phosphonate, silver acetate, and para-benzoquinone (Bq) and t-amyl alcohol as the solvent. The potential ligand exchanges that can be derived from the native palladium acetate and silver acetate, in both CMD and RE transition states, are provided in Fig. 1. The CMD transition states are grouped together on the basis of the ligand involved in the deprotonation step (Fig. 1(a)). It can be noticed that in the CMD step, bis-phosphonate is the most preferred ligand for the Pd–Ag bridge while a third phosphonate bound to Ag deprotonates the orthoaryl C–H bond. Although the function is different, phosphonate ligands are preferred in the RE step as well (Fig. 1(b)). Similarly, the presence of Pd–Ag interaction is found to be energetically beneficial for the RE transition state. It is instructive to note that homobimetallic catalytic systems were recently suggested to participate in similar catalytic reactions.38–40 However, such homobimetallic systems are found to be energetically less preferred in the case of the present examples.38
The above-mentioned analysis is based on the relative energies of the transition states computed with respect to a global reference point, i.e., the separated reactants. The most important aspect that we note here is that the inclusion of additives gives rise to reaction pathways that are evidently lower in energy than those in their absence.41 Hence, these catalytic reactions proceed through the lower energy pathway.
Fig. 2 provides a succinct and generalized representation of the most preferred ligand combinations around the metal(s) for each reaction. The important message that we wish to convey here is that the ligands involved in CMD (shown as X-O) are different for different reactions, and so are the ligands that form the intermetallic bridge. It is observed that in the conventional monometallic pathway for all the reactions, Pd-bound acetate is the preferred ligand that facilitates CMD, except in the case of the phosphorylation reaction (1), where Pd-bound phosphonate is the most preferred ligand for CMD. Another important aspect arising due to the Pd–Ag interaction is that the catalyst–substrate complexes in the case of heterobimetallic species are found to be of much lower energy than the corresponding complexes with monomeric palladium acetate.41 Such an energetic advantage can be regarded as a thermodynamic impetus toward a lower energy pathway involving the heterobimetallic Pd–Ag species. In other words, explicit participation of a silver salt in the mechanistic model provides access to a lower energy catalytic pathway that has generally remained overlooked in homogeneous palladium catalysis. Similar analyses of reactions other than phosphorylation considered in this study also revealed a similar energetic advantage for the Pd–Ag pathway (vide infra).
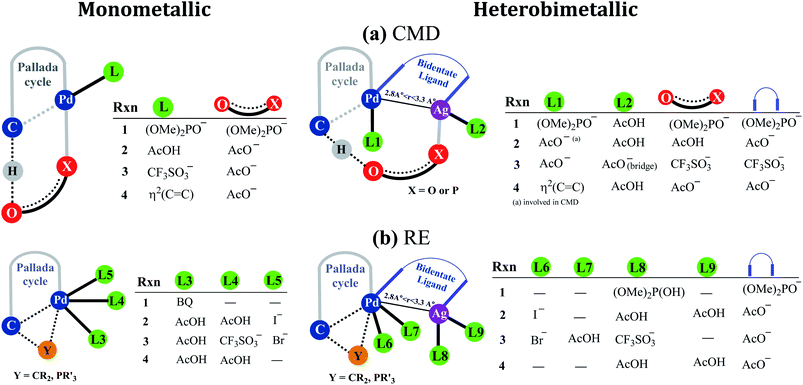 | ||
| Fig. 2 A generalized representation of (a) concerted metalation–deprotonation (CMD) and (b) reductive elimination (RE) transition states with monometallic and heterobimetallic catalysts.41 Only the most preferred ligand combinations, obtained by considering a much larger set of possibilities, are shown here. Details of various configurations considered are provided in Section 6 of the ESI.† | ||
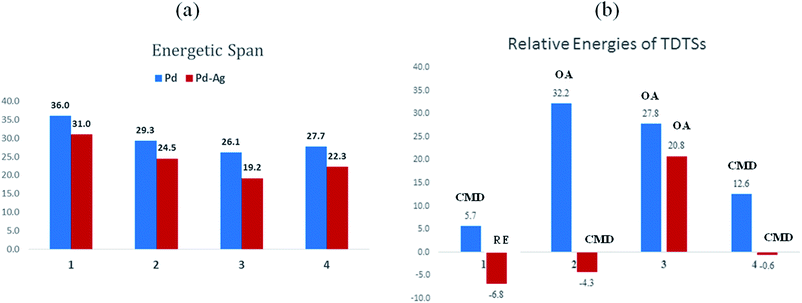
The influence of the heterobimetallic species can be better understood by assessing how the catalytic efficiency changes as compared to the monometallic pathway. One approach to do this is to compare the energetic span of the conventional monometallic pathway with that of the heterobimetallic pathway. As the first step toward this, we have investigated the full catalytic pathway, all the way from the reactants to the final product, and constructed the corresponding Gibbs free energy profiles. While the Gibbs free energy profile for a representative case (reaction 1) is shown in Fig. 3, similar analysis of the other reactions is provided in the ESI.†42 For phosphorylation (1), the C–H activation and the reductive elimination steps are the TDTSs, respectively, in the Pd and Pd–Ag pathways. Full knowledge of the reaction energy profile is found to be highly desirable to afford a comprehensive assessment of the role of silver salts. The nature of the catalytic step that contributes to the energetic span is identified to be different for different reactions as well as in a given reaction with and without the explicit inclusion of a silver salt. The most noticeable impacts arising due to the inclusion of the silver salt are (a) the involvement of lower energy transition states and intermediates, (b) improved catalytic efficiency as predicted using the lower energetic span (δE),43 and (c) lower activation barriers for the important elementary steps such as C–H activation, reductive elimination, and oxidative addition.
The most relevant question at this point is whether the key transition states gain any energetic advantages through the heterobimetallic interaction. To bring out this aspect more clearly, a comparison between the conventional monometallic and the refined heterobimetallic pathways is presented by using a graphical summary of the (a) energetic span and (b) relative energies of the TDTS in the catalytic cycles in Fig. 4. It can be observed that the presence of Pd–Ag interaction generally leads to lower energy TDTSs compared to the monometallic analogues. Depending on the nature of the reaction, the extent of lowering of δE is also different. Further, the relative energies of the TDTS, as given in Fig. 4(b), shed light on which catalytic step is likely to control the efficiency of the reaction and how the identity of the TDTS differs between the monometallic and heterobimetallic pathways.
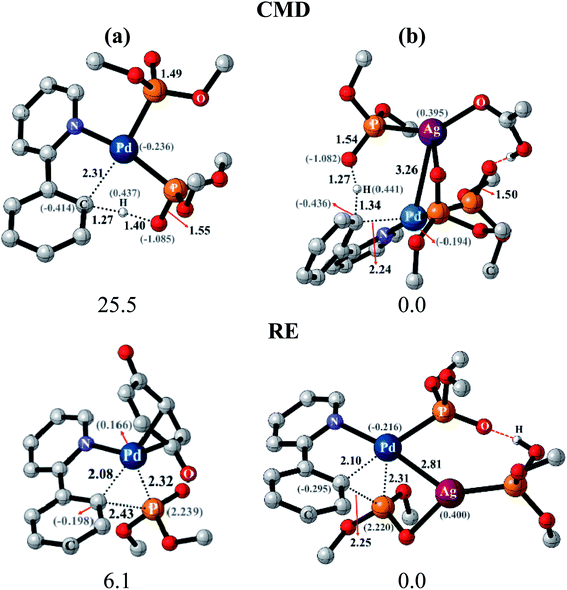
After identifying the most preferred set of transition states, we became more interested in rationalizing the predicted trends. In an effort to identify the origin of the transition state stabilization with the Pd–Ag bimetallic species, the structural and electronic features are analyzed. Succinct details of the aryl phosphorylation (reaction-1), chosen as the representative reaction, are provided in Fig. 5. The comparison of the transition state geometries between the monometallic and the heterobimetallic pathways for the CMD step points to a diminished strain in the latter. This is presumably due to the fact that a distant silver-bound ligand facilitates CMD in the heterobimetallic transition state, whereas in the mono-metallic analogue a proximal palladium-bound ligand is the one that is responsible for CMD through a relatively more strained transition state.44
The comparison of the electronic features between these two major modes of CMD and RE transition states offered additional insights. We notice that the hydrogen of the C–H bond that is being activated in the CMD step in the heterobimetallic case acquires a more protic character as compared to the corresponding monometallic counterpart. In the case of the RE transition states, the charges on the complementary pairs of atoms involved in the reductive elimination, i.e., the aryl carbon and the phosphorous of the phosphonate group, exhibited a larger difference in the heterobimetallic transition state as compared to the monometallic analogue.45 The nucleophilic aryl carbon in the Pd–Ag transition state exhibited an enhanced charge than in the monometallic case. Additionally, the aryl carbon tends to be more nucleophilic in both CMD and RE TSs in the heterobimetallic pathway (Fig. 5). Enhanced electron delocalization between the Pd–Ag bridge, the phosphorous and the aryl carbon is also identified in the heterobimetallic systems as compared to that in the monometallic case.44 Similar features are also noted for other reactions as detailed in Section 8 of the ESI.†
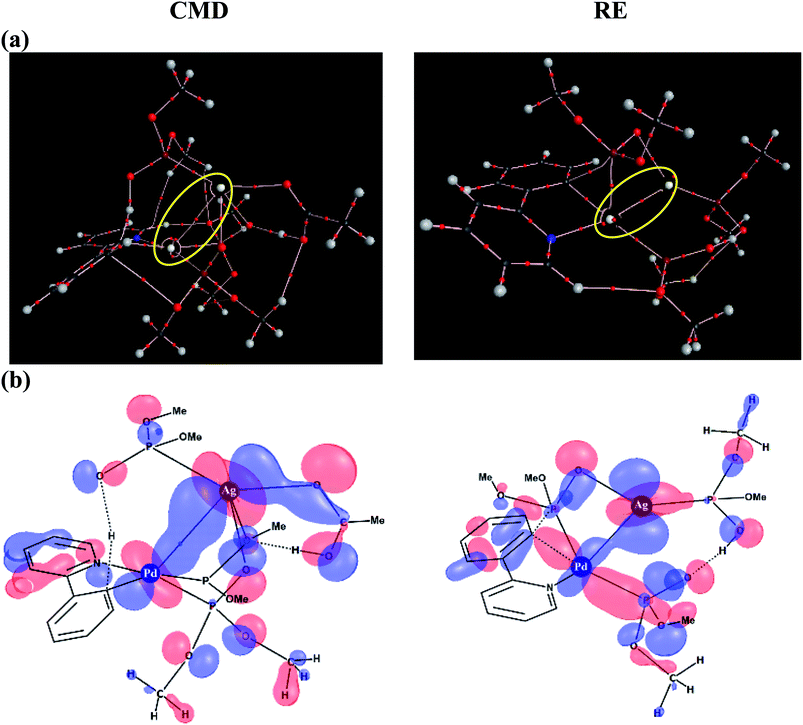
To delve further into the Pd–Ag interaction, topological analysis of the electron density using Bader's theory of Atoms-In-Molecules (AIM) has been performed, which identified a bond critical point, suggesting the presence of an intermetallic interaction. The Pd–Ag bond critical points, as shown in Fig. 6(a), exhibit electron densities (ρ) in the range of 1.59 to 3.55 (×10−2 a.u.), which are comparable to those of other known weak interactions.46,47
Similarly, an important Kohn–Sham molecular orbital that corresponds to the primary interaction between the Pd and Ag atoms is provided in Fig. 6(b). In both the CMD and RE transition states, a favorable bonding interaction between the d-orbitals of Pd and Ag is noticed. In the CMD transition state, dxy/dx2−y2(Pd) interacts with dxz/dx2−y2(Ag) whereas in the RE transition state dx2−y2(Pd) interacts with dyz(Ag).48 Thus, the presence of electronic communication between the metal centers is conspicuous in the Pd–Ag heterobimetallic transition states. Subtle differences in the electron population facilitated by such intermetallic interaction and the consequent lowering of the energies of the critical transition states are a valuable molecular insight. Further analysis using natural bond orbitals indicates relatively lower d-electron occupancy on Pd in the case of the CMD transition state with the Pd–Ag interaction as compared to that in the mono-metallic system.46–48 The cumulative effect of Pd–Ag interaction, as presented above, can offer access to a lower energy pathway and is thus expected to play a pivotal role in a broader class of single-site catalytic reactions centered on palladium. More importantly, the findings reported herein clearly suggest the need for considering the molecular participation of additives toward identifying the most preferred mechanistic pathway in a catalytic reaction.
Conclusions
Through this study, we have examined the molecular role of ubiquitous silver salt additives in four diverse sets of palladium-catalyzed C–H activation reactions. We have identified an important molecular interaction between the catalyst and the silver salt additive in the critical transition states for palladium acetate catalyzed sp2-aryl C–H bond activation reactions. Intermediates and transition states with the intermetallic Pd–Ag interaction are found to be energetically lower as compared to those of the conventional monometallic analogue suggesting that silver salts are likely to be involved throughout the catalytic cycle, and not just as terminal oxidants. The diminished strain and enhanced protic character of the C–H proton help stabilize the concerted metalation–deprotonation transition states. The improved electronic communication between Pd and Ag is identified to be responsible for a relatively more favorable reductive elimination via the heterobimetallic transition states. We learned that the knowledge of the full mechanistic cycle is necessary toward establishing the role of the silver salts, as the energetic impact of silver salts is not the same in different steps of the mechanism. The energetic span for the heterobimetallic pathway is noticeably lower than that for the monometallic pathway, evidently conveying that the explicit inclusion of silver salt additives is required for identifying the most preferred catalytic pathway. The molecular insights obtained through a set of four diverse sets of Pd-catalyzed C–H activation reactions, operating under a range of solvent polarities, reaction conditions, and different silver salts, all convey the involvement of an intermetallic Pd–Ag interaction. The findings are therefore expected to have a broader and general applicability in homogeneous transition metal catalysis.Conflicts of interest
There are no conflicts to declare.Acknowledgements
B. B. acknowledges a senior research fellowship from the University Grants Commission (UGC, New Delhi). We appreciate the SpaceTime supercomputing resource at IIT Bombay for the generous computing time. M. A. and H. F. S. acknowledge the National Science Foundation Grant CHE-1661604.References
- E. M. Simmons and J. F. Hartwig, Nature, 2012, 483, 70–73 CrossRef CAS.
- J. F. Hartwig, J. Am. Chem. Soc., 2016, 138, 2–24 CrossRef CAS.
- L. Yang and H. Huang, Chem. Rev., 2015, 115, 3468–3517 CrossRef CAS.
- M. P. Paudyal, A. M. Adebesin, S. R. Burt, D. H. Ess, Z. Ma, L. Kürti and J. R. Falck, Science, 2016, 353, 1144–1147 CrossRef CAS.
- S. Z. Tasker, E. A. Standley and T. F. Jamison, Nature, 2014, 509, 299–309 CrossRef CAS.
- P. Gandeepan, T. Müller, D. Zell, G. Cera, S. Warratz and L. Ackermann, Chem. Rev., 2019, 119, 2192–2452 CrossRef CAS PubMed.
- X. S. Xue, P. Ji, B. Zhou and J. P. Cheng, Chem. Rev., 2017, 117, 8622–8648 CrossRef CAS.
- J. L. Lee and C. K. Luscombe, ACS Macro Lett., 2018, 7, 767–771 CrossRef CAS.
- L. Ping, D. S. Chung, J. Bouffard and S. Lee, Chem. Soc. Rev., 2017, 46, 4299–4328 RSC.
- A. H. Cherney, N. T. Kadunce and S. E. Reisman, Chem. Rev., 2015, 115, 9587–9652 CrossRef CAS.
- C. G. Newton, S. G. Wang, C. C. Oliveira and N. Cramer, Chem. Rev., 2017, 117, 8908–8976 CrossRef CAS.
- J. He, M. Wasa, K. S. L. Chan, Q. Shao and J.-Q. Yu, Chem. Rev., 2017, 117, 8754–8786 CrossRef CAS.
- N. Decharin and S. S. Stahl, J. Am. Chem. Soc., 2011, 133, 5732–5735 CrossRef CAS PubMed.
- Z. K. Wickens, P. E. Guzmán and R. H. Grubbs, Angew. Chem., Int. Ed., 2015, 54, 236–240 CrossRef CAS.
- J. B. Gary, A. K. Cook and M. S. Sanford, ACS Catal., 2013, 3, 700–703 CrossRef CAS.
- D. C. Fabry and M. Rueping, Acc. Chem. Res., 2016, 49, 1969–1979 CrossRef CAS.
- J. L. Bras and J. Muzart, Chem. Rev., 2011, 111, 1170–1214 CrossRef.
- C. Colletto, A. Panigrahi, J. F. Casado and I. Larrosa, J. Am. Chem. Soc., 2018, 140, 9638–9643 CrossRef CAS.
- J. Kim and S. H. Hong, ACS Catal., 2017, 7, 3336–3343 CrossRef CAS.
- Y. –F. Yang, G. –J. Cheng, P. Liu, D. Leow, T. –Y. Sun, P. Chen, X. Zhang, J.-Q. Yu, Y.-D. Wu and K. N. Houk, J. Am. Chem. Soc., 2014, 136, 344–355 CrossRef CAS PubMed.
- K. D. Vogiatzis, M. V. Polynski, J. K. Kirkland, J. Townsend, A. Hashemi, C. Liu and E. A. Pidko, Chem. Rev., 2018, 119, 2453–2523 CrossRef.
- T. Sperger, I. A. Sanhueza and F. Schoenebeck, Acc. Chem. Res., 2016, 49, 1311–1319 CrossRef CAS.
- For additional details on computational methods, see Section 1 in the ESI.†.
- (a) C.-G. Feng, M. Ye, K.-J. Xiao, S. Li and J.-Q. Yu, J. Am. Chem. Soc., 2013, 135, 9322–9325 CrossRef CAS; (b) G.-W. Wang, T.-T. Yuan and D.-D. Li, Angew. Chem., Int. Ed., 2011, 50, 1380–1383 CrossRef CAS; (c) M. Tobisu, Y. Ano and N. Chatani, Org. Lett., 2009, 11, 3250–3252 CrossRef CAS; (d) L. Wang, J. Huang, S. Peng, H. Liu, X. Jiang and J. Wang, Angew. Chem., Int. Ed., 2013, 52, 1768–1772 CrossRef CAS; (e) For additional details on the reaction conditions and the mechanisms, see Section 2 in the ESI.†.
- See Section 3 in the ESI† for more details.
- A. P. Smalley and M. J. Gaunt, J. Am. Chem. Soc., 2015, 137, 10632–10641 CrossRef CAS.
- Y. Dang, S. Qu, J. W. Nelson, H. D. Pham, Z. –X. Wang and X. Wang, J. Am. Chem. Soc., 2015, 137, 2006–2014 CrossRef CAS.
- A. Gille and J. K. Stille, J. Am. Chem. Soc., 1980, 102, 4933–4941 CrossRef.
- M. Anand, R. B. Sunoj and H. F. Schaefer III, J. Am. Chem. Soc., 2014, 136, 5535–5538 CrossRef CAS PubMed.
- P. Braunstein, C. Frison, N. Oberbeckmann-Winter, X. Morise, A. Messaoudi, M. Benard, M. M. Rohmer and R. Welter, Angew. Chem., Int. Ed., 2004, 43, 6120–6125 CrossRef CAS.
- N. Y. Kozitsyna, S. E. Nefedov, A. P. Klyagina, A. A. Markov, Z. V. Dobrokhotova, Y. A. Velikodny, D. I. Kochubey, T. S. Zyubina, A. E. Gekhman, M. N. Vargaftik and I. I. Moiseev, Inorg. Chim. Acta, 2011, 370, 382–387 CrossRef CAS.
- K. L. Bay, Y.-F. Yang and K. N. Houk, J. Organomet. Chem., 2018, 864, 19–25 CrossRef CAS.
- J. P. McInnis, M. Delferro and T. J. Marks, Acc. Chem. Res., 2014, 47, 2545–2557 CrossRef CAS.
- P. Buchwalter, J. Rosé and P. Braunstein, Chem. Rev., 2015, 115, 28–126 CrossRef CAS PubMed.
- D. Whitaker, J. Bures and I. Larrosa, J. Am. Chem. Soc., 2016, 138, 8384–8387 CrossRef CAS PubMed.
- G. Jindal and R. B. Sunoj, J. Am. Chem. Soc., 2014, 136, 15998–16008 CrossRef CAS.
- Similar details pertaining to the other reactions are provided in Section 6 in the ESI.†.
- M. Aufiero, T. Sperger, A. S.-K. Tsang and F. Schoenebeck, Angew. Chem., Int. Ed., 2015, 54, 10322–10326 CrossRef CAS.
- G. Yin, I. Kalvet and F. Schoenebeck, Angew. Chem., Int. Ed., 2015, 54, 6809–6813 CrossRef CAS.
- M. D. Lotz, N. M. Camasso, A. J. Canty and M. S. Sanford, Organometallics, 2017, 36, 165–171 CrossRef CAS.
- See Section 5 in the ESI.†.
- See Section 4 in the ESI.†.
- The energetic span (δE) is calculated using δE = TDTS − TDI if the TDTS appears after the TDI or δE = TDTS − TDI + ΔGr if the TDTS appears before the TDI (where ΔGr is the Gibbs free energy of the reaction). For details see: S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101–110 CrossRef CAS.
- See Section 7 in the ESI.†.
- See Section 8 in the ESI.†.
- L.-C. Wu, C.-W. Hsu, Y.-C. Chuang, G.-H. Lee, Y.-C. Tsai and Y. Wang, J. Phys. Chem. A, 2011, 115, 12602–12615 CrossRef CAS.
- See Section 9 in the ESI† for details of AIM analysis.
- See Section 10 in the ESI.†.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc04540f |
| This journal is © The Royal Society of Chemistry 2020 |