Open Access Article
Open Access ArticleStudent discourse networks and instructor facilitation in process oriented guided inquiry physical chemistry classes†
Dilhara
Liyanage
 a,
Stanley M.
Lo
a,
Stanley M.
Lo
 b and
Sally S.
Hunnicutt
b and
Sally S.
Hunnicutt
 *a
*a
aVirginia Commonwealth University, Department of Chemistry, Richmond, VA 23284, USA. E-mail: sshunnic@vcu.edu
bUniversity of California San Diego, Section of Cell and Developmental Biology, Division of Biological Sciences and Program in Mathematics and Science Education, La Jolla, CA 92093, USA
First published on 10th September 2020
Abstract
A novel methodology has been developed to capture student interactions and engagement modes by mapping their discourse in Process Oriented Guided Inquiry Learning (POGIL) physical chemistry courses using graph theory and a modified ICAP (Interactive, Constructive, Active, Passive) framework. This work provides a deeply contextualized description of student teamwork in a POGIL setting with triangulation of data from talk-turn tracking and coding of student engagement. Graphs of student discussions in teams were constructed for 17 students in five teams in two courses taught by different instructors. Combined with the modified ICAP framework, our data illustrate the amount, extent, and quality of discussion along with students’ cognitive engagement. Specific facilitation strategies used by instructors appear to correlate with improved student discussion and interactivity. Such strategies include providing responsive versus prepared lectures and requiring students to publicly share their thinking.
Introduction
Traditional, lecture-based courses are not explicitly structured to encourage students to think about learning the material in real time or to promote student–student or student–instructor interactions. In contrast, students in an active-learning course process new concepts and communicate directly with peers while the instructor facilitates their learning (Farrell et al., 1999; Deslauriers et al., 2019). Classic learning theories focus on learning individually: the role of the instructor, development of a student's knowledge progressively, and a student's pre-existing knowledge. For example, Vygotsky emphasized the importance of guiding students when solving problems that are beyond their current abilities, highlighting the role of the instructor in the learning process (Vygotskiĭ and Kozulin, 1986). Piaget described the human development of intellectual abilities through four levels, sensory-motor, pre-operational, concrete operational, and formal operational, where each built upon the other (Herron, 1975), and Ausubel explained that learning is influenced by what students already know (Ausubel, 1963). However, Vygotsky also posits that person-to-person interactions are the origin of all cognitive functions and that learning occurs primarily on social level and secondarily on individual level (Vygotskiĭ, 1978). Thus, studying the interactions of students is important in education research, especially in active-learning courses where students must work in teams. More investigation of student interactions could provide insights into the relation of class discussion to overall performance and cognitive development (Mercer, 2004; Walker and Sampson, 2013).Research in post-secondary physical chemistry education in student-centered learning environments has focused on discourse analysis (Moon et al., 2017), student argumentation (Moon et al., 2016), and the role of the instructor (Becker et al., 2015; Stanford et al., 2016). Here, we develop a methodology to visualize and examine student interactions in POGIL physical chemistry courses using graph theory and a modified ICAP framework. In addition, we examine the divergence in student interactions due to instructor interventions to highlight effective facilitation strategies that may improve the productivity of collaborative learning in POGIL.
POGIL is an evidence-based, student-centered, active-learning pedagogy (Moog and Spencer, 2008). Students learn collaboratively in teams, and students’ interactions are a critical component of a POGIL course (Simonson, 2019). These interactions may vary depending on factors such as the students’ previous classroom experiences, interpersonal skills, and the instructor's facilitation methods (Forrest and Miller, 2003; Hillyard et al., 2010; Moon et al., 2017). Investigating student interactions within teams provides information related to the learning environment, student performance in the course, and the efficacy of instructor facilitation strategies.
Network analysis is a tool used to qualitatively and quantitatively analyze relationships within social structures (Wasserman and Faust, 1994). Network analysis uses mathematical graph theory to characterize affiliations between subjects or students within a team. Student teams in a POGIL course are social units or “networks” that can be analyzed using graph theory. The boundary of the graph is established by the students involved in the discussion. Using graph theory, discourse networks can be defined based on students in their teams and their relationships built through verbal communication (Wagner and González-Howard, 2018). Individual students are nodes (or vertices), and the relationships among the individuals are edges (or ties). Together, the nodes and edges form a graph, or network, allowing us to investigate characteristics of relationships and interactions (Wasserman and Faust, 1994; Wagner and González-Howard, 2018; Chai et al., 2019).
In addition to oral communication, students in a POGIL course engage in listening, reading, writing, and reflecting. Different modes of student behaviors in cognitive engagement have been categorized and linked to learning outcomes using the ICAP framework. In this framework, the levels of cognitive engagement range, in increasing order, from passive (P), to active (A), to constructive (C), to interactive (I) (Chi and Wylie, 2014). As students engage more with learning material and with their peers, their conceptual knowledge increases (Singer and Smith, 2013; Chi and Wylie, 2014; Chi et al., 2018).
The learning activities in a POGIL course vary during a single class meeting and from class to class (Hunnicutt and Ruder, 2008; Simonson, 2019). An instructor may choose to do some or all of the following: team quizzes, team-led learning-cycle activities, direct team-facilitator interactions, and various types of whole-class reporting out such as personal responder (“clicker”) questions, whole-class discussion, or team presentations on small white boards. Most instructors also spend some time in class to present a traditional lecture. The instructor's choices have been shown to affect students’ interactions and communication within their teams (Chase et al., 2013; Becker et al., 2015; Daubenmire et al., 2015; Stanford et al., 2016).
In this research study, we use graph theory to map the discourse networks of student discussions and the ICAP framework to examine the modes of student engagement – intellectual and otherwise – to gain a deeper understanding of students’ interactions in two POGIL physical chemistry courses. When graph theory is combined with the ICAP framework, we visualize simultaneously students’ social interactions, behavior, engagement modes, and collaborative discussions as these are influenced by the instructor's facilitation interventions, thus triangulating multiple data sources to examine learning and teaching (Lo and Mendez, 2019). Prior research shows that active learning is positively correlated with improved student learning outcomes and that teaching using POGIL has positive effects (Theobald et al., 2017; Walker and Warfa, 2017; Chi et al., 2018; Deslauriers et al., 2019; Lo and Mendez, 2019). However, implementing active-learning pedagogies in large classrooms with fixed seating arrangement is challenging for faculty (Shadle et al., 2017; Stains et al., 2018). Relatively few chemistry education research (CER) studies and discipline-based education research (DBER) studies in science, technology, engineering, and mathematics (STEM) focus on developing student-centered methodologies to understand instructor facilitation. Thus, rather than examining efficacy, the goal of this study is to advance a methodology to describe interactions and engagement behaviors of students that may not be evident to the instructor in POGIL classes in real time, leading to the following research questions.
Research questions
1. What can we learn by applying graph theory and the ICAP framework to study small-group interactions monitored in real time in a POGIL physical chemistry classroom?2. What, if any, patterns in teamwork emerge from combining graph theory and the ICAP framework?
Theoretical framework
Our research questions focus on student talk in the classroom. Both Piaget and Vygotsky considered learners’ discussion critical to development (Tudge and Winterhoff, 1993). Piaget theorized that peers’ interactions motivate learners to move through their learning stages. Vygotsky emphasized the individual learners’ mutual social interactions. These theories together emphasize the dialogic processes of learning (Mercer and Howe, 2012) and motivated the combination of ICAP with graph theory as a way to capture students’ peer-to-peer discussion in the classroom. ICAP affords a framework for the quality of the discussion, and graph theory objectively captures the whole team's interactivity. ICAP and graph theory are described in more detail next.ICAP: a theory of active learning
Some student behaviors with an assigned ICAP level are presented in Table 1 (Chi, 2009; Chi and Wylie, 2014). Students are Interactive when they are involved in comprehensive back-and-forth discussions that include justifying statements and questions. Students are Constructive when they express themselves by reflecting, comparing, or contrasting concepts. Students are Active when they are rephrasing, writing, and reading. Students are Passive when they are listening without writing or talking about classroom routines. Students at the Interactive level learn material at the deepest level by making or defending arguments and promote learning of other team members. Students at the Constructive level make simple explanations; students at the Active level read and write or ask simple questions. At the Passive level, individual student learning is expected to be minimal (Chi, 2009; Chi and Wylie, 2014; Chi et al., 2018).In our data set, we found that we needed to add an additional level, Disruptive or “D”, which represents off-topic or distracting discussions such as “they did put it online and it's really funny, you should watch it” or “put D bro. I’ve never let you wrong about life”. Each student is assigned to an ICAPD level according to their predominant engagement behavior.
Graph theory and discourse networks
Analyzing discourse networks can provide insights into the influence of student interactions on learning (Wagner and González-Howard, 2018). In a POGIL classroom, social interactions are a vital part of successful learning experiences, and therefore, discourse networks are an important feature to examine. Graph theory investigates questions involving relational data. When applied to discourse networks, it is used to study the factors that contribute to the generation and significance of connections among nodes (or students in this study) as well as the interventions that regulate these connections. One example of this methodology applied to a STEM college course collected student-reported interactions via a weekly administered survey in a physics course and showed an association between student performance and their position in the network during in-class social interactions (Bruun and Brewe, 2013).Another study adapted graph theory mathematics to examine the dynamics of small-group discussions in peer-led problem-solving sessions in post-secondary biological sciences (Chai et al., 2019). In this study, the trajectory of talk-turns among the team members for teams of five to seven students was analyzed to create discourse networks. Case studies of student discussions uncovered three distinct patterns: centralized sessions dominated by the peer facilitator; decentralized sessions with nearly equal participation from all students; and sessions with sub-groups hidden in the whole team. The talk-turn analysis is particularly well-suited for POGIL classrooms where students discuss course content in teams. We adapted this graph theory methodology to visualize the in-class student discourse within teams who are learning physical chemistry concepts.
Methods
Participants and setting
Students from two second-semester physical chemistry courses at a diverse, large, urban research university participated in this study. The course covered concepts from the POGIL physical chemistry text, Quantum Chemistry and Spectroscopy: A Guided Inquiry (Shepherd and Grushow, 2013). The same text and homework were used for both courses. Each course had a different instructor. Course I was offered in the fall semester, and the instructor is a trained, experienced POGIL practitioner. Course II was offered in the spring semester by a different instructor, who has implemented POGIL but not attended a workshop.Both courses (all days observed) began with a clicker question reviewing earlier content. The instructor in Course I facilitated whole-class discussions requiring students to give answers aloud, gave “just-in-time” mini-lectures when students seemed to be struggling to understand concepts or when a new topic was introduced, and called on each team to report out by displaying answers to questions on a small white board. This instructor interacted with teams by checking answers and pointing out mistakes, asking “Do you all agree with this answer?” or “Did you discuss the answer with others?”. The instructor in Course II assigned a ten-minute clicker question that students, working in teams, were expected to answer after completing a defined set of activity questions. The instructor and two teaching assistants directly answered students’ questions. Before class, a skeleton set of slides was made available to students; after class, the slides with all answers were made available.
The team members were pre-assigned to teams by the instructors according to the students’ GPAs at the beginning of the semester. This was done to ensure at least one student in each team was familiar with the mathematical tools used in physical chemistry. Each student was assigned one of four roles: (1) manager – directs team, (2) presenter – writes the team's answers on the white board when prompted, (3) reflector – completes and turn in the day's closure document, and (4) researcher – looks up pre-requisite knowledge, equations, and/or constants. Students rotated roles for each class. Neither instructor enforced student roles.
All students enrolled in the physical chemistry courses (41 students in Course I and 88 students in Course II) were invited to participate in the study during the second week of the course, and teams with all students who consented to participate in the study were recorded using a camera and a voice recorder. Both courses were held in medium-sized lecture halls. One contained tiered seating with fixed seats (Course I), and one had tiered seats that can be rotated (Course II). Each class session was taught twice weekly in 75 minute periods.
Data collection
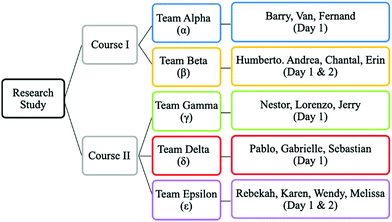
Institutional Review Board (IRB) approval for this research study was received from Virginia Commonwealth University (HM20013769). Audio and video recordings were collected for student discussion in two POGIL physical chemistry courses. A separate camera and audio recorder were used for each team. Student discussions were recorded for the entire class period and transcribed verbatim. Conversations from other groups were discernible from multiple devices, and we used this to verify the transcriptions. Recordings from different times during the semester were transcribed for the teams from Course I and II. This is because not all team members were present in each class meeting. Specific classes were also cancelled due to inclement weather. Some recordings could not be reliably transcribed due to technical difficulties such as when neighboring teams were too loud. The recordings transcribed and presented here are a representative sample of the class meetings recorded.Seven transcripts from five teams (Teams Alpha through Epsilon) in two courses (Course I, in the second week of the course, and Course II, mid-semester) (Fig. 1) were analyzed. The students in each team sat in a row. Fig. 1 summarizes the teams according to their seating order from left to right. For Course I, two team (Alpha and Beta) recordings were transcribed for the second week of class (Day 1), and one team (Beta) recording was transcribed on a second class day (Day 2) in the same week. For Course II, three team (Gamma, Delta, and Epsilon) recordings were transcribed for the ninth week of class (Day 1), and one team (Epsilon) was recorded in the 15th week of class (Day 2). The labeling is summarized in Fig. 1. The student names are pseudonyms. By random sampling, Teams Alpha and Gamma included all male, Team Epsilon all female, and Teams Beta and Delta a mix of female and male students.
Data analysis
Graphs showing the sequence of student talk-turns were generated from the transcripts. Each team discussion is represented by a graph of their discourse network, and the students are the nodes (or vertices) of the graph. An edge (or tie) between two students is generated every time two students speak in succession, which we define as a talk-turn; the edge is directed, pointing from the first to the second speaker. Fig. 2 describes a hypothetical trajectory of talk-turns in detail. The students’ talk-turn behavior was determined from class transcripts, and the resulting graphs were generated for episodes using the yEd graph editor (yEd Graph Editor). The nodes are arranged left to right in the figures according to the students’ seating order in class.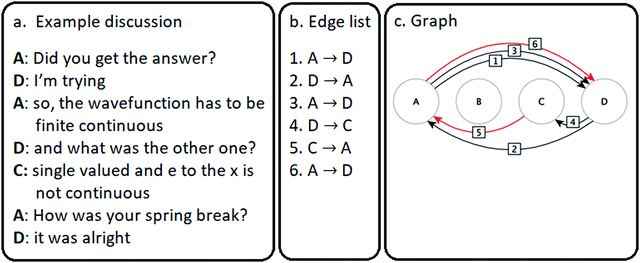 | ||
| Fig. 2 Graph construction from a discussion. The transcript of a sample discussion (a) is converted to a list of edges (b), and the edge list is used to construct a discourse network graph (c). | ||
The boundaries for each graph in our study are defined by the time periods, or episodes, during which student teams discuss a POGIL activity. An episode begins when the instructor tells the class to work in their teams on specific questions within an activity. An episode ends when the instructor stops the entire class to jointly discuss the material or to deliver a lecture or when the instructor directly interacts with a team. Thus, an episode is a time period in which, in a sense, the students control their interactive behaviors in a team-based setting. The teams are set up by the instructor, and each team has three or four students. In addition to the assigned teams, a graph may include students from neighboring teams, depending on the flow of discourse during a team activity. The nodes are thus based on the assigned teams (even if the students did not talk during an episode) and additional students who participated in discussion (even if the students were from a different team).
Fig. 2 illustrates how graphs are constructed using a hypothetical student discussion. The transcribed student discussion (Fig. 2a) is used to determine the students’ order of speaking and converted to an edge list (Fig. 2b). Each edge represents a talk-turn and is depicted as a directed arrow pointing from the student who has just spoken to the student who then speaks next. Therefore, an edge may represent how the discussion turns from one participant to another, who is willing to speak after others (whether with relevant or irrelevant information), and/or who contributes ideas that could be expanded upon or responded to. However, an edge does not trace if a student is speaking directly to another student or if a specific student is listening to the prior speaker. In fact, when one student speaks, everyone in the team could be listening. Using graph theory to model such listening behaviors instead of talk-turns would result in identical graphs completely saturated with edges for every episode.
The edge lists are imported to yEd to generate a network or graph (Fig. 2c). In the graph, the nodes (circles) represent the students in the team, and the edges (arrows) represent talk-turns. Thus, student A, then student D, and then student A speaking in turn is shown by arrows 1 and 2 (Fig. 2c). Student B does not engage in any discussion but is shown in the graph as a node without connected arrows because they are still in the team. Furthermore, black arrows represent productive, on-topic talk-turns relevant to the POGIL activity (e.g. “the wave function has to be finite continuous”), and red arrows represent off-topic talk-turns (e.g. “how was your spring break?”). In this sample discussion, the last two talk-turns are off-topic and represented by the red arrows labeled 5 and 6.
Graphs were generated for each of the episodes in all the class periods, and each graph is characterized by four measures: total edge frequency, on-topic edge frequency, reciprocity, and centralization. Here, we describe each parameter and then highlight some connections among these parameters, and we note special cases observed in our dataset.
Total edge frequency is a graph-level measure defined as the total number of talk-turns for each episode divided by the episode duration in minutes. Episodes that last different amounts of time may be compared by using total edge frequency rather than the raw number of talk-turns. Total edge frequency quantifies the number of times (or how much) students talk in an episode. A high total edge frequency suggests that each student who speaks does so for a short period of time and may speak in sentence fragments rather than complete sentences. Similarly, the on-topic edge frequency is the number of on-topic edges divided by the duration of the episode in minutes. A low on-topic edge frequency and high total edge frequency are correlated to low student ICAPD scores because of the larger proportion of off-topic talk.
Reciprocity (eqn (1)) is a graph-level measure of returned responses during the discussion (Wagner and González-Howard, 2018). Reciprocity, R, is calculated as
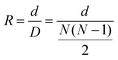 | (1) |
Centralization is a graph-level measure of the extent to which a small subset of nodes (students) dominates the graph. To calculate centralization, we first need to determine centrality for each node. Different types of centrality in graph theory are used to describe information flow among nodes in the graph. In this study, we track sequential talk-turns between pairs of students. Thus, degree centrality is the most appropriate centrality measurement because it relies only on an individual node and the number of edges directly connected to that node (Chai et al., 2019). Degree centrality for a given node is calculated as the number of edges pointing toward (in-degree centrality) and away (out-degree centrality) from that node. In Fig. 2, student D has the highest in-degree centrality, and student A has the highest out-degree centrality. Out-degree centrality is the number of times a student speaks and another student speaks next, regardless of whether that “response” is relevant (black arrows) or not (red arrows); in-degree centrality is the number of times a student responds verbally, again regardless of relevance. In some episodes, one (or more) team members never speaks. These students remain part of the graph during the episode although the non-speaking students did not generate ties to other students in that episode. Students in neighboring teams who take turns in the discussion also become part of the graph.
Centralization (eqn (2)) is the corresponding graph-level measure that describes the extent to which each node has an excess (higher) degree centrality compared to all other nodes. Centralization, C, ranges from 0 to 1 and is calculated as
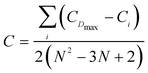 | (2) |
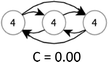
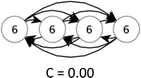
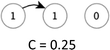
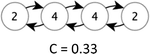
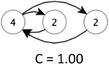
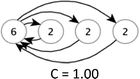
In this study, because of the size of the teams, graphs will have high centralization if one or two students take most of the talk-turns. Table 2 illustrates hypothetical teams with three or four nodes having examples of low, intermediate, and high centralization. A graph's centralization is 1 when a single node dominates the discourse network, i.e. when all team members respond to only one student but not anyone else. Centralization decreases to a minimum of 0 when all nodes (or students) are involved equivalently.
Combined, high reciprocity and low centralization suggest that each student in the team contributes to the discussion. Conversely, low reciprocity and high centralization suggest that one or two students lead or possibly dominate discussion. At times, a team of four students divides into two teams of two (talk turns only occurring between students “A” and “B” and between “C” and “D”). In this case, the centralization is 0 but reciprocity is 0.5. Hypothetically, team discussion is most interactive if the reciprocity is one and the centralization is zero.
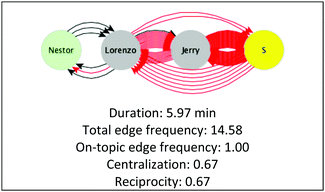
To illustrate how the graph-level measures come together and connect with the ICAPD framework, one representative graph for one episode from Course II is presented in Fig. 4. The students participated in minimal on-topic (black arrows) discussion, and they were at the Active and Disruptive levels. The node color is the most frequent level of engagement according to the student's ICAPD score (Table 1) because the episode is the unit of analysis. Yellow and blue nodes are exceptions, representing one or more students from neighboring teams or teaching assistants, respectively. The graph has a reciprocity of 0.67 and a centralization of 0.67. Jerry dominated discussion but was mostly off-topic (red arrows), and Nestor spoke little but mostly on topic.
During one of the recorded episodes, no students spoke, so there were no talk-turns. As a result, the total edge frequency, on-topic edge frequency, and reciprocity are all 0. This occurrence – when a team has zero talk-turns – demonstrates one limitation to using talk-turns as edges. The talk-turn methodology describes student teams solely by their discourse patterns. When there is no discourse, centralization is not defined. We included this episode in our data set although it has no edges because the team was defined as such by the instructor.
Results
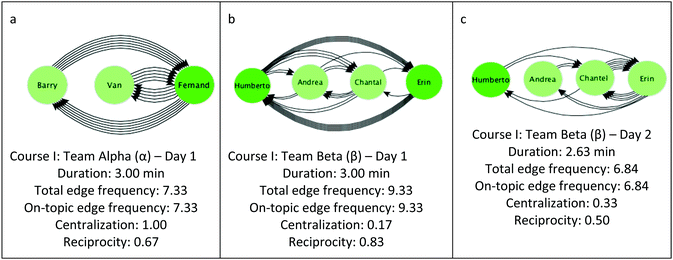
Fig. 5–7 highlight representative talk-turn graphs for Teams Alpha through Epsilon. Each graph includes the episode duration, the total edge frequency (talk-turns per minute), the on-topic edge frequency, the reciprocity, and the centralization. In the first section, we discuss each talk-turn graph in detail. In the second section, we discuss the measures for all talk-turn graphs together to illustrate patterns observed. The talk-turn graphs for all teams are included in the ESI.†Fig. 5 shows three representative talk-turn graphs for Teams Alpha and Beta (Course I) with one graph for each day recorded and transcribed. Each graph represents one episode, as defined in the Methods. The students in Teams Alpha (Day 1) and Beta (Day 1 and Day 2) participated in on-topic (black arrows) talk-turns with edge frequencies ranging from 6.84 to 9.33 talk-turns per minute, and they were primarily at the Active and Constructive levels. The episodes shown in Fig. 5 lasted about 2–3 minutes. In Team Alpha, Fernand led the discussion, and interacted with both Barry and Van; however, Barry and Van replied only to Fernand but not to each other. As a result, the talk-turn graph has a reciprocity of 0.67 (no talk-turns between Barry and Van) and a centralization score of 1.00 (talk-turns mediated through Fernand as a central node in the graph). For Team Beta (both days), Erin was engaged in the discussion with higher in- and out-degree values. On Day 1 Humberto and Erin were the most engaged in the discussion with the highest in- and out-degree values. They dominated the discussion although they were seated farthest apart, and they remained in the Constructive and Active levels for the whole episode. However, Chantel was more engaged in discussion than Humberto on Day 2. On both days Andrea was writing, reading, and likely listening but spoke rarely. As a result, team Beta's graphs for Day 1 and Day 2 have reciprocities of 0.83 and 0.50 and centralization scores of 0.17 and 0.33, respectively. We noted that as reciprocity decreases, centralization increases in these examples, although the two values are not linearly correlated.
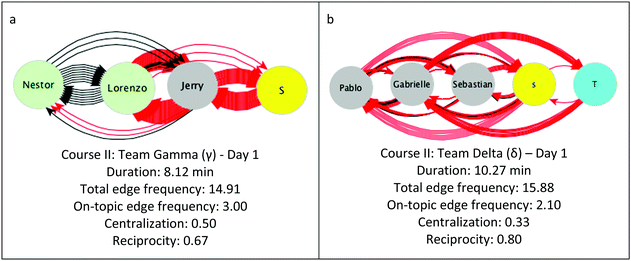
The discourse graphs and ICAPD results for Teams Gamma and Delta (Course II) are shown in Fig. 6. The episodes shown in Fig. 6 lasted about 8–10 minutes. Both teams had high edge frequencies (14.91 and 15.88 talk-turns per minute) with reciprocities of 0.67 and 0.80 and centralization scores of 0.50 and 0.33, respectively. Both teams engaged mostly in off-topic (red arrows) discussion. The students are all about equally engaged in discussion, but the primary focus of their talk-turns is not the POGIL activity. Only Nestor and Lorenzo (Team Gamma, Fig. 6a) engaged in on-topic discussion, while Jerry continually distracted his teammates and other students from neighboring teams. A student from a neighboring team (yellow node) was part of each team's graph, and a teaching assistant (blue node) was part of Team Delta's graph. Four of the six students, including all of Team Delta, remained at the Distracted level throughout this episode. While Lorenzo had some productive talk (black arrows) with Jerry, Jerry only responded with off-topic talk (red arrows) and therefore had an ICAPD score of zero (Distracted). Jerry was at the Active ICAPD level when he talked with Nestor, and Nestor was observed at the Active ICAPD level throughout this and all recorded episodes.
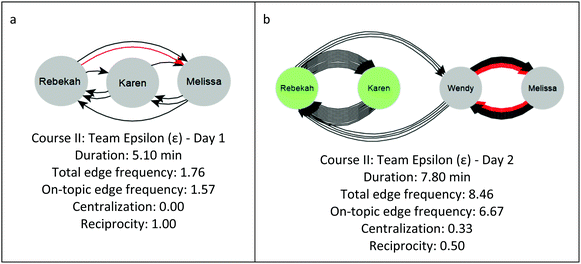
Two graphs for Team Epsilon (Course II) are shown in Fig. 7a and b. The episodes shown in Fig. 7 lasted under eight minutes. One team member was absent from class for the first day's recording (Fig. 7a), which was the same day as the graphs from Fig. 6. Team Epsilon had both on- and off-topic discussion, with edge frequencies of 1.76 and 8.46 talk-turns per minute for Day 1 and Day 2, respectively. The graphs in Fig. 7 show that Team Epsilon's behavior changed with three (Fig. 7a) versus four (Fig. 7b) team members present. With three team members, Team Epsilon's graph has a reciprocity of 1.00 (coherent discussion), but with four team members, their graph reciprocity decreases to 0.50 (split into two pairs of students engaging in parallel conversations). The centralization score stays low (0.00 and 0.33) in both cases. In two of the four episodes transcribed on Day 2 of the recording, all discussion occurred within the two pairs. In the other two episodes, discussion between the two pairs happened much less frequently than within the pairs. With three team members present, the average edge frequency over the four episodes is 5.49 talk-turns per minute; in comparison, the average edge frequency increases to 8.68 talk-turns per minute for the four episodes with all four team members present.
Fig. 8 compares the descriptive graph measures including total edge frequency (both on- and off-topic), on-topic edge frequency, centralization, reciprocity, and ICAPD scores for all teams for all transcribed episodes. All episode graphs are provided in the ESI.† The scores from the representative graphs shown in Fig. 4–7 are included in the scatter plots. We have transcribed recordings for Teams Beta and Epsilon on two days; the scores for these recordings are displayed separately (labeled Beta1, Beta2, Epsilon1, and Epsilon2) on the horizontal axis. Each horizontal axis entry represents the analyzed episodes for one team on one class day; the number of episodes ranged from four to eight and the episode lengths varied from about one to fifteen minutes. In Course I the average length of episodes was 3.55 minutes (range: 1.07–8.08 minutes), and in Course II the average episode length was 7.45 minutes (range: 1.92–15.50 minutes). The scores are displayed as scatter plots rather than as averages, so patterns of student engagement behavior during group activities (episodes) are more apparent. Moreover, considerably more recordings (multiple teams recorded on multiple days) are needed in order for averages to be statistically meaningful.
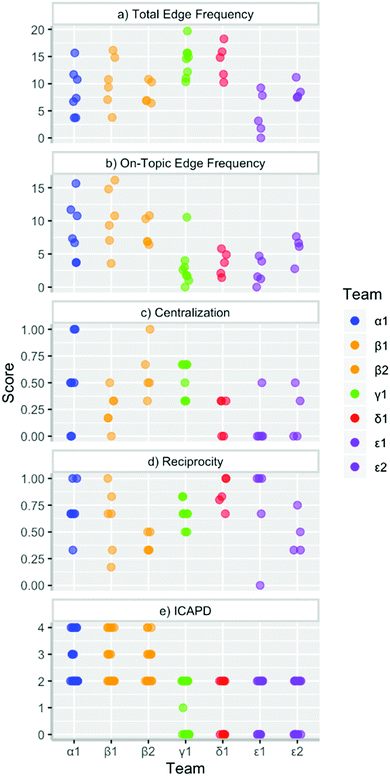 | ||
| Fig. 8 Scatterplots of graph measures: total edge frequency, on-topic edge frequency, centralization, reciprocity, and ICAPD scores for Teams Alpha (α) N = 7, Beta1 (β1) N = 6, Beta2 (β2) N = 5, gamma (γ) N = 8, delta (δ) N = 5, Epsilon1 (ε1) N = 5, and Epsilon2 (ε2) N = 4, where N is the number of episodes (total N = 40). The recorded class day is reported with the team label; for example, Alpha1 (α1) and Beta1 (β1) were recorded on the same day but Beta2 (β2) on a separate day. Teams Alpha and Beta were in Course I and Teams Gamma, Delta, and Epsilon were in Course II. The scores reported in Fig. 4–7 are included in these scatter plots. | ||
The graph measures and ICAPD scores appear to be consistent for the two teams recorded on two separate days. Team Epsilon's scores were similar for the two days although they had different team members present on each day. Their reciprocity – measuring the spread of discussion among the whole team – was slightly lower on the day when four students were in class, reflecting the team's split into two pairs. Likewise, Team Epsilon had lower edge frequencies on both days compared to the other teams, although their talk-turn rate was somewhat lower on the first versus the second day.
The teams in Course I were always on-topic (18 episodes for two teams), but the teams in Course II were mostly off-topic. Of the course discussion samples presented here (22 episodes for three teams), just two episodes were entirely on-topic, and in one of these two episodes, no student spoke. Teams Alpha and Beta (Course I) had reciprocities, centralization scores, and total edge and on-topic edge frequencies that ranged roughly from the minimum to maximum value for each network measure. The ICAPD scores for these Teams Alpha and Beta ranged from Active (2) to Interactive (4). However, Teams Gamma, Delta, and Epsilon had graph measures that were more clustered, and their ICAPD scores never went above Active (2). They have reciprocities closer to one and centralization and on-topic edge frequency scores closer to zero.
Fig. 8 thus implies the emergence of three patterns of team behaviors. We see teams in which students:
1. collaborate to answer the activity questions;
2. chat frequently, but mostly off-topic; and
3. work individually or engage in pair-wise discussion, depending on which team members are present.
Teams Alpha and Beta fall into the first category. The students’ teamwork was focused on the course, but it varied from episode to episode. Teams Gamma and Delta fall into the second category. The students in these teams had the most talk-turns, but these talk-turns were short and mostly off-topic. Team Epsilon falls into the third category. On the day when three students were present, Team Epsilon had one episode in which no students spoke and another in which there were just nine talk-turns (total edge frequency = 1.76 talk-turns per minute). Instead, the students mostly wrote in their activity books without discussion. On the day in which all members of Team Epsilon were present, the team split into two pairs, resulting in higher overall total edge frequencies but lower reciprocities. Future studies should examine how teamwork patterns change on class days when different team members are present.
Discussion
By combining graph theory and ICAPD (our modified ICAP framework), we successfully captured and visualized real-time student interactions and engagement in small groups, situated in the context of POGIL physical chemistry classrooms. In a previous study, using graph theory alone tracked only the sequential order of talk-turns by students in a small group but not the content of discussion (Chai et al., 2019). By adding the ICAPD framework, we were able to also monitor student engagement at different levels beyond simply talking, which could indicate varying levels of cognitive engagement. According to Vygotsky's social constructivism theory, students who cognitively engage in discourse begin to construct knowledge at a deeper level (Vygotskiĭ, 1978). Furthermore, interactive dialog leads to more cognitive engagement and conceptual learning (Chi, 2009; Chi and Wylie, 2014). Therefore, students who do not engage in these interactions or engage in off-topic discourse are not expected to derive the full benefits of an active-learning class.From our observations of student groups in POGIL physical chemistry classrooms, we identified three patterns, including groups that (1) collaborate to engage with the activity questions, (2) chat frequently but are mostly off-topic, or (3) mostly work individually or engage in pair-wise discussions. One possible reason for the observed engagement patterns may be the instructor's facilitation strategies; data collected from more teams over more courses are needed to definitively ascribe the patterns to the facilitation strategies. We note that the first group pattern of collaborative engagement was observed in Course I, where the instructor used a variety of evidence-based POGIL facilitation strategies: student groups reporting out on their findings either verbally or with visual displays of their work on small white boards, instructor providing “just-in-time” clarifications based on challenges that students were having with the activity, and instructor responding to student questions by requesting for reasoning instead of giving direct explanations (Simonson, 2019). These strategies were also implemented following an inquiry-based learning cycle, where students first collaboratively explore a problem before the instructor provides explanations and further elaboration on the course content (Simonson, 2019).
The second and third group patterns, in which students were either off-topic or not working collaboratively, coincided with Course II. The instructor in Course II followed a more didactic pedagogical approach, with prepared lectures as the main focus of the course supplemented by POGIL activities timed using open clicker questions. The instructor and teaching assistants also directly answered student questions by providing explanations to the content of the activity, as opposed to guiding students to use reasoning to make sense of the material, which has been shown in other active-learning contexts to likely result in the termination of student discussions (Knight et al., 2015). These strategies in Course II are less aligned with evidence-based POGIL facilitation strategies and inquiry-based learning cycles that have been shown to promote student learning (Lo and Mendez, 2019).
The mixed-method tools described here provide objective, unbiased data describing student behavior in the classroom in real time. In the future, the methodology could be used to evaluate the significance of instructional strategies in a POGIL course, answering the call for mechanistic studies (Lo and Mendez, 2019). For example, talk-turn graphs and ICAPD levels could be applied to a study of assigned roles (such as team manager or presenter) in a POGIL course. Enforcing roles may help more students take on specific tasks and responsibilities and thus promote more equitable contributions within a team. Furthermore, assigning roles may help foster interdependence in teamwork, which may be constructive or interactive and thus learn more effectively (Premo et al., 2018a; Premo et al., 2018b).
We were unable to draw definite conclusions regarding facilitation strategies and role assignment because our study is limited in the number of groups observed. However, our results are consistent with patterns described in previous studies in the existing literature, supporting the utility and validity of our methodology.
Limitations
This method, combining ICAP with graph theory, has several inherent limitations. First, we assigned a student's ICAPD level during an episode based on their most frequent engagement mode. Thus, the assignment of students into one ICAPD level for a given episode does not fully represent the student's moment to moment engagement during that episode. Second, the analysis of talk-turns does not capture who is listening, only who speaks in turn. Third, recording team discussion in the classroom was challenging. Many students were talking simultaneously because the teams were sitting close together. Last, the classroom environment is not controlled. Different instructors spent varying amounts of time lecturing in each class meeting. Teams changed during the semester as student attendance varied, as students withdrew from the course, or as students withdrew their consent to be included in the study.Conclusions
Generalizable conclusions about POGIL facilitation cannot be made because a limited number of groups was observed. However, the goal of this paper was to establish a methodology to examine student discussions in small groups by combining graph theory and ICAP. Even from the limited dataset, we were able to observe three distinct patterns of student group behaviors that correlated with different instructor facilitation strategies. Other quantitative methods already exist in the literature to analyze patterns of group discussions. For example, a computer-based method maps the content of the student group conversations (Barros and Felisa Verdejo, 2000). This previous study focused on how students contribute in a group and how such group dynamics may affect student learning. Our methodology complements this existing work by both tracking how students engage in talk-turns through graph theory and analyzing the level of cognitive engagement through our modified ICAPD framework.Our study captures and illustrates the nature of the students’ behaviors while working on POGIL activities in a physical chemistry classroom. Using graph theory and our modified ICAPD framework, we were able to quantify the dynamics of student discussion in POGIL group work and identify three potential archetypes of group behaviors: collaborative engagement, off-topic conversations, and individual or split paired work. Students’ engagement varies widely during group activities and from course to course, which suggests that the facilitation strategies used by instructors may influence and contribute to how students behave in group work. Overall, our methodology of talk-turn graphs and ICAPD scores combined together can track the dynamics of group discussions and cognitive engagement of individual students, opening up the possibilities for future studies to compare how students’ discussion varies with course content, facilitation strategies, and students’ individual personalities, attitudes, and attributes.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This material is based upon work supported by the National Science Foundation under Grant No. 1726066. We thank all the students and faculty who took part in this study.References
- Ausubel D. P., (1963), The psychology of meaningful verbal learning, New York: Grune & Stratton.
- Barros B. and Felisa Verdejo M., (2000), Analysing student interaction processes in order to improve collaboration. The DEGREE approach, Int. J. Artif. Intell. Educ., 11(3), 221–241.
- Becker N., Stanford C., Towns M., and Cole R., (2015), Translating across macroscopic, submicroscopic, and symbolic levels: the role of instructor facilitation in an inquiry-oriented physical chemistry class, Chem. Educ. Res. Pract., 16(4), 769–785.
- Borgatti S. P. and Halgin D. S., (2014), The SAGE Handbook of Social Network Analysis, SAGE.
- Bruun J. and Brewe E., (2013), Talking and learning physics: Predicting future grades from network measures and Force Concept Inventory pretest scores, Phys. Rev. ST Phys. Educ. Res., 9(2), 020109.
- Chai A., Le J. P., Lee A. S., and Lo S. M., (2019), Applying Graph Theory to Examine the Dynamics of Student Discussions in Small-Group Learning, CBE: Life Sci. Educ., 18(2), 1–12.
- Chase A., Pakhira D., and Stains M., (2013), Implementing Process-Oriented, Guided-Inquiry Learning for the First Time: Adaptations and Short-Term Impacts on Students’ Attitude and Performance, J. Chem. Educ., 90(4), 409–416.
- Chi M. T. H., (2009), Active-Constructive-Interactive: A Conceptual Framework for Differentiating Learning Activities, Top. Cogn. Sci., 1(1), 73–105.
- Chi M. T. H. and Wylie R., (2014), The ICAP Framework: Linking Cognitive Engagement to Active Learning Outcomes, Educ. Psych., 49(4), 219–243.
- Chi M. T. H., Adams J., Bogusch E. B., Bruchok C., Kang S., Lancaster M., et al., (2018), Translating the ICAP Theory of Cognitive Engagement Into Practice, Cogn. Sci., 42(6), 1777–1832.
- Daubenmire P. L., Bunce D. M., Draus C., Frazier M., Gessell A., and van Opstal M. T., (2015), During POGIL Implementation the Professor Still Makes a Difference, J. Coll. Sci. Teach., 44(5), 72–81.
- Deslauriers L., McCarty L. S., Miller K., Callaghan K., and Kestin G., (2019), Measuring actual learning versus feeling of learning in response to being actively engaged in the classroom, Proc. Natl. Acad. Sci. U. S. A., 116(39), 19251.
- Farrell J. J., Moog R. S., and Spencer J. N., (1999), A Guided Inquiry General Chemistry Course, J. Chem. Educ., 76(4), 570–574.
- Forrest K. and Miller R., (2003), Not another group project: Why good teachers should care about bad group experiences, Teach. Psychol., 30(3), 244–246.
- Freeman L. C., (1978), Centrality in Social Networks Conceptual Clarification, Soc. Networks, 215–239.
- Herron J. D., (1975), Piaget for chemists. Explaining what “good” students cannot understand, J. Chem. Educ., 52(3), 146.
- Hillyard C., Gillespie D., and Littig P., (2010), University students’ attitudes about learning in small groups after frequent participation, Active Learn. High. Educ., 11(1), 9–20.
- Hunnicutt S. S. and Ruder S. M., (2008), POGIL in Chemistry Courses at a Large Urban University: A Case Study, Process Oriented Guided Inquiry Learning (POGIL), ACS Symposium Series, American Chemical Society, pp. 12–133.
- Knight J. K., Wise S. B., Rentsch J., and Furtak E. M., (2015), Cues Matter: Learning Assistants Influence Introductory Biology Student Interactions during Clicker-Question Discussions, CBE: Life Sci. Educ., 14(4), 1–14.
- Lo S. M. and Mendez J. I., (2019), Learning - The Evidence, in POGIL: An Introduction to Process Oriented Guided Inquiry Learning for Those Who Wish to Empower Learners, Simonson S. R. (ed.), Stylus Publications, pp. 85–110.
- Mercer N., (2004), Sociocultural discourse analysis: analysing classroom talk as a social mode of thinking, J. Appl. Linguistics Prof. Pract., 1(2), 137–168.
- Mercer N. and Howe C., (2012), Explaining the dialogic processes of teaching and learning: The value and potential of sociocultural theory, Learn. Cult. Soc. Interact., 1(1), 12–21.
- Moog R. S. and Spencer J. N., (2008), POGIL: An Overview, Process Oriented Guided Inquiry Learning (POGIL), ACS Symposium Series, American Chemical Society, pp. 1–13.
- Moon A., Stanford C., Cole R., and Towns M., (2016), The nature of students’ chemical reasoning employed in scientific argumentation in physical chemistry, Chem. Educ. Res. Pract., 17(2), 353–364.
- Moon A., Stanford C., Cole R., and Towns M., (2017), Decentering: A Characteristic of Effective Student–Student Discourse in Inquiry-Oriented Physical Chemistry Classrooms, J. Chem. Educ., 94(7), 829–836.
- Premo J., Cavagnetto A., and Davis W. B., (2018a), Promoting Collaborative Classrooms: The Impacts of Interdependent Cooperative Learning on Undergraduate Interactions and Achievement, CBE: Life Sci. Educ., 17(2), 1–16.
- Premo J., Cavagnetto A., and Lamb R., (2018b), The Cooperative Classroom Environment Measure (CCEM): Refining a Measure that Assesses Factors Motivating Student Prosociality, Int. J. Sci. Math. Educ., 16(4), 677–697.
- Shadle S. E., Marker A., and Earl B., (2017), Faculty drivers and barriers: laying the groundwork for undergraduate STEM education reform in academic departments, Int. J. STEM Educ., 4(1), 8.
- Shepherd T. and Grushow A., (2013), Quantum Chemistry and Spectroscopy: A Guided Inquiry, Wiley.
- Simonson S. R., (2019), POGIL: an introduction to process oriented guided inquiry learning for those who wish to empower learners, Stylus.
- Singer S. and Smith K. A., (2013), Discipline-Based Education Research: Understanding and Improving Learning in Undergraduate Science and Engineering, J. Eng. Educ., 102(4), 468–471.
- Stains M., Harshman J., Barker M. K., Chasteen S. V., Cole R., DeChenne-Peters S. E., et al., (2018), Anatomy of STEM teaching in North American universities, Science, 359(6383), 1468.
- Stanford C., Moon A., Towns M., and Cole R., (2016), Analysis of Instructor Facilitation Strategies and Their Influences on Student Argumentation: A Case Study of a Process Oriented Guided Inquiry Learning Physical Chemistry Classroom, J. Chem. Educ., 93(9), 1501–1513.
- Theobald E. J., Eddy S. L., Grunspan D. Z., Wiggins B. L., and Crowe A. J., (2017), Student perception of group dynamics predicts individual performance: Comfort and equity matter, PLoS One, 12(7), e0181336.
- Tudge J. R. H. and Winterhoff P. A., (1993), Vygotsky, Piaget, and Bandura: Perspectives on the Relations between the Social World and Cognitive Development, Hum. Dev., 36(2), 61–81.
- Vygotskiĭ L. S. and Kozulin A., (1986), Thought and language, Translation newly rev. and edited, MIT Press.
- Vygotskiĭ L., (1978), Mind in Society: The Development of Higher Psychological Processes, Harvard University Press.
- Wagner C. J. and González-Howard M., (2018), Studying Discourse as Social Interaction: The Potential of Social Network Analysis for Discourse Studies, Educ. Res., 47(6), 375–383.
- Walker J. P. and Sampson V., (2013), Learning to Argue and Arguing to Learn: Argument-Driven Inquiry as a Way to Help Undergraduate Chemistry Students Learn How to Construct Arguments and Engage in Argumentation during a Laboratory Course, J. Res. Sci. Teach., 50(5), 561.
- Walker L. and Warfa A.-R. M., (2017), Process oriented guided inquiry learning (POGIL®) marginally effects student achievement measures but substantially increases the odds of passing a course, PLoS One, 12(10), e0186203.
- Wasserman S. and Faust K., (1994), Social network analysis: methods and applications, Cambridge University Press.
- yEd Graph Editor, yWorks the diagramming company, https://www.yworks.com.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0rp00031k |
| This journal is © The Royal Society of Chemistry 2021 |