Impact of arithmetic automaticity on students' success in second-semester general chemistry

Abstract

Completion of a first-semester chemistry (Chem I) course lays the foundation for understanding second-semester chemistry (Chem II) topics. The purpose of this study is to evaluate the influence of basic arithmetic skills on students’ Chem II success in understanding mathematics-grounded concepts (e.g., solutions and aqueous reactions, kinetics, equilibrium, acids and bases, solubility and equilibria, thermodynamics, electrochemistry, and nuclear chemistry). Previous studies suggest a strong correlation between arithmetic preparation and performance in general chemistry courses, though few have focused on the second-semester course. In this investigation, researchers from six higher-education institutions in Texas, USA of different sizes and with student bodies of different diversities have collaborated to determine whether the Math-Up Skills Test (MUST) is able to reliably identify at-risk students from a population of n = 1599 at the beginning of a Chem II course.

---

Background

As technology becomes a more vital component of our daily lives, the need for a workforce that is well-trained and conversant in the languages of science, technology, engineering and mathematics (STEM) is growing (CAE, 2019). Chemistry, as the central science, is a common denominator in STEM education and therefore success in teaching chemistry is a critical component in training the next generation of scientists. Freshman-level general chemistry is often identified as one of the “gateway courses” since it is typically a large-enrollment, lower-division course in which a relatively high number of students are at risk for failure. Failure in a gateway course is negatively correlated with degree completion (Flanders, 2017). Koch and Drake reported an average DFWI (grades of D and F, along with withdrawals and incompletes) rate of 29.4% for a sample of 20 987 students at 31 colleges and universities in the United States of America (USA) who were enrolled in an “introductory” freshman-level chemistry course (The Gardner Institute, 2018). Almost 50% of the students in the study who earned a mark of DFWI chose to leave the institution where they were enrolled putting degree completion at risk. These data are consistent with other reports of attrition in Chem I courses (e.g., Mason, 2015; Hartman and Nelson, 2016).

Mathematics/reasoning skills and chemistry course success

The statistics are sobering and chemistry faculty are under pressure to increase course retention by finding better ways to support students who enter university classrooms underprepared for success. As a first step, it is essential to identify factors that put a student at risk (Hanover Research, 2018). One well-documented concern surrounding STEM student preparation is their mathematics background. In 1927, Scofield described one of the first published efforts to devise a placement examination that would predict a student's success in a university-level chemistry course. The assessment included multiple sections, one of which was a set of five arithmetic questions (Scofield, 1927, p. 1168), obviously presented before the advent of the ubiquitous handheld calculator:

1. What is one and six-hundredths percent of five-hundred-sixty? (=5.936)

2. Express nine-hundred-seventy-five ten-thousandths as percent. (=9.75%)

3. Multiply eleven and eleven-hundredths by five-thousandths. (=0.05555)

4. Divide six and six-tenths by twenty-two-thousandths. (=300)

5. Subtract five and fifty-two-thousandths from ten and four-hundred-fifty-five-thousandths. (=5.403)

When looking at this list of questions, it is immediately obvious that the author assumed a certain level of quantitative literacy of students in that they should be able to interpret arithmetic problems written in sentence format. In light of today's learning standards, the calculations tested are more complex than current chemistry faculty would typically expect students to complete without a calculator. This begs the question: has calculator use changed approaches to teaching and expected learning?

The correlation of mathematics and/or reasoning ability (for example, that measured by the TOLT) with success in Chem I has been has been reported by many noted chemistry education researchers and continues to enter the literature (Deam, 1923; Tobin and Capie, 1981; Weisman, 1981; Goodstein, 1983; Craney and Armstrong, 1985; Bunce and Hutchinson, 1993; Spencer, 1996; Mason and Mittag, 2001; Lewis and Lewis, 2007; Nelson, 2018; Williamson et al., 2017; Williamson et al., 2020). Math SAT/ACT scores have been shown to be useful indicators of at-risk students in a Chem I course and have been used alongside demographic information, high school GPA or class rank, and assessments of motivation and/or self-efficacy to predict student performance (e.g., Andrews and Andrews, 1979; Bauer, 2008; Chan and Bauer, 2014; Kilner, 2014; Mason and Verdel, 2001; Ozsogomonyan and Loftus, 1979; Pickering, 1975; Pyburn et al., 2013; Spencer, 1996; Stone et al., 2018; Tai et al., 2006; Wagner et al., 2002; Zusho et al., 2003). Often SAT/ACT scores are not readily available to course instructors therefore local assessments are an important alternative. Most local tools that have been used to determine students’ preparation for chemistry include multiple items that test mathematics skills such as algebraic manipulations, probability, proportions and correlations where calculator use is often permitted (Bunce and Hutchinson, 1993; Cooper and Pearson, 2012; Hovey and Krohn, 1958; Karpp, 1995; Kolopajlo, 2019; Pienta, 2003; Srougi and Miller, 2018; Tobin and Capie, 1981) but a few professional exams like the Medical College Admission Test (MCAT) are calculator-free assessments (Leopold and Edgar, 2008). Only a few studies, like Scofield's five calculation questions mentioned above, are focused on local assessments of basic arithmetic abilities without the use of a calculator (Scofield, 1927; Hartman and Nelson, 2016; Albaladejo et al., 2018; Leopold, 2018; Williamson et al., 2020). Advances in educational technology, such as calculators, bring both opportunities and challenges.

Albaladejo et al. (2018) reported results of a pilot study comparing performance on a 16-item arithmetic instrument with and without the use of a calculator to final grades in Chem I courses. The instrument was adapted from a published assessment developed by Hartman and Nelson (2016) and included items on multiplication, interpretation of numbers in scientific notation, simple exponents, writing fractions in decimal notation, logarithms, square roots of numbers in scientific notation, as well as one item requesting rearrangement of an algebraic equation (ideal gas law) and some simple chemical equations to balance. Following the pilot semester, the instrument was updated with four additional questions that added more fraction-manipulation items. Data from the revised quiz was validated and internal consistency was confirmed; it was named the Math-Up Skills Test (MUST). Interestingly, the study found a stronger correlation between results of the assessments completed without a calculator and the course outcomes than between the results of the assessments completed with a calculator and course outcomes, leading the researchers to conclude that automaticity may be an important measure of preparation for general chemistry success. While it is not entirely evident why chemistry students may be exhibiting differences in automaticity despite many completing required pre-college mathematics coursework, variations in mathematical automaticity have been reported among student populations who are educated in different countries with different approaches to teaching and learning. Some suggest these differences may be influenced by the use of calculators (Cooper and Klymkowsky, 2013; Geary et al., 2008; Nelson, 2017).

Mathematical automaticity

How might mathematical automaticity impact chemistry students? By definition, mathematical automaticity is the ability to deliver a correct answer to a mathematics problem without conscious thought. The facts and processes necessary to complete a calculation are so familiar that they are “automatic” and are stored in long-term memory (Geary et al., 2008; Hartman and Nelson, 2015; Stickney et al., 2012). Research has shown that fluency in using automatic mathematics skills are essential to success in higher level mathematics and application of mathematics to unfamiliar problems (e.g., Cozad and Riccomini, 2016; Geary et al., 2013). It is not surprising that a student who is challenged by remembering how to multiply or divide fractions, would struggle with fraction concepts needed in using unit factors to complete calculations or a student who is still a novice at manipulating numbers using scientific notation might not realize that reporting a protein's molar mass as 5.003 × 10⁻³ g mol⁻¹ is nonsensical. A calculator could be used to do number crunching in each of these cases but cannot help the student set up the problem or provide an understanding of scale (Barouch, 1997; Jones and Taylor, 2009; Mason et al., 2004).

Cognitive scientists describe problem solving as an interaction between long-term memory (LTM) and working memory (WM). One retrieves memorized knowledge stored in LTM that has been integrated into the brain's conceptual frameworks and is able to use that memorized knowledge with automaticity (Hartman and Nelson, 2015). The LTM/WM framework suggests that if pertinent mathematics facts and calculation procedures along with understanding of scale required for a chemistry concept or to complete a chemistry calculation are not stored in LTM, a student is more likely to struggle and be at risk of failure (Barrouillet et al., 2011; Clark et al., 2012; Cowan, 2000; Miller, 1956; Cowan, 2010; Miller et al., 2018).

The constructivist framework

The constructivist description of learning supports the need for integration of foundational mathematics facts and skills as preparation for chemistry coursework. Researchers Piaget (1977), Osborne and Wittrock (1983), Bodner (1986), and Von Glaserfeld (1995) provided the basis for our understanding that knowledge is “constructed” by learners through interactions with materials and/or people and not simply transmitted from an instructor to a student (Williamson, 2008; Duit, 2016). Some researchers believe that prior knowledge can be the most important factor to influence how a student learns (Cooper and Stowe, 2018; Shell et al. 2010). Ausubel (1968) suggested that prior knowledge is the foundation upon which new knowledge is built and to which new knowledge is connected. Though much research on constructivism in chemistry education has centered on chemistry theory misconceptions such as misunderstandings of the particulate nature of matter (e.g., Taber, 2000), mathematics skills and concepts are also widely understood to be essential foundational knowledge. If they are not part of a student's prior knowledge, new chemistry knowledge construction that includes numerical data will be unstable and ephemeral (Duit, 2016; Taber, 2000, 2015).

First and second semester general chemistry curriculum

In the USA, first-year chemistry curriculum is often divided into two semesters. The American Chemical Society (ACS) exams institute identifies the first-term topics as: atomic structure, electronic structure, formula calculations and the mole, stoichiometry, solutions and aqueous reactions (part 1), heat and enthalpy, structure and bonding, and states of matter. (For additional information on testing general chemistry concepts, see Holme and Murphy (2012) and Murphy et al. (2012).) Mathematics manipulations important for these topics include straightforward addition, subtraction, multiplication, and division, use of scientific notation, calculations with fractions, and use of formulas to solve for an unknown quantity. The course which covers these topics is herein identified as Chem I. Ralph and Lewis (2018) identify the mole concept and stoichiometry as topics that students with bottom-quartile SAT mathematics scores find most challenging in the Chem I curriculum. In their analysis of student performance throughout Chem I coursework they determined that not all of the topics that are most difficult for students require algebraic manipulations or algorithmic approaches. Interestingly, at-risk students identified by the SAT mathematics score who mastered the mole concept and stoichiometry went on to outperform their peers deemed not at risk in the Ralph and Lewis study.

The ACS lists second-term topics as: solutions and aqueous reactions (part 2), kinetics, equilibrium, acids and bases, solubility and equilibria, thermodynamics, electrochemistry, and nuclear chemistry (Find Chem I and II topics at: https://uwm.edu/acs-exams/students/student-study-materials). More advanced mathematics and algebraic manipulations are required for these topics such as use of both base-10 and natural logarithms, graphical analysis of rates and slopes, solving systems of equations, and solving of quadratic equations. The course which covers these topics is herein identified as Chem II. A series of papers have elucidated student understanding of chemical kinetics and allowed researchers to draw conclusions about how students use mathematical models to interpret chemical processes including graphical representations of these processes. These studies point to the importance of integrating mathematical models into chemical problem solving and the key role symbolic reasoning plays in successful interpretation of chemical data (Bain et al., 2019; Rodriguez et al., 2018; Rodriguez et al., 2019).

At most institutions, students enrolled in Chem II have successfully completed Chem I as a prerequisite course. The default assumption is that the student who successfully completes Chem I should be well-prepared for Chem II, however, with a rising number of students transferring coursework from other institutions, completing courses via high-school dual credit, or returning to college after an extended break, prerequisite success is not always a dependable measure (Radunzel et al., 2014; Troutman et al., 2018). Furthermore, many faculty members report that access to student records allowing retrieval of Chem I course grades for a Chem II cohort is restricted, so specific Chem I passing grades of A, B, or C may not be available unless the faculty member has taught a student in the prerequisite course. It is also true that Chem I does not provide review or practice of the additional mathematics skills required by Chem II topics. Faculty are aware that the failure rate for students enrolled in Chem II can be substantial and there is a need for an accessible method of identifying at-risk students in this population that is easy to use, quick to administer and provides needed information very early in a Chem II semester, if we are to address remediation and retention in the second-semester course.

Previous work measuring students’ mathematics abilities

In 2016 the Networking for Science Advancement Team (NSA Texas team) began studying general chemistry students' numeracy ability and its correlations with students' success. The team was initially composed of eight chemical education research (CER) professionals from six institutions. Currently, there are instructors from ten universities who contribute to the Texas collaborative. In prior research studies (Petros et al., 2017; Albaladejo et al., 2018; Williamson et al., 2020), basic arithmetic automaticity (what students can accomplish without an electronic calculating device) was found to be a reliable predictor of success in Chem I. In the Chem I series of studies, the MUST (Math-Up Skills Test) was used to identify students who are considered to be at risk. The MUST has good internal consistency with the n = 1073 sample evaluated (Cronbach's alpha = 0.856). Results from the MUST support findings that arithmetic skills correlate well with course grades in Chem I. Poor automaticity may be an underlying contributor to lower performance by many Chem I students. With statistical modeling, the MUST, along with other demographic variables, was able to identify students who would go on to make a 69.5% or better in Chem I with almost an 80% accuracy.

In the evaluation presented here, the NSA team considered the automaticity skills of Chem II students as a continuing step needed to assess how learned basic skills can predict successful student outcomes in Chem II at six institutions in a majority–minority state in the southwestern part of the USA bordering Mexico. Other authors have reported on mathematics fluency and its association with the success of Chem II students (Kolopajlo, 2019; Leopold and Edgar, 2008), but these publications remain low in number as compared to publications for Chem I. Leopold and Edgar and Kolopajlo used the University of Minnesota mathematics assessment for second-semester chemistry (UnMMASSC), which is calculator-free and includes four sections: logarithms (7 items), scientific notation (5 items), graphs (4 items), and algebra (4 items) (Leopold and Edgar, 2008). Students taking the UnMASSC were permitted 30 minutes to complete the assessment and it included 10 choices for 17/20 of the questions, which may make it cumbersome for adopters wishing to use a standard five-choice response form. The shorter, 15 minute MUST assessment when paired with demographic information proved to be as strong a predictor of student success in Chem I courses and data from the present study also support a strong relationship with student success in Chem II courses.

The statistical analysis is sparse in Scofield's, 1927 study of student preparation for university-level chemistry coursework and no direct correlations were investigated between performance on only the mathematics section of the placement test and course outcomes, but the paper does state that the need for a placement test was due to the “widely varying abilities” of the entering freshmen chemistry students (Scofield, 1927, p. 1168). In the 90 years since this early publication, chemistry knowledge, curriculum and pedagogies have changed but the problem of uneven preparation persists. Investigators continue to look for methods of identifying students who may be at risk of failure and for new pedagogical approaches that will better support students so that they can successfully master essential chemistry concepts and calculations. We believe the MUST could be a very useful tool not only for predicting outcomes in Chem I, but also for identifying at-risk students and predicting outcomes in Chem II. The study presented here investigates this hypothesis.

Research questions

The research questions posed in this study are similar to those addressed in the NSA study on students enrolled in Chem I (Williamson et al., 2020). Prior knowledge is a known predictor of learning success in most disciplines (Shell et al., 2010) which might be evident as a contributor to success in the second-semester course. Like the NSA study of Chem I students, the purpose of this two-year study is to measure how arithmetic skills impact course averages in Chem II leading to the investigation of the following questions:

1. What relationships exist between scores from the diagnostic Math-Up Skills Test (MUST) instrument and students' course averages in Chem II?

2. Are any MUST-course average relationships influenced by students' self-reported demographic identifiers: personal characteristics (gender, ethnicity, prior knowledge in chemistry and mathematics, entrance college (STEM or non-STEM), and family education) and environmental factors (Hispanic-serving or Hispanic-emerging institution, classification, residence location, and employment level)?

Methodology

All participating instructors have expressed interest in chemical education research (CER). No restrictions were placed on curriculum choices or instructional pedagogies. Faculty members possess a wide-range of teaching experience from four to over forty years in the chemistry classroom. All Chem II lecture courses were offered for 3-credit hours; some lecture classes were taught two days a week and others met three days a week. Associated laboratory grades were not included in grades assigned for the lecture courses. Different textbooks and homework systems were used. For the purposes of this study, the course average for each student was calculated by dividing the points earned by points possible and reporting the result as a percentage. Some students earned extra credit points resulting in a percentage grade over 100%. MUST scores were based on a raw score of 0–20. The goal of this work is to investigate how the MUST diagnostic instrument predicts performance for students in Chem II courses taught in a variety of post-secondary settings across a broad geographic region. A strength of this study is that we have collected data from a sample that extends beyond a single institution (n = 1599) and includes a variety of instructors and teaching methodologies.

Research setting

The current two-year investigation continues the research initiated in a 2016 pilot study of the MUST correlation with Chem I performance (Petros et al., 2017; Albaladejo et al., 2018) and a second-year study that confirmed that the MUST is a strong predictor of students’ performance in Chem I (Williamson et al., 2020); four of the six universities in this study are the same as those in the Chem I study. In this investigation, two of the participating universities are mid-sized Hispanic-serving institutions (HSIs) that have greater than 25% of the student population reported as Hispanic ethnicity. One school's undergraduate Hispanic population is 72% of enrollment and 7% of the undergraduate population is African American. The second school has an undergraduate Hispanic enrollment of 41% and an African American enrollment of 9%. Chem II class sizes at these two institutions are in the range 30–60 students. The other four universities are considered Hispanic emerging institutions (greater than 16% but less than 25% Hispanic). Two of the Hispanic-emerging institutions are classified as large R1-research institutions (Carnegie classification, Chem II class size 300 students and 60–120 students) with undergraduate Hispanic populations closely approaching 25% and African American undergraduate populations in the range 5–15%. The fifth institution is a mid-sized Hispanic-emerging university with an undergraduate Hispanic enrollment of 22% and an African American enrollment of 24% (Chem II class size 50–100 students). The final participating institution is a small, private Hispanic-emerging university (Chem II class size 30–45 students) with an undergraduate Hispanic enrollment of 18.5% and an overall underrepresented minority enrollment of 33%. Only one university in Texas is not an HSI, Hispanic-emerging or historically black institution adding to the evidence that these data are descriptive of the current general chemistry population of the state. Reported standards identify a small university as one enrolling less than 5000 undergraduate students and a large university as one having over 30 000 with mid-size institutions between these limits. As in the Chem I study (Williamson et al., 2020) data collected were from six universities. Included are private and public institutions, small and large undergraduate student populations, various accountability groups (e.g., master's only, doctoral professional university, and emerging-R1 and R1 universities), and Hispanic-serving and Hispanic-emerging institutions. The undergraduate enrollment ranged from under 5000 students to almost 55 000. As noted above, the sizes of the lecture classes also varied from approximately 30 to 300 students.

All instructors obtained IRB approval at their respective institutions under the approved rules and regulations of that institution, and only students who agreed to participate in the study and earned a numerical average in the course above 10% were included in the following analyses. This study targeted Chem II on-sequence students in Springs 2018 and 2019 semesters combined. In general, students are admitted to Chem II upon their successful completion of Chem I with at least a grade of C, but as noted earlier, growing numbers of students are entering the Chem II classroom after completing Chem I in a dual-credit setting that may or may not be significantly different than the typical university campus experience or may have received AP credit. In addition, there are students who return to the classroom with Chem I credit after a lengthy absence. Student proficiency and success in Chem II rely on their understanding of foundational concepts in mathematics and chemistry. While some institutions have mathematics prerequisite requirements or mathematics placement tests, not all suggested prerequisites are strictly adhered to beyond the requirement of Chem I course completion.

Population

Demographic information requested and the grouping of data into personal characteristics and environmental factors were based on a review of the literature. Each demographic item collected has been reported in the literature as a predictor of academic success. Previous research reports that personal characteristics are primary contributors to student attrition, whereas institutional characteristics make only minimal contribution to attrition (Habley et al., 2012). According to Wilkerson (2008) personal characteristics are more useful for predicting retention than environmental factors. Personal characteristics include gender, ethnicity, prior knowledge in chemistry and mathematics, entrance college (STEM or not STEM), and education of parents/grandparents. Environmental factors describe the type of institution (HSI or Hispanic-emerging), university classification (accepted coursework, thus classification, is decided by the institution), residence location and employment status. For this study, the primary student outcome measure is a grade of C or better (average ≥69.5%) that qualifies the student to continue to the next course in a chemistry sequence, typically first-semester organic chemistry. Grandparent college-degree attainment was included in this investigation due to evidence that the current student population is significantly influenced by older relatives in addition to their parents (Monserud, 2011). It should be noted that the goal of predictive research, which seeks to produce the best possible predictive model, differs from the goal of explanatory research, which seeks to explain the phenomena (Pedhazur, 1997). The goal of this evaluation is to seek a predictive model for Chem II students who succeed with an average of at least 69.5% (grades of A, B and C).

In the combined study population of 1599 students, twelve students did not report a gender and one declared a gender of “other”. Therefore, the calculated gender breakdown is: 1029/1586 (64.9%) female and 557/1586 (35.1%) male. The majority of the students were classified as freshmen (n = 1076/1590, 67.9%); nine students did not report their classification. About 95% reported being of traditional college-student age and having attended high school in Texas, meaning that they have similar post-secondary background as they enter their Chem II classes. Over 90% (n = 1448/1567) intended to major in a STEM field of study with n = 120 (7.7%) reporting the intention to pursue a non-STEM major. The participating population completed Chem II with an overall course average and reported standard deviation (SD) and standard error (SE) of 78.9 (16.4) (0.410).

Assessment instrument

The 20-item version of the MUST as the measure of students’ automaticity ability was used in this investigation as in the Chem I study (Williamson et al., 2020). Near the beginning of the spring semesters, students responded to questions on the timed MUST (15 minutes) without the use of a calculator. Students were also asked to complete a demographics survey. The MUST items investigate a student's ability to accomplish the following tasks: multiplication of two-digit numbers, multiplication and division of two numbers in scientific notation, zeroth power application, division of fractions by a fraction, changing fraction to decimal notation, rearranging algebraic equation (combined gas law), recognition that division by zero is undefined, fraction simplification, determining the base-10 logarithms, square and square root of a number in scientific notation, fraction-decimal equivalents, and balancing simple chemical equations as an example of counting atoms supporting the conservation of mass. The graded MUST scores were collected by the last author. All un-useable student data sets were eliminated from the deidentified data (e.g., data sets for post-baccalaureates, students with final course grades of <10% and those who provided no demographic data). Copies of the 20-item MUST (both versions) are available in Appendix 1, ESI,† and the solutions for the items are found in Appendix 2, ESI.† Items were scored as either correct (1) or incorrect (0) resulting in whole number scores ranging from 0 to 20.

Two versions were distributed to the students on differently-colored paper in order to maintain the integrity of the test by reducing students’ chances of getting the correct answer by looking at their neighbor's paper. The content validity was established for both forms of the MUST by four professors (two full professors, each with a PhD in mathematics, one full professor with a PhD in physical chemistry, and one retired professor with a PhD in chemical education). These professionals investigated and confirmed that items on the instrument measured the intended tasks. Agreement on the answers and on the topic assessed for each item was 100%. For each student's MUST score, responses were identified as either correct or incorrect resulting in scores ranging from 0 to 20. The MUST is hand graded with no partial credit assigned to any item even when an equivalent fractional answer is given when a decimal response is required. One of the benefits of the MUST is that it is not multiple choice, so students cannot select a correct answer by guessing or working backwards from provided choices.

Results

The MUST has good internal consistency for this study as established by Cronbach's alpha = 0.853. The two analogous versions of the MUST produced t-test values between scores on the two forms of p = 0.524, supporting no significant difference between versions for the Chem II students. For example, in order to keep the two versions as similar as possible, one version asked students to multiply 78 by 96, while the other version used the multiplication of 87 by 96. It is possible that some students had participated in the prior research studies at four of the six institutions and may have taken the MUST before in their Chem I classes; this repetition was not controlled for and presumed to have minimal impact. The overall MUST average (SD) (SE) for this study was 11.86 (4.74) (0.12) out of 20 questions. Noteworthy is that the reported MUST average (SD) for Chem I course as assessed in a sample population during the Fall 2017 semester was only marginally lower at 10.36 (4.93) (Williamson et al., 2020). Chem II students are assumed to enter the course with stronger mathematics ability since most have completed at least of minimum of pre-calculus and Chem I. Chemistry students with weaker mathematics skills often will not successfully complete Chem I naturally culling the population enrolling in Chem II. The Chem II correlation of MUST scores to course average was r = 0.415. Fig. 1 shows the frequency of MUST scores with the sample of 1599. (Compare Fig. 1 in the Chem I Williamson et al. (2020) paper and Fig. 1 of this paper and note a shift to the right supporting the conclusion that the mean is slightly higher for Chem II as opposed to Chem I and that a greater number of Chem II students earned higher scores, while fewer earned very low scores.)

Fig. 1 Frequency of MUST scores (n = 1599).

The MUST score means were compared to course averages for 1599 students grouped as successful (average of ≥69.5%) and unsuccessful (average <69.5%) students (Table 1). In data analysis, there are some instances (like reported above) where the population varied slightly, due to data omitted for students who did not complete all sections of the demographics survey. Students who dropped the course before the end of the semester, thus not earning a grade, were not included in the analysis. Table 1 shows the MUST averages for students who were successful and unsuccessful in Chem II. The fact that the MUST is strongly correlated to Chem I course averages has been a consistent result since the NSA project began in Fall 2016. These data establish its correlation with Chem II course averages.

Table 1 Successful (average ≥69.5%) vs. unsuccessful (average <69.5%) students (n = 1599)

Success	n (%)	MUST (SD) (SE)
a Successful students significantly higher at p < 0.05 level.
Successful	1269 (79.4%)	12.72 (4.41) (0.124)^a
Unsuccessful	330 (20.6%)	8.57 (4.56) (0.251)

---

Fig. 2 presents the linear relationship between the MUST and course averages as a scatterplot. Most students who do well in the course have above average MUST scores as noted in Table 1. The given R² in Fig. 2 (0.172) is lower than that for the Chem I students of 0.288 in the prior study (Williamson et al., 2020) indicates a greater dispersion of data points. However, in Fig. 2 it is obvious that the students who entered with above average MUST scores do better in the course as indicated by the positive slope and the tighter grouping (less noise) of data points on the right side of the plot. This type of plot with its wide variability indicates that the MUST alone is not enough to predict class average. (Scatterplots of individual MUST scores versus course averages differentiated by institution are included in Appendix 4, ESI.†)

Fig. 2 Scatter plot (n = 1599) individual MUST scores plotted against course averages.

Table 2 presents the alignment of MUST mean scores with course averages. It is immediately obvious that higher performing students have better mean arithmetic automaticity ability as measured by the MUST. An average MUST score of 10 correct out of 20 questions (50%) appears to be the average minimum score for success in Chem II. Students who make an A in the course average about 15 (75%) on the MUST. There are statistical differences between the various grade groupings of students (i.e., A-student and B-student groups, B and C, C and D) but there is not a statistical difference between the groups of students who earned grades of D and F.

Table 2 MUST relationship to typical course average (n = 1599)

Classic averages	Number (%)	MUST (SD) (SE)^a
a Statistical difference between groups (grades of A vs. B, B vs. C, C vs. D) but no statistical difference between D vs. F at p < 0.05 level.
A: 89.5–100.0+%	455 (28.5%)	14.61 (3.87) (0.18)
B: 79.5–89.4%	467 (29.2%)	12.52 (4.16) (0.19)
C: 69.5–79.4%	347 (21.7%)	10.50 (4.31) (0.23)
D: 59.5–69.4%	175 (10.9%)	8.63 (4.62) (0.35)
F: 0–59.4%	155 (9.7%)	8.51 (4.51) (0.36)

---

Fig. 3 demonstrates that Chem II students at each participating institution have a similar pattern of success on the individual MUST assessment items despite the fact that students have experienced a Chem I course and college-level mathematics courses at different institutions in the same USA state. Over 94% of the students who participated in this Chem II study also attended high school in Texas, and therefore were exposed to the same education standards in a state-adopted isomorphic curriculum; the similar MUST assessment patterns may illustrate the weaknesses in a common curriculum. This is analogous to the trend seen in the Chem I study (Williamson et al., 2020).

Fig. 3 MUST scores by question for the participating institutions.

Demographic analysis

In addition to correlating MUST scores with course averages, we studied relationships between student success and self-reported demographic identifiers. The explored demographic predictor variables are categorized by those considered personal characteristics and those considered environmental factors, which are specific to an institution. Previous research has suggested that personal characteristics are reported to be more influential than environmental factors on the expected output of final course average (Habley et al., 2012). Personal characteristics for this study include gender, ethnicity, prior knowledge in chemistry and mathematics, choice of entrance college and parents’ academic degrees. Environmental factors for this study include type of institution, student classification (determined by what coursework is accepted the institution), residence location and employment. Self-reported survey data were collected and a complete analysis of the demographic data is available in Appendix 3, ESI.† The goal of this report was to seek a predictive model for the Chem II students.

Predictability of MUST

Previous research has determined that above average MUST scores are predictive of student success in Chem I (Williamson et al., 2020). In the Chem I study, the average MUST (SD) (SE) score was 10.36 (4.94) (0.15) while in this Chem II study, the average MUST score marginally improved to 11.86 (4.75) (0.12). For the Chem II collaborative we used one standard deviation around the mean MUST score to determine students above and below average and the following trends were established. The ranges established for the Chem II MUST (see Table 3) are: below average (0–9), average (10–14), and above average (15–20).

Table 3 Targeted MUST score ranges: below <10, average = 10–14, above >14

MUST range	n	Course (SD) (SE)^a	Number of unsuccessful		Percentage D + F
			D	F
a Significant difference at p < 0.05 level: upper outperformed medium, medium outperformed low, and upper outperformed low. Abbreviations correspond to those in Fig. 4: U = upper, M = middle, L = low.
Above average: U	550 (34.4%)	86.07 (13.17) (0.56)	25	19	44/550 = 8.0%
Average: M	555 (34.7%)	78.96 (15.63) (0.66)	52	43	95/555 = 17.1%
Below average: L	494 (30.9%)	70.94 (16.77) (0.75)	96	93	189/494 = 38.3%
Total	1599	78.93 (16.38) (0.41)	58	32	328/1599 = 20.5%

---

There was an approximate 8-point gain in course average for students in each successively higher MUST score category. Standard deviations and standard errors for each successively higher MUST category consistently decrease, and more importantly the percentages of unsuccessful students decrease by 21.2% (38.3% to 17.1%) as we move from the low MUST category to middle MUST category and by 9.1% (17.1% to 8.0%) when moving from the middle MUST category to the upper MUST category. The measure of success dropped rapidly as the average MUST ranges declined. Of the 328 students who made a grade of D or F in Chem II, 191 (57.9%) had below average MUST scores. About 90% of the students with average and above average MUST scores were successful (grades of A, B or C). The alluvial diagram (Fig. 4) helps us visualize the level of success for students who enter with MUST scores in each category. The majority of students with above average MUST scores did well in the course and few students who entered with below average MUST scores made a grade of A or B.

Fig. 4 Alluvial diagram illustrating the MUST ranges (upper: U, middle: M and low: L) as compared to the course grades (A, B, C, D, and F). Prepared using: https://rawgraphs.io/learning/how-to-make-an-alluvial-diagram/#01-paste-your-data.

Statistical modeling method for predictability

Data from Spring 2018 and 2019 collected from Chem II students were used to develop two regression models to predict future student outcomes. The first model is a linear regression model on course average while the second model is a logistic regression on course success (course average greater than 69.5%). To align with previous predictive analysis of Chem I, we started with the MUST score as our key linear predictor and include the following categorical variables similar to those selected for the model developed for the Chem I study (Williamson et al., 2020):

• student classification (freshman, sophomore, junior, or senior),

• gender (male or female),

• race/ethnicity (White, Hispanic, Black, Asian, or other),

• major (STEM, non-STEM major),

• which of the two MUST versions was completed (version 78 or 87),

• generations attending college (first generation—neither parents or grandparents earned a college degree, second generation—at least one parent earned a college degree, third generation at least one parent and grandparent earned a college degree, or don’t know)

• number of employment hours per week (0, 1–10, 11–19, 20–29, 30–39, or 40+),

• high school chemistry courses completed (none, high school chemistry, pre-AP chemistry, AP chemistry),

• student has met the mathematics requirement for Chem II (yes or no),

• the university is an HSI (yes or no),

• university (R1 large A, R1 large B*, small private, large public, midsize HSI A, midsize HSI B). *Special class with high minority populations at a Hispanic-emerging institution, and

• semester in which the survey was given.

Data from 2018 and 2019 were split into two unequal samples. The first sample consisted of a random selection two-thirds (n = 1005) of the total to set aside for training the models. The remaining one-third (n = 502) of the sample was held out to test the accuracy of the model's prediction (James et al., 2013). The LASSO method is a regression analysis method that regularizes, smooths, and shrinks model covariates in an effort to find the set of model coefficients that optimize prediction accuracies in balance with predictive effects for subject covariate variables (James et al., 2013; Hastie et al., 2015). Compared to a typical regression model that includes covariates based on theoretical assumptions, LASSO includes covariates based on statistical assumptions. For the linear model, the LASSO function's estimate of the mean square error was minimized. As a consequence, it selects the most parsimonious model with the largest explained variance. Similarly, cross validation selection for logistic regression minimizes the mean deviance of the model while selecting the most parsimonious model that maximizes the deviance ratio. While LASSO by its nature reduces multicollinearity, it is still useful to account for the assumption of no multicollinearity by calculating the mean variance inflation factor (VIF). The VIF for the linear model is 2.15 and the VIF for the logistic model is 3.01. A VIF of 1 indicates no multicollinearity and a VIF less than 5 can be considered low multicollinearity. The process of finding the LASSO penalty parameter (lambda) that minimizes mean square error and mean deviance in linear and logistic regressions, respectively, is visualized in Appendix 4, ESI,† in Fig. S3 and S4 (ESI†). In the top graph, the y-axis starts with the smallest mean square error from a cross-validation function containing no coefficients, and as the curve moves along the x-axis, the mean square error is reduced as lambda shrinks to the lowest penalty before the mean square error increases. In the bottom graph the selection of lambda corresponds directly to the number of covariates included in the predictive models and the strength of their coefficients. The MUST score is the first covariate selected and has the largest contribution to the prediction. In Appendix 4, ESI† in Table S12 (ESI†), we report post-selection coefficients for our linear-prediction model. For linear models, post-selection coefficients perform better than penalized coefficients (Belloni and Chernozhukov, 2013). In Appendix 4, ESI† in Table S13, we report the log odds from our logistic regression.

Coefficients derived from LASSO model selection are not interpretable in the same way that a typical linear or logistic regression coefficient is. They are not inferences of a parametric coefficient. Instead they are coefficients of a subset of possible covariates that have a non-zero contribution (Leeb and Pötscher, 2008). Covariates are either factors that are in the “true” model or factors that are correlated to factors in the “true” model. As such, the significance of each coefficient is not an indicator of its importance for a predictive model. LASSO selects only factors with a nonzero contribution. One notable result of this selection process is that some categories from a categorical dummy variable set may be selected by the model and others may not. For example, the classification of a student includes freshman, sophomore, junior, and senior yet our model only includes the freshman and junior categories. This can be thought of in two ways: (1) the coefficient or log odds of the two excluded categories is zero, or (2) the excluded categories collapse into one reference category for the dummy set—freshman or juniors compared to sophomores and seniors.

The MUST score is a numeric predictor while all of the other explanatory variables are categorical. For the linear regression on Chem II course average, the coefficients for categorical variables represent the mean differences compared to the reference, holding all other variables constant. The coefficient for the MUST score is the mean change in course average associated with a one-point increase on the MUST, again holding all other variables constant. For the logistic regression model the coefficient for each categorical variable represents the log odds of passing the course for someone in that category and the coefficient for the MUST is the predicted increase in the log odds of receiving a passing grade (≥69.5%) vs. a failing grade for a one-point increase in the MUST score, holding all else constant.

To make a prediction of a student's course average in Chem II, simply gather information corresponding to the coefficients in Tables S12 and S13 (ESI†). Since differences between universities can be significant, we do not recommend trying to match your institution to one in this study, but suggest using the average university coefficient, which is included in Tables S12 and S13 (ESI†).

As an example, consider a junior who is female, Hispanic (Hisp.), a third-generation college student (3rd gen. = both parents and grandparents have 4 year degrees), works 35 hours in a week, took pre-AP high school chemistry, has not completed pre-calculus, average university coefficient, and scored a 15 of 20 on the MUST. The linear prediction for our hypothetical student's course average would be as follows:

A student with our hypothetical characteristics is predicted to earn a grade of 80.02% with a score of 15 on the MUST. The same student with a score of 12 of 20 (in the middle range in Table 3 and Fig. 4) should be able to achieve a mid-range of a C grade (75.24%), and with only an 8 on the MUST (just below D/F average in Table 2) a grade of 68.87% (or a grade of D) would be predicted.

Similarly, the result of the logistic regression can be used to predict the log odds of succeeding in Chem II for the first hypothetical student by using the following equation:

The estimated probability of success in Chem II would be e^(1.78)/(1 + e^(1.78)) = 0.856. A student with these hypothetical characteristics is predicted to earn a passing grade 85.6% of the time. In the cases for the mid-range (12) and the low-range (8) on the MUST, the estimated probability of success would be 0.774 and 0.628, respectively. It appears from the logistic regression that the greatest negative effect for this student is the fact that she is working full-time and the greatest positive effect is having a well-educated family.

In both predictive models, the MUST score is a highly significant effect and it is the dominate covariate in both predictive models. The LASSO cross-validation process includes the MUST early in model selection and the LASSO penalty parameter finds its minimum at or near the apex of the MUST score's penalized standardized coefficient (see Fig. S3 and S4, ESI†). These factors indicate that the MUST is a robust part of performance in Chem II. When models are fit with only the MUST as a covariate, they produce strong model fit characteristics relative to the full LASSO models (see Table 4). However, it is clear that the predictive power of the MUST is bolstered by the inclusion of other predictive factors.

Table 4 Goodness of fit for linear and logistic LASSO regression predictive models

Model	Sample	Minimization criteria	Model fit	Observations
a Derived from a post-selection model with unpenalized coefficients. b Deviance ratio is analogous to r^2 for logistic regression.
LASSO linear^a		Mean square error	R-Squared
	Training	214.595	0.267	1005
	Validation	218.785	0.132	502
MUST only^a
	Training	238.789	0.184	1005
	Validation	221.652	0.120	502
LASSO logistic		Deviance	Deviance ratio
	Training	0.831	0.205	1005
	Validation	0.805	0.127	502
MUST only
	Training	0.900	0.140	1005
	Validation	0.848	0.081	502

---

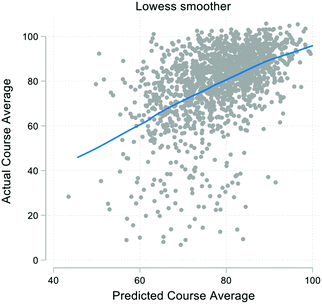
Using the selected logistic model on the validation sample, estimated is a balanced accuracy of 0.738 and classification accuracy of 0.829. The classification accuracy is the strict probability of predicting success or failure in Chem II based on the selected model. Here, 82.9% of predictions were found to be accurate. Balance accuracy weights sensitivity and specificity reducing bias for predicting the larger group. Applying the LASSO-selected linear regression model to the validation sample produced an MSE (mean squared error) of 218 and an R² = 0.13. Plotting the predicted course averages against the actual course averages gives more context for the MSE. Fig. 5 plots a smoothed LOWESS curve that fits the data in segments finding the local line of best fit. As a result, a LOWESS curve will take on non-linear characteristics if the data do not support linearity. The data have a slight inflection point but have a generally linear character. Additionally, the LOWESS curve's slope generally follows the line of equality. Both models can be used for predicting outcomes in Chem II. Furthermore, this evidence strongly supports using the MUST to predict course averages and overall success in Chem II.

Fig. 5 Actual vs. predicted course average.

Conclusions

The MUST instrument can be used to measure student performance on basic arithmetic manipulations without the use of a calculator. This study focused on the influence of arithmetic automaticity, which has been reported to be a concern since the advent of the handheld calculator (Gold, 1979; Nelson, 2018). Most of the mathematics skills tested by the MUST are taught before or during high school mathematics courses, but performance on the MUST indicates that either our freshman-level students have not achieved automaticity despite their high school preparation or their automaticity skills have become dormant before the beginning of chemistry coursework at the universities included in this study. We know that prior knowledge remains a very important contributor to success in Chem I as measured by the MUST (Williamson et al., 2020) and this study affirms that the MUST is also a good predictor of student success in Chem II courses.

Using the MUST to identify at-risk students in Chem II will allow faculty the opportunity to provide additional support and remediation to help students achieve greater success. The large effect size of the MUST and good correlation with course grades suggests that working to improve students’ basic number sense may initially have more advantages to their continued success than improving their more abstract algebraic skills. Specifically designed remedial lessons and/or courses, mandatory workshops (group and individual), arithmetic-focused introductory lectures in chemistry courses and focusing efforts on metacognitive-learning strategies may all be pathways to strengthening the STEM graduate pool. General chemistry courses are known gatekeeper courses, and as educators we strive to provide and to lead our students to becoming better problem solvers (Lagowski, 1993).

Consistent with the literature, the personal characteristics (gender, ethnicity, prior knowledge in both chemistry and mathematics, and students’ parents’ education) proved to be strongly aligned MUST scores and final course averages. Environmental factors (type of institution, classification, residence, and employment) were not as well aligned but showed trends favoring the importance of automaticity as a measure of potential for success in Chem II.

Limitations

The population of students who were study participants were all enrolled in institutions in the same USA state and the majority had graduated from high school in the same state that has uniform standards for high school graduation. However, the institutions from which data were collected included student populations of varied sizes, ethnicity distributions, and entrance requirements providing a broad student sample. This study includes students who were taking Chem II during a spring semester, which would be considered “on sequence” and the results for students who are enrolled in the course during “off sequence” semesters may vary from those reported here. Finally, although we report that the MUST paired with demographic factors does allow a high degree of predictability success, 82.9%, the prediction could be expected to be incorrect 17.1% of the time.

Future research

As educators, we are interested in helping every student reach their highest potential and providing pathways to success. The NSA team is currently gathering and analyzing data on high impact environments and practices that will support all at-risk students, in hopes of increasing success rates. Several HIPs (high impact practices) are currently being implemented and will be analyzed and reported in the future. Texas is classified as a majority–minority state due to the expanding Hispanic student population and also has a growing number of first-generation students. It is of interest to the NSA group to analyze how Hispanic students who attend one of our HSIs in Texas differ from the Hispanic students not attending an HSI (Villalta-Cerdas et al., (N.D.), in press). In addition, how MUST skills impact students’ success in first-semester organic chemistry and biochemical physical chemistry are being evaluated to see how automaticity skills effect success.

While strengthening mathematics preparation before or during chemistry enrollment seems an obvious and positive step toward supporting at-risk students, there is emerging research that elucidates the more complex nature of students’ conceptual understanding of chemistry as it is intertwined with mathematical calculations. In a recent publication, Ralph and Lewis (2019) addressed the observed differential performance of students with varying measures of mathematics aptitude and specifically identified methods of assessment design that could allow better evaluation of student mastery of chemistry concepts. They posit that this could lead to greater opportunities for an instructor to reinforce correct conceptual problem-solving strategies over potentially incorrect algorithmic problem solving. (For example, with regard to testing mastery of the mole concept and stoichiometry, they suggest using assessment items that evaluate student understanding of “the process” required to reach a conclusion, rather than simply a numerical outcome.) Bain et al. (2019) present an overview of research into student reasoning and problem solving strategies at the intersection of mathematics and physical sciences with the goal of highlighting “frameworks from other disciplines that may be useful in characterizing mathematical reasoning in chemical contexts,” (Bain et al., 2019, p. 2086). Aligning research in chemistry classrooms with research in other science disciplines and mathematics-intensive non-STEM courses would be helpful in determining the extent of the impact of mathematical automaticity on student success and its interaction with chemistry conceptual understanding. If the lack of mathematical automaticity is symptomatic of more wide-spread problems with logic and number sense and is correlated with quantitative reasoning/quantitative literacy, logical thinking and sense of scale that are so vital in our technology-saturated work environments, research is needed in methods of expanding student experiences at the high school and university levels so that our students will be better prepared for the future.

Conflicts of interest

There are no conflicts to declare.

References

1. Albaladejo J. D. P., Broadway S., Mamiya B., Petros A., Powell C. B., Shelton G. R., Walker D. R., Weber R., Williamson V. M. and Mason D., (2018), ConfChem conference on mathematics in undergraduate chemistry instruction: MUST-know pilot study—math preparation study from Texas, J. Chem. Educ., 95(8), 1428–1429.
2. Andrews M. H. and Andrews L., (1979), First-year chemistry grades and SAT math scores, J. Chem. Educ., 56(4), 231.
3. Ausubel D. P., (1968), Educational psychology: a cognitive view, New York: Holt, Rinehart & Winston.
4. Bain K., Rodriguez J. M. G., Towns M. H., (2019). Chemistry and Mathematics: Research and Frameworks To Explore Student Reasoning. J. Chem. Educ., 96(10), 2086–2096.
5. Bain K., Rodriguez J. M. G., Moon A., and Towns M. H., (2019), Mathematics in Chemical Kinetics: Which Is the Cart and Which Is the Horse? ACS Symp. Ser., 1316, 25–46.
6. Barouch D. H., (1997), Voyages in conceptual chemistry, Sudbury, MA: Jones & Bartlett Learning.
7. Barrouillet P., Portrat S., and Camos V., (2011), On the law relating processing to storage in working memory, Psychol. Rev., 118(2), 175.
8. Bauer C. F., (2008), Attitude toward chemistry: a semantic differential instrument for assessing curriculum impacts, J. Chem. Educ., 85(10), 1440.
9. Belloni A. and Chernozhukov V., (2013), Least squares after model selection in high-dimensional sparse models, Bernoulli, 19, 521–547.
10. Bodner G. M., (1986), Constructivism: a theory of knowledge, J. Chem. Educ., 63(10), 873.
11. Bunce D. M. and Hutchinson K. D., (1993), The use of the GALT (Group Assessment of Logical Thinking) as a predictor of academic success in college chemistry, ACS Publications.
12. CAE, (2019), (Council Aid to Education). CLA+ for higher education is a performance-based critical-thinking assessment of college students [online], available at: https://cae.org/flagship-assessments-cla-cwra/cla/, accessed December 2019.
13. Chan J. Y. and Bauer C. F., (2014), Identifying at-risk students in general chemistry via cluster analysis of affective characteristics, J. Chem. Educ., 91(9), 1417–1425.
14. Clark R., Sweller J. and Kirschner P., (2012), Putting students on the path to learning: the case for fully guided instruction, Am. Educ., 36(1), 6–11.
15. Cooper M. and Klymkowsky M., (2013), Chemistry, life, the universe, and everything: A new approach to general chemistry, and a model for curriculum reform, J. Chem. Educ., 90(9), 1116–1122.
16. Cooper C. I. and Pearson P. T., (2012), A genetically optimized predictive system for success in general chemistry using a diagnostic algebra test, J. Sci. Educ. Tech., 21(1), 197–205.
17. Cooper C. I. and Stowe R. L., (2018), Chemistry Education Research—From personal empiricism to evidence, theory, and informed practice, J. Chem. Educ., 118, 6053–6087.
18. Cowan N., (2000), The magical number 4 in short-term memory: a reconsideration of mental storage capacity, Behav. Brain Sci., 24, 87–185.
19. Cowan N., (2010), The magical mystery four: How is working memory capacity limited and why? Curr. Dir. Psychol. Sci., 19, 51–57 [online], available at: http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2864034/, accessed December 2019.
20. Cozad L. E., Riccomini P. J., (2016). Effects of Digital-Based Math Fluency Interventions on Learners with Math Difficulties: A Review of the Literature. J. Spec. Educ. Apprent., 5(2), n2.
21. Craney C. L. and Armstrong R. W., (1985), Predictors of grades in general chemistry for allied health students, J. Chem. Educ., 62(2), 127–129.
22. Deam M. T., (1923), Diagnostic algebra tests and remedial measures, Sch. Rev., 31(5), 376–379.
23. Duit R., (2016), The constructivist view in science education—what it has to offer and what should not be expected from it, Investigaçôes em ensino de ciências, 1(1), 40–75.
24. Flanders G. R., (2017), The effect of gateway course completion on freshman college student retention, J. Coll. Stud. Ret.: Res., Theory Prac., 19(1), 2–24.
25. Geary D. C., Boykin A. W., Embretson S., Reyna V., Siegler R., Berch D. B. and Graban J., (2008), Chapter 4: Report of the task group on learning processes, The final report of the National Mathematics Advisory Panel, retrieved from the Department of Education website at https://www2.ed.gov/about/bdscomm/list/mathpanel/report/learning-processes.pdf.
26. Geary D. C., Hoard M. K., Nugent L. and Bailey D. H., (2013), Adolescents’ functional numeracy is predicted by their school entry number system knowledge, PLoS One, 8(1), e54651.
27. Gold M., (1979), Chem ed compacts: Calculators in freshman chemistry—An alternative view, J. Chem. Educ., 56(8), 526.
28. Goodstein M. P., (1983), Reflections upon mathematics in the introductory chemistry course, J. Chem. Educ., 60(8), 665–667.
29. Habley W. R., Bloom J. L. and Robbins S., (2012), Increasing persistence: Research-based strategies for college success, San Francisco, CA: Jossey-Bass, A Wiley Imprint.
30. Hanover Research, (2018), Best practices in first year student support, Arlington, VA: Hanover Research [online], available at: https://insights.hanoverresearch.com/hubfs/Nurturing/Content%20Asset%20Downloads/Higher%20Education/Reports%20and%20Briefs/HE%20Trend%20Report%202018%20-%20Final.pdf, accessed December 2019.
31. Hartman J. R. and Nelson E. A., (2015), “Do we need to memorize that?” or cognitive science for chemists, Found. Chem., 17(3), 263–274.
32. Hartman J. R. and Nelson E. A., (2016), Automaticity in computation and student success in introductory physical science courses [online], available at: https://arxiv.org/abs/1608.05006, accessed December 2019, Quiz available at: http://bit.ly/1HyamPc, accessed December 2019.
33. Hastie T. J., Tibshirani R. J. and Wainwright M., (2015), Statistical Learning with Sparsity: The Lasso and Generalizations, Boca Raton, FL: CRC Press.
34. Holme T. and Murphy K., (2012), The ACS Exams Institute Undergraduate Chemistry Anchoring Concepts Content Map I: General Chemistry [online] updated information available at: https://uwm.edu/acs-exams/, accessed December 2019.
35. Hovey N. W. and Krohn A., (1958), Predicting failures in general chemistry, J. Chem. Educ., 35(10), 507.
36. James G., Witten D., Hastie T. and Tibshirani R., (2013), An Introduction to Statistical Learning: with Applications in R, New York: Springer.
37. Jones M. G. and Taylor A. R., (2009), Developing a sense of scale: Looking backward, J. Res. Sci. Teach., 46(4), 460–475.
38. Karpp E. R., (1995), Paths to Success, vol. III, Validating the California Chemistry Diagnostic Test for Local Use.
39. Kilner W. C., (2014), The chem-math project: Enhancing success in general chemistry through the integration of mathematics, problem-solving and conceptual understanding. An action-research study, University of New Hampshire.
40. Kolopajlo L., (2019), Attitudinal and Mathematical Assessments as Measures of Student Success in a College General Chemistry II Course, Ohio J. Sci., 119(2), 17–27.
41. Lagowski J. J., (1993), Editorially Speaking: Different Students, Different Needs, J. Chem. Educ., 70(12), 957.
42. Leeb H. and Pötscher B. M., (2008), Sparse estimators and the oracle property, or the return of Hodges’ estimator, J. Econom., 142, 201–211.
43. Leopold D. G., (2018), ConfChem Conference on Mathematics in Undergraduate Chemistry Instruction: Strengthening Students' Math Fluencies through Calculator-Free Chemistry Calculations, J. Chem. Educ., 95, 1432–1433.
44. Leopold D. F. and Edgar B., (2008), Degree of mathematics fluency and success in second-semester introductory chemistry, J. Chem. Educ., 85(5), 724–731.
45. Lewis S. E. and Lewis J. E., (2007), Predicting at-risk students in general chemistry: comparing formal thought to a general achievement measure, Chem. Educ. Res. Pract., 8(1), 32–51.
46. Mason D., (2015), Knowledge decay and content retention of students in first-semester general chemistry, LUMAT: Res. Pract. Math., Sci. Tech. Educ., 3(3), 341–352.
47. Mason D., Fies C. H., Taylor S. E. and Mittag K. C., (2004), How Scientists Communicate with Numbers, Texas Math. Teach., LI(1), 14–21.
48. Mason D. and Mittag K. C., (2001), Evaluating success of Hispanic-surname students in first-semester general chemistry, J. Chem. Educ., 78(2), 256–259. [Correction: J. Chem. Educ., 78(12), 1597].
49. Mason D. and Verdel E., (2001), Gateway to success for at-risk students in a large-group introductory chemistry class, J. Chem. Educ., 78(2), 252.
50. Miller G. A., (1956), The magical number seven, plus or minus two: some limits on our capacity for processing information, Psychol. Rev., 63(2), 81–97.
51. Miller E. K., Lundqvist M. and Bastos A. M., (2018), Working Memory 2.0. Neuron, 100(2), 463–475.
52. Monserud M. A., (2011), Changes in grandchildren's adult role statuses and their relationships with grandparents, J. Fam. Issues, 32(4), 425–451.
53. Murphy K., Holme T., Zenisky A., Caruthers H. and Knaus, K., (2012), Building the ACS Exams Anchoring Concept Content Map for Undergraduate Chemistry, J. Chem. Educ., 89(6), 715–720.
54. Nelson E. A., (2017). Cognitive Science and the Common Core Mathematics Standards, Nonpartisan Educ. Rev., 13(3), 1–18.
55. Nelson E. A., (2018), ConfChem Conference on Mathematics in Undergraduate Chemistry Instruction: Addressing Math Deficits with Cognitive Science, J. Chem. Educ., 95, 1440–1442.
56. Osborne R. J. and Wittrock M. C., (1983), Learning science: A generative process, Sci. Educ., 67(4), 489–508.
57. Ozsogomonyan A. and Loftus D., (1979), Predictors of general chemistry grades. J. Chem. Educ., 56(3), 173.
58. Pedhazur E. J., (1997), Multiple Regression in Behavioral Research, 3rd edn, Fort Worth, TX: Wadsworth/Thomson Learning.
59. Petros A., Weber R., Broadway S., Ford R., Powell C., Hunter K., Williamson V., Walker D., Mamiya B., Del Pilar J., Shelton G. R., and Mason D., (2017), MUST-Know Pilot—Math Preparation Study from Texas, ACS DivCHED CCCE (Committee on Computers in Chemical Education) online conference organized by Cary Kilner and Eric Nelson [online] available at: https://confchem.ccce.divched.org/2017FallConfChem, accessed December 2019.
60. Piaget J. (1977), The development of thought: Equilibration of cognitive structures, (Trans A. Rosin), Viking.
61. Pickering, M., (1975), Helping the high risk freshman chemist, J. Chem. Educ., 52(8), 512.
62. Pienta N. J. (2003), A placement examination and mathematics tutorial for general chemistry, J. Chem. Educ., 80(11), 1244.
63. Pyburn D. T., Pazicni S., Benassi V. A. and Tappin E. E., (2013), Assessing the relation between language comprehension and performance in general chemistry, Chem. Educ. Res. Pract., 14(4), 524–541.
64. Radunzel J., Noble J., Wheeler S., (2014), Dual-Credit/Dual-Enrollment Coursework and Long-Term College Success in Texas, Issue Brief, ACT, Inc.
65. Ralph V. R. and Lewis S. E., (2018), Chemistry topics posing incommensurate difficulty to students with low math aptitude scores. Chem. Educ. Res. Pract., 19(3), 867–884.
66. Ralph V. R., Lewis S. E., (2019). An explanative basis for the differential performance of students with low math aptitude in general chemistry. Chem. Educ. Res. Pract., 20(3), 570–593.
67. Rodriguez J. M. G., Bain K., Towns M. H., Elmgren M., Ho F. M., (2019). Covariational reasoning and mathematical narratives: investigating students’ understanding of graphs in chemical kinetics. Chem. Educ. Res. Pract., 20(1), 107–119.
68. Rodriguez J.-M. G., Santos-Diaz S., Bain K., and Towns M. H., (2018), Using Symbolic and Graphical Forms To Analyze Students’ Mathematical Reasoning in Chemical Kinetics. J. Chem. Educ., 95(12), 2114–2125.
69. Scofield M. B., (1927), An experiment in predicting performance in general chemistry, J. Chem. Educ., 4, 1168.
70. Shell D. F., Brooks D. W., Trainin G., Wilson K. M., Kauffman D. F. and Herr L. M., (2010), The unified learning model, Dordrecht, Netherlands: Springer.
71. Spencer H. E., (1996), Mathematical SAT test scores and college chemistry grades, J. Chem. Educ., 73(12), 1150.
72. Srougi M. C. and Miller H. B., (2018), Peer learning as a tool to strengthen math skills in introductory chemistry laboratories, Chem. Educ. Res. Pract., 19(1), 319–330.
73. Stickney E. M., Sharp L. B., Kenyon A. S., (2012), Technology-enhanced assessment of math fact automaticity: Patterns of performance for low-and typically achieving students. Assess. Eff. Interv., 37(2), 84–94.
74. Stone K. L., Shaner S. E. and Fendrick C. M., (2018), Improving the Success of First Term General Chemistry Students at a Liberal Arts Institution, Educ. Sci., 8(1), 5 [online], available at: https://www.mdpi.com/2227-7102/8/1/5, accessed October 2019.
75. Taber K. S., (2000), Chemistry lessons for universities? A review of constructivist ideas, Univ. Chem. Educ., 4(2), 63–72.
76. Taber K. S., (2015), Meeting educational objectives in the affective and cognitive domains: Personal and social constructivist perspectives on enjoyment, motivation and learning chemistry, Affective dimensions in chemistry education, Springer, pp. 3–27.
77. Tai R. H., Ward R. B. and Sadler P. M., (2006), High school chemistry content background of introductory college chemistry students and its association with college chemistry grades, J. Chem. Educ., 83(11), 1703.
78. The Gardner Institute, (2018), Koch A. K. and Drake B. M., Digging into the Disciplines: The Impact of Gateway Courses in Accounting, Calculus, and Chemistry on Student Success [online], available at: https://umaine.edu/provost/wp-content/uploads/sites/14/2018/11/Gardner-Institute-Digging-into-the-Disciplines-The-Impact-of-Gateway-Courses-in-Accounting-Calculus-and-Chemistry-on-Student-Success.pdf, accessed December 2019.
79. Tobin K. G. and Capie W., (1981), The development and validation of a group test of logical thinking, Educ. Psychol. Meas., 41(2), 413–423.
80. Troutman D. R., Handrix-Soto A., Creusere M., and Mayer E., (2018), The University of Texas System Dual Credit Study: Dual Credit and Success in College [online], available at: https://data.utsystem.edu/sites/default/files/upload/UTSystem-DualCreditStudy.pdf, accessed December 2019.
81. Villalta-Cerdas A., Dubrovskiy A., Mamiya B., Walker D. R., Powell C. B., Broadway S., Weber R., Shelton G. R., Mason D., (N.D.), Personal characteristics influencing college readiness of Hispanic students in a STEM gateway course: first-semester general chemistry, J. Coll. Sci. Teach., in press.
82. Von Glaserfeld E., (1995), Radical constructivism: A way of knowing and learning, London, England: Palmer Press.
83. Wagner E. P., Sasser H. and DiBiase W. J., (2002), Predicting students at risk in general chemistry using pre-semester assessments and demographic information, J. Chem. Educ., 79(6), 749.
84. Weisman R. L., (1981), A mathematics readiness test for prospective chemistry students, J. Chem. Educ., 58(7), 564.
85. Wilkerson S. L., (2008), An empirical analysis of ractors that influence the first year to second year retention of students at one large, Hispanic Serving Institution (HSI), Dissertation Texas A&M University.
86. Williamson K. C., Williamson V. M., and Hinze S., (2017), Administering spatial and cognitive instruments in-class and on-line: Are these equivalent? J. Sci. Educ. Tech., 26, 12–23.
87. Williamson V., (2008), The particulate nature of matter: an example of how theory-based research can impact the field, Nuts Bolts Chem. Educ. Res., 976, 67–78.
88. Williamson V. M., Walker D. R., Chuu E., Broadway S., Mamiya B., Powell C. B., Shelton G. R., Weber R., Dabney A. R. and Mason D., (2020), Impact of basic arithmetic skills on success in first-semester general chemistry, Chem. Educ. Res. Pract., 21, 51–61.
89. Zusho A., Pintrich P. R. and Coppola B. (2003), Skill and will: The role of motivation and cognition in the learning of college chemistry, Intern. J. Sci. Educ., 25(9), 1081–1094.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0rp00006j

---