Development of a measurement instrument to assess students' proficiency levels regarding galvanic cells

Abstract

The galvanic cell is a basic concept in electrochemistry. To assess mainland Chinese students’ proficiency levels in galvanic cells, the Galvanic Cell Proficiency Level Assessment (GCPA) was developed based on the Rasch model. The GCPA was developed through a pilot test and consists of seven multiple-choice questions and four open questions. The assessment instrument was administered to 621 high school students in the 11th grade, and the test results showed good reliability and validity. The interview results supported the validity of the data generated by the instrument.

---

Introduction

Conceptual learning is one of the core areas of science education research because it is very important for students to establish scientific concepts correctly, which will affect their subsequent reasoning and judgment regarding many issues. Researching and assessing students' concept learning has always been an active area of research in the science education community (Wren and Barbera, 2014).

In the past few decades, research on concept learning based on conceptual change theory has become a paradigm. Student alternative conceptions and conceptual change research has been embedded in various theoretical frameworks (Duit and Treagust, 2003). In the field of chemistry education, students' alternative conceptions regarding almost all subjects have been explored by researchers through the development of instruments (Treagust, 1986; Voska and Heikkinen, 2000; Tan et al., 2005; Brandriet and Bretz, 2014). Some researchers combine alternative conceptions with conceptual understanding and investigate whether students understand concepts by probing the students' alternative conceptions (Özkaya et al., 2006; Lu and Bi, 2016) or use the number of alternative conceptions as a criterion to assess the students' concept understanding level (Adadan et al., 2010). However, the actual research results have shown that conceptual change is very difficult (Hewson and Thorley, 1989). Alternative conceptions do not disappear with teaching (Tyson et al., 1997; Treagust and Duit, 2008) but change as students’ understanding of a concept deepens.

Science teaching focuses on achieving the following two main goals: promoting students' understanding of major scientific concepts and improving students' problem solving ability (Salta and Tzougraki, 2011). Focusing on alternative conceptions provides a good solution for understanding students' ideas, while mastering concepts and applying concepts to solve problems are also important aspects of student learning (Gillmore et al., 1975). Proficiency levels represent the performance levels of the abilities shown by students while solving problems (Gunstone, 2015). Compared with the number of studies that investigated alternative conceptions, relatively few studies have investigated students' proficiency levels in problem solving.

In a study investigating students' concept learning and problem solving, Nurrenbern and Pickering (1987) distinguished between two different reasoning methods used by students, namely, algorithmic and conceptual reasoning. Algorithmic reasoning indicates that students solve problems by memorizing a series of programs, while conceptual reasoning emphasizes that students solve problems by applying their understanding of core concepts (Cracolice et al., 2008; Talanquer, 2012). When different students solve problems, some students may memorize a series of routines, and some students may form a series of well-structured rules after obtaining a deep understanding of the concepts (Talanquer, 2012).

Electrochemistry has always been considered one of the most difficult topics in high school chemistry courses by students and teachers (Rogers et al., 2000; De Jong and Treagust, 2002). As Butts and Smith noted, high school students find galvanic cells and electrolytic cells to be very difficult to understand because these topics involve the concepts of electricity and redox, both of which are very challenging (Butts and Smith, 1987). In the past, researchers have developed some measurement instruments to investigate students' difficulties and alternative conceptions in learning about galvanic cells (Garnett and Treagust, 1992; Ogude and Bradley, 1994; Schmidt et al., 2007). However, no researchers have assessed students' proficiency levels in solving galvanic cell problems. To help teachers fully understand students' performance levels in solving galvanic cell problems, this study aims to develop an instrument to assess mainland Chinese students' proficiency levels in solving galvanic cell problems. On the one hand, this instrument could provide diagnostic feedback to teachers regarding their classroom teaching and allow the teachers to improve their teaching to improve their students' proficiency levels in solving galvanic cells problems. On the other hand, this instrument could provide a summary of the students’ proficiency levels in solving galvanic cell problems to the teachers and students after the course.

The question to be addressed in the study is: What evidence is indicative of the reliability and validity of the instrument developed in this study to assess students’ proficiency levels in galvanic cells?

Literature review

1. Basic knowledge in galvanic cell learning

Understanding the galvanic cell requires “complex and organized” conceptual knowledge. First, the concepts of electrolytes, electrodes, electrode reactions and potential differences are critical to the understanding of galvanic cells (De Jong and Treagust, 2002). Second, understanding the galvanic cell requires not only an understanding of the isolation of macroscopic components but also a systematic understanding of the formation of current in the galvanic cell from the microscopic perspective of the directional movement of electrons (external circuit) and the directional movement of ions (internal circuit). The basic scientific knowledge necessary to understand the galvanic cell has been summarized in related papers concerning the assessment of electrochemical concepts (Rahayu et al., 2011).

The Chemistry Curriculum Standard of High School in mainland China (2017) stipulates the content requirements for high school students' galvanic cell learning. Students are required to use redox reaction theory, metal activities and electrical knowledge in physics to qualitatively understand and analyze related issues (such as understanding the basic elements that constitute the galvanic cell, judging the positive and negative electrodes of the galvanic cell, judging the electrode reactants, writing electrode reactions and designing a galvanic cell device). Concepts, such as the electrode potential, are not required according to the curriculum standard.

Based on the content requirements for galvanic cell learning in the Chemistry Curriculum Standard of High School in mainland China (2017), we summarize the basic knowledge needed for galvanic cell learning in high school in Table 1.

Table 1 Basic knowledge in galvanic cell learning

Contents	Basic knowledge
Note: in physics, it is believed that electrons undergo a directional movement under the action of an electric field to display a current. It is stipulated that the direction of the positive charge is the direction of the current, and the current always flows from the positive pole with a high potential to the negative pole with a low potential, which is the opposite of the direction of the electron. According to this rule, electrons in the galvanic cell flow from the negative electrode (anode) to the positive electrode (cathode) in the external circuit. To maintain consistency with the definition of electrodes in physics, the Chemistry Curriculum Standard of High School in mainland China uses “positive electrode” and “negative electrode” uniformly in galvanic cells.
Galvanic cell	A galvanic cell is a device that directly converts chemical energy into electrical energy through an oxidation–reduction reaction.
	Electrode materials, electrode reactants, electronic conductors, and ionic conductors are the basic elements of a galvanic cell.
Electrode materials	Electrode materials are electrical conductors placed in electrolytes to provide a surface for oxidation or reduction reactions.
	Inert electrodes, such as graphite and platinum, are made of conductive materials and do not undergo chemical changes during cell reactions.
Electrode reactants	The electrode reactant is a substance involved in the electrode reaction (the half-reaction that occurs at the electrode).
	The relative tendency of electrode reactants to be oxidized or reduced determines the final redox reaction.
	The negative electrode reactant undergoes an oxidation reaction, while the positive electrode reactant undergoes a reduction reaction.
Electronic conductors	Electronic conductors, such as metals, graphite, and compounds of certain metals, rely on the directional movement of free electrons.
	Electrons are transferred from the negative reactant to the positive reactant through an external circuit or metal conductor connected to the electrode.
Ionic conductors	Ionic conductors, such as electrolyte solutions or molten electrolytes, conduct electricity by the directional motion of ions.
	The salt bridge is an aqueous solution containing a strong electrolyte that provides a continuous path for the movement of particles between half-cells.
	The anion passes through the electrolyte to the negative electrode, while the cation passes through the electrolyte to the positive electrode.
	The movement of ions completes the circuit and remains neutral.

---

2. Research concerning alternative conceptions of galvanic cells

Concepts in students' minds that are not consistent with scientific concepts are called alternative conceptions, which often hinder students' in-depth understanding of concepts and ability to solve practical problems. However, for teachers and test designers, alternative conceptions can not only be an important source of information for teachers but can also help them create an effective dialogue with learners by understanding their alternative conceptions and designing test propositions according to these conceptions. Previous researchers have performed many studies investigating alternative conceptions of galvanic cells. We summarized the main alternative conceptions of galvanic cells identified in these previous studies in Table 2.

Table 2 Alternative conceptions of galvanic cells

Contents	Alternative conceptions
Electrode (materials)	The polarity of the electrodes depend on the physical location of the half-cells (Sanger and Greenbowe, 1997).
	A lack of identifying electrodes (Schmidt et al., 2007).
	No reaction will occur if inert electrodes are used (Sesen and Tarhan, 2013).
	Inert electrodes can be oxidized or reduced (Sesen and Tarhan, 2013).
	The anode is positively charged because it has lost electrons; the cathode is negatively charged because it has gained electrons (Garnett and Treagust, 1992).
	The anode is negatively charged and therefore attracts cations; the cathode is positively charged and therefore attracts anions (Garnett and Treagust, 1992).
Electrode reactants	Reduction occurs at the anode, whereas oxidation occurs at the cathode (Karsli and Çalik, 2012).
	The anode electrode mass increases over time (Karsli and Çalik, 2012).
	Oxidizing metal and reducing metal ions react in 1 : 1 ratio irrespective of their charges (Rosenthal and Sanger, 2012).
	A lack of writing the cell and half-cell reaction correctly (Karsli and Çalik, 2012; Osman and Lee, 2014).
Electronic conductors	The cathode loses electrons, and the anode gains electrons (Karsli and Çalik, 2012; Osman and Lee, 2014).
	Electrons moved from one electrode to the other through the salt bridge (Rahayu et al., 2011).
Ionic conductors	The movement of ions in solution does not constitute an electric current (Garnett and Treagust, 1992).
	When an electrolyte conducts a current, electrons move to an ion at the cathode and are carried by that ion to the anode (Schmidt et al., 2007).
	The salt bridge supplies electrons to complete the circuit (Garnett and Treagust, 1992).
	Anions in the salt bridge moved to the cathode while cations moved to the anode (Rahayu et al., 2011).
	In an electrochemical cell, the anions and cations move until their concentrations in both half-cells are equal (Garnett and Treagust, 1992).

---

Theoretical framework

In 1956, Bloom and others divided the cognitive process of learners into six levels from simple to complex: knowledge, comprehension, application, analysis, synthesis, and evaluation (Bloom, 1956). Anderson revised the original taxonomy to incorporate new developments and achievements in cognitive psychology. The revised framework contains two basic dimensions. The first is the knowledge dimension. Knowledge is divided into four types: factual knowledge, conceptual knowledge, procedural knowledge, and metacognitive knowledge. The second dimension is the cognitive process, which is divided into six categories from low to high: remember, understand, apply, analyze, evaluate and create (Anderson and Krathwohl, 2001; Krathwohl and Anderson, 2009).

Based on the revised category of the cognitive process dimension and the content requirements of students' galvanic cell learning in the Chemistry Curriculum Standard of High School in mainland China, we propose three levels of student proficiency in solving galvanic cell problems, corresponding to the categories of “remember”, “understand” and “apply and analyze” in Bloom's classification of cognitive goals, the connotations and corresponding behaviors of each level are shown in Table 3.

Table 3 Levels of proficiency in galvanic cells

Level	Description	Behavior
Level 3	Solving chemical problems related to galvanic cells	Design a galvanic cell device, analyze the principle and real problems of unfamiliar chemical power sources
Level 2	Understanding the working principle of galvanic cells	Understand the electrode and the cell reaction and explain the working principle of the galvanic cell with a known device or a known cell reaction
Level 1	Remembering the related knowledge regarding the galvanic cell	Identify the galvanic cells and electrolytes that have been learned and recall the knowledge about galvanic cells that has been learned

---

First, students can recognize and recall knowledge about the galvanic cell content. For example, students can know the basic elements of galvanic cells, identify a galvanic cell device that they have learned, identify the electrolyte of the cell, and recall the knowledge of the galvanic cell that they have learned, such as the copper–zinc dilute sulfuric acid galvanic cell, to reach the “remember” category.

Second, students can understand the working principle of the galvanic cell. For example, students know that the activeness of the electrode material is not necessarily different and that the electrode material does not necessarily participate in the electrode reaction and can explain the principle of the galvanic cell within the context of a specific device or cell reaction, including judgements regarding the electrode materials and electrode reactants in a device and the change in acidity and alkalinity in the electrolyte solution and the writing of electrode reaction equations, to achieve the category of “understand”.

Finally, students can apply their understanding of the working principle of the galvanic cell to solve practical chemical problems, including the design of a galvanic cell device according to a given cell reaction and the analysis of an unfamiliar chemical power source by decomposing its constituting elements and determining their interrelation, corresponding to the “apply and analyze” categories.

Research method

1. Designing the items

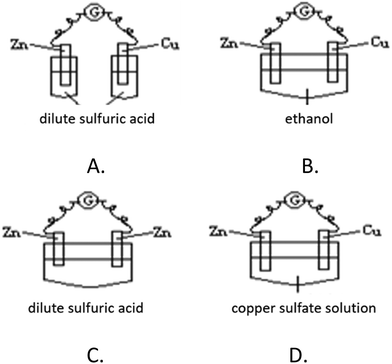
Various formats can be used to evaluate students' concept learning, including multiple-choice questions (Engelhardt and Beichner, 2004), two-tier diagnostic questions (Treagust, 1988), concept mapping (Novak and Cañas, 2008), interviews, etc. Different item formats play different roles in measuring students’ concept learning. Multiple-choice questions are appropriate for measuring teaching objectives at multiple levels and are particularly appropriate for item analysis and identifying student weaknesses (Sax and Newton, 1989). The use of open questions provides additional advantages, allowing students to articulate the understanding needed to craft their response in their own words (Loh and Subramaniam, 2018). According to the characteristics of the complexity of the concept of galvanic cells and the classification of the proficiency level in galvanic cells, we adopted various item formats, including multiple-choice questions (single-answer, multiple-answer and two-tier questions) and open questions. Among them, the level of remembering and understanding galvanic cells was mainly measured in the form of multiple-choice questions, while the higher level of problem solving was measured in the form of open questions.

Level 1 measures students' memory of galvanic cell knowledge. In high school chemistry textbooks, the copper–zinc dilute sulfuric acid galvanic cell appears as an example for teaching; thus, we use this cell as the context to examine students' memorization of the knowledge related to galvanic cells that they have learned (Fig. 1). The four choices examine the electrode in the cell, the direction of current flow, the type of electrode reaction and the phenomenon of electrode reactions. The students’ correct answer can be based on merely memorizing knowledge about galvanic cells. To design this item, we refer to the alternative conceptions of galvanic cells reported in existing research. Option A represents the difficulties a student experiences when identifying the electrodes in galvanic cells (Schmidt et al., 2007), and option C considers the alternative conception of “a reduction reaction occurs at the anode (negative electrode)” among students (Karsli and Çalik, 2012).

Fig. 1 Example of a level 1 item.

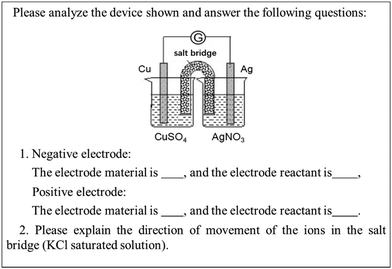
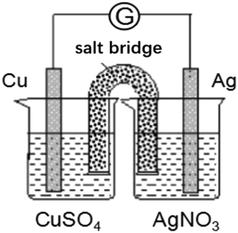
Level 2 examines students' understanding of the working principle of galvanic cells. If students understand the working principle of galvanic cells, they should be able to explain an uncomplicated galvanic cell device, determine the electrode reaction occurring in the device, and determine the electrode materials and electrode reactants. Accordingly, we designed the item shown in Fig. 2. In addition to the behavior of the students at the corresponding level, we also refer to the alternative conceptions reported in the literature. In the second question, we let students explain the direction of ion movement in the salt bridge. This question also considers the alternative conception of “anions in the salt bridge move to the cathode while cations move to the anode” (Rahayu et al., 2011).

Fig. 2 Example of a level 2 item.

Designing simple galvanic cells examines the students' ability to solve practical problems using the working principle of galvanic cells. Students need to analyze the cell reaction, determine the cell electrode reactants, choose a suitable electrode material and electrolyte, and design a galvanic cell as an operational cell device. We developed this item in the form of an open question (Fig. 3).

Fig. 3 Example of a level 3 item.

After the preliminary formulation of the items, two university chemistry professors and two experienced high school teachers were invited to examine the rationality and scientific integrity of the items and whether the items could reflect the development of students' proficiency level in galvanic cells. Then, the contents and descriptions of some items were revised according to the opinions of the experts. The 11 items of the assessment instrument were determined, including 8 multiple-choice questions (6 single-answer questions, 1 multiple-answer question and 1 two-tier question) and 3 open questions. Since the subjects were high school students from mainland China, the assessment instrument is presented in Chinese.

2. Measurement model and data analysis

The Rasch model is a type of a one-parameter logistic model of item response theory and is widely used in the construction of assessment instruments (Liu and Boone, 2006; Wang et al., 2017). The formula and uses of Rasch model can be referred to relevant literature (Liu and Boone, 2006). The Rasch model estimates both the difficulty of the items and the ability of the students, and the performance of individuals on an item (usually expressed as raw scores) is converted to equidistant logit values. By comparing the logit values, it is possible to compare the difficulty of different items and individuals’ ability (in this study, ability refers to the proficiency level in galvanic cells).

This study used the dichotomous Rasch model to encode and analyze the data. The students' answers are coded in the form of “0” and “1” using “all or nothing” as the standard. Thus, answering a question correctly is coded as “1”, and any mistake is coded as “0”. Notably, regarding the two-tier multiple choice questions, a correct choice in both tiers is coded as “1”; otherwise, the response is coded as “0”. Regarding the open questions, although all sub-items share background information, these sub-items are independent of each other. Therefore, we also make a correct or incorrect judgment of each sub-item in the open questions.

The data were imported into Winsteps 3.72.0 software for the statistical analysis. The interview serves as a secondary data source and an in-depth investigation of whether the assessment instrument can effectively measure and distinguish the levels of the students' proficiency.

3. Pilot test

The measurement based on the Rasch model requires participants to have differences in ability. Therefore, we adopted the cluster sampling method to select 224 students from 2 classes of grade 11 in a key high school and 3 classes of grade 11 in an ordinary high school in Jinan, Shandong Province, for the pilot test (key high schools refer to schools located in the central area of the city, and the students' academic performance is relatively good; ordinary high schools refer to schools located in remote areas in the city, and the students' academic performance is relatively poor). The test was approved by the school, the teacher and the students themselves and lasted for 30 minutes; the entire test process was supervised by the instructor. A total of 224 questionnaires were sent out, and 224 responses were received, for a recovery rate of 100%.

Since the Rasch model estimates the ability of the subject and the difficulty of the item based on the response of the subject on a series of items, it is necessary to test to the extent to which the measured data fit the theoretical model. Winsteps provides the following two forms of chi-square fit indicators: Outfit Mean Square (Outfit MNSQ) and Infit Mean Square (Infit MNSQ). These fitting indicators are calculated based on the residuals. Outfit MNSQ is the mean square of the residuals. Infit MNSQ is the mean square of the residuals after weighting (the performance of those close to the difficulty of the item receives more weight) (Bond and Fox, 2013). The Infit and Outfit indicators also have standardized forms expressed as Infit ZSTD and Outfit ZSTD, respectively. In addition to model-data-fit (or simply fit), the Rasch model reflects the quality of the measurement through multiple indicators. The meaning and significance of the indicators, including unidimensionality, local independence, subject and item separation index, reliability (separation reliability), etc., are described along with the results of the field test.

A Rasch analysis of the pilot test data was performed based on the above indicators. In general, in the pilot test, the Rasch analysis resulted in a person separation index of 1.00, a corresponding person reliability coefficient of 0.50, an item separation index of 5.31, and a corresponding item reliability coefficient of 0.97. We modified the items according to the results of the pilot test. First, a multiple-choice question in the pilot test was deleted (the item will no longer appear in the field test after deletion). The reason for the deletion was that the item not only did not meet the item fit criteria but also combined galvanic cells and electrolytic cells. The item assessed not only the students' understanding of the galvanic cell but also their relevant knowledge of the electrolytic cell. Second, an item was added to level 3 (this item corresponds to Q11 in the field test). This item is an open question concerning the background of a fuel cell, the principle of a fuel cell and the real problems existing in the cell.

4. Field test

After the modification of the items after the pilot test, 11 items of the assessment instrument for the proficiency level in galvanic cells were finally determined (see Appendix). The item list of the GCPA is shown in Table 4. The GCPA includes the following two item formats: multiple-choice questions and open questions. The multiple-choice questions include 5 single-answer questions (Q1, Q2, Q5, Q6, Q7), 1 multiple-answer question (Q3) and 1 two-tier multiple-choice question (Q4). Each open question contains 1 to 4 subquestions (Q8, Q9, Q10, Q11).

Table 4 GCPA item list

Level	Behavior	Item	Electrode materials	Electrode reactants	Ionic conductors	Electronic conductors
Level 3	Design a galvanic cell device	Q9	✓	✓	✓	✓
	Analyze the principle and real problems of unfamiliar chemical power sources	Q11.1		✓
		Q11.2			✓
		Q11.3		✓
Level 2	Understand the electrode and the cell reaction	Q2	✓	✓
		Q4		✓
	Explain the working principle of the galvanic cell with a known device	Q8.1	✓	✓
		Q8.2			✓
	Explain the working principle of the galvanic cell with a known cell reaction	Q7	✓	✓	✓	✓
		Q10.1		✓
		Q10.2		✓
		Q10.3			✓
		Q10.4				✓
Level 1	Identify the galvanic cells and the electrolytes that have been learned	Q1	✓	✓	✓	✓
		Q3			✓
	Recall knowledge about galvanic cells that has been learned	Q5	✓	✓
		Q6	✓	✓

---

To enable the test sample to cover as many students as possible, we selected a key high school and an ordinary high school in east, central and west Shandong province. Using the cluster sampling method, 621 students from 12 11th-grade classes of 6 schools were tested. Ethics clearance for the study was obtained from the schools’ institutional oversight board. All participants were informed of the purpose and procedure of the test and were told that their participation was voluntary and their anonymity would be guaranteed. The students consented to participate in the test and possible subsequent interviews. All students participating in the test covered the galvanic cell content in a high school chemistry course. The courses related to redox reaction theory and the acidity and alkalinity of solutions have also been completed. The testing process was approved by the school leaders and chemistry teachers, and the entire process was supervised by the teachers. The testing time was 30 minutes.

A total of 621 questionnaires were distributed during the testing process, and 621 questionnaires were collected. Excluding one questionnaire that was not seriously answered, the effective sample size was 620, and the effective recovery rate was 99.8%.

5. Interview

The Rasch model measures the difficulty of the items and the ability of the students on the same logit scale. The greater the difficulty of an item, the less likely the student will answer the item correctly. When the difficulty value of an item is greater than the average ability value of the student, the item is difficult for the student overall. Interviews related to items with which students have difficulty in responding can further validate the assessment instrument's differentiation of student proficiency levels.

A total of 10 students were interviewed, and each interviewee's questions were related to their answers. The interview lasted for 10–15 minutes. The interview was recorded.

Result and discussion

Unidimensionality and local independence

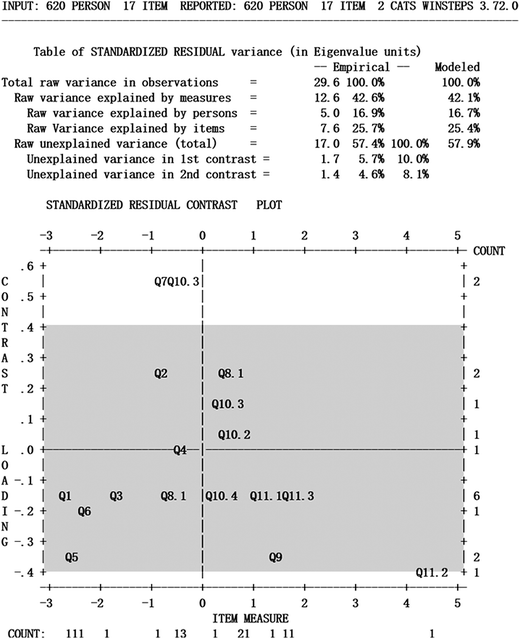
The unidimensionality of the measurement scale and the local independence of the measurements item are two basic assumptions of the Rasch model (Liu, 2010; Barbera, 2013). Regarding unidimensionality, the instrument must examine only content relevant to the students' proficiency level in the galvanic cell. The purpose of the unidimensionality test is search for data that are inconsistent with the latent trait of the “proficiency level in galvanic cells”, i.e., whether other components affect the students' responses to the item. The unidimensionality of the Rasch model is calculated based on the basic principle of residual analysis, which represents the correlation between the test scores and other components after controlling for the principal component (the proficiency level in galvanic cells). The results are shown in the residual comparison diagram (Fig. 4).

Fig. 4 Plot of item loading.

In Fig. 4, the horizontal axis represents the item measurement, and the vertical axis represents the correlation coefficient with other latent variables. The Rasch model explained 42.6% of the total variance, leaving 57.4% of the total variance unexplained. Among these dimensions, the dimension with the greatest influence in the unexplained variance only accounts for 5.7%, which is not greater than 10%. The influence of this largest dimension on the students' answers can be ignored, and other smaller dimensions can also be ignored. This finding suggests that although multiple extra dimensions may influence students' responses, none of these dimensions have a significant impact. Based on these data, it is believed that the GCPA is unidimensional.

Local independence requires that students are not affected by other items when answering a certain item. When the correlation coefficient is between −0.40 and 0.40, the item is considered to be in one dimension, which is marked with a gray area in the figure. Fig. 4 shows that most item correlation coefficients fall between −0.4 and +0.4, but items Q7 and Q10.3 fall beyond the scope of this range, with correlation coefficients of 0.56 and 0.55, respectively. An item can be considered highly locally dependent only when the correlation coefficient exceeds 0.7 (Linacre, 2011). Fig. 4 shows that the correlation coefficient of all items is less than 0.7; thus, the items can be considered locally independent. This finding indicates that the Rasch model can be used to analyze the data obtained from the GCPA.

In contrast to general item response theory, the Rasch model requires the collected data to meet the prior requirements of the model rather than using different parameters to adapt to the characteristics of the data. However, the Rasch model is an ideal mathematical model that is unlikely to be perfectly realized in realistic measurement because even simple tests may be disturbed by irrelevant factors (Yan zi, 2010). For example, in addition to proficiency in the galvanic cell, the performance of the student may be affected by the student's reading comprehension ability (ability to read the item), the student's physical condition, the student's willingness at the time of the test, and other unpredictable factors.

Research has demonstrated that data are difficult to render unidimensional and that deleting certain items in an assessment instrument requires rigorous consideration of whether these items obviously differ from other items given the assessment aim (Linacre, 2011). Q7 and Q10.3 evaluated whether the students reached level 2 by examining the students' description of the working principle of the galvanic cell given the cell reaction in the form of multiple-choice questions and open questions, respectively. Q10.3 specifically addressed changes in the acidity and alkalinity of the electrode solution. Judging from the test content, the two items did not extent beyond the scope of the galvanic cell; thus, we decided to retain these two items.

Reliability

Table 5 shows the overall statistics of the field test, including the person and item average measurement estimates (measure), fitting indicators (Infit and Outfit MNSQ and Infit and Outfit ZSTD), separation index (separation), and reliability.

Table 5 Summary person and item statistics

Parameter (N)	Measure	Infit		Outfit		Separation	Reliability
		MNSQ	ZSTD	MNSQ	ZSTD
Person (620)	0.63	1.00	0	1.03	0.1	1.51	0.69
Item (17)	0	0.99	−0.3	1.04	−0.1	14.27	1.00

---

In the Rasch analysis, the mean of the item estimates is set to 0 logit by default. As shown in Table 5, the average ability estimate of the subjects (0.63 logit) is higher than the average difficulty estimate of the items (0 logit), indicating that the instrument is easy for the test samples overall. The separation index is the ratio of the true standard deviation of a person (or item) to the error standard deviation. The separation index is used to reflect the discrimination of the different ability levels of the subjects by assessment tools. The larger the separation index, the better the discrimination effect. A separation index higher than 1.5 is acceptable, and a separation index greater than 2 is considered good (Duncan et al., 2003). As shown in Table 5, the person separation index is 1.51, and the item separation index is 14.27. The separation index of the items is very high, and the separation index of the person is acceptable.

Reliability refers to the reproducibility of relative measurement positions, and its relationship with the separation coefficient is Reliability = Separation coefficient²/(1 + Separation coefficient²) (Linacre, 2011). Analogous to Cronbach's alpha, reliability is bounded by 0 and 1. The data shown in Table 5 reveal that the reliability of the person is 0.69 and that the reliability of the item is 1.00.

Compared with the pilot test, the separation index and separation reliability of the person and item improved. The reliability of the item is very high, and the reliability of the person is also acceptable. This finding is similar to the research results reported by Luxford and Bretz (2014), who showed that the reliability did not exceed 0.7 when they tested high school students’ understanding of other chemistry concepts. Adams and Wieman (2011) proposed that one reason for the low value of Cronbach's α was the measurement of students’ fragmented knowledge with alternative frameworks. Because students' alternative conceptions are considered in the item design, the reliability of the person can be reduced. The acquisition of a high person reliability requires a sample with a large ability range and/or an instrument with many items (Linacre, 2011). Because the purpose of the instrument developed in this paper is related to low-risk classroom assessment and teacher teaching decisions, the reliability is acceptable (Lu and Bi, 2016).

Validity

Item fit. The Rasch model assumes that high-level students are more likely to answer a question correctly than low-level students (Barbera, 2013). Item fit analysis can verify whether the item conforms to the Rasch model and distinguish the problematic items accordingly. The estimate of the item difficulty and its accompanying error estimate in logits are given in Table 6. Of all items, the easiest is Q1 (−2.68 logit), and the most difficult is Q11.2 (+4.5 logit). The closer the standard error (SE) is to 0, the better. The standard error of all items is less than 1.0, and the maximum standard error is 0.21.

Table 6 Item fit statistics

Item	Measure	Model S.E.	Infit MNSQ	Outfit MNSQ	PTMEA corr.
Q1	−2.68	0.17	0.96	1.65	0.25
Q2	−0.91	0.11	1.26	1.78	0.22
Q3	−1.89	0.13	0.99	1.20	0.31
Q4	−0.36	0.10	1.23	1.47	0.29
Q5	−2.46	0.16	0.88	1.00	0.34
Q6	−2.36	0.15	1.03	0.95	0.29
Q7	−0.31	0.10	1.05	1.06	0.42
Q8.1	0.70	0.09	1.06	1.09	0.44
Q8.2	−0.56	0.10	0.92	0.83	0.50
Q9	1.41	0.10	1.13	1.12	0.40
Q10.1	0.70	0.09	0.86	0.81	0.57
Q10.2	0.88	0.09	0.78	0.69	0.63
Q10.3	−0.35	0.10	1.00	1.00	0.45
Q10.4	0.24	0.09	0.84	0.81	0.58
Q11.1	1.67	0.10	0.91	0.85	0.53
Q11.2	4.50	0.21	0.92	0.46	0.37
Q11.3	1.80	0.10	0.97	0.90	0.49

---

As described in the pilot test of the two forms of chi-square fitting indicators, Infit specifically notes the difference between the observed and expected response on those items that have a difficulty level near the person's ability level, and Outfit includes the differences across all items regardless of how far the item difficulty is from the person's ability (Tennant and Conaghan, 2007). A commonly accepted standard is that the Infit MNSQ and Outfit MNSQ should be in the range of 0.7–1.3 when the sample size is not large (Park and Liu, 2016). The data shown in Table 6 reveal that the Infit MNSQ of all items is within the acceptable range and that the Outfit MNSQ of some items is out of range. Determining the performance of persons whose ability is close to the item's difficulty should provide more sensitive insight into the item's performance, and many users of the Rasch model tend to pay more attention to Infit values than to Outfit values (Bond and Fox, 2013). Therefore, the data can basically be considered to fit the model.

The point-measure correlation (PTMEA corr.) indicates the correlation between a student's response to a specific item and the overall proficiency measure (Bond and Fox, 2013). A negative correlation indicates potential fit errors; thus, the higher the positive correlation, the better (Liu, 2010). The PTMEA corr. values of all items are positive with moderate to high positive correlations (from 0.22 to 0.63) (Bond and Fox, 2013). Based on the above analysis, it can be considered that the obtained data fit the Rasch model.

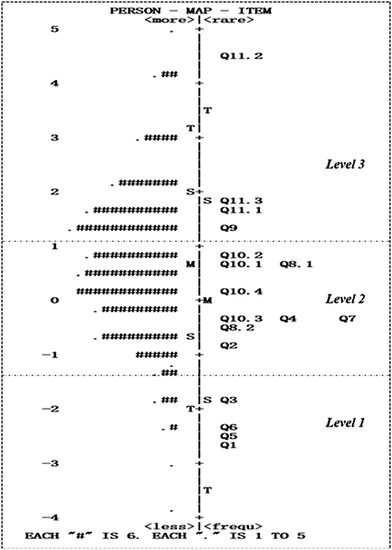
Wright map. Fig. 5 shows the Wright map, which estimates both the ability of a person and the difficulty of an item. The left side of the Wright map in the vertical direction shows the distribution of the proficiency levels of the sample; each “#” represents 6 people, and the level of proficiency ranges from low to high from bottom to top. The right side of the Wright map in the vertical direction shows how items are distributed from simple to difficult.

Fig. 5 Wright map of the GCPA.

According to the Wright map, the proficiency level of the sample presents a normal distribution, and the item difficulty estimation almost coincides with the sample proficiency level distribution. However, students of certain abilities still lack items that match their levels, and the gaps between Q2/Q3 and Q11.2/Q11.3 are slightly larger than ideal. However, in general, the distribution of the item difficulty level is consistent with the theoretical conception shown in Table 4, which indicates that the instrument can measure and distinguish between the three preset levels.

Interview findings

Students' proficiency level in solving galvanic cell problems. To statistically analyze the students' proficiency, we define the mean value of the difficulty value of all items corresponding to each level as the threshold for student proficiency (Wang et al., 2017). The difficulty value of each item is reported in Table 6, and using this value, we calculated that the threshold value of level 1 is −2.35, the threshold value of level 2 is 0.00, and the threshold value of level 3 is 2.35. If a student's measure value was below −2.35, his or her proficiency in galvanic cells could not reach level 1. According to the calculated thresholds for the proficiency levels in galvanic cells, we determined the proportion of students in the 11th grade at different proficiency levels. The results are shown in Fig. 6. As shown in Fig. 6, the assessment instrument distinguished students who are at different levels of proficiency in the galvanic cell concept. The proportions of grade-11 students with a level 1, level 2, and level 3 proficiency in galvanic cells were 28.39%, 62.26%, and 7.26%, respectively.

Fig. 6 Level of proficiency in galvanic cells of grade-11 students.

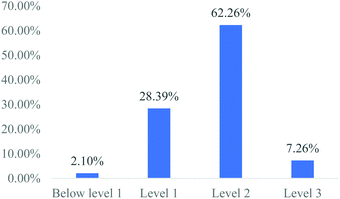
As shown in Table 5, the average student ability value is 0.63 logit. The data shown in Table 6 reveal that the difficulty values of items Q8.1, Q10.1, and Q10.2 in level 2 and items Q9, Q11.1, Q11.2, and Q11.3 in level 3 are greater than 0.63 logit, indicating that these items are difficult for students overall. We conducted interviews with students regarding these items to further verify whether the assessment instrument can measure and distinguish different proficiency levels among students in solving galvanic cell problems.

We transcribed all the recording materials obtained from the interview, and inferred students' proficiency levels in solving galvanic cell problems according to their answers to the items. The analysis results showed that the proficiency levels of the 10 students inferred from the interviews were consistent with the proficiency levels obtained from Rasch analysis process. This results supported the validity of the data generated by the instrument.

For example, item Q8.1 is at level 2. Students' judgments of electrode materials and electrode reactants in a galvanic cell device reflect whether the students reached the level of understanding the working principle of galvanic cells. Wang answered Q8.1 incorrectly, and in the Rasch analysis, his proficiency in galvanic cells was at level 1. Zheng answered Q8.1 correctly, and his proficiency in galvanic cells was at level 2. The following are excerpts from our interviews with these two students:

Wang: Potassium goes to the positive electrode and chloride goes to the negative electrode. Potassium seems to be more reactive than silver, it reacts with nitrate, and then the chloride ion reacts with copper.

Interviewer: How do you judge the reaction between the positive electrode and the negative electrode?

Wang: Copper does not react with copper sulfate, so it reacts with the chlorine ions that come in; the same thing occurs in the positive electrode: silver does not react with silver nitrate, so potassium ions react with nitrate ions.

Interviewer: So, how can you judge the positive and negative electrodes of the cell?

Wang: In the list of metal activities, copper is ranked before silver, so copper is more active than silver because it is a galvanic cell, so copper is the negative electrode. Active metal is used as the negative electrode.

Although Wang remembered the method of judging the positive and negative electrodes of a cell and the movement directions of anions and ions in the salt bridge, when faced with a real galvanic cell device, Wang could not analyze the cell reaction that occurred in the galvanic cell device or identify the electrode reactants for the positive and negative electrodes but could directly speculate regarding the role of each substance, and he understood the reduction or oxidation half-reaction occurring in the positive and negative electrodes as two pairs of substances reacting on the positive and negative electrodes, respectively. According to the interview, we can infer that Wang only remembered relevant knowledge about the galvanic cell and did not really understand the working principle of the galvanic cell, thus failing to reach level 2.

Zheng: The negative electrode loses electrons, so the copper rather than the copper ion is involved. The copper loses electrons and becomes the copper ion, and the positive electrode gains electrons, which involves the silver nitrate and the silver ion, and the silver ion gains electrons and becomes the silver element.

Interviewer: Can you explain the electrode reaction involving the copper and silver ions?

Zheng: According to the metal activity sequence table, copper is more active than silver, so copper can replace silver. According to the chemical reaction formula Cu + 2Ag ⁺ = Cu²⁺ + 2Ag, the silver ions have electrons, and copper loses electrons, so copper acts as a negative electrode and silver ions act as a positive electrode.

Interviewer: Did you first determine the electrode material and electrode reactants or the chemical reaction formula that you first wrote?

Zheng: The first reaction formula. The galvanic cell must be associated with chemical reactions.

Zheng first correctly judged the redox reaction in the device according to the relevant knowledge that he had learned and then connected the redox reaction with the principle of the galvanic cell and the galvanic cell device to correctly judge the electrode materials and reactants of the positive and negative electrodes. Therefore, his proficiency in galvanic cells reached level 2, which reflects an understanding of the working principle of the galvanic cell.

Conclusions and limitations

Based on Anderson's cognitive process goal taxonomy and the curriculum standards of chemistry in mainland China, this study divides students' proficiency level in solving galvanic cell problems into three levels. The Rasch model was used to develop the assessment instrument of the proficiency levels in galvanic cells through a two-round test process involving a pilot test and a field test. The analysis of the test data showed that the GCPA fulfill the unidimensionality and local independence requirements of the Rasch model and the test results have good reliability and validity. The assessment instrument developed in this research can help teachers diagnose students' proficiency in solving galvanic cell problems and determine their performance level in solving galvanic cell problems. In addition, teachers can understand their students' specific difficulties in solving galvanic cell problems according to the two way table of specifications and adopt more effective teaching intervention.

Students' proficiency in problem solving can be achieved by either understanding the core concepts or memorizing a sequence of procedures. The instrument developed in this study pays more attention to the performance level of the students' ability to solve galvanic cell problems. There is no measurement and discrimination of the students' problem solving methods, so it is difficult to determine exactly how students achieve proficiency. Achieving this will require in-depth interviews with students or continued development of corresponding assessment tools. The assessment instrument is designed according to the requirements of Chinese curriculum learning, so it is mainly suitable for high school students in mainland China. After the field test, the instrument was reviewed by experts again, and the expression of individual options (for example, option C in question 4.1 is not presented as a negative reason) is unreasonable. It is recommended to correct it when testing again.

Conflicts of interest

There are no conflicts to declare.

Appendix: galvanic cell test

This test includes a total of 11 questions; 7 are multiple-choice questions, one of which is a multiple-answer question, which has been noted in the question. Four of the questions are open questions. The test time is 30 minutes.

Relative atomic masses that may be used Zn: 65 Fe: 56 Cu: 64 C: 12 H: 1 O: 16

Multiple-choice questions

Q1. In which of the following devices does current flow through the galvanometer? ( )

Q2. The correct statement about positive and negative electrodes in galvanic cells is ()

A. the two electrode materials must be metal

B. the activity of the electrode materials must be different

C. the electrode materials do not necessarily participate in the cell reaction

D. the electrode materials must participate in the cell reaction

Q3. (multiple answers) Which can be used as a galvanic cell electrolyte solution?

A. sodium chloride solution

B. molten copper sulfate

C. sucrose solution

D. alcohol solution

Q4. (1) A chemical reaction that theoretically cannot be designed as a galvanic cell is ( )

A. CO₂(g) + C(s) = 2CO(g); ΔH > 0

B. CH₄(g) + 2O₂(g) = CO₂ + 2H₂O(g); ΔH < 0

C. Al(OH)₃(s) + NaOH(aq) = Na[Al(OH)₄](aq); ΔH < 0

(2) The reason for the answer for (1) is that ( )

A. endothermic reactions cannot be designed as galvanic cells

B. the reaction that needs to be ignited cannot be designed as a galvanic cell

C. the redox reaction can be designed as a galvanic cell

Q5. For a galvanic cell consisting of zinc, copper and dilute sulfuric acid, which of the following statements is correct?

A. The positive electrode is zinc.

B. Current flows from zinc to copper.

C. The zinc electrode undergoes a reduction reaction.

D. H₂ escapes around the copper electrode.

Q6. In a certain galvanic cell, two metals X and Y are connected with wires and inserted into the corresponding electrolyte solution at the same time, and it is found that the mass of the Y electrode increases, which may occur in which of the following cases?

A. Y is the negative electrode, and the electrolyte solution is a CuSO₄ solution.

B. Y is the negative electrode, and the electrolyte solution is a dilute H₂SO₄ solution.

C. Y is the positive electrode, and the electrolyte solution is a CuSO₄ solution.

D. Y is the positive electrode, and the electrolyte solution is a dilute H₂SO₄ solution.

Q7. Alkaline batteries have a large capacity and a large discharge current and thus have been widely used. The zinc–manganese alkaline battery uses potassium hydroxide solution as the electrolyte, and the battery reaction is:

Zn(s) + 2MnO₂(s) + H₂O(l) = Zn(OH)₂(s) + Mn₂O₃(s),

The mistake in the following statement is that ( )

A. when the battery is working, zinc loses electrons and zinc is negative

B. the reaction of the positive electrode of the battery is 2MnO₂(s) + H₂O(l) + 2e⁻ = Mn₂O₃(s) + 2OH⁻(aq)

C. the alkalinity of the solution in the negative area is enhanced during the discharge of the battery

D. the mass of zinc is theoretically reduced by 6.5 g for each pass of 0.2 mol electrons in the external circuit

Open questions

Q8. Please analyze the device shown and answer the following questions:

(a) Negative electrode:

The electrode material is ______, and the electrode reactant is ______.

Positive electrode:

The electrode material is ______, and the electrode reactant is ______.

(b) Please explain the direction of the movement of the ions in the salt bridge (KCl saturated solution).

Q9. The galvanic cell reaction is Fe + 2FeCl₃ → 3FeCl₂; please design and draw a galvanic cell diagram according to the generated cell reaction and indicate the positive and negative electrode materials, the electrolyte solution, the electron transfer direction and the movement direction of the anion and cation in the figure.

Q10. A high-speed rail battery is a new type of rechargeable battery that can maintain a stable discharge voltage for a long time compared with an ordinary battery. The total response of the high-speed rail battery is:

3Zn + 2K₂FeO₄ + 8H₂O = 3Zn(OH)₂ + 2Fe(OH)₃ + 4KOH

Please answer the following questions:

(a) When discharging (the same below), the equation of the negative electrode reaction is ______.

(b) The positive reaction equation is ______.

(c) The alkalinity of the solution near the ______ (“positive” or “negative”) electrode increases.

(d) Theoretically, the number of electrons transferred per 0.15 mol Fe(OH)₃ is ______.

Q11. Designing a fuel cell to oxidize gasoline directly to produce current is one of the most challenging topics of the century. Recently, a fuel cell was manufactured in which one electrode is supplied with air and the other electrode is supplied with gasoline vapor. The electrolyte of the battery is a ZrO₂ crystal doped with Y₂O₃, which conducts O²⁻ at a high temperature.

Please answer the following questions:

(a) Taking pentane (C₅H₁₂) for gasoline, the equation for the battery negative electrode reaction is ______.

(b) What do you think is the effect of substituting Y³⁺ for Zr⁴⁺ in ZrO₂ crystal doping Y₂O₃ on the conductivity of a solid electrolyte? What is the possible cause?

(c) The biggest obstacle to gasoline fuel cells is the incomplete oxidation reaction. What substances may be generated in the process that block the gas channels?

Acknowledgements

The authors thank all research participants for providing their time and responses during the data collection process. The authors also thank the instructors for their support.

References

1. Adadan E., Trundle K. C. and Irving K. E., (2010), Exploring grade 11 students' conceptual pathways of the particulate nature of matter in the context of multirepresentational instruction, J. Res. Sci. Teach., 47(8), 1004–1035.
2. Adams W. K. and Wieman C. E., (2011), Development and validation of instruments to measure learning of expert-like thinking, Int. J. Sci. Educ., 33(9), 1289–1312.
3. Anderson L. W. and Krathwohl D. R., (2001), A taxonomy for learning, teaching, and assessing: A revision of Bloom's Taxonomy of Educational Objectives, New York: Longman.
4. Barbera J., (2013), A psychometric analysis of the chemical concepts inventory, J. Chem. Educ., 90(5), 546–553.
5. Bloom B. S., (1956), Taxonomy of Educational Objectives, vol. 1, Cognitive Domain, New York: McKay.
6. Bond T. G. and Fox C. M., (2013), Applying the Rasch model: Fundamental measurement in the human sciences, Psychology Press.
7. Brandriet A. R. and Bretz S. L., (2014), The development of the redox concept inventory as a measure of students’ symbolic and particulate redox understandings and confidence, J. Chem. Educ., 91(8), 1132–1144.
8. Butts B. and Smith R., (1987), What do students perceive as difficult in HSC chemistry, Australian Sci. Teach. J., 32(4), 45–51.
9. Cracolice M. S., Deming J. C. and Ehlert B., (2008), Concept learning versus problem solving: a cognitive difference, J. Chem. Educ., 85(6), 873.
10. De Jong O. and Treagust D., (2002), The teaching and learning of electrochemistry, in Chemical education: towards research-based practice, Dordrecht: Springer, pp. 317–337.
11. Duit R. and Treagust D. F., (2003), Conceptual change: a powerful framework for improving science teaching and learning, Int. J. Sci. Educ., 25(6), 671–688.
12. Duncan P. W., Bode R. K., Lai S. M. and Perera S., (2003), Rasch analysis of a new stroke-specific outcome scale: the Stroke Impact Scale, Arch. Phys. Med. Rehabil., 84(7), 950–963.
13. Engelhardt P. V. and Beichner R. J., (2004), Students’ understanding of direct current resistive electrical circuits, Am. J. Phys., 72(1), 98–115.
14. Garnett P. J. and Treagust D. F., (1992), Conceptual difficulties experienced by senior high school students of electrochemistry: electrochemical (galvanic) and electrolytic cells. J. Res. Sci. Teach., 29(10), 1079–1099.
15. Gillmore G. M., Stallings W. M., Heil D. K. and Smock H. R., (1975), A study of the educational benefits of proficiency testing for students, Res. High. Educ., 3(2), 187–194.
16. Gunstone R., (2015), Encyclopedia of Science Education; With 88 Figures and 32 Tables, Springer.
17. Hewson P. W. and Thorley N. R., (1989), The conditions of conceptual change in the classroom, Int. J. Sci. Educ., 11(5), 541–553.
18. Karsli F. and Çalik M., (2012), Can Freshman Science Student Teachers' Alternative Conceptions of' Electrochemical Cells' Be Fully Diminished? Asian J. Chem., 24(2), 485–491.
19. Krathwohl D. R. and Anderson L. W., (2009), A taxonomy for learning, teaching, and assessing: A revision of Bloom's taxonomy of educational objectives, Longman.
20. Linacre J. M., (2011), A User's Guide to Winsteps: Rasch-Model Computer Programs, winsteps.com.
21. Liu X., (2010), Using and Developing Measurement Instruments in Science Education: A Rasch Modeling Approach, Information Age Publishing, Inc.
22. Liu X. and Boone W. J., (2006), Applications of Rasch measurement in science education, JAM Press.
23. Loh A. S. L. and Subramaniam R., (2018), Mapping the knowledge structure exhibited by a cohort of students based on their understanding of how a galvanic cell produces energy, J. Res. Sci. Teach., 55(6), 777–809.
24. Lu S. and Bi H., (2016), Development of a measurement instrument to assess students' electrolyte conceptual understanding, Chem. Educ. Res. Pract., 17(4), 1030–1040.
25. Luxford C. J. and Bretz S. L., (2014), Development of the bonding representations inventory to identify student misconceptions about covalent and ionic bonding representations, J. Chem. Educ., 91(3), 312–320.
26. Novak J. D. and Cañas A. J., (2008), The theory underlying concept maps and how to construct and use them, Florida Institute for Human and Machine Cognition.
27. Nurrenbern S. C. and Pickering M., (1987), Concept learning versus problem solving: Is there a difference? J. Chem. Educ., 64(6), 508.
28. Ogude A. N. and Bradley J. D., (1994), Ionic conduction and electrical neutrality in operating electrochemical cells: pre-college and college student interpretations, J. Chem. Educ., 71(1), 29–34.
29. Osman K. and Lee T. T., (2014), Impact of interactive multimedia module with pedagogical agents on students’ understanding and motivation in the learning of electrochemistry, Int. J. Sci. Math. Educ., 12(2), 395–421.
30. Özkaya A. R., Üce M., Saricayir H. and Sahin M., (2006), Effectiveness of conceptual change-oriented teaching strategy to improve students' understanding of galvanic cells, J. Chem. Educ., 83(11), 1719.
31. Park M. and Liu X., (2016), Assessing understanding of the energy concept in different science disciplines, Sci. Educ., 100(3), 483–516.
32. Rahayu S., Treagust D. F., Chandrasegaran A. L., Kita M. and Ibnu S., (2011), Assessment of electrochemical concepts: a comparative study involving senior high-school students in Indonesia and Japan, Res. Sci. Technol. Educ., 29(2), 169–188.
33. Rogers F., Huddle P. A. and White M. D., (2000), Using a teaching model to correct known misconceptions in electrochemistry, J. Chem. Educ., 77(1), 104–110.
34. Rosenthal D. P. and Sanger M. J., (2012), Student misinterpretations and misconceptions based on their explanations of two computer animations of varying complexity depicting the same oxidation–reduction reaction, Chem. Educ. Res. Pract., 13(4), 471–483.
35. Salta K. and Tzougraki C., (2011), Conceptual versus algorithmic problem-solving: focusing on problems dealing with conservation of matter in chemistry, Res. Sci. Educ., 41(4), 587–609.
36. Sanger M. J. and Greenbowe T. J., (1997), Common student misconceptions in electrochemistry: galvanic, electrolytic, and concentration cells, J. Res. Sci. Teach., 34(4), 377–398.
37. Sax G. and Newton J. W., (1989), Principles of Educational and Psychological Measurement and Evaluation, Belmont: Wadsworth Publishing Co.
38. Schmidt H. J., Marohn A. and Harrison A. G., (2007), Factors that prevent learning in electrochemistry, J. Res. Sci. Teach., 44(2), 258–283.
39. Sesen B. A. and Tarhan L., (2013), Inquiry-based laboratory activities in electrochemistry: high school students’ achievements and attitudes, Res. Sci. Educ., 43(1), 413–435.
40. Talanquer V., (2012), Chemistry education: ten dichotomies we live by, J. Chem. Educ., 89(11), 1340–1344.
41. Tan K. C. D., Taber K. S., Goh N. K. and Chia L. S., (2005), The ionisation energy diagnostic instrument: a two-tier multiple-choice instrument to determine high school students’ understanding of ionisation energy, Chem. Educ. Res. Pract., 6(4), 180–197.
42. Tennant A. and Conaghan P. G., (2007), The Rasch measurement model in rheumatology: what is it and why use it? when should it be applied, and what should one look for in a Rasch paper? Arthrit. Rheumat., 57(8), 1358–1362.
43. Treagust D., (1986), Evaluating students' misconceptions by means of diagnostic multiple choice items, Res. Sci. Educ., 16(1), 199–207.
44. Treagust D. F., (1988), Development and use of diagnostic tests to evaluate students’ misconceptions in science, Int. J. Sci. Educ., 10(2), 159–169.
45. Treagust D. F. and Duit R., (2008), Conceptual change: a discussion of theoretical, methodological and practical challenges for science education, Cult. Stud. Sci. Educ., 3(2), 297–328.
46. Tyson L. M., Venville G. J., Harrison A. G. and Treagust D. F., (1997), A multidimensional framework for interpreting conceptual change events in the classroom, Sci. Educ., 81(4), 387–404.
47. Voska K. W. and Heikkinen H. W., (2000), Identification and analysis of student conceptions used to solve chemical equilibrium problems, J. Res. Sci. Teach., 37(2), 160–176.
48. Wang Z., Chi S., Luo M., Yang Y. and Huang M., (2017), Development of an instrument to evaluate high school students' chemical symbol representation abilities, Chem. Educ. Res. Pract., 18(4), 875–892.
49. Wren D. and Barbera J., (2014), Psychometric analysis of the thermochemistry concept inventory, Chem. Educ. Res. Pract., 15(3), 380–390.
50. Yan zi, (2010), Objective Measurement in Psychological Science: An Overview of Rasch Model, Adv. Psychol. Sci., 18(8), 1298–1305.

---