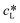Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Process analytical technology (PAT) as a versatile tool for real-time monitoring and kinetic evaluation of photocatalytic reactions†
Martin
Rößler
 ,
Philipp U.
Huth
,
Philipp U.
Huth
 and
Marcel A.
Liauw
and
Marcel A.
Liauw
 *
*
Institut für Technische und Makromolekulare Chemie (ITMC), RWTH Aachen University, Worringerweg 1, 52074 Aachen, Germany. E-mail: liauw@itmc.rwth-aachen.de; Tel: +49 241 80 26470
First published on 14th September 2020
Abstract
In this work, we present a methodology for the real-time monitoring of light induced reactions. Employing process analytical technology (PAT) permits an in situ approach to disclose kinetic insights into photocatalytic reactions. The applicability of this methodology was tested on the eosin Y (EY) catalysed photooxidation of 4-methoxythiophenol (4-MTP) to bis(4-methoxyphenyl)disulfide (4-MPD). The reaction was monitored by in situ Raman and UV/Vis spectroscopy under various process conditions including the stirrer speed, oxygen pressure, EY concentration and light intensity. Evaluation by an indirect hard modelling approach (IHM) disclosed the contributions of rate limiting effects like the oxygen mass transport and the degradation of EY. Detailed investigations on the influence of EY concentration and light intensity led to an empirical model for the correlation of the initial photooxidation rate with the averaged rate of photon absorption. These results confirmed the applicability of the methodology to support the development of photocatalytic reactions.
Introduction
Despite their historical roots going back to Ciamician in 1912, light driven reactions have gained tremendous attention over the last years.1,2 The use of light as an abundant, selective and traceless energy source has motivated researchers of various fields to investigate light-driven equivalents of existing techniques.3,4 Besides its application in air5–8 and water treatment,9–12 photochemistry has gained great importance in the field of synthetic organic chemistry.13 In particular, photoredox catalysis in the visible range is a fast growing field due to the possible utilisation of sunlight.14–16 While tremendous research efforts focus on challenging C–H activations17,18 or enantioselective synthesis,19,20 an evaluation of the underlying reaction kinetics is rarely performed. Nevertheless, detailed knowledge about the interdependence of process parameters like catalyst concentration and light intensity is indispensable for reaction modelling and further industrial application. Reasons for this lack of information may stem from the experimental effort that comes along with offline sampling.A promising approach to cut down the experimental effort is given by in situ monitoring that has become a state of the art technique to evaluate reaction kinetics. Various methods like IR or Raman spectroscopy as well as NMR spectroscopy have already been applied to conventional heat activated reaction networks.21–23 The application of in situ monitoring in photocatalysis is challenging in terms of experimental equipment and the possible interference with the light used to drive the reaction. Recently, Yu et al. demonstrated an approach of using probe electrospray ionisation mass spectrometry for the monitoring of methylene blue photo-degradation over TiO2 under UV-light irradiation.24 This methodology provides detailed qualitative information about the reaction intermediates but requires physical sampling of the reaction solution. Addressing this, various in situ or non-invasive approaches towards the application of UV/Vis-, IR- and NMR spectroscopy have been developed.25–27 As one example for a UV/Vis-based methodology, Lu et al. reported a microfluidic device with an immobilised TiO2 layer for kinetic investigations on the degradation kinetics of methylene blue.25 A similar design was presented by Wang et al. to study the degradation of methylene blue and methyl orange.12 Further studies by Bukman et al. revealed the degradation kinetics of textile dyes from a TiO2 suspension.28 In spite of the low detection limits, the applicability of UV/Vis spectroscopy is limited to UV/Vis active compounds. Furthermore, reasonable distinction between different species is often challenging. In contrast, measurements based on molecular vibrations, e.g. IR spectroscopy, are applicable to a wider range of compounds. In the context of photocatalysis, IR-based investigations were mainly focused on surface activities in heterogeneous catalysis.29 For that purpose, Bürgi et al. presented a flow cell utilising the principle of attenuated total reflection (ATR) within an internal reflection element (IRE).26 Irradiation of the flow cell by UV-light allowed a kinetic investigation of malonic acid mineralisation by TiO2. This principal design was adopted by various groups to investigate the photooxidation of cyclohexane30 and ethanol.31 Furthermore, NMR spectroscopy has become a versatile tool in photocatalysis. Besides bypass enabled inline monitoring,32,33in situ approaches have been developed.27 By guiding the excitation light via an optical fibre into the reaction solution, Gschwind and co-workers enabled an in situ approach that allowed the study of flavin photocatalysis. Further application of this methodology led to a detailed understanding of a photoinduced cycloisomerisation to form cyclic enol ethers.34 However, in particular, NMR-based systems suffer from a low pressure compatibility and the absence of forced convection (stirring). Thus, photocatalytic reactions that involve either a reactive or inert gas-atmosphere could only be studied at low performance including mass transport limitation or are simply not feasible.35
Process analytical technology (PAT) combine in situ real-time analysis with chemometric data evaluation for the monitoring and evaluation of chemical processes.36 The use of in situ techniques like UV/Vis, IR or Raman spectroscopy enables in-process monitoring of the relevant information without physical sampling.37 With this, PAT was successfully implemented for the determination of reaction kinetics,22 real-time optimization38 and quality control.39 The easy implementation and robustness allows PAT to support the development from the laboratory to an industrial scale.40,41 This makes PAT a promising candidate for the in situ monitoring of visible light induced photocatalytic reactions.
Herein, we present a methodology for the real-time in situ monitoring of photocatalytic reactions by employing PAT tools. Simultaneous irradiation and monitoring were conducted in a home-designed reactor. To verify the applicability of this methodology, we investigated the eosin Y (EY) mediated photocatalytic oxidation of 4-methoxythiophenol (4-MTP) to bis(4-methoxyphenyl)disulfide (4-MPD).42,43 Disulfides are of fundamental interest due to their application in pharmacy,44 agriculture45 and as a crosslinker in polymer synthesis.46 The reaction is driven by green light and utilises ethanol and oxygen as cheap and sustainable reactants. The additive N,N,N′,N′-tetramethylethylenediamine (TMEDA) is reported to enhance the overall reaction. Besides the evaluation of possible mass transport limitations, the methodology provided valuable insights into the interdependence between light intensity, EY concentration and the photooxidation rate. Additionally, the versatility of the developed methodology was demonstrated by resolving EY degradation by bleaching as a competing reaction pathway.
Methodology
Photoreactor design
Monitoring photocatalytic reactions during irradiation imposes requirements that are not fulfilled by commercially available equipment. With the proposed setup, in situ monitoring under realistic reaction conditions is accessible by various PAT methods. As illustrated in Fig. 2, the setup involves a Schlenk-based vessel that is irradiated by light emitting diodes (LEDs) around its lower end. According to their small size, high efficiency and narrow emission bands, LEDs became a suitable light source for driving photochemical reactions.47 Utilising a circular arrangement of twelve high-power LEDs located on six LED plates, a uniform light distribution across the reactor wall is expected. Reproducibility was enhanced by fixing the LED plates and the reaction vessel at a constant distance in a 3D-printed holder. With this setup, photon fluence rates of up to 0.08 μmol cm−2 s−1 were reached.Suitable fibre optical probes (outer diameter up to 6.5 mm) were fixed on opposite positions at a 45° angle with Teflon fittings. Equipped with either an ATR-UV/Vis, an ATR-mIR and/or a Raman spectrometer, a sufficient probability to trace the relevant components was ensured. It should be noted that Raman measurements are sensitive to ambient light since any small proportion of stray light overlays the weak Raman scattering. As a consequence, an additional cover was designed for further in situ Raman application (see section 2, ESI†). Compared to the ambient light, no negative impact was found for the LED illumination that was used to drive the photocatalytic reaction.
The lower end of the reactor was fabricated from quartz glass in order to extend the field of application to UV activated photochemistry. With an inner diameter of 12 mm and a volume of 7 mL, the reactor dimensions are comparable to those of commonly used reaction vials. The irradiated area (shell surface) was about 28 cm2. With the Schlenk-based design, we envisioned an application not only for single-phase reactions, but also for multiphase reactions. This ability broadens the scope of the methodology to various photocatalytic reactions that are either oxygen sensitive or require the latter in the photocatalytic cycle. Stirring of the reaction solution was conducted via a magnetic stirrer. It is worth noting that the reactor features a challenging height to diameter ratio that caused an insufficient mixing behaviour using commercially available stirrers. In order to address this issue, a customised stirrer was designed and fabricated with particular attention paid to the stirrer height (see section 2, ESI†).
Benchmark reaction
In this work, we have chosen the photooxidation of 4-MTP to 4-MPD as a benchmark reaction (Fig. 1). Employing oxygen as the oxidant, EY as a metal-free photosensitizer and TMEDA as a proton acceptor, Noël and co-workers reported an efficient protocol to transform the aromatic thiol to its corresponding disulfide under batch and flow conditions.42 Since the reaction is performed in a biphasic regime, oxygen transport from the gas to the liquid phase (R6) becomes a potentially rate limiting step in the catalytic cycle. In this context, we see the photooxidation of 4-MTP as a promising candidate for testing the capabilities of the developed methodology. As postulated by Noël and co-workers, the photooxidation of 4-MTP is initiated by exciting EY (R1) at its main absorption band around 525 nm to EY* (see section 3, ESI†). Subsequently, the excited state can either undergo intersystem crossing to the triplet state or directly return to the ground state by radiative relaxation (fluorescence) (R2). From the triplet state, the next step includes a proton coupled electron transfer (PCET) to reduce EY* to EY− and generate a thiyl radical 4-MTP˙ (R3). Afterwards, product formation occurs from the radical coupling (R4). In order to close the photocatalytic cycle, the reduced EY− undergoes an oxygen assisted single electron transfer to again form its ground-state (R5). Additionally, preliminary investigations revealed the bleaching of certain reaction solutions, especially when low EY concentrations were used. We attribute this decolorisation of EY to a degradation pathway occurring from the excited state (R7) yielding EYdeg. | ||
| Fig. 2 Representation of the developed setup for studying photocatalytic reaction kinetics. The setup allows simultaneous LED irradiation and in situ monitoring by various PAT techniques. | ||
Spectroscopic feasibility
In order to select a suitable spectroscopic method for following the reaction progress, we initially performed a feasibility study on UV/Vis, mid-IR and Raman spectroscopy. While a spectral correlation with the concentration was found in the mid-IR and Raman spectra, UV/Vis spectroscopy showed no reasonable distinction between 4-MTP and 4-MDP. The additive TMEDA showed an overall weak signal intensity and was not considered for further investigations. Focusing on the vibrational methods, binary mixtures of 4-MTP and 4-MPD in ethanol revealed the superior performance of Raman spectroscopy due to higher signal intensities and a weaker signal overlapping (see section 5, ESI†). With high signal/noise ratios, the Raman spectra provided the most valuable information in the spectral range of 1000–1200 cm−1 (Fig. 3). In this region, both components show a characteristic signal that can be assigned to the aromatic C–S stretching vibration. However, in this particular range, especially at 1100 cm−1, the Raman bands of ethanol, 4-MTP and 4-MPD showed a strong overlap. This renders the use of univariate methods not feasible and therefore requires a multivariate approach.Since Raman spectroscopy is sensitive to competing radiative events like fluorescence or stray light, we investigated the influence from the excitation light that was used to drive the reaction. Encouragingly, no interference was observed in the Raman spectra as long as the excitation light is at a sufficient distance to the Raman laser at 785 nm. However, recording Raman spectra in the presence of EY led to a significant increase in the baseline intensity. This effect was further reinforced under green light excitation (see section 5, ESI†). We see this as evidence that the baseline shift originates from the EY fluorescence. Further proof was given by the decreasing intensity upon the addition of 4-MTP and TMEDA, respectively. Both compounds are expected to quench EY fluorescence. Interestingly, the decrease in fluorescence was less pronounced for TMEDA than that for 4-MTP. Stern–Volmer analysis confirmed this observation by revealing a 7-fold higher quenching ability of 4-MTP compared to that of TMEDA (see section 6, ESI†).
Since the typical EY loadings were in the range of 10−3–10−5 M, the overall impact of the fluorescence was small enough to be subtracted by a baseline correction combined with a peak normalisation (see section 5, ESI†). Upon this spectral pretreatment, a chemometric evaluation of the spectra was possible in the presence of both EY and external excitation.
Chemometric modeling
Extracting information about a component's concentration from a spectrum sets the basic idea in chemometric modeling. Caused by the aforementioned signal overlap in the spectral region of 700–1200 cm−1, a multivariate chemometric model was necessary to analyse 4-MTP and 4-MPD quantitatively. Utilising the indirect hard modelling (IHM) approach enabled the deconvolution of the mixture spectrum into its single components.48 Since a mixture spectrum is the sum of its single components, quantitative monitoring is feasible via the relative weighting of the components. By adjusting the component weights, the concentrations were calculated on the basis of a model calibration. As the in situ Raman spectra were affected by the catalyst fluorescence, the model includes a data pretreatment that subtracts the background and normalises the spectra to the characteristic ethanol band at 880 cm−1 (for a detailed description, see section 7, ESI†).Model calibration was carried out on a total number of 41 calibration samples including binary and ternary mixtures of ethanol, 4-MTP and 4-MPD. In order to use an unbiased calibration set, we used a calibration routine based on the nearest neighbour statistic (see section 7, ESI†). The calibration covers a concentration range of 0–0.38 M for 4-MTP and 0–0.26 M for 4-MPD. As only 4-MTP and 4-MPD showed characteristic Raman bands in the chosen spectral range, the additive TMEDA and EY were not included in the calibration. However, both components were considered for a model validation to obtain the root mean square error of prediction (RMSEP). Measurements of representative mixture samples revealed a robust and reliable model that predicts the component concentration with reasonable RMSEP values, 0.014 M for 4-MTP (4% relative error at 0.38 M) and 0.010 M for 4-MPD (4% relative error at 0.26 M), even in the presence of a strong fluorescence background (see section 7, ESI†).
Results and discussion
Reaction monitoring
Applying the developed method, we monitored the photooxidation of 4-MTP in both the presence and absence of oxygen using in situ Raman spectroscopy. Spectra were recorded with a temporal resolution of about one minute to provide a high level of information that would otherwise not be accessible by offline sampling. Particularly for fast photocatalytic reactions like the photooxidation of 4-MTP, this is one of the main advantages of PAT and makes it a versatile tool for kinetic analyses. Spectral evaluation was conducted on the basis of the IHM prediction model. As demonstrated in Fig. 4a, no spectral change was observed in the absence of light and oxygen (argon atmosphere). Upon exposing the reaction to oxygen, 4-MTP is consumed as indicated by the decreasing signal intensity at 1100 cm−1. The 4-MPD related signal intensity (1088 cm−1) increased in a similar manner. Since no light was present during this stage, a background reaction pathway through direct oxidation is assumed.Assuming first order reaction kinetics, a rate constant of 0.013 min−1 was found in the dark. Within 11 min, a conversion of 20% was reached. Exposing the reaction to green light irradiation caused a significant acceleration of the reaction. With a 16-fold increase in the reaction rate constant (0.21 min−1), the light induced pathway outperforms the direct oxidation. During irradiation, a conversion of 90% was reached within 15 minutes. These results demonstrate that the setup is capable of dealing with biphasic reactions involving an inert or reactive atmosphere. This makes the reaction and the developed methodology a perfect match to investigate mass transport limitations and the interplay of catalyst concentration and light intensity.
Overcoming oxygen mass transport limitations
Performing gas–liquid reactions is challenging not only in terms of the implementation but also when it comes to reaction monitoring. In particular, with kinetic analysis, care must be taken since transport limitations may lead to incorrect interpretations. In the case of the benchmark reaction, oxygen is needed to complete the catalytic cycle. With a gas solubility of 5.71 × 10−4 mol mol−1, oxygen reaches an equilibrium concentration of 0.01 M in ethanol at 20 °C and atmospheric pressure (see section 8, ESI†).49 Comparing this to the initial concentration of 4-MTP (0.2 M), it becomes evident that with a slow replenishment, the overall photooxidation rate is limited by R6. The oxygen transfer to a liquid phase is described by eqn (1). Accordingly, the rate is a function of the mass transfer coefficient (kL), the effective interfacial area (a) and the concentration gradient between the actual concentration (cL) and the saturation concentration of oxygen. The latter can be derived from Henry's law (2).
of oxygen. The latter can be derived from Henry's law (2).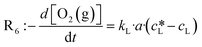 | (1) |
 | (2) |
As reported in the literature, the product kL·a, the volumetric mass transfer coefficient, is a measure that depends on specific equipment parameters (reactor and stirrer diameter, stirrer type), process conditions (stirrer speed, partial pressure, filling height) and the physical properties of the liquid (viscosity, density).50,51 Since the physical properties as well as the filling height could not be varied, further investigations were focused on the effect of stirring speed and oxygen pressure. In order to determine the extent of mass transport limitation, we investigated the benchmark reaction at stirring speeds ranging from 250–1300 rpm and in a pressure range of 0–2.5 bar. For the evaluation, the initial photooxidation rate was determined from the numerical differentiation of the concentration–time profiles. Using the RMSEP as the error on the concentration values, the uncertainty on the photooxidation rate was calculated as 0.005 M min−1 (see section 10, ESI†). With this level of accuracy, the developed methodology provides reliable data for further evaluation of the reaction kinetics.
Fig. 5(a) shows the evaluated initial photooxidation rates at various stirring speeds and a constant pressure of 2 bar. By increasing the stirring speed, we observed a significant increase in the initial reaction rate from 0.008 M min−1 to 0.03 M min−1. While a linear increase in the photooxidation rate became visible in the range of 250–1000 rpm, no further increase was observed by increasing the stirring speed to 1300 rpm, hence, indicating that the increased stirring speed shifts the reaction from a mass transport limitation to a kinetic limitation. A similar behaviour of gas–liquid transport in pressurised “dead-end” reactors was described by Hofmann and co-workers.52 Increasing the stirrer speed led to an increase in kLa due to the change in the interfacial area. Throughout the literature, various empirical attempts have been made to calculate kLa values for stirred tank reactors of different shapes and sizes.53,54 In spite of discrepancies, authors agreed on a direct correlation of kLa with the stirring speed N by the power of a factor b that depends on the geometrical properties of the reactor (eqn (3)).
| kL·a ∝ Nb | (3) |
Effects of insufficient mixing may also contribute at lower stirring speeds. However, changing the stirrer geometry to have a larger blade width to diameter ratio (see section 2, ESI†) maximised the specific power input and hence minimised insufficient mixing.
At the beginning of our investigation, we explored that the typical use of an oxygen balloon resulted in a weak performance. In fact, low reaction rates and reproducibility were observed from this commonly used technique. Hence, we optimised the setup towards a continuous oxygen supply. Besides improving reproducibility, it enabled investigations on the applied oxygen pressure. Based on the findings of Hofmann and co-workers,52 oxygen was directly introduced to the liquid phase by a capillary in order to further improve mass transport. Fig. 5(b) illustrates the response of the initial photooxidation rate to an increasing oxygen pressure. Here, the benchmark reaction was monitored at a stirring speed of 1300 rpm and various pressures in the range of 0 to 2.5 bar. Increasing the oxygen pressure resulted in an increase in the reaction rate from 0 to 0.03 M min−1. Beyond 2 bar, the photooxidation rate showed an independent response to the applied oxygen pressure. We see this as evidence for a shift from a mass transport limitation to a kinetic limitation. The observed pressure dependence of the photooxidation rate can be traced back to the oxygen concentration in the liquid phase. As described by Henry's law (eqn (2)), the saturation concentration increases linearly with the partial pressure. In the case of the benchmark reaction, the available oxygen content rises from 0.005 M at 0.5 bar to 0.024 M at 2 bar (see section 8, ESI†). Combining these results, we have identified a process window where the transfer rate (R6) becomes much greater than that of the consecutive reaction R4. As a consequence, steady-state conditions for the oxygen concentration can be assumed. With this, further investigations were performed at 1300 rpm and 2 bar.
Monitoring EY bleaching
During preliminary studies on the benchmark reaction, we observed decolorisation for some of the irradiated samples. In particular, reactions performed at low initial EY concentrations (0.002 to 0.05 M) seemed to face a strong loss in active (colored) photocatalyst during the irradiation (see section 9, ESI†). We attribute this observation to the photodegradation of EY.55 As a consequence, we added a degradation pathway (R7) to the photocatalytic cycle in Fig. 1. In order to quantify the extent of the catalyst degradation and its influence on the overall reaction kinetics, we tested the capability of the presented methodology to monitor the catalyst degradation during the photooxidation.Initially, we attempted to record in situ absorption spectra by applying ATR-UV/Vis spectroscopy. Aside from a weak absorption due to the short optical path length (50 to 120 nm), we discovered that this approach enabled the in situ observation of the catalyst fluorescence. Since the green LED light does not only drive the reaction, but also triggers the catalyst fluorescence, the emitted fluorescence light dominates the measured UV/Vis spectra (see section 9, ESI†). Interestingly, discrepancies were found in the fluorescence spectra obtained from the in situ and offline measurements. While the emission maximum was at 540 nm in the offline spectra, it underwent a bathochromic shift in the in situ measurement. Going to higher initial EY concentrations, this shift was even more pronounced. Due to the concentration difference in the offline and in situ measurements, the spectral shift is assigned to the inner filter effect (IFE). The IFE arises from re-absorption of emitted fluorescence light whenever a molecule shows a sufficient spectral overlap in the absorption and emission spectra.56 As a consequence, both the emission maximum and its corresponding intensity are affected, hence making the IFE a common challenge in fluorescence spectroscopy.57
Encouraged by this observation, we tested the applicability of the IFE for monitoring the temporal change in EY concentration. A direct correlation of the EY concentration with the observed emission maximum confirmed the applicability of this approach (see section 9, ESI†). Accordingly, we see this as evidence that the IFE can assist in the evaluation of the EY degradation during the photooxidation.
Based on these results, we simultaneously monitored the photooxidation of 4-MTP by in situ Raman and UV/Vis-spectroscopy at four different EY concentrations in the range of 0.005 to 0.037 mM. As illustrated in Fig. 6, irradiating the reaction mixtures with green light caused continuous bleaching of EY in all four reactions. Nevertheless, it becomes apparent that the evaluation by the IFE method mainly covers high EY concentrations. Reaching a lower concentration of around 0.003 mM, the observed fluorescence spectra are no longer affected by the IFE, thus specifying the detection limit of this method. However, we still observed a bathochromic shift in the emission maximum upon reaching this particular concentration (see section 9, ESI†). Upon closer inspection, we assigned this to a gradual shift of contributions from the decreasing EY fluorescence, as a consequence of ongoing EY bleaching, and an increasing proportion of LED light falling onto the ATR-probe (for a detailed description, see section 9, ESI†). Deconvolution of the fluorescence spectra by an indirect hard model into the EY fluorescence and the LED emission revealed the time to reach an almost complete EY degradation (Fig. 6 bottom). The results clearly show that compared to the time scale of a typical 4-MTP photooxidation (<30 min), the degradation of EY is significantly slower. This difference in time scales becomes even more pronounced at higher initial EY concentrations. Additionally, a short induction period in the temporal change of EY concentration confirmed that EY degradation preferably happens at a high degree of 4-MTP conversion. These results not only demonstrate the applicability of in situ fluorescence measurements towards the monitoring of EY concentration but also reveals that the slow degradation pathway plays only a minor role in the catalytic cycle. Thus, it can be neglected in further kinetic evaluation.
Influence of light intensity and EY concentration
In the case of the benchmark reaction, the first step in the photocatalytic cycle includes the excitation of EY to EY* (Fig. 1). The corresponding rate law depends on the rate of photon absorption Lap, the quantum yield ϕ and the initial EY concentration (eqn (4)). In order to investigate the individual contributions of the applied light intensity and the EY concentration to the observed reaction kinetics, we performed reactions at photon fluence rates spanning from 0 to 0.08 μmol cm−2 s−1 and EY concentrations ranging from 0 to 0.5 mM. Reactions were monitored by in situ Raman spectroscopy and evaluated by the developed chemometric model.| R1 = k1·[EY] = Lap·ϕ·[EY] | (4) |
Fig. 7 shows the initial photooxidation rate as a function of the applied reaction conditions. As previously assumed, the benchmark reaction implies a background reaction that is independent of the photocatalytic pathway. Consequently, all reactions, performed in the absence of light or a photocatalyst, showed a low reaction rate of 0.05 mM s−1.
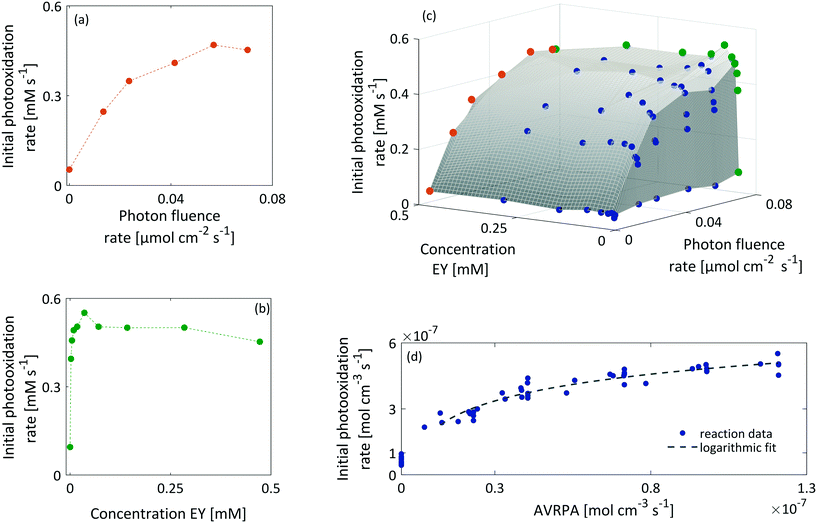
As a consequence of increasing the photon fluence rate at fixed EY concentrations, we observed an increasing trend in the photooxidation rate (Fig. 7a and c). Particularly, in the range of 0 to 0.02 μmol−2 s−1, the photooxidation rate increased almost linearly. However, when exposing the reaction to photon fluence rates exceeding 0.02 μmol cm−2 s−1, the increase in the photooxidation rate slowed down. We claim that this saturation behaviour corresponds to a gradual shift from a photon limitation to a kinetic limitation. Based on Lambert–Beer's law (eqn (5)), all photoreactions, regardless of the utilised reactor, suffer from attenuation of the incident light due the absorption by the photocatalyst. Consequently, the reactor will have local differences in the rate of photon absorption, which can be approximated by the negative derivative of Lambert–Beer's law (eqn (6)). The local volumetric rate of photon absorption (LVRPA) Lap depends on the photon fluence rate I0 and the catalyst concentration c0, and is approximated as a function of the reactor depth z.
| I(z) = I0·10−ε·[EY]·z | (5) |
| Lap = −dI(z)/dz = ε·ln(10)·I0·[EY]·10−ε·[EY]·z | (6) |
Simulation of the LVRPA for the given reaction setup confirms the expected differences in the photon absorption throughout the reactor (see section 10, ESI†). While the largest photon absorption occurs close to the reactor walls, the LVRPA decreases exponentially towards the center of the reactor. This effect is further reinforced by increasing the photon fluence rate. Also, as a consequence of the local differences in the photon absorption, the rate of EY excitation (R1) becomes a function of the position within the reactor. In particular, close to the reactor walls, photon absorption might be high enough so that the rate of EY excitation (R1) could exceed the rate of the subsequent steps R3 and R4 in the photocatalytic cycle, hence causing a change in the rate limiting step. We see this as evidence that the observed photooxidation rate has to be perceived as an average of local reaction rates that gradually shift from a photon limitation to a kinetic limitation with an increasing photon fluence rate.
As Fig. 7(b and c) illustrates, the photooxidation rate was also observed to be a function of the EY concentration. While a strong increase was found at low EY concentrations (0 to 0.05 mM), any further addition of EY led to a decrease in the photooxidation rate. At low EY concentrations (up to 0.05 mM), we again attribute this trend to the increase in the local photon absorption according to the LVRPA (see section 10, ESI†). Assuming a complete and homogeneous irradiation of the reactor surface, the complexity arising from the local differences in photon absorption can be reduced by averaging along one direction of the reactor. The averaged volumetric rate of photon absorption (AVRPA) 〈Lap〉 is then estimated from the mean value of the LVRPA within an interval corresponding to the reactor depth (eqn (7)). In the reaction setup, a radius of 0.58 cm was used as the effective reactor depth.
 | (7) |
Comparing the simulation of the AVRPA (see section 10, ESI†) and the observed photooxidation rate revealed a matching trend up to a concentration of 0.05 mM. We see this correlation as evidence that the approximation of the AVRPA is valid in the case of the presented methodology. However, the AVRPA could not explain the slight decrease in the observed photooxidation rate upon reaching an EY concentration of 0.05 mM. Since the AVRPA becomes independent of the EY concentration upon reaching 0.05 mM, we claim that this trend corresponds to a change in the lifetime τ of the triplet state, which appears in eqn (8). By means of a decreasing triplet lifetime, the concentration [EY*] decreases which directly affects R3 (eqn (9)).
| R2 = k2·[EY*] = τ−1·[EY*] | (8) |
| R3 = k3·[EY*]·[4-MTP] | (9) |
In particular, a change in the lifetime of the triplet state can occur as a consequence of an increasing probability of competing events occurring from the excited state (e.g. self-quenching). Furthermore, also, the formation of dimers, which is a known phenomenon for concentrated solutions, could lead to a change in the photochemistry of EY.58
Fig. 7(d) illustrates the observed initial photooxidation rate as a function of the AVRPA. Different than expected from the determined rate law (see section 10, ESI†), the initial photooxidation rate shows a logarithmic increase, rather than a linear increase, within the range of the applied AVRPA. Such a saturation behaviour can be traced back to an overall loss in efficiency of the photocatalytic process. It can be assumed that with a specific photon absorption (Lap, crit), the kinetic limit of the reaction network is reached. Since the LVRPA is a function of the reactor depth, this will mainly occur close to the reactor walls. The corresponding reactor depth (dcrit), in which the local reaction rate exceeds the photon limitation, is calculated from Lap(z) = Lap, crit. In these locations, an increased amount of light is absorbed without further enhancing the reaction kinetics. The resulting excess of absorbed photons lowers the overall efficiency of the photocatalytic process. In order to cover this issue, an effective quantum yield ϕeff(z) has to be used for certain locations in the reactor. With this, the observed reaction rate becomes a sum of the photon limited and kinetically limited reaction rates weighted by their individual contributions (eqn (10)).
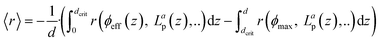 | (10) |
Simulation of 〈r〉 confirmed the hypothesis by showing a comparable logarithmic trend (see section 10, ESI†). With this non-linear behaviour, it becomes evident that photochemical processes imply a maximum performance in terms of the formed product per mol photons and unit of time. With the local difference in reaction rates, the photocatalytic reaction kinetics can get very complex. However, it could be demonstrated that PAT can assist in breaking down this complex behaviour to a simpler, in this case logarithmic, model. This model could then be used as a basis for further process optimisation. Further on, PAT and the developed chemometric model can be easily translated to a flow application thus accompanying the scale-up from a lab-based batch process to a continuous industrial application.
Conclusions
We showed that the combination of PAT and chemometric modeling is a versatile approach to obtain real-time data for kinetic insights into photocatalytic reaction networks. In particular, the photooxidation of 4-MTP has been monitored and evaluated by utilising in situ Raman spectroscopy together with an indirect hard modeling approach for data analysis. With this, we verified an, albeit slow, direct oxidation pathway that occurs independently of the photooxidation. Furthermore, by studying crucial process conditions like the stirring speed and the applied oxygen pressure, we were able to decouple mass transport phenomena from the reaction kinetics. Extending the methodology by in situ ATR-UV/Vis spectroscopy enabled the recording of real-time fluorescence spectra which then allowed for quantification of EY degradation during the photooxidation of 4-MTP. The results showed that EY degradation is a comparably slow side reaction that becomes more prominent at low 4-MTP concentrations. Consequently, this implies only a minor contribution to the photooxidation kinetics. A far greater effect was observed for the applied light intensity and EY concentration. While the optimal EY concentration was verified to be 0.05 mM, a constant increase in the rate of 4-MTP consumption was observed with increasing light intensity. However, the methodology revealed a saturation behaviour that arose from a gradual shift in the reaction limiting step. With the largest amount of absorbed photons occurring close to the reactor walls, these locations undergo a change from a photon limitation to a kinetic limitation. Increasing the light intensity further, these locations were seeing an excess of absorbed photons which did not contribute to the photocatalytic cycle. As a consequence, the overall observed photooxidation kinetics became a function of decreasing effective quantum yield lowering the overall efficiency of the photocatalytic process. Lastly, we have proposed an empirical model, on a logarithmic basis, that describes the correlation of the photooxidation rate with the averaged rate of photon absorption.These results clearly showcased the versatility of PAT in combination with chemometric analysis towards an in situ real-time monitoring of photocatalytic reactions. With this, kinetic insights into photocatalytic reactions are easily accessible while reducing the experimental effort arising from sampling. In particular, fast and biphasic reactions, like the photooxidation of 4-MTP, will benefit from this in situ approach. Lastly, PAT is known for its easy implementation in continuous flow reactors as an online monitoring tool. Thus, PAT is a promising approach that could assist early stage research and follow the scale-up towards a continuous photocatalytic process.
Experimental section
Materials
4-Methoxythiophenol (97%) (4-MTP) and bis(4-methoxyphenyl)disulfide (98%) (4-MPD) were provided by ABCR. N,N,N′,N′-Tetramethylethylenediamine (99%) (TMEDA), eosin Y (dye content > 85%) (EY) and ethanol (>99.8%, HPLC grade) were provided by Sigma-Aldrich. All chemicals were used without further purification.Photocatalytic oxidation of 4-MTP
Photooxidation reactions of 4-MTP to 4-MPD were performed in a home-designed reactor setup that allows for simultaneous irradiation and monitoring using various PAT tools. The setup was composed of a customised Schlenk-tube and a 3D-printed illumination unit equipped with 12 high-power LEDs (Nichia NCSG219B-V1, peak wavelength 520 nm, FWHM 30 nm) in a circular arrangement around the glass reactor. The LEDs operated at a constant current of 500 mA. The light intensity was further controlled by a microcontroller using pulse width modulation. Cooling of the LEDs and the reaction mixture to room temperature was conducted with compressed air. Under standard conditions, the reaction solution contained 0.2 M 4-MTP, 0.2 M TMEDA and 0.00015 M EY in 7 mL ethanol. After dissolving all reactants, the reaction mixture was transferred to the reactor. Prior to irradiation, the reaction solution was saturated with oxygen in the dark for 5 min. Under standard conditions, the reaction was performed at a stirring rate of 1300 rpm and a constant oxygen pressure of 2 bar.Real-time monitoring
In situ Raman spectra were acquired on an RXN2 spectrometer (Kaiser Optical Systems, Lille, France). The spectrometer was equipped with a laser source (785 nm) that operated at an output power of 400 mW. A short focus immersion probe with a sapphire tip was mounted in the photoreactor with GL-screw fittings (Bohlender, Grünsfeld, Germany). In situ fluorescence spectra were acquired using an AvaSpec2048 spectrometer (Avantes, Apeldoorn, Netherlands) coupled to an ATR probe (type KATANA, Hellma Analytics, Mülheim/R., Germany). The probe was equipped with an internal reflection element made of sapphire with three reflections. In situ Raman spectra were acquired using an exposure time of 5 s and were averaged over 10 measurements. Under these conditions, the reaction progress was monitored with a resolution of 1 min. In situ fluorescence spectra were acquired with an integration time of 2 ms and were averaged over 5 measurements.Chemometric modeling
Spectral evaluation of the in situ Raman and fluorescence data was conducted using PEAXACT 4 (S-PACT, Aachen, Germany). The concentration of 4-MTP and 4-MPD was predicted by an indirect hard model (IHM) in the spectral range of 700 to 1200 cm−1. Spectra were pretreated by linear baseline subtraction and peak normalisation to the EtOH band at 880 cm−1. The IHM was built from single component models according to ethanol, 4-MTP, 4-MPD and the background produced from the sapphire tip of the immersion probe. The model was calibrated from gravimetrically prepared samples including binary and ternary mixtures of ethanol, 4-MTP (0–0.38 M) and 4-MPD (0–0.27 M). Linear regression of the IHM led to a R2 of 0.99. The model was validated with samples that additionally contained EY and TMEDA to give a RMSEP of 0.014 M (4-MTP) and 0.01 M (4-MPD).Abbreviations and symbols
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors like to thank Prof. Dr. Dominik Wöll for scientific discussion.References
- G. Ciamician, Science, 1912, 36, 385–394 CrossRef CAS.
- B. König, Eur. J. Org. Chem., 2017, 15, 385–394 Search PubMed.
- S. Protti and M. Fagnoni, Photochem. Photobiol. Sci., 2009, 8, 1499–1516 RSC.
- N. Hoffmann, Photochem. Photobiol. Sci., 2012, 11, 1613–1641 RSC.
- L. Di, H. Haneda, S. Hishita and N. Ohashi, Chem. Mater., 2005, 17, 2596–2602 CrossRef.
- H. Sun, R. Ullah, S. Chong, H. M. Ang, M. O. Tadé and S. Wang, Appl. Catal., B, 2011, 108–109, 127–133 CrossRef.
- F. Dong, Z. Wang, Y. Li, W.-K. Ho and S. C. Lee, Environ. Sci. Technol., 2014, 48, 10345–10353 CrossRef CAS.
- P. Chen, H. Wang, H. Liu, Z. Ni, J. Li, Y. Zhou and F. Dong, Appl. Catal., B, 2019, 242, 19–30 CrossRef CAS.
- O. M. Alfano, D. Bahnemann, A. E. Cassano, R. Dillert and R. Goslich, Catal. Today, 2000, 58, 199–230 CrossRef.
- M. F. J. Dijkstra, H. Buwalda, A. W. F. de Jong, A. Michorius, J. G. M. Winkelman and A. A. C. M. Beenackers, Chem. Eng. Sci., 2001, 56, 547–555 CrossRef.
- R. Monsef, M. Ghiyasiyan-Arani and M. Salavati-Niasari, J. Environ. Manage., 2019, 230, 266–281 CrossRef.
- W. Wang, P. Serp, P. Kalck, C. G. Silva and J. L. Faria, Mater. Res. Bull., 2008, 43, 958–967 CrossRef.
- M. H. Shaw, J. Twilton and D. W. C. MacMillan, J. Org. Chem., 2016, 81, 6898–6926 CrossRef.
- D. Dondi, S. Protti, A. Albini, S. M. Carpio and M. Fagnoni, Green Chem., 2009, 11, 1653–1659 RSC.
- D. Cambié, F. Zhao, V. Hessel, M. G. Debije and T. Noël, Angew. Chem., Int. Ed., 2017, 56, 1050–1054 CrossRef.
- P. E. da Silva Júnior, H. I. M. Amin, A. M. Nauth, F. da Silva Emery, S. Protti and T. Opatz, ChemPhotoChem, 2018, 2, 878–883 CrossRef.
- K. A. Margrey, A. Levens and D. A. Nicewicz, Angew. Chem., Int. Ed., 2017, 56, 15644–15648 CrossRef CAS.
- N. Holmberg-Douglas, N. P. R. Onuska and D. A. Nicewicz, Angew. Chem., Int. Ed., 2020, 59, 7425–7429 CrossRef CAS.
- H.-H. Zhang, J.-J. Zhao and S. Yu, J. Am. Chem. Soc., 2018, 140, 16914–16919 CrossRef CAS.
- M. Leverenz, C. Merten, A. Dreuw and T. Bach, J. Am. Chem. Soc., 2019, 141, 20053–20057 CrossRef.
- A. Ohligschläger, C. Gertig, D. Coenen, S. Brosch, D. Firaha, K. Leonhard and M. A. Liauw, Chem. Eng. J., 2019, 368, 649–658 CrossRef.
- T. Eifert and M. A. Liauw, React. Chem. Eng., 2016, 1, 521–532 RSC.
- F. Dalitz, M. Cudaj, M. Maiwald and G. Guthausen, Prog. Nucl. Magn. Reson. Spectrosc., 2012, 60, 52–70 CrossRef.
- Z. Han, X. Gu, S. Wang, L. Liu, Y. Wang, Z. Zhao and Z. Yu, Analyst, 2020, 145, 3313–3319 RSC.
- Y. Li, B. Lin, L. Ge, H. Guo, X. Chen and M. Lu, Sci. Rep., 2016, 6, 28803 CrossRef.
- I. Dolmiac and T. Bürgi, J. Catal., 2017, 248, 268–276 CrossRef.
- C. Feldmeier, H. Bartling, E. Riedle and R. M. Gschwind, J. Magn. Reson., 2013, 232, 39–44 CrossRef CAS.
- L. Bukman, C. F. de Freitas, W. Caetano, N. R. C. Fernandes, N. Hioka and V. R. Batistela, Spectrochim. Acta, Part A, 2019, 211, 330–335 CrossRef CAS.
- M. J. Muñoz-Batista, M. M. Ballari, A. Kubacka, O. M. Alfano and M. Fernández-García, Chem. Soc. Rev., 2019, 48, 637–682 RSC.
- A. R. Almeida, J. A. Moulijn and G. Mul, J. Phys. Chem. C, 2008, 112, 1552–1561 CrossRef CAS.
- D. Gong, V. P. Subramaniam, J. G. Highfield, Y. Tang, Y. Lai and Z. Chen, ACS Catal., 2011, 1, 864–871 CrossRef CAS.
- L. Bliumkin, R. Dutta Majumdar, R. Soong, A. Adamo, J. P. D. Abbatt, R. Zhao, E. Reiner and A. J. Simpson, Environ. Sci. Technol., 2016, 50, 5506–5516 CrossRef CAS.
- A. M. R. Hall, R. Broomfield-Tagg, M. Camilleri, D. R. Carbery, A. Codina, D. Whittaker, S. Coombes, J. P. Lowe and U. Hintermair, Chem. Commun., 2018, 54, 30–33 RSC.
- D. Lehnherr, Y. Ji, A. J. Neel, R. D. Cohen, A. P. J. Brunskill, J. Yang and M. Reibarkh, J. Am. Chem. Soc., 2018, 140, 13843–13853 CrossRef CAS.
- Y. Ji, D. A. DiRocco, J. Kind, C. M. Thiele, R. M. Gschwind and M. Reibarkh, ChemPhotoChem, 2019, 3, 984–992 CrossRef CAS.
- R. W. Kessler, Prozessanalytik, Wiley-VCH, Weinheim, 2012 Search PubMed.
- K. A. Bakeev, Process Analytical Technology: Spectroscopic Tools and Implementation Strategies for the Chemical and Pharmaceutical Industries, Wiley, 2010 Search PubMed.
- D. C. Fabry, S. Heddrich, E. Sugiono, M. A. Liauw and M. Rueping, React. Chem. Eng., 2019, 4, 1486–1491 RSC.
- M. EscribÃ-Gelonch, E. Shahbazali, M. Honing and V. Hessel, Tetrahedron, 2018, 74, 3143–3151 CrossRef.
- P. Sagmeister, J. D. Williams, C. A. Hone and C. O. Kappe, React. Chem. Eng., 2019, 4, 1571–1578 RSC.
- D. Müller, B. Dercks, E. Nabati, M. Blazek, T. Eifert, J. Schallenberg, U. Piechottka and K. Dadhe, Chem. Ing. Tech., 2017, 89, 1464–1470 CrossRef.
- A. Talla, B. Driessen, N. J. W. Straathof, L.-G. Milroy, L. Brunsveld, V. Hessel and T. Noël, Adv. Synth. Catal., 2015, 357, 2180–2186 CrossRef CAS.
- Y. Su, A. Talla, V. Hessel and T. Noël, Chem. Eng. Technol., 2015, 38, 1733–1742 CrossRef CAS.
- B. Sun, C. Luo, H. Yu, X. Zhang, Q. Chen, W. Yang, M. Wang, Q. Kan, H. Zhang, Y. Wang, Z. He and J. Sun, Nano Lett., 2018, 18, 3643–3650 CrossRef CAS.
- H. Zhang, K. Mehmood, X. Jiang, W. Yao, M. Iqbal, M. Waqas, M. Ur Rehman, A. Li, Y. Shen and J. Li, Environ. Sci. Pollut. Res., 2018, 25, 28264–28274 CrossRef CAS.
- I. Azcune and I. Odriozola, Eur. Polym. J., 2016, 84, 147–160 CrossRef CAS.
- M. Sender and D. Ziegenbalg, Chem. Ing. Tech., 2017, 89, 1159–1173 CrossRef CAS.
- F. Alsmeyer, H.-J. Koß and W. Marquardt, Appl. Spectrosc., 2004, 58, 975–985 CrossRef.
- T. Sato, Y. Hamada, M. Sumikawa, S. Araki and H. Yamamoto, Ind. Eng. Chem. Res., 2014, 53, 19331–19337 CrossRef.
- K. Van't Riet, Ind. Eng. Chem. Process Des. Dev., 1979, 18, 357–364 CrossRef.
- F. Garcia-Ochoa and E. Gomez, Biotechnol. Adv., 2009, 27, 153–176 CrossRef.
- R. V. Chaudhari, R. V. Gholap, G. Emig and H. Hofmann, Can. J. Chem. Eng., 1987, 65, 744–751 CrossRef.
- V. Meille, N. Pestre, P. Fongarland and C. D. Bellefon, Ind. Eng. Chem. Res., 2004, 43, 924–927 CrossRef.
- M. Lopes, M. Mota and I. Belo, Chem. Eng. Technol., 2013, 36, 1779–1784 Search PubMed.
- A. Alvarez-Martin, S. Trashin, M. Cuykx, A. Covaci, K. De Wael and K. Janssens, Dyes Pigm., 2017, 145, 376–385 CrossRef.
- J. R. Lakowicz, Principles of Fluorescence Spectroscopy, Springer, Berlin, 2006 Search PubMed.
- M. Kubista, R. Sjoback, S. Eriksson and B. Albinsson, Analyst, 1994, 119, 417–419 RSC.
- M. Enoki and R. Katoh, Photochem. Photobiol. Sci., 2018, 17, 793–799 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Absorption and fluorescence spectra of eosin Y, Raman spectra of pure components, detailed description of model calibration, theoretical calculation of LVRPA and AVRPA and kinetic rate laws. See DOI: 10.1039/d0re00256a |
| This journal is © The Royal Society of Chemistry 2020 |