Open Access Article
Open Access ArticleCloud-inspired multiple scattering for light intensified photochemical flow reactors†
Lu
Zheng‡
a,
Hansong
Xue‡
 a,
Wai Kuan
Wong
a,
Hui
Cao
b,
Jie
Wu
a,
Wai Kuan
Wong
a,
Hui
Cao
b,
Jie
Wu
 *b and
Saif A.
Khan
*b and
Saif A.
Khan
 *a
*a
aDepartment of Chemical and Biomolecular Engineering, National University of Singapore, 4 Engineering Drive 4, Singapore 117576, Singapore. E-mail: saifkhan@nus.edu.sg
bDepartment of Chemistry, National University of Singapore, 3 Science Drive 3, Singapore 117543, Singapore. E-mail: chmjie@nus.edu.sg
First published on 14th May 2020
Abstract
The development of light-promoted organic synthesis has gained great momentum in recent years. However, the rates of photochemical reactions are dependent on the photon flux, which is typically limited by Beer–Lambert attenuation, and hampers their broad application in large-scale production. When photochemistry takes place inside clouds, photochemical reaction rates exceed clear-sky values due to the increased photon path lengths resulting from multiple reflections and refractions at droplet-air interfaces. Herein, by mimicking how nature accelerates photochemical reactions, we present a flow reactor scheme that utilizes the liquid–solid interfaces provided by densely packed glass beads as efficient light scatterers to enable homogeneous distribution and intensification of light absorption within the reaction media. With this design, we are able to scale up photo flow-reactors from micro-scale to meso-scale without compromising their performance.
The past decade has seen significant developments in photocatalysis, which have enabled previously inaccessible transformations.1 Photocatalysts can trigger single-electron transfer (SET), hydrogen-atom transfer (HAT) or energy transfer to access reactive open-shell radicals or excited intermediates, allowing hitherto unforeseen opportunities to construct organic molecules in a mild and efficient manner. However, the rate of a majority of photochemical transformations is limited by photon transport.2 Therefore, despite the exciting opportunities enabled by novel photocatalysts, their industrial application is significantly hampered by scalability challenges associated with conventional batch reactors, owing to the attenuation of photon transport by the Beer–Lambert law.3 For instance, with a 1 mM solution of commonly utilized Ru(bpy)3Cl2 photocatalyst, the transmitted light intensity is attenuated to ∼20% at a mere 0.5 mm into the liquid phase, and drops further to ∼5% at a distance of 1 mm.2 Moreover, the typically inhomogeneous irradiation inside reactors not only slows down the reaction rate, but also results in the formation of by-products4 In this regard, continuous microflow reactors have emerged as an attractive solution to overcome the issues associated with batch photochemistry.2,3,5 Notably, Noël et al. have recently demonstrated a leaf-inspired luminescent solar concentrator, where solar light was efficiently collected and converted into a narrower spectral range, and subsequently transported to microchannel reactors via total internal reflection in a polydimethylsiloxane (PDMS) light guide.5c Commonly employed flow reactor inner diameters (IDs) range between 0.25 to 2 mm, and further increment of reactor IDs without employing high power light sources still remains an outstanding challenge, due to Beer–Lambert attenuation.5b,6 The use of higher power light sources often leads to elevated temperatures, promoting undesirable side reactions and leading to a high risk of thermal runaway.5b,7 A higher production rate is often achieved by increasing the reactor length to allow increased flow rates for the same residence time. However, when flow reactors with small dimensions become longer and are operated at higher flow rates, high back pressures are typically generated.5b There have been a few notable examples of kg scale flow photochemistry.7b,8 However, in all reported approaches, high power lamps (e.g. 400 W) or lasers were employed to provide sufficient light to support high production rate in larger reaction vessels, and the excess heat generated required intensified cooling measures. In this work, we address an important gap in photochemical reactor technology development by attempting to answer the question – can the size of a ‘micro’ flow reactor (e.g. 1 mm ID) be scaled up to ‘meso’ scale (e.g. 10 mm ID), by increasing the photon absorption efficiency, without also necessitating the use of a higher power light source?
To do this, we draw inspiration from atmospheric photochemistry, a significant amount of which takes place inside cloud water droplets.9 Examples include the photodissociation of O2 and O3 and the photochemical smog caused by strong solar irradiation of automobile emissions. The photodissociation rate coefficient inside cloud droplets exceeds clear-sky values due to the increased photon path lengths within the clouds, which is a result of multiple reflections and refractions at droplet-air interfaces (Fig. 1a).10 Multiple scattering effectively traps photons and thus maximizes photon absorption/utilization; it explains why tropospheric ozone absorbs UV-radiation more efficiently than stratospheric ozone.11 The enhancement of the actinic flux also occurs within the aerosol layer,12 which accelerates photochemical reactions.13 The concept of mimicking photochemistry in cloud water droplets was previously demonstrated by Vassilikogiannakis et al. in a nebulizer-based flow reactor.14 The authors have shown how increased specific area can facilitate biphasic photo-oxygenations with improved light penetration using aerosols. However, aerosol-based flow reactors face challenges for photochemical reactions that occur in timescales of minutes, due to limited aerosol stability arising from droplet coalescence.
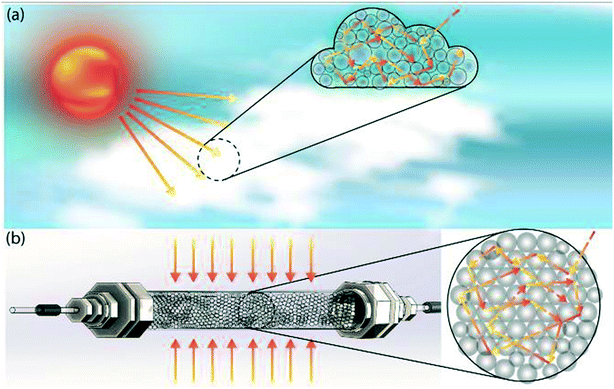 | ||
| Fig. 1 Schematic depiction of (a) multiple scattering in cloud water droplets, and (b) translation of this scheme from nature into our proposed multiple scattering flow reactor. | ||
In this study, by mimicking how nature accelerates photochemical reaction rates by multiple scattering in clouds and aerosols, we have designed a flow reactor scheme that utilizes high refractive index contrast liquid–solid interfaces provided by densely packed glass beads as efficient light scatterers (Fig. 1b). As we will describe in detail below, this reactor scheme significantly increases the photon absorption efficiency by increasing photon path lengths, while also mitigating the spatial inhomogeneity of photon distribution caused by the Beer–Lambert attenuation, thus offering a potential path to scale up flow photochemical reactors without requiring a proportional increase in the power of the light source. A packed glass bead-based reactor for heterogeneous photochemistry was previously demonstrated by Inagawa et al.,15 in which a fused glass bead monolith was coated with anatase photocatalyst, and the fused glass bead network functioned as a waveguide. The intensification of photochemistry was mainly achieved through the increased surface-to-volume ratio provided by the catalyst-coated glass beads, with no light absorption intensification within the substrate-carrying liquid phase. Herein, we demonstrate how scattering-based light absorption intensification within the liquid phase can accelerate homogeneous photochemical reactions.
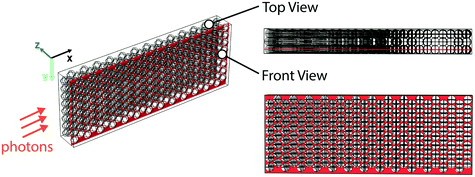
As a proof of concept, we first conducted a comparative study between the glass bead packed flow reactor scheme and a single-phase micro-flow reactor for a visible-light-promoted E/Z isomerization16 as a model reaction (Fig. 2a). The photocatalyst behaves as an uphill catalyst, which promotes isomerization of the thermodynamically more stable E-alkene to the less stable Z-isomer via an energy transfer process. Perfluoroalkoxy (PFA) tubes were chosen as the reactor material due to the high transparency of PFA to visible light and good resistance to organic reagents.2 A blue light-emitting diode (LED) stripe (center ∼460 nm) was wrapped around a glass cylinder (with an inner diameter of 9 cm), at the center of which the reactor tube was placed to receive light radially (Fig. S1†). Glass beads (diameter ∼75 μm, refractive index nD = 1.52) were densely packed into PFA reactor tubes of three different diameters (1 mm, 5 mm and 10 mm ID respectively) and reactor lengths (7 cm, 1.8 cm and 2.7 cm respectively). The corresponding mass loading of glass beads was 40, 260, 1560 mg respectively, with a liquid volume per unit length of 2, 50, 200 μL cm−1 respectively. The reaction was conducted in 1,2-dichloroethane (DCE, refractive index, nD = 1.445). The residence time was controlled by tuning the flow rates of the reaction mixture (reaction details can be found in the ESI†).
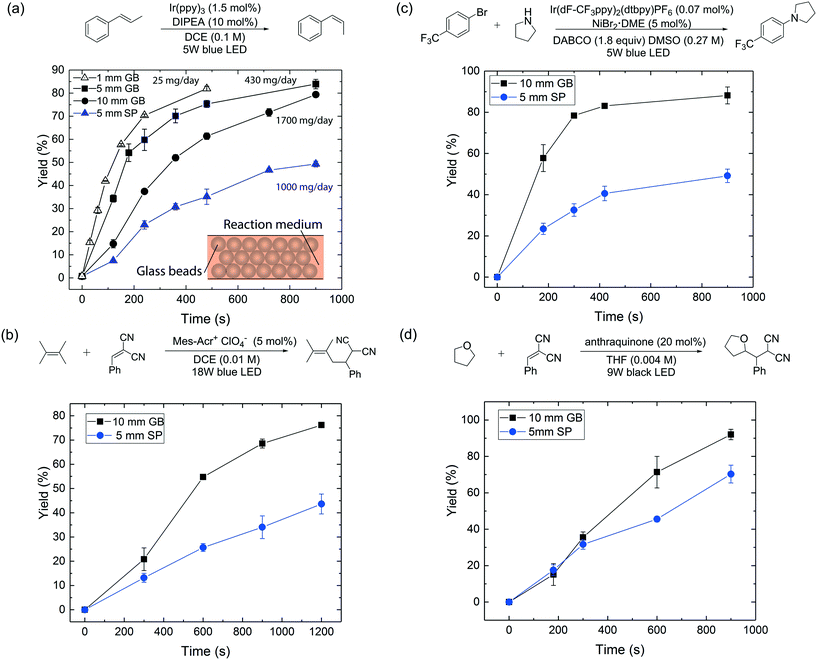 | ||
| Fig. 2 (a) Reactor performance comparison between 1 mm, 5 mm, 10 mm ID glass bead and 5 mm ID single-phase flow reactors for the photocatalytic E-to-Z isomerization16 under visible-light irradiation. (b)–(d) Reactor performance comparison between 5 mm ID single-phase (SP) and 10 mm ID glass bead (GB) flow reactors for (b) photoredox transformation;17 (c) aryl amination using ligand-free Ni(II) catalyst and photoredox catalysis;18 (d) photo-mediated hydrogen-atom-transfer.19 A 40 psi back-pressure regulator was used for all flow reactions. DIPEA = N,N-diisopropylethylamine; Mes–Acr+ = 9-mesityl-10-methylacridinium; DABCO = 1,4-diazobicyclo[2.2.2]octane; DMSO = dimethyl sulfoxide; THF = tetrahydrofuran. | ||
Fig. 2a provides yield versus residence time curves for the three glass bead reactors and a 5 mm ID reactor run in single-phase flow mode. First, we note that yields exceeding 80% could be obtained with all three glass bead reactors within 15 minutes of residence time, with estimated daily production rates of 25 mg per day, 430 mg per day and 1700 mg per day respectively (values calculated based on a reactor length of 10 cm and yields at residence times of 8 min, 15 min and 15 min respectively). An ∼70× enhancement of production rate was thus achieved by moving from the 1 mm to the 10 mm ID reactor, without significantly compromising reaction performance or, equally importantly, changing the light source. We further underscore this important point, by comparing the performance of a 10 mm ID glass bead reactor to that of a 5 mm ID single-phase reactor (Fig. 2a), which has the same liquid volume per unit length (200 μL cm−1); the glass bead reactor clearly outperformed the latter (80% vs. 50% yield at 15 min residence time). Further, to rule out radial mixing as a major contributor to the superior performance of the packed glass bead reactor, a control experiment was performed with a 1 mm ID reactor packed with opaque beads (see ESI†). This packed reactor led to a significantly compromised performance (16% vs. 75% yield at 8 min residence time) compared to a 1 mm ID single-phase reactor.
To demonstrate the generality and applicability of our reactor scheme, the 10 mm ID glass bead reactor and the 5 mm ID single-phase flow reactor, which possesses the same liquid volume per unit length, were further compared for another three representative photochemical transformations (with the same setup shown in Fig. S1†), including a photoredox transformation,17 dual photoredox and nickel catalysis,18 and a photo-mediated HAT reaction.19 The results are summarized in Fig. 2b–d; all experiments were conducted in duplicate. In all cases, the glass bead reactor outperforms its single-phase counterpart under the same reaction conditions. This study shows that the glass bead packed reactor can enhance the performance of a wide range of photochemical transformations where photon transport is important.
Finally, we also performed optical ray-tracing simulations in COMSOL Multiphysics20 to visualize photon transport in the glass bead reactor system and compared it with photon transport in a single-phase flow reactor. We used a three-dimensional model and assumed a planar monochromatic light wave to represent the incident light. The geometry of the model is shown in Fig. 3; representative volumes of 2.5 mm × 0.98 mm × 0.38 mm dimension, either filled with layers of close-packed glass beads (26 × 8 × 3 glass beads, each of 100 μm diameter) or empty were used for the simulation. In essence, the representative volume filled with glass beads was used to simulate a section of the glass bead reactor while the representative volume kept empty was used to represent its equivalent single-phase reactor. Now, since the experimental reactor system is axisymmetric, the simulated propagation length of the planar wave along the incident direction (X-axis) was chosen to be 2.5 mm (for a 5 mm diameter reactor) as a proof-of-concept. The incident wavelength of 470 nm was chosen based on maximum emission wavelength of the blue LED utilized. As shown in Fig. 3, the rays were normally incident onto the Y–Z plane, and the incident power of the light source used was 1.4 × 10−4 W, based on the illumination geometry of the experiment. Only absorption, reflection and refraction were considered in the modelling. Rays were only allowed to leave the modelled representative volume from the Y–Z plane by setting specular reflection wall conditions for all surfaces of the representative volume except for the surfaces parallel to the Y–Z plane (Fig. 3); specular reflection was taken into consideration as the surfaces of the glass beads were treated as smooth (see ESI† and the ray-tracing plots). The absorption properties of the reaction medium were accounted for in the simulations by the imaginary part of the complex refractive index, which was estimated as follows. The molar extinction coefficient (ε) of the reaction medium for the photocatalytic E-to-Z isomerization reaction was first experimentally measured to be 1700 M−1 cm−1 (at 470 nm and catalyst concentration of 1.5 mM) using a UV-vis spectrometer (see ESI† for details). This value was subsequently used to estimate the imaginary part of the complex refractive index in single-phase ray tracing simulations, where it was a fitting parameter used to match experimentally measured absorbance with that obtained from the ray tracing.
Based on the output power of rays leaving the representative volume, total absorption of the rays by the reaction medium was 66% of the incident power for the glass bead case, whereas it was 77% for the single-phase case, based on the Beer–Lambert law. Interestingly, though the total absorption was slightly smaller for the glass bead case, it is also crucial to note that there is ∼4× less absorbing liquid medium inside the glass bead reactor. Next, following the same rationale as in our experiments, we then modelled a representative volume of 5.0 mm × 0.98 mm × 0.38 mm filled with glass bead layers to simulate the case for 10 mm diameter glass bead reactor, and compared its performance to a 5 mm diameter single-phase reactor. This time, the absorption for glass bead case was estimated to be ∼84%; this demonstrates that the glass bead flow reactor has higher light absorption efficiency than its single-phase counterpart given the same amount of absorbing medium. Given that the concentrations and molar extinction coefficients are identical in the two cases, this difference can be attributed to the increased optical path length in the glass bead reactor. To verify this hypothesis, we compared photon residence times inside the 5 mm diameter glass bead and single-phase reactors. To estimate this quantity from ray tracing, 24 evenly spaced incident rays on the YZ plane were chosen such that each ray passed through the centre of the first layer of glass beads on the YZ plane. The average residence time for glass bead reactor was 12.4 ps, which is 7% longer than the single-phase reactor case (11.6 ps).
Lastly, we also carried out another simulation for the dual photoredox and nickel catalysis reaction (Fig. 2c) with a molar extinction coefficient value of 567 M−1 cm−1 (at 450 nm (ref. 8b) and catalyst concentration of 0.189 mM). Based on the Beer–Lambert law, the single-phase reactor is expected to absorb only 6% of the incident power, and any enhancement in the optical path length is expected to have a more prominent effect than in the above case of the E–Z isomerization reaction, where even the single-phase case leads to 77% absorption of the incident power. Our results show that the 5 mm diameter glass bead system leads to an absorption efficiency of 19%, an ∼3× enhancement over the expected value for the single-phase case. Interestingly, this is despite the fact that there is 4× less reaction medium in the glass bead case. When simulated for a 10 mm diameter glass bead reactor, the absorption was found to be ∼28%. These simulation results also agree well with the experimental trends reported in Fig. 2, where a greater performance enhancement is observed in Fig. 2c compared to Fig. 2a.
In conclusion, inspired by accelerated photochemical reaction rates via multiple scattering in clouds and aerosols in nature, we have developed a platform that employs solid–liquid interfaces to enhance photon absorption efficiency while circumventing the inhomogeneous illumination caused by the attenuation effect in photochemical processes, making scaling up of microflow photochemical reactors possible. We have demonstrated superior performance of the 10 mm ID glass bead packed reactor over a volume-equivalent 5 mm ID single-phase flow reactor in four different types of photochemical transformations and also validated these findings for the E-to-Z isomerization and the dual photoredox and nickel catalysis reactions through optical ray-tracing simulations. Multiple scattering enabled by solid–liquid interfaces allows intensification of light absorption inside the reactor, which then enhances the efficiency of photochemistry. Further scale-up of the mass throughput of such systems (into the kg per day range) via further increasing reactor dimensions (both radial and axial), is currently ongoing in our laboratory. We expect this technology to pave the way for scaled-up application of photocatalytic reactions in the pharmaceutical and fine chemical industries.
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
We thank Mr. Habimana Jean Willy for assistance with running the COMSOL Multiphysics ray tracing model, and Prof. Ding Jun (Department of Materials Science & Engineering, NUS) for providing the COMSOL Multiphysics program. We are grateful for the financial support provided by the GSK-EDB Fund for Green and Sustainable Manufacturing (R-143-000-687-592 and R-279-000-507-592), Ministry of Education (R-279-000-534-514), and A*STAR via the Pharmaceutical Innovation Programme Singapore (grant number A19B3a0008).References
- For selected reviews, see: (a) L. Marzo, S. K. Pagire, O. Reiser and B. König, Angew. Chem., Int. Ed., 2018, 57, 10034–10072 ( Angew. Chem. , 2018 , 130 , 10188–10226 ) CrossRef CAS PubMed; (b) M. Silvi and P. Melchiorre, Nature, 2018, 554, 41–49 CrossRef CAS PubMed; (c) N. A. Romero and D. A. Nicewicz, Chem. Rev., 2016, 116, 10075–10166 CrossRef CAS PubMed; (d) D. Ravelli, S. Protti and M. Fagnoni, Chem. Rev., 2016, 116, 9850–9913 CrossRef CAS PubMed; (e) K. L. Skubi, T. R. Blum and T. P. Yoon, Chem. Rev., 2016, 116, 10035–10074 CrossRef CAS PubMed; (f) C. K. Prier, D. A. Rankic and D. W. C. MacMillan, Chem. Rev., 2013, 113, 5322–5363 ( Angew. Chem. , 2012 , 124 , 6934–6944 ) CrossRef CAS PubMed; (g) J. Xuan and W.-J. Xiao, Angew. Chem., Int. Ed., 2012, 51, 6828–6838 CrossRef CAS PubMed; (h) J. M. R. Narayanam and C. R. J. Stephenson, Chem. Soc. Rev., 2011, 40, 102–113 RSC; (i) Q.-L. Shi and J.-T. Ye, Angew. Chem., Int. Ed., 2020, 59, 4998–5001 CrossRef CAS PubMed; (j) G. Masson and B. König, Eur. J. Org. Chem., 2020, 1191–1192 CrossRef CAS.
- D. Cambié, C. Bottecchia, N. J. Straathof, V. Hessel and T. Noël, Chem. Rev., 2016, 116, 10276–10341 CrossRef PubMed.
- M. B. Plutschack, B. U. Pieber, K. Gilmore and P. H. Seeberger, Chem. Rev., 2017, 117, 11796–11893 CrossRef CAS PubMed.
- B. Shen, M. W. Bedore, A. Sniady and T. F. Jamison, Chem. Commun., 2012, 48, 7444–7446 RSC.
- (a) O. Shvydkiv, A. Yavorskyy, S. B. Tan, K. Nolan, N. Hoffmann, A. Youssef and M. Oelgemöller, Photochem. Photobiol. Sci., 2011, 10, 1399–1404 RSC; (b) Y. Su, N. J. Straathof, V. Hessel and T. Noël, Chem. – Eur. J., 2014, 20, 10562–10589 ( Angew. Chem. , 2017 , 129 , 1070–1074 ) CrossRef CAS PubMed; (c) D. Cambié, F. Zhao, V. Hessel, M. G. Debije and T. Noël, Angew. Chem., Int. Ed., 2017, 56, 1050–1054 CrossRef PubMed; (d) C. Sambiagio and T. Noël, Trends Chem., 2020, 2, 92–106 CrossRef; (e) G. X. de Oliveira, J. O. B. Lira, D. Cambié, T. Noël, H. G. Riella, N. Padoin and C. Soares, Chem. Eng. Res. Des., 2020, 153, 626–634 ( Angew. Chem. , 2019 , 131 , 14512–14516 ) CrossRef CAS; (f) D. Cambié, J. Dobbelaar, P. Riente, J. Vanderspikken, C. Shen, P. H. Seeberger, K. Gilmore, M. G. Debije and T. Noël, Angew. Chem., Int. Ed., 2019, 58, 14374–14378 ( Angew. Chem. , 2019 , 131 , 13164–13168 ) CrossRef PubMed; (g) X.-J. Wei, I. Abdiaj, C. Sambiagio, C.-F. Li, E. Zysman-Colman, J. Alcázar and T. Noël, Angew. Chem., Int. Ed., 2019, 58, 13030–13034 CrossRef CAS PubMed.
- B. D. Hook, W. Dohle, P. R. Hirst, M. Pickworth, M. B. Berry and K. I. Booker-Milburn, J. Org. Chem., 2005, 70, 7558–7564 CrossRef CAS PubMed.
- (a) I. Abdiaj, C. R. Horn and J. Alcazar, J. Org. Chem., 2019, 84(8), 4748–4753 CrossRef CAS PubMed; (b) J. W. Beatty, J. J. Douglas, R. Miller, R. C. McAtee, K. P. Cole and C. R. Stephenson, Chem, 2016, 1, 456–472 CrossRef CAS PubMed; (c) T. Noël, J. Flow Chem., 2017, 7, 87–93 CrossRef.
- (a) L. D. Elliott, M. Berry, B. Harji, D. Klauber, J. Leonard and K. I. Booker-Milburn, Org. Process Res. Dev., 2016, 20, 1806–1811 CrossRef CAS; (b) K. C. Harper, E. G. Moschetta, S. V. Bordawekar and S. J. Wittenberger, ACS Cent. Sci., 2019, 5, 109–115 CrossRef CAS PubMed.
- W. Chameides and D. Davis, J. Geophys. Res., C: Oceans Atmos., 1982, 87, 4863–4877 CrossRef CAS.
- S. Madronich, J. Geophys. Res.: Atmos., 1987, 92, 9740–9752 CrossRef.
- C. Brühl and P. J. Crutzen, Geophys. Res. Lett., 1989, 16, 703–706 CrossRef.
- D. V. Michelangeli, M. Allen, Y. L. Yung, R. L. Shia, D. Crisp and J. Eluszkiewicz, J. Geophys. Res.: Atmos., 1992, 97, 865–874 CrossRef CAS PubMed.
- R. Dickerson, S. Kondragunta, G. Stenchikov, K. Civerolo, B. Doddridge and B. Holben, Science, 1997, 278, 827–830 CrossRef CAS PubMed.
- G. I. Ioannou, T. Montagnon, D. Kalaitzakis, S. A. Pergantis and G. Vassilikogiannakis, ChemPhotoChem, 2017, 1, 173–177 CrossRef CAS.
- H. Usami, K. Ohta and S. Inagawa, J. Photochem. Photobiol., A, 2017, 332, 595–601 CrossRef CAS.
- K. Singh, S. J. Staig and J. D. Weaver, J. Am. Chem. Soc., 2014, 136, 5275–5278 CrossRef CAS PubMed.
- R. Zhou, H. Liu, H. Tao, X. Yu and J. Wu, Chem. Sci., 2017, 8, 4654–4659 RSC.
- E. B. Corcoran, M. T. Pirnot, S. Lin, S. D. Dreher, D. A. DiRocco, I. W. Davies, S. L. Buchwald and D. W. MacMillan, Science, 2016, 353, 279–283 CrossRef CAS PubMed.
- X.-Z. Fan, J.-W. Rong, H.-L. Wu, Q. Zhou, H.-P. Deng, J. D. Tan, C.-W. Xue, L.-Z. Wu, H.-R. Tao and J. Wu, Angew. Chem., Int. Ed., 2018, 57, 8514–8518 ( Angew. Chem. , 2018 , 130 , 8650–8654 ) CrossRef CAS PubMed.
- For COMSOL, see https://www.comsol.com/ for Comsol multiphysics 5.4a.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI:10.1039/d0re00080a |
| ‡ Lu Zheng and Hansong Xue contributed equally to the manuscript. |
| This journal is © The Royal Society of Chemistry 2020 |