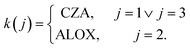Optimization of the direct synthesis of dimethyl ether from CO2 rich synthesis gas: closing the loop between experimental investigations and model-based reactor design†
Received
30th January 2020
, Accepted 31st March 2020
First published on 1st April 2020
Abstract
Reaction kinetic modeling, model-based optimization and experimental validation are performed for the direct synthesis of dimethyl ether from CO2 rich synthesis gas. Among these disciplines, experimental methods and models are aligned in a stringent way of action, i.e., the same setup and models are applied throughout the whole contribution. First, a lumped reaction kinetic model from the literature is modified and parametrized to fit a vast array of 240 data points measured in a laboratory fixed bed reactor. The data were acquired using a mechanical mixture of the commercial catalysts CuO/ZnO/Al2O3 and γ-Al2O3. For this setup, a predictive model is derived and applied within dynamic model-based optimization. Here, the single-pass COx conversion serves as objective function while the operating conditions and composition of the mixed catalyst bed are the optimization variables. Finally, the optimization results obtained numerically are validated experimentally verifying the identified performance enhancement qualitatively. The remaining quantitative deviations yield valuable insights into model and methodological weaknesses or inaccuracies, closing the loop between kinetic investigations, model-based optimization and experimental validation.
1 Introduction
A good mathematical model covers the description of all relevant physicochemical processes with an adequate level of detail to answer a specific question, while its numerical manageability is not compromised by an unnecessary high complexity. Consequently, models are often simplified by a number of context dependent assumptions that facilitate their solution. In the context of model-based optimization of chemical reactors as for example during multi-level reactor design (MLRD),1–3 a proper degree of detail is crucial. This so called model adequacy is especially relevant when the models are extrapolated. Therefore, it is of general importance to review optimization results critically by using experimental data for the validation of the predictions and analysis of the models extrapolation capabilities. For this purpose, it is necessary to closely link the gathering of experimental data, the development and parametrization of mathematical models and the model-based optimization in a systematic approach as proposed in Fig. 1.
 |
| | Fig. 1 Proposed systematic approach. | |
Dimethyl ether (DME) serves as an example system in our work since it is subject of current research due to its manifold possible applications in a world of changing fuel feedstocks, especially in the vehicle technology as a diesel alternative, as well as in the chemical industry as feedstock for the manufacturing of short-chain olefins.4–6 Dimethyl ether is one of the so called multi-source fuels since it can be produced from different raw materials such as petroleum, natural gas, coal and also from renewable resources such as biomass.7
DME can be produced directly from syngas over a dual catalyst system in one reactor. This process is thermodynamically more favorable than the traditional two-step process used in industry (i.e. methanol synthesis, followed by dehydration), allowing a better utilization of the synthesis gas at comparable conditions.8–12 The direct route is more efficient and selective in comparison with other methods used in the production of synthetic fuels.13–15 New possible applications of DME lead to an increase of the global production, but also to the search for new ways to optimize the processes efficiency, especially if CO2 is used as co-feed.
One of the most challenging aspects during the direct DME synthesis is the prevention of deactivation phenomena which affect the catalyst service life and yield. It has also been shown that the synergetic effect of the metallic components in methanol catalysts strongly depends on the feed composition, temperature and mixing methods of the dual catalyst system.16,17 In previous studies, the direct DME synthesis process has been studied using different reactor configurations and corresponding kinetic models, and optimized reactor configurations have been proposed.18–20 However, to the best of our knowledge there is hardly any study in which a kinetic model has been correlated using a vast array of data points and in which the obtained model-based optimization results were validated experimentally in order to assess both its extrapolation capability and the model fidelity.
The scope of our work is to establish the link between experimental investigations, model development and model-based optimization by setting a joint basis for each of the disciplines. Compared to other DME synthesis works, we further address the fundamental difficulties associated with possible model shortcomings caused by assumptions and uncertainties of a mathematical system description in application-oriented research. The experimental validation of optimization results helps to develop enhancement strategies for avoiding loss in catalytic performance and yield for the direct synthesis of dimethyl ether, while also serving for the identification of possible model weaknesses and critical factors influencing the quality of model predictions.
2 Laboratory reactor for the one-step DME synthesis
In the following sections, the laboratory reactor setup is presented (section 1) and the corresponding model for this reactor is developed and explained (section 2.2). The setup and its corresponding model are applied in all further parts of this contribution ensuring consistency between experimental and model-based results.
2.1 Experimental setup
The reactor setup is depicted in Fig. 2. It consists of a tube made of stainless steel with an inner concentric tube which allows to ensure isothermal conditions. The reactor is divided into four independent heating zones, each of which is surrounded by brass jaws equipped with heating cartridges for temperature control. Gas is supplied via mass flow controllers (MFC) by using proportional integral derivative (PID) control. The product composition was measured by means of a gas chromatograph (GC) G1530A from Agilent equipped with a thermal conductivity (TCD) and flame ionization (FID) detectors. Within the scope of this study a mechanical 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of two commercially available catalysts was used. The catalysts were a CZA (CuO/ZnO/Al2O3) catalyst for the methanol synthesis and ALOX (γ-Al2O3) for the selective methanol dehydration to dimethyl ether. Both catalysts were milled and sieved to a particle size dp between 250 and 500 μm. To ensure an isothermal mode of operation, the catalyst mixture was diluted with silicon carbide (SiC) of the same grain size. Details of the experimental setup and further information about the used materials can be found in the ESI.†
1 mixture of two commercially available catalysts was used. The catalysts were a CZA (CuO/ZnO/Al2O3) catalyst for the methanol synthesis and ALOX (γ-Al2O3) for the selective methanol dehydration to dimethyl ether. Both catalysts were milled and sieved to a particle size dp between 250 and 500 μm. To ensure an isothermal mode of operation, the catalyst mixture was diluted with silicon carbide (SiC) of the same grain size. Details of the experimental setup and further information about the used materials can be found in the ESI.†
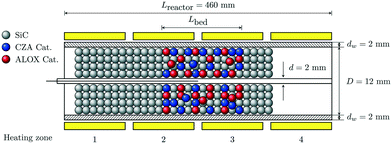 |
| | Fig. 2 Schematic representation of the reactors geometry. | |
2.2 Predictive model for laboratory reactor
As a major objective of this work is to establish a joint basis for the reaction kinetic investigations and model-based design of chemical reactors via optimization, the laboratory reactor has to be described in terms of a predictive model. Using different implementations, this model will be used for both, the parametrization of the reaction kinetic model and the model-based optimization of the laboratory reactor. It hence constitutes the aforementioned link between these disciplines and is introduced in the following sections.
2.2.1 Balance equations.
eqn (1) represents the species mass balance formulated in terms of the molar fraction that is valid for the considered system under the assumptions of steady state, isothermal and isobaric operation, no relevant gradients in radial direction and negligible back-mixing effects. In order to justify the assumption of plug flow, the Bodenstein number (Bo) was calculated for the worst case scenario (lowest inlet volume flow). In this case, the Bo computed is 436, a value at which according to Baerns et al.21 the influence of back-mixing in the gas phase can be neglected. The assumption of plug flow applies. The influence of internal mass transport was ruled out in all measurements on the basis of the Weisz criterion,21,22 which was fulfilled in each case (maximal reported value: 0.87). Additionally, an expression for the change of the gas velocity (u in m s−1) along the reactor coordinate, is derived based on the total mass balance to account for the effects of volume contraction caused by reaction, and presented in eqn (2).| |  | (1) |
| |  | (2) |
In eqn (1) and (2), R represents the universal gas constant in J mol−1 K−1, T the temperature in K, p the pressure in Pa, Z the mixture's compressibility factor (eqn (8)), and yi the mole fraction of component i. The molar rate of depletion or formation of component i due to chemical reaction (Ri in mol m−3 s−1) is defined by:| |  | (3) |
In eqn (3), νi,j represents the stoichiometric coefficient of component i in reaction j, and rj represents the rate of the same reaction.
For the solution of the system of equations, Dirichlet boundary conditions (eqn (4) and (5)) at the reactor inlet (z = 0) are used.
| | | Species mole fraction : yi,0 = yi,in | (4) |
| | | Gas velocity : u0 = uin | (5) |
2.2.2 Thermodynamic considerations.
The equilibrium constants Kf,j of each reaction j were computed based on the stoichiometry of the involved reactions with the commercial software Aspen Plus® using the built-in reactor model REquil in the relevant temperature range of 200–300 °C at 50 bar, and fitted to the simplified function given in eqn (6). The parameters Aj and Bj are reported in Table 2.| |  | (6) |
The Peng Robinson equation of state23 is used to describe the real gas behavior of the gaseous mixture, and Van der Waals mixing rules are employed to account for inter-molecular interactions. Relevant information obtained from these equations are the fugacity coefficients ϕi which are used for the calculation of the fugacities fi based on eqn (7), and the mixture's compressibility factor Z which characterizes the nonideality of the gas mixture.
| | | Z3 − (1 − B)Z2 − (A − 3B2 − 2B)Z − (AB − B2 − B3) = 0 | (8) |
The parameters
A and
B are defined by:
| |  | (9) |
The mixture parameters
a and
b are calculated with the mixing rules:
| |  | (10) |
where
δik is the empirically determined binary interaction coefficient for the species
i and
k, taken from Meng and Duan
24 and Meng
et al.25 The pure component parameters are defined by:
| | a = a(Tc)α(Tr,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω), b = b(Tc), ω), b = b(Tc), | (11) |
| | 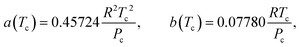 | (12) |
| |  | (13) |
while the fugacity coefficient of a component
i in a mixture is given by
eqn (14):
| |  | (14) |
The required data on chemical substances in the gas mixture such as the critical temperature
Tc, critical pressure
Pc and the acentric factor
ω were taken from the Yaws Handbook.
26
3 Reaction kinetic investigations
For predicting the system behavior in the proximity of a well-known operating point it is best practice to use kinetic models developed under the assumption of a given environmental setting, i.e., a given range of operating conditions, a given setup, and so on. In the context of model-based reactor optimization, however, this assumption not necessarily holds true since the aforementioned environmental setting might be changing due to the selected optimization variables. Accordingly, the formulation of suitable reaction kinetic models is much more challenging and subject to increasingly sophisticated demands. In this regard, besides accounting for measurable quantities, the effects of optimized design variables also have to be considered already at the development stage of a reaction kinetic model. In case of the direct synthesis of DME, this triggers, e.g., the consideration of the composition of the mixed catalytic bed. Hence, the scope of the reaction kinetic investigations in this work is set onto the identification of a suitable model and a corresponding set of parameters that satisfy these specific needs. The reaction kinetic model developed in section 3.2 is compiled from literature and modified accordingly.
3.1 Reaction kinetic measurements: procedure and operating conditions
Prior to any measurement, the catalysts were reduced at atmospheric pressure. The initial reduction was performed with 5% hydrogen (H2) diluted in argon (Ar); the temperature was increased from 100 °C to 200 °C with a heating rate of 20 °C h−1. In the second step, the hydrogen concentration was increased to 50% and the temperature was increased from 200 °C to 240 °C with a heating rate of 12 °C h−1. The catalyst was kept at this temperature for 5 h, then the reactor was flushed with Ar and cooled down to 220 °C.
The measured kinetic data are provided in the ESI.† The kinetic experiments were carried out at the conditions outlined in Table 1. These conditions were chosen in order to minimize the amount of water and methanol produced as by-products, since an accurate measurement of these species was not possible with the analytical equipment used in this study. To avoid stoichiometric limitations, the hydrogen content in the feed gas was calculated using eqn (15),
| | | yH2,in = 2.3 (yCO,in + yCO2,in) + yCO2,in. | (15) |
Table 1 Conditions for kinetic measurements
| Param. |
Value |
Unit |
|
Standard liters per minute, T = 0 °C and p = 1.01325 bar.
|
|
T
|
220, 230, 240, 250, 260 |
°C |
|
V
iṅ
|
0.2, 0.3, 0.4, 0.5, 0.6, 0.7 |
SLPMa |
|
y
CO2in
|
0, 1, 3 |
% |
|
y
CO,in
|
4, 8, 15 |
% |
|
d
p
|
250–500 |
μm |
|
m
ALOX/mCZA |
0, 1 |
gALOX/gCZA |
|
p
|
50 |
bar |
Catalyst reduction and the experimental procedure were controlled using an automated measurement routine to set up the experimental conditions (i.e., temperature, total volumetric flow and inlet feed). Each operating point was measured under steady state conditions. In all kinetic experiments, the carbon balance featured a maximal deviation of 2.5%.
3.2 Reaction kinetic model and parameter estimation
Reviewing the reaction kinetic approaches in literature,20,27–30 the model proposed by Lu et al.20 was found to be particularly suitable. In contrast to the original formulation using partial pressures, in our work the influence of higher pressure levels is accounted for by using fugacities. The modified rate expressions are described by eqn (16) to (18) for the methanol synthesis from carbon dioxide (reaction 1), the methanol dehydration to dimethyl ether (reaction 2) and the water gas shift reaction (reaction 3), respectively.
| Reaction 1) CO2 + 3H2 ⇌ CH3OH + H2O |
| Reaction 2) 2CH3OH ⇌ CH3OCH3 + H2O |
| Reaction 3) CO + H2O ⇌ CO2 + H2 |
| |  | (16) |
| |  | (17) |
| |  | (18) |
To minimize strong correlation between the parameters in the Arrhenius and the Van't Hoff equations for each reaction, the reparametrization proposed by Pritchard and Bacon31 is applied for a reference temperature (TR) of 503 K. The reparametrized equations used for the reaction kinetic modeling are described by eqn (19) for the Arrhenius, and by eqn (20) for the Van't Hoff approach. Additionally, the activation energy EA,j and the adsorption enthalpy ΔHAds,i were scaled according to eqn (21) and (22) in order to reduce the difference in magnitude between these parameters and the frequency factors kj,TR and adsorption coefficients Ki,TR respectively. According to Espie and Macchietto32 this procedure increases the numerical stability of the fitting procedure and increases the statistical significance of the estimated parameters.
| |  | (19) |
| |  | (20) |
| |  | (21) |
| | 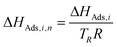 | (22) |
The parameters A and B associated to eqn (6) for the calculation of the equilibrium constants (Kf,j) are reported in Table 2 for reactions (1) to (3).
Table 2 Fitted parameters for the equilibrium constants calculated with Aspen Plus®
The expressions for the reaction rates were extended as illustrated by eqn (23) in order to enable the model-based optimization of the catalytic bed composition by introducing the term ξk(j) which characterizes this composition. In eqn (23), rj represents the reaction rate as described in eqn (16) to (18) in mol kg−1 s−1, and rj,mod is the modified reaction rate of reaction j in mol m−3 s−1:
| | | rj,mod = [(1 − εbed) ρcat,k(j)ξk(j)] rj. | (23) |
Here, the term ξk(j) is defined as the catalyst volume fraction related to the total volume of solid in the mixed catalytic bed (eqn (24)), εbed is the porosity of the catalytic bed and ρcat,k(j) the density of the catalyst which promotes reaction j. As reported in the literature,33 the water-gas shift reaction is promoted by the methanol catalyst only. Hence, a possible influence of the dehydration catalyst on its reaction rate is neglected.
| |  | (24) |
Parameter estimation was carried out with gProms® using the built-in maximum likelyhood function, based on the outlet mole fraction of the main species,
| | | yi(z = Lbed) i = CO, CO2, DME, H2. | (25) |
3.3 Reaction kinetic investigations results
The derived reaction kinetic model was fitted to a total of 240 experiments. The experimental data basis considered 10 different feed compositions at 5 different temperature levels and 6 residence times. The estimated parameters for the modified Arrhenius and Van't Hoff approaches (eqn (19) and (20), respectively) are reported in Table 3, along with the corresponding 95% confidence intervals. The goodness of fit of this model is illustrated by means of parity plots (Fig. 3) where the measured molar fraction of CO, CO2, DME and H2 in the product stream is plotted against the one predicted by the reaction kinetic model for all experiments. This Figure depicts a very good agreement between measurements and predictions without noticeable systematic deviations. A particularly wide random scattering can be observed in the low concentration range (<0.5%) of DME which can mainly be attributed to measurement limitations, since these concentrations are outside the calibration range of the analytics. Additionally, the estimated enthalpy ΔHads,CO2,n indicates a weak to almost nonexistent temperature dependence of the CO2 adsorption. In general it can be observed that the selected kinetic approach delivers a satisfactory fitting of the experimental data within a broad validity range (Table 4). The reaction kinetic model as presented here is employed in section 4 for the model-based reactor optimization.
Table 3 Estimated parameters in reparametrized form and 95% confidence intervals
|
|
Reaction (1)
|
Reaction (2)
|
Reaction (3)
|
|
Parameters were fixed, no statistical information available.
|
| ln(kj,TR) |
−6.94 (±0.03) |
−2.07 (±0.31) |
−2.75 (±0.11) |
|
E
Aj,n
|
21.81 (±0.84) |
42.77 (±9.1) |
10.82 (±2.51) |
|
|
CO |
CO2 |
H2 |
| ln(ki,TR) |
−15.32a |
−0.57a |
−19.51a |
| ΔHads,i,n |
−14.03a |
0a |
−14.68a |
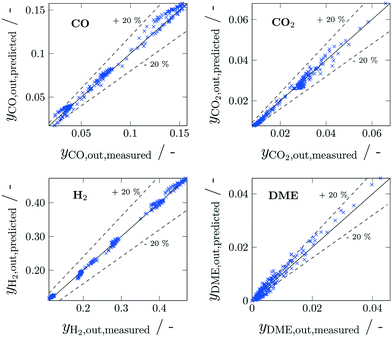 |
| | Fig. 3 Parity plots for measured and predicted CO, CO2, H2 and DME concentrations in the product stream. Experimental conditions reported in Table 1. | |
Table 4 Validity range of parametrized kinetic model
|
|
y
CO2
|
y
CO
|
y
H2
|
y
DME
|
y
CH3OH
|
y
H2O
|
T
|
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in
in
|
p
|
| % |
% |
% |
% |
% |
% |
°C |
SLPM |
bar |
| Min. |
0.8 |
2.2 |
11.0 |
0.0 |
0.0 |
0.0 |
220 |
0.2 |
50 |
| Max. |
6.6 |
16.2 |
48.4 |
4.3 |
1.4 |
2.0 |
260 |
0.7 |
50 |
4 Model-based reactor optimization
With the newly developed reaction kinetic model described in section 3, the laboratory reactor setup can now be optimized using the reactor model of section 2.2. It is to be highlighted that, since the same laboratory reactor applied for kinetic measurements is optimized here, any errors resulting from the transfer of an unknown setup with unknown flow field and other unknown nonidealities are reduced to a minimum. That way it is possible to disregard these transfer errors in the interpretation of the optimization results. Accordingly, a general uncertainty when comparing model-based with experimental results is also reduced to a minimum, increasing the reliability of the findings in this work.
4.1 Problem statement
In this Section, the optimization scenario consisting of the objective function, optimization variables and constraints is described.
4.1.1 Objective function.
Since the direct synthesis of dimethyl ether does not involve any significant problems with selectivity at the studied conditions, the main purpose of the optimization problems considered in this work is to identify the reaction concept that yields the highest single-pass carbon conversion,| |  | (26) |
4.1.2 Optimization variables.
The temperature (T), total gas flow (![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in) and the composition of the catalytic bed (ξk(j)) are obvious optimization variables considering that these are the control variables of the experimental facilities, which is advantageous and even necessary for the posterior experimental validation of the optimization results. Additionally, these are the key parameters for the reactor operation. By optimizing the temperature, the inherent trade-off associated to exothermic reversible reactions is taken into account. In general, high process temperatures lead to high reaction rates, which for a defined constant residence time or reactor size allows for high conversions to be reached. However, the equilibrium conversion is lower at higher temperatures. The total gas flow on the other side affects directly the DME productivity due to its reciprocal influence on the residence time, the gas load and selectivity. Finally, the composition of the catalyst bed was also considered as an optimization variable because of its direct influence on the modified reaction rates rj,mod (eqn (23)). In a mixed catalytic bed like the one used in this work, the optimization of the catalyst distribution serves the enhancement of the synergy effects that characterize the direct DME synthesis. Here, two cases are evaluated: an axially constant catalytic bed composition where the ratio between the three materials (two catalysts and inert material) in the catalytic bed is constant along the reactor coordinate, and an axially variable catalytic bed composition where the ratio between the three materials is adjusted continuously along the reactor coordinate, resulting in a distribution profile. Since the kinetic measurements were all carried out at a constant pressure of 50 bar, this parameter was not optimized in order to avoid extrapolation of the kinetic model. Furthermore, an optimization of the pressure gives trivial results since for the considered reaction system a higher pressure is always thermodynamically favorable.
in) and the composition of the catalytic bed (ξk(j)) are obvious optimization variables considering that these are the control variables of the experimental facilities, which is advantageous and even necessary for the posterior experimental validation of the optimization results. Additionally, these are the key parameters for the reactor operation. By optimizing the temperature, the inherent trade-off associated to exothermic reversible reactions is taken into account. In general, high process temperatures lead to high reaction rates, which for a defined constant residence time or reactor size allows for high conversions to be reached. However, the equilibrium conversion is lower at higher temperatures. The total gas flow on the other side affects directly the DME productivity due to its reciprocal influence on the residence time, the gas load and selectivity. Finally, the composition of the catalyst bed was also considered as an optimization variable because of its direct influence on the modified reaction rates rj,mod (eqn (23)). In a mixed catalytic bed like the one used in this work, the optimization of the catalyst distribution serves the enhancement of the synergy effects that characterize the direct DME synthesis. Here, two cases are evaluated: an axially constant catalytic bed composition where the ratio between the three materials (two catalysts and inert material) in the catalytic bed is constant along the reactor coordinate, and an axially variable catalytic bed composition where the ratio between the three materials is adjusted continuously along the reactor coordinate, resulting in a distribution profile. Since the kinetic measurements were all carried out at a constant pressure of 50 bar, this parameter was not optimized in order to avoid extrapolation of the kinetic model. Furthermore, an optimization of the pressure gives trivial results since for the considered reaction system a higher pressure is always thermodynamically favorable.
4.1.3 Constraints and further considerations.
Both the temperature and total gas flow are limited by the design specifications of the described experimental setup. In order to avoid the extrapolation of the formal kinetic model, the variable bounds are here determined by the validity range of the derived reaction kinetic model. The bounds as displayed in eqn (27) and (28) apply:| | 0.2 SLPM ≤ ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in ≤ 0.7 SLPM. in ≤ 0.7 SLPM. | (28) |
The validity range of the kinetic model is also limited regarding the concentration of the different species in the system. However, for the model-based optimization an extrapolation in this regard cannot be avoided. Otherwise, only a trivial optimization result could be obtained within the experimentally explored operation range.
An extrapolation of the kinetic model regarding the catalyst distribution is also inevitable when pursuing the optimization of this variable since the kinetic measurements were all carried out with the same catalytic bed. However, to avoid obtaining too small amounts of catalyst and in order to stay above the measuring accuracy of the employed electronic balance used in the laboratory in context of the experimental validation, the amount of each catalyst was set to:
Additionally, the share of inert material (SiC) was kept constant over the length of the catalytic bed (eqn (30)). The optimization of an axially variable share of inert material along the reactor coordinate could be used to avoid hot spot formation, however, this approach is out of the scope of this work.
| | ξSiC(z) = const. ∀ z ∈ [0,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Lbed]. Lbed]. | (30) |
The species balance and velocity field (section 2.2.1) along with the thermodynamic considerations (section 2.2.2) and the derived reaction kinetic model (section 3.2) constitute a predictive model to describe the system behavior. Based on this and the optimization scenario described in this section, a continuous nonlinear optimization problem can be formulated as:
4.2 Case studies
Two examples (A and B) with two optimization cases each were considered. The examples differ in the chosen reference case regarding the feed composition. In Example A, the experiment of the kinetic measurements at which the highest COx conversion was achieved was chosen as a reference case in order to evaluate if an optimized catalyst distribution can lead to an even higher conversion within the same range of conditions. In Example B, the reference case is based on a recent campaign performed in the DME pilot plant at KIT (bioliq®34), where the feed gas was under stoichiometrical regarding the hydrogen amount. The optimization cases, on the other hand, differ regarding the optimization variables. In case 1, the optimization variables were the temperature, the total gas flow and an axially constant catalytic bed composition (opt. variables: T, ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in, ξk(j)), while in case 2 the catalyst distribution was axially variable (opt. variables: T,
in, ξk(j)), while in case 2 the catalyst distribution was axially variable (opt. variables: T, ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in, ξk(j) (z)). Table 5 provides an overview of the considered case studies.
in, ξk(j) (z)). Table 5 provides an overview of the considered case studies.
Table 5 Overview of optimization examples, cases and variables
| Ex. |
y
CO,in
|
y
CO2,in
|
y
H2,in
|
Case |
Opt. variables |
Case-ID |
| A |
16.07 |
2.82 |
48.42 |
1 |
T, ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in, ξk(j) in, ξk(j) |
A1 |
|
|
|
|
|
2 |
T, ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in, ξk(j) (z) in, ξk(j) (z) |
A2 |
| B |
12.00 |
3.00 |
13.00 |
1 |
T, ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in, ξk(j) in, ξk(j) |
B1 |
|
|
|
|
|
2 |
T, ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in, ξk(j) (z) in, ξk(j) (z) |
B2 |
4.3 Numerical solution approach
The techniques for discretization and solution of the optimization problem are adopted from the works on multi-level reactor design (MLRD)2,35 and will be introduced in the following.
For discretization, the method of orthogonal collocation on finite elements is employed, whereby the optimization problem (including reactor model, control variables and constraints) is transformed into a system of algebraic equations. By that, the numerical solution of the system of differential equations in a function space spanned by polynomials at a set of collocation points distributed over the discretized domain36 is facilitated. The discretized problem was then implemented within the modeling environment AMPL® (a mathematical programming language) which uses a high-level algebraic representation for the description and solution of large-scale optimization problems. The modeling language for mathematical programming uses a syntax similar to mathematical or algebraic notation and allows the use of solvers based on different mathematical approaches suitable for different kinds of optimization problems.37 The solver used in this work is called IPOPT (Interior Point OPTimizer). It is an open source nonlinear solver that converges to local optima using an interior-point method, whose foundations are the newton approach based on the local quadratic Taylor-series model.38
4.4 Optimization results
4.4.1 Example A.
Example A allows to determine if an even better performance can be obtained in the same range of conditions in which the kinetic measurements were taken by simultaneously optimizing the catalyst distribution and the operating conditions (temperature and total gas flow). Since the reference case is taken from the measurements carried out for the development of the reaction kinetic model, this example does not represent a model extrapolation and it therefore delivers a suitable basis for comparison in section 5 (experimental validation of optimization results). The optimization results of the reference and the optimized cases for this example are displayed in Table 6.
Table 6 Example A – optimization results
| Param. |
Unit |
Ref. Case |
Opt. Case A1 |
Opt. Case A2 |
|
T
|
°C |
260.0 |
256.0 |
256.1 |
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in
in
|
SLPM |
0.2 |
0.2 |
0.2 |
|
ξ
CZA
|
— |
0.16 |
0.38 |
Fig. 5
|
|
ξ
ALOX
|
— |
0.42 |
0.20 |
Fig. 5
|
|
ξ
SiC
|
— |
0.42 |
0.42 |
0.42 |
|
X
COx
|
% |
48.5 |
59.5 |
59.5 |
|
Y
DME
|
% |
45.4 |
55.2 |
55.2 |
|
S
DME
|
% |
69.3 |
70.9 |
70.9 |
4.4.1.1 Optimization case A1.
As reported in Table 6, the optimal temperature is below the maximally allowed value, suggesting that this operating point is not dominated by kinetics, and thermodynamic equilibrium is approached. The lower constraint for the total gas flow is active, i.e., this variable is set to its lower bound. Regarding the catalytic bed, the optimal configuration consists of a higher share of methanol catalyst (and a lower share of dehydration catalyst) than in the reference case.
For a comprehensive understanding of the optimization results, the modified reaction rates (rj,mod) in eqn (23) along the axial coordinate are presented in Fig. 4 for both the reference and the optimization case A1. Reviewing the first 4 centimeters of the catalytic bed, the reaction rates for the configuration in A1 (dashed lines) are higher than the respective rates in the reference case (solid lines). This effect was expected for the methanol synthesis and the water-gas shift reaction, which are both promoted by the catalyst with an increased share in the optimal configuration. Additionally, a higher reaction rate of the methanol dehydration to dimethyl ether is also noticeable, although the share of the dehydration catalyst was significantly reduced in comparison to the reference case. This can be explained by the synergetic effects characteristic of the direct DME synthesis: a faster production of methanol and consumption of water enhance the potential term in the methanol dehydration reaction, creating a strong driving force for the overall reaction, and allowing for a higher conversion of the synthesis gas. These effects not only compensate for the decrease of the reaction rate of the methanol dehydration caused by the lower amount of dehydration catalyst, but they also lead to an overall rate increase of the direct synthesis of dimethyl ether from synthesis gas. The computed enhancement of the performance indicators conversion of COx, yield and selectivity of dimethyl ether are shown in Table 6.
 |
| | Fig. 4 Example A – modified reaction rates. Solid lines: reference case, dashed lines: optimization case A1. Conditions reported in Tables 5 and 6. Lbed = 5.5 cm. | |
At the reactor outlet, the modified reaction rates of the optimized case (dashed lines) are all at a level close to zero, indicating (as well as the optimal temperature not taking the maximal possible value) a proximity to the thermodynamic equilibrium. This is confirmed and illustrated in the state space diagram in Fig. 6, where the COx conversion is plotted against the temperature for the optimal total gas flow and the catalytic bed composition of the reference and the two optimization cases. The conversion achieved through optimization exhibits indeed a proximity to the thermodynamic equilibrium and represents the maximal possible conversion of COx that can be achieved regarding the systems inherent limitations (particle size, pressure, etc.) and the considered optimization variables (T, ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in, ξk(j)).
in, ξk(j)).
4.4.1.2 Optimization case A2.
The optimal conditions for case A2 are also summarized in Table 6, while the obtained optimal catalytic bed composition profiles are illustrated in Fig. 5, in comparison to the composition of the reference and the optimization case A1.
 |
| | Fig. 5 Example A – optimal catalytic bed composition. Left: methanol catalyst, right: dehydration catalyst. ξSiC(z) = 0.42 ∀ z ∈ [0,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Lbed]. Lbed]. | |
The first half of the catalytic bed exhibits a continuously increasing amount of methanol catalyst followed by the second half of the bed, which shows a nearly constant fraction of this catalyst. For all cases, the axial share of the dehydration catalyst is complementary this profile. The composition of the second half of the bed represents the optimal catalyst ratio that potentiates the synergy effects of the direct synthesis of dimethyl ether and it is similar to the constant composition obtained in case A1. The optimized temperature and total gas flow as well as the performance indicators (refer to Table 6 and Fig. 6) are also very similar to the ones obtained in case A1, showing that virtually no further performance improvement is achieved by an axially variable catalytic bed composition.
 |
| | Fig. 6 Example A – state space diagram for different catalyst distributions. ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in = 0.2 SLPM, Lbed = 5.5 cm. Feed composition in Table 5. in = 0.2 SLPM, Lbed = 5.5 cm. Feed composition in Table 5. | |
4.4.2 Example B.
The composition of the syngas used in the DME pilot plant at KIT was used in this example as a basis for optimization. Since the syngas produced from biomass exhibits lower hydrogen content than stoichiometrically necessary for the synthesis, this example aims to evaluate to what extent the optimization of the chosen optimization variables can enhance the process performance for a hydrogen-lean feed. This is of particular interest for the synthesis of biofuels, considering that industrially, the customization of the synthesis gas is carried out by adding hydrogen produced by expensive technologies such as steam reforming or electrolysis which compromises the profitability of the process.34,39
For the simulation and optimization of the DME synthesis from syngas obtained in the pilot plant, the feed species that can not be taken into account by the reaction kinetic model (e.g. methane, propane, etc.) are replaced in the simulations by inert gas. The adapted feed gas composition used for the optimization (reported in Table 5) was used to simulate the DME synthesis in the laboratory reactor setup. The predicted performance indicators are outlined in Table 7 along with the optimization results of the two optimization cases described below.
Table 7 Example B – optimization results
| Param. |
Unit |
Ref. Case |
Opt. Case B1 |
Opt. Case B2 |
|
T
|
°C |
250.0 |
260.0 |
260.0 |
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in
in
|
SLPM |
0.2 |
0.2 |
0.2 |
|
ξ
CZA
|
— |
0.12 |
0.29 |
Fig. 7
|
|
ξ
ALOX
|
— |
0.31 |
0.14 |
Fig. 7
|
|
ξ
SiC
|
— |
0.57 |
0.570 |
0.57 |
|
X
COx
|
% |
9.58 |
17.09 |
17.12 |
|
Y
DME
|
% |
8.89 |
16.26 |
16.24 |
|
S
DME
|
% |
67.80 |
66.31 |
66.17 |
4.4.2.1 Optimization case B1.
In this case study, the optimal temperature was determined to be at its upper limit and the optimal total gas flow corresponds to the maximal residence time possible. Similarly to example A, the catalyst distribution was optimized by an increased amount of methanol catalyst and a decreased amount of dehydration catalyst, promoting the same synergetic effects explained before and leading to an enhancement of the COx conversion and the yield of dimethyl ether (Table 7).
 |
| | Fig. 7 Example B – optimal catalytic bed composition. Left: Methanol catalyst, right: Dehydration catalyst. ξSiC(z) = 0.57 ∀ z ∈ [0,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Lbed]. Lbed]. | |
The fact that the optimal temperature is at the upper limit of the available range indicates that the conversion is not yet significantly influenced by the thermodynamic equilibrium. The optimal operating point for this case is primarily dominated by the reaction kinetics. This suggests that at the given pressure, feed composition and length of catalytic bed, even at the maximal possible residence time, highest temperature and optimized catalyst distribution the low amount of hydrogen in the feed inhibits the reaction rate to such an extent that the equilibrium conversion can not be achieved. The state space diagram is depicted in Fig. 8. The conversion achieved at different temperatures was calculated for the reference and optimized catalyst distributions obtained in this example. In this plot, it can be observed how the optimized catalyst distribution leads to a positive shift of the conversion for each temperature. However, Fig. 8 also outlines the further optimization potential of this example, which, however, can only be exploited by including additional optimization variables such as e.g., the hydrogen content in the feed.
 |
| | Fig. 8 Example B – state space diagram for different catalyst distributions. ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in = 0.2 SLPM, Lbed = 8 cm. Feed composition in Table 5. in = 0.2 SLPM, Lbed = 8 cm. Feed composition in Table 5. | |
5 Experimental validation of optimization results
The experimental validation of optimization results was carried out to close the loop between kinetic investigations and reactor optimization via rigorous mathematical modeling. For this aim, the conditions of the reference and the first optimization case (with an optimized axially constant catalytic bed composition) of both examples are realized in the experimental facilities in which the kinetic measurements were performed. The optimization results were hereby assessed both qualitatively and quantitatively.
The measured values of the relevant process parameters (composition of the inlet gas stream, temperature and composition of the catalytic bed as arranged for the experiments) are outlined in Table 8. Simulations were carried out for the reported process parameters in order to account for the deviations between set point and actual measured value in order to provide a suitable basis for comparison.
Table 8 Experimental validation - measured operating conditions, setup and performance
| Param. |
Unit |
Example A |
Example B |
| Ref. Case |
Case A1 |
Ref. Case |
Case B1 |
|
y
H2,in
|
% |
46.5 |
46.5 |
14.0 |
14.0 |
|
y
CO,in
|
% |
15.6 |
15.6 |
12.3 |
12.3 |
|
y
CO2,in
|
% |
3.4 |
3.4 |
3.2 |
3.2 |
|
T
|
°C |
261.5 |
260.6 |
250.1 |
259.3 |
|
p
|
bar |
49.9 |
50.1 |
50.1 |
50.0 |
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in
in
|
SLPM |
0.2 |
0.2 |
0.2 |
0.2 |
|
L
bed
|
cm |
5.2 |
5.4 |
7.4 |
7.8 |
|
ξ
CZA
|
% |
16 |
38 |
11 |
29 |
|
ξ
ALOX
|
% |
41 |
20 |
29 |
14 |
|
ξ
SiC
|
% |
43 |
42 |
60 |
57 |
5.1 Validation results example A
To assess the quality of the model predictions in this example, the simulated and experimentally achieved COx conversion, yield and selectivity of DME are presented graphically in Fig. 9 for both, the reference and the optimized operating points.
 |
| | Fig. 9 Example A – experimental validation of optimization results. Conditions and feed composition according to Table 8 – example A. | |
Qualitative validation.
The experimental validation of the optimized results demonstrate a successful performance enhancement of the direct synthesis of dimethyl ether. The COx conversion and the yield of dimethyl ether were indeed increased by operation at the determined optimal conditions and catalytic bed configuration. However, the performance enhancement was compromised by an unexpected slight decrease of selectivity.
Quantitative validation.
Regarding the quality of the model predictions, the following observations can be made:
• Ref. case – no extrapolation.
Since the reference operating point was also considered in the modeling of the reaction kinetics, simulation at these conditions do not represent an extrapolation of the model, thus leading to an almost perfect agreement between the predicted and the measured performance with an absolute error of 0.1% regarding the single-pass conversion of COx. The higher deviations between measured and predicted yield and selectivity of dimethyl ether are due to the model's inferior ability to predict DME compared to CO and CO2, as described in section 3.3.
• Opt. case A1 – extrapolation to consider an optimized catalyst bed composition.
The catalytic bed configuration obtained in optimization case A1 differs from the composition used for the reaction kinetic measurements and modeling. Thus, simulating the performance of this operating point means forcing the model to predict the behaviour of a setup that lies outside its validity range. The experimental validation resulted in a discrepancy between predictions and measurements (Fig. 9) where the simulated performance indicators COx conversion, selectivity and yield of DME were all higher than the measured ones. Additional practical reasons for the observed deviations are nonidealities regarding the mixing and dilution of the catalyst bed.
5.2 Validation results example B
The analysis of the extrapolation capability of the model, is again conducted for the two measured operating points. The measured and predicted performance indicators are displayed for both, the reference and the optimized operating points in Fig. 10.
 |
| | Fig. 10 Example B – experimental validation of optimization results. Conditions and feed composition according to Table 8 – example B. | |
Qualitative validation.
The synthesis gas used in this example exhibited a hydrogen content lower than the one stoichiometrically required for the conversion of COx, which directly affects the process performance. Additionally, all kinetic measurements were carried out with a higher hydrogen to COx ratio than the one presented in this example. Thus, conducting simulations with such a hydrogen-lean feed represents an extrapolation of the reaction kinetic model, even though the hydrogen amount is within its validity range. These aspects, along with nonidealities regarding the packing of the mixed catalyst bed, affect the performance enhancement and the agreement between model predictions and measurements. Nevertheless, experimentally, the single-pass conversion of COx and the yield of dimethyl ether could be increased using the optimal conditions, while a marginal decrease of the DME selectivity was observed.
Quantitative validation.
• Ref. case – extrapolation to consider a hydrogen-lean feed.
The extrapolation of the reaction kinetic model for the consideration of a hydrogen-lean synthesis gas leads to an underprediction of the COx conversion and of the yield of DME, while an overprediction of the selectivity is observed.
• Opt. case B1 – extrapolation to consider a hydrogen-lean feed and an optimized catalyst bed composition.
Predicting the performance of this operating point implies the extrapolation of the kinetic model regarding two factors, thus, a higher deviation than the one observed for the reference case was expected. However, as displayed in Fig. 10, the agreement between prediction and measurement for this operating point is slightly better than in the reference case.
From the deviations exhibited for the reference case, it can be concluded that an extrapolation regarding a low hydrogen content in the feed leads to an underprediction of the performance indicators. On the other hand, the validation of A1 shows that the extrapolation regarding the optimized catalytic bed composition leads to an overprediction. The combination of these two opposite effects leads in this case to a partial mutual compensation, resulting in a better agreement between prediction and measurement than for the reference case.
6 Summary and conclusions
The model-based optimization of a laboratory reactor for the direct synthesis of dimethyl ether from CO2 rich synthesis gas was carried out and experimentally validated. Referring to the sections above, the novelty and main results of this contribution are summarized as follows.
Reaction kinetic investigations
To improve versatility, a kinetic model from the literature was modified in order to account for the nonideal behavior of the gaseous mixture and improved to increase numerical stability. The resulting model was used to fit a vast array of data points (i.e. 240 experiments, available in the ESI†) in a range of conditions broader than usually covered in literature. A further modification of the model allows its application for the model-based optimization of the catalyst bed composition along the reactor coordinate.
Model-based reactor optimization
Although the optimization of direct DME synthesis has been subject of research for years, this contribution is, to the best of our knowledge, the first to apply a dynamic scheme for rigorous optimization of the operating conditions and the composition of the mixed catalytic bed along the reactor coordinate. Model-based optimization, as applied here, indicates for which parameters the validity range of the model should be extended, namely for catalyst bed compositions with larger CZA-to-ALOX ratios.
Experimental validation of optimization results
Critically reviewing the extrapolation capability of the models is of general importance, but not a common practice in the open literature. In this contribution, the optimization results were validated experimentally and the predictive power of the derived model is evaluated both qualitatively and quantitatively for operating conditions beyond its validity range. Since the same setup was used for all tasks, it is to be highlighted that the prediction error is mainly caused by underlying model assumptions. The revealed prediction error caused by the extrapolation highlights the necessity for high-fidelity kinetic models that allow for extrapolation in a sensible range. The predictions, however, were qualitatively accurate and the enhancement of the single-pass conversion of COx and of the yield of dimethyl ether at the optimal conditions was demonstrated experimentally in both examples, proving the adequacy of the model and the qualitative correctness of the numerically obtained optimization results.
Final remarks
Our findings encourage the use of mechanistically motivated assumptions, broad validity ranges with respect to the applied degrees of freedom during optimization and a critical statistical evaluation of identified parameter sets.
In addition to established reactor modeling methods, this work contributes with an extensive database which is being made available to other researchers in the ESI.†
The systematic approach followed in this work can as well be applied to other dual catalyst systems that have not yet been thoroughly investigated in order to clarify promising operating windows at an early stage of process design. Furthermore, this approach is also generally applicable for the identification of optimal catalyst dilution strategies (relevant for exothermic reactions) or the optimal mixing of different catalyst generations (extended catalyst lifetime). This list of possible fields of applications illustrates that the approach presented in this work is powerful and versatile.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors from FAU Erlangen-Nürnberg gratefully acknowledge funding of the German Research Foundation (DFG) for the Cluster of Excellence “Engineering of Advanced Materials” within the framework of the “Excellence Initiative”. The authors from KIT acknowledge the financial support from the Helmholtz Research Program “Storage and Cross-linked Infrastructures” and Dr. Stephan Pitter for his support during the project.
References
- H. Freund, A. Peschel and K. Sundmacher, Chem. Ing. Tech., 2011, 83, 420–426 CrossRef CAS.
- A. Peschel, H. Freund and K. Sundmacher, Ind. Eng. Chem. Res., 2010, 49, 10535–10548 CrossRef CAS.
- H. Freund, J. Maußner, M. Kaiser and M. Xie, Curr. Opin. Chem. Eng., 2019, 26, 46–57 CrossRef.
- B. Niethammer, S. Wodarz, M. Betz, P. Haltenort, D. Oestreich, K. Hackbarth, U. Arnold, T. Otto and J. Sauer, Chem. Ing. Tech., 2018, 90, 99–112 CrossRef CAS.
- N. Dahmen, U. Arnold, N. Djordjevic, T. Henrich, T. Kolb, H. Leibold and J. Sauer, J. Supercrit. Fluids, 2015, 96, 124–132 CrossRef CAS.
- P. Haltenort, K. Hackbarth, D. Oestreich, L. Lautenschütz, U. Arnold and J. Sauer, Catal. Commun., 2018, 109, 80–84 CrossRef CAS.
-
DME Handbook, ed. Japan DME Forum, Tokyo, 2007, vol. 1 Search PubMed.
-
M. Müller and U. Hübsch, Ullmann's encyclopedia of industrial chemistry, 2000 Search PubMed.
- K. Waugh, Catal. Today, 1992, 15, 51–75 CrossRef CAS.
-
E. Fiedler, G. Grossmann, D. B. Kersebohm, G. Weiss and C. Witte, Ullmann's encyclopedia of industrial chemistry, 2000 Search PubMed.
- M. Kasaie and M. Sohrabi, J. Mex. Chem. Soc., 2009, 53, 233–238 CAS.
- B. Sabour, M. H. Peyrovi, T. Hamoule and M. Rashidzadeh, J. Ind. Eng. Chem., 2014, 20, 222–227 CrossRef CAS.
-
H. G. Roh and C. S. Lee, in Fuel Properties and Emission Characteristics of Dimethyl Ether in a Diesel Engine, ed. A. K. Agarwal, A. Dhar, A. Gautam and A. Pandey, Springer Singapore, Singapore, 2017, pp. 113–128 Search PubMed.
- E. Catizzone, G. Bonura, M. Migliori, F. Frusteri and G. Giordano, Molecules, 2017, 23, 31 CrossRef PubMed.
- M. Gentzen, W. Habicht, D. Doronkin, J.-D. Grunwaldt, J. Sauer and S. Behrens, Catal. Sci. Technol., 2016, 6, 1054–1063 RSC.
- J.-D. Grunwaldt, A. Molenbroek, N.-Y. Topsøe, H. Topsøe and B. Clausen, J. Catal., 2000, 194, 452–460 CrossRef CAS.
- S. Ren, S. Li, N. Klinghoffer, M. Yu and X. Liang, Carbon Resour. Convers., 2019, 2, 85–94 CrossRef CAS.
- R. Peláez, P. Marín, F. V. Díez and S. Ordóñez, Fuel Process. Technol., 2018, 174, 149–157 CrossRef.
- R. Peláez, P. Marín and S. Ordóñez, Fuel Process. Technol., 2017, 168, 40–49 CrossRef.
- W.-Z. Lu, L.-H. Teng and W.-D. Xiao, Chem. Eng. Sci., 2004, 59, 5455–5464 CrossRef CAS.
-
M. Baerns, A. Behr, A. Brehm, J. Gmehling, H. Hofmann and U. Onken, Technische Chemie, John Wiley & Sons, 2013 Search PubMed.
-
E. Fitzer and W. Fritz, Technische Chemie: Einführung in die Chemische Reaktionstechnik, Springer, Berlin, Heidelberg, 2013 Search PubMed.
- D.-Y. Peng and D. B. Robinson, Ind. Eng. Chem. Fundam., 1976, 15, 59–64 CrossRef CAS.
- L. Meng and Y.-Y. Duan, Fluid Phase Equilib., 2005, 238, 229–238 CrossRef CAS.
- L. Meng, Y.-Y. Duan and X.-D. Wang, Fluid Phase Equilib., 2007, 260, 354–358 CrossRef CAS.
-
C. L. Yaws, The Yaws Handbook of Physical Properties for Hydrocarbons and Chemicals: Physical Properties for More Than 54,000 Organic and Inorganic Chemical Compounds, Coverage for C1 to C100 Organics and Ac to Zr Inorganics, Gulf Professional Publishing, 2015 Search PubMed.
- T. Henrich, J. Abeln and M. Betz, Chem. Ing. Tech., 2018, 90, 307–315 CrossRef CAS.
- A. T. Aguayo, J. Ereña, D. Mier, J. M. Arandes, M. Olazar and J. Bilbao, Ind. Eng. Chem. Res., 2007, 46, 5522–5530 CrossRef CAS.
- J. Ereña, I. Sierra, A. T. Aguayo, A. Ateka, M. Olazar and J. Bilbao, Chem. Eng. J., 2011, 174, 660–667 CrossRef.
- M. Mollavali, F. Yaripour, H. Atashi and S. Sahebdelfar, Ind. Eng. Chem. Res., 2008, 47, 3265–3273 CrossRef CAS.
- D. Pritchard and D. Bacon, Chem. Eng. Sci., 1975, 30, 567–574 CrossRef CAS.
- D. M. Espie and S. Macchietto, Ind. Eng. Chem. Res., 1988, 27, 2175–2179 CrossRef CAS.
- T. Shishido, M. Yamamoto, D. Li, Y. Tian, H. Morioka, M. Honda, T. Sano and K. Takehira, Appl. Catal., A, 2006, 303, 62–71 CrossRef CAS.
-
N. Dahmen, E. Dinjus and E. Henrich, Renewable Energy. Sustainable Energy Concepts for the Future, 2008, p. 61 Search PubMed.
- M. Kaiser and H. Freund, Chem. Eng. Sci., 2019, 206, 401–423 CrossRef CAS.
- L. T. Biegler, Comput. Chem. Eng., 1984, 8, 243–247 CrossRef CAS.
-
R. Fourer, D. M. Gay and B. W. Kernighan, AMPL: A Modeling Language for Mathematical Programming, 2002, vol. 36 Search PubMed.
-
Y. Kawajir, C. Laird and A. Wachter, Introduction to IPOPT: A tutorial for downloading, installing, and using IPOPT, 2006 Search PubMed.
- S. Schemme, R. C. Samsun, R. Peters and D. Stolten, Fuel, 2017, 205, 198–221 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0re00041h |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab,
Markus
Kaiser
ab,
Markus
Kaiser
 *a,
Karla
Herrera Delgado
*b,
Stefan
Wild
b,
Jörg
Sauer
*a,
Karla
Herrera Delgado
*b,
Stefan
Wild
b,
Jörg
Sauer
 b and
Hannsjörg
Freund
b and
Hannsjörg
Freund
 a
a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of two commercially available catalysts was used. The catalysts were a CZA (CuO/ZnO/Al2O3) catalyst for the methanol synthesis and ALOX (γ-Al2O3) for the selective methanol dehydration to dimethyl ether. Both catalysts were milled and sieved to a particle size dp between 250 and 500 μm. To ensure an isothermal mode of operation, the catalyst mixture was diluted with silicon carbide (SiC) of the same grain size. Details of the experimental setup and further information about the used materials can be found in the ESI.†
1 mixture of two commercially available catalysts was used. The catalysts were a CZA (CuO/ZnO/Al2O3) catalyst for the methanol synthesis and ALOX (γ-Al2O3) for the selective methanol dehydration to dimethyl ether. Both catalysts were milled and sieved to a particle size dp between 250 and 500 μm. To ensure an isothermal mode of operation, the catalyst mixture was diluted with silicon carbide (SiC) of the same grain size. Details of the experimental setup and further information about the used materials can be found in the ESI.†






![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω), b = b(Tc),
ω), b = b(Tc),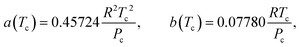








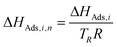


![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in
in

![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in) and the composition of the catalytic bed (ξk(j)) are obvious optimization variables considering that these are the control variables of the experimental facilities, which is advantageous and even necessary for the posterior experimental validation of the optimization results. Additionally, these are the key parameters for the reactor operation. By optimizing the temperature, the inherent trade-off associated to exothermic reversible reactions is taken into account. In general, high process temperatures lead to high reaction rates, which for a defined constant residence time or reactor size allows for high conversions to be reached. However, the equilibrium conversion is lower at higher temperatures. The total gas flow on the other side affects directly the DME productivity due to its reciprocal influence on the residence time, the gas load and selectivity. Finally, the composition of the catalyst bed was also considered as an optimization variable because of its direct influence on the modified reaction rates rj,mod (eqn (23)). In a mixed catalytic bed like the one used in this work, the optimization of the catalyst distribution serves the enhancement of the synergy effects that characterize the direct DME synthesis. Here, two cases are evaluated: an axially constant catalytic bed composition where the ratio between the three materials (two catalysts and inert material) in the catalytic bed is constant along the reactor coordinate, and an axially variable catalytic bed composition where the ratio between the three materials is adjusted continuously along the reactor coordinate, resulting in a distribution profile. Since the kinetic measurements were all carried out at a constant pressure of 50 bar, this parameter was not optimized in order to avoid extrapolation of the kinetic model. Furthermore, an optimization of the pressure gives trivial results since for the considered reaction system a higher pressure is always thermodynamically favorable.
in) and the composition of the catalytic bed (ξk(j)) are obvious optimization variables considering that these are the control variables of the experimental facilities, which is advantageous and even necessary for the posterior experimental validation of the optimization results. Additionally, these are the key parameters for the reactor operation. By optimizing the temperature, the inherent trade-off associated to exothermic reversible reactions is taken into account. In general, high process temperatures lead to high reaction rates, which for a defined constant residence time or reactor size allows for high conversions to be reached. However, the equilibrium conversion is lower at higher temperatures. The total gas flow on the other side affects directly the DME productivity due to its reciprocal influence on the residence time, the gas load and selectivity. Finally, the composition of the catalyst bed was also considered as an optimization variable because of its direct influence on the modified reaction rates rj,mod (eqn (23)). In a mixed catalytic bed like the one used in this work, the optimization of the catalyst distribution serves the enhancement of the synergy effects that characterize the direct DME synthesis. Here, two cases are evaluated: an axially constant catalytic bed composition where the ratio between the three materials (two catalysts and inert material) in the catalytic bed is constant along the reactor coordinate, and an axially variable catalytic bed composition where the ratio between the three materials is adjusted continuously along the reactor coordinate, resulting in a distribution profile. Since the kinetic measurements were all carried out at a constant pressure of 50 bar, this parameter was not optimized in order to avoid extrapolation of the kinetic model. Furthermore, an optimization of the pressure gives trivial results since for the considered reaction system a higher pressure is always thermodynamically favorable.
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in ≤ 0.7 SLPM.
in ≤ 0.7 SLPM.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Lbed].
Lbed].![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in, ξk(j)s.t.:Component mass balance eqn (1)Velocity field eqn (2)Boundary conditions eqn (4) and (5)Reaction kinetics eqn (16) to (24)Thermodynamics eqn (6) and (7)–(14) System constrainst eqn (27) to (30).
in, ξk(j)s.t.:Component mass balance eqn (1)Velocity field eqn (2)Boundary conditions eqn (4) and (5)Reaction kinetics eqn (16) to (24)Thermodynamics eqn (6) and (7)–(14) System constrainst eqn (27) to (30).![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in, ξk(j)), while in case 2 the catalyst distribution was axially variable (opt. variables: T,
in, ξk(j)), while in case 2 the catalyst distribution was axially variable (opt. variables: T, ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in, ξk(j) (z)). Table 5 provides an overview of the considered case studies.
in, ξk(j) (z)). Table 5 provides an overview of the considered case studies.
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in, ξk(j)
in, ξk(j)![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in, ξk(j) (z)
in, ξk(j) (z)![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in, ξk(j)
in, ξk(j)![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in, ξk(j) (z)
in, ξk(j) (z)
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in, ξk(j)).
in, ξk(j)).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Lbed].
Lbed].
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in = 0.2 SLPM, Lbed = 5.5 cm. Feed composition in Table 5.
in = 0.2 SLPM, Lbed = 5.5 cm. Feed composition in Table 5.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Lbed].
Lbed].
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in = 0.2 SLPM, Lbed = 8 cm. Feed composition in Table 5.
in = 0.2 SLPM, Lbed = 8 cm. Feed composition in Table 5.![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) in
in