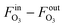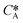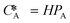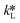Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Determination of fast gas–liquid reaction kinetics in flow†
Jisong
Zhang
 ab,
Andrew R.
Teixeira
ab,
Andrew R.
Teixeira
 bc,
Haomiao
Zhang
bc,
Haomiao
Zhang
 b and
Klavs F.
Jensen
b and
Klavs F.
Jensen
 *b
*b
aThe State Key Laboratory of Chemical Engineering, Department of Chemical Engineering, Tsinghua University, Beijing 100084, China
bDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: kfjensen@mit.edu
cDepartment of Chemical Engineering, Worcester Polytechnic Institute 100 Institute Road, Worcester, MA 01609, USA
First published on 8th November 2019
Abstract
We present a flow concept to measure fast gas–liquid reaction kinetics. A tube-in-tube reactor design with semipermeable Teflon AF-2400 tubes is adopted to achieve fast gas–liquid mass transfer without direct contact of gas and liquid. By performing a steady-state flux balance of both gas and liquid flowing into the reactor and developing a mathematical model based on the film theory, the reaction kinetic parameters can be determined with excellent precision with the use of only a single gas flow meter. Reactions of CO2 with alkanolamines and ozonolysis of organics serve as case studies to assess the ability of the technique to resolve reaction kinetics in situ. The proposed strategy presents a new opportunity for the study of fundamental aspects of gas–liquid reactions in a simple, safe, automated and high-throughput manner.
Introduction
Gas–liquid reactions are ubiquitous chemical transformations that include well known examples such as absorption of CO2 into aqueous alkanolamines, absorption of H2S into ferric sulphate solutions, and ozonolysis, hydrogenation, or chlorination of organic substances.1,2 A detailed knowledge of the reaction kinetics and thermodynamic characteristics is essential for developing a new and efficient chemical process. For example, to generate an efficient CO2 capture process, it is highly desirable to study the reaction kinetics of CO2 with amines as a function of temperature, amine type and concentrations.3,4 Ozone is widely used as an oxidant in drinking water and wastewater treatments, and chemical synthesis using ozone has attracted considerable attention.5,6 However, it is challenging to perform kinetic studies with ozone due to safety concerns with the strong oxidizer and the facile and rapid decomposition of O3.7 Recent efforts in micro-scale multiphase flow have revealed strategies to understand and minimize interfacial mass transfer limitations in reacting systems.8,9 This, in turn, has led to microreactor designs that operate in the absence of transport limitations and approach the desired kinetic rate limit, thus motivating the need for a precise understanding of intrinsic multiphase kinetics.The determination of gas–liquid reaction kinetics is often performed with a stirred cell reactor by recording the pressure decay over time with no analysis of the liquid phase.10,11 This method is simple to operate and widely applied. However, it can involve a labour-intensive reloading operation and large variations due to its sensitivity to stirring conditions and poorly defined gas–liquid interface.12 Continuous systems such as laminar jets,13 wetted wall columns14 and microfluidic contactors4,15 partially solve this problem, but they are more complex to operate and rippling on the liquid surface could lead to erroneous results. For more details of such techniques, readers are referred to relevant reviews.12,16
Recently, several gas–liquid reactions such as oxidation,17,18 hydrogenation,19 carboxylation,20 methoxycarbonylation21 and ozonolysis22 have been applied in a class of membrane reactors named “tube-in-tube” reactors, which are based on a gas-permeable Teflon AF-2400 membrane. In this strategy, gas diffuses through the gas-permeable membrane where it is then equilibrated with a contacting liquid stream. The reactor achieves rapid gas–liquid mass transfer rates (10–30 s)23 owing to the small diffusion length scales (0.3 mm) while avoiding the direct and chaotic contact of the gas and liquid. The liquid flow in the inner tubing is laminar so the mass transfer process can be precisely described.24 The physical separation of gas and liquid flow by the Teflon AF membrane produces a well-defined gas–liquid interface at the inner tubing wall, which effectively circumvents erroneous surface rippling and hydrodynamically varying mass transfer rates (kLa). Additionally, this highly stable reactor works well with a wide range of reactive gases and liquids because of the chemically inert fluoropolymer characteristics. Woodley et al.25 developed an automated system to collect kinetic data of enzyme-mediated oxidation based on this tube-in-tube reactor demonstrating that the precise control of O2 concentration in the solution allows accurate studies of oxidation kinetics. Thus, the tube-in-tube reactor is a highly promising tool to study the fundamental aspects of gas–liquid reactions.
In our previous work, we have developed a fully automated strategy based on the tube-in-tube reactor geometry for fast in situ measurements of gas solubility21 and diffusivity24 in liquids. Here we extend the application of this strategy to the determination of reaction kinetics. A mathematical model of gas–liquid mass transfer process in the reactor coupled with chemical reactions is first developed and validated. This model is then used to determine the kinetic reaction rate from gas uptake data at various liquid flow rates. The technique is illustrated with two reaction systems, CO2 absorption and ozonolysis, demonstrating both good accuracy and efficiency.
Experimental
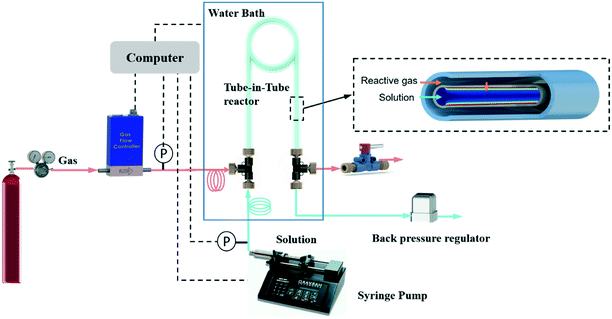
Carbon dioxide (99.99%, pure) and oxygen (99.994%, pure) were all supplied by Airgas (Salem, NH). Methyl diethanolamine (99%) and propionaldehyde (98%) were obtained from Sigma-Aldrich. Deionized water was obtained from VWR, meeting ASTM type II specifications.Fig. 1 shows a schematic illustration of the automated system, which builds on our previous flow platforms for measuring gas solubility23 and diffusivity.24 In brevity, the system is composed of the tube-in-tube reactor, a pump, a gas flow meter and a back pressure regulator. Before experiments were conducted, all liquid feeds were degassed according to literature procedures26 to avoid erroneous effects of the dissolved air on the kinetic measurements. The tube-in-tube reactor was composed of inner Teflon AF-2400 tubing (O.D. 0.8 mm, I.D. 0.6 mm) and outer PTFE tubing (O.D. 3.18 mm, I.D. 1.59 mm) with a length of 0.7 m. During experiments, liquid solutions were pumped from a syringe pump (Harvard Apparatus PHD 2000), through a PTFE feed tube (O.D. 1.59 mm, I.D. 1.2 mm, length 2 m), into the inner reactor tube. The pressure of liquid flow in this tube-in-tube reactor was controlled by a back pressure regulator placed at the outlet of the liquid flow. The reactive gas was delivered through an impermeable PTFE tube (O.D. 1.59 mm, I.D. 1.2 mm, length 2 m) into the shell side of the tube-in-tube reactor from the regulated cylinder. A shut-off valve (IDEX, P-732) placed at the outlet of the gas flow prevented gas flow out of the reactor during the experiments. Hence, the inlet pressure regulator solely controlled the gas flow pressure.
The gas flow was measured by a thermal mass flow controller (Brooks Instruments, 5850i, 5 sccm O2) located downstream of the pressure regulator but just upstream of the tube-in-tube reactor inlet. The mass flow controller was set to a fully open state, effectively acting solely as a gas flow meter in the experiments. When using gases other than O2, the flow meter was used with a gas-specific correction factor provided by Brooks Instruments or calibrated following the method reported in our previous study.22 Two pressure transducers (Omega PX409) at the inlets of the reactor monitored the pressures of the gas and liquid flows separately. The feed tubing and the entire tube-in-tube reactor were all immersed in a stirred water bath with a PID controlled immersion heater to ensure an isothermal operation. LabVIEW software controlled the liquid flow and the temperature of the water bath while acquiring gas flow rates and pressures.
Measurement principles
Most gas–liquid reactions are second-order reactions with first order dependencies on gas A and reactant B, respectively. To simplify the kinetic model, reaction kinetics are usually measured under pseudo-first-order regimes whereby an excess liquid reagent is present and reaction rates are measured at low conversion. To describe the gas–liquid mass transfer, the well-established two-film theory27 is usually adopted, describing the mass transfer as molecular diffusion through a stagnant gas/liquid layer of thickness δ and the bulk gas/liquid is well mixed as depicted in Fig. 2.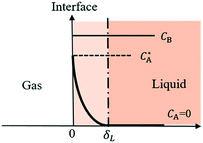 | ||
| Fig. 2 Concentration profiles in the liquid film for gas absorption with chemical reactions in pseudo-first-order regime. | ||
The Hatta number, Ha, describes the ratio of reaction to diffusion rates in the thin film:
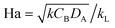 | (1) |
When the reaction is in the pseudo-first-order regime, the concentration of reactant B in the liquid film is considered constant and equal to the bulk liquid concentration (Fig. 2). In that case, eqn (1) transforms to:
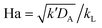 | (2) |
| 2 < Ha ≪ Ei | (3) |
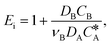 | (4) |
An illustration relating the mathematical model to determine reaction kinetics is included in Fig. 3. In brevity, the gas mass transfer flux, NA, can be directly measured by transforming the gas flow rate.
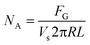 | (5) |
According to the Danckwerts mass transfer model,28 the mass transfer flux NA in the fast pseudo first order regime is proportional to the liquid phase equilibrium concentration:
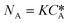 | (6) |
According to Henry's law 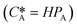 , the following equation is obtained:
, the following equation is obtained:
| NA = KHPA | (7) |
By equating eqn (5) and (7), the overall mass transfer coefficient, K, can be directly determined from the measured gas flow, FG, as the only factor requiring experimental determination. This overall mass transfer coefficient is a weighted average of the respective liquid-side and membrane-side mass transfer coefficients. As the mass transfer across the membrane km is known, the mass transfer coefficient in liquid with chemical reaction, 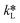 , can now be deconvoluted from the overall mass transfer coefficient according to the resistance-in-series model29,30 as follows:
, can now be deconvoluted from the overall mass transfer coefficient according to the resistance-in-series model29,30 as follows:
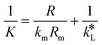 | (8) |
The Ha value is then determined based on the following relationship.31
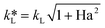 | (9) |
Finally, the value of k′ and corresponding reaction rate constant, k, can be calculated. It should be noted that the thermodynamic and transport characteristics (gas solubility and diffusivity in liquids) are also required for the determination of reaction kinetics. Both can be obtained in this platform according to the aforedescribed methods.23,24 In addition, the reactor should operate in a laminar flow regime. The maximum Reynolds number in the current experiments is only 96.
Experimentally, a constant rate of liquid flow was applied and allowed to achieve well-developed steady flow in the inner tube; the corresponding constant gas flux was measured at the inlet flow meter capturing the flux through the membrane into the liquid at steady state. For kinetics measurements in the gas–liquid reaction system, a relatively high liquid flow rate is required to achieve the low conversions needed to accurately measure the reaction rate constant. This original strategy overcomes the slow sampling and poor interfacial control present in classical pressure decay and microfluidic approaches while retaining the advantages of easy operation, fast transport time and improved safety.
Results and discussion
To demonstrate the accuracy and efficiency of this automated platform for reaction kinetics determination, we considered two case studies: absorption of CO2 into aqueous methyl diethanolamine (MDEA) (Scheme 1) and ozonolysis of propionaldehyde (Scheme 2).CO2 absorption kinetics
MDEA is a tertiary amine, which can provide a higher capacity, smaller reaction enthalpy with CO2 and lower vapour pressure compared with traditionally used primary and secondary amines.32 Therefore, the reaction kinetics of CO2 with aqueous MDEA are well described in the literature using different techniques.33–35 To ensure that the reaction is in the pseudo-first-order regime (2 < Ha ≪ Ei), the following conditions were chosen: temperature: 20, 40 and 60 °C; MDEA concentration: 10 and 20 wt%.Fig. 4 shows the measured transient gas flow rate as the liquid flow rate is stepped from 0.2 to 2.7 ml min−1 during the reaction. At low liquid flow rates, FG increases with increasing FL before becoming nearly constant as FL is increased above 1 mL min−1. However, according to eqn (5) and (7), FG should be independent of FL across the entire flow window for a reaction-controlled process. This behaviour occurs at low flow rates because the large absorption rate of CO2 leads to a decrease of MDEA concentration in the liquid phase, which invalidates the pseudo-first-order approximation that MDEA is in excess and not changing substantially over the course of the experiment. When the liquid flow rate is sufficiently large, the decrease of MDEA concentration is negligible and the measured gas flow rate is constant. Therefore, a relatively high liquid flow rate was used to ensure that the conversion of MDEA remained less than 2%. The reaction enthalpy of absorption of CO2 in MDEA solution is only in the range of 20–30 kJ mol−1.36 As a result, the temperature rise due to the heat of reaction is negligible. In addition, there is no increase in the liquid phase molar volume from the dissolution of gas into the liquid because of the small amount of gas absorption. The typical measurement process progressed by recording the gas flow rate at a large liquid flow rate and then the kinetic rate constant was calculated. It is recommended that at least two liquid flow rates are tested to verify that the measured gas flow rate is constant in the experiments. To improve the accuracy, the flow rate at several pressures can be recorded and linear regression of gas flow rate versus pressure should be performed to extract the overall mass transfer coefficient in accordance with eqn (5) and (7).
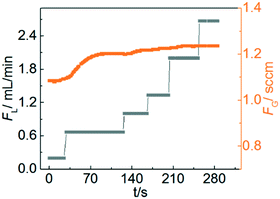 | ||
| Fig. 4 Measured gas flow rate as a function of set liquid flow rate for the CO2–MDEA system. Gas pressure: 1.1 bar; temperature: 40 °C; MDEA concentration: 20 wt%. | ||
The final measurement results including reaction rate constants at three temperatures and two MDEA concentrations are summarized in Table 1, while the detailed calculations are outlined in Table S1.† Fitting k values versus temperature with an Arrhenius relationship, the activation energy is determined to be 52.9 ± 4.4 kJ mol−1, in good agreement with the literature value (stirred cell reactor) of 49.2 kJ mol−1.34 The uncertainty in the activation energy results from the standard error of linear fitting.
| T (°C) | C MDEA (mol L−1) | F G/PA (sccm bar−1) | k′ (s−1) | k average (L mol−1 s−1) |
|---|---|---|---|---|
| a Liquid flow rate: 2.7 mL min−1. | ||||
| 20 | 0.85 | 1.13 | 1.6 | 2.0 ± 0.1 |
| 1.71 | 1.19 | 3.4 | ||
| 40 | 0.84 | 1.12 | 5.9 | 6.7 ± 0.3 |
| 1.69 | 1.17 | 11.2 | ||
| 60 | 0.84 | 1.08 | 15.7 | 26.8 ± 0.5 |
| 1.68 | 1.15 | 45.1 | ||
Ozonolysis kinetics
There are two obstacles to determining ozonolysis kinetics: 1) ozone gas from an ozone generator is not pure O3, but rather a mixture of O3 and O2. The current experimental setup is not suitable for the mixed gas because the outlet of gas flow is blocked and the unreacted gas would accumulate as the reaction progresses. This would decrease the partial pressure of reacted gas in the gas phase of the reactor and thus would decrease the corresponding O3 gas flux. 2) There is no reported literature on the Teflon AF 2400 O3 permeability, which is needed for the above analysis.To measure gas–liquid reaction kinetics involving a mixed gas stream, the system required some modifications (Fig. S1†) to prevent the accumulation of diluent gases present in the reacting gas mixture from the ozone generator. A back pressure regulator was placed on the gas flow outlet instead of the shut-off valve. The gas flowing into the reactor was controlled by a thermal gas flow controller at a constant rate and a gas flow meter was placed downstream of the reactor before the back pressure regulator to measure the gas flow rate exiting the reactor. The corresponding gas flux into the liquid was calculated with the difference of these two gas flows. To account for the decreased driving force for O3 into the liquid, the length of the tube-in-tube reactor was increased to 2.1 m to increase the value of the measured gas flow rate.
For O3 permeability, we proposed a simple method to determine it by leveraging the automated system as shown in Fig. 1. A pressure larger than atmospheric pressure at the gas phase of the reactor was set by the upstream pressure regulator. The liquid inlet was sealed to prevent liquid-flow into the system and gas-flow out from it. The back pressure on the inner tube was set to atmospheric pressure with the outlet directly vented. In this way, the gas flow through the Teflon AF membrane can be directly determined with the gas flux through the flow meter. Thus, the gas permeability can be calculated in a similar fashion to established approaches in the literature.37
To determine the permeability of pure O3, the O2 flow rate through the membrane was first measured and then that of the O3 mixture. The permeability of pure O3 could then be determined with the difference of the two permeances. Table 2 summarizes the results for the O3 permeability determination. The measured permeability of O2 was 7.2 × 10−6 mL (STP) cm cm−2 s−1 bar−1, which is in good agreement with the established literature value of 7.4 × 10−6 mL (STP) cm cm−2 s−1 bar−1.37 Furthermore, the permeability of O3 was substantially lower, consistent with the size-dependent permeability through Teflon AF. Note that the reading of steady gas flow of the O3 mixture must be taken immediately after flow stabilization to ensure that the concentration of O3 between the inner and outer tubes does not drift due to the changes in the permeabilities of O2 and O3 through the membrane.
| Temperature | F O2 (sccm) | F O3 (sccm) | κ O2 (mL (STP) cm cm−2 s−1 bar−1) | κ O3 (mL (STP) cm cm−2 s−1 bar−1) |
|---|---|---|---|---|
| a Gas pressure difference across the membrane: 1.72 bar, inner tube length: 2.1 m. b O3 gas concentration: 14%, O2 gas concentration: 86%. | ||||
| 20 | 3.01 | 3.29 | 7.23 × 10−6 | 1.209 × 10−5 |
| 30 | 3.00 | 3.28 | 7.21 × 10−6 | 1.207 × 10−5 |
| 40 | 2.99 | 3.27 | 7.19 × 10−6 | 1.206 × 10−5 |
The ozonolysis of propionaldehyde (Scheme 2) was chosen to further verify the ability to extract kinetic rate parameters from a multiphase reaction system with a diluent gas. To suppress the decomposition of O3 in aqueous solution, pH control (<7) and scavenger addition are typically required during the kinetics determination of ozonolysis.7 In our system, the overall residence time of liquid in the reactor is less than 40 s, during which negligible O3 decomposition occurs,6 so the solution requires no pH control (pH = 7) or scavenger addition. To ensure that the reaction was in the pseudo-first-order regime, the following conditions were chosen: temperature: 20, 30 and 40 °C; propionaldehyde concentration: 1 mol L−1.
The measurement results are given in Table 3 with a detailed calculation process outlined in Table S2.† The decrease of gas flow rate (FG = FinG − FoutG) was used to derive the O3 absorption rate 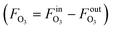 by assuming that oxygen is not absorbed and the O2 flow rate is constant. With the method described in the Measurement principle section, the reaction rate constants were determined. The obtained reaction rate constant (0.83 ± 0.10 L mol−1 s−1 at 20 °C) is lower than that in the literature (2.5 ± 0.4 L mol−1 s−1 at 20 °C),38 which could result from different reaction conditions (pH and scavengers) or errors from the O3 solubility and diffusivity data. The activation energy is determined to be 48.9 ± 2.1 kJ mol−1, at the upper end of the range of 35–50 kJ mol−1 for ozonolysis of most organic compounds.38
by assuming that oxygen is not absorbed and the O2 flow rate is constant. With the method described in the Measurement principle section, the reaction rate constants were determined. The obtained reaction rate constant (0.83 ± 0.10 L mol−1 s−1 at 20 °C) is lower than that in the literature (2.5 ± 0.4 L mol−1 s−1 at 20 °C),38 which could result from different reaction conditions (pH and scavengers) or errors from the O3 solubility and diffusivity data. The activation energy is determined to be 48.9 ± 2.1 kJ mol−1, at the upper end of the range of 35–50 kJ mol−1 for ozonolysis of most organic compounds.38
| T (°C) | F in G − FoutG (sccm) | (sccm) | k (L mol−1 s−1) |
|---|---|---|---|
| a Propionaldehyde concentration: 1 mol L−1, liquid flow rate: 2.7 mL min−1, gas pressure: 2.23 bar, O3 concentration: 14%. | |||
| 20 | 0.38 | 0.330 | 0.83 ± 0.10 |
| 30 | 0.43 | 0.342 | 1.55 ± 0.21 |
| 40 | 0.47 | 0.357 | 3.01 ± 0.41 |
The strategy is demonstrated to be a simple and fast (<2 min) method to measure fast gas–liquid reaction kinetics in multiphase systems. In addition, it can provide direct tabulation determination of reaction kinetics under different conditions such as liquid phase composition, temperature and pressure. Similar to the gas solubility and gas diffusivity determination, the system should be operated below the glass transition temperature of Teflon AF-2400 (240 °C).37 To improve the accuracy of this method, the gas flow rate obtained from the gas flow meter should be large, which is usually larger than 0.1 sccm. As a result, a high pressure (>5 bar) is adopted during the gas solubility and diffusivity determination. During the reaction kinetics determination, low pressures (<5 bar) prove to be accurate due to the enhancement of chemical reactions in terms of mass transfer rate. Notably, this automated system can work at even higher pressures (<7 MPa) without causing mechanical strain on the Teflon tubing and the fittings. Also, as with gas diffusivity determination,24 the mass transfer coefficient across the membrane km should be close to or much larger than the mass transfer coefficient in liquid flow kL to ensure the accuracy of measurement. This should be confirmed before performing the reaction kinetics measurement for other reactants or temperatures.
Conclusions
In this paper, we have developed a flow strategy to measure fast gas–liquid reaction kinetics based on the tube-in-tube reactor geometry using gas-permeable Teflon AF-2400. The reaction rate constant can be determined with only a measured gas flow rate within 2 min. Using the reaction of CO2 with an alkanolamine and the challenging ozonolysis of organics as the examples, we demonstrate the viability of this technique for rapid determination of reaction rate constants for multiphase, multicomponent gas/liquid systems. The determined kinetic parameters using this technique agree well with the literature values from classical batch analyses. The proposed strategy opens a new opportunity for the studies of kinetics of fast gas–liquid reactions in a simple, automated and high-throughput manner.Nomenclature
Dimensionless numbers
| Ha | Hatta number, 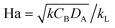 |
| E i | Enhancement factor for an irreversible instantaneous reaction, 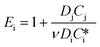 |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from the Novartis-MIT Centre for Continuous Manufacturing is acknowledged.Notes and references
- G. T. Rochelle, Science, 2009, 325, 1652–1654 CrossRef CAS PubMed
.
- M. Brzozowski, M. O'Brien, S. V. Ley and A. Polyzos, Acc. Chem. Res., 2015, 48, 349–362 CrossRef CAS PubMed
.
- M. Abolhasani, A. Gunther and E. Kumacheva, Angew. Chem., Int. Ed., 2014, 53, 7992–8002 CrossRef CAS PubMed
.
- W. Li, K. Liu, R. Simms, J. Greener, D. Jagadeesan, S. Pinto, A. Gunther and E. Kumacheva, J. Am. Chem. Soc., 2012, 134, 3127–3132 CrossRef CAS PubMed
.
- M. D. Lundin, A. M. Danby, G. R. Akien, P. Venkitasubramanian, K. J. Martin, D. H. Busch and B. Subramaniam, AIChE J., 2017, 63, 2819–2826 CrossRef CAS
.
- J. L. Sotelo, F. J. Beltran, F. J. Benitez and J. Beltran-Heredia, Ind. Eng. Chem. Res., 1987, 26, 39–43 CrossRef CAS
.
- T. T. Dang, P.-F. Biard and A. Couvert, Ind. Eng. Chem. Res., 2016, 55, 8058–8069 CrossRef CAS
.
- A. Gavriilidis, A. Constantinou, K. Hellgardt, K. K. Hii, G. J. Hutchings, G. L. Brett, S. Kuhn and S. P. Marsden, React. Chem. Eng., 2016, 1, 595–612 RSC
.
- C. Yang, A. R. Teixeira, Y. Shi, S. C. Born, H. Lin, Y. Li Song, B. Martin, B. Schenkel, M. Peer Lachegurabi and K. F. Jensen, Green Chem., 2018, 20, 886–893 RSC
.
- B. Lu, X. Wang, Y. Xia, N. Liu, S. Li and W. Li, Energy Fuels, 2013, 27, 6002–6009 CrossRef CAS
.
- L. Kucka, J. Richter, E. Y. Kenig and A. Górak, Sep. Purif. Technol., 2003, 31, 163–175 CrossRef CAS
.
- P. D. Vaidya and E. Y. Kenig, Chem. Eng. Commun., 2007, 194, 1543–1565 CrossRef CAS
.
- N. Ramachandran, A. Aboudheir, R. Idem and P. Tontiwachwuthikul, Ind. Eng. Chem. Res., 2006, 45, 2608–2616 CrossRef CAS
.
- Q. Li, Y. Wang, S. An and L. Wang, Energy Fuels, 2016, 30, 7496–7502 CrossRef CAS
.
- C. Zheng, B. Zhao, K. Wang and G. Luo, AIChE J., 2015, 61, 4358–4366 CrossRef CAS
.
- H. Kierzkowska-Pawlak, Ecol. Chem. Eng. S, 2012, 19, 175–196 CAS
.
- G. Wu, A. Constantinou, E. Cao, S. Kuhn, M. Morad, M. Sankar, D. Bethell, G. J. Hutchings and A. Gavriilidis, Ind. Eng. Chem. Res., 2015, 54, 4183–4189 CrossRef CAS
.
- T. P. Petersen, A. Polyzos, M. O'Brien, T. Ulven, I. R. Baxendale and S. V. Ley, ChemSusChem, 2012, 5, 274–277 CrossRef CAS PubMed
.
- M. O'Brien, N. Taylor, A. Polyzos, I. R. Baxendale and S. V. Ley, Chem. Sci., 2011, 2, 1250 RSC
.
- A. Polyzos, M. O'Brien, T. P. Petersen, I. R. Baxendale and S. V. Ley, Angew. Chem., Int. Ed., 2011, 50, 1190–1193 CrossRef CAS PubMed
.
- P. Koos, U. Gross, A. Polyzos, M. O'Brien, I. Baxendale and S. V. Ley, Org. Biomol. Chem., 2011, 9, 6903–6908 RSC
.
- M. O'Brien, I. R. Baxendale and S. V. Ley, Org. Lett., 2010, 12, 1596–1598 CrossRef PubMed
.
- J. Zhang, A. R. Teixeira, H. Zhang and K. F. Jensen, Anal. Chem., 2017, 89, 8524–8530 CrossRef CAS PubMed
.
- J. Zhang, A. Teixeira, H. Zhang and K. F. Jensen, Anal. Chem., 2019, 91, 4004–4009 CrossRef CAS PubMed
.
- R. H. Ringborg, A. Toftgaard Pedersen and J. M. Woodley, ChemCatChem, 2017, 9, 3285–3288 CrossRef CAS PubMed
.
- R. Battino, M. Banzhof, M. Bogan and E. Wilhelm, Anal. Chem., 1971, 43, 806–807 CrossRef CAS
.
- W. K. Lewis and W. G. Whitman, Industrial & Engineering Chemistry, 1924, 16, 1215–1220 Search PubMed
.
- J.-C. Charpentier, Adv. Chem. Eng., 1981, 11, 1–133 CAS
.
- S. Atchariyawut, C. Feng, R. Wang, R. Jiraratananon and D. T. Liang, J. Membr. Sci., 2006, 285, 272–281 CrossRef CAS
.
- A. Mansourizadeh and A. F. Ismail, J. Hazard. Mater., 2009, 171, 38–53 CrossRef CAS PubMed
.
- M. M. Sharma and P. V. Danckwerts, Br. Chem. Eng., 1970, 522–528 CAS
.
- P. D. Vaidya and E. Y. Kenig, Chem. Eng. Technol., 2007, 30, 1467–1474 CrossRef CAS
.
- A. Jamal, A. Meisen and C. Jim Lim, Chem. Eng. Sci., 2006, 61, 6590–6603 CrossRef CAS
.
- H. Kierzkowska-Pawlak and A. Chacuk, Ecol. Chem. Eng. S, 2010, 17, 463–475 CAS
.
- N. J. M. C. Penders-van Elk, P. W. J. Derks, S. Fradette and G. F. Versteeg, Int. J. Greenhouse Gas Control, 2012, 9, 385–392 CrossRef CAS
.
- M. Gupta, E. F. da Silva, A. Hartono and H. F. Svendsen, J. Phys. Chem. B, 2013, 117, 9457–9468 CrossRef CAS PubMed
.
- I. Pinnau and L. G. Toy, J. Membr. Sci., 1996, 109, 125–133 CrossRef CAS
.
- J. Hoigné and H. Bader, Water Res., 1983, 17, 173–183 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9re00390h |
| This journal is © The Royal Society of Chemistry 2020 |