Open Access Article
Open Access ArticleCarboxylated cellulose nanofiber/montmorillonite nanocomposite for the removal of levofloxacin hydrochloride antibiotic from aqueous solutions†
Junfeng Li *a,
Junhong Tao
*a,
Junhong Tao a,
Chengxiao Maa,
Jie Yanga,
Tiantian Gub and
Jianchao Liu
a,
Chengxiao Maa,
Jie Yanga,
Tiantian Gub and
Jianchao Liu c
c
aCollege of Water Conservancy and Architecture Engineering, Shihezi University, Shihezi 832000, Xinjiang, PR China. E-mail: ljfshz@126.com
bKey Laboratory for Green Process of Chemical Engineering of Xinjiang Bingtuan, School of Chemistry and Chemical Engineering, Shihezi University, Xinjiang 832003, PR China
cKey Laboratory of Integrated Regulation and Resources Development, College of Environment, Hohai University, Nanjing 210098, China
First published on 17th November 2020
Abstract
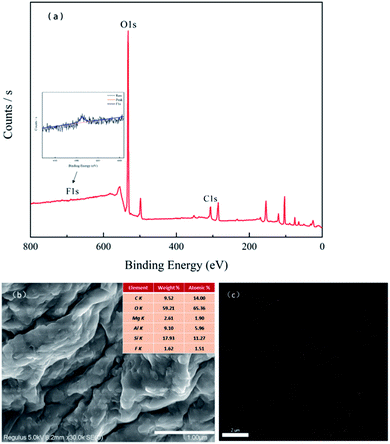
Herein, we report the facile two-step synthesis of an effective carboxylated cellulose nanofiber/montmorillonite nanocomposite (CMNFs–MMT) adsorbent for levofloxacin hydrochloride (Levo-HCl). CMNFs–MMT was characterized using scanning electron microscopy, energy dispersive X-ray spectrometry, Brunauer–Emmett–Teller measurements, X-ray photoelectron spectroscopy, X-ray diffraction, and Fourier transform infrared spectroscopy. Based on the central composite design, the effects of various factors on the removal of Levo-HCl by the CMNFs–MMT were explored, wherein the effect of pH was the most significant. To gain a clearer perspective on the adsorption process of Levo-HCl onto CMNFs–MMT, the adsorption kinetics and isotherms were also measured, revealing that the reaction is pseudo-second-order and the Sips models provide the best fit with experimental data. Comparing the adsorption in pure water with the removal in river water, the rate of river water removal (90.37%) was slightly lower than that of pure water (93.97%) when adsorption equilibrium was reached, confirming that CMNFs–MMT is not easily influenced by environmental conditions. Reusability experiments indicate that CMNFs–MMT can maintain a certain adsorption capacity for Levo-HCl after six uses. Overall, this work indicates that CMNFs–MMT is an effective adsorbent for eliminating Levo-HCl from aqueous media in future engineering applications.
Introduction
Antibiotics are widely used to treat human or animal diseases, and also as growth-promoting agents in aquaculture and animal husbandry. Since the discovery of penicillin, the number of different types of antibiotics has reached tens of thousands, and the use of antibiotics has become an indispensable part of the medical and breeding industries.1,2 In recent years, along with their contribution to longer, healthier lives and advances in medical technology and farming, the abuse of antibiotics has brought new challenges, while the pollution caused by the manufacturing process has become a widespread concern.3 Among them, fluoroquinolone antibiotics are produced synthetically, as opposed to by fermentation or semi-synthetic methods. Fluoroquinolone drugs were first developed in 1962 and are now mass-produced and used worldwide due to their broad-spectrum, long half-life, strong tissue penetration, low toxicity, and low price, in addition to their high efficiency and safety.4 With the gradual improvement in antibiotic research and development technology, the stability and antibacterial or bactericidal properties of fluoroquinolone products are continuously improving. A typical example is the third-generation fluoroquinolone antibiotic levofloxacin hydrochloride.5 Fluoroquinolone antibiotics are only partly absorbed by the humans and livestock during use, so large amounts of residual antibiotics are discharged into the water environment during the sewage treatment process. Therefore, fluoroquinolone antibiotics are often detected in water environments or even groundwater, with levofloxacin hydrochloride being particularly abundant.6 As a new type of organic pollutant, antibiotics are mostly soluble in water and are not volatile. However, antibiotics remaining in the environment are not indestructible. In nature, photolysis,7 adsorption,8 hydrolysis,9 and biodegradation methods10 can remove residual antibiotics. Due to the continuous discharge of human activities, antibiotics enter the environment and spread through water bodies and food chains. Eventually, they are naturally enriched in air, water, and soil, and become a persistent environmental pollutants. Therefore, there is an urgent need for reasonable and feasible antibiotic pollution control strategies. In recent years, many different methods for removing antibiotics, including adsorption, oxidation, photocatalysis, and biodegradation have been explored.11–13 Among them, the adsorption technique is widely used owing to easy operation, flexibility, low energy consumption, high removal rates, low secondary pollution, and low adsorbent regeneration cost. Thus, various types of adsorbents such as activated carbon,14 porous resin,15 zeolites,16 carbon nanotubes,17 biochar,18 bentonite,19 activated sludge,20 fly ash,21 and graphite oxide22 have been widely used. However, these materials have low adsorption efficiency and can be difficult to recover. These shortcomings have greatly hampered their practical applications; therefore, developing an inexpensive and efficient adsorbent is crucial.23,24 The comparison of the ability of different adsorbents to remove multiple pollutants is depicted in Table 1.| Pollutants | Absorbents | pH | T (°C) | qm (mg g−1) | References |
|---|---|---|---|---|---|
| Cr(VI) | Acid-treated algae activated carbon | 2.0 | 25 | 25.60 | 53 |
| Cr(VI) | Activated carbon prepared from Terminalia arjuna nuts | 1.0 | 25 | 28.40 | 54 |
| Cd(II) | Sardinian clinoptilolite | — | — | 0.34 | 55 |
| Pb(II) | Natural phillipsite | — | — | 0.23 | 56 |
| Ni(II) | Brazilian scolecite | — | — | 2.08 | 57 |
| Al | Cattle manure biochar | 4.3 | 25 | 0.30 | 58 |
| As(V) | Pine wood biochar | 7.0 | 22 | 0.93 | 59 |
| Hg(II) | Wheat straw biochar | 7.0 | 25 | 0.85 | 60 |
| As(III) | Anatase nanoadsorbent | — | — | 16.98 | 61 |
| F | Fe–Ti bimetallic magnetic oxide | — | — | 57.22 | 62 |
| Remazol red 3BS | Hexagonal mesoporous silica | — | — | 15.00 | 63 |
| Remazol red 3BS | Chitosan-MIPs | — | — | 35.00 | 64 |
| Malachite green | Clinoptilolite | — | — | 19.70 | 65 |
| Reactive red 239 | CTAB-clinoptilolite | — | — | 15.90 | 66 |
| Reactive yellow 176 | HTAB-clinoptilolite | — | — | 13.20 | 67 |
| Methylene blue dye | Eucalyptus biochar | — | 40 | 2.06 | 68 |
| Trichloroethylene | Peanut shells biochar | — | 25 | 12.12 | 69 |
| Paraquat | Swine manure biochar | — | 25 | 14.79 | 70 |
| K-NYT (humic acid) | Natural zeolites | — | 60 | 6.58 | 71 |
Cellulose is one of the most abundant compounds in nature.25 Crystalline and amorphous regions are randomly distributed in cellulose molecules. The crystalline regions are tightly arranged, and the crystal form is not easily damaged by chemicals and various enzymes, while the amorphous regions are loosely arranged and are more susceptible to attack and cracking by chemicals and various enzymes. Cellulose has the advantages of good biocompatibility, degradability, renewability, lack of pollution, and easy derivatization.26 The development and application of cellulose-based functional materials is of great significance for the development of new materials. Nanocellulose is a derivative of cellulose that has received extensive attention owing to its unique properties. First, nanocellulose has a nanometer size and excellent mechanical properties. Second, because of the large number of hydroxyl groups on the surface of nanocellulose, various chemical groups can be used to modify nanocellulose to achieve surface modification, such as oxidation, etherification, silanization, and polymer graft copolymerization. While successfully modifying nanocellulose, the hydroxyl groups also facilitate the dispersion of nanocellulose into different polymers.27–30 In addition, nanocellulose has the advantages of high width ratio, low energy consumption, low density, reproducibility, biodegradability, and biocompatibility.31,32
Montmorillonite is an aluminosilicate with a nano-level planar layered structure that determines the permanent negative charge in the montmorillonite sheet.33 The layered structure contains an aluminum octahedral layer sandwiched between two silica tetrahedral layers, and interlayer cations (Na+ and Ca2+) are intercalated to balance the charges.34 Layered MMT crystals have weak cation interaction between sandwich flakes, so they have high cation exchange capacity. This exchange property gives the montmorillonite sheets water swellability and strong adsorption capacity for cations. At the same time, since there is no hydrogen bond in the structure of montmorillonite, it also has the property of being intercalated or peeled off.35 At the same time, because the crystal layer in the montmorillonite structure is connected by two oxygen atomic layers, there is no hydrogen bond, so its lamellar bonding force is very weak, and it is easy to translate and peel off between the lamellar layers, which makes montmorillonite also has the property of being intercalated or stripped.36 In addition, montmorillonite is widely used in wastewater treatment because of its dispersion and suspension, thixotropy, cohesiveness, plasticity, thermal stability, and high adsorption capacity for organics.37–39 However, due to the swelling and dispersing and properties of aqueous montmorillonite suspensions, its use in applications requiring high adsorption has been limited. Montmorillonite need to be modified to improve its water dispersibility and adsorption capacity.35 In recent years, research on nanocomposites has begun to appear, and polymer/layered silicate nanocomposites have attracted wide attention owing to their superior comprehensive properties.40–47 This type of material has the characteristics of both organic and inorganic materials, and many desirable properties can be achieved through compounding, giving these materials good prospects for use in many applications.48 Therefore, a carboxylated cellulose nanofiber/montmorillonite nanocomposite combining the advantages of desirable adsorption capacity and excellent comprehensive performance can be used as a cost-effective and promising adsorbent to remove a wide range of organic pollutants, including Levo-HCl. However, to the best of our knowledge, little is known about the preparation of carboxylated cellulose nanofiber/montmorillonite nanocomposites and their effectiveness in the removal of Levo-HCl from water. In the existing research on cellulose/silicate materials, the preparation is mainly a composite process of alkali-modified cellulose/nanocellulose and silicate/modified silicate.49–52 However, this study proves that a composite material made of nanocellulose and alkalized montmorillonite has high adsorption capacity, and there are no published research on the adsorption performance of a material prepared by this method.
Therefore, the proposed study aims to use nanocellulose and alkalized montmorillonite as raw materials to prepare a new composite material (CMNFs–MMT) and to explore the adsorption performance of the material for antibiotics, using levofloxacin hydrochloride (Levo-HCl) as a typical pollutant. The microscopic structure and surface chemical composition of the nanocomposite (CMNFs–MMT) were investigated. The intermittent adsorption method was adopted, and the influencing factors such as solution pH, CMNFs–MMT dosage, initial Levo-HCl concentration, and contact time were investigated. The optimum adsorption conditions were found through the response surface method, isothermal adsorption model, and kinetic modelling. The adsorption mechanisms of Levo-HCl onto CMNFs–MMT and the adsorption effect and reproducibility in environmental water samples were discussed. We believe that the results obtained herein will provide a new strategy for removal of levofloxacin hydrochloride antibiotics from aqueous solutions.
Results and discussion
Characterization of the adsorbent
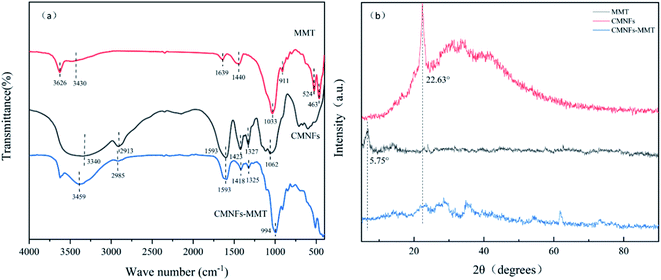
The FT-IR patterns of CMNFs, MMT, and CMNFs–MMT are depicted in Fig. 1a. The CMNF spectrum reveals absorption peaks at 3340, 2913, 1593, 1423, and 1062 cm−1, which correspond to the C–OH stretching vibration of the methylene group, C–H asymmetric stretching vibration, O–H bending vibration, C–OH stretching vibration, and C–O stretching vibration in the carboxyl group, respectively. In the FT-IR spectrum of MMT, there is an absorption peak at 3626 cm−1, corresponding to the –OH stretching vibration, and the absorption peaks at 1639 and 1440 cm−1 correspond to the H–O–H stretching and bending vibrations, respectively.72 This shows that the layered crystal structure of MMT adsorbs water and water of crystallization is present in the crystal lattice. The Si–O stretching peak is at 1033 cm−1, and the Al–O stretching peak is at 911 cm−1.73 In the FT-IR spectrum of CMNFs–MMT, the –OH bending peak of MMT at 3430 cm−1 in H2O and C–OH stretching peak of CMNFs at 3340 cm−1 both moved to a higher wavenumber (3459 cm−1), which proves that C–OH in CMNFs has a complex interaction with –OH in MMT.74 The CMNFs attenuated the C–H asymmetric stretching peak at 2913 cm−1 and moved toward a higher wavenumber (2985 cm−1), whereas the C–O stretching vibration at 1062 cm−1 moved toward a lower wavenumber (994 cm−1). The Si–O stretching peak at 1033 cm−1 of MMT weakened,75 and the Al–O stretching peak at 911 cm−1 disappeared. These results indicate that the nanocomposite comprises both an MMT framework structure and CMNFs macromolecules. This is consistent with the XPS analysis (Fig. S1†). CMNFs molecules are dispersed into the interlayer of MMT through intercalation. Active groups such as C–H, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, C–OH, –OH, O
O, C–OH, –OH, O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–O, C–O–C, and other active groups of CMNFs may interact with –CH2, –OH, Al–O, Si–O, and other groups in MMT and cations between layers. Chemical reactions such as coordination and complexation have occurred, forming carboxymethyl cellulose/montmorillonite intercalation stripping nanocomposite adsorption materials.
C–O, C–O–C, and other active groups of CMNFs may interact with –CH2, –OH, Al–O, Si–O, and other groups in MMT and cations between layers. Chemical reactions such as coordination and complexation have occurred, forming carboxymethyl cellulose/montmorillonite intercalation stripping nanocomposite adsorption materials.
 | ||
| Fig. 1 (a) FT-IR spectra of MMT, CMNFs and CMNFs–MMT; (b) X-ray diffraction patterns of MMT, CMNFs, CMNFs–MMT. | ||
The XRD patterns of MMT, CMNFs, and CMNFs–MMT are shown in Fig. 1b. It can be seen that MMT has obvious characteristic diffraction peaks at the diffraction angle 2θ = 5.75°.76 According to the Bragg equation: 2dsin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = kλ (k = 1, 2, 3…), the interlayer spacing of MMT is d = 1.54 nm, indicating that MMT has a relatively complete crystal structure and has the typical structural characteristics of nanomaterials. After MMT is combined with CMNFs, the characteristic diffraction peak of MMT at 2θ = 5.75° disappears, and the characteristic diffraction peak of CMNFs at 2θ = 22.63° also disappears, indicating that CMNFs molecules are inserted between MMT sheets by destroying the crystal structure of MMT to form a nanocomposite with an intercalation–exfoliation structure.77
θ = kλ (k = 1, 2, 3…), the interlayer spacing of MMT is d = 1.54 nm, indicating that MMT has a relatively complete crystal structure and has the typical structural characteristics of nanomaterials. After MMT is combined with CMNFs, the characteristic diffraction peak of MMT at 2θ = 5.75° disappears, and the characteristic diffraction peak of CMNFs at 2θ = 22.63° also disappears, indicating that CMNFs molecules are inserted between MMT sheets by destroying the crystal structure of MMT to form a nanocomposite with an intercalation–exfoliation structure.77
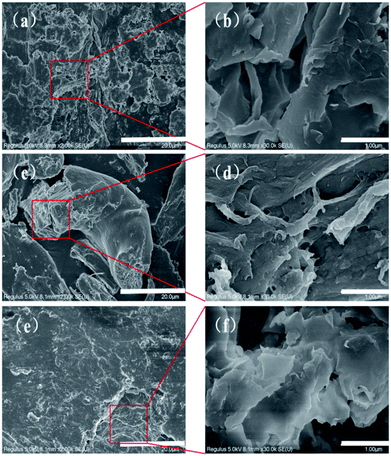
Fig. 2a and b present SEM images of MMT at 5000× and 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000× magnifications, respectively. Montmorillonite has a sheet-like structure with agglomeration and close arrangement, and its flat surface stretches with crystallographic features.78 There are many small gaps between closely connected sheet structures. These gaps are the channels through which CMNFs can enter the MMT sheets.79 Fig. 2c and d show the 5000× and 30
000× magnifications, respectively. Montmorillonite has a sheet-like structure with agglomeration and close arrangement, and its flat surface stretches with crystallographic features.78 There are many small gaps between closely connected sheet structures. These gaps are the channels through which CMNFs can enter the MMT sheets.79 Fig. 2c and d show the 5000× and 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000× SEM images for CMNFs, respectively. The size of CMNFs is small, and the original compact structure is decomposed to form more dispersed CMNFs, which increases the specific surface area. At the same time, the dispersed surface, with its greater specific surface area, exposes a greater number of the hydroxyl groups present on the surface of CMNFs, resulting in more opportunities for hydrogen bonds to form.80,81 The analogous SEM images for the CMNFs–MMT are presented in Fig. 2e and f. In this case, CMNFs are inserted into the gaps between the MMT sheets by changing the crystal structure of the MMT, so that the nanocomposite forms a curled or clumped, porous surface. This proves that after CMNFs enter, the crystalline region of MMT is destroyed, and CMNFs are effectively dispersed into the MMT sheets, forming intercalated-peeling nanocomposites.
000× SEM images for CMNFs, respectively. The size of CMNFs is small, and the original compact structure is decomposed to form more dispersed CMNFs, which increases the specific surface area. At the same time, the dispersed surface, with its greater specific surface area, exposes a greater number of the hydroxyl groups present on the surface of CMNFs, resulting in more opportunities for hydrogen bonds to form.80,81 The analogous SEM images for the CMNFs–MMT are presented in Fig. 2e and f. In this case, CMNFs are inserted into the gaps between the MMT sheets by changing the crystal structure of the MMT, so that the nanocomposite forms a curled or clumped, porous surface. This proves that after CMNFs enter, the crystalline region of MMT is destroyed, and CMNFs are effectively dispersed into the MMT sheets, forming intercalated-peeling nanocomposites.
 | ||
| Fig. 2 SEM of CMNFs, MMT and CMNFs–MMT: (a) and (b) SEM of MMT; (c) and (d) SEM of CMNFs; (e) and (f) SEM of CMNFs–MMT. | ||
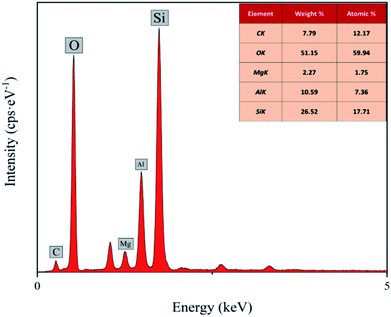
The EDS spectra of the CMNFs, MMT, and CMNFs–MMT presented in Fig. 3 show that the CMNFs contain mostly C and O atoms. There are some unlabelled elements in the energy spectrum, which may be the elements that were not cleaned during the preparation and washing process. Comparing the mass ratio and element ratio data, Mg, Al, and Si elements not detected in CMNFs appear in the composite material, which is the main component of MMT. Thus, the EDS analysis also provides clear support for successful composite formation.
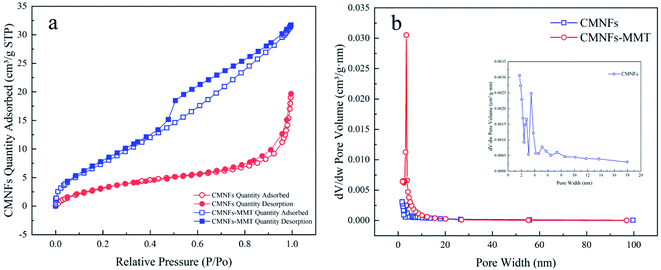
The N2 adsorption–desorption isotherms and Barrett–Joyner–Halenda (BJH) pore volume distributions for the CMNFs and CMNFs–MMT are shown in Fig. 4. The CMNFs produce type II isotherms, in contrast to CMNFs–MMT, which produce type IV isotherms. In the low-pressure range of P/P0 < 0.1, the N2 adsorption–desorption curves of the CMNFs and CMNFs–MMT increased sharply, and the low-pressure end deviated toward the Y axis, indicating that the two materials have a strong interaction with N and both materials have a certain amount of micropores. The N2 adsorption–desorption curve of the CMNFs has no obvious hysteresis loop in the 0.4–1.0 relative pressure range, indicating that this material has no mesoporous or hollow structures. In the relative pressure range of 0.4–1.0, there is a significant H4 type hysteresis loop in the N2 adsorption–desorption curve of the CMNFs–MMT, indicating the existence of a mesoporous structure containing narrow fissure pores, which is different from particle accumulation. This type of pore is caused by a layered structure.82 In the relative pressure range of 0.8–1.0, the curve of the CMNFs-MMT increases significantly, indicating the presence of large cavities in the composite. Fig. 4b presents the pore size distribution curves for CMNFs and CMNFs–MMT calculated using the BJH model. Detailed structural parameters for the two materials are shown in Table 2. The nanocomposites have a larger specific surface area and pore volume the CMNFs. These results show that the CMNFs–MMT composite material with ultra-high surface area and adsorption sites is effective for the adsorption of antibiotics.
| Sample | Unit | CMNFs | CMNFs–MMT |
|---|---|---|---|
| BET | m2 g−1 | 13.8885 | 30.7006 |
| BJH adsorption cumulative volume of pores | cm3 g−1 | 0.025913 | 0.044702 |
| Single point surface area | m2 g−1 | 12.0508 | 29.3846 |
| Adsorption average pore diameter | nm | 6.30784 | 7.52589 |
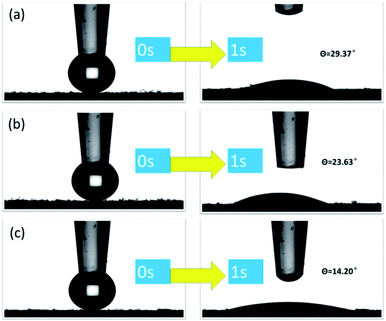
Generally, the hydrophilicity of the adsorbent is an important factor affecting its adsorption performance. The hydrophilic and hydrophobic properties of CMNFs, MMT, and CMNFs–MMT composites were investigated by contact angle analysis. The contact angles of montmorillonite, nanocellulose, and nanocellulose/montmorillonite composite material were measured as 29.37°, 23.63°, and 14.20°, respectively (Fig. 5a–c). All three materials have good hydrophobicity. With strong hydrophilic nanocellulose and montmorillonite as materials, a composite material with a small contact angle and good hydrophilicity is synthesized, which can be easily immersed in an aqueous solution to ensure that antibiotic molecules can diffuse into the adsorbent smoothly internally.
Response surface analysis
The statistical software Design-Expert 10.0 was used to fit the multiple regression equations to the experimental data from the response surface in Table S1† to obtain the dosage of adsorbent (A), initial pollutant concentration (B), pH (C), contact time (D), and the quadratic polynomial equation for the Levo-HCl removal rate (η), as shown in eqn (1).| η = 91.54 + 1.03A + 0.14B − 5.53C + 0.21D − 0.40AB − 2.30AC + 0.56AD − 0.80BC + 2.25BD − 0.55CD − 2.96A2 − 1.37B2 − 14.07C2 − 5.60D2 | (1) |
Eqn (1) shows that the influence of the four test factors on the response value is interactive and not a simple linear relationship.83 An analysis of variance and significance test was performed on the response surface model to test whether the model could be used to optimize the test conditions. The statistical significance of the model's equations was each regression coefficient were determined by the F and P values, respectively. Among the P values, if an item is p < 0.05, the effect of the item on the response value is significant; if a certain item is p < 0.01, the effect of the item on the response value is very significant. The smaller the lack of fit of the model, the better, and the larger the p-value corresponding to the lack of fit, the better. If p > 0.05, it means that the obtained multiple regression equation and the actual fitting have a small proportion of abnormal errors. The variance analysis of the model and the fitting results of the quadratic regression equation are shown in Table 3.
| Source | Sum of squares | df | Mean square | F Value | p-Value Prob > F |
|---|---|---|---|---|---|
| a Comment: R2 = 0.9775, Radj2 = 0.9564, Rpred2 = 0.8806, CV = 3.31%, adequate precision = 19.027. | |||||
| Model | 4236.25 | 14 | 302.59 | 46.47 | <0.0001 |
| A | 19.18 | 1 | 19.18 | 2.95 | 0.1067 |
| B | 0.34 | 1 | 0.34 | 0.052 | 0.8233 |
| C | 550.79 | 1 | 550.79 | 84.58 | <0.0001 |
| D | 0.76 | 1 | 0.76 | 0.12 | 0.7366 |
| AB | 2.54 | 1 | 2.54 | 0.39 | 0.5420 |
| AC | 84.78 | 1 | 84.78 | 13.02 | 0.0026 |
| AD | 4.94 | 1 | 4.94 | 0.76 | 0.3975 |
| BC | 10.35 | 1 | 10.35 | 1.59 | 0.2266 |
| BD | 80.87 | 1 | 80.87 | 12.42 | 0.0031 |
| CD | 4.85 | 1 | 4.85 | 0.74 | 0.4017 |
| A2 | 22.68 | 1 | 22.68 | 3.48 | 0.0817 |
| B2 | 4.86 | 1 | 4.86 | 0.75 | 0.4015 |
| C2 | 513.20 | 1 | 513.20 | 78.81 | <0.0001 |
| D2 | 81.37 | 1 | 81.37 | 12.49 | 0.0030 |
| Residual | 97.68 | 15 | 6.51 | ||
| Lock of fit | 86.92 | 10 | 8.69 | 4.04 | 0.0683 |
| Pure error | 10.76 | 5 | 2.15 | ||
| Cor total | 4333.93 | 29 | |||
The F value of the model was 46.47, with p < 0.01, indicating that the correlation between the four factors described by the regression equation and the removal rate is extremely significant. In addition, the P value of the misfit term of the model is 0.0683, indicating that the misfit of the prediction model is not significant, i.e., the model can describe the nonlinear relationship between each influencing factor and the response value.84 The fitting degree of the prediction model R2 = 0.9775 indicate that the model fits well with the test results, and the test accuracy is high.85 The correction decision coefficient Radj2 = 0.9564, indicating that approximately 95.64% of the response value changed, can be explained by the model.86 The difference between the corrected complex correlation coefficient (Radj2) and the predicted complex correlation coefficient (Rpred2) is 0.0758, which is less than 0.2, the coefficient of variation CV = 3.31%, and the precision is 19.027, which is much greater than 4.0, indicating that the model has high precision and reliability.87 Therefore, the model can be used to optimize and predict the experimental conditions for the removal of Levo-HCl by CMNFs–MMT in water.
From Table 3, the independent variables C, AC, BD, C2, D2, and C2 respond significantly (p < 0.05), that is, pH, interaction between adsorbent dosage and pH, interaction between initial concentration of pollutants and contact time, the square of the pH, the square of contact time all have significant effects, and other factors have little effect on the response value η. From the F value, it can be concluded that pH, adsorbent concentration, and contact time (in that order of significance) have an influence on the removal rate. In contrast, the initial concentration of pollutants had no significant effect on the removal rate. Considering the interactions between adsorbent dosage and contact time with pH, both factors were found to have a significant effect on the removal rate.
The Stat-Ease Design-Expert 10.0 software was used to generate 3D images, each with two independent variables as coordinates, to allow us to more intuitively explain the effects of adsorbent dosage, initial concentration of pollutants, pH, and contact time on the removal rate, and to characterize the response surface function. The results are shown in Fig. 6 and 7.
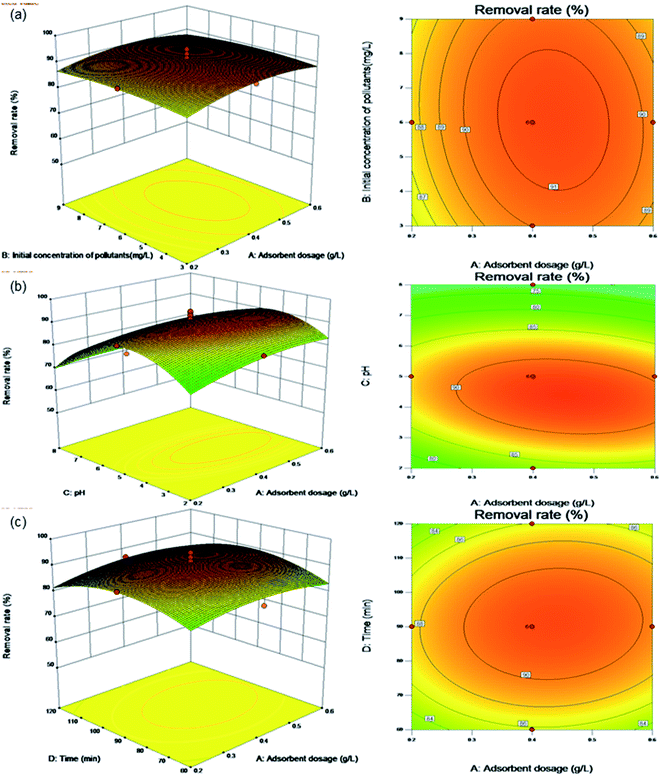 | ||
| Fig. 6 Surface and contour plots for Levo-HCl removal (%) interaction between independent parameters. (a) Levo-HCl concentration–adsorbent dosage. (b) pH–adsorbent dosage. (c) Time–adsorbent dosage. | ||
Fig. 6a shows the effects of the adsorbent dosage and initial pollutant concentration on the removal rate under the center point conditions of pH (pH 5.0) and contact time (90 min). The contour plot shows that the interaction between the initial concentration of pollutants and the dosage of adsorbent is not significant. The removal rate increases with increasing adsorbent dosage, but does not change significantly upon increasing the initial concentration of pollutants. This shows that within the parameters of the test conditions, the composite adsorption material is little affected by the change in the concentration of antibiotics in wastewater and is suitable for wide range of applications.
Fig. 6b shows the effects of the adsorbent dosage and pH on the removal rate under the center point conditions of an initial concentration of pollutants (6.0 mg L−1) and contact time (90 min). The contour plot shows a clear interaction between pH and the adsorbent dosage. When the pH is between 2.0 and 8.0 and adsorbent dosage is between 0.2 and 0.6 g L−1, the removal rate increases with the increasing adsorbent dosage, while increasing pH, causing an initial increase followed by a decrease in the removal rate. This is because as the number of adsorption sites increases, the amount of adsorbent added increases. Similarly, when the pH increases under acidic conditions, the OH− in the solution neutralizes the positive charge on the surface of the composite material, which increases the negative charge on the surface. The Levo-HCl antibiotic has a positive charge under acidic conditions, which is conducive its adsorption on the composite material. In an alkaline environment, Levo-HCl is negatively charged and a high concentration of OH− in the solution will also make the surface of the composite material negatively charged, causing electrostatic repulsion between the Levo-HCl and the composite and thereby inhibiting adsorption.
Fig. 6c shows the effects of the adsorbent dosage and contact time on the removal rate under the center point conditions of initial concentration of pollutants (6.0 mg L−1) and pH (pH 5.0). The contour plot shows a clear interaction between the dosage of adsorbent and the contact time. The removal rate increases with both increasing contact time and adsorbent dosage. The reason is that as the amount of adsorbent added increase, the greater number of adsorption sites causes an increase in the removal rate, as the contact time increases along with the amount of adsorbent, the adsorption sites have more time to contact and adsorb antibiotic molecules, resulting in a further increase in the removal rate.
Fig. 7a shows the effects of the pH and initial concentration of pollutants on the removal rate under the center point conditions of an adsorbent dosage (0.4 g L−1) and contact time (90 min). Contour plots show a clear interaction between the initial concentration of pollutants and pH. In an acidic environment, as the pH and initial concentration of pollutants increase, the removal rate increases. The reason is that with higher initial concentrations of pollutants, the higher number of antibiotic molecules increases the likelihood of contact between the adsorbent and an antibiotic molecule. At the same time, as the pH in the acidic environment increases, the OH− in the solution neutralizes the positive charge on the surface of the composite material to increase the negative charge on the surface, and since the Levo-HCl antibiotic is positively charged under acidic conditions, the removal rate increases due to electrostatic attraction.
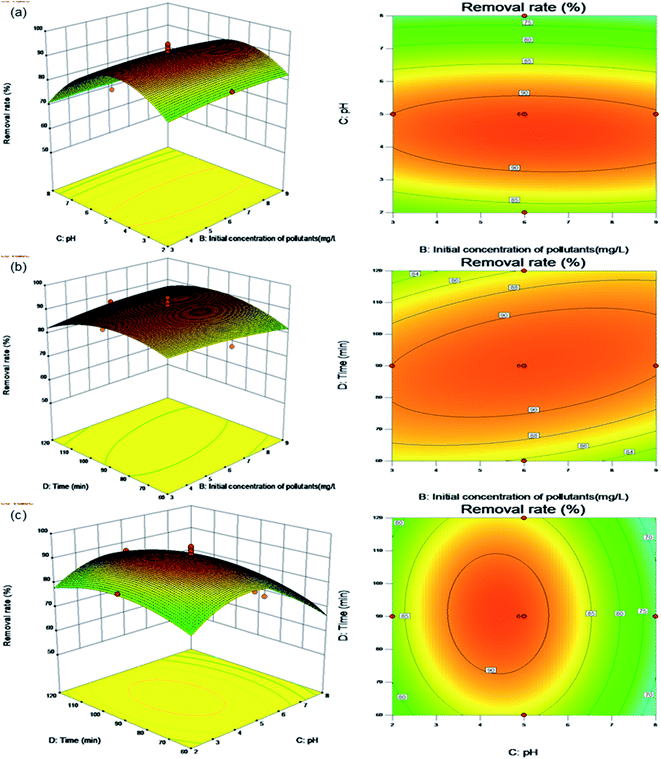 | ||
| Fig. 7 Surface and contour plots for Levo-HCl removal (%) interaction between independent parameters. (a) pH–Levo-HCl concentration. (b) Time–Levo-HCl concentration. (c) Time–pH. | ||
Fig. 7b shows the effects of the contact time and initial concentration of pollutants on the removal rate under the center point conditions of adsorbent dosage (0.4 g L−1) and pH (5.0). The contour plot shows a clear interaction between the initial concentration of pollutants and the contact time. When the initial pollutant concentration is between 3.0 and 6.5 mg L−1 and the contact time is between 60 and 90 min, the removal rate increases with both increasing initial pollutant concentration and contact time. As discussed in relation to Fig. 6c above, the reason is that the increased contact time and initial pollutant concentration increases the likelihood that a pollutant will come into contact with an adsorption site, resulting in a higher removal rate. As the influencing factors increase, the removal rate starts to flatten until adsorption equilibrium is established and the maximum removal rate is obtained.
Fig. 7c shows the effects of contact time and pH on the removal rate under the center point conditions of an adsorbent dosage (0.4 g L−1) and initial pollutant concentration (6.0 mg L−1). The contour plot shows that the interaction between contact time and pH is not significant. When the contact time is between 60 and 120 min, the removal rate initially increases first before decreasing with increasing of pH.
The Design-Expert 10.0 program was used to predict the optimal experimental conditions for the adsorption of Levo-HCl by the CMNFs–MMT. The optimal conditions were as follows: adsorbent dosage, 0.45 g L−1; initial pollutant concentration, 6.40 mg L−1; solution pH, 4.33; and contact time, 92 min. Under these conditions, the Levo-HCl removal rate reached 92.30%. To verify the accuracy of the response surface model, three parallel experiments were performed under the predicted optimal conditions. The average value of the measured removal rate was 92.44%, indicating that the model has excellent predictive ability.
The response surface analysis of the second-order polynomial regression equation for the removal rate of Levo-HCl indicates that the optimal adsorption conditions can be obtained. At the same time, single-factor experiments were performed to verify the results (Fig. S2†). The optimal conditions obtained by the two methods are the same, which proves that the model can accurately predict the actual values and can be used to assess the materials utility in practical applications.
Adsorption kinetics
Adsorption kinetics were used to study the adsorption and desorption rates of adsorbents and the influences of the aforementioned factors. The results of such studies are important indicators of the adsorption performance of the material. Kinetic data can clarify the adsorption mechanism and confirm which of the three processes of chemical reaction, diffusion, and mass transfer is the rate-determining step. The characteristics of the adsorption kinetics are shown in Fig. 8. The adsorption capacity gradually increased over time, exhibiting rapid adsorption in the initial stage (0–60 min), reaching 89% of the equilibrium adsorption amount after only 60 min. The adsorption amount changes linearly with time, during which the active sites on the CMNFs–MMT surface become occupied and the adsorption rate gradually decreases, eventually reaching saturation. The reason for this may be that CMNFs–MMT can easily be dispersed in the solution, so that levofloxacin hydrochloride in the solution can quickly bind to the adsorption sites of CMNFs–MMT. As the reaction progresses, the adsorption rate is slowed as the levofloxacin hydrochloride pore migration, diffusion, and mass transfer resistance on CMNFs–MMT increase. At the same time, the influence of pH, temperature, and other factors causes the adsorption rate to decrease gradually, and the reaction reaches equilibrium.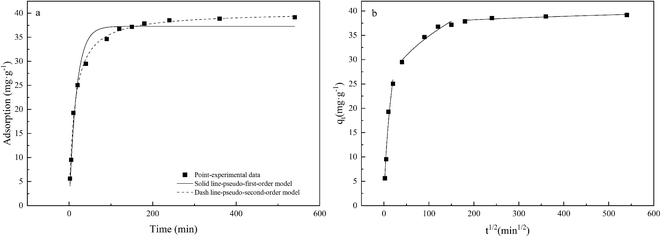 | ||
| Fig. 8 Adsorption kinetics of Levo-HCl on CMNFs–MMT: (a) pseudo-first-order kinetic model, pseudo-second-order kinetic model; (b) intra-particle diffusion model. | ||
The adsorption kinetics and linear fitting results are shown in Table 4 and Fig. 8. The linear correlation coefficient of the pseudo-second-order kinetic model (R2 = 0.9944) is significantly greater than the R2 value of the pseudo-first-order kinetic model (R2 = 0.9702), indicating that the adsorption of Levo-HCl by CMNFs–MMT is a pseudo-second-order process. This may be due to the boundary layer control in the initial stage of adsorption. The adsorption rate is proportional to the square of pollutant concentration, which also indicates that chemical adsorption may be the limiting factor of Levo-HCl adsorption. This process is affected by the electron exchange and interaction between the adsorbent and the adsorbate.88,89 Previous FT-IR characterization found that there are a large number of oxygen-containing functional groups on the surface of CMNFs–MMT, and the hydrogen bonds formed by them with antibiotic molecules play an important role in adsorption. In addition, –OH, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, and C
C, and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O on the surfaces of the adsorbent and antibiotics interact through π–π interactions to enhance the adsorption capacity. This also confirms that the adsorption process is chemical adsorption.
O on the surfaces of the adsorbent and antibiotics interact through π–π interactions to enhance the adsorption capacity. This also confirms that the adsorption process is chemical adsorption.
| Kinetic model | Parameters | Values | |
|---|---|---|---|
| Pseudo-first-order | qe (mg g−1) | 37.2822 | |
| K1 (min−1) | 0.0576 | ||
| R2 | 0.9702 | ||
| Pseudo-second-order | qe (mg g−1) | 40.2959 | |
| K2 (g mg−1 min−1) | 0.0019 | ||
| R2 | 0.9944 | ||
| Intra-particle diffusion | Stage I | Kd1 (mg (g min1/2)−1) | 6.6747 |
| C1 | −3.9498 | ||
| R12 | 0.9531 | ||
| Stage II | Kd2 (mg (g min1/2)−1) | 1.3606 | |
| C1 | 21.2568 | ||
| R22 | 0.9488 | ||
| Stage III | Kd3 (mg (g min1/2)−1) | 0.1216 | |
| C1 | 36.4721 | ||
| R32 | 0.8118 | ||
Generally, the intra-particle diffusion model is used to evaluate the rate-determining steps of the adsorption process to determine whether intra-particle diffusion is the main factor controlling the adsorption rate. The adsorption kinetics and linear fitting results are shown in Table 4 and Fig. 8b. The adsorption of levofloxacin hydrochloride by CMNFs–MMT has a multilevel linear relationship. In the initial stage, the adsorption amount increases rapidly with time, after which the adsorption rate gradually decreases and tends to equilibrium in the subsequent two stages. Based on the experimental data, three-stage fitting was used. In the first stage, the easily accessible adsorption sites on the outer surface of the adsorbent were in contact with more antibiotic molecules in the solution, resulting in a rapid increase in the adsorption rate. In the second stage, the number of adsorption sites decreases, and the adsorbed antibiotics gradually enter the interior of the adsorbent via the intra-particle diffusion process, resulting in a gradual flattening of the curve. In the third stage, the intra-particle diffusion decreases, the solid–liquid phase distribution gradually balances, and the amount of antibiotic adsorbed gradually reaches the adsorption–desorption equilibrium.90 If the linear part of the intra-particle diffusion model passes through the origin of the coordinates, the rate-determining step is intra-particle diffusion; if it does not pass through the origin, it means that intra-particle diffusion is not the only control step, and there are other processes that control the reaction rate, which together constitute the control step.91,92 Therefore, the adsorption of antibiotics may be controlled by various factors such as surface adsorption and intra-particle diffusion. The results in Table 4 show that the R2 value of the first and second stages are greater than 0.900, indicating that the adsorption process is determined by two or more steps. Meanwhile, other mechanisms such as complexation, π–π reaction, electrostatic reaction, and other specific interactions may be involved in the adsorption process of Levo-HCl.
Adsorption isotherms
The adsorption isotherm characterizes the relationship between the adsorption amount and equilibrium concentration at a given temperature, which can infer the interaction mechanism between the adsorbent and the adsorbate and serve as the basis for the selection of the adsorbent. In this study, Langmuir, Freundlich, and Sips adsorption isotherm models were used to fit the experimental data and calculate relevant parameters.Table 5 and Fig. 9 show the three isotherm models and parameters. The linear correlation coefficients of the Langmuir, Freundlich, and Sips isothermal models are all greater than 0.9, and the R2 of the Langmuir isothermal model is greater than that of the Freundlich isothermal model, which indicates that the adsorption mechanism of CMNFs–MMT composites mainly involves single-layer adsorption.93 The Langmuir model assumes that the adsorption sites are evenly distributed on the surface of the adsorbent and the adsorption energy is the same at each adsorption site, which is not consistent with the actual conditions on the CMNFs–MMT surface. Therefore, the Sips isothermal model was used to fit the data. The results showed that the R2 of the Sips isothermal model was greater than 0.99, higher than both of the other isothermal models. The average non-uniform coefficient γ = 0.6438, which shows that the adsorption of antibiotics on CMNFs–MMT occurs heterogeneous monolayer chemisorption.
| Isotherm model | Temperature | |||
|---|---|---|---|---|
| Model | Parameter | 293.15 K | 303.15 K | 313.15 K |
| Langmuir | qm (mg g−1) | 53.0712 | 60.3618 | 65.9009 |
| KL (L mg−1) | 0.1167 | 0.1093 | 0.1033 | |
| R2 | 0.9736 | 0.9779 | 0.9692 | |
| Freundlich | KF (mg1−1/n L1/n g−1) | 7.4238 | 8.1025 | 8.4923 |
| 1/n | 0.5770 | 0.5801 | 0.5864 | |
| R2 | 0.9464 | 0.9533 | 0.9463 | |
| Sips | qm (mg g−1) | 36.7688 | 42.5212 | 45.1044 |
| Ks (L mg−1) | 0.2308 | 0.2099 | 0.2070 | |
| γ | 0.6316 | 0.6621 | 0.6378 | |
| R2 | 0.9924 | 0.9928 | 0.9874 | |
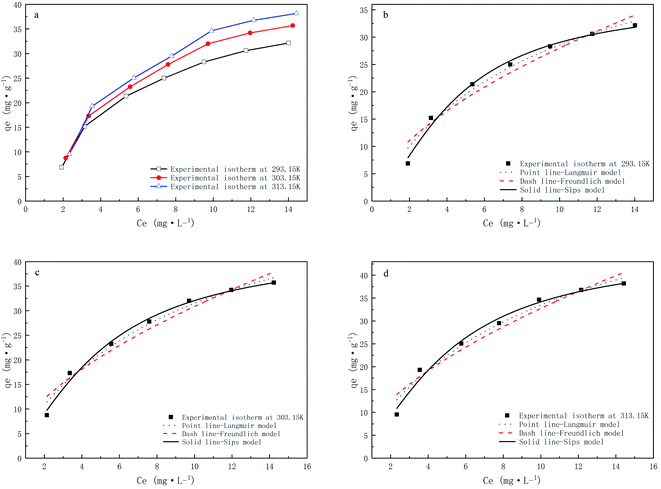 | ||
| Fig. 9 Adsorption isotherms of CMNFs–MMT for Levo-HCl at different temperatures and fitting of Langmuir, Freundlich and Sips models. | ||
Study on environmental water sample treatment effect and adsorbent regeneration and comparison of CMNFs–MMT with other adsorbents
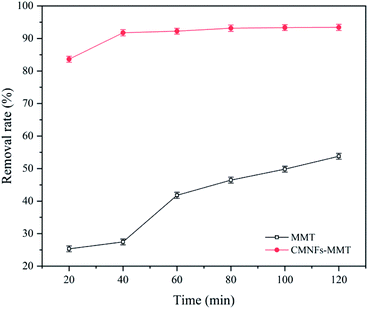
The results of antibiotic adsorption on single MMT and CMNFs–MNT are shown in Fig. 10. It can be seen that MMT has an adsorption effect on Levo-HCl, but the effect is not good, and the optimal removal rate is approximately 53%. The removal effect of CMNFs–MMT on Levo-HCl is significantly better than that on MMT, with a maximum removal rate of 93%. In addition, the adsorption performances of CMNFs–MMT and existing antibiotic adsorbents were compared. The results are shown in Table 6.| Antibiotic | Absorbents | T (h) | Dose (g L−1) | pH | T (°C) | qm (mg g−1) | References |
|---|---|---|---|---|---|---|---|
| Sulfadiazine | Molecularly imprinted polymers | 2.00 | 1.42 | 7.0 | 25 | 7.098 | 94 |
| Tetracycline | Alkali biochar | 60.00 | 5.00 | 7.0 | 30 | 58.82 | 95 |
| Tetracycline | Diatomite | 2.00 | 5.00 | 7.0 | 45 | 34.00 | 96 |
| Metronidazole | Multiwall carbon nanotube | 24.00 | — | 7.0 | 25 | 49.80 | 97 |
| Norfloxacin | Iron-doped activated alumina | 16.00 | 3.00 | 6.5 | 21 | 32.55 | 98 |
| Tetracycline | Crystalline nanocellulose | 2.00 | — | 5.0 | 45 | 7.73 | 99 |
| Levofloxacin hydrochloride | CMNFs–MMT | 1.53 | 0.05 | 4.0 | 40 | 65.90 | This study |
The removal effect of Levo-HCl in actual water samples is shown in Fig. 11a. It can be seen that compared with the Levo-HCl solution prepared with ultrapure water, the CMNFs–MMT has a smaller loss of adsorption capacity in the Levo-HCl solution prepared with actual water samples. This shows that CMNFs–MMT still has good utility in actual water bodies.
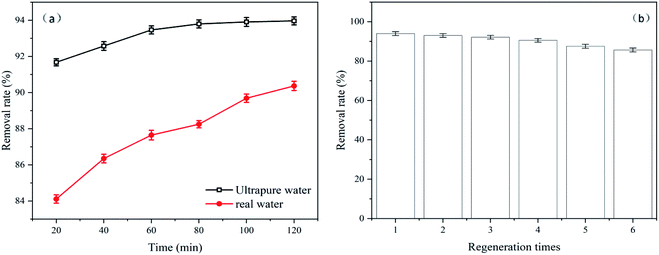 | ||
| Fig. 11 (a) Comparison of actual water body and pure water removal effect. (b) The regeneration experiment of CMNFs–MMT. | ||
For commercial applications, the reusability of adsorbents is an extremely important factor to consider. Therefore, reusability experiments were designed to evaluate the regeneration ability of CMNFs–MMT. Fig. 11b shows the adsorption capacities of Levo-HCl onto CMNFs–MMT during six regeneration cycles. As shown in Fig. 11b, CMNFs–MMT maintained ∼92% removal efficiency after three cycles. After six cycles, CMNFs–MMT still maintained ∼85% removal efficiency. This demonstrates that CMNFs–MMT possesses the clear advantages of high adsorption performance and low cost, making them ideal for practical applications on a large scale.
The mechanism study of Levo-HCl removal on CMNFs–MMT
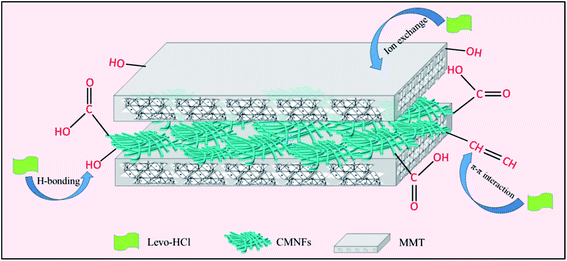
To further investigate the possible potential adsorption sites and bonding modes, XPS and SEM-EDS were used to detect the synthesized CMNFs–MMT after Levo-HCl adsorption. Fig. 12a shows the XPS wide-scan spectra of the CMNFs–MMT composite after Levo-HCl adsorption. A distinct peak appeared after adsorption at a binding energy of approximately 686.4 eV and was assigned to Levo-HCl, suggesting that the Levo-HCl was entirely removed. In addition, the composition of the composites after Levo-HCl adsorption was verified by SEM-EDS (Fig. 12b and c). The ratio of Levo-HCl was estimated to be approximately 1.62% and it was evenly dispersed on the surface of the material.The surface area of CMNFs–MMT nanocomposites is larger than the surface area of each component, which is consistent with the removal rate results. The larger surface area, which can provide more adsorption sites, is due to the large pore area of the nanocomposite and the large core–shell space.100 At the same time, the MMT component has a high ion exchange capacity,101,102 so that the nanocomposite can significantly improve the adsorption capacity through the cation exchange reaction. A large number of oxygen-containing functional groups exist on the surface of CMNFs–MMT, and the hydrogen bonds formed with antibiotic molecules also play an important role in adsorption. In addition, the –OH, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, and C
C, and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds on the surface of the adsorbents can act as π-electron-donors. The O and N-hetero-aromatic rings of Levo-HCl might serve as π-electron-acceptors, which may enhance the adsorption capacity through π–π interactions. Therefore, CMNFs–MMT rely on the abundant adsorption sites provided by the larger surface area, hydrogen bonding, π–π interactions, and electrostatic attraction to effectively adsorb Levo-HCl in water (Fig. 13).
O bonds on the surface of the adsorbents can act as π-electron-donors. The O and N-hetero-aromatic rings of Levo-HCl might serve as π-electron-acceptors, which may enhance the adsorption capacity through π–π interactions. Therefore, CMNFs–MMT rely on the abundant adsorption sites provided by the larger surface area, hydrogen bonding, π–π interactions, and electrostatic attraction to effectively adsorb Levo-HCl in water (Fig. 13).
Conclusions
In this study, CMNFs–MMT was synthesized and its application in removing Levo-HCl from aqueous solution was demonstrated. According to the optimization results obtained from response surface graphs and practical operation, the optimal conditions for adsorption were determined as an initial pollutant concentration of 6.40 mg L−1, initial pH of 4.33, adsorbent dosage of 0.45 g L−1, and contact time of 92 min. The adsorption kinetics and isotherms revealed that the adsorption of Levo-HCl by CMNFs–MMT conforms to the monolayer chemisorption of heterogeneous surfaces. Studies on the adsorption effect in different water bodies show that the removal rate of river water (90.37%) was slightly lower than that of pure water (93.97%) when it reached adsorption equilibrium, which proved that the performance of CMNFs–MMT was not significantly influenced by realistic environmental conditions. In addition, regeneration experiments showed that CMNFs–MMT had the excellent potential as an adsorbent for Levo-HCl in large-scale practical applications. In conclusion, CMNFs–MMT has obvious potential for application in the environment to remove Levo-HCl as an outstanding, reliable, and recyclable adsorbent.Experimental
Materials and methods
Levofloxacin hydrochloride (98%) and montmorillonite were purchased from Shanghai Macklin Biochemical Co., Ltd. Deionized water was used for all experiments. All the other chemicals were of analytical grade and used as received. The pulp board was purchased from X.J.H. Zbiotechnology Co., Ltd. For water matrix experiments, deionized water and environmental water samples were obtained from laboratories and Manas River, respectively.Preparation of carboxymethyl nanocellulose (CMNFs)
Herein, 5 g of dry pulp board, 0.5 mol L−1 sodium hydroxide, and 85% ethanol aqueous solution were added to a 250 mL three-necked flask, and the mixture was stirred and alkalized at 25 °C for 8 h. Then, 0.5 mol L−1 monochloroacetic acid/ethanol solution was continuously added, and the reaction was stirred at 70 °C for 3 h in the mixture. After the reaction, the cellulose ether mixed solution was neutralized with 1 mol L−1 hydrochloric acid solution to obtain carboxymethyl-modified cellulose, the carboxymethylated cellulose was dispersed into a 2.0% concentration suspension with deionized water, and then subjected to a homogenization treatment with a nano-microjet homogenizer, adjusting the pressure to 138.0 MPa.Preparation of carboxymethyl nanocellulose/montmorillonite nanocomposite (CMNFs–MMT)
Herein, 1 g of carboxymethyl nanocellulose suspension was added to 30 mL of deionized water and stirred at room temperature for 30 min. Then, 1 g montmorillonite was dissolved in 30 mL of NaOH solution with 12.5% mass fraction stirring ultrasonically at 25 °C for 30 min to form a suspension. The carboxymethyl nanocellulose suspension was mixed with the montmorillonite suspension, ultrasonically stirred at 60 °C for 2 h, and the product was centrifuged and washed with deionized water to neutrality. After 48 h of freeze drying (CHRIST ALPHA 1-2 LD plus, Germany), CMNFs–MMT nanocomposites were obtained.Characterization
For the characterization of the CMNFs, MMT, and CMNFs–MMT samples, the FT-IR spectra were recorded using a Nicolet 6700 FT-IR instrument (USA). The surface morphology was analyzed using a Quanta 650FEG emission scanning electron microscope (USA). The specific surface area and the pore volume were measured using an ASAP 2020 surface and porosity analyzer (USA). Powder X-ray diffraction (XRD) patterns were obtained using a Bruker D8 X-ray powder diffractometer (Germany) accompanied by Cu-Kα radiation, and X-ray photoelectron spectroscopy (XPS) was performed using a Thermo Fisher Scientific Escalab 250Xi (USA) accompanied by Al-Kα mono. All parameters were set following our previous study.103Adsorption experiments
The initial concentration of the Levo-HCl solution, CMNFs–MMT composite adsorption material, initial pH value, and configured suspension for the batch adsorption experiments followed our previous study.103 The supernatant was removed and the concentration of Levo-HCl in the liquid phase was measured by HPLC (Agilent-1200, USA). The adsorption kinetic data were measured with 6 mg L Levo-HCl solution at 293.15 K. At time intervals of 2, 5, 10, 20, 40, 90, 120, 150, 180, 240, 360, and 540 min, the solution was centrifuged (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm, 5 min), filtered, and its composition was determined. Adsorption isotherms were investigated by carrying out adsorption studies at 293.15, 303.15, and 313.15 K, respectively, with varying initial concentrations of Levo-HCl (5, 15, 25, 35, 45, 60, and 70 mg L−1), and the pH of the solution was adjusted to 4. The residual Levo-HCl concentration was obtained from a standard curve derived from a series of Levo-HCl solutions with known antibiotic content. The adsorption ability of Levo-HCl was calculated using eqn (2),
000 rpm, 5 min), filtered, and its composition was determined. Adsorption isotherms were investigated by carrying out adsorption studies at 293.15, 303.15, and 313.15 K, respectively, with varying initial concentrations of Levo-HCl (5, 15, 25, 35, 45, 60, and 70 mg L−1), and the pH of the solution was adjusted to 4. The residual Levo-HCl concentration was obtained from a standard curve derived from a series of Levo-HCl solutions with known antibiotic content. The adsorption ability of Levo-HCl was calculated using eqn (2),
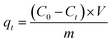 | (2) |
The percentage removal (R%) of the Levo-HCl was calculated using eqn (3),
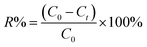 | (3) |
Recyclable experiment
The recyclability of the CMNFs–MMT nanocomposites was determined as follows. We first used CMNFs–MMT to adsorb antibiotics in an aqueous solution, and then the CMNFs–MMT containing the adsorbed antibiotic was immersed in 5 wt% NaOH solution for 5 h to ensure complete desorption. Subsequently, the nanocomposite material was separated, recovered, and washed with distilled water. Finally, the cleaned CMNFs–MMT nanocomposite was freeze-dried under vacuum to obtain a regenerated adsorbent. To test the performance of the adsorbent after regeneration, 0.45 g L−1 regenerated adsorbent was added to 6 mg L−1 Levo-HCl, and the adsorption effect was tested. The adsorption–desorption cycles were performed six times.Statistical analysis and response surface design
Data analysis was performed using the IBM SPSS statistics 19.0 (USA) and Stat-Ease Design-Expert 10.0 (USA) software. According to RSM design principles, the central composite model was used to study the four factors impacting Levo-HCl removal from water by the CMNFs–MMT, which are initial pollutant concentration, initial pH of the solution, contact time, and amount of adsorbent. We predicted the optimal conditions in the experimental range and the center point experiment using 3 parallel experiments. The experimental values are listed in Table 7.| Factor | Coding | Values for each level of coding | ||
|---|---|---|---|---|
| −1 | 0 | +1 | ||
| Dosage of adsorbent, g L−1 | A | 0.2 | 0.4 | 0.6 |
| Initial pollutant concentration, mg L−1 | B | 3 | 6 | 9 |
| pH | C | 2 | 5 | 8 |
| Time, min | D | 60 | 90 | 120 |
Author contributions statement
Junhong Tao, Chengxiao Ma and Jie Yang: conceptualization, methodology, software, writing-original draft preparation, Tiantian Gu and Jianchao Liu: visualization, investigation; Junfeng Li: supervision, software, validation, writing-reviewing and editing, project administration and funding acquisition.Conflicts of interest
The authors declare that they have no conflict of interest.Acknowledgements
Financial support from the National Natural Science Foundation of China (U1803244), the National Key R&D Program of China (2017YFC0404304) are gratefully acknowledged.References
- B. Halling-Sørensen, S. N. Nielsen, P. F. Lanzky, F. Ingerslev, H. C. H. Lützhøft and S. E. Jørgensen, Chemosphere, 1998, 36, 357–393 CrossRef.
- J. L. Martinez, Environ. Pollut., 2009, 157, 2893–2902 CrossRef CAS.
- D. Barceló and M. Petrovic, Anal. Bioanal. Chem., 2007, 387, 1141–1142 CrossRef.
- A. J. Ramirez, R. A. Brain, S. Usenko, M. A. Mottaleb, J. G. O'Donnell, L. L. Stahl, J. B. Wathen, B. D. Snyder, J. L. Pitt, P. Perez-Hurtado, L. L. Dobbins, B. W. Brooks and C. K. Chambliss, Environ. Toxicol. Chem., 2009, 28, 2587–2597 CrossRef CAS.
- J. Shi-Yun and Z. Jun-Ying, Prog. Pharm. Sci., 2008, 032, 323–325 Search PubMed.
- F. Sacher, F. T. Lang, H. J. Brauch and I. Blankenhorn, J. Chromatogr. A, 2001, 938, 199–210 CrossRef CAS.
- P. A. Lara-Martin, E. Gonzalez-Mazo and B.-N. Rosa Maria, Environ. Sci. Technol., 2017, 51, 3148–3156 CrossRef.
- A. D. Jones, G. L. Bruland, S. G. Agrawal and D. Vasudevan, Environ. Toxicol. Chem., 2005, 24, 761–770 CrossRef CAS.
- T. Haddad, E. Baginska and K. Kuemmerer, Water Res., 2015, 72, 75–126 CrossRef CAS.
- L. Xiaobin, L. Bingxin, Z. Rusen, D. Yu and X. Shuguang, Environ. Sci. Pollut. Res., 2016, 23, 7911–7918 CrossRef.
- K. Kummerer, D. A. Skoog, D. M. West, F. J. Holler, S. R. Couch, W. Sanchez, W. Sremski, B. Piccini, O. Palluel and E. Maillotmaréchal, J. Hazard. Mater., 2007, 149, 631–642 CrossRef.
- X. Yu, L. Zhang, M. Liang and W. Sun, Chem. Eng. J., 2015, 279, 363–371 CrossRef CAS.
- V. A. Tsihrintzis and G. D. Gikas, Water Sci. Technol., 2010, 61, 2653 CrossRef CAS.
- V. Rakic, V. Rac, M. Krmar, O. Otman and A. Auroux, J. Hazard. Mater., 2015, 282, 141–149 CrossRef CAS.
- W. Yang, Y. Lu, F. Zheng, X. Xue, L. Na and D. Liu, Chem. Eng. J., 2012, 179, 112–118 CrossRef CAS.
- H. M. Ötker and I. Akmehmet-Balcıoğlu, J. Hazard. Mater., 2005, 122, 251–258 CrossRef.
- M. C. Ncibi and M. Sillanpää, J. Hazard. Mater., 2015, 298, 102–110 CrossRef CAS.
- Y. Hong, L. Jian, J. Wu, Z. Lu, P. C. Wilson and S. Yan, Water, Air, Soil Pollut., 2013, 224, 1370 CrossRef.
- E. K. Putra, R. Pranowo, J. Sunarso, N. Indraswati and S. Ismadji, Water Res., 2009, 43, 2419–2430 CrossRef CAS.
- K. Li, F. Ji, Y. Liu, Z. Tong, X. Zhan and Z. Hu, Water Sci. Technol., 2013, 67, 1490 CrossRef CAS.
- M. E. Essington, J. Lee and Y. Seo, Soil Sci. Soc. Am. J., 2010, 74, 1577 CrossRef CAS.
- P. Liao, Z. Zhan, J. Dai, X. Wu, W. Zhang, K. Wang and S. Yuan, Chem. Eng. J., 2013, 228, 496–505 CrossRef CAS.
- L. H. Hu, Z. P. Yang, L. M. Cui, Y. Li, H. H. Ngo, Y. G. Wang, Q. Wei, H. M. Ma, L. G. Yan and B. Du, Chem. Eng. J., 2016, 287, 545–556 CrossRef CAS.
- C. J. Madadrang, H. Y. Kim, G. H. Gao, N. Wang, J. Zhu, H. Feng, M. Gorring, M. L. Kasner and S. F. Hou, ACS Appl. Mater. Interfaces, 2012, 4, 1186–1193 CrossRef CAS.
- L. Brinchi, F. Cotana, E. Fortunati and J. M. Kenny, Carbohydr. Polym., 2013, 94, 154–169 CrossRef CAS.
- M. Barsbay, O. Guven, M. H. Stenzel, T. P. Davis, C. Barner-Kowollik and L. Barner, Macromolecules, 2007, 40, 7140–7147 CrossRef CAS.
- O. J. Rojas, G. A. Montero and Y. Habibi, J. Appl. Polym. Sci., 2009, 113, 927–935 CrossRef CAS.
- R. Batmaz, N. Mohammed, M. Zaman, G. Minhas and K. C. Tam, Cellulose, 2014, 21, 1655–1665 CrossRef CAS.
- M. Suzelei, R. Mohamad, H. Laurent and M. R. Vignon, Macromolecules, 2005, 38, 1665–1671 CrossRef.
- K. H. M. Kan, L. Jian, K. Wijesekera and E. D. Cranston, Biomacromolecules, 2013, 14, 3130–3139 CrossRef CAS.
- I. Siró and D. Plackett, Cellulose, 2010, 17, 459–494 CrossRef.
- W. Yang, F. Dominici, E. Fortunati, J. M. Kenny and D. Puglia, RSC Adv., 2015, 5, 32350–32357 RSC.
- S. S. Ray and M. Okamoto, Prog. Polym. Sci., 2003, 28, 1539–1641 CrossRef CAS.
- Y. F. Xi, R. L. Frost, H. P. He, T. Kloprogge and T. Bostrom, Langmuir, 2005, 21, 8675–8680 CrossRef CAS.
- D. Trache, A. F. Tarchoun, M. Derradji, T. S. Hamidon, N. Masruchin, N. Brosse and M. H. Hussin, Front. Chem., 2020, 8, 392 CrossRef CAS.
- C. C. Yang, Int. J. Hydrogen Energy, 2011, 36, 4419–4431 CrossRef CAS.
- A. Gil, F. C. C. Assis, S. Albeniz and S. A. Korili, Chem. Eng. J., 2011, 168, 1032–1040 CrossRef CAS.
- F. Parisi, G. Lazzara, M. Merli, S. Milioto, F. Princivalle and L. Sciascia, Nanomaterials, 2019, 9, 1699 CrossRef CAS.
- G. Fijalkowska, K. Szewczuk-Karpisz and M. Wisniewska, J. Mol. Liq., 2019, 293 Search PubMed.
- Q. Qin, Y. Liu, S. C. Chen, F. Y. Zhai, X. K. Jing and Z. W. Yu, J. Appl. Polym. Sci., 2012, 126, 1556–1563 CrossRef CAS.
- J. Zicans, R. D. Maksimov, E. Plume, R. M. Meri and J. Jansons, Compos. Struct., 2018, 183, 483–488 CrossRef.
- A. Kurt and P. Yilmaz, Kuwait J. Sci., 2016, 43, 172–184 CAS.
- D. W. Mbui, D. M. Andala, D. A. Abong'o and J. N. Mmbaga, MRS Adv., 2018, 1–9 Search PubMed.
- R. D. Maksimov and E. Plume, Mech. Compos. Mater., 2014, 50, 613–622 CrossRef CAS.
- A. I. Alateyah, H. N. Dhakal and Z. Y. Zhang, Adv. Polym. Technol., 2013, 32, 5153–5162 CrossRef.
- T. S. Volkova, E. Y. Beider and P. L. Zhuravleva, Russ. J. Gen. Chem., 2011, 81, 1047–1052 CrossRef CAS.
- F. Kadar, L. Szazdi, E. Fekete and B. Pukanszky, Langmuir, 2006, 22, 7848–7854 CrossRef CAS.
- S. W. Jang, J. C. Kim and J. H. Chang, Cellulose, 2009, 16, 445–454 CrossRef CAS.
- M. M. Wang, L. Wang and A. Q. Wang, in Progress in Environmental Science and Engineering, ed. H. Li, Q. J. Xu and D. Zhang, 2012, vol. 356–360, p. 325 Search PubMed.
- M. M. Wang, L. Wang and A. Q. Wang, Desalin. Water Treat., 2013, 51, 7120–7129 CrossRef CAS.
- H. L. Xie, Y. F. Pan, H. N. Xiao and H. Y. Liu, J. Appl. Polym. Sci., 2019, 136, 47941 CrossRef.
- H. F. Heiba, A. A. Taha, A. R. Mostafa, L. A. Mohamed and M. A. Fahmy, Korean J. Chem. Eng., 2018, 35, 1844–1853 CrossRef CAS.
- M. Y. Arica, I. Tuzun, E. Yalcin, O. Ince and G. Bayramoglu, Process Biochem., 2005, 40, 2351–2358 CrossRef CAS.
- K. Mohanty, M. Jha, B. C. Meikap and M. N. Biswas, Chem. Eng. Sci., 2005, 60, 3049–3059 CrossRef CAS.
- A. Cincotti, A. Mameli, A. M. Locci, R. Orru and G. Cao, Ind. Eng. Chem. Res., 2006, 45, 1074–1084 CrossRef CAS.
- A. Al-Haj-Ali and T. Al-Hunaidi, Environ. Technol., 2004, 25, 1009–1019 CrossRef CAS.
- S. M. Dal Bosco, R. S. Jimenez and W. A. Carvalho, J. Colloid Interface Sci., 2005, 281, 424–431 CrossRef CAS.
- L. B. Qian and B. L. Chen, Environ. Sci. Technol., 2013, 47, 8759–8768 CAS.
- S. S. Wang, B. Gao, Y. C. Li, A. Mosa, A. R. Zimmerman, L. Q. Ma, W. G. Harris and K. W. Migliaccio, Bioresour. Technol., 2015, 181, 13–17 CrossRef CAS.
- Z. O. Kocabas-Atakli and Y. Yurum, Chem. Eng. J., 2013, 225, 625–635 CrossRef CAS.
- C. Zhang, L. Chen, T. J. Wang, C. L. Su and Y. Jin, Appl. Surf. Sci., 2014, 317, 552–559 CrossRef CAS.
- D. D. Asouhidou, K. S. Triantafyllidis, N. K. Lazaridis and K. A. Matis, Colloids Surf., A, 2009, 346, 83–90 CrossRef CAS.
- G. Z. Kyzas, N. K. Lazaridis and D. N. Bikiaris, Carbohydr. Polym., 2013, 91, 198–208 CrossRef CAS.
- S. Wang and E. Ariyanto, J. Colloid Interface Sci., 2007, 314, 25–31 CrossRef CAS.
- D. Karadag, M. Turan, E. Akgul, S. Tok and A. Faki, J. Chem. Eng. Data, 2007, 52, 1615–1620 CrossRef CAS.
- D. Karadag, E. Akgul, S. Tok, F. Erturk, M. A. Kaya and M. Turan, J. Chem. Eng. Data, 2007, 52, 2436–2441 CrossRef CAS.
- L. Sun, S. G. Wan and W. S. Luo, Bioresour. Technol., 2013, 140, 406–413 CrossRef CAS.
- M. Ahmad, S. S. Lee, X. M. Dou, D. Mohan, J. K. Sung, J. E. Yang and Y. S. Ok, Bioresour. Technol., 2012, 118, 536–544 CrossRef CAS.
- W. T. Tsai and H. R. Chen, Int. J. Environ. Sci. Technol., 2013, 10, 1349–1356 CrossRef CAS.
- S. Capasso, S. Salvestrini, E. Coppola, A. Buondonno and C. Colella, Appl. Clay Sci., 2005, 28, 159–165 CrossRef CAS.
- S. Capasso, E. Coppola, P. Iovino, S. Salvestrini and C. Colella, Microporous Mesoporous Mater., 2007, 105, 324–328 CrossRef CAS.
- M. Alshabanat, A. Al-Arrash and W. Mekhamer, J. Nanomater., 2013, 2013, 1–12 CrossRef.
- L. Aljerf, J. Environ. Manage., 2018, 225, 120–132 CrossRef CAS.
- S. Zhu, M. Xia, Y. Chu, M. A. Khan, W. Lei, F. Wang, T. Muhmood and A. Wang, Appl. Clay Sci., 2019, 169, 40–47 CrossRef CAS.
- L. Vaculíková, E. Plevová and M. Ritz, J. Nanosci. Nanotechnol., 2019, 19, 2775–2781 CrossRef.
- E. Cohen, T. Joseph, I. Lapides and S. Yariv, Clay Miner., 2005, 40, 223–232 CrossRef CAS.
- L. Wang and A. Wang, Chem. Eng. J., 2007, 143, 43–50 CrossRef.
- M. T. Caccamo, G. Mavilia, L. Mavilia, D. Lombardo and S. Magazu, Materials, 2020, 13, 1100 CrossRef CAS.
- A. Vatansever, H. Dogan, A. Sirkecioglu, T. Inan and S. Sezer, Polym. Eng. Sci., 2015, 55, 2922–2928 CrossRef CAS.
- J. Yang, C. R. Han, J. F. Duan, F. Xu and R. C. Sun, ACS Appl. Mater. Interfaces, 2013, 5, 3199–3207 CrossRef CAS.
- K. Y. Lee, Y. Aitomäki, L. A. Berglund, K. Oksman and A. Bismarck, Compos. Sci. Technol., 2014, 105, 15–27 CrossRef CAS.
- M. Hayati-Ashtiani, Part. Part. Syst. Charact., 2011, 28, 71–76 CrossRef.
- M. Arulkumar, P. Sathishkumar and T. Palvannan, J. Hazard. Mater., 2011, 186, 827–834 CrossRef CAS.
- K. M. Helen, I. Regupathi, M. G. Pillai and L. R. Miranda, Colloids Surf., B, 2009, 70, 35–45 CrossRef.
- M. Zbair, Z. Anfar and H. A. Ahsaune, RSC Adv., 2019, 9, 6935 RSC.
- K. Sen, N. K. Mondal, S. Chattoraj and J. K. Datta, Environ. Earth Sci., 2017, 76, 22 CrossRef.
- M. Roosta, M. Ghaedi, A. Daneshfar and R. Sahraei, Spectrochim. Acta, Part A, 2014, 122, 223–231 CrossRef CAS.
- H. Hu, L. Sun, B. Jiang, H. Wu, Q. Huang and X. Chen, Miner. Eng., 2018, 124, 123–136 CrossRef CAS.
- X. Zhao, X. Li, X. Xie, Z. Wang and R. Li, Environ. Sci. Pollut. Res., 2018, 25, 31136–31148 CrossRef.
- J. Ma, J. Chen, J. Huai, L. Chen, Z. Yuan, F. Yu, W. Gong and J. Wang, J. Colloid Interface Sci., 2012, 378, 175–183 CrossRef.
- M. Arami, N. Y. Limaee and N. M. Mahmoodi, Chem. Eng. J., 2008, 139, 2–10 CrossRef CAS.
- I. Turku, T. Sainio and E. Paatero, Environ. Chem. Lett., 2007, 5, 225–228 CrossRef CAS.
- H. Liu, W. Liu, J. Zhang, C. Zhang, L. Ren and Y. Li, J. Hazard. Mater., 2011, 185, 1528–1535 CrossRef CAS.
- P. F. Ma, Z. P. Zhou, W. M. Yang, B. Q. Tang, H. Liu, W. Z. Xu and W. H. Huang, J. Appl. Polym. Sci., 2015, 132, 41769 CrossRef.
- P. Liu, W. J. Liu, H. Jiang, J. J. Chen, W. W. Li and H. Q. Yu, Bioresour. Technol., 2012, 121, 235–240 CrossRef CAS.
- Y. H. Chao, W. S. Zhu, F. Chen, P. Wang, Z. L. Da, X. Y. Wu, H. Y. Ji, S. Yan and H. M. Li, Sep. Sci. Technol., 2014, 49, 2221–2227 CrossRef CAS.
- D. H. Canales-Alvarado, R. Ocampo-Perez, R. Leyva-Ramos and J. Rivera-Utrilla, J. Colloid Interface Sci., 2014, 436, 276–285 CrossRef.
- W. F. Liu, J. Zhang, C. L. Zhang and L. Ren, Chem. Eng. J., 2011, 171, 431–438 CrossRef CAS.
- M. Rathod, S. Haldar and S. Basha, Ecol. Eng., 2015, 84, 240–249 CrossRef.
- R. Nadra and L. Aljerf, Int. J. Nanomanuf., 2019, 15, 269–289 CrossRef.
- L. Chen, X. L. Chen, C. H. Zhou, H. M. Yang, S. F. Ji, D. S. Tong, Z. K. Zhong, W. H. Yu and M. Q. Chu, J. Cleaner Prod., 2017, 156, 648–659 CrossRef CAS.
- Y. Yao, B. Gao, J. Fang, M. Zhang, H. Chen, Y. Zhou, A. E. Creamer, Y. Sun and L. Yang, Chem. Eng. J., 2014, 242, 136–143 CrossRef CAS.
- J. Tao, J. Yang, C. Ma, J. Li, K. Du, Z. Wei, C. Chen, Z. Wang, C. Zhao and X. Deng, R. Soc. Open Sci., 2020, 7, 200857 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra08987g |
| This journal is © The Royal Society of Chemistry 2020 |