Open Access Article
Open Access ArticleAmino acid interacting network in the receptor-binding domain of SARS-CoV-2 spike protein†
Puja Adhikari and
Wai-Yim Ching
and
Wai-Yim Ching
Department of Physics and Astronomy, University of Missouri-Kansas City, Kansas City, Missouri, USA. E-mail: chingw@umkc.edu
First published on 2nd November 2020
Abstract
The relation between amino acid (AA) sequence and biologically active conformation controls the process of polypeptide chains folding into three-dimensional (3d) protein structures. The recent achievements in the resolution achieved in cryo-electron microscopy coupled with improvements in computational methodologies have accelerated the analysis of structures and properties of proteins. However, the detailed interaction between AAs has not been fully elucidated. Herein, we present a de novo method to evaluate inter-amino acid interactions based on the concept of accurately evaluating the amino acid bond pairs (AABP). The results obtained enabled the identification of complex 3d long-range interconnected AA interacting network in proteins. The method is applied to the receptor binding domain (RBD) of the SARS-CoV-2 spike protein. We show that although nearest-neighbor AAs in the primary sequence have large AABP, other nonlocal AAs make substantial contribution to AABP with significant participation of both covalent and hydrogen bonding. Detailed analysis of AABP in RBD reveals the pivotal role they play in sequence conservation with profound implications on residue mutations and for therapeutic drug design. This approach could be easily applied to many other proteins of biomedical interest in life sciences.
Introduction
Amino acids (AAs) together with the nucleobases in deoxyribonucleic acid (DNA) and ribonucleic acid (RNA) structures with specific base pairs are the fundamental entities in biological science and human evolution.1 The primary structure of a protein refers to the sequence of AAs in the polypeptide chain held together by peptide bonds and controls its stability and functionality. Amino acid mutation refers to random changes in the sequence and minor modifications in the structure that are related to the genetic evolution of species over a long time. All AAs contain a central carbon (C) atom, an amine group and a lone hydrogen (H) atom but they differ from each other with different side chains known as the R group. Some AAs have charged side chains important to their linkage and mutual interaction. The elements C, N and O in AAs form strong covalent or ionic bonds and also the weaker hydrogen bonds (HBs). Cysteine (Cys) and methionine (Met) are the only two AAs that contain S which can form disulfide bonds.Conservation of AA sequence is considered to hold the key for understanding many of the biological and evolution process.2 A highly conserved sequence is one that has remained relatively unchanged far up in the phylogenetic tree, and hence way back into geological time scale. Traditional analysis of conservation is based on the comparative study of the alignment of AA sequence of different proteins from closely related species or at different times. The compensatory effect in these important interactions exclusively relied on the linear sequence of residue numbers of the AAs. In other words, for a specific AA in the sequence, it only considers the two nearest neighbor (NN) AAs with little consideration of the interactions with other non-local AAs in the real three dimensional (3d) space which form secondary or tertiary structures. There have been some recent efforts to go beyond this liner sequence model.2 However, most such analysis depend on statistical methods and probability theory such as multiple sequence alignment (MSA),2 statistical coupling analysis (SCA),3 direct coupling analysis (DCA)4 etc. They all based on the homologous sequence, and sequence alone, of the AAs in the protein. The use of efficient algorithm and combinatory data analysis scheme had some success in the directional dependence of AAs.2 Nevertheless, they all share the same drawback of lack of numerical quantification of AA–AA interaction that are not NNs. The distance of separation between two neighboring AAs is not a precisely defined quantity as in the case for atoms or small molecules. AAs are essentially biomolecules with different sizes, compositions, structures and orientations. They cannot be easily quantified as a viable parameter routinely used in some published literatures.5 Precise quantification requires accurate first-principles calculation at the atomistic level.
Historically and not too long ago, the Holy Grail in biological research is to predict the structure of unknown proteins using a variety of techniques including existing protein data, various sequence analysis, experimental crystallography and NMR spectroscopy. The discovery of cryogenic electron microscopy (cryo-EM) that can determine bio-molecular structures at near-atomic resolution is the game changer.6–9 AA sequences can be reliably determined and their structures are deposited in data banks such as PDB, CNBI, GenBank, etc. with specific identity codes. More recently, it has been reported that the resolution of cryo-EM can be further increased from the current 3.5 Å to less than 1.3 Å with the visualization of H atoms.10,11 The new goal now is to accurately determine the structures of new proteins, to verify and validate many unproved hypotheses and to explain some intrigue phenomena. In this regard, their structural refinement to even higher precision using large-scale computational modeling is absolutely necessary. The computationally refined structure can be used to investigate the details of intra- and inter-protein interactions at the atomistic level12 and reveal the possible mechanism of biological interaction under different environments. Currently the atomic resolution from cryo-EM is about 3.2–3.5 Å.13 Most of the data deposited have the AA sequence but not the H atoms that saturate the dangling bonds. In addition, the atomic coordinates of some AAs in the sequence are sometimes missing for various technical reasons.
The outbreak of the coronavirus disease in late 2019 (COVID-19) has rapidly emerged as an appalling epidemic with no end in sight. It is caused by the new severe acute respiratory syndrome corona virus 2 (SARS-CoV-2). The key to combat this virus is to understand its complex structure and functionality.12–16 Wrapp et al.13 is among the earliest in the determination the prefusion structure of spike (S) glycoprotein (S-protein) of the SARS-CoV-2 using cryo-EM (PDB ID: 6VSB). The S-protein is the key element in understanding the anatomy of the virus since it makes the first contact with angiotensin-converting enzyme 2 (ACE2) in human cell. Other computational work17–19 have prompted computational research at atomistic level possible.12 In this paper, we describe the development of a de novo method that go beyond the current statistical approach in analyzing the interaction between all AAs in 3d with a quantitative descriptor called amino acid bond pair (AABP) (see Methods). The ability to perform accurate and detailed calculation of AABP using ab initio quantum chemical methods enabling the investigation of proteins and their evolution at a much deeper level. The method is applied to the receptor binding domain (RBD) of the S-protein. The data generated is used to quantify and correlate with the sequence conservation in RBD. We also show the significant role played by the HBs in addition to the strong covalent bonds between atoms in different AAs in three dimensions.
Methods
Structural construction and relaxation
The structure for the S-protein in SARS-CoV-2 is downloaded from PDB (ID: 6VSB). The missing H atoms in the coordinates are added using standard software Chimera.20 This initial structure is then fully relaxed using The Vienna ab initio simulation package (VASP).21 We used the projector augmented wave (PAW) method with the Perdew–Burke–Ernzerhof (PBE) exchange correlation functional22 within the generalized gradient approximation (GGA). While it is possible to use more elaborate potentials within the density functional theory but they are computationally prohibitive due to the large and complex structure of the S-protein and the use of PBE potential is reasonably accurate for biomolecular systems. The input parameters used are: energy cut-off 500 eV, electronic convergence criterion of 10–4 eV; force convergence criteria for ionic relaxation −10–2 eV Å−1 and a single k-point sampling. All VASP structure relaxations were carried out at the National Energy Research Scientific Computing (NERSC) facility at the Lawrence Berkeley Laboratory and Research Computing Support Services (RCSS) of the University of Missouri System. They are fully relaxed and the resulting accuracy in atomic positions is estimated to be less than 0.01 Å. The initial unrelaxed and fully relaxed total energy from VASP relaxation for the small SD1 subdomain is −2370.8472 eV and −2379.2055 eV respectively. The reduction in the total energy of 8.3533 eV lower for 24 AAs with 391 atoms in SD1 implies a reduction of 0.02 eV (1.93 kcal mol−1) per atom.Electronic structure, interatomic bonding and partial charge on amino acids
For the electronic structure calculations of the protein domains, we use the in-house developed all-electron orthogonalized linear combination of atomic orbitals (OLCAO) method23 with the VASP-relaxed structure as input. The merit of combining the two different DFT codes (VASP for accurate structure optimization and atomic orbital based OLCAO method for bonding analysis) is well documented24–27 and it is especially effective for large complex biomolecular systems such as COVID-19 virus. The key point of the success of the OLCAO method is provision of the effective charge (Q*) on each atom and the bond order (BO) values ραβ between any pairs of atoms. They are obtained from the ab initio wave functions with atomic basis expansion calculated quantum mechanically:
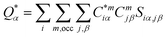 | (1) |
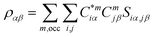 | (2) |
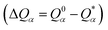 is the deviation of the effective charge
is the deviation of the effective charge 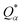 from the neutral atomic charge Q0α on the same atom α. The BO signifies the strength of the bond between two atoms. The calculation of PC and BO are based on the Mulliken scheme.28,29 Hence such calculations are basis-dependent. Comparisons of BO values using different basis or different methods should be treated with caution. The atomic-scale interactions based on DFT calculations are critical for providing the accurate information necessary for their fundamental understanding and are rarely done on large proteins. In the present case, the RBD has a total of 2100 atoms and it is obviously quite challenging to obtain accurate atomic partial charges and bond order values between all pairs of atoms. More details on the OLCAO method can be found in ref. 12 and 23.
from the neutral atomic charge Q0α on the same atom α. The BO signifies the strength of the bond between two atoms. The calculation of PC and BO are based on the Mulliken scheme.28,29 Hence such calculations are basis-dependent. Comparisons of BO values using different basis or different methods should be treated with caution. The atomic-scale interactions based on DFT calculations are critical for providing the accurate information necessary for their fundamental understanding and are rarely done on large proteins. In the present case, the RBD has a total of 2100 atoms and it is obviously quite challenging to obtain accurate atomic partial charges and bond order values between all pairs of atoms. More details on the OLCAO method can be found in ref. 12 and 23.
Amino acid bond pair (AABP)
In the OLCAO method, the bond order (BO) values ραβ described above are calculated for every pairs of atoms (α, β) within a cut-off distance of 2.5 Å. The position of the atoms is a well-defined quantity, whereas the positions of amino acids in the biological system are not because they are essentially biomolecules with different atoms, configurations and orientations. Strictly speaking, to assign a distance of separation between different amino acids in a protein in order to describe their interactions is an ill-conceived parameter based on some vague and arbitrary criteria.However, with the quantum mechanically based OLCAO method and with the interatomic interaction between all atoms available, we can defined the bonding between two amino acids u and v with no ambiguity which we coin as amino acid bond pair (AABP):
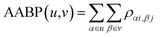 | (3) |
In principle, interatomic bonding between every pair of atoms in RBD of the S-protein with 2100 atoms in this work is already well defined in eqn (1) and (2) above and calculated by the full diagonalization of the secular equation in the OLCAO method. However, it requires the eqn (3) above to decipher them into pair-wise inter-amino acid bonding from the interatomic bonding that has not been done except may be in few isolated cases of a few amino acids. The merit of the above scheme is that AABP for selected groups can obtained by adding their BO in that group for relative comparisons such as those listed in Table 1 for SD1.
| Bond type | Sum of BO of type | No. of Bonds |
|---|---|---|
| C–H | 0.4074 | 1 |
| N–C | 61.6410 | 140 |
| N–H | 0.3395 | 1 |
| N⋯H | 0.2297 | 4 |
| O–H | 0.2555 | 1 |
| O⋯H | 2.9788 | 89 |
| S–S | 0.3324 | 2 |
| Total | 66.1843 | 238 |
Matrix presentation of nonlocality in AABP
To prepare data for effective representation for AABP (u, v), we design a matrix representation in which the rows (u) and columns (v) designate the each of the amino acids in the sequence. The matrix element represents the (u, v) is the numerical value of AABP (u, v) in unit of electrons. Obviously, this matrix is symmetric and AABP (u, v) = 0 for u = v and AABP (u ± 1, v) ≠ 0 since they represent the nearest neighbor (NN) interaction of the primary sequence of the AAs in the protein. Even though AABP (u, v) is not diagonal but it shows diagonal nature so, we name this NN interaction to be pseudo-diagonal cell in this paper. The nonzero AABP (u, v) represent the nonlocal AABP (u, v) interactions in 3d. The empty cell box in AABP (u, v) simply indicate these pairs are non-interacting since they are too far apart with negligibly small calculated BO between the atoms of different AAs. The RBD domain has 144 AAs and listing a 144 × 144 matrix is obviously unpractical. They are divided into 10 submatrices as shown in Fig. S1.† The smaller subdomain SD1 with 24 AAs, the matrix is 24 × 24. The matrix presentation for data for AABP (u, v) for SD1 and RBD are shown in Tables S1 and S2† respectively.Result and discussion
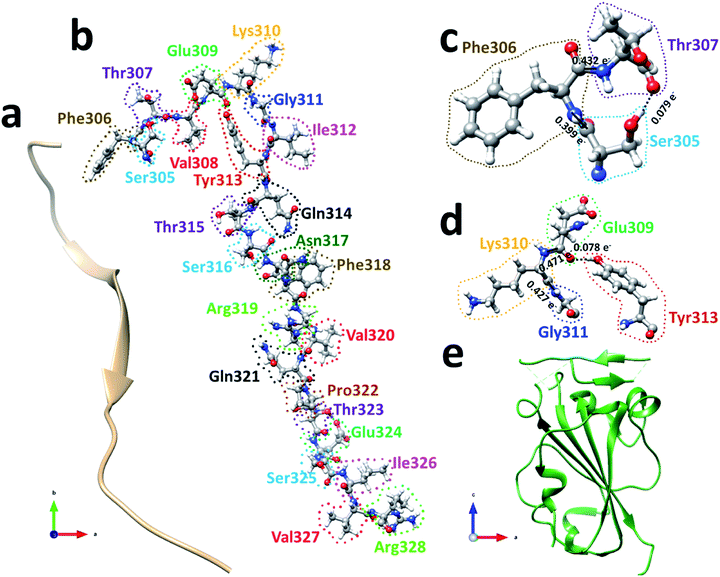
The spike protein or S-protein in SARS-CoV-2 consists of three chains A, B, C with the chain A in the up conformation most critical since it is receptor accessible. Each chain in S-protein has two subunits, receptor binding S1 and membrane binding S2. S1 consists of N-terminal domain (NTD), receptor binding domain (RBD), SD1 and SD2. S1 has 526 AAs and S2 has 433 AAs as depicted in Fig. 1. So, S-protein has a total of 959 AAs excluding the ones with missing coordinates due to either technical difficulties or because they were deemed to be less important for biological interactions related to coronavirus.13 SD1 is the smallest subdomain with only 24 AAs and has been used to illustrate new methods, approaches and data analysis, whereas RBD is the most important domain in S-protein since it directly contacts the ACE2. A somewhat minor complication in RBD is that the atomic coordinates on three flexible segments of the AA sequences are missing. The region for SD1 (305–328) also has missing position coordinates for some AAs, which we have simply ignored. Under this scheme, the RBD (330–521) has 144 AAs excluding missing ones as indicated in Fig. 1. This will be alerted in later presentation of figures and tables. Furthermore, there are 6 AAs (329–334) missing their positions between SD1 and RBD.13 Another critically missing positions are 14 AAs (673–686) near the junction of S1 and S2. This is at the polybasic furin cleavage sites instrumental for viral infection when RBD in S-protein fuses with the ACE-2 cell in human.30 The ribbon structures of SD1 and RBD are shown in Fig. 2(a) and (e) respectively.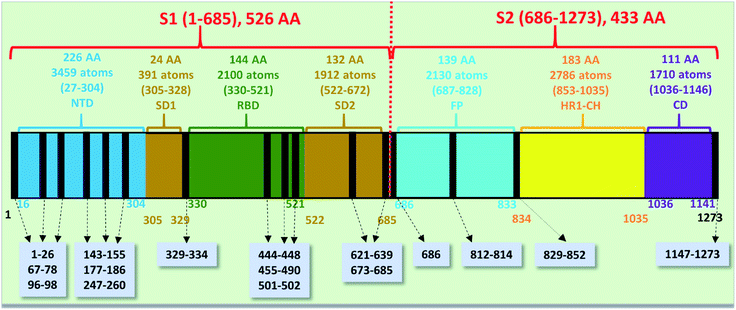 | ||
| Fig. 1 The S-protein in SARS-CoV-2 (6VSB) divided into two subunits S1 and S2 with their domains. The missing position coordinates are indicated by vertical black lines with their sequence numbers shown in grey boxes pointed with dashed arrows. The overall number of amino acids, atoms and their sequence number range are marked in upper part of the horizontal bar. The numbers at the bottom of the horizontal bar show the sequence numbers for the domains with their respective color. | ||
We will first use the data for subdomain SD1 (Fig. 2(b)) with only 24 AAs as an example to illustrate the type of results that can be obtained making it easier to understand the results for RBD. The results of AABP for SD1 are listed in Table S1 in the ESI† in the form of a 24 × 24 matrix (see Methods section). The pseudo-diagonal blocks of cells representing the calculated AABP values between the NN pairs are highlighted in yellow. There are only 2 off-diagonal AABP in the matrix for SD1, one between Ser305 and Thr307 with AABP = 0.079 e− and the other one is between Glu309 and Tyr313 with AABP = 0.078 e−. The main reason that there are only two off-diagonal AABP pairs is because SD1 is an elongated protein and the AAs are further separated unless they are NNs. This is certainly not the case with RBD to be discussed later. In SD1, the largest AABP value from NN is Val327 (0.587 e−) and the smallest is Arg328 (0.399 e−). The total AABP value for each AA is the sum of NN pairs and off-diagonal AAs. It should be pointed out that both Ser305 and Arg328 have only one NN AA to the right and left respectively giving lower total AABP values. For Ser305 has total AABP value is 0.399 e− + 0.079 e− = 0.478 e−. The total AABP values for the other AAs will be twice as larger since they will have contributions from two NNs. For example, Thr307 will have a total AABP value of 0.496 e− + 0.432 e− + 0.079 e− = 1.007 e− including the contribution from the off-diagonal pairs Ser305–Thr307. A typical AA in the middle of SD1 without off-diagonal contribution such as Asn317 has a total AABP value of 0.485 e− + 0.466 e− = 0.951 e−, one from the left (Ser316) and the other from right (Phe318).
Fig. 2(c) and (d) show the details of inter-amino acid interactions between 3 AAs (Ser305, Phe306, Thr307) and four AAs (Glu309, Lys310, Gly311, Tyr313) respectively in SD1. In Fig. 2(c) the two covalent bonds are between a C in Ser305 and a N in Phe306 and a C in Phe306 and a N in Thr307 with BO values of 0.399 e− and 0.432 e− respectively. Specific interatomic bonds, covalent and HB, are marked with solid and dashed lines. There is only one HB between an H atom in Ser305 and an O atom in Thr307 with a BO value of 0.079 e−. Fig. 2(d) with four AAs have two covalent bonds and one HB.
AABP analysis of RBD
RBD is a very large biomolecule with 144 residues and a total of 2100 atoms. Structural relaxation of proteins with accuracy in atomic coordinates up to 0.01 Å is very important for realistic quantum chemical calculations.12 It is anticipated that such high precision calculations could significantly compliment the experimental work at a much reduced cost in addition to providing the fundamental understanding on various aspects of viral infection. Since RBD has 144 AAs, the data for AABP is massive, with a much larger number of off-diagonal AABP and its presentation for the 3d-connected network will be extremely challenging. The diversity of the distribution of these 144 AAs among the 20 distinct residues in RBD is shown in Fig. 3. All AAs are present except Met and they are very unevenly distributed. Tyr and Val have 13 each followed by Ser has 12. The smallest presence are Glu, Trp and His with frequencies of 3, 2, and 1 respectively. There are 5 Cys (336, 361, 379, 391, 432), less than half of the average. Cys and Met are the only AAs with S–S bonds. It turns out that Cys is quite different from other AAs in the context of the present paper with large contributions to the AABP from the off-diagonal Cys–Cys pairs due to the unique S–S bonds. More details will be detailed later in this section.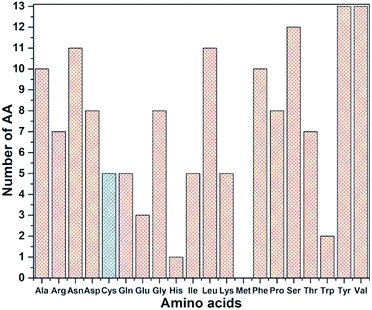 | ||
| Fig. 3 Frequency distribution of 144 AA among 20 amino acids in RBD. Cys highlighted with blue color. | ||
Like in SD1, the bonding between different AAs consist of covalent bonds and HBs. We first surmise the gross picture of binding in RBD in Table 1. Out of 238 bonds, there are 93 HBs (39.1%), 89 are O⋯H bonds (95.7% of HBs) and only 4 are N⋯H bonds (4.3% of HBs). For the bond strength, we list the total bond order (BO) values for each bond types in Table 1. Since HBs are weaker than covalent bonds, its total bond order of 0.2297 + 2.9788 = 3.2085 is only 4.78% (3.21/66.18). This does not mean that HBs are less important in AA interactions since the data in Table 1 constitutes all possible bonds in RBD. We will return to this point later.
Fig. S1† shows the summary of the ten 36 × 36 matrices (MT) data (MT1–MT10) shown in Table S2† for RBD which lists the actual data for the AABP in the form of ten matrices covering all 144 × 144 possible inter-AA interacting pairs. It is similar to Table S1† for SD1 showing all possible interactions among NN pairs with pseudo-diagonal cells highlighted with yellow and non-local AA pairs in off-diagonal cells. The pseudo-diagonal cells represent the primary AA sequence where the AA–AA interaction are between NN pairs with AAs with residue number next to each other (see Methods section). As expected, the pseudo-diagonal cells have much larger AABP values compared to those from off-diagonal cells which constitute the AA interactions in 3d. It should be pointed out that in MT4, MT7, MT9 and MT10, the position coordinates of some AA are missing as shown in Fig. 1 (444–448, 455–490, 501–502) which results in total 36 AAs in the sequence range 443–521. These AA positions are simply eliminated in the RBD calculations (see ref. 12). The missing part in MT4, MT7, MT9 and MT10 are those marked by vertical black line in Fig. 1. In this way, the MTs (s = 4, 7, 9, 10) all have dimension 36 × 36 similar to the other 6 MTs. Table S2† shows the 140 AABP values in the primary sequence with an average AABP value of 0.445 electron (e−) ranging from 0.397 e− (Ala372–Ser373 and Leu517–Leu518) to 0.939 e− (Val503–Gly504). There are 75 off-diagonal AABP values with a much smaller average AABP value of 0.052 e− ranging from 0.010 e− (Gly416–Asp420) to 0.407 e− for (Thr500–Tyr505).
Fig. 4(a) shows the sketch of the possible connection among the 144 AAs in the RBD as reflected by their finite AABP values listed in Table S2.† This is a very busy figure in order to show the 3d connection map in a 2d plane by connecting those AAs that are off-diagonal cells in Table S2.† The connected circles with the AA name and sequence number labeled are the primary AA sequence. This figure with a lot of details shows the true nature of the AA interaction in 3d and their nonlocal network in RBD. There are only 41 AAs (no color) or 28.5% that do not have off-diagonal AABP. Careful inspection of Fig. 4(a) shows that there are 68 AAs have 1 off-diagonal AABP (yellow), 26 AAs have 2 off-diagonal AABP (green), 7 AAs have 3 off-diagonal AABP (blue), and 2 AAs have 4 off-diagonal AABP (pink). The amino acids Cys are marked by red star to emphasize the unique Cys–Cys off-diagonal bonding.
 | ||
| Fig. 4 (a) Distribution of AABP in RBD using the data from Table S2† (10 matrix tables). Circle with no color represents the AA with no off-diagonal AABP. Colored circles represent following AAs: yellow represents one off-diagonal AABP, green two off-diagonal AABP, blue three off-diagonal AABP, and pink four off-diagonal AABP. The colored lines are used to show multiple off-diagonal AABP. (b) and (c) are examples for chains with off-diagonal connections. | ||
The above analysis enables us to quantitatively designate a number characterizing the stability or binding strength for each amino acid in RBD based on the total inter-AA interactions in 3d space. It consists of two parts: (1) AABP from NN AAs in the primary sequence. (2) Contribution from off-diagonal AAs. Each of these two parts can be further divided into those formed with covalent bonds and by HBs. Such detailed analysis of inter-AAs interaction in 3d space is truly de novo and unprecedented. Moreover, they can be connected to the conservation of the amino acid sequence itself.
Table S3† lists the calculated AABP values in RBD from the inter-amino acid interaction. There are two columns: one from NN (pseudo-diagonal) AAs and the other from nearby AAs (off-diagonal). The green cells in Table S3† mark those AAs having a total AABP larger than 0.90 e−, a reasonable estimation for the high AA binding strength that controls the formation of the 3d-network. Of the 144 AAs in RBD, 60% have AABP sum higher than 0.9 e−. These data are plotted in Fig. 5 in the form of histogram bars. The three vertical dashed lines show the locations of AA with missing position coordinates. The AAs with only one NN are marked light blue (Leu335, Ser443, Tyr449, Arg454, Pro491, Thr500, Val503 and Pro521). They all have much lower total AABP values. In particular, we note that the AAs that have much higher total AABP than the average are those with large contributions from the off-diagonal parts. Ostensibly, both Gly504 and Tyr505 have large total AABP values which will be discussed in more detail in the next section. Another interesting observation is that the total AABP values show some have a correlation with the absolute value of the partial charge (PC) |ΔQ*| (Fig. 2 of ref. 12). They are identified and marked with blue arrows for higher positive PC or red arrows for higher negative PC in Fig. 5. Most of these AAs have AABP values equal or higher than 0.9 e−. Interestingly, the five Cys mentioned earlier (marked pink in Table S3†) have large contribution from the off-diagonal contribution but they do not correlate with the PC. The blue bold color in Table S3† indicates those amino acids that have contribution from only one NN. They are either the first or last AA in the sequence, or they are next to the omitted AA with missing coordinates (Fig. 1). In other words, the contribution to the strength of AABP for these AAs should have the NN part doubled. More detailed breakdown of different types of interatomic bonding between all amino acid pairs in RBD are listed in Table S4.†
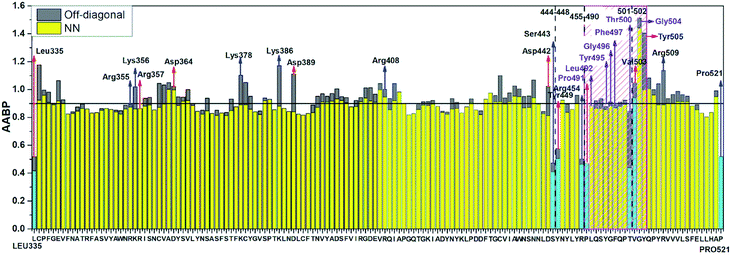 | ||
| Fig. 5 Distribution of AABP in RBD using the data from Table S2† (10 matrix Tables) and Table S3†. The three dashed lines shows missing position coordinates of AA. The color bar represents following, light blue: sum AABP of AA with single nearest neighbor, yellow: sum AABP of AA with two nearest neighbors, grey: AA with off-diagonal AABP. The AA marked with purple are conserved ones in the ACE2 receptor binding contact residue area according to Anderson et al. (marked with striped pink box). The red and blue arrow represents the AA with higher negative and positive partial charge. | ||
Details of amino acid interactions
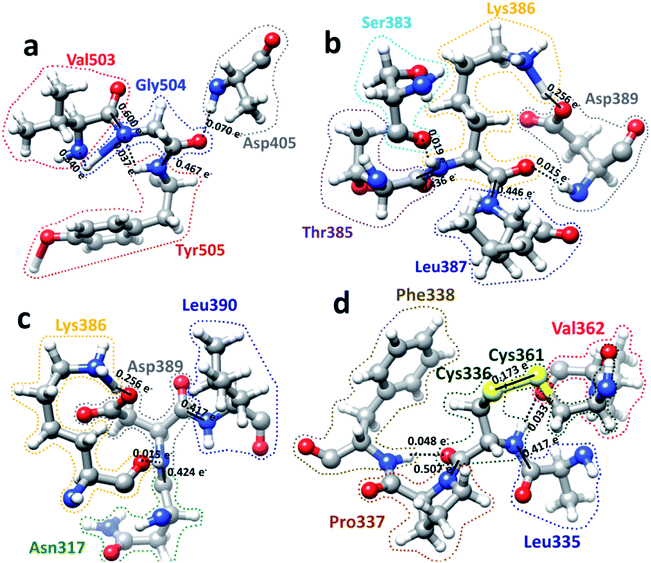
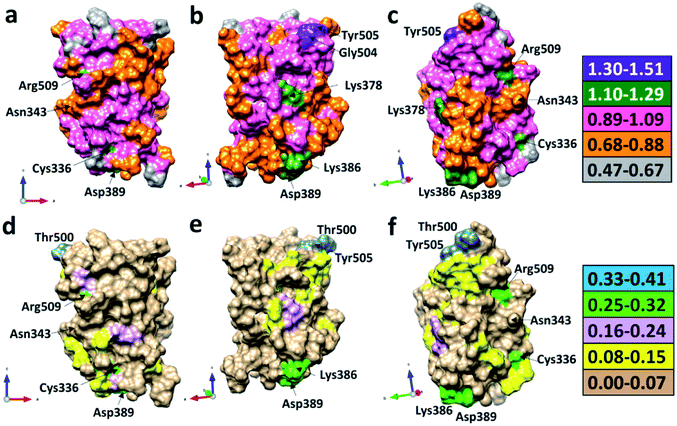
We now present some selected examples vividly illustrating the intricate details on the inter-amino acid interaction that have not been revealed before. Fig. 6 shows the bonding of: (a) Gly504 with three AAs: Val503, Asp405, and Tyr505; (b) Lys386 with four AAs: Ser383, Asp389, Leu387, and Thr385; (c) Asp389 with three AAs: Lys386, Leu390, and Asn317; (d) Cys336 with five AAs: Cys361, Val362, Phe338, Pro337, and Leu335. Details are described in the figure caption. The entire RBD has been analyzed similarly with detailed results presented in Table S4.† Moreover, we show in Fig. 7, the AABP of entire RBD on the surface. The total AABP value is displayed in different orientations in Fig. 7(a)–(c) and those from the off-diagonal component in Fig. 7(d)–(f). The AAs with higher sum AABP and off-diagonal AABP are marked. The residue Asn343 is the only AA in RBD out of the 22 N-linked glycosylation in the S protein.31 Detailed description is in the figure caption.Off-diagonal connections of RBD
We now discuss the nonlocality of AA–AA interactions in 3d based on their quantitative values in AABP. Off-diagonal connections form chains from multiple off-diagonal AABP, each contributed from two AAs. This is sketched in Fig. 4(a) using colorful lines. They are summarized in Table S5.† Off-diagonal connections can be complicated since they involve all AAs in the long-range nonlocal interactions, and demonstrate the twists and turns in the protein which is very difficult to characterize based purely on sequence alignment. Table S5† lists the AAs involved in unique chains. The left side of table lists all AAs involved and the right side of table shows the number of AAs involved in each unique chain or the count. The lower limit of the count is 3 since the ones with 2 counts are just off-diagonal AABP shown in Fig. 4(a) (marked with yellow color). Please note that some off-diagonal connections shown in Table S5† might be connected to NN AA. One of such example is Ala344, with 9 different AAs involved in including itself which connects to its NN Thr345. Among the 144 AAs in RBD, 12.5% of AAs has 9 counts, 4.9% of AA has 7 counts, 12.5% of AAs has 6 counts, 6.9% of AAs has 5 counts, 5.6% of AAs has 4 counts, 8.3% of AAs has 3 counts, 20.8% of AAs has 2 counts (off-diagonal AABP) and 28.5% of AAs has 1 count (no off-diagonal AABP). Strangely, there is no chain with 8 counts. An interesting fact regarding Cys is that out of 5 Cys AAs present in RBD two of them Cys379 and Cys432 falls under 9-count off-diagonal connections. The other 2 Cys336 and Cys361 falls under 6-count off-diagonal connections. The remaining one Cys391 does not have any off-diagonal AABP since it is bonded with Cys525 in SD2.AABP off-diagonal connections and conservation
AABP with its off-diagonal connections is related to conservation of AAs. In ref. 12, we attempted to connect sequence conservation with intramolecular binding in RBD of SARS-CoV-2. In RBD the AA sequence number from 455 to 505 is considered to be the residues in the binding region in contact with ACE2 receptor.30 As described in Fig. 1, there are only 13 AAs with their position coordinates available in this area. Pro499 is one of the 13 AAs with off-diagonal connections with 7 AAs (Table S5† and Fig. 4(b)) and serves as a simple example of branching of off-diagonal connections from Asn439. Among the 13 AAs in the ACE2 receptor binding area only 7 are considered to be conserved.12 They are Pro491, Leu492, Tyr495, Gly496, Phe497, Thr500, and Gly504. Two of them, Pro491 and Leu492 do not have any off-diagonal AABP. Four of the 7 conserved AAs each has one off-diagonal AABP and no off-diagonal connections. They are from pairs Tyr495–Phe497, Gly496–Gln498 and Thr500–Tyr505 with off-diagonal contribution of 0.023 e−, 0.029 e− and 0.407 e− respectively. The last one, Gly504 has 6 off-diagonal connections (Gly504–Asp405–Arg408–Thr376–Ala435–Ser375) (see Table S5† and Fig. 4(c)). In addition, Gly504 has a large off-diagonal AABP of 0.070 e− from Asp405–Gly504 pair and the highest total AABP sum of 1.513 e− (see Table S3,† and Fig. 5) among all AAs in RBD. This astonishly high value approaches that of the pseudo-diagonal contributions in the primary sequence. It is remarkable that Gly504, which falls under conserved ACE2 receptor binding segment of RBD has the largest sum AABP and large off-diagonal connections. All these factors point to the important role of 3d inter-amino acid bonding in sequence conservation. The NNs of Gly504 are Val503 and Tyr505 with pseudo-diagonal AABP contributions of 0.939 e− with AABP 0.503 e− respectively. It turns out that both Val503 and Tyr505 have higher negative partial PC12 and marked with red arrows in Fig. 5. AAs with higher negative or positive PC are mostly the conserved ones consistent with our claim.12 We also note that Tyr505–Thr500 pair has the highest off-diagonal AABP value of 0.407 e−. It should be pointed out that Thr500 has only one NN with AABP of 0.437 e− yet their sum still has a very respectable value of 0.845 e−. Thr500 is one of the 7 conserved AAs, this again supports the notion of positive correlation between conservation and AABP.Hinge movement in S-protein RBD
S-protein undergoes a conformational change during infection in which RBD of S1 carries out a hinge-like movement into a receptor-binding active state.32 Interaction between Ser359 (located in RBD) and Pro561 (located in SD2) are the key for this conformation change according to Roy et al.33 From Table S5† and Fig. 4, we show that the off-diagonal connections for Ser359 falls under 5 counts (Ser359–Asn394–Glu516–Thr393–Ala520) and is linear with no branching out. Four of these AAs except Thr393 are conserved.12 The ball and stick figure of these five amino acids are shown in Fig. 8. In this case, all off-diagonal bonding is due to HBs. This shows the nature of most of the off-diagonal bonding in the entire RBD. HBs are one of the important factors in the interaction within the S-protein. In this regard, our method and analysis go beyond NN interaction in the primary sequence and includes the contributions from all nonlocal off-diagonal AAs, identifying their HBs. This is one level deeper in explaining the hinge movement of RBD in S-protein during viral infection. We believe that other AAs with longer 3d chains with their HBs also play key roles which are not revealed yet. Table S5† shows all unique chains and we would like to point out 2 unique chains each with 9 AAs (maximum count), may also have key function in the S-protein.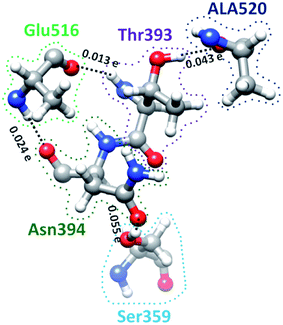 | ||
| Fig. 8 Ball and stick figure showing off-diagonal bonding among five amino acids including Ser359. The dashed lines represent the HB. The BO for all off-diagonal bonding are marked. | ||
Conclusions
In this paper, we have accomplished the following: (1) presented a de novo method for inter-amino acid interactions based on quantitative quantum mechanical calculation of the bonding between AAs called AABP (u, v) and confirmed that the nearest neighbor AAs predominate the interactions consistent with using primary amino acid sequence as the key descriptor used in the past theory. (2) Demonstrated quantitatively the nonlocal network structure of amino acids in 3-dimensions and its implication to the conservation of the amino acid sequence. (3) Confirmed the significant contribution of AABP with off-diagonal contributions to the sequence conservation in the receptor binding domain of the S-protein of SARS-CoV-2 virus. (4) Offered detailed site-specific analysis of intricate complex bonding processes in RBD including glycosylation and the prominent role of residue Gly504. (5) Identified the unique bonding of amino acid Cys which contains sulphur in the AABP (u, v) and its specific role in the formation of the AA network. (6) Correlated the AAs involved in the hinge movement around Ser359 with their HBs.In summary, based on the clearly delineated steps of the proposed methodology and meticulously displayed of the data collected and discussed in various aspects of the impacts of the existence of the non-local amino acid interaction network in RBD of SARS-CoV-2 Spike protein. To the best of our knowledge, this important issue has not been touched upon, at least at the quantitative level in the research community. This new concept and method of AABP for interaction between amino acids is clearly one step beyond the simpler interatomic interactions in proteins.12 More importantly, the method can be readily applied to and play a crucial role in large-scale computation for protein design34–37 and understanding the mutation process38–40 leading to effective vaccine and therapeutic drug design41–43 in combating COVID-19 pandemics. This is because such urgent research topics require the information on the details of the interaction under different environments, involving a single amino acid or clusters of multiple amino acids. Some of such calculations are currently in progress and will be reported in near future.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research used the resources of the National Energy Research Scientific Computing Center supported by DOE under Contract No. DE-AC03-76SF00098 and the Research Computing Support Services (RCSS) of the University of Missouri System. This project is funded by the National Science Foundation of USA: RAPID DMR/CMMT-2028803. We would like to thank Professor Reidun Twarock for discussion and valuable suggestions.Notes and references
- C. B. Anfinsen, Science, 1973, 181, 223–230, DOI:10.1126/science.181.4096.223.
- C. Sruthi and M. Prakash, PLoS One, 2018, 13, e0198645, DOI:10.1371/journal.pone.0198645.
- S. W. Lockless and R. Ranganathan, Science, 1999, 286, 295–299, DOI:10.1126/science.286.5438.295.
- M. Weigt, R. A. White, H. Szurmant, J. A. Hoch and T. Hwa, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 67–72, DOI:10.1073/pnas.0805923106.
- I. Anishchenko, S. Ovchinnikov, H. Kamisetty and D. Baker, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 9122–9127, DOI:10.1073/pnas.1702664114.
- Y. Cheng, N. Grigorieff, P. A. Penczek and T. Walz, Cell, 2015, 161, 438–449, DOI:10.1016/j.cell.2015.03.050.
- A. Doerr, Nat. Methods, 2017, 14, 34, DOI:10.1038/nmeth.4115.
- J. Dubochet and A. McDowall, J. Microsc., 1981, 124, 3–4, DOI:10.1111/j.1365-2818.1981.tb02483.x.
- M. Adrian, J. Dubochet, J. Lepault and A. W. McDowall, Nature, 1984, 308, 32–36, DOI:10.1038/308032a0.
- K. M. Yip, N. Fischer, E. Paknia, A. Chari and H. Stark, bioRxiv, 2020, 1–21, DOI:10.1101/2020.05.21.106740.
- E. Callaway, Nature, 2020, 582, 156–157, DOI:10.1038/d41586-020-01658-1.
- P. Adhikari, N. Li, M. Shin, N. F. Steinmetz, R. Twarock, R. Podgornik and W.-Y. Ching, Phys. Chem. Chem. Phys., 2020, 22, 18272–18283, 10.1039/D0CP03145C.
- D. Wrapp, N. Wang, K. S. Corbett, J. A. Goldsmith, C.-L. Hsieh, O. Abiona, B. S. Graham and J. S. McLellan, Science, 2020, 367, 1260–1263, DOI:10.1126/science.abb2507.
- W. Tai, L. He, X. Zhang, J. Pu, D. Voronin, S. Jiang, Y. Zhou and L. Du, Cell. Mol. Immunol., 2020, 1–8, DOI:10.1038/s41423-020-0400-4.
- F. Wu, S. Zhao, B. Yu, Y.-M. Chen, W. Wang, Z.-G. Song, Y. Hu, Z.-W. Tao, J.-H. Tian and Y.-Y. Pei, Nature, 2020, 579, 265–269, DOI:10.1038/s41586-020-2008-3.
- R. Lu, X. Zhao, J. Li, P. Niu, B. Yang, H. Wu, W. Wang, H. Song, B. Huang and N. Zhu, Lancet, 2020, 395, 565–574, DOI:10.1016/s0140-6736(20)30251-8.
- J. Wang, ChemRxiv, 2020, 1–23, DOI:10.26434/chemrxiv.11875446.v1.
- J. Zou, J. Yin, L. Fang, M. Yang, T. Wang, W. Wu and P. Zhang, ChemRxiv, 2020, 1–13, DOI:10.26434/chemrxiv.11902623.v2.
- M. Smith and J. C. Smith, ChemRxiv, 2020, 1–29, DOI:10.26434/chemrxiv.11871402.v4.
- E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612, DOI:10.1002/jcc.20084.
- VASP - Vienna Ab initio Simulation Package, https://www.vasp.at/ Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865, DOI:10.1103/PhysRevLett.77.3865.
- W.-Y. Ching and P. Rulis, Electronic Structure Methods for Complex Materials: The orthogonalized linear combination of atomic orbitals, Oxford University Press, 2012 Search PubMed.
- L. Poudel, N. F. Steinmetz, R. H. French, V. A. Parsegian, R. Podgornik and W.-Y. Ching, Phys. Chem. Chem. Phys., 2016, 18, 21573–21585, 10.1039/c6cp04357g.
- L. Poudel, R. Twarock, N. F. Steinmetz, R. Podgornik and W.-Y. Ching, J. Phys. Chem. B, 2017, 121, 6321–6330, DOI:10.1021/acs.jpcb.7b02569.
- P. Adhikari, A. M. Wen, R. H. French, V. A. Parsegian, N. F. Steinmetz, R. Podgornik and W.-Y. Ching, Sci. Rep., 2014, 4, 5605, DOI:10.1038/srep05605.
- J. Eifler, R. Podgornik, N. F. Steinmetz, R. H. French, V. A. Parsegian and W. Y. Ching, Int. J. Quantum Chem., 2016, 116, 681–691, DOI:10.1002/qua.25089.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840, DOI:10.1063/1.1740588.
- R. Mulliken, J. Chem. Phys., 1955, 23, 1841–1846, DOI:10.1063/1.1740589.
- K. G. Andersen, A. Rambaut, W. I. Lipkin, E. C. Holmes and R. F. Garry, Nat. Med., 2020, 26, 450–452, DOI:10.1038/s41591-020-0820-9.
- Y. Watanabe, J. D. Allen, D. Wrapp, J. S. McLellan and M. Crispin, Science, 2020, 369(6501), 330–333, DOI:10.1126/science.abb9983.
- A. C. Walls, Y.-J. Park, M. A. Tortorici, A. Wall, A. T. McGuire and D. Veesler, Cell, 2020, 181, 281–292, DOI:10.1016/j.cell.2020.02.058.
- S. Roy, bioRxiv, 2020, 1–30, DOI:10.1101/2020.04.20.052290.
- F. Sesterhenn, C. Yang, J. Bonet, J. T. Cramer, X. Wen, Y. Wang, C.-I. Chiang, L. A. Abriata, I. Kucharska, G. Castoro, S. S. Vollers, M. Galloux, E. Dheilly, S. Rosset, P. Corthésy, S. Georgeon, M. Villard, C.-A. Richard, D. Descamps, T. Delgado, E. Oricchio, M.-A. Rameix-Welti, V. Más, S. Ervin, J.-F. Eléouët, S. Riffault, J. T. Bates, J.-P. Julien, Y. Li, T. Jardetzky, T. Krey and B. E. Correia, Science, 2020, 368, 1–12, DOI:10.1126/science.aay5051.
- Y. Han and P. Král, ACS Nano, 2020, 14, 5143–5147, DOI:10.1021/acsnano.0c02857.
- B. Qiao and M. Olvera de la Cruz, ACS Nano, 2020, 14, 10616–10623, DOI:10.1021/acsnano.0c04798.
- A. A. Glasgow, Y.-M. Huang, D. J. Mandell, M. Thompson, R. Ritterson, A. L. Loshbaugh, J. Pellegrino, C. Krivacic, R. A. Pache, K. A. Barlow, N. Ollikainen, D. Jeon, M. J. S. Kelly, J. S. Fraser and T. Kortemme, Science, 2019, 366, 1024–1028, DOI:10.1126/science.aax8780.
- T. N. Starr, A. J. Greaney, S. K. Hilton, K. H. Crawford, M. J. Navarro, J. E. Bowen, M. A. Tortorici, A. C. Walls, D. Veesler and J. D. Bloom, bioRxiv, 2020, 1–40, DOI:10.1101/2020.06.17.157982.
- L. Zhang, C. B. Jackson, H. Mou, A. Ojha, E. S. Rangarajan, T. Izard, M. Farzan and H. Choe, bioRxiv, 2020, 1–25, DOI:10.1101/2020.06.12.148726.
- B. Korber, W. M. Fischer, S. Gnanakaran, H. Yoon, J. Theiler, W. Abfalterer, N. Hengartner, E. E. Giorgi, T. Bhattacharya, B. Foley, K. M. Hastie, M. D. Parker, D. G. Partridge, C. M. Evans, T. M. Freeman and T. I. d. Silva, Cell, 2020, 182, 812–827, DOI:10.1016/j.cell.2020.06.043.
- P. K. Panda, M. N. Arul, P. Patel, S. K. Verma, W. Luo, H.-G. Rubahn, Y. K. Mishra, M. Suar and R. Ahuja, Sci. Adv., 2020, 6, eabb8097, DOI:10.1126/sciadv.abb8097.
- W. Dai, B. Zhang, X.-M. Jiang, H. Su, J. Li, Y. Zhao, X. Xie, Z. Jin, J. Peng, F. Liu, C. Li, Y. Li, F. Bai, H. Wang, X. Cheng, X. Cen, S. Hu, X. Yang, J. Wang, X. Liu, G. Xiao, H. Jiang, Z. Rao, L.-K. Zhang, Y. Xu, H. Yang and H. Liu, Science, 2020, 368, 1331–1335, DOI:10.1126/science.abb4489.
- R. K. Guy, R. S. DiPaola, F. Romanelli and R. E. Dutch, Science, 2020, 368, 829–830, DOI:10.1126/science.abb9332.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra08222h |
| This journal is © The Royal Society of Chemistry 2020 |