Significant changes in yields of 7-hydroxy-coumarin-3-carboxylic acid produced under FLASH radiotherapy conditions

Abstract

FLASH radiotherapy appears to kill off tumor cells while sparing healthy tissues, by irradiation at ultra high dose rate (>40 Gy s⁻¹). The present study aims to clarify the mechanism of the sparing effect by proton irradiation under the FLASH conditions from a viewpoint of radiation chemistry. To do so, we evaluate radiation chemical yields (G values) of 7-hydroxy-coumarin-3-carboxylic acid (7OH–C3CA), which is produced by water radiolysis using coumarin-3-carboxylic acid (C3CA) solution as a radical scavenger of hydroxyl radicals. We shoot 27.5 MeV protons in the dose rate ranging from 0.05 to 160 Gy s⁻¹. The recombination process of hydroxyl radicals produced is followed by varying the concentration of C3CA from 0.2 to 20 mM, which corresponds to the scavenging time scale from 7.1 to 714 ns. The G value of 7OH–C3CA produced decreases with increasing dose rate on the same scavenging time scale. Additionally, the trend of the relative G value normalized at a scavenging time scale of 100 ns, where radical–radical reaction subsides, is consistent in the examined dose rate range. This finding implies that G values of 7OH–C3CA produced reduce with increasing dose rate due to the oxygen depletion. We experimentally present that the sparing effect for healthy tissues would be seen even with a proton beam under the FLASH conditions due to the depletion of oxygen.

---

Introduction

FLASH radiotherapy targets tumor treatment while minimizing the damage to the surrounding normal tissues by ultra-high dose rate (>40 Gy s⁻¹ = 2400 Gy min⁻¹).^1,2 The FLASH effect has been observed not only in electrons and photons³ but also in protons.^4,5 Now, the implementation of FLASH to C ion therapy is being discussed.⁶ Thanks to this radiation methodology, healthy tissues have an increased tolerance, the so called sparing effect, compared to conventional (CONV) radiation therapy performed at relatively low dose rate (<0.1 Gy s⁻¹ = 6 Gy min⁻¹). While the toxicity due to radiotherapy is suppressed by FLASH irradiation, the effectiveness of the treatment can be maintained.⁷ The FLASH effect has been investigated in many radiobiological studies with cells and mice [e.g., ref. 1 and 5]. Furthermore, some important studies were done using a computer simulation^8,9 and a kinetic model was developed to understand the mechanism of the FLASH effect.¹⁰ However, the mechanism of the FLASH effect has not been experimentally investigated.

It has been observed that the amount of hydrogen peroxide (H₂O₂) generated decreased under the FLASH conditions.¹¹ Consequently, the oxygen dependence of radiochemical process is proposed (i.e., dissolved oxygen in water is consumed to form reactive organic hydroperoxides under the FLASH condition).¹² Adrian et al. reported that FLASH effect highly depends on the intracellular oxygen concentration, indicating the importance of the depletion and rediffusion of oxygen and/or radical–radical interaction for the FLASH effect.¹³ This view was also pointed out over 60 years ago.^14,15 Under ionizing radiations, cells have been affected by the depletion of an oxygen-containing solute by radiation-chemical reactions, when replenishment by diffusion is insufficient.¹⁴ It is understood that this “suffocation” effect was due to cells being oxygenated and then anoxic; the use of the double-pulse method, which two radiation pulses were separated by a defined interval, enabled to observe both oxygen depletion and its replenishment by diffusion.¹⁵ These findings implied that radiation induced radicals could play important roles for the sparing effect under the FLASH condition.¹⁶

In the present study, we experimentally evaluate yields of 7-hydroxy-coumarin-3-carboxylic acid (7OH–C3CA), which is formed by water radiolysis using coumarin-3-carboxylic acid (C3CA) as a scavenger of hydroxyl radicals¹⁷ under the FLASH condition.¹⁸ Changes in radiation chemical yields (G value) of 7OH–C3CA, the number of entities formed or destroyed per unit energy (traditionally 100 eV), with time after the irradiation are followed from 7.4 to 714 ns using C3CA solutions. Additionally, the dose rate dependence of the G value is investigated in a wide range from 0.05 to 160 Gy s⁻¹.

Materials and methods

Radiation-induced hydroxyl radicals efficiently react with benzene ring in C3CA to form fluorescent 7OH–C3CA.¹⁹ C3CA (purity > 98%; Fujifilm/Wako Pure Chemical Industries Ltd.) solutions were prepared using 1/15 M phosphate buffer of nominal pH of 6.8 (Fujifilm/Wako Pure Chemical Industries Ltd.). The concentration of prepared C3CA solutions were 20, 10, 5, 1.4, 0.5 and 0.2 mM. The C3CA solutions were contained in a 200 μL PCR tube. The purity of C3CA was enough to quantitatively evaluate the amount of 7OH–C3CA.

Proton irradiations with an energy of 27.5 MeV were performed in ambient air at the AVF-930 cyclotron equipped in the National Institutes for Quantum and Radiological Science and Technology (QST), the National Institute of Radiological Sciences (NIRS), Chiba, Japan.²⁰ We used only beam field of the center with 3 cm in diameter, where uniform beam intensity (within ±5%) was guaranteed. The beam intensity was verified using EBT3 Gafchromic film. The room temperature during irradiation was 29 °C and the atmospheric pressure was 1000 hPa. Under this condition, the saturation solubility of oxygen in the solution is about 8 mg L⁻¹. The beam intensity was monitored and controlled with a beam monitor (parallel plate ionization chamber) installed in front of the samples. The monitor count is characterized with the absorbed dose at the samples measured with a Markus ionization chamber. The proton beam easily passed through the C3CA solution in the 200 μL PCR tube. The thickness of the PCR tube was 0.5 mm and that of solution was 6.0 mm coaxial with beam trajectory. An average linear energy transfer (LET) in the solution was calculated to be 2.9 eV nm⁻¹ with SRIM code.²¹

The absorbed dose rates of 0.05, 0.8, 7.7, 80 and 160 Gy s⁻¹ were chosen for verifying changes in the amount of 7OH–C3CA produced. The first was the CONV condition and the last two were FLASH conditions. The others were in between. The irradiated absorbed doses were from 30 to 80 Gy. The beam currents were measured to be 0.2 (CONV), 3, 30, 300 (FLASH) and 600 nA (FLASH) measured with a Faraday cup installed in the beam line. The beam pulses were controlled to 561 (CONV), 40, 4, 0.4 (FLASH) and 0.2 s (FLASH) for 30 Gy irradiation with a mechanical shutter.

After the irradiations, C3CA solutions were analyzed using a fluorescence spectrophotometer connected to the HPLC system (RF-20A equipped with Prominence-2200, SHIMADZU, Japan). The 7OH–C3CA formed was separated using Hypersil Fold C18 column (250 × 4.6 mm, i.d. 5 μm) at a flow rate of 0.8 mL min⁻¹ at 25 degree of Celsius. Fluorescence detection was done with excitation at 370 nm by a Xe lamp and measurement of emission at 410 nm. To determine the amount of 7OH–C3CA formed after the irradiation, we used an analytical curve, which was previously obtained.²²

Results

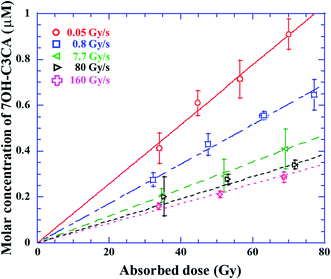
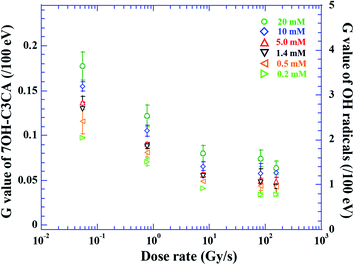
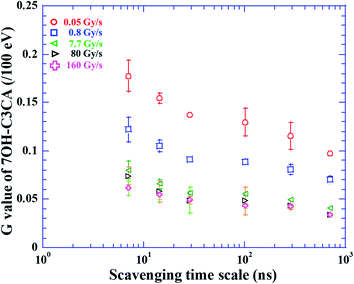
The molar concentration of 7OH–C3CA after the irradiation with dose rates of 0.05 (circles), 0.8 (squares), 7.7 (leftward triangles), 80 (rightward triangles) and 160 (crosses) Gy s⁻¹ in 1.4 mM C3CA solution is shown as a function of the absorbed dose (Fig. 1). As is well known, 4.7% of hydroxyl radicals generated in water are scavenged by C3CA.²³ This constant fraction is independent of ion species.²³ The concentration of 7OH–C3CA increases linearly with increasing the absorbed dose. The fitted lines are obtained using a linear function made by the least-squares method. As mentioned above, the G value is the number of entities formed or destroyed per unit energy, so that the slope of fitted lines in Fig. 1 is equivalent to the G values. Fig. 2 represents G values of 7OH–C3CA produced with molar concentrations of C3CA solutions of 20 (circles), 10 (diamonds), 5.0 (upward triangles), 1.4 (downward triangles), 0.5 (leftward triangles) and 0.2 mM (rightward triangles) as a function of the dose rate (left axis). G values of hydroxyl radicals produced with each molar concentration of C3CA solutions under the CONV condition are also shown (right axis). Overall, G values of 7OH–C3CA (and hydroxyl radicals) produced decrease monotonically with increasing the dose rate. At each dose rate, the G value increases with increasing the concentration of C3CA solution (i.e., time after ion pass). Similarly, the G value of 7OH–C3CA reduces with increasing the scavenging time scale (Fig. 3). Note that the inverse of the scavenging capacity, kS, where k is the rate constant of the reaction and S concentration of the scavenger, indicates the scavenging time scale. This technique enables us to evaluate the time dependent yield of 7OH–C3CA. The k for the reaction between C3CA and hydroxyl radicals was determined as 6.8 × 10⁹ M⁻¹ s⁻¹.²⁴ We clearly find the dose rate dependence of G values of 7OH–C3CA. At each scavenging time, the G value of 7OH–C3CA decreases monotonically with increasing dose rate. Under the FLASH condition (i.e., 80 and 160 Gy s⁻¹), the G values are almost constant at all scavenging time scales, meaning that the G value of 7OH–C3CA seems to be saturated under the FLASH condition.

Fig. 1 Molar concentration of 7OH–C3CA produced in C3CA solution with 1.4 mM as a function of the absorbed dose. The lines are fitting line obtained from the least square fitting. The trends of 7OH–C3CA produced are shown at each dose rate; 0.05 Gy s⁻¹: circles, 0.8 Gy s⁻¹: squares, 7.7 Gy s⁻¹: leftward triangles, 80 Gy s⁻¹: rightward triangles, 160 Gy s⁻¹: crosses.

Fig. 2 G value of 7OH–C3CA (left axis) and that of hydroxyl radicals (right axis) as a function of dose rates. The trends of G values are represented at each molar concentration of C3CA solution; 20 mM: circles, 10 mM: diamonds, 5.0 mM: upward triangles, 1.4 mM: downward triangles, 0.5 mM: leftward triangles, 0.2 mM: rightward triangles.

Fig. 3 G value of 7OH–C3CA produced as a function of the scavenging time scale. The trends of G values produced are shown at each dose rate; 0.05 Gy s⁻¹: circles, 0.8 Gy s⁻¹: squares, 7.7 Gy s⁻¹: leftward triangles, 80 Gy s⁻¹: rightward triangles, 160 Gy s⁻¹: crosses.

Discussions

The G values of hydroxyl radicals produced are 3.6 ± 0.3 and 2.6 ± 0.3/100 eV at scavenging time scales of 7.4 and 100 ns, respectively, under the CONV condition (right axis of Fig. 2). These G values are consistent with experimental results reported by Brabcová et al. of 3.5 ± 0.3 at 7 ns. This experiment was performed under the condition close to the CONV dose rate.²⁵ Additionally, the present G value under the CONV condition is in agreement with previous simulations of 2.6 and 2.5 at 100 ns.^23,25,26 In fact, the production of 7OH–C3CA is strongly affected by dissolved oxygen in the C3CA solution as discussed below, so that the reduction of the G value of 7OH–C3CA with increasing the dose rate is understandable (Fig. 3). However, yields of OH radicals have never been influenced by dose rate. Therefore, the G value of hydroxyl radicals produced (right axis of Fig. 2) is for validation of the present result under the CONV condition.

The G values of 7OH–C3CA decrease monotonically with increasing the dose rate (Fig. 2 and 3). As is well known, hydroxyl radicals efficiently react with proteins and DNA molecules and produce damages to them leading cell killing (indirect action).¹⁸ Therefore, simply speaking, the contribution of indirect action becomes low with increasing the dose rate, especially under the FLASH condition, because G values of 7OH–C3CA produced reduces with increasing the dose rate (Fig. 2). This view agrees with the sparing effect is seen under the FLASH condition.¹³

From the reduction behavior of G values of 7OH–C3CA with dose rate, there would be two plausible interpretations to understand the mechanism of the FLASH effect;

(1) The first is that the radical–radical reaction is likely to occur under the FLASH condition than that under the CONV condition. A significant contribution of radical–radical reaction was proposed by a physicochemical model of reaction kinetics.¹⁰ In the case of proton tracks, separate clusters of reactive species, which would be spherical in shape, so-called “spur”, could be continuous. Consequently, proton tracks can be considered as cylinders. In accordance with the diffusion coefficient and a Monte Carlo simulation, a maximum radius of the proton track is estimated as 200 nm.^27,28 Based on the track overlapping model, in which tracks are treated as cylinder,^29–31 more than 1.5 Gy of protons must be irradiated in 1 μs for the track overlapping to occur. In the case of the dose rate of 160 Gy s⁻¹, the absorbed dose is 1 × 10⁻⁴ Gy in 1 μs. Therefore, it is unlikely that the radical–radical reaction is facilitated under the FLASH condition.

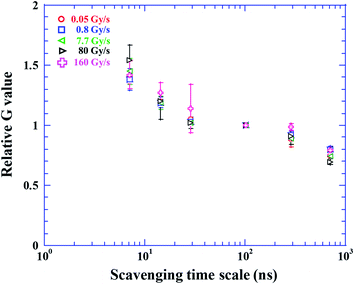
Additionally, apparent LET might become higher under the FLASH condition than the CONV condition by collective energy loss.³² Indeed, the beam bunch under the CONV condition is about 3000 times shorter than that under the FLASH condition. Fig. 4 shows the reduction of the relative G value normalized at scavenging time scale of 100 ns, where radical–radical reaction subsides. There is consistency in each data point within error bar. Generally, the relative G value decreases more rapidly with increasing LET in earlier scavenging scale (<100 ns),²³ for instance, the relative G value of Fe ion with a LET of 205 eV nm⁻¹ is twice higher than that of gamma rays with a LET of 0.3 eV nm⁻¹ at scavenging time scale of 6.4 ns.²³ This is explained by the efficient radical–radical reactions in the track core of high LET particles. In this study, the relative G value and its reduction trend are universal within error bar even at the dose rate of 160 Gy s⁻¹. The apparent LET is not modified under the FLASH condition. Therefore, it is unlikely that G value decreases with increasing the dose rate due to the radical–radical reaction.

Fig. 4 Relative G value of 7OH–C3CA produced as a function of the scavenging time scale. The G values at each scavenging time scale are normalized by that at 100 ns. The trends of relative G values are described at each dose rate; 0.05 Gy s⁻¹: circles, 0.8 Gy s⁻¹: squares, 7.7 Gy s⁻¹: leftward triangles, 80 Gy s⁻¹: rightward triangles, 160 Gy s⁻¹: crosses.

(2) The second is that a decrease of oxygen concentration in the C3CA solution. The mechanism of 7OH–C3CA was investigated by pulse radiolysis with a 35 MeV electron beam.³³ There are two main different pathways of stabilization (disproportionation or elimination) from the intermediate OH-adduct radicals to 7OH–C3CA existed, depending on the presence of oxygen (Fig. 5). We note that the kinetic constant of the pathway of disproportionation is almost equivalent to that of elimination.³³ In the case of the hypoxia condition, the pathway with oxygen is occluded. Therefore, the disproportionation is a key phenomenon for the production of 7OH–C3CA under the hypoxia condition. Two moles of intermediate OH-adduct radicals are necessary for disproportionation to form one mole of 7OH–C3CA. In comparison to this, under the aerated condition, the peroxidation by the presence of oxygen followed by elimination of HO₂˙ is a dominant reaction for producing 7OH–C3CA. Under the FLASH condition, oxygen could be rapidly consumed, leading the lower G values of 7OH–C3CA. Furthermore, under the FLASH condition, oxygen is rapidly consumed by secondary reactions, for instance,

H˙ + O₂ → HO₂˙, (1)

e_aq⁻ + O₂ → O₂˙⁻, (2)

where H˙ and e_aq⁻ are hydrogen radicals and hydrated electrons, respectively, produced by water radiolysis. Thus, the C3CA solution is momentarily in as pseudo-hypoxic state. Since accumulation of the intermediate radicals changes the balance between both second order and pseudo first order reactions, intermediate species including the OH-adduct, amongst others involved in elimination, is highly sensitive to high dose rate. This view regarding radiolytic oxygen depletion is supported from a computational model.³⁴ The FLASH effect could disappear in the region where radiation pulse duration is less than 1 s. It suggests that the oxygen flow plays an important role in the FLASH effect. In addition, the sparing effect observed under the FLASH condition.¹³ The sparing effect was seen when the relative partial oxygen pressure was 4.4, 2.7 and 1.6%, namely under the hypoxia condition. In comparison to this, the sparing effect was not confirmed at the relative partial oxygen pressure of 8.8 and 20%. However, the therapeutic effectiveness for cancer tissue is maintained at any oxygen pressure because the damage to DNA molecules leading to cell killing is less dependent on the oxygen concentration around the Bragg peak, at which high LET relative to the other region can be expected. Around the Bragg peak energy, the contribution of direct action is dominant for cell killing. Also, G values of hydroxyl radicals around Bragg peak energies are smaller than those at high energy region. Thus, our interpretation, which significantly lower G value under the FLASH condition is due to the reduction of the relative partial oxygen pressure, is reasonable and is consistent with the previous observation from experiments using X-rays.¹¹ In other words, the sparing effect could occur due to the suppression of indirect action under the low oxygen concentration. To verify our interpretation, we should take into account the difference in the radiation quality. In the case of X-rays, spurs are sparsely distributed. As a result, lowering the likelihood that radicals from different spurs react together before its diffusion. The reactions between different spurs are not expected in low LET region below 3 eV nm⁻¹.³⁵ In the present study, the average LET of the proton beam is 2.9 eV nm⁻¹, which is slightly lower than 3 eV nm⁻¹. Therefore, the comparison of our results to previously obtained one by X-rays would be valid.

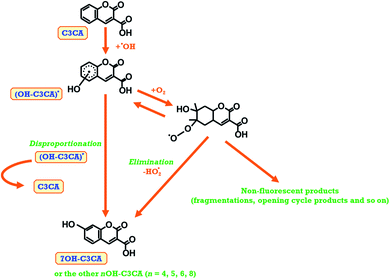Fig. 5 A schematic view of the formation of 7OH–C3CA due to the reaction of C3CA with hydroxyl radicals under oxygen sufficient and oxygen depletion conditions.

In the present study, we have evaluated the G values of 7OH–C3CA produced by proton beams under the CONV and FLASH conditions using C3CA solution. As is well known, clustered DNA damage leading to cell killing is more easily induced by direct action than indirect action. Of course, damage to DNA by indirect action mainly due to hydroxyl radicals could occur. However, the types of damage by indirect action (e.g., single strand break or base mismatch) are quickly reparable except for the rare case damage by clustered hydroxyl radicals occurring near the DNA (i.e., in the hydration shell with a distance ∼ 1 nm). In such cases, it would be reasonable to think that the DNA damage induced by “clustered hydroxyl radicals” is a part of direct action because its time scale is <1 ns. Thus, cell killing results from multiple hits from a single densely ionizing track from any combination of radiolysis products (e.g., hydroxyl radicals and e_aq⁻) and ionized or excited DNA molecules (e.g., DNA˙⁺ and DNA˙⁻), namely radiation-induced radicals contribute not only for indirect action but also for direct action. The minimum scavenging time scale in the present study is 7.4 ns. To elucidate the FLASH effect in more detail, roles played by water radiolysis products in earlier scavenging time scale (<7.4 ns) should be evaluated using the pulse radiolysis method.^36,37 Additionally, yields of other water radiolysis species will be investigated in near future.^38,39 The FLASH effect is multi-factorial and proceeds from a delicate balance between dose, oxygen availability, reactions induced by radicals and DNA repair and the target cells intrinsic tolerance to peroxyl radicals.¹⁰ To have a holistic view regarding FLASH effect, it is necessary to quantitatively evaluate yields not only of hydroxyl radicals but also of other water radiolysis products and to consider the roles played by peroxyl radicals in the further step. Moreover, additional experiments with shorter pulse proton beams will be crucial for investigating the contribution of radical–radical reaction. A view from radiation chemistry could largely contribute to develop of FLASH radiotherapy not only using proton beam but also using heavy ion beams.

Conclusions

We evaluated G values of 7OH–C3CA produced using C3CA solution, while varying the dose rate of proton beam from 0.05 to 160 Gy s⁻¹. The G value of 7OH–C3CA produced decreased monotonically with increasing the dose rate. This finding implied that a rapid consumption of oxygen by high dose irradiation was the main reason for the reduction of G values of hydroxyl radicals produced. This view was in agreement with that the sparing effect was seen under the hypoxia condition. In the present study, we indicated that the oxygen concentration was important for minimizing the toxicity of radiotherapy by ultra-high dose irradiation from the radiochemical approach.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors express our thanks to the NIRS-Cyclotron crew for providing excellent beams.

References

1. I. Lohse, S. Lang, J. Hrbacek, S. Scheidegger, S. Bodis, N. S. Macedo, J. Feng, U. M. Lütolf and K. Zaugg, Radiother. Oncol., 2011, 101, 226–232.
2. V. Favaudon, L. Caplier, V. Mounceau, F. Pouzoulet, M. Sayarath and C. Fouillade, Sci. Transl. Med., 2014, 16, 245ra93.
3. M. Durante, E. Brauer-Krisch and M. Hill, Br. J. Radiol., 2018, 91, 20170628.
4. M. Buonanno, V. Grilj and D. J. Brenner, Radiother. Oncol., 2019, 139, 51–55.
5. A. Patriarca, C. Fouillade, M. Auger, F. Martin, F. Pouzoulet, C. Nauraye, S. Heinrich, V. Facaudon, S. Meyroneinc, R. Dendale, A. Mazal, P. Poortmans, P. Verrelle and L. De Marzi, Int. J. Radiat. Oncol., Biol., Phys., 2018, 102, 619–622.
6. N. W. Colangelo and E. Azzam, Radiat. Res., 2020, 193, 1–4.
7. P. Montay-Gruel, A. Bouchet, M. Jaccard, D. Patin, R. Serduc, W. Aim, K. Petersson, B. Petit, C. Bailat, J. Bourhis, E. Brauer-Krisch and M.-C. Vozenin, Radiother. Oncol., 2018, 129, 582–588.
8. J. Ramon-Méndez, N. Domínguez-Kondo, J. Schuemann, A. McNamara, E. Moreno-Barbosa and B. Faddegon, Radiat. Res., 2020, 194.
9. D. Boscolo, M. Krämer, M. C. Fuss, M. Durante and E. Scifoni, Int. J. Mol. Sci., 2020, 21(2), 424.
10. R. Labarbe, L. Hotoiu, J. Barbier and V. Favaudon, Radiother. Oncol., 2020 DOI:10.1016/j.radonc.2020.06.001.
11. M. O'Leary, D. Boscolo, N. Breslin, J. M. C. Brown, I. P. Dolbnya, C. Emerson, C. Figueira, O. J. L. Fox, D. R. Grimes, V. Ivosev, A. K. Kleppe, A. McCulloch, I. Pape, C. Polin, N. Wardlow and F. J. Currell, Sci. Rep., 2018, 8, 4735.
12. D. R. Spitz, G. R. Buettner, M. S. Petronek, J. J. St-Aubin, R. T. Flynn, T. J. Waldron and C. L. Limoli, Radiother. Oncol., 2019, 139, 23–27.
13. G. Adrian, E. Konradsson, M. Lempart, S. Back, C. Ceberg and K. Petersson, Br. J. Radiol., 2020, 93, 20190702.
14. D. L. Dewey and J. W. Boag, Nature, 1959, 183, 1450–1451.
15. C. C. Ling, H. B. Michaels, E. R. Epp and E. C. Peterson, Radiat. Res., 1978, 76, 522–532.
16. P. Wardman, Radiat. Res., 2020, 194 DOI:10.1667/RADE-19-00016.
17. H. B. Michaels and J. W. Hunt, Radiat. Res., 1978, 74, 23–34.
18. N. Ludwig, T. Kusumoto, C. Galindo, P. Peaupardin, S. Pin, J.-P. Renault, D. Muller, T. Yamauchi, S. Kodaira, R. Barillon and Q. Raffy, Radiat. Meas., 2018, 116, 55–59.
19. T. Karin and O. Stefan, FEMS Microbiol. Ecol., 2002, 40, 13–20.
20. M. Kanazawa, S. Hojo, A. Sugiura, T. Honma, K. Tashiro, T. Okada, T. Kamiya, Y. Takahashi, H. Suzuki, Y. Uchihori and H. Kitamura, in: Proceedings of the 19^th International Conference on Cyclotrons and Their Applications, 2010.
21. J. F. Ziegler, Nucl. Instrum. Meth. B, 2004, 219–220, 1027–1036.
22. T. Kusumoto, R. Ogawara R, N. Ludwig, Q. Raffy and S. Kodaira, Radiat. Phys. Chem., 2020, 174, 108978.
23. T. Maeyama, S. Yamashita, G. Baldacchino, M. Taguchi, A. Kimura, T. Murakami and Y. Katsumura, Radiat. Phys. Chem., 2011, 80, 535–539.
24. G. Baldacchino, T. Maeyama, S. Yamashita, M. Taguchi, A. Kimura, Y. Katsumura and T. Murakami, Chem. Phys. Lett., 2009, 468, 275–279.
25. K. P. Brabcová, V. Štěpán, M. Karamitros, M. Karabín, P. Dostálek, S. Incerti, M. Davídková and L. Sihver, Radiat. Prot. Dosim., 2015, 166, 44–48.
26. J. Meesungnoen and J.-P. Jay-Gerin, J. Phys. Chem. A, 2005, 109, 6406–6419.
27. Y. Muroya, I. Plante, E. I. Azzam, J. Meesungnoen, Y. Katsumura and J.-P. Jay-Gerin, Radiat. Res., 2006, 165, 485–491.
28. Y. Frongillo, T. Goulet, M.-J. Fraser, V. Cobut, J. P. Patau and J.-P. Jay-Gerin, Radiat. Phys. Chem., 1998, 51, 245–254.
29. T. Yamauchi, Radiat. Meas., 2003, 36, 73–81.
30. S. Seki, S. Tsukuda, K. Maeda, Y. Matsui, A. Saeki and S. Tagawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 144203.
31. T. Kusumoto, Y. Mori, M. Kanasaki, K. Oda, S. Kodaira, R. Barillon and T. Yamauchi, Radiat. Phys. Chem., 2019, 157, 60–64.
32. A. Ogata, T. Kondoh, K. Norizawa, J. Yang, Y. Yoshida, S. Kashiwagi and T. Kaneko, Nucl. Instrum. Meth. A, 2011, 637, S95–S98.
33. S. Yamashita, G. Baldacchino, T. Maeyama, M. Taguchi, Y. Muroya, M. Lin, A. Kimura, T. Murakami and Y. Katsumura, Free Radical Res., 2012, 46(7), 861–871.
34. G. Pratx and D. S. Kapp, Phys. Med. Biol., 2020, 65, 109501.
35. J. A. LaVerne, Radiat. Res., 2000, 153, 487–496.
36. N. Chitose, Y. Katsumura, Y. Zuo, Z. Domae, K. Ishigure and T. Murakami, J. Chem. Soc., Faraday Trans., 1997, 93(22), 3939–3944.
37. F. Wang, U. Schmidhammer, J.-P. Larbre, Z. Zong, J.-L. Marignier and M. Mostafavi, Phys. Chem. Chem. Phys., 2018, 20, 15671.
38. S. Yamashita, Y. Katsumura, M. Lin, Y. Muroya, T. Maeyama and T. Murakami, Radiat. Phys. Chem., 2008, 77, 1224–1229.
39. J. A. Ghormley and A. C. Stewart, J. Am. Chem. Soc., 1956, 78(13), 2934–2939.

---