DOI:
10.1039/D0RA07838G
(Paper)
RSC Adv., 2020,
10, 42733-42743
In silico approach: biological prediction of nordentatin derivatives as anticancer agent inhibitors in the cAMP pathway†
Received
13th September 2020
, Accepted 6th November 2020
First published on 25th November 2020
Abstract
A combination of computational techniques has been carried out to predict the binding of nordentatin derivatives based on pyranocoumarin semi-synthesis with the target protein from the expression of the PDE4B gene. The inhibition of the cAMP pathway is the main target of anti-cancer drugs, which is responsible for uncontrolled cell division in cancer. Modeling was done using a combination of semi-empirical methods and the density functional theory (PM3-DFT/6-31G*/B3LYP) to obtain the optimal structure of a small ligand that could be modeled. Studies on the interaction of the ligands and amino acid residues on protein targets were carried out using a combination of molecular docking and molecular dynamic simulation. Molecular docking based on functional grid scores showed a very good native ligand pose with an RMSD of 0.93 Å in determining the initial coordinates of the ligand–receptor interactions. Furthermore, the amino acid residues responsible for interaction through H-bonds were Tyr103, His104, His177, Met217, and Gln313. The binding free energy (kcal mol−1) results of the candidates were PS-1 (−36.84 ± 0.31), PS-2 (−35.34 ± 0.28), PS-3 (−26.65 ± 0.30), PS-5 (−42.66 ± 0.26), PS-7 (−35.33 ± 0.23), and PS-9 (−32.57 ± 0.20), which are smaller than that of the native ligand Z72 (−24.20 ± 0.19), and thus these have good potential as drugs that can inhibit the cAMP pathway. These results provide theoretical information for the efficient inhibition of the cAMP pathway in the future.
Introduction
Phosphodiesterase-4 (PDE4) plays an important role in the cyclic adenosine-3,5-monophosphate (cAMP) pathway that involves the G Protein-Coupled Receptors (GPCRs) located on the surface of the cell membrane, which plays an important role in the signal transduction process in cells.1 Signal transduction plays an important role in physiological processes that are related to resistance and cell growth in normal cells.2 The signal received from ligand-bound GPCRs is forwarded by the G protein, which consists of 3 subunits, namely protein α, which is bound to guanosine diphosphate (GDP), protein β, and protein γ. The transmitted signal changes the GDP bound to the α-protein to guanosine triphosphate (GTP), activating the α-protein. The activated α protein binds to the enzyme adenylyl cyclase, which plays a role in the phosphorylation process of changing adenosine triphosphate (ATP) into cAMP, a second messenger that activates a protein kinase. The activation of protein kinase A (PKA) is the main step in the cAMP pathway in the process of activating DNA transcription.3 Understanding the cAMP pathway is very important for understanding uncontrolled cell division in cancer cells.4 Some cases of cancers that are affected by the cAMP pathway are human colorectal cancer5,6 and diffuse large B-cell lymphoma.7 The development and study of drugs that inhibit the cAMP pathway are desirable to suppress the growth and survival of cancer cells.
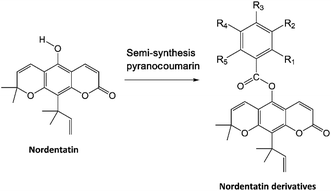
Coumarin derivatives have been reported in several studies with a focus on their biological activity as anticancer agents,8,9 specifically regarding their inhibition of the cAMP pathway in cancer.10 The isolation and synthesis of coumarin derivatives have been the centre of attention in recent decades toward their development as anticancer agents.8–10 Nordentatin is a type of natural product obtained from coumarin derivatives that can be isolated from the Clausena excavata Burm. plant.11 The semi-synthesis of pyranocoumarin and the structural modification of coumarin derivatives by substituting a hydroxy group with an aromatic ring containing a halogen element have shown very promising results in increasing its biological activity.12
The in silico approach is a complex and systematic approach to designing drugs based on predictions of the nature, structure, and interaction of drugs and target molecules efficiently and effectively through calculations without sacrificing accuracy.13 Drug modeling based on quantum mechanical approaches using a combination of semi-empirical methods and the density functional theory (DFT) is based on the efficiency to accurately predict the physicochemical properties of the structure of a drug molecule.14–17 Several computational chemistry techniques developed for drug design, such as Molecular Docking (MD) and Molecular Dynamic Simulation (MDS), using in silico approaches have shown very good accuracy in studying interactions between drugs and protein targets.18,19 Molecular docking has shown good performance in studying the initial coordinates of drug interactions (ligands) with protein targets (receptor).20 Additionally, molecular dynamic simulation can predict the free energy of ligand–receptor binding by using the Molecular Mechanics-Generalized Born Surface Area (MM-GBSA) method that has been widely used.21,22 In this article, we present the application of several alternative choices for the combination of computational chemistry techniques and some important parameters systematically used in the design of nordentatin derivatives to inhibit the cAMP pathway and function as anticancer agents.
Methodology
Computational resource and data set
The hardware and operating systems used were Windows (Intel Dual-Core 2.48 GHz and 2 GB Memory RAM) and Linux (Intel Core i7-8700, 32 GB RAM, graphical processing unit (GPU) NVidia GTX 1080 Ti 11 GB, SSD M.2 250 GB, SSD SATA 500 GB). The Windows-based software used for preparing the ligands and receptors was Chimera version 1.13 besides other supporting applications including, Chem-Office 2016, Putty, WinSCP, Notepad++, and Modeller 9.21. Linux-based software Gaussian 09W, Dock6, and Amber18 were used to perform a series of molecular docking and molecular dynamic simulation processes. Meanwhile, the visualization of the calculations and simulation results was done using the Discovery Studio software.
The study materials used in this study were the 10 candidate nordentatin derivatives based on the semi-synthesis of pyranocoumarin in previous research.23 The selection of compounds modeled in this study included new-derivatives of nordentatin that have been successfully synthesized from the main structure of nordentatin and characterized. Their synthesis was carried out based on the semi-synthesis of pyranocoumarin with the addition of several halogen groups to the structure. The protein target was selected from the protein data bank using the PDB code: 3LY2 (resolution: 2.6 Å; https://www.rcsb.org/structure/3LY2), which is a protein expressed by the PDE4B gene that plays a role in the cAMP pathway.24 Additionally, one of the native ligands of protein 3LY2 is a coumarin-derived compound (code Z72).
Modeling based quantum mechanical method
The candidate total energy was calculated using the semi-empirical quantum mechanical method Parametric Method 3 (PM3) to find the optimal molecular geometry of the candidate. Then, it was optimized again using the DFT method with the 6-31G* base set, and the functional hybrid Becke 3-parameter Lee–Yang–Parr (B3LYP) was used to obtain a more stable molecular geometry with the least energy.25 The nordentatin derivatives were optimized for their molecular geometry based on the Self Consistent Field (SCF) procedure with a convergence limit of 0.01.26,27
The stages of molecular geometry optimization were based on gradient-based energy minimization involving the evaluation of the gradient function of the error parameters.28 The parameter changes in each property reference were predicted and calculated using the Taylor expansion centred on the initial parameter value, as shown in eqn (1), where x is the parameter change (n), and q is the property reference.
| |
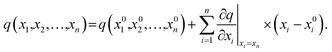 | (1) |
The approach used to solve several calculation parameters was uses the Density Functional Theory which states the electrons density as energy. In this, the ground state energy is expressed as a function of the probable electron density (ρ) and can be determined using the Khon–Sham (KS) equation, which is the basis for DFT calculations.29
| | |
E[ρ] = Vne[ρ] + Ts[ρ] + J[ρ] + Exc[ρ]
| (2) |
where the KS theory that states the ground state energy in a system is a functional application, as shown in
eqn (2).
| | |
Vne[ρ] = ∫ρ(r1)v(r1)dr1
| (3) |
The values of ρ(r1) and v(r1) are stated as
| |
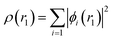 | (4) |
| |
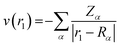 | (5) |
The components of the ground state energy include several energies, such as the nucleus potential energy eqn (2), the kinetic energy of the KS noninteracting reference system eqn (6), the classical electron–electron repulsion energy eqn (7), and the exchange–correlation functional eqn (8).30
| |
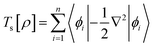 | (6) |
| |
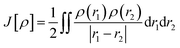 | (7) |
| |
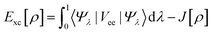 | (8) |
Finally, the ground state energy (E0) was determined by the KS formula shown in eqn (9).
| |
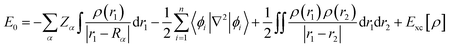 | (9) |
The heat of formation (ΔHf) for some of the modelled compounds was determined in two stages using DFT.31 The first stage aims to minimize the error function (S), as shown in eqn (10). Meanwhile, the second step is the contribution of the compound containing element X to the total energy in the calculation using the first-stage equation. Thus, in the second stage, the error function is expressed as a selection of the ΔHf reference with the predicted value using the DFT calculation, as given in eqn (11), where Ci is a constant for every atom i, Cx is an unknown constant multiplier, and n represents the sum of each atomic type i and x.
| |
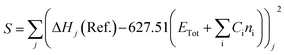 | (10) |
| |
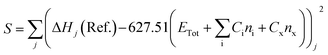 | (11) |
Cluster sphere selection and the grid score functional
Sphere selection with a 10.0 Å radius was made to select specific regions or clusters that are occupied by ligands on the active site of the receptor. Meanwhile, other parameters that were used as a reference to successfully obtain the coordinates of the ligand–receptor interactions were box size and spacing grid box. The grid score-based calculation used in this study used a spacing of 0.3 with box sizes required for the calculation. Additionally, the grid score-based calculations enhance the efficiency and speed of finding the coordinates of the active site, where ligand–receptor interactions take place.32| |
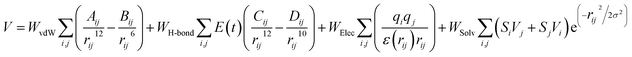 | (12) |
The scoring function in molecular docking aims to describe the pose of the interaction between the ligand and receptor. The interaction has been simplified in eqn (12) by using different functions and approaches. Some simplified functions include force field, empirical, and knowledge-based scoring functions.33 The value of W is the weighted factor for calibrating the empirical free energy, and V is the pair-wise energy. The scoring function formulate is the total number of parameters evaluated such as van der Waals, hydrogen bonds, electrostatic, and desolvation.
Molecular docking and molecular dynamic simulation
The combination of molecular docking and molecular dynamic simulation can accurately predict the coordinates and energy components of the ligand–receptor interactions considered for drug design.34 The conformation-type ligand–receptor interactions use flexibility to find the best coordinates of the native ligands that are expressed as ligand poses. The pose of molecular docking is declared good if it meets the criterion of Root Mean Square Deviation (RMSD) ≤ 1.5 Å at the validation stage.35 The force field used in this study was ff14SB with the ligand charge calculated using the Austin Model 1-Bond Charge Correction (AM1-BCC) method.
The coordinate based on the grid-score functional obtained from molecular docking was used as the initial coordinate of the interaction during Molecular Dynamic simulation using the General AMBER Force Field (GAFF). The force fields were very influential in the simulation results as the ff14SB force field was very well used in AMBER during the simulation process.36 Several parameters were calculated, including the energy minimization stage, the heating stage, the density stage, the equilibrium stage, and the production stage. The topology created through the leap played an important role in the success of the molecular dynamic simulation process. The production stage used in this study was 120 ns to obtain the trajectories needed for analysing several properties in the molecular dynamic simulation process.
The molecular dynamics simulation calculation using the Taylor series algebraic equations aims to approach simpler differential terms. Thus, it can be used to describe the motion of molecules through the computer simulation calculation shown in eqn (13). The movement of molecules in the system can be followed by the time variable (t). The determination of the force field and total system energy of the molecular dynamics simulation algorithm was implemented by dividing the volume of the simulation box into cube cells of its size (rcut). These parameters were determined using a linked-cell algorithm (LCA) that has been simplified in eqn (14).
| |
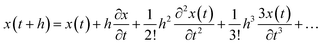 | (13) |
| |
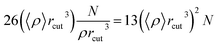 | (14) |
Binding free energy calculation
The binding free energy (ΔG) was determined based on the trajectories generated during the simulation and was then used to calculate the binding energy of each ligand with a receptor using the MM-GBSA method, as shown in eqn (15), and its terms are detailed in eqn (16) and (17).37 The gXji notation is defined as the interaction between the i and j loads agreed to be determined by different complex gji functions (LR), receptor (R), and ligand (L).| | |
ΔGGB = GGB(LR) − GGB(R) − GGB(L)
| (15) |
| |
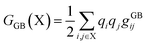 | (16) |
| |
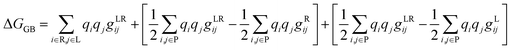 | (17) |
The calculation process using the MM-GBSA method provided some information about the complete energy components in the gas state (eqn (18)) and the solvation state (eqn (19)). The candidates that gave good results were evaluated by comparing them with the binding free energy of the native ligand as a benchmark for the criterion of ΔG candidate ligand < ΔG native ligand.
| | |
ΔGGas = EElec + EvdW
| (18) |
| | |
ΔGSolv = GGB + GSASA
| (19) |
Drug-likeness, pharmacokinetics, and toxicity properties
The criteria of the candidates as a drug, such as drug-likeness and bioavailability, were predicted using the SwissADME web service (http://www.swissadme.ch/index.php).38 Furthermore, the drug-likeness was predicted based on Lipinski's rule and Veber's rule using the 2D structures (SMILES format) of the modelled compounds. Studies on the absorption, distribution, metabolism, excretion, and toxicity (ADMET) of the drug candidates were conducted to assess their biological activities in the body. Prediction of their pharmacokinetic properties was carried out using the pkCSM web service (http://biosig.unimelb.edu.au/pkcsm/prediction), which can help describe the ADMET properties of the candidates in detail.39
Results and discussion
Geometry optimization of nordentatin derivatives
The modeling of molecules in this research was performed based on semi-pyranocoumarin synthesis on the structure of nordentatin as the main compound, resulting in 9 nordentatin derivatives with variations in the number and position of different substitution groups (Table 1). The differences in the structure of the nordentatin derivatives are expected to provide better interaction with the receptor than that with the main compound. Several studies have shown that the addition of a group of halogens to natural compounds provides better anticancer activity.40,41
Table 1 The structure of nordentatin derivatives
|
| Candidates |
R1 |
R2 |
R3 |
R4 |
R5 |
| PS-1 |
–H |
–CF3 |
–H |
–CF3 |
–H |
| PS-2 |
–H |
–CF3 |
–H |
–H |
–H |
| PS-3 |
–H |
–Br |
–H |
–H |
–H |
| PS-4 |
–H |
–Cl |
–F |
–H |
–H |
| PS-5 |
–Cl |
–H |
–NO2 |
–H |
–H |
| PS-6 |
–H |
–H |
–Br |
–H |
–H |
| PS-7 |
–H |
–C4H9 |
–H |
–H |
–H |
| PS-8 |
–Cl |
–H |
–H |
–H |
–H |
| PS-9 |
–Cl |
–H |
–Cl |
–H |
–Cl |
Molecular geometry optimization was performed using the Gaussian 09 W package through a combination of PM3-DFT/6-31G*/B3LYP as initial preparation of the nordentatin derivatives used in this study.42 The molecular geometry of the structures with low total energy is expected to give the best conformation of the molecules.43 The variables measured in this stage include total energy (a.u), charge distribution (eV), dipole moment (D), and molecular length (Å), which are primary data on their physicochemical properties (Table 2). The lowest total energy value indicates the molecule with the optimum structural conformation. Based on the results of geometry optimization using a combination of quantum mechanics methods, it was found that all candidates showed good results with energy values < 0 a.u. Some other important variables, such as charge distribution and dipole moment, showed that each candidate met the dipole moment criterion > 0. The polarity difference between the candidates was due to the effect of the number and position of the functional groups. Thus, it impacts the partial charge distribution of each atom. This could be seen in PS-8 and PS-9 candidates, both of which have –Cl atom substitutions. However, these candidates had different dipole moments because the PS-8 candidate only has one –Cl atom because of which the partial negative charge tends to be attracted to itself, which causes the dipole moment to increase. Meanwhile, the PS-9 candidate has 3 –Cl atoms at 3 different positions R1, R3, and R5, which cause a balanced partial negative charge distribution on each atom (–Cl). As a result, the dipole moment of PS-9 was lower than that of PS-8. Meanwhile, molecular length plays an important role in the initial relationship, which has a major effect on the ability of small molecules to penetrate the cell membrane.44
Table 2 Geometry optimization of the nordentatin derivatives using the PM3 semi-empirical and density functional theory with the basis set 6-31G*/B3LYP
| Candidates |
ETotal (a.u) |
Charge dis. (eV) |
μ (D) |
Molecular length (Å) |
| P |
−1036.92 |
−0.64 → 0.59 |
7.40 |
10.58 |
| PS-1 |
−2055.39 |
−0.57 → 0.80 |
5.77 |
15.15 |
| PS-2 |
−1718.36 |
−0.57 → 0.79 |
7.16 |
15.14 |
| PS-3 |
−3952.42 |
−0.57 → 0.60 |
7.24 |
14.39 |
| PS-4 |
−1940.14 |
−0.57 → 0.60 |
6.65 |
14.26 |
| PS-5 |
−2045.40 |
−0.54 → 0.60 |
5.51 |
15.13 |
| PS-6 |
−3952.42 |
−0.57 → 0.60 |
6.45 |
14.87 |
| PS-7 |
−1538.58 |
−0.57 → 0.59 |
7.65 |
18.02 |
| PS-8 |
−1840.90 |
−0.54 → 0.60 |
8.07 |
14.10 |
| PS-9 |
−2760.08 |
−0.55 → 0.60 |
7.16 |
14.49 |
Active site determination
The molecular validation stage of docking (re-docking) was carried out to determine active-site binding through interactions between the native ligand and the receptor on the target protein.45,46 The validation result showed that the native ligand had a good pose with the RMSD value of 0.93 Å, which meets the criterion (Table 3). A smaller RMSD that is closer to ∼0 Å represents increasingly accurate coordinates. The grid score was also included as one of the evaluation criteria for molecular docking assessment based on the grid score functional. Meanwhile, the hydrogen bonds (H-bond) measured at the validation stage showed that the hydrogen bonds in the strong category had a distance of 2.11 Å and those in the medium category had a distance of 2.83 Å. The results of the interaction between the native ligand and the amino acid residues at the receptor active site showed a radius of 6.0 Å and included several types of bonds (Fig. 1).
Table 3 Molecular docking validation of the native ligand
| Native ligand |
RMSD (Å) |
H-bond distance (Å) |
Grid score (kcal mol−1) |
| Z72 |
0.93 |
2.11 (Gln313:HE22-Z72:O10) |
−63.90 |
| 2.83 (Gln313:HE22-Z72:O3) |
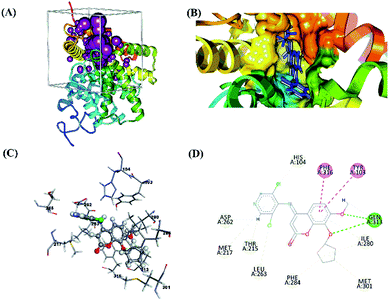 |
| | Fig. 1 Visualization of molecular docking validation: (A) cluster sphere selected; (B) the active site where the native ligand binds; (C) interaction between the native ligand and amino acid residues; (D) the types and 2D-diagram of the interactions. | |
Molecular docking validation showed that the native ligands interacted with the Gln313 residue as a hydrogen bond acceptor precisely at the O3 and O10 atoms in the coumarin structure (Z72). These results identified the Gln313 residue as one of the important residues for studying ligand–receptor interactions. The selection of protein targets was based on the similarity of their structure to that of the native ligand. Z72 has a basic structure of coumarin, which is expected to provide a stable interaction, resulting in drug design using coumarin derivative candidates.
Candidate–receptor interactions at the molecular level
The interactions between the candidates and the receptor were determined by docking the candidate molecule back to the receptor active site based on the initial coordinates obtained from the re-docking process. The results showed that all the candidates could occupy the active site very well (Fig. 2). The energy component determination of the molecular docking results using the dock6 package provided details of energy calculations, such as grid scores, van der Waals energy (EvdW), electrostatic energy (EElec), and internal energy repulsive (EInt). The results showed that the candidates PS-1, PS-2, PS-3, PS-5, PS-7, and PS-9 had better grid scores than the native ligand (Table 4). This shows that their binding pose is very promising in interacting with the receptors on the target proteins as a reference basis for the next analysis. The data obtained by molecular docking are very helpful in determining the initial coordinates of the ligand–receptor interaction. Therefore, it is necessary to do a combination study with dynamic molecular simulation to obtain more reliable data for studying the candidate's binding free energy with the receptor.47,48
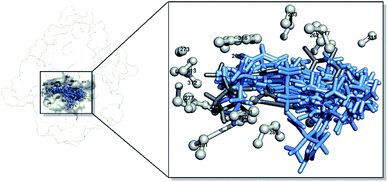 |
| | Fig. 2 Visualization of the pocket area of the active site: Z72 (dim gray), candidates (cornflower blue), and amino acid residues in a radius of 4 Å (gray). | |
Table 4 Molecular docking results of the candidates on the receptor
| Candidate ligands |
Grid score (kcal mol−1) |
EvdW (kcal mol−1) |
EElec (kcal mol−1) |
EInt (kcal mol−1) |
| P |
−51.60 |
−45.52 |
−6.08 |
17.06 |
| PS-1 |
−69.95 |
−67.18 |
−2.77 |
34.06 |
| PS-2 |
−67.40 |
−64.79 |
−2.61 |
38.88 |
| PS-3 |
−64.53 |
−62.03 |
−2.50 |
20.92 |
| PS-4 |
−63.16 |
−62.02 |
−1.14 |
20.96 |
| PS-5 |
−68.48 |
−66.14 |
−2.33 |
38.50 |
| PS-6 |
−63.58 |
−61.61 |
−1.97 |
29.18 |
| PS-7 |
−70.81 |
−70.06 |
−0.75 |
21.77 |
| PS-8 |
−61.61 |
−58.77 |
−2.83 |
26.15 |
| PS-9 |
−66.60 |
−65.27 |
−1.33 |
21.89 |
The binding of the nordentatin derivatives as a cAMP pathway inhibitor can be predicted based on the stability and types of interactions that occur at the molecular level. This can help us understand the mechanism of the interaction that occurs between the candidate and the receptor. Interaction modeling was conducted on candidates that met the criterion of a lower grid score than that of the native ligand. The results showed that the six candidates had different types of interactions with the amino acid residues on the polypeptide side chains of the receptor (Fig. S1†). Further, one of the important variables that determine the stability of ligand–receptor bonds and play an important role in the interactions is the hydrogen bond (H-bond).49
The molecular docking results showed that PS-9 did not have H-bond interactions, while the rest of them had H-bonds. Besides, the amino acid residues Tyr103, His104, His177, Met217, and Gln313 were the hydrogen donors responsible for interaction through H-bonds.
Molecular dynamic simulation: stability, flexibility, compactness and solvent accessibility
The molecular dynamic simulation was carried out in several stages to assess the level of bond stability in each complex. The stages included minimization, heat, density, equilibrium, and production. These stages were summarized and analysed in the form of frames recorded during the simulation, which showed the stability of the system based on several considerations, such as total energy and complex RMSD (Fig. 3). The analysis of the total energy in each system shows the energy stability of the system through the stages of minimization, heat, density, equilibrium, and production as a pre-analysis for the molecular dynamic simulation. The total energy analysis was performed considering that each system (topology) consisted of a solvent (TIP3P-water), Na+ ions (charge neutralization system), and the complex (ligand–receptor). The total energy of the system was evaluated in the simulation to examine if any of the molecular systems remained energetically stable.50 The analysis of total energy output in each system during the simulation time of 120 ns showed that the system stability was very good with no significant changes (average value (kcal mol−1): Z72: −155997 ± 669.93, PS-1: −155910 ± 677.5423, PS-2: −155928 ± 665.45, PS-3: −154234 ± 669.85, PS-5: −155883 ± 681.97, PS-7: −155908 ± 671.69, and PS-9: −155947 ± 693.56) (Fig. 3A). The analysis of the trajectory showed that, especially at the simulation time of 1–30 ns, the systems experienced a significant increase in RMSD and continued with steady RMSD values between ∼3 Å to ∼4 Å until the end of (120 ns) simulation with insignificant fluctuation (Fig. 3B). In this study, the analysis was performed over the last 20 ns trajectories to analyse some important variables of MD simulation, such as flexibility, the radius of gyration, the surface area of solvent accessibility, and binding free energy.51
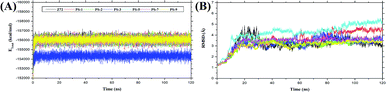 |
| | Fig. 3 System stability during the simulation time of 120 ns: (A) output file analysis for total energy; (B) trajectory analysis of the root-mean-square displacement of the complexes. | |
The root-mean-square fluctuations of the complexes were analysed by looking at the fluctuations that occur in the receptor backbone (Fig. 4A). The RMSF analysis for each complex was carried out during the last 20 ns when system stability was achieved. Fluctuation in each complex could be seen in the loop region, especially in the PS-1 complex. The largest PS-1 fluctuation occurred in the loop region of the residues: 194–199, 232–255, and 300–308 with fluctuation over ∼8.0 Å. This indicated that the loop region of this complex was more flexible during simulation time than the loop regions of the other complexes.52 A radius of gyration analysis was performed to analyse the bond compactness between the ligand and receptor in each system in the last 20 ns. The RoG analysis identified stable folding of the protein when it was bound to the ligand in all the complexes. The average values of RoG (Å) were Z72: 21.14 ± 0.08, PS-1: 20.78 ± 0.06, PS-2: 21.12 ± 0.06, PS-3: 21.36 ± 0.09, PS- 5: 20.82 ± 0.07, PS-7: 21.13 ± 0.08, and PS-9: 20.99 ± 0.06 (Fig. 4B). This indicated that each complex had good bond compactness, which is characterized by a fixed RoG value, and there was no significant change in the RoG values.53
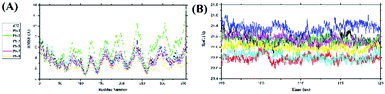 |
| | Fig. 4 Trajectory analysis during simulation over the last 20 ns: fluctuations in the (A) root-mean-square values and (B) radii of gyration of the complexes. | |
Solvent-accessible surface area (SASA) analysis was carried out for all surface areas and the active site surface areas of the complexes to determine the role of water molecules as solvents in accessing the residues in both areas (Fig. 5). Additionally, this analysis was done to see the interaction of water molecules with each complex during the last 20 ns of simulation time. Specifically, the PS-5 complex showed the smallest SASA value, suggesting water solvent access in all surface areas of the complex and the active site surface area was lower than that in other complexes. However, the overall results showed that there was no insignificant fluctuation in the average SASA value on all surface areas of the complexes and the active site surface areas (Table 5).
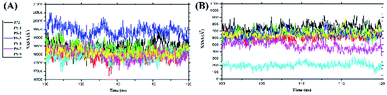 |
| | Fig. 5 Solvent-accessible surface area (SASA): (A) all surface areas and (B) active-site surface areas of the complexes. | |
Table 5 The average values of SASA: all surface areas and active-site surface areas of the complexes
| Candidate ligands |
Average of SASA (Å) |
| All surface areas |
Active site |
| Z72 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 490.63 ± 310.11 490.63 ± 310.11 |
752.12 ± 56.23 |
| PS-1 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 932.83 ± 293.98 932.83 ± 293.98 |
612.20 ± 44.73 |
| PS-2 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 377.30 ± 317.14 377.30 ± 317.14 |
668.03 ± 55.49 |
| PS-3 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 420.68 ± 312.39 420.68 ± 312.39 |
658.13 ± 51.06 |
| PS-5 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 919.90 ± 300.25 919.90 ± 300.25 |
202.63 ± 37.64 |
| PS-7 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 032.12 ± 330.13 032.12 ± 330.13 |
489.92 ± 59.43 |
| PS-9 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 111.43 ± 260.49 111.43 ± 260.49 |
660.57 ± 47.99 |
Binding free energy prediction
The determination of binding free energy was done by extracting the trajectories from the results of the production stages in the last 20 ns simulation. The calculations produced several energy components that were read in detail using the MM-GBSA method. These energies included the binding free energy (ΔG), gas-phase free energy gas (ΔGGas), solvation free energy (ΔGSolv), van der Waals energy (EvdW), electrostatic energy (EEles), generalized Born energy (EGB), and solvent-accessible surface area energy (ESASA).54 The contribution of each energy component determined the binding free energy of each complex (Table 6). The energy components that had the biggest contribution against ΔG, namely EVDW and EGB (EvdW and EEles) contributed to ΔGGas. On the other side, the energy components (EGB and ESASA) contributed to ΔGSolv. Besides, the EGB value shows the contribution of the polar properties of the solvent, and the ESASA value shows the contribution of the nonpolar properties of the solvent in each system.
Table 6 Determination of energy components using the MM-GBSA approach. Data are shown as mean ± standard error of mean (SEM)
| Ligand |
ΔG (kcal mol−1) |
ΔGGas (kcal mol−1) |
ΔGSolv (kcal mol−1) |
EvdW (kcal mol−1) |
EElec (kcal mol−1) |
EGB (kcal mol−1) |
ESASA (kcal mol−1) |
| Z72 |
−24.20 ± 0.19 |
−30.64 ± 0.28 |
6.43 ± 0.23 |
−32.75 ± 0.20 |
2.10 ± 0.28 |
10.12 ± 0.23 |
−3.69 ± 0.02 |
| PS-1 |
−36.84 ± 0.31 |
−58.53 ± 0.43 |
21.69 ± 0.24 |
−47.66 ± 0.30 |
−10.87 ± 0.27 |
27.65 ± 0.25 |
−5.96 ± 0.03 |
| PS-2 |
−35.34 ± 0.28 |
−60.70 ± 0.55 |
25.35 ± 0.44 |
−45.34 ± 0.27 |
−15.35 ± 0.50 |
31.62 ± 0.45 |
−6.26 ± 0.02 |
| PS-3 |
−26.65 ± 0.30 |
−32.47 ± 0.46 |
5.82 ± 0.30 |
−36.51 ± 0.32 |
4.03 ± 0.30 |
10.37 ± 0.31 |
−4.55 ± 0.03 |
| PS-5 |
−42.66 ± 0.26 |
−73.97 ± 0.56 |
31.31 ± 0.44 |
−59.44 ± 0.28 |
−14.53 ± 0.58 |
38.82 ± 0.44 |
−7.51 ± 0.02 |
| PS-7 |
−35.33 ± 0.23 |
−63.53 ± 0.31 |
28.19 ± 0.20 |
−45.25 ± 0.26 |
−18.27 ± 0.20 |
34.17 ± 0.21 |
−5.97 ± 0.03 |
| PS-9 |
−32.57 ± 0.20 |
−49.48 ± 0.26 |
16.91 ± 0.19 |
−40.40 ± 0.21 |
−9.08 ± 0.23 |
21.24 ± 0.18 |
−4.32 ± 0.02 |
The smallest binding free energy represents the formation of a highly stable complex structure. The data showed that the ΔG value of the native ligand was −24.20 ± 0.19 kcal mol−1. Its value was considered as a reference criterion for candidates with good potential. Overall, candidates PS-1, PS-2, PS-3, PS-5, PS-7, and PS-9 showed good binding free energy values (ΔG ≤ ΔG Z72). Thus, this variable can be used as one of the main conditions in selecting candidates that have a good binding with the target protein. Candidates with small free energy bonds are expected to be able to bind more easily and strongly with the amino acid residues at the active site of the target protein. The binding free energy of the native ligand was used as the standard criterion for ligands that can bind to the active site of the target protein (receptor). The candidates bound to the target protein expressed by the PDEB4 gene changed the protein conformation. This conformational change is expected to block the ability of cAMP, which relies heavily on phosphodiesterase compartmentalization to elicit a cell surface receptor-specific response.55 The phosphodiesterases (PDE) play an important role in the hydrolysis of the cAMP pathway. Therefore, phosphodiesterase becomes an important target protein to control the cAMP pathway and prevent hyperproliferation, which can lead to uncontrolled cell development.
Analysis of the contribution of residues that have good bonds was performed using the MM-GBSA method (Fig. S2†). Residues that meet the contribution criteria are residues that have ΔGresiduebind ≤ −1.0 kcal mol−1.56 The overall results showed that 15 residues (Met217, Leu263, Asn265, Ile280, Phe284, Gln287, Ile298, Ser299, Pro300, Ser312, Gln313, Gly315, Phe316, Tyr319, and Ile320) had good contribution energy criteria. Additionally, the amino acid residue with good energy contribution is expected to bind strongly to the modelled candidate.
Hydrogen bond analysis: molecular docking and molecular dynamic simulation
The H-bonds were determined using molecular docking analysis and molecular dynamic simulation based on force field ff14SB. Molecular docking provides results in the form of initial coordinates of the H-bond interaction. However, molecular dynamic simulation provides a series of treatments to verify the durability of the H-bond interactions during the simulation process. The results of molecular docking show a good image of the interaction of the donor–acceptor hydrogen bonds in the active site area.57 Meanwhile, the analysis of H-bonds through molecular dynamic simulation provides a more accurate analysis of the durability of the H-bonds during the simulation.
H-bond analysis through molecular dynamic simulation provided several variables in the form of frames, fractions, residues interaction, and distance of the H-bonds (Table 7). The results showed that the PS-2 and PS-3 candidates had H-bond fractions > 10% recorded during the 120 ns simulation time during the molecular dynamic simulation process at 42.27%, and 38.34%, respectively. This implies that the H-bonds formed between the PS-2 and PS-3 candidates and the Gln313 residue were quite stable with a bond distance of around 2.98 Å and 2.96 Å, respectively, which fall in the category of moderate bond strength. This was supported by the lifetime of the PS-2 and PS-3 H-bonds, which were 9.00 ns and 7.27 ns, respectively, showing longer H-bond occupancy in a row compared with the other complexes during simulation (Fig. S3†). Meanwhile, the undetected H-bond during the simulation process does not identify when it is given the influence of parameters such as temperature, pressure, accuracy, and equilibrium during the H-bond simulation process that cannot be detected on the trajectory. The H-bonds that were read both in molecular docking and molecular dynamic simulation show good stability. Therefore, the combination of molecular docking and molecular dynamic simulation provides a more convincing and accurate prediction of H-bonds.58
Table 7 Simulation of H-bond strength between the ligands and amino acid residues
| Ligand |
Frames |
Fraction (%) |
H-bond |
Distance (Å) |
| Acceptor |
Donor (H) |
MDSa |
MDb |
| Molecular dynamic simulation. Molecular docking. Non-detected. |
| Z72 |
1716 |
13.41 |
Z72_358:O10 |
GLN_313:NE2 (HE22) |
2.99 |
2.11 |
| 743 |
5.80 |
Z72_358:O3 |
GLN_313:NE2 (HE22) |
3.15 |
2.83 |
| PS-1 |
306 |
2.39 |
PS1_358:F5 |
GLN_313:NE2 (HE22) |
3.22 |
NDc |
| 9 |
0.07 |
PS1_358:F2 |
GLN_313:NE2 (HE21) |
3.25 |
2.50 |
| 1 |
0.01 |
PS1_358:F2 |
GLN_313:NE2 (HE22) |
3.05 |
2.26 |
| 1 |
0.01 |
PS1_358:F6 |
TYR_103:OH (HH) |
3.41 |
2.42 |
| PS-2 |
5410 |
42.27 |
PS2_358:O3 |
GLN_313:NE2 (HE22) |
2.98 |
2.44 |
| 411 |
3.21 |
PS2_358:F3 |
MET_217:N (H) |
3.16 |
2.39 |
| PS-3 |
4908 |
38.34 |
PS3_358:O3 |
GLN_313:NE2 (HE22) |
2.96 |
2.38 |
| PS-5 |
621 |
4.85 |
PS5_358:O6 |
GLN_313:NE2 (HE22) |
3.00 |
2.23 |
| PS-7 |
93 |
0.73 |
PS7_358:O5 |
HIE_104:NE2 (HE2) |
3.01 |
2.31 |
| NDc |
NDc |
PS7_358:O3 |
HIE_177:NE2 (HE2) |
NDc |
3.01 |
| PS-9 |
2.37 |
1.85 |
PS9_358:O1 |
HIE_104:NE2 (HE2) |
3.05 |
NDc |
Drug-likeness, bioavailability, and ADMET prediction
Predictions about drug-likeness, bioavailability, and ADMET provide an important image of the pharmacokinetics of a structure. The drug-likeness prediction of the nordentatin derivatives provided different biological results when the measured parameters were evaluated based on Lipinski's rule (RO5) and Veber's rule (Table 8). Candidates with two or more violations of RO5 have poor drug permeability and potentially fall into the bRO5 drug category.59 The effects of the biological properties evaluated by using the RO5 criteria were established by Lipinski and his research group. The RO5 rule provides good reference drug criteria for the process of absorption, distribution, metabolism, and excretion (ADME) when the drug is delivered in the body.60 The M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P data shows the solubility of a drug candidate. The result showed that the average violation of RO5 occurred in the log
P data shows the solubility of a drug candidate. The result showed that the average violation of RO5 occurred in the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P and MW variables (molecular weight). Based on the data, the PS-5 candidate showed no violations, and candidate PS-2, PS-3, and PS-7 were still acceptable.
P and MW variables (molecular weight). Based on the data, the PS-5 candidate showed no violations, and candidate PS-2, PS-3, and PS-7 were still acceptable.
Table 8 Drug-likeness: physicochemical properties, Lipinski's rule of five and Veber's rule
| Code |
Physicochemical properties |
Lipinski's rule |
Veber's rule |
Lipinski and Veber validations/n |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Po/w (XLogP3) Po/w (XLogP3) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S (ESOL) S (ESOL) |
Fraction Csp3 |
M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P P |
MW (Da) |
∑HBD |
∑O + N |
Rotatable bonds |
TPSA (Å2) |
| PS-1 |
7.96 |
−8.12 |
0.29 |
5.37 |
552.46 |
0 |
5 |
7 |
65.74 |
2 |
| PS-2 |
7.07 |
−7.24 |
0.26 |
4.89 |
484.46 |
0 |
5 |
6 |
65.74 |
1 |
| PS-3 |
6.88 |
−7.29 |
0.23 |
4.97 |
495.36 |
0 |
5 |
5 |
65.74 |
1 |
| PS-5 |
6.65 |
−7.05 |
0.23 |
3.95 |
495.91 |
0 |
8 |
6 |
111.56 |
0 |
| PS-7 |
8.07 |
−7.66 |
0.33 |
5.18 |
472.57 |
0 |
5 |
8 |
65.74 |
1 |
| PS-9 |
8.07 |
−8.17 |
0.23 |
5.80 |
519.80 |
0 |
5 |
5 |
65.74 |
2 |
Meanwhile, candidates PS-1 and PS-9 that violate RO5 show that this category of compounds has the potential to fall into the bRO5 drug molecule category. Previous work has reported that several anticancer drugs used in the area of oncology therapy, such as venetoclax and ceritinib, on an average, have a low degree of solubility with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P: 6–11 and relatively large molecular mass: 500–900 dalton but have proven to be effective in inhibiting cancerous growth.61
P: 6–11 and relatively large molecular mass: 500–900 dalton but have proven to be effective in inhibiting cancerous growth.61
The candidates predicted to have good permeability were PS-2, PS-3, PS-5, and PS-7. Several parameters considered in the prediction process can be used as benchmark criteria for a drug. The criteria for acceptance of candidates as drugs based on Lipinski's rule (M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ≤ 4.15, MW ≤ 500 dalton, HBD ≤ 5, and O + N ≤ 10) and Veber's rule (rotatable bonds ≤ 10, and TPSA ≤ 140 Å2) predict the drug-likeness and bioavailability of the candidates.62,63 Furthermore, predictions regarding the oral bioavailability give a better image of the candidate's physicochemical properties (Fig. S4†). Several parameters, namely lipophilicity (−0.7 < XLogP3 < 5.0), size (150 D < MW < 500 D), polarity (20 Å2 < TPSA < 130 Å2), insolubility (0 < ESOL < 6), saturation (0.25 < Csp3 < 1), and flexibility (0 < rot. bonds < 9) were measured.64 Overall, the prediction results showed low compatibility of the candidates as oral drugs because they violated more than two criteria.65 In the end, the prediction of drug-likeness and bioavailability can be used as preliminary data for testing in a wet lab.
P ≤ 4.15, MW ≤ 500 dalton, HBD ≤ 5, and O + N ≤ 10) and Veber's rule (rotatable bonds ≤ 10, and TPSA ≤ 140 Å2) predict the drug-likeness and bioavailability of the candidates.62,63 Furthermore, predictions regarding the oral bioavailability give a better image of the candidate's physicochemical properties (Fig. S4†). Several parameters, namely lipophilicity (−0.7 < XLogP3 < 5.0), size (150 D < MW < 500 D), polarity (20 Å2 < TPSA < 130 Å2), insolubility (0 < ESOL < 6), saturation (0.25 < Csp3 < 1), and flexibility (0 < rot. bonds < 9) were measured.64 Overall, the prediction results showed low compatibility of the candidates as oral drugs because they violated more than two criteria.65 In the end, the prediction of drug-likeness and bioavailability can be used as preliminary data for testing in a wet lab.
For ADMET prediction (absorption, distribution, metabolism, excretion, and toxicity), we used the pkCSM service website (Table S1†). Absorption prediction showed that each candidate had Caco-2 permeability with a predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Papp value > 0.90. Human intestinal absorption showed perfect absorption > 30%, which indicates that the candidates would be absorbed in the human small intestine. The prediction of skin permeability aimed to analyse the initial data as a basis for transdermal drug delivery. The results showed that each candidate had relatively high skin permeability with a log
Papp value > 0.90. Human intestinal absorption showed perfect absorption > 30%, which indicates that the candidates would be absorbed in the human small intestine. The prediction of skin permeability aimed to analyse the initial data as a basis for transdermal drug delivery. The results showed that each candidate had relatively high skin permeability with a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kp value < −2.5. Volume distribution (VDss) is a predictor that is defined as the theoretical volume of the total dose of the drug needed for distribution at the same concentration in the blood plasma. Prediction results showed that no candidate in the high VDss category (log
Kp value < −2.5. Volume distribution (VDss) is a predictor that is defined as the theoretical volume of the total dose of the drug needed for distribution at the same concentration in the blood plasma. Prediction results showed that no candidate in the high VDss category (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L > 0.45), while low VDss was found for candidate PS-5 (log
L > 0.45), while low VDss was found for candidate PS-5 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L < −0.15), and the other candidates fell in the moderate VDss category.66 Thus, overall, the candidates can be distributed evenly at the same concentration in the blood plasma. Prediction of permeability through the blood–brain barrier (BBB) shows the ability of the drug to penetrate the BBB and affect the central nervous system. The BBB criterion was that candidates that can penetrate BBB have BB log values > 0.3 and candidates that are not distributed to BBB have BB log values < −1.0. The prediction results indicated that the candidates would not permeate the BBB.
L < −0.15), and the other candidates fell in the moderate VDss category.66 Thus, overall, the candidates can be distributed evenly at the same concentration in the blood plasma. Prediction of permeability through the blood–brain barrier (BBB) shows the ability of the drug to penetrate the BBB and affect the central nervous system. The BBB criterion was that candidates that can penetrate BBB have BB log values > 0.3 and candidates that are not distributed to BBB have BB log values < −1.0. The prediction results indicated that the candidates would not permeate the BBB.
The predicted metabolism showed that each candidate was a non-inhibitor and non-substrate of the cytochrome isoenzymes (CYP), especially CYP2D6 and CYP1A2. These results identified that the candidates are promising drugs because they do not interfere with the activity of the cytochrome isoenzymes. Disruption or inhibition of the working system of cytochrome enzymes, which are the main enzymes in the metabolic process, usually causes undesirable side effects on the body.67 Meanwhile, the expenditure predictions showed that each candidate was an OCT2 renal substrate in the non-subarctic category with a total clearance range from −0.36 to 0.08![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log mL per min per kg. Organic cation transporter 2 plays a crucial role in the disposal of drugs and cleansing of the kidney. The toxicity parameters calculated in this study showed promising results for each candidate. All candidates were not toxic because the data predictions indicated criteria, such as non-AMES toxicity, non-HERG I inhibitors, and non-skin sensitivity.68 Especially, PS-7 and PS-9 showed non-hepatotoxicity, that is, do not damage the liver, which is the main criterion for a ligand to act as a drug. ADMET prediction using the pkCSM server showed that each candidate had promising ADMET properties and can be considered a drug candidate.
log mL per min per kg. Organic cation transporter 2 plays a crucial role in the disposal of drugs and cleansing of the kidney. The toxicity parameters calculated in this study showed promising results for each candidate. All candidates were not toxic because the data predictions indicated criteria, such as non-AMES toxicity, non-HERG I inhibitors, and non-skin sensitivity.68 Especially, PS-7 and PS-9 showed non-hepatotoxicity, that is, do not damage the liver, which is the main criterion for a ligand to act as a drug. ADMET prediction using the pkCSM server showed that each candidate had promising ADMET properties and can be considered a drug candidate.
Conclusions
The prediction of nordentatin derivatives as anticancer candidates that inhibit the cAMP pathway using the in silico approach offered a systematic and efficient pathway without sacrificing accuracy. The use of several computational chemical techniques, such as modeling, molecular docking, and molecular dynamic simulation for drug design in a systematic and integrated manner played an important role in understanding the nature, interactions, and pharmacokinetics of the nordentatin derivatives. In addition, several variables and parameters played an important role in predicting the promising candidates. The important approaches used in this study, namely a combination of quantum mechanical methods (PM3-DFT/6-31G*/B3LYP), force field (ff14SB), AM1-BCC, and MM-GBSA methods, were very influential on the variables specified. Meanwhile, the variables that played an important role in the selection of candidates that meet the criteria were RMSD validation, grid scores, RMSD complex, binding free energy, hydrogen bond properties, drug-likeness, and ADMET properties. Overall, the PS-1, PS-2, PS-3, PS-5, PS-7, and PS-9 candidates were promising as drug candidates among the 10 nordentatin derivatives as they fulfilled most of the variables considered as criteria in this research.
Conflicts of interest
There are no conflicts to declare.
References
- L. Rinaldi, R. Delle Donne, B. Catalanotti, O. Torres-Quesada, F. Enzler, F. Moraca, R. Nisticò, F. Chiuso, S. Piccinin, V. Bachmann, H. H. Lindner, C. Garbi, A. Scorziello, N. A. Russo, M. Synofzik, U. Stelzl, L. Annunziato, E. Stefan and A. Feliciello, Nat. Commun., 2019, 10, 1–14 CrossRef CAS.
- X. Kong, G. Ai, D. Wang, R. Chen, D. Guo, Y. Yao, K. Wang, G. Liang, F. Qi, W. Liu and Y. Zhang, Anal. Cell. Pathol., 2019, 2019, 1–5 CrossRef.
- J. Huang, J. R. Yang, J. Zhang and J. Yang, Org. Biomol. Chem., 2013, 11, 3212–3222 RSC.
- K. Li, H. Zhang, J. Qiu, Y. Lin, J. Liang, X. Xiao, L. Fu, F. Wang, J. Cai, Y. Tan, W. Zhu, W. Yin, B. Lu, F. Xing, L. Tang, M. Yan, J. Mai, Y. Li, W. Chen, P. Qiu, X. Su, G. Gao, P. W. L. Tai, J. Hu and G. Yan, Mol. Ther., 2016, 24, 156–165 CrossRef CAS.
- T. Tsunoda, T. Ota, T. Fujimoto, K. Doi, Y. Tanaka, Y. Yoshida, M. Ogawa, H. Matsuzaki, M. Hamabashiri, D. R. Tyson, M. Kuroki, S. Miyamoto and S. Shirasawa, Mol. Cancer, 2012, 11, 1–12 CrossRef.
- B. Mahmood, M. M. B. Damm, T. S. R. Jensen, M. B. Backe, M. S. Dahllöf, S. S. Poulsen, N. Bindslev and M. B. Hansen, BMC Cancer, 2016, 16, 1–12 CrossRef.
- A. N. Suhasini, L. Wang, K. N. Holder, A. P. Lin, H. Bhatnagar, S. W. Kim, A. W. Moritz and R. C. T. Aguiar, Leukemia, 2016, 30, 617–626 CrossRef CAS.
- T. M. Thant, N. S. Aminah, A. N. Kristanti, R. Ramadhan, H. T. Aung and Y. Takaya, Nat. Prod. Commun., 2020, 15, 1–15 CrossRef.
- A. Sabt, O. M. Abdelhafez, R. S. El-Haggar, H. M. F. Madkour, W. M. Eldehna, E. E. D. A. M. El-Khrisy, M. A. Abdel-Rahman and L. A. Rashed, J. Enzyme Inhib. Med. Chem., 2018, 33, 1095–1107 CrossRef CAS.
- S. Sengupta and G. Mehta, Org. Biomol. Chem., 2018, 16, 6372–6390 RSC.
- I. A. Arbab, C. Y. Looi, A. B. Abdul, F. K. Cheah, W. F. Wong, M. A. Sukari, R. Abdullah, S. Mohan, S. Syam, A. Arya, M. Mohamed Elhassan Taha, B. Muharram, M. Rais Mustafa and S. Ibrahim Abdelwahab, Evid.-Based Complementary Altern. Med., 2012, 2012, 1–15 CrossRef.
- R. Chen, L. Huo, Y. Jaiswal, J. Wei, D. Li, J. Zhong, L. Williams, X. Xia and Y. Liang, Int. J. Mol. Sci., 2019, 20, 1–17 CAS.
- P. Paudel, S. H. Seong, H. A. Jung and J. S. Choi, ACS Omega, 2019, 4, 11621–11630 CrossRef CAS.
- Q. Cui and M. Elstner, Phys. Chem. Chem. Phys., 2014, 16, 14368–14377 RSC.
- E. Cortes, E. Márquez, J. R. Mora, E. Puello, N. Rangel, A. De Moya and J. Trilleras, Processes, 2019, 7, 1–12 CrossRef.
- E. S. Kryachko and E. V. Ludeña, Phys. Rep., 2014, 544, 123–239 CrossRef CAS.
- J. G. Hill, Int. J. Quantum Chem., 2013, 113, 21–34 CrossRef CAS.
- F. Ntie-Kang, J. N. Nwodo, A. Ibezim, C. V. Simoben, B. Karaman, V. F. Ngwa, W. Sippl, M. U. Adikwu and L. M. a. Mbaze, J. Chem. Inf. Model., 2014, 54, 2433–2450 CrossRef CAS.
- A. Balupuri, P. K. Balasubramanian and S. J. Cho, Arabian J. Chem., 2020, 13, 1052–1078 CrossRef CAS.
- L. G. Ferreira, R. N. Dos Santos, G. Oliva and A. D. Andricopulo, Molecules, 2015, 20, 13384–13421 CrossRef CAS.
- J. Kongsted, P. Söderhjelm and U. Ryde, J. Comput.-Aided Mol. Des., 2009, 23, 395–409 CrossRef CAS.
- T. Hou, J. Wang, Y. Li and W. Wang, J. Chem. Inf. Model., 2011, 51, 69–82 CrossRef CAS.
- T. M. Thant, N. S. Aminah, R. Ramadhan, H. T. Aung and Y. Takaya, Open Chem., 2020, 18, 890–897 Search PubMed.
- S. P. Govek, G. Oshiro, J. V. Anzola, C. Beauregard, J. Chen, A. R. Coyle, D. A. Gamache, M. R. Hellberg, J. N. Hsien, J. M. Lerch, J. C. Liao, J. W. Malecha, L. M. Staszewski, D. J. Thomas, J. M. Yanni, S. A. Noble and A. K. Shiau, Bioorg. Med. Chem. Lett., 2010, 20, 2928–2932 CrossRef CAS.
- A. S. Christensen, T. Kubař, Q. Cui and M. Elstner, Chem. Rev., 2016, 116, 5301–5337 CrossRef CAS.
- P. Echenique and J. L. Alonso, Mol. Phys., 2007, 105, 3057–3098 CrossRef CAS.
- É. Brémond, N. Golubev, S. N. Steinmann and C. Corminboeuf, J. Chem. Phys., 2014, 140, 0–11 CrossRef.
- A. Allouche, J. Comput. Chem., 2012, 32, 174–182 CrossRef.
- M. E. Foster and K. Sohlberg, Phys. Chem. Chem. Phys., 2010, 12, 307–322 RSC.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Chem. Rev., 2012, 112, 289–320 CrossRef CAS.
- J. J. P. Stewart, J. Mol. Model., 2007, 13, 1173–1213 CrossRef CAS.
- N. S. Pagadala, K. Syed and J. Tuszynski, Biophys. Rev., 2017, 9, 91–102 CrossRef CAS.
- X.-Y. Meng, H.-X. Zhang, M. Mezei and M. Cui, Curr. Comput.-Aided Drug Des., 2012, 7, 146–157 CrossRef.
- V. Salmaso and S. Moro, Front. Pharmacol., 2018, 9, 1–16 CrossRef.
- S. Debnath, T. Debnath, S. Bhaumik, S. Majumdar, A. M. Kalle and V. Aparna, Sci. Rep., 2019, 9, 1–14 CrossRef CAS.
- J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713 CrossRef CAS.
- T. Simonson, Rep. Prog. Phys., 2003, 66, 737–787 CrossRef CAS.
- A. Daina, O. Michielin and V. Zoete, Sci. Rep., 2017, 7, 1–13 CrossRef.
- D. E. V. Pires, T. L. Blundell and D. B. Ascher, J. Med. Chem., 2015, 58, 4066–4072 CrossRef CAS.
- X.-M. Peng, G. L. V. Damu and C.-H. Zhou, Curr. Pharm. Des., 2013, 19, 3884–3930 CrossRef CAS.
- Y. Y. Zhang, Q. Q. Zhang, J. L. Song, L. Zhang, C. S. Jiang and H. Zhang, Molecules, 2018, 23, 1–19 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- F. Pereira and J. Aires-de-Sousa, J. Cheminf., 2018, 10, 1–11 Search PubMed.
- C. G. Mayne, M. J. Arcario, P. Mahinthichaichan, J. L. Baylon, J. V. Vermaas, L. Navidpour, P. C. Wen, S. Thangapandian and E. Tajkhorshid, Biochim. Biophys. Acta, Biomembr., 2016, 1858, 2290–2304 CrossRef CAS.
- T. Ban, M. Ohue and Y. Akiyama, Comput. Biol. Chem., 2018, 73, 139–146 CrossRef CAS.
- X. Li, Z. Chu, X. Du, Y. Qiu and Y. Li, RSC Adv., 2019, 9, 11465–11475 RSC.
- A. L. Da Fonseca, R. R. Nunes, V. M. L. Braga, M. Comar, R. J. Alves, F. D. P. Varotti and A. G. Taranto, J. Mol. Graphics Modell., 2016, 66, 174–186 CrossRef.
- Y. Xu, Z. He, H. Liu, Y. Chen, Y. Gao, S. Zhang, M. Wang, X. Lu, C. Wang, Z. Zhao, Y. Liu, J. Zhao, Y. Yu and M. Yang, RSC Adv., 2020, 10, 6927–6943 RSC.
- M. Ajmal Ali, J. King Saud Univ., Sci., 2020, 32, 891–895 CrossRef.
- Z. Zhou and Y. Li, J. Comput.-Aided Mol. Des., 2009, 23, 705–714 CrossRef CAS.
- T. Joshi, T. Joshi, P. Sharma, S. Chandra and V. Pande, J. Biomol. Struct. Dyn., 2020, 1–18 Search PubMed.
- L. Piao, Z. Chen, Q. Li, R. Liu, W. Song, R. Kong and S. Chang, Int. J. Mol. Sci., 2019, 20, 1–17 Search PubMed.
- M. Arnittali, A. N. Rissanou and V. Harmandaris, Procedia Comput. Sci., 2019, 156, 69–78 CrossRef.
- P. Mahalapbutr, K. Thitinanthavet, T. Kedkham, H. Nguyen, L. thi ha Theu, S. Dokmaisrijan, L. Huynh, N. Kungwan and T. Rungrotmongkol, J. Mol. Struct., 2019, 1180, 480–490 CrossRef CAS.
- B. A. Fertig and G. S. Baillie, J. Cardiovasc. Dev. Dis., 2018, 5, 1–14 Search PubMed.
- B. Nutho, P. Mahalapbutr, K. Hengphasatporn, N. C. Pattaranggoon, N. Simanon, Y. Shigeta, S. Hannongbua and T. Rungrotmongkol, Biochemistry, 2020, 59, 1769–1779 CrossRef CAS.
- A. K. Varma, R. Patil, S. Das, A. Stanley, L. Yadav and A. Sudhakar, PLoS One, 2010, 5, 1–10 Search PubMed.
- S. M. Noha, H. Schmidhammer and M. Spetea, ACS Chem. Neurosci., 2017, 8, 1327–1337 CrossRef CAS.
- L. Z. Benet, C. M. Hosey, O. Ursu and T. I. Oprea, Adv. Drug Delivery Rev., 2016, 101, 89–98 CrossRef CAS.
- A. Amin, N. A. Chikan, T. A. Mokhdomi, S. Bukhari, A. M. Koul, B. A. Shah, F. R. Gharemirshamlu, A. H. Wafai, A. Qadri and R. A. Qadri, Sci. Rep., 2016, 6, 1–13 CrossRef.
- D. A. Degoey, H. J. Chen, P. B. Cox and M. D. Wendt, J. Med. Chem., 2018, 61, 2636–2651 CrossRef CAS.
- C. A. Lipinski, F. Lombardo, B. W. Dominy and P. J. Feeney, Adv. Drug Delivery Rev., 2012, 64, 4–17 CrossRef.
- D. F. Veber, S. R. Johnson, H. Y. Cheng, B. R. Smith, K. W. Ward and K. D. Kopple, J. Med. Chem., 2002, 45, 2615–2623 CrossRef CAS.
- F. T. Ndombera, G. K. K. Maiyoh and V. C. Tuei, J. Pharm. Pharmacol., 2019, 7, 165–176 Search PubMed.
- S. Yasmeen and P. Gupta, Bioinf. Biol. Insights, 2019, 13, 1–11 Search PubMed.
- Y. Han, J. Zhang, C. Q. Hu, X. Zhang, B. Ma and P. Zhang, Front. Pharmacol., 2019, 10, 1–12 CrossRef.
- J. D. Tyzack and J. Kirchmair, Chem. Biol. Drug Des., 2019, 93, 377–386 CrossRef CAS.
- C. F. Araujo-Lima, R. J. M. Nunes, R. M. Carpes, C. A. F. Aiub and I. Felzenszwalb, BioMed Res. Int., 2017, 2017, 1–8 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra07838g |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab,
Imam Siswantoa,
Tin Myo Thantcd,
Alfinda Novi Kristantiab and
Yoshiaki Takayae
*ab,
Imam Siswantoa,
Tin Myo Thantcd,
Alfinda Novi Kristantiab and
Yoshiaki Takayae
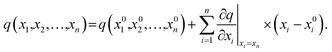
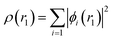
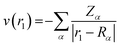
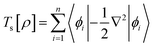
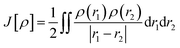
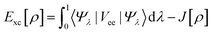
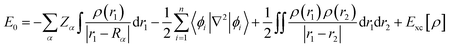
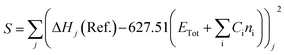
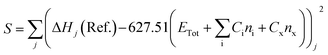
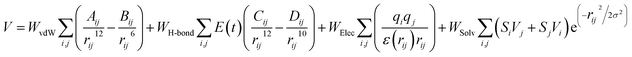
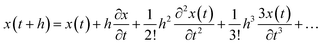
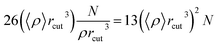
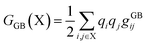
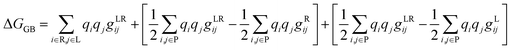




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 490.63 ± 310.11
490.63 ± 310.11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 932.83 ± 293.98
932.83 ± 293.98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 377.30 ± 317.14
377.30 ± 317.14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 420.68 ± 312.39
420.68 ± 312.39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 919.90 ± 300.25
919.90 ± 300.25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 032.12 ± 330.13
032.12 ± 330.13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 111.43 ± 260.49
111.43 ± 260.49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P data shows the solubility of a drug candidate. The result showed that the average violation of RO5 occurred in the log
P data shows the solubility of a drug candidate. The result showed that the average violation of RO5 occurred in the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P and MW variables (molecular weight). Based on the data, the PS-5 candidate showed no violations, and candidate PS-2, PS-3, and PS-7 were still acceptable.
P and MW variables (molecular weight). Based on the data, the PS-5 candidate showed no violations, and candidate PS-2, PS-3, and PS-7 were still acceptable.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Po/w (XLogP3)
Po/w (XLogP3)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S (ESOL)
S (ESOL)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P
P![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P: 6–11 and relatively large molecular mass: 500–900 dalton but have proven to be effective in inhibiting cancerous growth.61
P: 6–11 and relatively large molecular mass: 500–900 dalton but have proven to be effective in inhibiting cancerous growth.61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ≤ 4.15, MW ≤ 500 dalton, HBD ≤ 5, and O + N ≤ 10) and Veber's rule (rotatable bonds ≤ 10, and TPSA ≤ 140 Å2) predict the drug-likeness and bioavailability of the candidates.62,63 Furthermore, predictions regarding the oral bioavailability give a better image of the candidate's physicochemical properties (Fig. S4†). Several parameters, namely lipophilicity (−0.7 < XLogP3 < 5.0), size (150 D < MW < 500 D), polarity (20 Å2 < TPSA < 130 Å2), insolubility (0 < ESOL < 6), saturation (0.25 < Csp3 < 1), and flexibility (0 < rot. bonds < 9) were measured.64 Overall, the prediction results showed low compatibility of the candidates as oral drugs because they violated more than two criteria.65 In the end, the prediction of drug-likeness and bioavailability can be used as preliminary data for testing in a wet lab.
P ≤ 4.15, MW ≤ 500 dalton, HBD ≤ 5, and O + N ≤ 10) and Veber's rule (rotatable bonds ≤ 10, and TPSA ≤ 140 Å2) predict the drug-likeness and bioavailability of the candidates.62,63 Furthermore, predictions regarding the oral bioavailability give a better image of the candidate's physicochemical properties (Fig. S4†). Several parameters, namely lipophilicity (−0.7 < XLogP3 < 5.0), size (150 D < MW < 500 D), polarity (20 Å2 < TPSA < 130 Å2), insolubility (0 < ESOL < 6), saturation (0.25 < Csp3 < 1), and flexibility (0 < rot. bonds < 9) were measured.64 Overall, the prediction results showed low compatibility of the candidates as oral drugs because they violated more than two criteria.65 In the end, the prediction of drug-likeness and bioavailability can be used as preliminary data for testing in a wet lab.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Papp value > 0.90. Human intestinal absorption showed perfect absorption > 30%, which indicates that the candidates would be absorbed in the human small intestine. The prediction of skin permeability aimed to analyse the initial data as a basis for transdermal drug delivery. The results showed that each candidate had relatively high skin permeability with a log
Papp value > 0.90. Human intestinal absorption showed perfect absorption > 30%, which indicates that the candidates would be absorbed in the human small intestine. The prediction of skin permeability aimed to analyse the initial data as a basis for transdermal drug delivery. The results showed that each candidate had relatively high skin permeability with a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kp value < −2.5. Volume distribution (VDss) is a predictor that is defined as the theoretical volume of the total dose of the drug needed for distribution at the same concentration in the blood plasma. Prediction results showed that no candidate in the high VDss category (log
Kp value < −2.5. Volume distribution (VDss) is a predictor that is defined as the theoretical volume of the total dose of the drug needed for distribution at the same concentration in the blood plasma. Prediction results showed that no candidate in the high VDss category (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L > 0.45), while low VDss was found for candidate PS-5 (log
L > 0.45), while low VDss was found for candidate PS-5 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L < −0.15), and the other candidates fell in the moderate VDss category.66 Thus, overall, the candidates can be distributed evenly at the same concentration in the blood plasma. Prediction of permeability through the blood–brain barrier (BBB) shows the ability of the drug to penetrate the BBB and affect the central nervous system. The BBB criterion was that candidates that can penetrate BBB have BB log values > 0.3 and candidates that are not distributed to BBB have BB log values < −1.0. The prediction results indicated that the candidates would not permeate the BBB.
L < −0.15), and the other candidates fell in the moderate VDss category.66 Thus, overall, the candidates can be distributed evenly at the same concentration in the blood plasma. Prediction of permeability through the blood–brain barrier (BBB) shows the ability of the drug to penetrate the BBB and affect the central nervous system. The BBB criterion was that candidates that can penetrate BBB have BB log values > 0.3 and candidates that are not distributed to BBB have BB log values < −1.0. The prediction results indicated that the candidates would not permeate the BBB.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log mL per min per kg. Organic cation transporter 2 plays a crucial role in the disposal of drugs and cleansing of the kidney. The toxicity parameters calculated in this study showed promising results for each candidate. All candidates were not toxic because the data predictions indicated criteria, such as non-AMES toxicity, non-HERG I inhibitors, and non-skin sensitivity.68 Especially, PS-7 and PS-9 showed non-hepatotoxicity, that is, do not damage the liver, which is the main criterion for a ligand to act as a drug. ADMET prediction using the pkCSM server showed that each candidate had promising ADMET properties and can be considered a drug candidate.
log mL per min per kg. Organic cation transporter 2 plays a crucial role in the disposal of drugs and cleansing of the kidney. The toxicity parameters calculated in this study showed promising results for each candidate. All candidates were not toxic because the data predictions indicated criteria, such as non-AMES toxicity, non-HERG I inhibitors, and non-skin sensitivity.68 Especially, PS-7 and PS-9 showed non-hepatotoxicity, that is, do not damage the liver, which is the main criterion for a ligand to act as a drug. ADMET prediction using the pkCSM server showed that each candidate had promising ADMET properties and can be considered a drug candidate.

