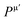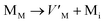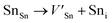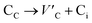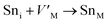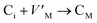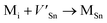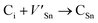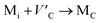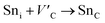Open Access Article
Open Access ArticleChemically stable new MAX phase V2SnC: a damage and radiation tolerant TBC material
M. A. Hadi *a,
M. Dahlqvist
*a,
M. Dahlqvist b,
S.-R. G. Christopoulosc,
S. H. Naqib
b,
S.-R. G. Christopoulosc,
S. H. Naqib a,
A. Chroneoscd and
A. K. M. A. Islamae
a,
A. Chroneoscd and
A. K. M. A. Islamae
aDepartment of Physics, University of Rajshahi, Rajshahi 6205, Bangladesh. E-mail: hadipab@gmail.com
bThin Film Physics Division, Department of Physics (IFM), Linköping University, SE-581 83 Linköping, Sweden
cFaculty of Engineering, Environment and Computing, Coventry University, Priory Street, Coventry CV1 5FB, UK
dDepartment of Materials, Imperial College, London SW7 2AZ, UK
eInternatinal Islamic University Chittagong, Kumira, Chittagong 4318, Bangladesh
First published on 8th December 2020
Abstract
Using density functional theory, the phase stability and physical properties, including structural, electronic, mechanical, thermal and vibrational with defect processes, of a newly synthesized 211 MAX phase V2SnC are investigated for the first time. The obtained results are compared with those found in the literature for other existing M2SnC (M = Ti, Zr, Hf, Nb, and Lu) phases. The formation of V2SnC is exothermic and this compound is intrinsically stable in agreement with the experiment. V2SnC has potential to be etched into 2D MXene. The new phase V2SnC and existing phase Nb2SnC are damage tolerant. V2SnC is elastically more anisotropic than Ti2SnC and less than the other M2SnC phases. The electronic band structure and Fermi surface of V2SnC indicate the possibility of occurrence of its superconductivity. V2SnC is expected to be a promising TBC material like Lu2SnC. The radiation tolerance in V2SnC is better than that in Lu2SnC.
1. Introduction
MAX phases are a family of more than 80 ternary carbides, nitrides and borides in hexagonal crystal symmetry.1,2 This family is chemically represented as Mn+1AXn, where M is an early transition metal, A is an A-group element, X is C or N or B, and the integer ‘n’ ranges from 1 to 3.3 Depending on the value of layer index n, MAX phases are categorized as 211, 312 and 413 phases for n = 1, 2, 3, respectively. MAX phases crystallize in the hexagonal space group P63/mmc (194). In their crystal structures, M6X-octahedra with the X-elements fill the octahedral positions between the M-elements as do in the corresponding MX binaries. The octahedra exchange with the A-atomic layers placed at the centers of trigonal prisms, which are larger, and thus more accommodating of the larger A-atoms. The interposing pure metallic A-atomic planes are mirror planes to the meandering ceramic Mn+1Xn slabs. Due to alternating metallic and ceramic layers in MAX phases they possess a unique set of metallic and ceramic properties.4 The common metallic properties are electrical and thermal conductivities, high fracture toughness, machinability, damage tolerant and thermal shock resistance. The typical ceramic properties are lightweight, oxidation and corrosion resistance, elastic stiffness, resistant to fatigue and ability to maintain the strength to high temperature.5 The MAX phases also experience plastic-to-brittle transitions at high temperatures, and can resist high compressive stresses at ambient temperature.6 These exceptional properties of MAX phases make them suitable for potential uses as tough and machinable, coatings for electrical contacts, thermal shock refractories, and heating elements at high temperature. Additionally, their neutron irradiation resistance makes them suitable in nuclear applications. A common recent use of MAX phases is as precursors for producing two-dimensional MXenes.7 The MAX phases are attractive due to their unique combination of structural characteristics, wide range of properties, and many prospective uses.Early studies on M2SnC phases by Jeitschko et al. in mid 1960s resulted in synthesized phases with M = Ti, Zr, Hf, and Nb.8–10 Kuchida et al.11 synthesized the first Lu-based MAX phase Lu2SnC in the M2SnC family. Lu is the last element in the lanthanide series although it is sometimes mentioned as the first member in the 6th-period transition metals. Lu replaced the common early transition metals “M” in the M2SnC MAX phases. Theoretical investigations reveal that Lu2SnC is softer and more easily machinable than the other existing M2SnC phases. It is also a promising candidate as a thermal barrier coating (TBC) material owing to its high thermal shock resistance, low minimum thermal conductivity, high melting temperature and characteristically good oxidation resistance.12 Xu et al.13 focused their attention on M2SnC phases and synthesized V2SnC by sintering V, Sn, and C powder mixture at 1000 °C. They identified the crystal structure of V2SnC as 211 MAX phases through X-ray diffraction, first-principles calculation, and high-resolution transmission scanning electron microscopy.
M2SnC compounds show diversity in their properties. Nb2SnC and Lu2SnC show superconducting transition, Nb2SnC has also better radiation tolerance in the M2SnC family, Hf2SnC is highly dense, and Zr2SnC is highly elastically anisotropic in this group.5,12 Additionally, the lattice constants of Sn-containing 211 MAX phases show an increasing trend with the crystal radius of M-elements.12 The diverse properties of M2SnC motivated the use of density functional theory (DFT) calculations to explore the physical properties of V2SnC and the analysis of the trend of physical properties in M2SnC MAX phases. In this study, the mechanical, lattice dynamical and thermodynamic phase stability is examined for the new phase V2SnC. Mechanical behaviors, elastic anisotropy, Debye temperature, melting point, lattice thermal conductivity, minimum thermal conductivity, lattice dynamics and defect processes of V2SnC are investigated for the first time.
2. Methodology
All calculations are performed with the DFT method as implemented in CASTEP.14 The non-spin polarized Perdew–Burke–Ernzerhof (PBE) functional within generalized gradient approximation (GGA) is chosen to describe the electronic exchange-correlation potential.15 Ultra-soft pseudo-potential developed by Vanderbilt is used to model the interactions between electrons and ion cores.16 A Γ-centered k-point mesh of 15 × 15 × 3 grid in the Monkhorst-Pack (MP) scheme is used to integrate over the first Brillouin zone in the reciprocal space of the MAX phase hexagonal unit cell.17 To expand the eigenfunctions of the valence and closely valence electrons in terms of a plane-wave basis, a cutoff energy of 700 eV is chosen. Total energy and internal forces are minimized during the geometry optimization with the BFGS minimization technique named after by the first letter of the name of Broyden–Fletcher–Goldfarb–Shanno.18 The self-consistence convergence is achieved with the difference in the total energy within 5 × 10−6 eV per atom, the maximum ionic Hellmann–Feynman force within 0.01 eV Å−1, maximum ionic displacement within 5 × 10−4 Å, and maximum stress within 0.02 GPa. For self-consistent field calculations, the tolerance is chosen as 5 × 10−7 eV per atom.The elastic stiffness constants and moduli are calculated from the first-principles investigations using finite-strain method implemented in the CASTEP code.19 This method involves setting the deformation to a predetermined value, relaxing all free parameters and computing the stress. The convergence criteria for elastic calculations are chosen as: the difference in total energy within 10−6 eV per atom, the maximum ionic Hellmann–Feynman force within 2 × 10−3 eV Å−1, and the maximum ionic displacement within 10−4 Å. Elastic calculations with CASEP code have been successful for all kind of crystal systems.20–31 The lattice dynamic properties such as phonon dispersion and phonon density of states are calculated by means of the finite displacement supercell method executed with a 3 × 3 × 1 supercell within the code.
Defect calculations are performed with a 72-atomic site (36M, 18A, and 18C) supercell using a 3 × 3 × 1 MP k-point mesh under constant pressure. Allowing for all possible interstitial sites, an intensive computational search is carried out to identify the potential interstitial sites. The defect energies are defined as effectively energy differences between the isolated defects.
3. Results and discussion
3.1. Structural aspects and phase stability
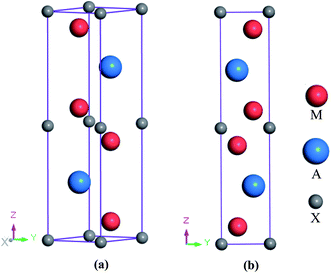
The newly synthesized V2SnC phase crystalizes in the hexagonal MAX phase crystal structure with space group P63/mmc (no. 194). The position of each atom is found as V at 4f (1/3, 2/3, 0.0744), Sn at 2d (2/3, 1/3, 1/4), and C at 2a (0, 0, 0). The V and Sn atoms stack along the z-direction (c-axis) (see Fig. 1, where M represents V, A refers to Sn and X is C). There are two layers of V atoms in each V–C slab, and every two layers of V atoms and one layer of Sn atoms are consecutively arranged along the z-direction. The optimized lattice constants a and c and internal parameter zM are in agreement with the experimental and theoretical values.13 The present values (a = 3.121 Å, c = 12.947 Å, zM = 0.0759) are closer to the experimental results (a = 2.981 Å, c = 13.470 Å, zM = 0.0776) compared with the previous theoretical values (a = 3.134 Å, c = 12.943 Å, zM = 0.0751). The reason may be the use of coarse k-point mesh (9 × 9 × 2) and low cutoff energy (400 eV) in the previous theoretical study. In the M2SnC systems, we observed that the unit cell parameters show a better relationship with the crystal radius of M atoms.12 In this relation, the lattice parameters exhibit increasing trend with the increase of crystal radius of transition metal M. The newly synthesized V2SnC also obeys this relationship (refer to Fig. 2) (Table 1).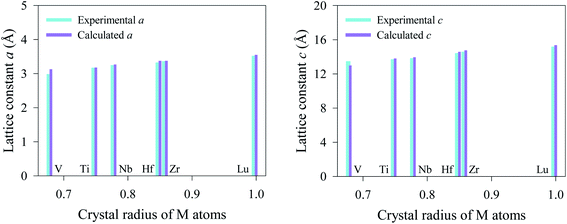 | ||
| Fig. 2 Lattice parameters of M2SnC as a function of crystal radius of M atoms.33 | ||
| Compound | a | c | c/a | zM | V | Remarks |
|---|---|---|---|---|---|---|
| V2SnC | 3.121 | 12.947 | 4.148 | 0.0759 | 109.2 | Calc. (This work) |
| 2.9792 | 13.4441 | 4.513 | 0.0744 | 103.3 | Expt.13 | |
| Ti2SnC | 3.172 | 13.772 | 4.342 | 0.0806 | 120.0 | Calc.12 |
| 3.1635 | 13.675 | 4.323 | — | 118.5 | Expt.32 | |
| Nb2SnC | 3.258 | 13.918 | 4.272 | 0.0820 | 128.0 | Calc.12 |
| 3.2408 | 13.802 | 4.259 | — | 125.5 | Expt.32 | |
| Hf2SnC | 3.367 | 14.548 | 4.320 | 0.0865 | 142.9 | Calc.12 |
| 3.3199 | 14.388 | 4.334 | — | 137.3 | Expt.32 | |
| Zr2SnC | 3.367 | 14.730 | 4.374 | 0.0849 | 144.7 | Calc.12 |
| 3.3576 | 14.568 | 4.339 | — | 142.2 | Expt.32 | |
| Lu2SnC | 3.546 | 15.323 | 4.320 | 0.0850 | 166.9 | Calc.12 |
| 3.514 | 15.159 | 4.314 | — | 162.1 | Expt.32 |
Phase stability of MAX phases with respect to the constituent elements cannot be used to predict whether a material is thermodynamically stable. Instead, all competing phases need to be included in the analysis. The thermodynamic stability of the recently synthesized V2SnC MAX phase is examined at 0 K with respect to decomposition into any combination of competing phases. The most competitive set of competing phases, designated as equilibrium simplex, is identified using a linear optimization procedure.34 This procedure has already been successful to confirm the experimentally known MAX phases in addition to predicting the existence of new ones.35 The stability of V2SnC is quantified in terms of formation enthalpy ΔHcp by comparing its energy to the energy of the equilibrium simplex according to
| ΔHcp = E(V2SnC) − E(equilibrium simplex) | (1) |
The phase V2SnC is considered to be stable if ΔHcp < 0. The considered competing phases for V2SnC are listed in Table 2. V2C and Sn are identified as the most competing phases according to linear optimization procedure. The eqn (1) can be rewritten as
| ΔHcp = E(V2SnC) − E(V2C) − E(Sn) | (2) |
| Phase | Prototype structure | Pearson symbol | Space group | a (Å) | b (Å) | c (Å) | V (Å3) | E (eV fu−1) |
|---|---|---|---|---|---|---|---|---|
| C | C (graphite) | hP4 | P63/mmc (194) | 2.462744 | 2.462744 | 8.985673 | 47.2 | −155.088 |
| C | Diamond | cF8 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (227) m (227) |
3.567776 | 3.567776 | 3.567776 | 45.4 | −154.901 |
| V | W | cI2 | Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (229) m (229) |
3.011843 | 3.011843 | 3.011843 | 27.3 | −1976.398 |
| α-Sn | Diamond | cF8 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (227) m (227) |
8.596983 | 8.596983 | 8.596983 | 635.4 | −94.217 |
| β-Sn | β-Sn | tI4 | I41/amd (141) | 5.973130 | 5.973130 | 3.183849 | 113.6 | −95.465 |
| SnC | ZnS | cF8 | F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m (216) 3m (216) |
5.134950 | 5.134950 | 5.134950 | 135.4 | −248.722 |
| SnC | NaCl | cF8 | Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (225) m (225) |
4.921133 | 4.921133 | 4.921133 | 119.2 | −247.793 |
| VC | CrB | oC8 | Cmcm (63) | 2.784524 | 7.500027 | 3.378178 | 70.5 | −2131.336 |
| VC | α-MoB | tI16 | I41/amd (141) | 2.875169 | 2.875169 | 19.390061 | 160.3 | −2131.692 |
| V2C | β-V2N | hP9 | P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1m (162) 1m (162) |
5.017396 | 5.017396 | 4.546570 | 99.1 | −4109.186 |
| V2C | Inverse CdI2 | hP3 | P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (164) m1 (164) |
2.908853 | 2.908853 | 4.555253 | 33.4 | −4109.146 |
| α-V2C | ζ-Fe2N (Fe2N0.94) | oP12 | Pbcn (60) | 4.563895 | 5.751247 | 5.040818 | 132.3 | −4109.208 |
| β-V2C | W2C | hP3 | P63/mmc (194) | 2.908607 | 2.908606 | 4.555192 | 33.4 | −4109.147 |
| β′-V2C | ε-Fe2N | hP9 | P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (164) m1 (164) |
5.003269 | 5.003269 | 4.535382 | 98.3 | −4109.191 |
| VC2 | MoB2 | tR18 | R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (166) m (166) |
2.599774 | 2.599774 | 24.095326 | 141.0 | −2285.036 |
| VC2 | AlB2 | hP3 | P6/mmm (191) | 2.554138 | 2.554138 | 4.407399 | 24.9 | −2284.212 |
| VC3 | Ni3Ti | hP16 | P63/mmc (194) | 4.471182 | 4.471182 | 7.239285 | 125.3 | −2439.254 |
| V6C5 | V6C5 | hP33 | P3112 (151) | 5.122689 | 5.122689 | 14.387631 | 327.0 | −12639.362 |
| V8C7 | cP60 | P4332 (212) | 8.328377 | 8.328377 | 8.328377 | 577.7 | −16905.598 | |
| VSn2 | Mg2Cu | cF48 | Fddd (70) | 5.523603 | 9.500626 | 18.914470 | 992.6 | −2167.631 |
| V3Sn | Cr3Si | cP8 | Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n (223) n (223) |
5.003758 | 5.003758 | 5.003758 | 125.3 | −6024.943 |
| V3Sn | Mg3Cd | hP6 | P63/mmc (194) | 5.664976 | 5.664976 | 4.517371 | 125.5 | −6025.165 |
| V3Sn2 | Cr3Si2 | tP10 | P4/mbm (127) | 7.107742 | 7.107742 | 3.555283 | 179.6 | −6118.656 |
| VSnC | MoAlB | oC12 | Cmcm (63) | 2.966421 | 22.230689 | 2.858936 | 188.5 | −2226.001 |
| V2SnC | Cr2AlC | hP8 | P63/mmc (194) | 3.136333 | 3.136333 | 13.011838 | 110.8 | −4204.700 |
| V2Sn2C | Mo2Ga2C | hP10 | P63/mmc (194) | 3.185703 | 3.185703 | 18.846330 | 165.6 | −4299.833 |
| V3SnC | CaTiO3 | cP5 | Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (221) m (221) |
4.081427 | 4.081427 | 4.081427 | 68.0 | −6180.677 |
| V3SnC2 | Ti3SiC2 | hP12 | P63/mmc (194) | 3.055478 | 3.055478 | 18.163485 | 146.9 | −6336.856 |
| V4SnC3 | Ta4AlN3 | hP16 | P63/mmc (194) | 3.009399 | 3.009399 | 23.156747 | 181.6 | −8469.124 |
3.2. Elastic properties
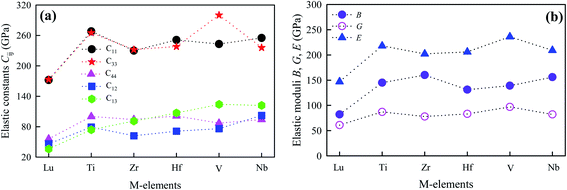
Elastic constants estimate the response of the crystalline solids to external stresses and measure the strength of the materials. Elastic constants also provide a fundamental insight into the nature of bonding character between adjacent atomic planes and the anisotropic character of the bonding and structural stability. They can link between a material's dynamical behaviour and its mechanical and thermal properties. For hexagonal MAX phases, five nonzero independent elastic constants, namely C11, C12, C13, C33, and C44 are obtained.36 Table 3 lists the elastic constants of the newly synthesized V2SnC calculated at zero pressure and zero temperature along with the values found in literatures for existing M2SnC phases for comparison. For Ti2SnC, Nb2SnC, Hf2SnC, and Zr2SnC, we have listed Cij calculated with either different codes or different functionals. The CASTEP-GGA results are consistent to the VASP-GGA values. Fig. 3a presents Cij calculated with CASTEP-GGA, in which the M-elements are shown along the x-axis according to the order of their groups for seeking a trend. All Cij show a tendency of monotonic increase when the M-element moves from left to right across the group-3 to −5, though C13 shows almost linear increase. The constant C66 is not independent as C66 = (C11 − C12)/2. The elastic constants of M2SnC including newly synthesized V2SnC fulfills the mechanical stability criteria for hexagonal crystals:37| C11, C33, C44 > 0; C11 > |C12| and (C11 + C12)C33 > 2C13C13 | (3) |
| Phases | C11 | C33 | C44 | C66 | C12 | C13 | B | G | E | v | B/G | Remarks |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| V2SnC | 243 | 300 | 87 | 84 | 76 | 124 | 156 | 82 | 209 | 0.276 | 1.91 | CASTEP-GGA (This work) |
| 336 | 304 | 85 | 105 | 126 | 122 | 190 | 95 | 244 | 0.286 | 2.00 | CASTEP-GGA13 | |
| Lu2SnC | 172 | 173 | 56 | 64 | 46 | 36 | 82 | 61 | 147 | 0.199 | 1.33 | CASTEP-GGA12 |
| Ti2SnC | 268 | 265 | 100 | 95 | 79 | 74 | 139 | 97 | 236 | 0.217 | 1.43 | CASTEP-GGA12 |
| 253 | 254 | 93 | 79 | 91 | 74 | 138 | 87 | 217 | 0.238 | 1.57 | VASP-GGA46 | |
| 337 | 329 | 169 | 126 | 86 | 102 | 176 | 138 | 329 | 0.188 | 1.27 | FP-L/APW + lo47 | |
| 303 | 308 | 121 | 109 | 84 | 88 | 160 | 114 | 275 | 0.212 | 1.40 | CASTEP-LDA48 | |
| 152 | 83.9 | 207.4 | 0.24 | Experimental39,41 | ||||||||
| Zr2SnC | 230 | 232 | 94 | 84 | 62 | 91 | 131 | 83 | 206 | 0.237 | 1.57 | CASTEP-GGA12 |
| 225 | 227 | 87 | 77 | 72 | 90 | 131 | 78 | 196 | 0.251 | 1.68 | VASP-GGA46 | |
| 269 | 290 | 148 | 94 | 81 | 107 | 157 | 110 | 268 | 0.215 | 1.42 | FP-L/APW + lo47 | |
| 279 | 272 | 111 | 104 | 70 | 89 | 147 | 104 | 252 | 0.215 | 1.42 | CASTEP-LDA48 | |
| 178 | Experimental39 | |||||||||||
| Hf2SnC | 251 | 238 | 101 | 90 | 71 | 107 | 145 | 87 | 218 | 0.250 | 1.67 | CASTEP-GGA12 |
| 249 | 252 | 99 | 85 | 73 | 101 | 144 | 87 | 218 | 0.247 | 1.65 | VASP-GGA46 | |
| 330 | 292 | 167 | 138 | 54 | 126 | 173 | 132 | 316 | 0.195 | 1.30 | FP-L/APW + lo47 | |
| 311 | 306 | 119 | 109 | 92 | 97 | 167 | 112 | 275 | 0.225 | 1.49 | CASTEP-LDA48 | |
| 169 | 237 | Experimental40 | ||||||||||
| Nb2SnC | 255 | 236 | 94 | 77 | 102 | 122 | 160 | 78 | 202 | 0.290 | 2.05 | CASTEP-GGA12 |
| 253 | 250 | 98 | 74 | 103 | 120 | 160 | 80 | 206 | 0.286 | 2.00 | VASP-GGA46 | |
| 341 | 321 | 183 | 118 | 106 | 169 | 209 | 126 | 315 | 0.250 | 1.67 | FP-L/APW + lo47 | |
| 315 | 309 | 124 | 108 | 99 | 141 | 189 | 107 | 189 | 0.262 | 1.77 | CASTEP-LDA48 | |
| 180 | 216 | Experimental40 |
Furthermore, for all M2SnC phases, it is observed that the principal elastic constants C11 and C33 are larger than all other Cij. While for the three systems with M = V, Lu, or Zr, the principal elastic constants are classified as C33 > C11, and the remaining three systems with M = Hf, Ti, or Nb, exhibit C11 > C22 within the same code and functional (CASTEP-GGA). It implies that the former group is more incompressible along the c-axis. Either C11 > C33 or C33 > C11 is the evident of elastic anisotropy of M2SnC MAX phases. The phases Ti2SnC, Zr2SnC and Lu2SnC are elastically less anisotropic than other phases as their C11 and C33 values are very close to each other. The shear elastic constants C12 and C13 lead mutually to a functional stress component in the crystallographic a-axis with a uniaxial strain along the crystallographic b- and c-axis, respectively. This stress component measures the resistance of shear deformation of a material along the crystallographic b- and c-axis, when stress is applied along the a-axis. The phase Nb2SnC is most capable to resist such deformation, while Lu2SnC will deform easily under the same stress along the a-axis. The new compound V2SnC is the next most capable phase to resist the deformation in M2SnC systems if a rank is made one obtains: Nb2SnC > V2SnC > Hf2SnC > Ti2SnC > Zr2SnC > Lu2SnC.
We have obtained the bulk modulus B and shear modulus G of polycrystalline aggregates from individual elastic constants, Cij by the Hill approximations as implemented within the code.38 Using B and G, the average Young's modulus E and the Poisson ratio ν can be obtained:
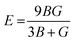 | (4) |
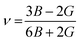 | (5) |
All the elastic moduli B, G, and E and Poisson's ratio v are also listed in Table 3, from which we observe that the results obtained with the CASTEP-GGA and VASP-GGA are consistent to each other, while the other results deviate considerably. Fig. 3b presents elastic moduli calculated with the CASTEP-GGA scheme. B is highly correlated to the chemical composition and structure, while G is linked to chemical bonding. On the other hand, E measures the response under uniaxial tension averaged over all directions. Within the results of this scheme, B is highest for Nb2SnC (160 GPa) and lowest for Lu2SnC (82 GPa). The new phase V2SnC has second highest value of 156 GPa. Ti2SnC has highest G (97 GPa) and E (236 GPa) values. The lowest values of G (61 GPa) and E (147 GPa) are found for Lu2SnC. The new phase V2SnC has an intermediate value of G (80 GPa) and E (209 GPa). When we move from left to right in the Fig. 3b, we cross the group-3 element (Lu) to group-5 elements (V, Nb) via the group-4 elements (Ti, Zr, Hf). The elastic moduli G and E show the almost similar trend. B of the phases containing groups 3 and 4 elements as M-atom show the similar trend of G and E but the phases containing the group-5 elements show the reverse trend. For comparison, we have found 152 ± 3, 180 ± 5, and 169 ± 4 GPa as the measured values of B for Ti2SnC, Nb2SnC, and Hf2SnC, respectively.39,40 These values are larger than the values calculated with GGA within CASTEP and VASP codes by 9–14% and smaller than the other values by 2–16%. The experimental shear modulus is found for Ti2SnC, which is comparable with the GGA-value and much smaller than the other theoretical values listed in Table 3.41 The experimental Poisson's ratio for Ti2SnC is 0.24, which is also very close to the GGA-values rather than other values.41 The experimental value of E for Ti2SnC, Nb2SnC, Zr2SnC, and Hf2SnC are 207.4, 216, 178, and 237 GPa, respectively.40,41 For Nb2SnC and Hf2SnC, the experimental E is larger than the theoretical E calculated with both the CASTEP-GGA and VASP-GGA by 7–8%, while the experiment E of Ti2SnC and Zr2SnC is smaller than the theoretical E derived with GGA within CASTEP and VASP codes by 5–16%. From other theoretical values listed in Table 3, the experimental E deviates within 13–51%. Therefore, the GGA values of B and E obtained with the CASTEP and VASP codes deviates from experimental values within a reasonable range. The larger the E value, the stiffer the system, and therefore the larger the exfoliation energy.42 Amongst the productively etched MAX phases into two-dimensional (2D) MXenes, V2AlC has the largest theoretical exfoliation energy, whose E is reported 311 and 316 GPa.43,44 Accordingly, the exfoliation energy of new MAX phase V2SnC and previously observed M2SnC have lower exfoliation energy than V2AlC. It is evident that all M2SnC (M = V, Ti, Zr, Hf, Nb, and Lu) phases have potential to etch into 2D MXenes.
Poisson's ratio ν provides the information regarding the bonding forces and reflects the stability of a material against shear. The M2SnC MAX phases including newly synthesized V2SnC have Poisson's ratio within 0.195–0.290. As the obtained values with CASTEP-GGA for V2SnC, Hf2SnC and Nb2SnC fall in the range of 0.25–0.5; their interatomic forces can be considered as central forces.45 Literature values of v for Hf2SnC46–48 lie on the lower side of this range, while a literature value for Zr2SnC46 falls within this range. The values outside this range indicate that the interatomic force is non-central. The low value of v for Lu2SnC indicates that it is more stable against shear than other M2SnC phases including the new phase V2SnC.1 Additionally, a pure covalent crystal has a Poisson's ratio of 0.1 and a totally metallic compound has a value of 0.33. As the Poisson's ratio for M2SnC MAX phases lies between these two characteristic values their atomic bonding is expected to be a mixture of covalent and metallic in nature. Furthermore, Poisson's ratio can classify the solid materials as either brittle or ductile with a value of 0.26.49,50 Brittle materials have values less than 0.26 and ductile materials have values larger than this value. Accordingly, the new phase V2SnC and Nb2SnC are ductile and the remaining phases are brittle. Therefore, V2SnC and Nb2SnC are predicted to be damage tolerant.
Bulk modulus to shear modulus ratio (B/G), known as Pugh's ratio can serve as a tool for measuring the ductile/brittle nature of a material.51 If the Pugh's ratio is greater than 1.75 the material is expected to be ductile, otherwise it is brittle in nature. Accordingly, V2SnC and Nb2SnC are ductile in nature as predicted from their Poisson's ratio.
Indeed, it is essential to analyze and visualize the directional dependence of elastic properties – such as Young's modulus (E), linear compressibility (β), shear modulus (G) and Poisson's ratio (ν) of anisotropic materials – rather than their averages. For the M2SnC phases, the directional dependency of E, β, G and ν are calculated using the ELATE suit program52 and the 2D presentations are shown in Fig. 4 for V2SnC, indicating that there is no directional dependence in the xy plane as the plots are uniformly circular but in both xz and yz planes there are directional dependences and which are similar in nature as the hexagonal crystal symmetry of V2SnC. The linear compressibility for some compounds can be negative in some directions, which is represented with an additional curve of red color. For V2SnC, no negative value is found for any direction. The shear modulus G and Poisson's ratio ν are not so straightforward to represent, as they depend on two orthogonal unit vectors a and b, which respectively represent the direction of the stress applied and the direction of measurement. For G and ν there are two curves: translucent blue curve represents the maximal values and green curve represents the minimal positive values. There are a lot of compounds having negative Poisson's ratio in some directions. In this case, an additional curve of translucent red represents the negative values. For V2SnC, no negative Poisson's ratio is found for any directions. For other M2SnC phases, the above discussions are applicable. The directional dependence of E, β, G and ν in xz and yz planes is almost identical for Nb2SnC, Hf2SnC and Zr2SnC. Ti2SnC shows almost isotropic nature of E, β, G and ν in xz and yz planes also. The directional dependence of E, β, G and ν in Lu2SnC is different compared to other M2SnC phases. Linear compressibility in Ti2SnC and Lu2SnC is almost directional independent.
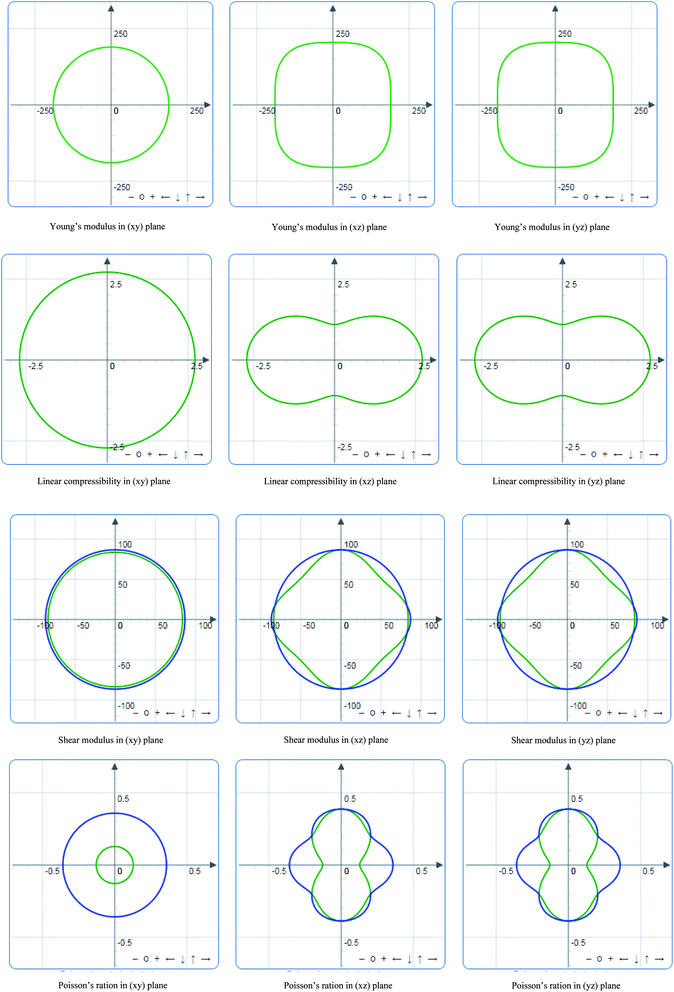 | ||
| Fig. 4 Directional dependence of Young's modulus (E), linear compressibility (β), shear modulus (G) and Poisson's ratio (ν) of V2SnC. | ||
ELATE also provides a quantitative analysis by reporting the minimal and maximal values of each modulus as well as the directions along which these extrema occur. This allows the determination of directions of particular interest in the elastic properties, which are not necessarily along the crystallographic axes of the material. Minimal and maximal values of each modulus are listed in Table 4. A measure of the anisotropy AX of each elastic modulus X is defined as follows:
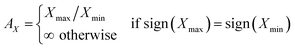 | (6) |
| Phases | Young's modulus (GPa) | Linear compressibility (TPa−1) | Shear modulus (GPa) | Poisson's ratio | ||||
|---|---|---|---|---|---|---|---|---|
| Emin | Emax | βmin | βmax | Gmin | Gmax | νmin | νmax | |
| V2SnC | 188.79 | 223.85 | 1.0964 | 2.7112 | 71.355 | 86.673 | 0.12849 | 0.38828 |
| Hf2SnC | 168.97 | 236.44 | 1.9579 | 2.4813 | 66.846 | 99.802 | 0.12198 | 0.38969 |
| Lu2SnC | 143.59 | 167.39 | 3.8307 | 3.9590 | 56.841 | 70.092 | 0.16641 | 0.26442 |
| Nb2SnC | 168.47 | 237.13 | 1.7785 | 2.1490 | 66.303 | 97.202 | 0.15262 | 0.41665 |
| Ti2SnC | 233.72 | 239.43 | 2.4154 | 2.4509 | 95.408 | 100.210 | 0.19446 | 0.22531 |
| Zr2SnC | 174.63 | 222.77 | 2.1404 | 2.7889 | 68.418 | 94.736 | 0.13615 | 0.33803 |
| Elastic anisotropy AX | ||||
|---|---|---|---|---|
| AE | Aβ | AG | Aν | |
| V2SnC | 1.186 | 2.4729 | 1.215 | 3.0219 |
| Hf2SnC | 1.399 | 1.2674 | 1.493 | 3.1947 |
| Lu2SnC | 1.166 | 1.0335 | 1.233 | 1.5889 |
| Nb2SnC | 1.408 | 1.2083 | 1.466 | 2.7300 |
| Ti2SnC | 1.024 | 1.0147 | 1.050 | 1.1586 |
| Zr2SnC | 1.276 | 1.3030 | 1.385 | 2.4828 |
The obtained elastic anisotropy AX for each elastic modulus is also listed in Table 4. It is observed that Young's modulus shows maximum anisotropy for Nb2SnC and minimum for Ti2SnC. Anisotropy in linear compressibility is maximum for V2SnC and minimum for Ti2SnC. Anisotropy in shear modulus is highest for Hf2SnC and lowest for Ti2SnC. Maximum anisotropy of Poisson's ratio is observed in Hf2SnC and minimum in Ti2SnC. Considering all parameters Ti2SnC is the least anisotropic in M2SnC family.
Here, we want to quantify the degree of elastic anisotropy of V2SnC and compare with previously synthesized M2SnC phases. For hexagonal M2SnC crystals, there are three shear anisotropy factors linked to Cij that can be determined using the succeeding expressions:53
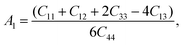 | (7) |
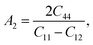 | (8) |
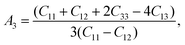 | (9) |
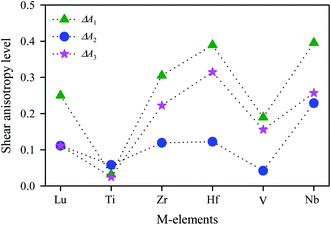
The calculated values of Ai for V2SnC are listed in Table 5 along with reported values for other M2SnC phases and the anisotropy level ΔAi is shown in Fig. 5, suggesting that all M2SnC phases including V2SnC are elastically anisotropic in shear. Shear anisotropy level is highest in Nb2SnC and lowest in Ti2SnC in all respects. The anisotropy level in the new phase V2SnC is higher than that in Ti2SnC and lower than those in other M2SnC phases. It is observed that the shear anisotropy level within a group of M atoms of M2SnC phases increases in the descending order. A different anisotropy factor for hexagonal crystals depending on Cij, i.e. kc/ka = (C11 + C12 − 2C13)/(C33 − C13) is used to quantify the elastic anisotropy upon compression; where ka and kc are the linear compressibility coefficients along the a- and c-axis, respectively.54 Deviation of kc/ka from unity (Δ(kc/ka)), determines the anisotropy level upon linear compression. The calculated value reveals that the compressibility along the c-axis is smaller than that along the a-axis for the new phase V2SnC as well as for Zr2SnC, Hf2SnC, and Nb2SnC. For Lu2SnC and Ti2SnC the compressibility along the c-axis is greater than that along the a-axis.
| Phases | A1 | A2 | A3 | kc/ka | AB% | AG% | AU | Remarks |
|---|---|---|---|---|---|---|---|---|
| V2SnC | 0.8103 | 1.0419 | 0.8443 | 0.4034 | 1.8476 | 0.7283 | 0.1110 | CASTEP-GGA (This work) |
| Lu2SnC | 1.2500 | 0.8889 | 1.1111 | 1.0657 | 0.0256 | 0.3781 | 0.0385 | CASTEP-GGA12 |
| Ti2SnC | 0.9683 | 1.0582 | 1.0247 | 1.0419 | 0.0088 | 0.0284 | 0.0030 | CASTEP-GGA12 |
| Zr2SnC | 0.6950 | 1.1190 | 0.7778 | 0.7801 | 0.2082 | 0.9355 | 0.0986 | CASTEP-GGA12 |
| Hf2SnC | 0.6106 | 1.1222 | 0.6852 | 0.8244 | 0.1093 | 1.6814 | 0.1732 | CASTEP-GGA12 |
| Nb2SnC | 0.6046 | 1.2288 | 0.7429 | 0.9912 | 0.0020 | 1.6962 | 0.1726 | CASTEP-GGA12 |
According to Hill, the difference between BV and BR as well as GV and GR is proportional to the degree of elastic anisotropy of crystals, which leads to define the percentage anisotropy factors AB and AG with the succeeding equations:55
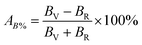 | (10) |
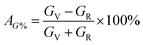 | (11) |
The percentage anisotropy factors AB and AG calculated for V2SnC are also listed in Table 5 together with the literature value of other M2SnC phases. These two factors assign zero values for completely isotropic crystals in view of compressibility and shear, respectively. A positive value quantifies the level of anisotropy. It is evident that the new phase V2SnC is more anisotropic in compression, whereas Nb2SnC is more anisotropic in shear. Nb2SnC is less anisotropic in compression and Ti2SnC is less anisotropic in shear. An anisotropy factor named “universal anisotropy index” is recently proposed for an appropriate universal measure of elastic anisotropy of crystals and defined as:56
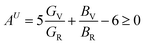 | (12) |
This index has either zero or positive value. Zero value signifies the completely isotropic nature and positive value indicates the anisotropy level in elastic properties of crystals. According to this index (see Table 5), the new phase V2SnC is more anisotropic than Lu2SnC, Ti2SnC and Zr2SnC and less anisotropic than Hf2SnC and Nb2SnC. It is evident that the universal anisotropy level follows the trend of shear anisotropy level. That is, the universal anisotropy level within a group of M atoms of M2SnC phases increases in the descending order.
3.3. Electronic properties
Electronic structure plays a significant role in understanding of material properties at the microscopic level. Electronic energy band structure calculated along high symmetry points of the Brillouin zone for V2SnC is shown in Fig. 6a. Similar to other M2SnC and remaining MAX phases, the band structure of V2SnC reveals the metallic characteristics as a large number of its valence bands cross the Fermi level EF and overlap with the conduction bands. The position of Fermi level in V2SnC is just below the valence band maximum near the Γ-point as in Ti2SnC.5 In Nb2SnC, the Fermi level is above the valence band maximum at the Γ-point.5 The Γ-point, where the maximum of the valence bands accumulate, lies above the Fermi levels of Sn-based other MAX phases Hf2SnC, Zr2SnC and Lu2SnC (see Fig. 6 in ref. 5). The band structure of V2SnC is very similar to that of Nb2SnC rather than other M2SnC phases.5 Nb2SnC is a superconducting phase. Resemblance of two band structures indicates the possibility of superconductivity in V2SnC. The main characteristic of the band structure is the significantly anisotropic nature with less energy dispersion along the c-axis. It is evident from the reduced dispersion along the short H–K and M–L directions. The anisotropic band structure near and below the Fermi level implies that the electrical conductivity is also anisotropic for the new MAX phase studied here.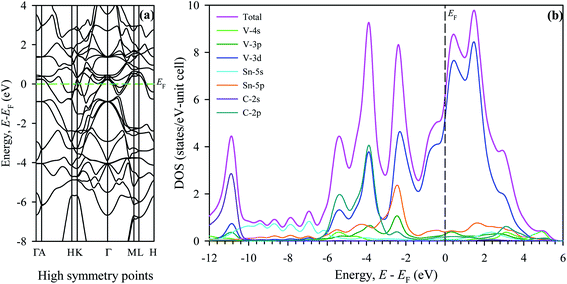 | ||
| Fig. 6 Electronic structures of V2SnC, (a) band structure and (b) density of states; EF denotes the Fermi level. | ||
To realize the bonding nature, the total and partial density of states (DOS) are calculated for V2SnC and presented in Fig. 6b. The Fermi level of V2SnC lies far from a pseudogap at the left instead of near a pseudogap as found for other existing M2SnC MAX phases.5 Consequently, the new phase V2SnC is not as stable as other M2SnC phases. In fact, the Fermi level of V2SnC lies at the wall of a large peak and as a result V2SnC has a large total DOS of 6.12 states per eV per unit cell at EF, whereas the total DOS at EF for other M2SnC phases ranges from 2.35–3.93 states per eV per unit cell.5 The valence band of V2SnC contains two main parts. An intermediate low flat-type valence band arises due to Sn-s orbitals in similar to in other M2SnC and M3SnC2 compounds.5,27 The lower valence band consists of a single peak arising owing to the hybridization between V-3d and C-2s states, which indicate strong covalent V–C bond in V2SnC similar to the M–C bonds in M2SnC. The higher valence band contains three distinct peaks similar to those of Nb2SnC.5 The small peak at the left of the higher valence band arises due to the interaction between V-3d and C-2p-orbitals. The middle peak is the highest peak and arises owing to the hybridization between V-3d and C-2p electrons. The third peak corresponds to the interaction between V-3d and Sn-5p states. This interaction results in weaker covalent V–Sn bonding due to closeness of the peak to the Fermi level. It is clear that the V–C bond is stronger than V–Sn bond as M–C bonds are stronger than M–A bonds. Weaker M–A bond favours the exfoliation of M2SnC MAX phases to 2D MXenes.59 The overall bonding nature in the new phase V2SnC is a combination of metallic, covalent, and, due to the difference in electronegativity between the constituent atoms, ionic like other MAX phase compounds.1,3,5,27,57
We have calculated the electron charge density map and Fermi surface to understand the nature of chemical bonding in V2SnC. In the contour map of electron charge density (Fig. 7a) it is seen that the charge distributions around V atoms are practically spherical and its intensity specifies the amount of charge accumulation. The charge accumulated around the V atom is 0.32e, whereas the charge accumulation around the M atoms in other M2SnC systems ranges from 0.28–0.45e.5 The highest charge is deposited around the Lu atom (0.45e) and lowest charge around the Hf atom (028e). The V-charge overlaps with the C-charge and slightly edges with the Sn-charge, which indicates the strong V–C and weak V–Sn bonds, respectively. Analogous bonds are also seen in the contour maps of other M2SnC compounds.5 The spherical charge distributions around the atoms also indicate some ionic nature in chemical bonds in V2SnC as well as in other M2SnC MAX phases.
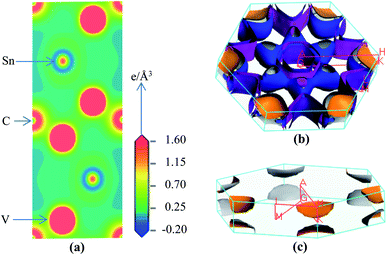 | ||
| Fig. 7 Electronic structures of V2SnC; (a) charge density map, (b) Fermi surface and (c) fourth Fermi sheet. | ||
The Fermi surface (FS) calculated for the V2SnC MAX phase is shown in Fig. 7b, which contains four different sheets. All sheets are seen to be centered along the Γ–A direction. The first and second sheets are cylindrical. They have an extra part like a half-folded plain sheet along each L–M direction. The third sheet shows a lot of nesting nature. It has also an additional part along H–K directions, whose shape is like a cylinder cutting parallel to its axis. The fourth sheet consists of two identical parts along the H–K directions. The lower part is just the mirror inversion of the upper part (Fig. 7c). As seen from Fig. 5a, near the Γ (0,0,0) point, two hole-like bands appear, giving rise to two hole-like Fermi surface sheets near the Γ point (first and second sheets). Conversely, the calculated band structure near the H(1/3, 1/3, 1/3) point consists of two electron-like bands, corresponding to two electron-like Fermi surface sheets near the H point (third and fourth sheets). The FS of V2SnC has a lot of similarities to that of superconducting Nb2SnC among all M2SnC MAX phases.5 Nb2SnC is a superconducting phase having nesting nature in its FS. This nesting plays a role in strong electron–phonon interactions and is ultimately able to enhance the superconducting order of the material.58 Nesting nature is an indication of superconductivity of V2SnC. We hope that the experimentalists will be stimulated to confirm the prediction.
3.4. Thermal properties
In this section, we have reported the elastic Debye temperature, melting point, lattice thermal conductivity and minimum thermal conductivity of V2SnC. Debye temperature θD is a characteristic temperature of solid materials that can be calculated from the elastic moduli using Anderson method.59 This method is simple and rigorous, which determines θD using average sound velocity calculated from the shear and bulk moduli via the equation:
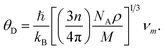 | (13) |
In this equation, ℏ and kB are respectively the Plank and Boltzmann constants, NA is Avogadro's number, ρ is the mass density, n is the number of atoms in a molecule, and M is the molecular weight. The average sound velocity vm is obtained from the longitudinal and transverse sound velocities vl and vt by the equation:
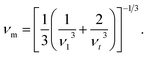 | (14) |
With the bulk modulus B and shear modulus G, vl and vt can be determined as:
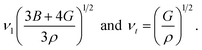 | (15) |
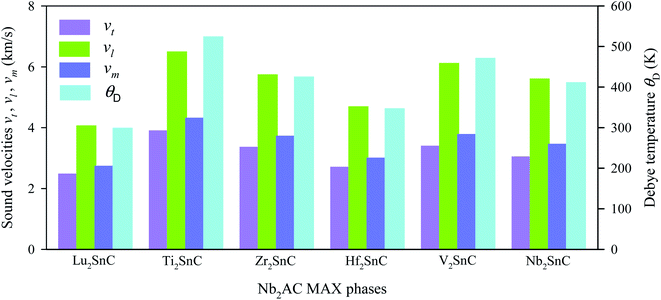
The obtained sound velocities and Debye temperature of V2SnC is listed in Table 6 along with the literature values for existing M2SnC phases and the CASTEP-GGA values are given in Fig. 8. There are several sets of literature values of θD for M = Ti, Zr, Hf, and Nb. It is observed that the values derived with the GGA functional using the CASTEP and VASP codes are consistent as we have a close measured value (380 K) and a theoretical value (412 K) of θD for Nb2SnC.60,61 The remaining two sets of θD values show large deviations from the former sets as well as from the available experimental and theoretical values. It is evident from the Fig. 8 that the sound velocities and Debye temperature follow the reverse trend of shear and universal anisotropy level. That is, the sound velocities and Debye temperature within a group of M atoms of M2SnC phases decrease in the descending order.
| Phases | ρ | vl | vt | vm | θD | Tm | κmin | κphb | Remarks |
|---|---|---|---|---|---|---|---|---|---|
| a Calculated from published data.b Calculated at 300 K. | |||||||||
| V2SnC | 7.073 | 6.125 | 3.405 | 3.792 | 472 | 1533 | 1.20 | 14.38 | CASTEP-GGA (This work) |
| Lu2SnC | 9.847 | 4.073 | 2.489 | 2.748 | 300 | 1130 | 0.51 | 14.91 | CASTEP-GGA12 |
| Ti2SnC | 6.346 | 6.503 | 3.910 | 4.325 | 525 | 1556 | 0.99 | 29.98 | CASTEP-GGA12 |
| 6.346 | 6.327 | 3.703 | 4.106 | 498 | 1494 | 1.23 | 22.24 | VASP-GGA46,a | |
| 6.473 | 7.113 | 4.337 | 4.790 | 585 | 1859 | 1.45 | 49.51 | FP-L/APW + lo47 | |
| 6.76 | 6.783 | 4.099 | 4.532 | 561 | 1725 | 1.08 | 36.87 | CASTEP-LDA48 | |
| Zr2SnC | 7.313 | 5.749 | 3.369 | 3.735 | 426 | 1392 | 0.76 | 20.61 | CASTEP-GGA12 |
| 7.313 | 5.669 | 3.266 | 3.627 | 414 | 1370 | 0.73 | 17.22 | VASP-GGA46,a | |
| 7.280 | 6.357 | 3.831 | 4.236 | 483 | 1596 | 0.86 | 34.67 | FP-L/APW + lo47 | |
| 7.75 | 6.111 | 3.683 | 4.073 | 472 | 1599 | 0.86 | 31.82 | CASTEP-LDA48 | |
| Hf2SnC | 11.796 | 4.704 | 2.716 | 3.015 | 348 | 1464 | 0.63 | 15.92 | CASTEP-GGA12 |
| 11.796 | 4.695 | 2.716 | 3.015 | 348 | 1479 | 0.63 | 16.15 | VASP-GGA46,a | |
| 11.828 | 5.228 | 3.118 | 3.446 | 398 | 1782 | 0.72 | 32.92 | FP-L/APW + lo47 | |
| 12.06 | 5.121 | 3.050 | 3.376 | 393 | 1746 | 0.71 | 26.94 | CASTEP-LDA48 | |
| Nb2SnC | 8.369 | 5.616 | 3.053 | 3.469 | 412 | 1473 | 0.76 | 12.38 | CASTEP-GGA12 |
| 8.369 | 5.645 | 3.092 | 3.448 | 410 | 1488 | 0.76 | 12.61 | VASP-GGA46,a | |
| 8.388 | 6.358 | 3.626 | 4.030 | 480 | 1859 | 0.89 | 29.96 | FP-L/APW + lo47 | |
| 8.53 | 6.150 | 3.493 | 3.883 | 469 | 1763 | 0.87 | 22.92 | CASTEP-LDA48 | |
The Debye temperatures of M2SnC MAX phases follow the order of Lu2SnC < Hf2SnC < Nb2SnC < Zr2SnC < V2SnC < Ti2SnC. High average sound velocity corresponds to a high Debye temperature of Ti2SnC. The new phase V2SnC has the second highest Debye temperature. Lu2SnC has a low Debye temperature because of its low average sound velocity. Generally, the higher the Debye temperature the stiffer the material. Therefore, V2SnC is softer than Ti2SnC and stiffer than the other existing M2SnC MAX phases. A low Debye temperature results in low thermal conductivity of a material, which favors it for being a promising thermal barrier coating (TBC) material.62 The Debye temperature of a promising TBC material, Y4Al2O9 is 564 K,63 which is larger than those of existing M2SnC phases. Therefore, M2SnC phases including new phase V2SnC have possibility to be potential TBC materials if they have low thermal conductivity, high thermal expansion coefficient, high melting point and oxidation resistance. For comparison, we have experimental Debye temperature only for Nb2SnC (380 K),60 which is comparable to the theoretical value (412 K).13
Lattice thermal conductivity is one of the most fundamental properties of solids. As the MAX phases have dual characters of metals and ceramics, therefore, to determine their lattice thermal conductivity, the Slack model is appropriate as it deals with materials having partial ceramic nature.64 The model considers the average of the atoms (M/n) in a “molecule” (or the atoms in the formula unit of the crystal) and their average atomic weight. This model is useful to determine the temperature-dependent lattice thermal conductivity of materials. On the other hand, Clarke's model is very advantageous for calculating the temperature-independent minimum thermal conductivity of compounds.1 Slack's equation for calculating the lattice thermal conductivity is
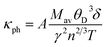 | (16) |
In this formulation, Mav is the average atomic mass in kg mol−1, θD is the Debye temperature in K, δ is the cubic root of average atomic volume in m, n is the number of atoms in a conventional unit cell, T is the temperature in K, and γ is the Grüneisen parameter, which is calculated from the Poisson's ratio with the equation
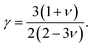 | (17) |
The factor A(γ) due to Julian65 can be obtained as
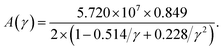 | (18) |
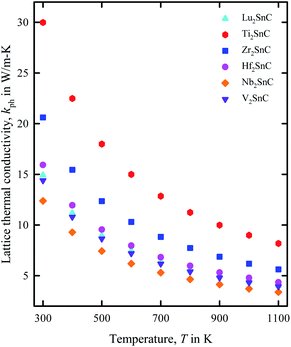
The lattice thermal conductivity of V2SnC calculated at room temperature (300 K) is listed in Table 6 and its temperature dependence is shown in Fig. 9. Table 5 also lists the literature values for other existing M2SnC phases. Lattice thermal conductivity is highly sensitive to the Debye temperature. As the Debye temperature agrees fairly with the experimental value for the theoretical results with the GGA functional within the CASTEP and VASP codes, the room temperature lattice thermal conductivity calculated with the same functional within the same codes is expected to be consistent with the experiment if it is done in future. The reliability of Slack model has been established for MAX phases as their calculated lattice thermal conductivity agrees fairly well with the experimental values. For instance, the calculated (experimental) lattice thermal conductivity at 1300 K for Ta4AlC3 and Nb4AlC3 are 5 (6) W m−1 K−1 and 7 (7) W m−1 K−1, respectively.61 The lattice thermal conductivity at room temperature for M2SnC MAX phases ranges from 14 to 30 W m−1 K−1 within the CASTEP-GGA calculations, which does not exceed the typical range for MAX phases.66 Fig. 9 exhibits the gradual decrease of lattice thermal conductivity of M2SnC with the increase of temperature. The new phase V2SnC has lattice thermal conductivities very close to those of Lu2SnC for the whole range of temperatures. Lu2SnC is already predicted as better TBC materials among M2SnC (M = Lu, Ti, Nb, Zr, Hf) phases.12 Therefore, the new phase V2SnC is expected to be a promising TBC material as Lu2SnC.
The theoretical lower limit of intrinsic thermal conductivity of a material at high temperature is defined as its minimum thermal conductivity. The phonons become unpaired at high temperature and hence the heat energy is transferred to the adjacent atoms. In this situation, the mean free path of phonons is supposed to be the average interatomic distance. According to this approximation, different atoms can be substituted within a molecule with an equivalent atom having average atomic mass of M/n (n is the number of atoms in a primitive cell). A single “equivalent atom” within the cell never exhibits optical modes and hence it can be used to derive a formulation to determine the minimum thermal conductivity κmin at high temperature, as Clarke described in his model:67
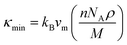 | (19) |
The symbols used in this expression carry the same meanings of those used in eqn (4). The minimum thermal conductivity calculated for the new MAX phase V2SnC is listed in Table 6 along with literature values for other M2SnC MAX phases. In the similar fashion of other properties, the minimum thermal conductivity calculated with GGA functional within CASTEP and VASP codes show more consistency than other results listed in Table 6. For comparison, we have another theoretical result of 0.755 W m−1 K−1 for Nb2SnC,61 which is identical to 0.76 W m−1 K−1 obtained in the present and a previous46 calculations with GGA within CASTEP and VASP codes. The new phase has the highest value of 1.20 W m−1 K−1 among M2SnC phases considering same functional within same code, which is very close to 1.13 W m−1 K−1 of a promising TBC material, Y4Al2O9.63 Additionally, the ultralow minimum thermal conductivity of 1.25 W m−1 K−1 is used for selecting appropriate materials for TBC applications.68 Therefore, M2SnC phases including new phase V2SnC have the possibility to be promising TBC materials.
3.5. Vibrational properties
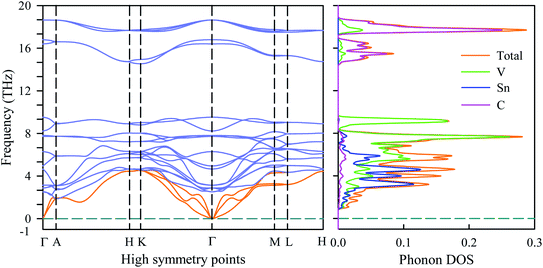
To verify the dynamical stability of the newly synthesized V2SnC MAX phase, the phonon dispersion and phonon density of states are investigated. The phonon dispersion curve is shown in the left panel of Fig. 10. There is no negative phonon frequency in the whole Brillouin zone. The absence of negative phonon frequency ensures the absence of soft phonon modes, indicating that the phase V2SnC is dynamically stable against the mechanical perturbation at ambient state like the other existing M2SnC phases.12 211 MAX phases have eight atoms in their unit cell, which lead to 24 vibrational modes including three acoustic and 21 optical modes. The lower branches correspond to the acoustic modes (orange) and the upper branches with frequencies greater than 2 THz correspond to the optical modes (light blue). Lower optical branches overlap with the acoustic branches and consequently there is no phononic band gap between the acoustic and optical branches. The zero phonon frequency of the acoustic modes at the Γ point is another indication of dynamical stability of the V2SnC MAX phase. The phonon DOS shown in the right panel of Fig. 10, reveals that the acoustic and lower optical modes arise due to the vibration of heavier atoms Sn and V. The higher optical modes mainly originate from the vibration of lighter atom C. Acoustic phonon is caused by the coherent vibrations of atoms in a lattice outside their equilibrium position. On the other hand, when an atom moves to the left and its neighbour to the right, the optical phonon is originated due to the out-of-phase oscillation of the atom in a lattice. Optical phonons control the most of the optical properties of crystals.3.6. Vickers' hardness
Herein, the theoretical method based on Mulliken population developed by Gou et al.69 is used to calculate the Vickers' hardness of partial metallic compounds. Within this method, the bond hardness Hμv is calculated as:
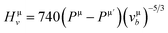 | (20) |
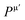 is the metallic population and can be calculated with the unit cell volume V and the number of free electrons in a cell, nfree as follows:
is the metallic population and can be calculated with the unit cell volume V and the number of free electrons in a cell, nfree as follows: 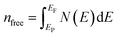 and
and 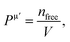 EP and EF are the energy at the pseudogap and at the Fermi level, respectively, vμb is the volume of μ-type bond and is calculated from the bond length dμ of μ-type and the number of bonds Nvb of v type per unit volume using the equation
EP and EF are the energy at the pseudogap and at the Fermi level, respectively, vμb is the volume of μ-type bond and is calculated from the bond length dμ of μ-type and the number of bonds Nvb of v type per unit volume using the equation 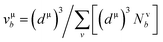 . Then, the theoretical Vickers hardness for complex multiband crystal can be determined as a geometric average of all bond hardness values as follows:
. Then, the theoretical Vickers hardness for complex multiband crystal can be determined as a geometric average of all bond hardness values as follows:
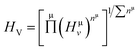 | (21) |
 , and hardness HV (GPa) of M2SnC MAX phases
, and hardness HV (GPa) of M2SnC MAX phases
| Compound | Bond | nμ | dμ | Pμ | vμb | Hμν | HV | HV (expt.) | |
|---|---|---|---|---|---|---|---|---|---|
| V2SnC | V–C | 4 | 2.0526 | 1.02 | 0.05432 | 27.30 | 2.9 | 2.9 | |
| Ti2SnC | Ti–C | 4 | 2.1414 | 1.08 | 0.01525 | 30.00 | 2.7 | 2.7 | 3.5,32 3.570 |
| Zr2SnC | Zr–C | 4 | 2.3118 | 1.05 | 0.01302 | 36.18 | 1.9 | 1.9 | 3.5,32 3.970 |
| Lu2SnC | Sn–C | 4 | 4.3478 | 0.12 | 0.00348 | 41.82 | 0.2 | 0.2 | |
| Hf2SnC | Hf–C | 4 | 2.3158 | 1.39 | 0.00541 | 35.73 | 2.6 | 2.6 | 3.8,32 4.570 |
| Nb2SnC | Nb–C | 4 | 2.2014 | 0.99 | 0.00139 | 31.98 | 2.3 | 2.3 | 3.8,70 3.570 |
The theoretical HV of Lu2SnC is very small compared to the lower limit of measured value for MAX phases. The reason may be the absence of typical M–C bond in the structure of Lu2SnC. This also reduces the elastic constants, elastic moduli and melting and Debye temperature in Lu2SnC. Consequently, Lu2SnC is the most soft and easily machinable compound in M2SnC as well as in MAX family. Indeed, the hardness of MAX phases is very small compared to their corresponding binary phases. Low hardness of MAX phases makes them machinable compounds. All phases in M2SnC family are easily machinable compared to many other MAX phases.
3.7. Defect processes
Frenkel defect energies provide the information regarding nuclear applications of a material as the low pair formation energy is linked to a higher content of more persistent defects. These in turn cause the loss of ordering in the structure of a crystal. An accumulation of defects in a crystal that are formed by the displacement cascades are indicative of radiation tolerance of the material.71,72 In Table 8, the relations (1–3) are the key reactions for the Frenkel defects in Kröger–Vink notation73 for M2SnC phases.Antisite defects are point defects formed due to either recombination or occupation of atoms at alternative lattice sites during radiation damage.71 Low energy antisite formation energy indicates that a major population of residual defects will persist in a material, as a net reduction of defect mobility arises due to change of an interstitial into an antisite,71,74 The antisite formation mechanisms are given by the reactions (4)–(6) in Table 8.
Displacive radiation causes an athermal concentration of Frenkel pairs, as it is assumed that the radiation tolerance of materials depends on the resistance to form persistent populations of Frenkel (and antisite) defects.72 In this context, high defect energy is indicative of radiation tolerance. In a previous study of M2SnC (M = Lu, Ti, Zr, Hf, and Nb) phases, Nb2SnC is predicted as most radiation tolerant MAX phase in these systems.5 If the new phase V2SnC is included in these systems Nb2SnC remains at the same position. Comparing with other M2SnC phases, the radiation tolerance in V2SnC is better than Lu2SnC and lower than remaining ones.
Although the M interstitials, according to reaction (9), will recombine with 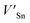 to form MA antisites for all the M2SnC MAX phases studied here, there will be very little concentration of Mi in the first place due to the very high reaction energies of reaction (1) listed in Table 8. Under equilibrium conditions, this will effectively render reaction (7) practically irrelevant. Similar arguments are also applicable for the other antisite reactions (8) and (9). These reactions may become pertinent in the case of a non-equilibrium environment (i.e., under irradiation) where an increased defect concentration is feasible. In this environment, it is expected that Mi will recombine with
to form MA antisites for all the M2SnC MAX phases studied here, there will be very little concentration of Mi in the first place due to the very high reaction energies of reaction (1) listed in Table 8. Under equilibrium conditions, this will effectively render reaction (7) practically irrelevant. Similar arguments are also applicable for the other antisite reactions (8) and (9). These reactions may become pertinent in the case of a non-equilibrium environment (i.e., under irradiation) where an increased defect concentration is feasible. In this environment, it is expected that Mi will recombine with 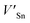 to produce MA antisites. Moreover, the creation of CSn through the reaction (8) should be anticipated for Ti2SnC. After irradiation, these processes may only be relevant, given that the formation energies of the Mi defects according to the Frenkel reaction (relation-(1)) are high for all the M2SnC MAX phases studied here (6.40–9.34 eV, refer to Table 8). The processes considered for the displacement of lattice atoms by interstitials (reactions (13)–(18)) are all positive in energy. The new phase requires lowest energy in Schottky reaction. From an experimental point of view, the radiation tolerance and oxidation resistance of M2SnC phases have to be determined at high temperature. A detailed understanding of the radiation tolerance of V2SnC requires systematic experimental work and simulation over a range of timescales and system sizes.
to produce MA antisites. Moreover, the creation of CSn through the reaction (8) should be anticipated for Ti2SnC. After irradiation, these processes may only be relevant, given that the formation energies of the Mi defects according to the Frenkel reaction (relation-(1)) are high for all the M2SnC MAX phases studied here (6.40–9.34 eV, refer to Table 8). The processes considered for the displacement of lattice atoms by interstitials (reactions (13)–(18)) are all positive in energy. The new phase requires lowest energy in Schottky reaction. From an experimental point of view, the radiation tolerance and oxidation resistance of M2SnC phases have to be determined at high temperature. A detailed understanding of the radiation tolerance of V2SnC requires systematic experimental work and simulation over a range of timescales and system sizes.
4. Conclusions
In summary, the density functional theory is employed to investigate the phase stability and physical properties of a newly synthesized 211 MAX phase, V2SnC for the first time. The calculated results are compared with those of other existing M2SnC (M = Ti, Zr, Hf, Nb, and Lu) phases. The newly synthesized compound V2SnC has passed the mechanical, dynamic and thermodynamic stability tests. The new phase V2SnC is the second most capable phase to resist the deformation in M2SnC systems following the order: Nb2SnC > V2SnC > Hf2SnC > Ti2SnC > Zr2SnC > Lu2SnC. It also has the second highest value of B and θD and an intermediate value of G and E in the M2SnC family. V2SnC is softer than Ti2SnC and stiffer than other existing M2SnC MAX phases. V2SnC has potential to be etched into 2D MXene like the other M2SnC phases. V2SnC and Nb2SnC are ductile and damage tolerant and the remaining phases are brittle in nature. The directional dependence of E, β, G and ν of M2SnC is calculated. All M2SnC phases show directional dependence of E, G, and ν in the xz and yz planes. Ti2SnC and Lu2SnC show almost directional independency on β. Elastic anisotropy in V2SnC is higher than Ti2SnC and less than the other M2SnC phases. The band structure and Fermi surface are indicative of possible superconductivity of V2SnC. V2SnC is anticipated to be a promising TBC material as Lu2SnC among M2SnC phases. V2SnC is more radiation tolerant than Lu2SnC and less than the remaining other M2SnC phases.Authors contribution
M. A. Hadi: conceptualization, data curation, investigation, methodology, formal analysis, writing – original draft. M. Dahlqvist: software, formal analysis, review & editing; S.-R. G. Christopoulos: investigation, data curation; S. H. Naqib: project administration, review & editing; A. Chroneos: formal analysis, writing, review & editing. A. K. M. A. Islam: formal analysis, review & editing.Data availability
Supplementary data will be made available on request.Conflicts of interest
There are no conflicts of interest to declare.References
- M. A. Hadi, J. Phys. Chem. Solids, 2020, 138, 109275 CrossRef CAS.
- T. Rackl, L. Eisenburger, R. Niklaus and D. Johrendt, Phys. Rev. Mater., 2019, 3, 054001 CrossRef CAS.
- M. W. Barsoum, Prog. Solid State Chem., 2000, 28, 201–281 CrossRef CAS.
- D. Horlait, S. Grasso, A. Chroneos and W. E. Lee, Mater. Res. Lett., 2016, 4, 137–144 CrossRef CAS.
- M. A. Hadi, N. Kelaidis, S. H. Naqib, A. Chroneos and A. K. M. A. Islam, Comput. Mater. Sci., 2019, 168, 203–212 CrossRef CAS.
- D. J. Tallman, E. N. Hoffman, E. N. Caspi, B. L. Garcia-Diaz, G. Kohse, R. L. Sindelar and M. W. Barsoum, Acta Mater., 2015, 85, 132–143 CrossRef CAS.
- M. A. Hadi, M. A. Rayhan, S. H. Naqib, A. Chroneos and A. K. M. A. Islam, Comput. Mater. Sci., 2019, 170, 109144 CrossRef CAS.
- H. Nowotny and F. Benesovsky, J. Less-Common Met., 1964, 7, 133–138 CrossRef.
- W. Jeitschko and H. N. F. Benesovsky, Monatsh. Chem., 1963, 94, 1198–1200 CrossRef CAS.
- F. Benesovsky, Monatsh. Chem., 1963, 94, 332–333 CrossRef.
- S. Kuchida, T. Muranaka, K. Kawashima, K. Inoue, M. Yoshikawa and J. Akimitsu, Physica C Supercond., 2013, 494, 77–79 CrossRef CAS.
- M. A. Hadi, N. Kelaidis, S. H. Naqib, A. Chroneos and A. K. M. A. Islam, J. Phys. Chem. Solids, 2019, 129, 162–171 CrossRef CAS.
- Q. Xu, Y. Zhou, A. Jiang, H. Zhang, Q. Tao, J. Lu, J. Rosen, S. Grasso and C. Hu, J. Adv. Ceram., 2020, 9, 481–492 CrossRef CAS.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567 CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188 CrossRef.
- T. H. Fischer and J. Almlof, J. Phys. Chem., 1992, 96, 9768 CrossRef CAS.
- F. D. Murnaghan, Finite Deformation of an Elastic Solid, Wiley, New York, 1951 Search PubMed.
- M. A. Hadi, M. T. Nasir, M. Roknuzzaman, M. A. Rayhan, S. H. Naqib and A. K. M. A. Islam, Phys. Status Solidi B, 2016, 253, 2020–2026 CrossRef CAS.
- M. A. Hadi, M. Roknuzzaman, A. Chroneos, S. H. Naqib, A. K. M. A. Islam, R. V. Vovk and K. Ostrikov, Comput. Mater. Sci., 2017, 137, 318–326 CrossRef CAS.
- M. H. K. Rubel, M. A. Hadi, M. M. Rahaman, M. S. Ali, M. Aftabuzzaman, R. Parvin, A. K. M. A. Islam and N. Kumada, Comput. Mater. Sci., 2017, 138, 160–165 CrossRef CAS.
- M. Roknuzzaman, M. A. Hadi, M. A. Ali, M. M. Hossain, N. Jahan, M. M. Uddin, J. A. Alarco and K. Ostrikov, J. Alloys Compd., 2017, 727, 616–626 CrossRef CAS.
- M. T. Nasir, M. A. Hadi, M. A. Rayhan, M. A. Ali, M. M. Hossain, M. Roknuzzaman, S. H. Naqib, A. K. M. A. Islam, M. M. Uddin and K. Ostrikov, Phys. Status Solidi B, 2017, 254, 1700336 CrossRef.
- S.-R. G. Christopoulos, P. P. Filippatos, M. A. Hadi, N. Kelaidis, M. E. Fitzpatrick and A. Chroneos, J. Appl. Phys., 2018, 123, 025103 CrossRef.
- A. M. M. Tanveer Karim, M. A. Hadi, M. A. Alam, F. Parvin, S. H. Naqib and A. K. M. A. Islam, J. Phys. Chem. Solids, 2018, 117, 139–147 CrossRef CAS.
- M. A. Hadi, S.-R. G. Christopoulos, S. H. Naqib, A. Chroneos, M. E. Fitzpatrick and A. K. M. A. Islam, J. Alloys Compd., 2018, 748, 804–813 CrossRef CAS.
- M. A. Hadi, M. N. Islam and M. H. Babu, Z. Naturforsch., A: Phys. Sci., 2019, 74, 71 CAS.
- P. P. Filippatos, M. A. Hadi, S.-R. G. Christopoulos, A. Kordatos, N. Kelaidis, M. E. Fitzpatrick, M. Vasilopoulou and A. Chroneos, Materials, 2019, 12, 4098 CrossRef CAS.
- M. N. Islam, M. A. Hadi and J. Podder, AIP Adv., 2019, 9, 125321 CrossRef.
- M. Mozahar Ali, M. A. Hadi, M. L. Rahman, F. H. Haque, A. F. M. Y. Haider and M. Aftabuzzaman, J. Alloys Compd., 2020, 821, 153547 CrossRef.
- M. W. Barsoum, G. Yaroschuck and S. Tyagi, Scr. Mater., 1997, 37, 1583–1591 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751 CrossRef.
- M. Dahlqvist, B. Alling, I. A. Abrikosov and J. Rosén, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 024111 CrossRef.
- A. S. Ingason, A. Petruhins, M. Dahlqvist, F. Magnus, A. Mockute, B. Alling, L. Hultman, I. A. Abrikosov, P. O. Å. Persson and J. Rosen, Mater. Res. Lett., 2014, 2, 89–93 CrossRef CAS.
- M. A. Hadi, S. H. Naqib, S.-R. G. Christopoulos, A. Chroneos and A. K. M. A. Islam, J. Alloys Compd., 2017, 724, 1167–1175 CrossRef CAS.
- M. Born, On the stability of crystal lattices. I, Mathematical Proceedings of the Cambridge Philosophical Society, Cambridge University Press, 1940, p. 160 Search PubMed.
- R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349 CrossRef.
- B. Manoun, S. K. Saxena, G. Hug, A. Ganguly, E. N. Hoffman and M. W. Barsoum, J. Appl. Phys., 2007, 101, 113523 CrossRef.
- T. El-Raghy, S. Chakraborty and M. W. Barsoum, J. Eur. Ceram. Soc., 2000, 20, 2619–2625 CrossRef CAS.
- T. Lapauw, K. Vanmeensel, K. Lambrinou and J. Vleugels, J. Alloys Compd., 2015, 631, 72–76 CrossRef CAS.
- A. Champagne, F. Ricci, M. Barbier, T. Ouisse, D. Magnin, S. Ryelandt, T. Pardoen, G. Hautier, M. W. Barsoum and J.-C. Charlier, Phys. Rev. Mater., 2020, 4, 013604 CrossRef CAS.
- S. Aryal, R. Sakidja, M. W. Barsoum and W.-Y. Ching, Phys. Status Solidi B, 2014, 251, 1480–1497 CrossRef CAS.
- M. F. Cover, O. Warschkow, M. M. M. Bilek and D. R. McKenzie, J. Phys.: Condens. Matter, 2009, 21, 305403 CrossRef CAS.
- M. A. Hadi, Comput. Mater. Sci., 2016, 117, 422–427 CrossRef CAS.
- S. Aryal, R. Sakidja, M. W. Barsoum and W.-Y. Ching, Phys. Status Solidi B, 2014, 251, 1480–1497 CrossRef CAS.
- M. B. Kanoun, S. Goumri-Said and A. H. Reshak, Comput. Mater. Sci., 2009, 47, 491–500 CrossRef CAS.
- A. Bouhemadou, Phys. B, 2008, 403, 2707 CrossRef CAS.
- I. N. Frantsevich, F. F. Voronov and S. A. Bokuta, Elastic Constants and Elastic Moduli of Metals and Insulators Handbook, Naukova Dumka, Kiev, 1983, pp. 60–180 Search PubMed.
- G. Vaitheeswaran, V. Kanchana, A. Svane and A. Delin, J. Phys.: Condens. Matter, 2007, 19, 326214 CrossRef.
- S. F. Pugh, Philos. Mag., 1954, 45, 823 CAS.
- R. Gaillac, P. Pullumbi and F.-X. Coudert, J. Phys.: Condens. Matter, 2016, 28, 275201 CrossRef.
- M. A. Ali, M. A. Hadi, M. M. Hossain, S. H. Naqib and A. K. M. A. Islam, Phys. Status Solidi B, 2017, 254, 1700010 CrossRef.
- M. Roknuzzaman, M. A. Hadi, M. J. Abedin, M. T. Nasir, A. K. M. A. Islam, M. S. Ali, K. Ostrikov and S. H. Naqib, Comput. Mater. Sci., 2016, 113, 148–153 CrossRef CAS.
- D. H. Chung and W. R. Buessem, in Anisotropy in Single Crystal Refractory Compound, ed. F. W. Vahldiek and S. A. Mersol, vol. 2 Plenum, New York, 1968, p. 217 Search PubMed.
- I. S. Ranganathan and M. Ostoja-Starzewski, Phys. Rev. Lett., 2008, 101, 055504 CrossRef.
- M. A. Hadi, U. Monira, A. Chroneos, S. H. Naqib, A. K. M. A. Islam, N. Kelaidis and R. V. Vovk, J. Phys. Chem. Solids, 2019, 132, 38–47 CrossRef CAS.
- D. Yan, D. Geng, Q. Gao, Z. Cui, C. Yi, Y. Feng, C. Song, H. Luo, M. Yang, M. Arita, S. Kumar, E. F. Schwier, K. Shimada, L. Zhao, K. Wu, H. Weng, L. Chen, X. J. Zhou, Z. Wang, Y. Shi and B. Feng, Phys. Rev. B, 2020, 102, 205117 CrossRef.
- O. L. Anderson, J. Phys. Chem. Solids, 1963, 24, 909 CrossRef CAS.
- S. E. Lofland, J. D. Hettinger, T. Meehan, A. Bryan, P. Finkel, S. Gupta, M. W. Barsoum and G. Hug, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 174501 CrossRef.
- C. Dhakal, S. Aryal, R. Sakidja and W.-Y. Ching, J. Eur. Ceram. Soc., 2015, 35, 3203–3212 CrossRef CAS.
- D. R. Clarke and S. R. Phillpot, Mater. Today, 2005, 8, 22–29 CrossRef CAS.
- Y. Zhou, H. Xiang, X. Lu, Z. Feng and Z. Li, J. Adv. Ceram., 2015, 4, 83–93 CrossRef CAS.
- D. T. Morelli and G. A. Slack, in High Thermal Conductivity Materials, ed. S.L. Shinde and J. S. Goela, Springer, New York, 2006, pp. 37–68 Search PubMed.
- C. L. Julian, Phys. Rev., 1965, 137, A128 CrossRef.
- M. W. Barsoum, MAX Phases: Properties of Machinable Ternary Carbides and Nitrides, John Wiley & Sons, Weinheim, Germany, 2013 Search PubMed.
- D. R. Clarke, Surf. Coat. Technol., 2003, 163, 67–74 CrossRef.
- Y. Liu, V. R. Cooper, B. Wang, H. Xiang, Q. Li, Y. Gao, J. Yang, Y. Zhou and B. Liu, Mater. Res. Lett., 2019, 7, 145–151 CrossRef CAS.
- H. Gou, L. Hou, J. Zhang and F. Gao, Appl. Phys. Lett., 2008, 92, 241901 CrossRef.
- T. El-Raghy, S. Chakraborty and M. W. Barsoum, J. Eur. Ceram. Soc., 2000, 20, 2619–2625 CrossRef CAS.
- S. C. Middleburgh, G. R. Lumpkin and D. Riley, J. Am. Ceram. Soc., 2013, 96, 3196–3201 CrossRef CAS.
- K. E. Sickafus, L. Minervini, R. W. Grimes, J. A. Valdez, M. Ishimaru, F. Li, K. J. McClellan and T. Hartmann, Science, 2000, 289, 748–751 CrossRef CAS.
- F. A. Kröger and H. J. Vink, Solid State Phys., 1956, 3, 307–435 Search PubMed.
- R. E. Voskoboinikov, G. R. Lumpkin and S. C. Middleburgh, Intermetallics, 2013, 32, 230–232 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |