Open Access Article
Open Access ArticleThe thermal stability of FAPbBr3 nanocrystals from temperature-dependent photoluminescence and first-principles calculations
Xiaozhe Wang,
Qi Wang,
Zhijun Chai* and
Wenzhi Wu *
*
School of Electronic Engineering, Heilongjiang University, Harbin, Heilongjiang 150080, China. E-mail: 2002076@hlju.edu.cn; wuwenzhi@hlju.edu.cn
First published on 16th December 2020
Abstract
The temperature dependence of FAPbBr3 perovskite nanocrystals (PNCs) is investigated experimentally by steady-state and time-resolved photoluminescence (PL) spectroscopies. With the temperature increase, photon energies of line width and emission peak become larger due to stronger exciton–phonon coupling. Furthermore, theoretical calculations of first-principles simulations are used to estimate comparatively the thermal stability of typical FAPbBr3 PNCs. It is found that the PL peaks of PNCs slightly change with increasing temperature below 175 K and then blueshift steeply decreases rapidly till 400 K, which is related to phase transition from orthorhombic to tetragonal and cubic phase. The simulated results show the PL and the crystal structure of FAPbBr3 are largely dependent on the temperature. With higher temperature, the photon energy of the PL peak becomes larger, and the calculated band gap of FAPbBr3 is about 2.15 eV at 80 K, which is in good agreement with the experimental results. It is confirmed that temperature-dependent PL is composed of a band-edge exciton state and trapping state emission. The results obtained will be of certain significance to further expand other hybrid organometal perovskite materials.
1. Introduction
Organic–inorganic hybrid Pb-based perovskite materials have achieved remarkable successes of being used as luminescent materials in optoelectronic devices, and possess excellent characteristics of broadly tunable photoluminescence (PL), high photoluminescence quantum yields (PLQYs), and narrow bandwidths.1 Hybrid Pb-based perovskites with a general formula of APbX3 (A = CH3NH3+ (MA), or CH(NH2)2+ (FA); and X = Br−, I−, or Cl−) are now emerging as a new generation of functional semiconductors for photonics and optoelectronics due to their outstanding device performance and low-cost solution processability.2 Compared with their corresponding bulk materials, perovskite nanocrystals (PNCs) with remarkable quantum confinement and enhanced optical performance, have potential applications such as in bioimaging,3 photocatalysis,4 solar cells,5 lasing,6 and light-emitting diodes (LEDs).7 Within this class of materials, formamidinium lead halide (FAPbX3) PNCs have been extensively investigated and reported.8,9 Besides their application to photovoltaic devices, FAPbX3 PNCs are desired as light emitters with characteristics of being bright, color-tunable, and narrow-band, which make them attractive working materials for fabricating LEDs10 and lasers.11 Since high-efficiency LEDs usually use organic components such as methylamine, formamidine and the like contained in organic–inorganic hybrid metal halide perovskite, they are is easy to decompose in the presence of high working temperature and photobleaching, affecting their performance, thus causing the thermal stability to become another important performance parameter for evaluating perovskite materials.In addition to remaining the network structure of perovskite,12 the substances generated in the decomposition process can further interfere with the charge transfer and recombination process inside perovskite devices, also lead to the decline of optoelectronic performance of the device due to its poor optical performance and weak absorption capacity. Consequently, it is important to understand the mechanisms on temperature-dependent exciton recombination for LEDs and lasers. Compared to the bulk counterparts, PNCs show a higher PLQY and exciton binding energy due to the strong spin–orbit coupling in the conduction band of perovskite combined with Rashba effect.13 The temperature dependence of FAPbX3 perovskite has been investigated experimentally using spectroscopic ellipsometry,2 PL spectroscopy,14,15 Raman spectroscopy16, neutron diffraction17 and photocurrent18 techniques. For FAPbBr3 material, its temperature-dependent phase transitions are orthorhombic (α), tetragonal (β), and cubic (γ) with the temperature increasing. Following photoinduced excitation, various relaxation processes typically occur, in which other photons are re-radiated. This re-radiated process comes from the recombination of the excited pair of electron and hole (exciton). The observation of PL at a certain energy can be viewed as an indication that an electron populated an excited state associated with this transition energy. Temperature-dependent PL spectroscopy is an extremely important method to characterize the internal structure of perovskite material. Peak shift, intensity and line width of PL can be provided to investigate the mechanism on exciton–phonon coupling, which is closely related to the optical band gap of the light absorption layer and the existence of material structure and internal defects. The broadening of the PL in FAPbBr3 PNCs at room temperature is due to the presence of emissions from the free carriers as well as the excitons, and the scattering by phonons.19 FAPbBr3 undergoes a tetragonal phase transition at about 240 K, and a successive phase transformation to low symmetrical orthorhombic phase at lower temperature monitored by Raman spectroscopy.20 Exciton–phonon (EP) couplings of MAPbX3 or FAPbX3 are ascribed to the scattering from longitudinal optical phonons via Fröhlich interaction based on first-principles calculations, which underlines the suitability of an electronic band-structure picture for describing charge carriers in hybrid perovskites.21 Experimental measurement and theoretical EP couplings in hybrid lead halide perovskites are significant for the performance of hybrid perovskite in photovoltaics and LEDs. Therefore, we choose one typical FAPbBr3 PNCs to investigate comparatively the thermal properties using temperature-dependent PL spectroscopy and Monte Carlo simulation.
In this study, the photophysical properties of FAPbBr3 PNCs are investigated by temperature-dependent steady-state and time-resolved PL spectroscopies, and Monte Carlo simulation. Compared with the experimental results, based on Monte Carlo simulation, the thermal stability of FAPbBr3 perovskite material is discussed through the PL properties of its temperature dependence under PL spectra at different temperatures. The combined experimental-theoretical analysis indicates that temperature is a key factor for the performance of FAPbBr3 PNCs, which induces the structural phase transition and influences the band gap and exciton–phonon couplings.
2. Experimental and theoretical methods
2.1 Preparation of perovskite FAPbBr3 PNCs
The FAPbBr3 PNCs are synthesized by ligand-assisted reprecipitation method.22 FAPbBr3 PNCs in n-hexane are dropped on a BK7 glass substrate due to the volatilization of solvent closed-packed PNC films are prepared for temperature-dependent PL measurements.2.2 Experimental methods
The ground-state absorption spectrum of FAPbBr3 PNCs is performed on a UV-Vis spectrometer (TU-190, Persee). A continuous-wave (CW) laser (MLL-III-200 mW, CNI) at 405 nm is used as an excitation light source for steady-state excitation. A supercontinuum picosecond laser (Surperk Extreme EXB-4, NKT Photonics) is employed as the excitation source at 405 nm, which provides the pulse with the width of 60 ps. The measurement of temperature-dependent steady-state and time-resolved PL is described previously.23 The temperature-dependent steady-state and time-resolved PL measurements are performed using a vacuum liquid-nitrogen cryostat (Cryo-77, Oriental Koji), with the capability to have temperature variation from 80 to 400 K.2.3 Theoretical method
In our theoretical investigation, both Monte Carlo and density functional methods (DFT) are applied to study the PL mechanism, including the intensity dependency on temperature, which is set from 80 to 400 K with every 40 K interval. In order to optimize the structure of FAPbBr3 PNCs, 106 Monte Carlo steps are set at every temperature. After that, the DFT calculations are performed to obtain the optical properties of FAPbBr3 PNCs.24 The epsilon function is obtained from the DFT calculation and then calculated to analyze the PL. All the DFT calculation is done under the package of CASTEP25 of Material Studio. Heyd–Scuseria–Ernzerhof (HSE) hybrid pseudopotential is applied to better describe the exchange–correlation functionals than that of PBE functional. The energy cutoff is set at 490 eV, which is large enough to make sure the convergence. The Brillouin zone is set to be within a 3 × 3 × 3 k point mesh, and the maximum displacement is set 1.0 × 10−4 nm. In the optimization calculation, Broyden–Fletcher–Goldfarb–Shanno algorithm is applied to obtain a better lattice structure. Furthermore, the energy and force thresholds for optimization are 10−5 eV and 0.3 eV nm−1, respectively.3. Results and discussions
3.1 Characterization of FAPbBr3 PNCs
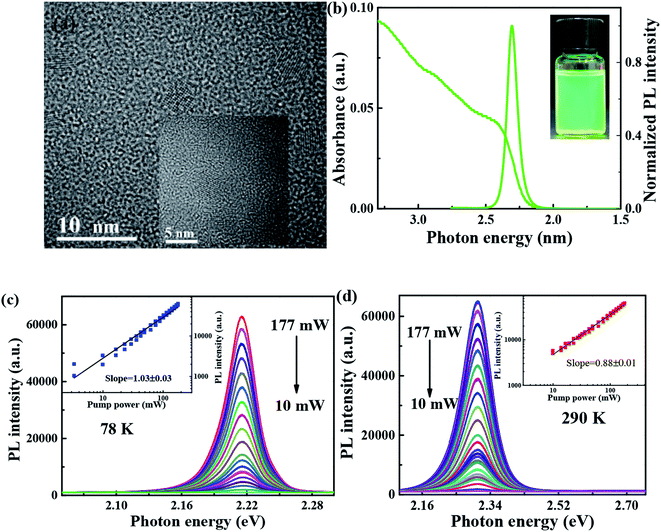
As shown in Fig. 1(a), transmission electron microscopy (TEM) image is utilized to characterize the morphology of FAPbBr3 PNCs, of which average sizes, is 6–8 nm, and the corresponding lattice distance of nanoparticle can be observed clearly. As shown in Fig. 1(b), the absorption spectrum of FAPbBr3 PNCs is measured at room temperature, of which lowest energy excitonic band is centered at 2.4 eV. PL spectrum excited by 405 nm CW laser is centered at 2.3 eV, with full width at half-maximum (FWHM) of 22.6 nm (97 meV). Stokes shift between absorption peak (first exciton peak) and the emission peak can be observed in traditional II–VI or perovskite NCs due to the band-edge emission, which is similar to those of MAPbX3 PNCs via LARP synthetization at room temperature.26 The photograph of FAPbBr3 PNCs in hexane is green under UV lamp irradiation as shown in the inset of Fig. 1(b). With the pump laser fluence decreasing from 177 to 10 mW, the 405 CW laser pump-power dependent FAPbBr3 PNCs PL spectra at 78 and 290 K are measured as shown in Fig. 1(c) and (d), which shows the negligible variation in the shape of the integrated PL spectrum with increasing excitation density. The black line is linear fitting curve with a slope of 1.03 and 0.88, respectively, which reveals the existence of one-photon absorption. The PL intensity of FAPbBr3 PNCs has a better linear increase with the pump power changing, suggesting that thermal effects can be considered when the laser pulses interact with perovskite materials.3.2 Temperature-dependent steady-state PL properties
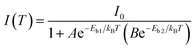 | (1) |
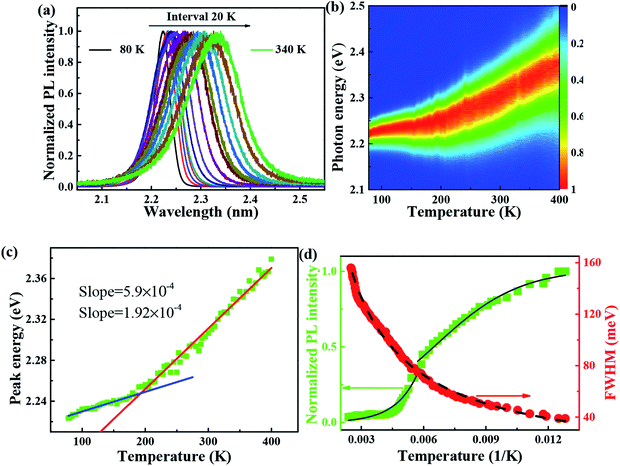
It is reported that FAPbBr3 PNCs have structural evolution driven by temperature, in which the decrease of temperature makes the band gap in FAPbBr3 structure network smaller and changes the energy distribution of carriers. Based on the space group symmetry, the structure of FAPbBr3 can be classified as α, β and γ phase, with Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, P4/mbm and Pnma symmetry, respectively, under different temperatures. It can be seen from the steep slope change in PL peak of FAPbBr3 that it experienced two phase transitions from 80 to 400 K, from γ to β at 150 and 125 K and from β to α at 275 and 250 K, this phenomenon is found in PL spectrum of MAPbI3 and MAPbBr3 PNCs.29
m, P4/mbm and Pnma symmetry, respectively, under different temperatures. It can be seen from the steep slope change in PL peak of FAPbBr3 that it experienced two phase transitions from 80 to 400 K, from γ to β at 150 and 125 K and from β to α at 275 and 250 K, this phenomenon is found in PL spectrum of MAPbI3 and MAPbBr3 PNCs.29
Simulation of FWHM and temperature based on Bose–Einstein statistics function as:30
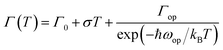 | (2) |
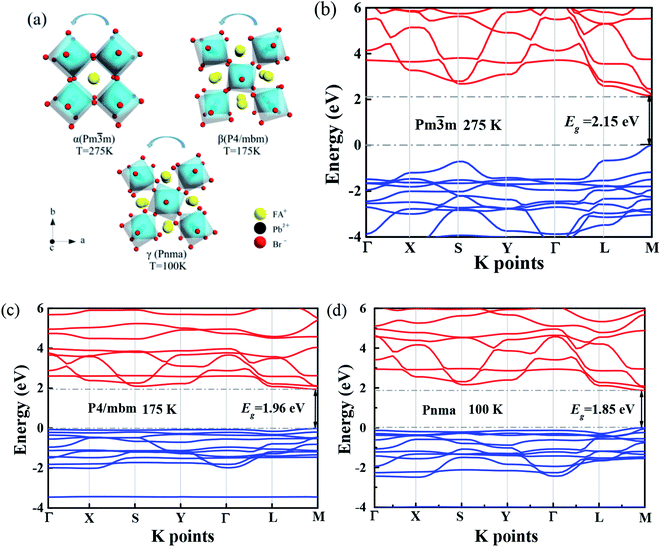
Several research groups have investigated temperature influences on the properties of FAPbX3 materials experimentally and theoretically. From previous investigations, the increase in temperature can induce the phase transition of FAPbBr3.31,32 By steady-state PL, transient PL, and photocurrent measurements, Tan et al. have studied the temperature-dependent optoelectronic properties of FAPbI3 films. As the temperature decreases from 295 to 77 K, FAPbI3 undergoes a series of phase transition, from α to β, and finally γ phase. The crystal structure of the ABX3 type perovskite is shown in Fig. 3(a). It belongs to the equiaxed crystal system. The atomic coordinate parameters in cells are A (0, 0, 0), B (0.5, 0.5, 0.5) and X (0.5, 0.5, 0), the space group is Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. The crystal structure can be regarded that formed by BX6 octahedra connected by common apex angle, and the cations at a site are in the center of the gap formed by the octahedra, and the coordination number is 12. Since the ionic radii of A and X are very similar, from the point of view of dense stacking, the structure can be regarded as the formation of A and X atomic layers by the hexagonal packing along the direction of [111], and B ions filling in the octahedral voids. However, this structure is prone to deformation under the pressure of temperature changes or the arrangement of atoms space. The change of temperature may lead to the disorder orientation or fluidity of organic cations, which is difficult to be bound in octahedral lattice, so the phase transition occurs. Furthermore, the phase transition temperature varies with the size, and the symmetry of the structure of the ions is higher. For example, for FAPbBr3 PNCs, the phase transition temperature from cubic phase of α transition to tetragonal phase of β transition, then from the tetragonal phase of β transition to orthogonal phase of γ transition is 175 and 100 K, respectively. The phase transition of FAPbBr3 induced by temperature can be seen in Fig. 3(a). Generally, the higher temperature, the crystal symmetry is higher. In the first-principles calculation, the default temperature is 0 K. At such a low temperature, the orthogonal phase is usually the most stable. At 275 K, the crystal structure has the space group Pm
m. The crystal structure can be regarded that formed by BX6 octahedra connected by common apex angle, and the cations at a site are in the center of the gap formed by the octahedra, and the coordination number is 12. Since the ionic radii of A and X are very similar, from the point of view of dense stacking, the structure can be regarded as the formation of A and X atomic layers by the hexagonal packing along the direction of [111], and B ions filling in the octahedral voids. However, this structure is prone to deformation under the pressure of temperature changes or the arrangement of atoms space. The change of temperature may lead to the disorder orientation or fluidity of organic cations, which is difficult to be bound in octahedral lattice, so the phase transition occurs. Furthermore, the phase transition temperature varies with the size, and the symmetry of the structure of the ions is higher. For example, for FAPbBr3 PNCs, the phase transition temperature from cubic phase of α transition to tetragonal phase of β transition, then from the tetragonal phase of β transition to orthogonal phase of γ transition is 175 and 100 K, respectively. The phase transition of FAPbBr3 induced by temperature can be seen in Fig. 3(a). Generally, the higher temperature, the crystal symmetry is higher. In the first-principles calculation, the default temperature is 0 K. At such a low temperature, the orthogonal phase is usually the most stable. At 275 K, the crystal structure has the space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. As the temperature decreases, the symmetry of FAPbBr3 becomes lower, from P4/mbm at 175 K to Pnma at 100 K. Different perovskite crystal structure results in different electronic band structure, which influences the band gap of our FAPbBr3, as it is shown in our theoretical result in Fig. 3(b)–(d) for these three kinds of phases. The band gap of FAPbBr3 for phase Pm
m. As the temperature decreases, the symmetry of FAPbBr3 becomes lower, from P4/mbm at 175 K to Pnma at 100 K. Different perovskite crystal structure results in different electronic band structure, which influences the band gap of our FAPbBr3, as it is shown in our theoretical result in Fig. 3(b)–(d) for these three kinds of phases. The band gap of FAPbBr3 for phase Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m in our calculation is about 2.15 eV, which is quite close to our experimental results, as shown in Fig. 2(a). For phases P4/mbm and Pnma, the gaps are a little smaller, which is 1.96 and 1.85 eV, respectively. Both the experimental and theoretical PL results show wider broadening at the high temperature, and this temperature-dependent broadening is close related to the density of excitons in FAPbBr3 materials.33
m in our calculation is about 2.15 eV, which is quite close to our experimental results, as shown in Fig. 2(a). For phases P4/mbm and Pnma, the gaps are a little smaller, which is 1.96 and 1.85 eV, respectively. Both the experimental and theoretical PL results show wider broadening at the high temperature, and this temperature-dependent broadening is close related to the density of excitons in FAPbBr3 materials.33
The band structure is plotted along with the high symmetrical K point (Γ–X–S–Y–Γ–L–M). The valence band maximum (VBM) and conduction band minimum (CBM) are located at the same high symmetry point M, which indicates that FAPbBr3 is a semiconductor with direct band gap. As we can see from the electronic band structure, the band gap is about 2.2 eV, located at M. Compared with our simulation and experimental results, the peak of PL is in the range of 2.2–2.3 eV. This band gap is quite close to our peak of PL, which can explain the location of the peak. Because the crystal structure of FAPbBr3 depends on the temperature, the band gap should be temperature-dependent. According to the research,34 the VBM of FAPbBr3 PNCs is composed of 4p electrons of Pb and 6s electrons of Br, and the CBM is composed of 4p orbitals of Pb. The electronic states of FA cation are far below the VBM, so the main factors affecting low energy electrons and holes are Pb and Br elements. The energy band structure is related to the symmetry of the crystal and affected by the temperature. The symmetry decreases gradually from cubic phase to quadrate phase, and part of the energy band collapses.
After obtaining the optimized cell structure, the electronic structure properties are further calculated as shown in Table 1. PL spectrum calculation is based on the following Van Roosbroeck–Shockley formula:35
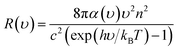 | (3) |
| Simulation parameters | T (K) | δ (meV) | N (%) | EB (meV) | E0 (meV) | τ0 (ns) | τ0ν0 | Nα |
|---|---|---|---|---|---|---|---|---|
| FAPbBr3 | 80–400 | 13 | 25 | 70 | 50 | 10–120 | (1 × 1011) × τ0 | 0.5 |
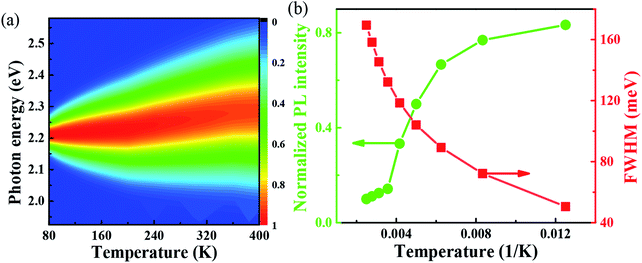
With the change of temperature, the peak value of PL is continuously transferred to higher energy. In the PL spectrum changing with temperature, no sudden change of spectrum is observed, which indicates that the main peak comes from the same phase of materials. When the temperature is from 80 to 100 K, the number of excitons is dominant, the occupation of optical phonons can be basically ignored, and only phonons contribute to the spectrum broadening. When the temperature is from 100 to 200 K, the width of PL line gradually widens with the temperature increasing. At this temperature, and the spectrum broadening is mainly due to the interaction between excitons and phonons, with the increase in temperature, the proportion of free charge increases gradually. The experimental relationship between PL line width and phonon scattering is also described in above eqn (2), the first term Γ0 dominate at low temperature, and electrons have less energy at a lower temperature (less than 100 K) and cannot emit optical phonons, although phonons still exist. The obtained acoustic phonons coupling strength σ (0.1 meV K−1) is higher than that of FAPbBr3 bulk crystals (0.06 meV K−1),21 indicating that in FAPbBr3, acoustic phonons scattering contributes more than in the bulk counterpart. As the temperature increases, the optical phonon contribution dominates and the PL linewidth increases almost linearly with temperature.36 At the high temperature, high-energy electrons fully emit optical phonons, and the thermal occupation of optical phonons also increases the probability of optical phonon scattering. Evidently, the temperature is an important factor, which leads to the thermal expand coefficient due to the high temperature.
One important factor may be the temperature, which leads to the change of coefficient of thermal expansion due to high temperature. From the Van Roosbroeck–Shockley formula, the temperature plays an important role in the PL of FAPbBr3,37 the intensity of PL spectrum should be much more extended. With temperature reaches 400 K, the energy is up to 2.36 eV. So, from our simulation, we can conclude that, the temperature plays an important role to the PL, through the thermal expand coefficient, which may change the volume of FAPbBr3,38 thus leads to the changes of electronic property.30 The PL is quite closely related to exciton in the materials, which is related to defects with optical phonons in FAPbBr3.39 Fig. 4(a) shows the simulated variable temperature PL spectra of FAPbBr3 at 80–400 K, we use the Monte Carlo simulation method to show the blue shift behavior of PL peaks and the change of FWHM at different temperatures. When the temperature rises from 80 to 400 K, the blue shift of λmax shifts from 555 nm to 525 nm, and the shift of peak is 30 nm. The blue shift of the PL of FAPbBr3 is similar to that of MAPbI3, which is caused by the phase transition from orthogonal to cubic, and the blue shift of photoluminescence is accompanied by the increase of FWHM. The blue shift of PL spectra is a typical characteristic of lead-based composite semiconductors, which may be caused by the inverse arrangement of the band edges or may be related to the electron–phonon renormalization interaction. According to the thermal distribution, when the temperature is 80–190 K, the exciton population increases, although the electron and the hole are still bounded to the FA molecule. As the temperature continues to rise above about 190 K, the exciton energy continues to increase. The delocalization becomes stronger, even to the nearest transition dipole moment molecule, where the electron or hole may be transferred or the charge transferred to the nearest molecule. The electrons and holes on the same molecule are separated from each other. Because the distance between the organic molecules is quite large, the electrons and the holes cannot return to the same molecule after separation. Thus, reducing the probability of radiation recombination, and greatly increases the probability of nonradiative deexcitation. Due to the change of exciton energy and its interaction with phonons, the photoluminescence spectra have a monotonic blue shift as shown in Fig. 4(b). The FWHM shows the interaction between the phonon and exciton, and the simulation results are in good agreement with the experimental results.40
3.3 Temperature-dependent time-resolved PL properties
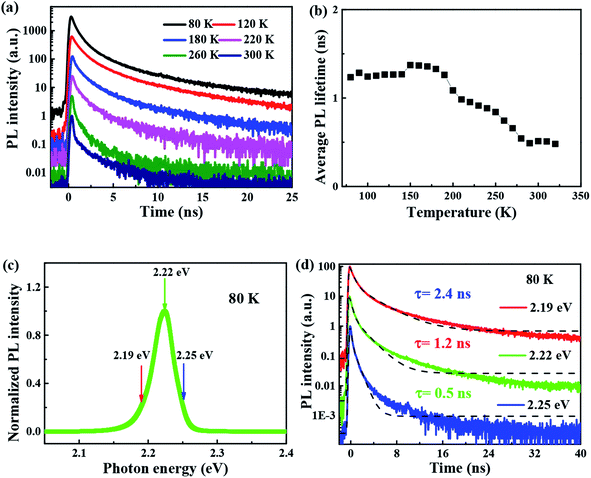
The time-resolved wavelength and temperature-dependent PL dynamics of FAPbBr3 PNCs film is shown in Fig. 5(c). The lifetime is similar to that of other FAPbBr3 PNCs, and can be fitted as a double exponential function, the PL decay dynamics is fitted41,42 as:
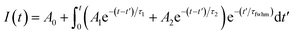 | (4) |
| τ = (A1τ12 + A2τ22)/(A1τ1 + A2τ2) | (5) |
It is noted that the PL decays are basically unchanged at the temperature below 180 K, and then become shorter with the increasing temperature to 320 K, which is different with that of all-inorganic CsPbX3 PNCs43 due to the incorporation of organic ligands. The wavelength dependence of the PL decays provides an evidence that surface excitonic emission indicates the difference between the populations of different sizes of PNCs as shown in Fig. 5(d). The larger PNCs, emitting at the longer wavelength, have a longer PL lifetime.
4. Conclusion
The simulation results of local exciton dynamics enable us to quantitatively explain the anomalous temperature behavior of photoluminescence spectra of perovskite materials from 80 to 400 K. In our work, we apply Monte Carlo simulation method to analyze the phonon assisted dynamics of local exciton and its effect on the PL spectra of FAPbBr3. The simulation results are in good agreement with the experimental results. From our simulation and experimental results, we conclude that, the peak is temperature-dependent: with higher temperature, the peak of location increases. This is because of the temperature-dependent crystal structure and band gap of electronic band structure.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful for the financial support from Key Project of Scientific Foundation by Heilongjiang Province (JJ2018ZZ0010), Young Scholar Innovation Team of Heilongjiang University (RCYJTD201901) and Innovative Scientific Research Project for Postgraduates of Heilongjiang University (YJSCX2020-161HLJU).References
- C. M. Sutter-Fella, Y. Li, M. Amani, J. W. Ager, III, F. M. Toma, E. Yablonovitch, I. D. Sharp and A. Javey, Nano Lett., 2016, 16, 800–806 Search PubMed.
- G. Mannino, I. Deretzis, E. Smecca, A. La Magna, A. Alberti, D. Ceratti and D. Cahen, J. Phys. Chem. Lett., 2020, 11, 2490–2496 Search PubMed.
- H. Zhang, X. Wang, Q. Liao, Z. Xu, H. Li, L. Zheng and H. Fu, Adv. Funct. Mater., 2017, 27, 1604382–1604389 Search PubMed.
- X. Zhu, Y. Lin, J. San Martin, Y. Sun, D. Zhu and Y. Yan, Nat. Commun., 2019, 10, 2843–2852 Search PubMed.
- H. Tan, A. Jain, O. Voznyy, X. Lan, F. P. G. de Arquer, J. Z. Fan, R. Quintero-Bermudez, M. Yuan, B. Zhang, Y. Zhao, F. Fan, P. Li, L. N. Quan, Y. Zhao, Z.-H. Lu, Z. Yang, S. Hoogland and E. H. Sargent, Science, 2017, 355, 722–726 Search PubMed.
- X. Tang, Z. Hu, W. Chen, X. Xing, Z. Zang, W. Hu, J. Qiu, J. Du, Y. Leng, X. Jiang and L. Mai, Nano Energy, 2016, 28, 462–468 Search PubMed.
- H. Cho, S.-H. Jeong, M.-H. Park, Y.-H. Kim, C. Wolf, C.-L. Lee, J. H. Heo, A. Sadhanala, N. Myoung, S. Yoo, S. H. Im, R. H. Friend and T.-W. Lee, Science, 2015, 350, 1222–1225 Search PubMed.
- Y.-L. Tong, Y.-W. Zhang, K. Ma, R. Cheng, F. Wang and S. Chen, ACS Appl. Mater. Interfaces, 2018, 10, 31603–31609 Search PubMed.
- R. Ding, H. Liu, X. Zhang, J. Xiao, R. Kishor, H. Sun, B. Zhu, G. Chen, F. Gao, X. Feng, J. Chen, X. Chen, X. Sun and Y. Zheng, Adv. Funct. Mater., 2016, 26, 7708–7716 Search PubMed.
- M. Cao, Y. Xu, P. Li, Q. Zhong, D. Yang and Q. Zhang, J. Mater. Chem. C, 2019, 7, 14412–14440 Search PubMed.
- Y. Fu, H. Zhu, A. W. Schrader, D. Liang, Q. Ding, P. Joshi, L. Hwang, X. Y. Zhu and S. Jin, Nano Lett., 2016, 16, 1000–1008 Search PubMed.
- F. Zhu, L. Men, Y. Guo, Q. Zhu, U. Bhattacharjee, P. M. Goodwin, J. W. Petrich, E. A. Smith and J. Vela, ACS Nano, 2015, 9, 2948–2959 Search PubMed.
- M. A. Becker, R. Vaxenburg, G. Nedelcu, P. C. Sercel, A. Shabaev, M. J. Mehl, J. G. Michopoulos, S. G. Lambrakos, N. Bernstein, J. L. Lyons, T. Stoferle, R. F. Mahrt, M. V. Kovalenko, D. J. Norris, G. Raino and A. L. Efros, Nature, 2018, 553, 189–193 Search PubMed.
- L. Yang, K. Wei, Z. Xu, F. Li, R. Chen, X. Zheng, X. Cheng and T. Jiang, Opt. Lett., 2018, 43, 122–125 Search PubMed.
- O. Pfingsten, J. Klein, L. Protesescu, M. I. Bodnarchuk, M. V. Kovalenko and G. Bacher, Nano Lett., 2018, 18, 4440–4446 Search PubMed.
- S. Ruan, D. P. McMeekin, R. Fan, N. A. S. Webstereb, H. Ebendorff-Heidepriem, Y.-B. Cheng, J. Lu, Y. Ruan and C. R. McNeill, J. Phys. Chem. C, 2020, 124, 2265–2272 Search PubMed.
- A. Franz, D. M. Toebbens, F. Lehmann, M. Kaergell and S. Schorr, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2020, 76, 267–274 Search PubMed.
- M. Tan, B. Chen, Y. Zhang, M. Ni, W. Wang, H. Zhang, Q. Zhou, Y. Bao and Y. Wang, J. Phys. Chem. C, 2020, 124, 5093–5098 Search PubMed.
- S. Ghosh, Q. Shi, B. Pradhan, P. Kumar, Z. Wang, S. Acharya, S. K. Pal, T. Pullerits and K. J. Karki, J. Phys. Chem. Lett., 2018, 9, 4245–4250 Search PubMed.
- S. Govinda, B. P. Kore, D. Swain, A. Hossain, C. De, T. N. Guru Row and D. D. Sarma, J. Phys. Chem. C, 2018, 122, 13758–13766 Search PubMed.
- A. D. Wright, C. Verdi, R. L. Milot, G. E. Eperon, M. A. Perez-Osorio, H. J. Snaith, F. Giustino, M. B. Johnston and L. M. Herz, Nat. Commun., 2016, 7, 11755–11763 Search PubMed.
- D. Han, M. Imran, M. Zhang, S. Chang, X.-g. Wu, X. Zhang, J. Tang, M. Wang, S. Ali, X. Li, G. Yu, J. Han, L. Wang, B. Zou and H. Zhong, ACS Nano, 2018, 12, 8808–8816 Search PubMed.
- Q. Wang, W. Wu, R. Wu, S. Yang, Y. Wang, J. Wang, Z. Chai and Q. Han, J. Colloid Interface Sci., 2019, 554, 133–141 Search PubMed.
- A. A. Sutanto, V. I. Queloz, I. Garcia-Benito, K. Laasonen, B. Smit, M. K. Nazeeruddin, O. A. Syzgantseva and G. J. A. M. Grancini, APL Mater., 2019, 7, 041110 Search PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570 Search PubMed.
- F. Zhang, H. Zhong, C. Chen, X.-g. Wu, X. Hu, H. Huang, J. Han, B. Zou and Y. Dong, ACS Nano, 2015, 9, 4533–4542 Search PubMed.
- Q. Wang and W. Wu, Opt. Lett., 2018, 43, 4923–4926 Search PubMed.
- W. Wu, W. Liu, Q. Wang, Q. Han and Q. Yang, J. Alloys Compd., 2019, 787, 165–172 Search PubMed.
- Y. Liu, H. Lu, J. Niu, H. Zhang, S. Lou, C. Gao, Y. Zhan, X. Zhang, Q. Jin and L. Zheng, AIP Adv., 2018, 8, 095108–095116 Search PubMed.
- S. Huang, S. Yang, Q. Wang, R. Wu, Q. Han and W. Wu, RSC Adv., 2019, 9, 42430–42437 Search PubMed.
- M. C. Gélvez-Rueda, N. Renaud and F. C. Grozema, J. Phys. Chem. C, 2017, 121, 23392–23397 Search PubMed.
- A. G. Kontos, G. K. Manolis, A. Kaltzoglou, D. Palles, E. I. Kamitsos, M. G. Kanatzidis and P. Falaras, J. Phys. Chem. C, 2020, 124, 8479–8487 Search PubMed.
- Z. Zhao, M. Zhong, W. Zhou, Y. Peng, Y. Yin, D. Tang and B. Zou, J. Phys. Chem. C, 2019, 123, 25349–25358 Search PubMed.
- Y. Pan, Y. Su, C. Hsu, L. Huang, K. Dou and C. J. J. A. N. Kaun, Journal of Advances in Nanomaterials, 2016, 1, 33–38 Search PubMed.
- J. Li, L. Xu, T. Wang, J. Song, C. Jiawei, J. Xue, Y. Dong, B. Cai, Q. Shan, B. Han and H. Zeng, Adv. Mater., 2016, 29, 1603885–1603893 Search PubMed.
- K. Wu, A. Bera, C. Ma, Y. Du, Y. Yang, L. Li and T. Wu, Phys. Chem. Chem. Phys., 2014, 16, 22476–22481 Search PubMed.
- S. Peng, Z. Wen, T. Ye, X. Xiao, K. Wang, J. Xia, J. Sun, T. Zhang, G. Mei, H. Liu, B. Xu, X. Li, R. Chen, G. Xing, K. Wang and Z. Tang, ACS Appl. Mater. Interfaces, 2020, 12, 31863–31874 Search PubMed.
- H. Alehdaghi, A. Kanwat, M. Zirak, E. Moyen, W. C. Choi and J. Jang, Org. Electron., 2020, 79, 105626–105632 Search PubMed.
- S. K. Si, S. Paria, S. K. Karan, S. Ojha, A. K. Das, A. Maitra, A. Bera, L. Halder, A. De and B. B. Khatua, Nanoscale, 2020, 12, 7214–7230 Search PubMed.
- Q. Shi, S. Ghosh, P. Kumar, L. C. Folkers, S. K. Pal, T. Pullerits and K. J. Karki, J. Phys. Chem. C, 2018, 122, 21817–21823 Search PubMed.
- W. Wu, D. Yu, H.-a. Ye, Y. Gao and Q. Chang, Nanoscale Res. Lett., 2012, 7, 301–308 Search PubMed.
- W. Wu and Y. Wang, Opt. Lett., 2015, 40, 64–67 Search PubMed.
- Q. Han, W. Wu, W. Liu, Q. Yang and Y. Yang, J. Lumin., 2018, 198, 350–356 Search PubMed.
| This journal is © The Royal Society of Chemistry 2020 |