Open Access Article
Open Access ArticleElectrical properties of Ca12Al14O33 synthesised through polymer assisted deposition and glass crystallization routes
Yun Lv,
Huaibo Yi,
Tianjie Wei,
Junwei Liu,
Xiangyu Xu and
Jungu Xu *
*
MOE Key Laboratory of New Processing Technology for Nonferrous Metal and Materials, Guangxi Universities Key Laboratory of Non-ferrous Metal Oxide Electronic Functional Materials and Devices, College of Materials Science and Engineering, Guilin University of Technology, Guilin 541004, P. R. China. E-mail: xujungu@glut.edu.cn
First published on 30th September 2020
Abstract
In this paper, two new methods, polymer assisted deposition (PAD) and glass crystallization (GC) methods were reported for the first time to prepare oxide ion conductor Ca12Al14O33, with their microstructures and electrical properties compared to that of a sample prepared by the traditional solid-state reaction (SSR) method. The results showed that these two new methods are effective for improving ceramic densities and oxide ion conductivities compared to the SSR method, and the ceramic prepared from the GC method in the present work possessed the highest level of ∼94% of the theoretical density and ∼1.0 × 10−3 S cm−1 at 900 °C for the bulk conductivity. A new bond valence method was applied to study the oxide ion conducting mechanism, which revealed an exchange process between the free oxide ion and the framework ion, and the wide windows connecting the Ca–Al–O framework cages were shown to be the key factor limiting oxide ion transport.
Introduction
Oxide ion conductors are attracting increasing attention due to their application as electrolytes in solid-oxide fuel cells (SOFCs).1–4 The state-of-the-art electrolyte used for commercially available SOFCs is yttria-stabilized zirconia (YSZ). However, this material can only meet the oxide ion conductivity demand at a working temperature higher than 800 °C.5–7 Such a high temperature imposes a technical challenge for electrode material selection and their long-term stability, which therefore limits the widespread application of SOFCs and stimulates the discovery of new oxide ion conductors with high conductivities at intermediate temperature (400–700 °C). To date, some new structural families, such as apatites,8,9 scheelites,10,11 mayenites,12,13 melilites,14–17 and so on, have been identified to possess pure oxide ion conductivities and have good application potential in SOFCs. Among these new structural families, the mayenite Ca12Al14O33 is also well-known for its optical properties,18 electronic conducting properties when being converted into electride,19 and the more recently reported thermal energy storage properties.20 For the oxide ion conducting properties, these were first reported by M. Lacerda et al. with a modest level, inferior to that of YSZ at a given temperature.21–23 Nevertheless, its relatively low cost of raw materials makes it still competitive if the oxide ion conductivity could be improved. To this end, several works using a cation doping strategy have been carried out, such as zinc single doping or zinc and phosphorus co-doping,24,25 iron-doping,26 cobalt-doping,27 gallium-doping,28 and vanadium-doping29 on Al atom sites. For the zinc-, phosphorus-, or iron-doped materials, an even lower conductivity was observed when compared to that of parent Ca12Al14O33. While for the cobalt, gallium, and vanadium doped samples, although the conductivities could be slightly improved, the low solid solution hindered their further conductivity enhancements. Other elements, including copper,30,31 nickel,32 manganese,33 iridium,34 bismuth,35 and Ln3+[Tb/Sm/Er/Nd/Yb/Ho/Pr]36 were also reported to be incorporated into the mayenite structure, but without oxide ion conductivity being investigated.All these doped samples with low solid solution limits as stated above are mainly synthesized by traditional solid-state reaction method or through growing single crystals using the floating zone technique37 or Czochralski method.38 To investigate the effect of preparation condition on sinterability and electrical property, M. Matsuda et al. prepared the parent Ca12Al14O33 material by mixing the raw materials through a solution method.21 The sinterability and electrical property were then compared to the sample synthesized by the traditional solid-state reaction method in which the raw materials were mechanically mixed. The results showed a great enhancement in conductivity for the solution method prepared sample due to the better sinterability and densification. As in a similar hydrothermal synthesis, S. Fujita et al.39 prepared Si-substituted mayenite Ca12Al14−xSixO33+0.5x with the high solid solution of 0 ≤ x ≤ 4. Although these Si-substituted materials are stable only below 600 °C and without oxide ion conductivities being reported, it gave us a hint that the low doping level as reported in previous works may be remarkably improved by a new synthesis method. Thus, developing new methods to prepare the mayenite-based materials may be an important way to optimize their sinterability, extend the solid solution limit, and finally improve their oxide ion conductivities. In addition, as debates existing in the oxide ion conduction mechanism in Ca12Al14O33,12,13,22 it is essential to make it clear to indicate a direction for its performance optimization.
In this paper, two new methods, polymer assisted deposition (PAD) method and glass crystallization (GC) method, are applied to prepare Ca12Al14O33 material for the first time, with their electrical properties and microstructures being studied in detail and compared with that yielded from solid-state reaction method. Moreover, the oxide ion diffusion path in Ca12Al14O33 was investigated by a new approach, the bond valence (BV) method, for the first time. This method had been proved to be reliable and successful in simulating the conduction mechanism for ionic conductors.40,41
Methods
Synthesis
(1) For samples prepared by polymer assisted deposition (PAD) method, Ca(NO3)2·4H2O (Alfa Aesar, >99% purity) and Al(NO3)3·9H2O (Alfa Aesar, >99.99% purity) were used as metal precursors and soluble polyethyleneimine (PEI) (Alfa Aesar, >99% purity) as the complexing agent. The Ca and Al precursor were first separately deposited in PEI in deionized water solution, and these two solutions were then mixed together, followed by a heating treat to evaporate water until finally burning out the PEI, yielding amorphous Ca12Al14O33 precursor which was then fired at 1000 °C to obtain crystallized powder Ca12Al14O33 product. To prepare ceramic samples for electrical property measurements, the powders were pressed into pellets and then calcined at 1300 °C for 12 h. (2) For the glass crystallization (GC) method, the well-mixed and grounded raw materials were first pressed into pellets with a diameter of 4 mm, which was then placed in an aerodynamic levitator coupled to a CO2 laser heating system to achieve vitrification. The pellets were thus heated up to about 1850 °C for a few seconds to homogenize and subsequently quenched down to room temperature at a rate of roughly 300 °C s−1 by simply turning off the lasers, yielding glass beads. The crystallization process was then studied by heat treatment performed in the open air at 920 °C or higher temperature. (3) For comparison, Ca12Al14O33 samples were also prepared by a solid-state reaction (SSR) method, using CaCO3 (Alfa Aesar, >99% purity), Al2O3 (Alfa Aesar, >99% purity) as starting raw materials. The stoichiometric weighted, evenly mixed, and well-ground raw materials were first fired at 1000 °C for 12 hours to drive off CO2. After regrinding, the pre calcined powders were uniaxially pressed into pellets and sintered at 1300 °C for 12 hours. Archimedes principle was applied to estimate the densities for all these prepared ceramics.Characterization
The XRD characterizations were performed on a Panalytical X'pert Pro X-ray diffractometer with Cu Kα radiation. In situ variable temperature, XRD (VTXRD) measurements were carried out using a HTK1200N Anton Paar oven chamber. The morphology was investigated using scanning electron microscopy (SEM) (S-4800, Hitachi, Japan). HRTEM imaging and EDS analysis were performed on a JEM-2100F (Japan) transmission electron microscopy. Electrochemical impedance spectroscopy (EIS) measurements were performed with a Bio-Logic VSP instrument over a 106 to 10−1 Hz frequency range. Before the EIS measurements, electrodes were formed by coating platinum paste on opposite faces of the pellets and fired at 750 °C for 3 hours to remove any organic components. Before the impedance measurements, the temperature was equilibrated at each setpoint for 30 minutes. Differential Scanning Calorimetry (DSC) was performed on the STA8000 thermal analysis instrument in airflow. The crystallization temperatures of glass were determined from 25 mg powder samples, with a heating rate of 10 °C min−1.Bond valence-based energy landscapes (BVELs) for a test ion O2− in the Ca12Al14O33 crystal structure (ICSD #6287) were calculated using the program 3DBVSMAPPER.42 The spatial resolution was set to 0.2 Å.
Results and discussions
Phases and microstructures
As for the PAD method, fully crystallized and pure phase Ca12Al14O33 material can be obtained by calcining the amorphous precursor at 1000 °C, as checked by the XRD pattern shown in Fig. 1a. However, the density of a pellet fired at this temperature is only ∼69% of the theoretical density. The particle sizes observed in SEM analysis (Fig. 1b) on such a pellet are typically around 100–200 nm, and the pores demonstrated in the picture can be ascribed to the combustion of incompletely burned polymer in the precursor. Thus, to get a dense ceramic for electrical property measurement, the powders calcined at 1000 °C were then reground, pressed into pellets, and fired at 1300 °C. The phase purity and microstructure are displayed in Fig. 1a and c, respectively. It is seen that a pure phase with an average particle size of ∼3.0 μm can be gained. The particle sizes are thus apparently increased and even larger than that prepared by the SSR method (0.25–1.5 μm and average in ∼1.0 μm as shown in Fig. 1d) at the same firing temperature. The ceramic density was also improved to ∼92% of the theoretical density, higher than the ceramic from the SSR method in this work (∼90%).For the glass crystallization method, the as-made colorless and transparent glass beads achieve a maximum size of ∼3.0 mm in diameter. These glass beads were first ground into powders for DSC measurement, which reveals a single crystallization peak at ∼920 °C, as presented in Fig. 2a. The presence of a single peak and no further exothermic peak at higher temperatures seem to indicate a congruent crystallization process which is required to eventually elaborate a dense and single-phase ceramic.43 To confirm this congruent crystallization process, in situ variable temperature powder XRD measurements were then carried out from room temperature to 1000 °C (Fig. 2b). It reveals that only the mayenite phase crystallizes from 900 °C and no other crystalline phase was formed over the whole measured temperature range. The minor deviation in crystallization temperatures derived from DSC and VTXRD results can be ascribed to the different temperature detection precisions for the furnaces used for DSC and VT-XRD. Thermal treatment at temperature 900 °C in a furnace under the air atmosphere was then performed on glass beads in order to synthesize a fully crystallized mayenite material, i.e. a ceramic, in a single step, for subsequent electrical property measurements. However, heat treat at this temperature did not result in crystallized samples, regardless of heat treatment time, suggesting the thermodynamically inaccessible nature at this temperature. Thus, the annealing was then performed at a higher temperature of 920 °C. For 2 hours, the products show a partial crystallization behavior, as indicated by a broad rise in background centered at ∼22° 2θ in the XRD pattern, and the obtained beads are also transparent, as the inset shows in Fig. 2c. This partial crystallization behavior was also further verified by HRTEM (Fig. 2d), from which we can see that besides the nano-crystalline region, the remaining part in the picture can be ascribed to amorphous Ca12Al14O33. The element distribution analysis (Fig. 2e) revealed high homogeneity of the product and no segregation was observed. Prolong the annealing time to 5 hours would, however, lead to cracks of these beads into many little pieces (<1 mm in diameter) with irregular shapes. Although these little pieces have better crystallinity that can be checked by subsequent XRD measurement, such a small size makes it almost impossible to carry out electrical study experiments on an individual piece. Thermal treats at 950 °C or even higher temperatures for 2 hours or longer were also tried, but all failed and resulted in well-crystallized but cracked little pieces. The crack in these beads mainly arises from the huge internal thermal stress introduced in the glass beads preparing stage by extremely heating and cooling rates. Optimized annealing processes, e.g. using a much slower heating and cooling rates (1 °C min−1), did not work either. Therefore, to obtain a well-crystallized ceramic pellet for electrical property studies, the partially or completely crystallized samples that pre-calcined at 920 °C or 950 °C has to be ground into powders and then pressed into pellets, followed by firing at 1300 °C that is the same as used in the SSR and PAD method in this work. The phase and microstructure of the final product obtained at 1300 °C were demonstrated in Fig. 2c and f, respectively. We can see that the product is phase pure and particle sizes are around 10–20 μm, with a ceramic density of ∼95% of its theoretical value, close to the density of a ceramic that prepared by sintering at a higher temperature of 1350 °C as described in previous works.21,44 The particle size and ceramic density thus pronounced larger than that for the SSR and PAD methods. The particle sizes and densities of ceramics prepared by these three different methods but with the same final firing temperature of 1300 °C are summarized in Table 1.
| Method | Ceramic density | Particle size |
|---|---|---|
| SSR | 90% of theory | 0.25–1.5 μm, average in ∼1.0 μm |
| PAD | 92% of theory | 2.0–5.0 μm, average in 3.0 μm |
| GC | 94% of theory | 10.0–20.0 μm, average in ∼15.0 μm |
Electrical properties
The oxide ion conductions of Ca12Al14O33 materials prepared by SSR, PAD, and GC methods as stated above were studied by AC impedance spectroscopy, and the Arrhenius plots for bulk conductivities in these samples are shown in Fig. 3a. It can be seen that for the ceramics prepared at the same final firing temperature 1300 °C, the sample prepared from the glass crystallization method has the highest bulk conductivity, and about one order of magnitude higher than that of the sample from the SSR method which shows the lowest conductivity among these three samples. A medium conductivity was revealed for the sample synthesized by the PAD method. The conductivities in these samples can be well related to their particle sizes and ceramic densities. The larger particle size and higher ceramic density with reduced grain boundary lead to higher conductivity, as the bulk conductivity of a ceramic is deduced from the total impedance of grain and grain boundary, thus the higher density with less grain boundary would reduce the total resistance and result in higher conductivity. In fact, as had been reported by Irvine and West et al., the controlled sintering is imperative to lower the grain boundary impedance,44 and the optimum sintering temperature is around 1350 °C, close to the melting pointing. In the present work, we just fixed the final sintering temperature at 1300 °C and to investigate the effects of sample preparation methods on the conductivity. The conductivity for the sample prepared from the GC method here is comparable with that reported in Matsuda's work21 where the sample was finally fired at 1350 °C. The nature of oxide ion conduction in these samples can be confirmed by the collapse of electrode response in a complex plot at elevated temperature. Fig. 3b shows typical complex plots recorded at 900 °C for samples prepared by both PAD and GC methods. We can see that the arcs at low frequency for these two samples show capacitances of ∼10−5 F cm−1, which can be no doubt ascribed to electrode responses, corresponding to the enhanced kinetics of the oxygen ion diffusion and charge transfer reaction of O2 + 2e ↔ 2O2− along with the sample–electrode interface.43 Therefore, here we can make a conclusion that the PAD and GC methods can effectively improve the ceramic sinterability and hence resulted in higher oxide ion conduction. These two methods may also have great potential in preparing doped Ca12Al14O33 materials with a high substitution degree.Oxide ion migration paths
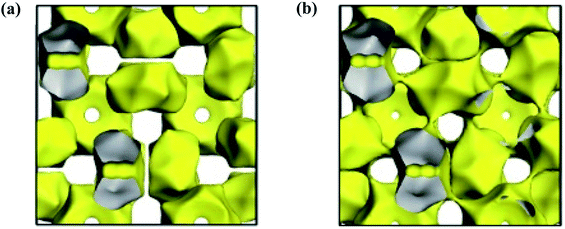
The oxide ion conduction in Ca12Al14O33 is relative to its particular crystal structure, a cubic nanoporous zeolite-like structure (a = 11.98 Å, space group I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3d, Z = 2). There are 64 out of 66 oxide ions fixed in the Ca–Al–O framework composed of 12 cages per unit cell. Each cage has a width of ∼6 Å and is surrounded by 8 other cages with ∼3.7 Å wide windows. The remaining two oxygen ions randomly occupy the centers of two of these cages, and thus loosely coordinated by cations and termed as ‘free’ oxygen. Therefore, the unit cell can be expressed by the chemical formula [Ca24Al28O64]4+·2O2−, and the schematic crystal structure is demonstrated in Fig. 4. The high mobility of free oxygen ions is an important factor for Ca12Al14O33 to become an oxide-ion conductor, and these free oxide ions are initially thought to transport directly through the wide windows to a neighboring cage,12 i.e. interstitial diffusion mechanism. This mechanism was then questioned by molecular dynamics and ab initio calculations by Sushko et al.,22 which suggested that the diffusion processes are dominated by the exchange of free oxide ions with the framework. In this exchange mechanism, the migrating free oxygen ion will kick-out and replace one framework oxygen ion, which then goes into the next cage. This exchange mechanism was then further supported by high-temperature neutron powder diffraction,13,23 and oxygen isotope exchange experiments.45,46
3d, Z = 2). There are 64 out of 66 oxide ions fixed in the Ca–Al–O framework composed of 12 cages per unit cell. Each cage has a width of ∼6 Å and is surrounded by 8 other cages with ∼3.7 Å wide windows. The remaining two oxygen ions randomly occupy the centers of two of these cages, and thus loosely coordinated by cations and termed as ‘free’ oxygen. Therefore, the unit cell can be expressed by the chemical formula [Ca24Al28O64]4+·2O2−, and the schematic crystal structure is demonstrated in Fig. 4. The high mobility of free oxygen ions is an important factor for Ca12Al14O33 to become an oxide-ion conductor, and these free oxide ions are initially thought to transport directly through the wide windows to a neighboring cage,12 i.e. interstitial diffusion mechanism. This mechanism was then questioned by molecular dynamics and ab initio calculations by Sushko et al.,22 which suggested that the diffusion processes are dominated by the exchange of free oxide ions with the framework. In this exchange mechanism, the migrating free oxygen ion will kick-out and replace one framework oxygen ion, which then goes into the next cage. This exchange mechanism was then further supported by high-temperature neutron powder diffraction,13,23 and oxygen isotope exchange experiments.45,46
In this work, we investigated the possible oxide ion migration paths by the bond valence method for the first time. This method has been discussed in a range of earlier studies about how it be used to analyze ion transport pathways statistically from crystal structure data.41,47–50 In a nutshell, it is based on the bond-valence sum (BVS) rule from Pauling's electrostatic valence concept.51 It postulates that the BVS of an atom in a crystal structure almost equals the absolute value of its oxidation state, which can be expressed as the following relation:
| Vi = ∑Sij | (1) |
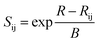 | (2) |
Conclusion
In this paper, the oxide ion conductor Ca12Al14O33 was prepared by two new ways, PAD and GC methods, along with microstructures and electrical properties reported. The results show that the new methods can effectively increase the particle sizes and densities of Ca12Al14O33 ceramic, and the product obtained from the GC method has the highest level, which therefore resulted in the highest conductivities among the ceramics prepared using the methods reported in the present work, ∼1.0 × 10−3 S cm−1 at 900 °C for the bulk conductivity. A new bond valence method was applied for the first time to investigate the oxide ion transporting mechanism in Ca12Al14O33. The results strongly suggest an exchange mechanism involving the free oxide ions and framework ion, and passing through the centers of the wide windows between Ca–Al–O cages is inevitable and a rate-limiting step for the 3D oxide ion migration.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Guangxi Natural Science Foundation (2017GXNSFAA198203), National Natural Science Foundation of China (No. 21965008), “High-level innovation team and outstanding scholar program of Guangxi Institutes” are acknowledged for financial support.References
- L. Yu, M. Tade and Z. Shao, Solid Oxide Fuel Cells: From Materials to System Modeling, 2013, vol. 123, pp. 26–55 Search PubMed.
- A. Subardi, K. Y. Liao and Y. P. Fu, RSC Adv., 2017, 7, 14487–14495 RSC.
- D. Jeong and G. Kim, Ceramist, 2018, 21 Search PubMed.
- Y. Lyu, J. Xie, D. Wang and J. Wang, J. Mater. Sci., 2020, 55, 7184–7207 CrossRef CAS.
- Z. L. M. Botello, A. Montenegro, N. G. Osorio, M. Huvé, C. Pirovano, D. R. Småbråten, S. M. Selbach, A. Caneiro, P. Roussel and G. H. Gauthier, J. Mater. Chem. A, 2019, 7, 18589–18602 RSC.
- S. Ryu, W. Yu, I. Chang, T. Park and S. W. Cha, Ceram. Int., 2020, 46, 12648–12655 CrossRef CAS.
- N. Chuankrerkkul, S. Chauoon, M. Meepho and R. Pornprasertsuk, Key Eng. Mater., 2017, 751, 467–470 Search PubMed.
- Y. Tianrang, Z. Hailei, F. Mengya, W. Konrad, W. Jie and D. Zhihong, J. Eur. Ceram. Soc., 2019, 424–431 Search PubMed.
- D. Marrero-Lopez, P. Diaz-Carrasco, J. Pena-Martinez, J. C. Ruiz-Morales and J. R. Ramos-Barrado, Fuel Cells, 2011, 11, 65–74 CrossRef CAS.
- X. Yang, A. J. Fernandezcarrion, J. Wang, F. Porcher, F. Fayon, M. Allix and X. Kuang, Nat. Commun., 2018, 9, 4484 CrossRef.
- R. J. Packer, S. J. Skinner, A. A. Yaremchenko, E. V. Tsipis, V. V. Kharton, M. V. Patrakeev and Y. A. Bakhteeva, J. Mater. Chem., 2006, 16, 3503–3511 RSC.
- J. T. S. Irvine and M. Lacerda, Nature, 1988, 23, 1033–1038 CAS.
- H. Boysen, M. Lerch, A. Stys and A. Senyshyn, Acta Crystallogr., 2007, 63, 675–682 CAS.
- J. Xu, J. Wang, X. Tang, X. Kuang and M. Rosseinsky, Inorg. Chem., 2017, 56, 6897–6905 CrossRef CAS.
- X. Kuang, M. A. Green, H. Niu, P. Zajdel, C. Dickinson, J. B. Claridge, L. Jantsky and M. J. Rosseinsky, Nat. Mater., 2008, 7, 498–504 CrossRef CAS.
- J. Xu, X. Kuang, E. Veron, M. Allix, M. R. Suchomel, F. Porcher, C. Liang, F. Pan and M. Wu, Inorg. Chem., 2014, 53, 11589–11597 CrossRef CAS.
- J. Xu, J. Wang, A. Rakhmatullin, S. Ory, A. J. Fernández-Carrión, H. Yi, X. Kuang and M. Allix, ACS Appl. Energy Mater., 2019, 16, 3503–3511 Search PubMed.
- M. M. Rashad, A. G. Mostafa and D. A. Rayan, J. Mater. Sci.: Mater. Electron., 2015, 27, 1–10 Search PubMed.
- S. Matsuishi, Y. Toda, M. Miyakawa, K. Hayashi, T. Kamiya, M. Hirano, I. Tanaka and H. Hosono, Science, 2003, 301, 626–629 CrossRef CAS.
- A. Zaki, A. Gutierrez, M. Schmidt, D. Bielsa, M. Linder and A. Faik, J. Energy Storage, 2020, 31, 101647 CrossRef.
- M. Matsuda, Y. Inda, W. Hisamatsu, K. Yamashita and T. Umegaki, J. Mater. Sci. Lett., 1996, 15, 933–934 CrossRef CAS.
- P. V. Sushko, A. L. Shluger, K. Hayashi, M. Hirano and H. Hosono, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 014101 CrossRef.
- H. Jian, L. Valenzano and G. Sant, Chem. Mater., 2015, 27, 4731–4741 CrossRef.
- J. T. S. Irvine and A. R. West, Solid State Ionics, 1990, 40, 896–899 CrossRef.
- K. Khan, A. K. Tareen, M. Aslam, K. H. Thebo, U. Khan, R. Wang, S. S. Shams, Z. Han and Z. Ouyang, Prog. Solid State Chem., 2019, 54, 1–19 CrossRef CAS.
- S. G. Ebbinghaus, H. Krause, D. Lee and J. Janek, Cryst. Growth Des., 2014, 14, 2240–2245 CrossRef CAS.
- H. Yi, Y. Lv, V. Mattick and J. Xu, Ionics, 2019, 25, 5105–5115 CrossRef CAS.
- H. Yi, Y. Lv, Y. Wang, X. Fang, V. Mattickb and J. Xu, RSC Adv., 2019, 9, 3809–3815 RSC.
- A. S. Tolkacheva, S. N. Shkerin, S. V. Plaksin, A. A. Pankratov, N. I. Moskalenko and I. Ceramics, Refract. Ind. Ceram., 2019, 60, 109–114 CrossRef CAS.
- S. Maurelli, M. Ruszak, S. Witkowski, P. Pietrzyk, M. Chiesa and Z. Sojka, Phys. Chem. Chem. Phys., 2010, 12, 10933–10941 RSC.
- J. R. Salasin, S. E. A. Schwerzler, M. R. Koehler, D. J. Keffer and C. Rawn, Materialia, 2018, 4, 466–477 CrossRef.
- M. Teusner, R. A. De Souza, H. Krause, S. G. Ebbinghaus and M. Martin, Solid State Ionics, 2016, 284, 25–27 CrossRef CAS.
- L. Palacios, S. Bruque and M. A. G. Aranda, Phys. Status Solidi, 2008, 245, 666–672 CrossRef CAS.
- R. Stoser, M. Nofz, W. Gesner, C. Schroter and G. Kranz, J. Solid State Chem., 1989, 81, 152–164 CrossRef.
- K. Kurashige, Y. Toda, S. Matstuishi, K. Hayashi and H. Hosono, Cryst. Growth Des., 2006, 6, 1602–1605 CrossRef CAS.
- J. R. Salasin and C. Rawn, Crystals, 2017, 7, 1–25 Search PubMed.
- S. G. Ebbinghaus, H. Krause and F. Syrowatka, Cryst. Growth Des., 2013, 13, 2990–2994 CrossRef CAS.
- X. Tao, Y. Yin, Z. Jia, W. Mu, Z. Gao, J. Zhang and X. Tao, Cryst. Growth Des., 2016, 16, 1903–1906 CrossRef.
- S. Fujita, H. Nakano, K. Suzuki, T. Mori and H. Masuda, Catal. Lett., 2006, 106, 139–143 CrossRef CAS.
- S. Adams and J. Swenson, Solid State Ionics, 2004, 175, 665–669 CrossRef CAS.
- S. Adams and R. P. Rao, in Bond Valences, ed. I. D. Brown and K. R. Poeppelmeier, Springer, Berlin, Heidelberg, 2014, ch. 137, pp. 129–159, DOI:10.1007/430_2013_137.
- M. Sale and M. Avdeev, J. Appl. Crystallogr., 2012, 45, 1054–1056 CrossRef CAS.
- M. Boyer, X. Yang, A. J. Fernández Carrión, Q. Wang, E. Véron, C. Genevois, L. Hennet, G. Matzen, E. Suard, D. Thiaudière, C. Castro, D. Pelloquin, L. B. Kong, X. Kuang and M. Allix, J. Mater. Chem. A, 2018, 6, 5276–5289 RSC.
- J. T. S. Irvine and A. R. West, J. Appl. Electrochem., 1989, 19, 410–412 CrossRef CAS.
- M. Kilo, S. Swaroop and M. Lerch, Defect Diffus. Forum, 2009, 289–292, 511–516 CAS.
- M. Teusner, R. A. De Souza, H. Krause, S. G. Ebbinghaus, B. Belghoul and M. Martin, J. Phys. Chem., 2015, 119, 9721–9727 CAS.
- S. Adams and R. P. Rao, J. Mater. Chem., 2012, 22, 1426–1434 RSC.
- S. Adams, in Structure and Bonding, ed. I. D. Brown and K. R. Poeppelmeier, Springer, Berlin, Heidelberg, 2013, vol. 158, ch. 96, pp. 91–128 Search PubMed.
- E. Niwa and M. Yashima, ACS Appl. Energy Mater., 2018, 1, 4009–4015 CrossRef CAS.
- Y. Yasui, E. Niwa, M. Matsui, K. Fujii and M. Yashima, Inorg. Chem., 2019, 58, 9460–9468 CrossRef CAS.
- L. Pauling, J. Am. Chem. Soc., 1929, 51, 1010–1026 CrossRef CAS.
- M. Avdeev, M. Sale, S. Adams and R. P. Rao, Solid State Ionics, 2012, 225, 43–46 CrossRef CAS.
- I. D. Brown, Chem. Rev., 2009, 109, 6858–6919 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |