Donor–acceptor duality of the transition-metal-like B₂ core in core–shell-like metallo-borospherenes La₃&[B₂@B₁₇]⁻ and La₃&[B₂@B₁₈]⁻

Abstract

Transition-metal doping induces dramatic structural changes and leads to earlier planar → tubular → spherical → core–shell-like structural transitions in boron clusters. Inspired by the newly discovered spherical trihedral metallo-borospherene D_3h La₃&B₁₈⁻ (1) (Chen, et al., Nat. Commun., 2020, 11, 2766) and based on extensive first-principles theory calculations, we predict herein the first and smallest core–shell-like metallo-borospherenes C_2v La₃&[B₂@B₁₇]⁻ (2) and D_3h La₃&[B₂@B₁₈]⁻ (3) which contain a transition-metal-like B₂ core at the cage center with unique donor–acceptor duality in La₃&B_n⁻ spherical trihedral shells (n = 17, 18). Detailed energy decomposition and bonding analyses indicate that the B₂ core in these novel complexes serves as a π-donor in the equatorial direction mainly to coordinate three La atoms on the waist and a π/σ-acceptor in the axial direction mainly coordinated by two B₆ triangles on the top and bottom. These highly stable core–shell complexes appear to be spherically aromatic in nature in bonding patterns. The IR, Raman, and photoelectron spectra of 2 and 3 are computationally simulated to facilitate their spectroscopic characterizations.

---

1. Introduction

As a prototypical electron-deficient element, boron exhibits diverse geometrical structures and bonding patterns in both bulk allotropes and polyhedral molecules.^1,2 Persistent joint photoelectron spectroscopy (PES) and first-principles theory investigations in the past two decades have unveiled a rich landscape for size-selected boron nano-clusters (B_n^−/0) from planar or quasi-planar (2D) structures (n = 3–38, 41–42)^3–8 to cage-like borospherenes (C₃/C₂ B₃₉⁻ and D_2d B₄₀^−/0) which are all characterized with delocalized multi-centre bonding.^9,10 Seashell-like borospherenes C₂ B₂₈⁻ and C_s B₂₉⁻ were later confirmed in PES measurements to be minor isomers of the monoanions.^11,12 The borospherene family has been systematically expanded at first-principles theory level to the cage-like B_n^q series (n = 36–42, q = n − 40) in different charge states.^13–16 More complicated structural competitions exist in medium-sized boron clusters, with B₄₆ being theoretically predicted to be the smallest core–shell-like boron cluster reported to date, while B₄₈, B₅₄, B₆₀, and B₆₂ are proposed to possess bilayer structures.^17,18 Joint ion-mobility experiments and density functional theory (DFT) investigations, on the other hand, indicated that bare B_n⁺ boron cluster monocations possess double-ring tubular structures in the size range between n = 16–25.¹⁹

Transition-metal-doping induces dramatic structural changes and leads to earlier planar → tubular → spherical → core–shell-like structural transitions in boron clusters. Perfect transition-metal-centred 2D boron wheels D_8h Co@B₈⁻, D_9h Ru@B₉⁻, and D_10h Ta@B₁₀⁻, half-sandwich SmB₆⁻, PrB₇⁻, CoB₁₂⁻, and RhB₁₂⁻,^20–23 double-ring tubular CoB₁₆⁻ (ref. 24) and RhB₁₈⁻,²⁵ and perfect inverse sandwich D_7h La₂B₇⁻,²⁶D_8h La₂B₈⁻,²⁷ and D_9h La₂B₉⁻ (ref. 26) have been successively characterized in PES experiments. The first experimentally observed tri-lanthanide-doped inverse triple-decker C_2v La₃B₁₄⁻ (ref. 28) contains two conjoined B₈ rings which share a B₂ unit on the waist. With four more B atoms added in, the first perfect spherical trihedral metallo-borospherene D_3h La₃&B₁₈⁻ (1) with three equivalent deca-coordinate La atoms as integral parts of the cage surface were discovered very recently in a joint PES experimental and theoretical investigation.²⁹ Exohedral metallo-borospherenes M&B₄₀ (M = Be, Mg)³⁰ and Ni_n&B₄₀ (n = 1–4)³¹ were previously proposed in theory which contain hepta-coordinate metal centres in η⁷-B₇ rings on the cage surface of B₄₀. Our group proposed very recently at first-principles theory level the smallest perfect spherical trihedral metallo-borospherenes D_3h Ta₃&B₁₂⁻ which contains three equivalent octa-coordinate Ta centres as integral parts of the cage surface.³² However, to the best of our knowledge, there have been no core–shell-like metallo-borospherenes reported to date in either theory or experiments.

Based on extensive global minimum (GM) searches and first-principles theory calculations, we predict herein the first and smallest core–shell-like (CSL) spherical trihedral metallo-borospherenes C_2v La₃&[B₂@B₁₇]⁻ (2) and D_3h La₃&[B₂@B₁₈]⁻ (3) which contain three equivalent La atoms as integral parts of cage surface and, more importantly, a B₂ core with unusual donor–acceptor duality at the cage centre (Fig. 1 and TOC) which exhibits obvious transition-metal-like behaviour. With the formation of effective coordination interactions between B₂ and La₃@B_n⁻ spherical shells (n = 17, 18), the B₂ core plays an essential role in stabilizing these spherically aromatic CSL complexes. La₃&[B₂@B₁₇]⁻ (2) and La₃&[B₂@B₁₈]⁻ (3) prove to possess the optimum core–shell combinations to demonstrate the donor–acceptor duality of a B₂ core in La₃&B_n⁻ spherical shells (n = 17, 18).

Fig. 1 Side (a) and top (b) views of the global minimum structures of D_3h La₃&B₁₈⁻ (1), C_2v La₃&[B₂@B₁₇]⁻ (2), and D_3h La₃&[B₂@B₁₈]⁻ (3) at PBE0/B6-311+G(d)/La/ECP28MWB level, with the B₂ core highlighted in red and important bond lengths indicated in Å.

2. Theoretical procedure

Extensive global minimum (GM) searches were performed on B_nLa₃⁻ (n = 19 and 20) using the TGmin 2.0 algorithms,^33,34 in conjunction with manual structural constructions. Approximately 2000 trial structures were probed on the potential energy surface for each species in both singlet and triplet states. The low-lying isomers were then fully re-optimized at both the hybrid PBE0 (ref. 35) and TPSSh³⁶ DFT levels with the 6-311+G(d)³⁷ basis set for B and Stuttgart relativistic small-core pseudopotential (ECP28MWB) for La^38,39 using the Gaussian 09 program suite (with the self-consistent-field convergence criteria of scf = tight),⁴⁰ with vibrational frequencies checked to make sure all the low-lying isomers obtained are true minima of the systems. Relative energies of the five lowest-lying isomers were further refined at the more accurate CCSD(T) level^41–43 at PBE0 geometries using the MOLPRO program,⁴⁴ with the same basis sets. Bonding analyses were performed using the adaptive natural density partitioning (AdNDP)^45,46 approach. Born–Oppenheimer molecular dynamics (BOMD) simulations were performed on La₃&[B₂@B₁₇]⁻ (2) and La₃&[B₂@B₁₈]⁻ (3) for 30 ps at different temperatures using the CP2K software package⁴⁷ with the time step of 10 fs at the PBE/TZVP level, starting from the equilibrium GM geometry with random velocities assigned to the atoms in a cubic box with 15 Å on each side. The initial conditions were chosen to correspond to a microcanonical ensemble with the energy cutoff of 300 eV. The iso-chemical shielding surfaces (ICSSs)^48,49 were generated with the Multiwfn 3.7 code.⁵⁰ A detailed energy decomposition analysis with natural orbitals for chemical valence (EDA-NOCV)^51–53 was carried out using the ADF program package⁵⁴ at the PBE0/TZP-ZORA level where scalar relativistic effects were considered for the metals using the zeroth-order regular approximation (ZORA).^55–57 The frozen core approximation was not employed in these computations. In the EDA analysis, the interaction energy (ΔE_int) between two fragments is decomposed into the electrostatic interaction energy (ΔE_elstat), the Pauli repulsion (ΔE_Pauli), and the orbital interaction energy (ΔE_orb) in eqn (1).

ΔE_int = ΔE_elstat + ΔE_Pauli + ΔE_orb (1)

3. Results and discussions

We start from closed-shell D_3h La₃&[B₂@B₁₈]⁻ (3, ), the smallest perfect CSL metallo-borospherene which can be obtained by adding a B₂ core directly inside the experimentally observed La₃&B₁₈⁻ (1) shell²⁹ (Fig. 1). Extensive global searches indicate that La₃&[B₂@B₁₈]⁻ (3) is the well-defined GM of La₃B₂₀⁻ in thermodynamics in both singlet and triplet states, with the lowest vibrational frequency of ν_min = 113.2 cm⁻¹ (e′) and large HOMO–LUMO gap of ΔE_gap = 2.30 eV at PBE0/B6-311+G(d)/La/ECP28MWB level.^37–39 It lies 0.51, 0.52, 0.29 eV lower than the second lowest-lying triple-decker C_s La₃&B₂₀⁻ at PBE0,³⁵ TPSSh,³⁶ and CCSD(T)^41–43 levels with the same basis sets, respectively (Fig. S1†). The D_3h La₃&B₁₈⁻ shell in La₃&[B₂@B₁₈]⁻ (3) contains three equivalent deca-coordinate La atoms at the centres of three conjoined η¹⁰-B₁₀ rings which share two B₆ triangles on the top and bottom interconnected by three B₂ units on the waist. All the fifteen lowest-lying isomers within 1.1 eV possess 3D structures in singlet states, with the second, third, and fourth CSL La₃&[B_n@B_20−n]⁻ isomers (n = 1–3) lying 0.65, 0.88, and 1.08 eV higher than the GM at PBE0 level, respectively. Triplet isomers are found to be much less stable than the GM, with the first triplet structure C_s La₃&[B₂@B₁₈]⁻ (14) possessing the relative energies +0.97 eV at PBE0 (Fig. S1†). Removing one B atom from a B₂ unit on the waist in La₃&[B₂@B₁₈]⁻ (3) results in the doublet C_2v La₃&[B₂@B₁₇]⁻ (2, ²A₁) which, with one η¹⁰-B₁₀ ring in the front and two equivalent η⁹-B₉ rings on the back, is also the GM of the system (Fig. S2†).

Extensive BOMD simulations are performed on La₃&[B₂@B₁₇]⁻ (2) and La₃&[B₂@B₁₈]⁻ (3) at 300, 700 and 1000 K to check their dynamical stabilities in gas-phases, respectively (Fig. S3 and S4†). Both of these CSL species appear to be dynamically stable at 1000 K, with the small calculated average root-mean-square-deviations of RMSD = 0.13, 0.14 Å and maximum bond length deviations of MAXD = 0.40, 0.47 Å, respectively. No high-lying isomers were observed during the simulations.

Natural bonding orbital (NBO) analyses⁵⁸ show that the three equivalent La centres in La₃&[B₂@B₁₈]⁻ (3) possess the electronic configuration of La [Xe]6s^0.125d^1.46, natural atomic charge of q_La = +1.28|e|, and total Wiberg bond index of WBI_La = 3.11, respectively, indicating that each La centre in these complexes donates its 6s² electrons almost completely to the B₂₀ ligand, while, in return, accepts about half an electron in its partially filled 5d orbitals from the CSL B₂₀ framework (Table S1†). As a commonly used indicator of bond order,^13–16 the calculated B–B Wiberg bond index of WBI_B–B = 0.73 in the B₂ core indicates the formation of a B–B single bond, the B⋯B bond orders of WBI_B–B = 0.27–0.43 between the two B₆ triangles and B₂ core suggest the existence of B₆⋯B₂ coordination interactions in axial direction, while the B⋯La bond order of WBI_La⋯B = 0.26 between the B₂ core and three La atoms evidences the formation of B₂⋯La coordination interactions on the equator. The B₂ core thus forms effective coordination interactions with the La₃B₁₈⁻ shell around it, akin to a transition metal centre in traditional complexes.

Detailed EDA-NOCV analyses^51–53 at PBE0/TZP-ZORA level^35,55–57 – with various interacting fragments in different charge states⁵⁹ considered (Table S2†) indicate that, with the smallest orbital interaction energy of ΔE_orb = −717.9 kcal mol⁻¹, the B₂ and La₃&B₁₈⁻ fragments interaction is best suited to describe the bonding scheme of La₃&[B₂@B₁₈]⁻ (3). Such a scheme is well in line with the experimental observation that a spherical trihedral La₃B₁₈⁻ cage is highly stable in gas phase.²⁹ As for the B₂ core, previous theoretical and experimental investigations demonstrated that the isolation of B₂ allotropes with a B≡B triple bond can be achieved in the formula of L→B≡B←L, where L is N-heterocyclic carbene (NHC),^60,61 carbonyl (CO),⁶² or boronyl anion (BO⁻).⁶³ The third excited state (¹Σ_g⁺) of B₂ with two electrons excited from 1σ_u to 1π_u rather than the ground state (³Σ_g⁻) with the valence electron configuration of 1σ²_g1σ²_u1π²_u was proven to have the most suitable electron configuration (1σ²_g1π⁴_u) to describe the bonding nature of (NHC)→B≡B←(NHC).^64,65 For La₃&[B₂@B₁₈]⁻ (3), the B₂ core in the third excited state [¹Σ_g⁺] produces a smaller orbital interaction energy (ΔE_orb) than that in the ground state [³Σ_g⁻] by 261.8 kcal mol⁻¹. We thus choose to use B₂ [¹Σ_g⁺] and La₃B₁₈⁻ [¹A₁] fragments as interacting species to demonstrate the bonding scheme of La₃&[B₂@B₁₈]⁻ (3) in Fig. 2.

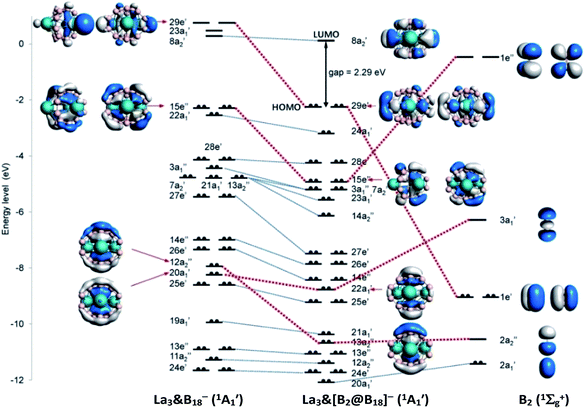Fig. 2 Bonding scheme of D_3h La₃&[B₂@B₁₈]⁻ (3) using the fragments B₂ (¹Σ_g⁺) and La₃&B₁₈⁻ (¹A₁) as interacting species at PBE0/TZP-ZORA level.

The bonding molecular orbitals (MOs) 29e′, 15e′′, and which represent coordination bonding between the B₂ core and La₃B₁₈⁻ shell are connected with the corresponding fragmental orbitals by red lines in Fig. 2, with the orbital compositions listed in Table S3.† The doubly degenerate MOs 29e′ are mainly composed of contributions from the occupied 1e′ of B₂ core with π character and vacant 29e′ of La₃B₁₈⁻ with π feature. The doubly degenerate 15e′′ are a linear combination of the occupied 15e′′ of La₃B₁₈⁻ with π feature and vacant 1e′′ of B₂ core with π* antibonding character. The non-degenerate and mainly originate from the occupied and of La₃B₁₈⁻ with π character and vacant and of B₂ core with σ bonding and σ* antibonding characters, respectively. The non-degenerate originates almost completely from the 2a′ of B₂ which represents the B–B σ single bond in the B₂ core. As detailed in Table 1, EDA analyses clearly demonstrate that the interaction energy ΔE_int between the B₂ core and La₃&B₁₈⁻ shell in La₃&[B₂@B₁₈]⁻ (3) consists of Pauli repulsion ΔE_Pauli, coulombic attraction ΔE_elstat, and orbital interaction ΔE_orb, with slightly more covalent contribution (51.2%) than electrostatic contribution (48.8%). The decompositions of the orbital interactions ΔE_orb into pairwise contributions between occupied and vacant MOs of the fragments provide quantitative insight into the charge flow. The strongest orbital interaction ΔE_orb(1) (43.9%) arises mainly from [B₂ (π)] → [La₃B₁₈⁻ (π_La(s+d))] in which the B₂ core serves as a π-donor in equatorial direction mainly to coordinate the three La atoms on the waist, while the relatively weaker orbital interaction ΔE_orb(2) (17.8%) originates from [B₂ (π*)] ← [La₃B₁₈⁻ (π_B(p))] where the B₂ core is a π*-acceptor in axial direction mainly coordinated by two B₆ triangles on the top and bottom. The orbital interactions ΔE_orb(3) (19.4%) and ΔE_orb(4) (11.0%) correspond to [B₂ (σ_p)] ← [La₃B₁₈⁻ (π_B(p))] and [B₂ ()] ← [La₃B₁₈⁻ (π_B(p))], respectively, in which the B₂ core functions as both σ- and σ*-acceptors in axial direction coordinated mainly by two B₆ triangles on the top and bottom. Fig. S5† further shows the deformation densities Δρ associated with the pairwise interactions ΔE_orb(1)–(4) in La₃&[B₂@B₁₈]⁻ (3).

Table 1 EDA-NOCV analysis of the donor–acceptor interactions of La₃&[B₂@B₁₈]⁻ (3) at PBE0/TZP-ZORA level using the fragments B₂ [¹Σ_g⁺] and B₁₈La₃⁻ [¹A₁] as interacting species. All energy values are in kcal mol⁻¹

Energy terms	Orbital interaction	B2 [^1Σg^+] + B18La3^− [^1A1]
a The value in parentheses gives the percentage contribution to the total attractive interactions (ΔEelstat + ΔEorb). b The value in parentheses gives the percentage contribution to the total orbital interactions.
ΔEint		−349.9
ΔEPauli		1053.5
ΔEelstat^a		−685.5 (48.8%)
ΔEorb^a		−717.9 (51.2%)
ΔEorb(1)^b	[B2 (π)] → [La3B18^−(πLa(s+d))]	−315.4 (43.9%)
ΔEorb(2)^b	[B2 (π*)] ← [La3B18^− (πB(p))]	−127.6 (17.8%)
ΔEorb(3)^b	[B2 (σp)] ← [La3B18^− (πB(p))]	−139.3 (19.4%)
ΔEorb(4)^b	[B2 (σs*)] ← [La3B18^− (πB(p))]	−79.1 (11.0%)
ΔEorb(rest)^b		−57.2 (7.9%)

---

Our EDA-NOCV results quantitatively indicate that the B₂ core in the spherically trihedral La₃&[B₂@B₁₈]⁻ (3) is a considerably strong π-donor to three equivalent La centres in equatorial directions rather than mainly a σ-acceptor in axial direction in the previously reported linear L→B≡B←L complexes.^60–63 The π-donation of the B₂ core effectively weakens the B–B π interactions in the B₂ core and results in a B–B single bond in La₃&[B₂@B₁₈]⁻ (3) with the B–B bond length of r_B–B = 1.63 Å (rather than a B≡B triple bond with the B–B distances of r_B≡B = 1.45–1.48 Å in L→B≡B←L complexes).^60–63 The π-donation of B₂ core in La₃&[B₂@B₁₈]⁻ (3) to three equivalent La centers evenly distributed in three equatorial directions is also different from the activation of CO by transition-metal-like NHC→B≡B←NHC in one direction in which an HOMO–LUMO swap occurs in B₂(NHC)₂ to form effective electron back-donations with the π* MO of CO.⁶⁵ The B₂ unit at the centre serves as both π-donor and σ-acceptor in B₂(NHC)₂.^60,61,65

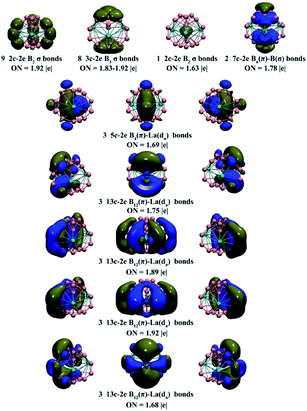
Detailed adaptive natural density partitioning (AdNDP) bonding analyses^45,46 recover both the localized and delocalized bonds of the concerned complexes. As shown in Fig. 3 in the first row, La₃&[B₂@B₁₈]⁻ (3) possesses 9 localized 2c–2e σ bonds on three edges on the waist, 8 3c–2e σ bonds on two B₆ triangles on the top and bottom, 1 2c–2e B–B σ bond inside the B₂ core, and 2 7c–2e B₆(π) → B(σ) coordination bonds between the B₂ core and two B₆ triangles on the top and bottom (in which the B₂ core serves as a σ-acceptor). The 3 5c–2e B₄(π)–La(d_σ) bonds in axial direction in the second row mainly represent B₂ → La coordination interactions between the B₂ core and three La atoms (in which the B₂ core functions as a π-donor). There exist 3 13c–2e B₁₂(π)–La(d_π) bonds in axis direction in the third row (in which the B₂ core serves as a π*-acceptor), 3 13c–2e B₁₂(π)–La(d_π) bonds in equatorial direction in the fourth row, and 3 13c–2e B₁₂(π)–La(d_σ) bonds in equatorial direction in the fifth row. The nine delocalized (p–d) π interactions evenly distributed on the cage surface form a local 6π-aromatic system over each La&B₁₀ pyramidal subunit (similar to the 6π-aromatic system in benzene) and render overall spherical aromaticity to La₃&[B₂@B₁₈]⁻ (3). The 3 13c–2e (p–d) δ bonds in the sixth row help to further stabilize the CSL complex. As shown in Fig. S6,† a closed-shell C_2v La₃&[B₂@B₁₇]²⁻ (¹A₁) possesses a similar bonding pattern with La₃&[B₂@B₁₈]⁻(3). The open-shell C_2v La₃&[B₂@B₁₇]⁻ (2) has the same bonding pattern as La₃&[B₂@B₁₇]²⁻, with the 5c–2e B₄(π)–La(d_σ) bond at the centre in the second row in Fig. S6† singly occupied (which corresponds to its singly occupied HOMO (a₁)).

Fig. 3 AdNDP bonding patterns of D_3h La₃&[B₂@B₁₈]⁻ (3) with the occupation numbers (ON) indicated.

The spherical aromaticity of La₃&[B₂@B₁₇]⁻ (2) and La₃&[B₂@B₁₈]⁻ (3) is further evidenced by their calculated negative nucleus-independent chemical shift (NICS) values⁶⁶ of NICS = −80.05 and −80.18 ppm at the cage centres, respectively. Based on the calculated NICS-ZZ components, Fig. S7† plots their iso-chemical-shielding surfaces (ICSSs)^48,49 with Z-axis parallel to the designated C₂ molecular axes of the systems to illuminate the chemical shielding around the La&B₁₀ pyramids in these complexes. Obviously, the space inside the spherical trihedron and within about 1.0 Å above the La centres in vertical direction belongs to the chemical shielding region with negative NICS-ZZ values, while the chemical de-shielding areas with positive NICS values are located outside the B₁₀ ring in the horizontal direction. The ICSSs of these complexes in C₂ axial directions appear to be similar to that of the prototypical aromatic benzene C₆H₆ in C₆ axial direction (Fig. S7†).

Finally, we simulate the IR, Raman, and PES spectra of La₃&[B₂@B₁₈]⁻ (3) in Fig. 4 to facilitate its future spectroscopic characterizations in gas-phases. Its major IR bands occur at 365(e′), 517(e′), 728(e′), 824(e′), 1169(e′) and 1421(e′) cm⁻¹, with the corresponding Raman active vibrations located at 158(e′′), 366(e′), 521(), 824(e′) and 1006() cm⁻¹, respectively. Detailed vibrational analyses indicate that the symmetrical vibrations at 521() cm⁻¹ represent typical radial breathing modes (RBMs) of the boron skeleton which can be used to characterize single-walled hollow boron nanostructures.⁶⁷ The calculated PES spectrum of La₃&[B₂@B₁₈]⁻ in Fig. 4c exhibits major spectral features at 2.46, 2.51, 2.98, 3.73–4.94, 5.81 and 6.02 eV, respectively, which correspond to vertical electronic transitions from the ground state of the anion to the ground and excited states of the neutral at the ground-state geometry of the anion. The simulated IR, Raman, and photoelectron spectra of La₃&[B₂@B₁₇]⁻ (2) are depicted in Fig. S8.†

Fig. 4 Simulated (a) IR, (b) Raman and (c) photoelectron spectra of La₃&[B₂@B₁₈]⁻ (3) at PBE0/B6-311+G(d)/La/ECP28MWB level.

4. Summary

In summary, we have presented in this work a comprehensive first-principles theory investigation on the first and smallest spherically aromatic CSL metallo-borospherenes La₃&[B₂@B₁₇]⁻ and La₃&[B₂@B₁₈]⁻ in which the B₂ core and La₃&B_n⁻ spherical trihedral shells (n = 17 and 18) match both geometrically and electronically. The donor–acceptor duality of the transition-metal-like B₂ core plays an essential role in stabilizing these novel complexes, in particular, its strong π-donation to the three equivalent La atoms in equatorial directions makes major contributions to the overall orbital interaction. Initial results indicate that the experimentally observed spherical trihedral D_3h Tb₃&B₁₈⁻ (ref. 29) can also be used as a cage-like shell to host a B₂ core with donor–acceptor duality. A similar B₂ core in a tubular molecular rotor La₂&[B₂@B₁₈]⁻ has been reported recently.⁶⁸ It is anticipated that more B_n units with donor–acceptor dualities could exist in 3D complexes or low-dimensional nanostructures which may have important applications in materials science, molecular devices, and chemical catalysis.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the National Natural Science Foundation of China (21720102006 and 21973057 to S.-D. Li). We thank the helpful discussions on EDA-NOCV analysis with Prof. Lili Zhao from Nanjing Tech University and Dr Jun Liu from FermiTech (Beijing) Co. Ltd.

Notes and references

1. F. A. Cotton, G. Wilkinson, C. A. Murillo and M. Bochmann, Advanced Inorganic Chemistry, Wiley-Interscience, New York, 6th edn, 1999, p. 1355, ISBN 0-471-19957-5.
2. L. S. Wang, Int. Rev. Phys. Chem., 2016, 35, 69.
3. H. J. Zhai, A. N. Alexandrova, K. A. Birch, A. I. Boldyrev and L. S. Wang, Angew. Chem., Int. Ed., 2003, 42, 6004–6008.
4. A. P. Sergeeva, D. Y. Zubarev, H. J. Zhai, A. I. Boldyrev and L. S. Wang, J. Am. Chem. Soc., 2008, 130, 7244–7246.
5. W. Huang, A. P. Sergeeva, H. J. Zhai, B. B. Averkiev, L. S. Wang and A. I. Boldyrev, Nat. Chem., 2010, 2, 202–206.
6. Q. Chen, T. T. Chen, H. R. Li, X. Y. Zhao, W. J. Chen, H. J. Zhai, S. D. Li and L. S. Wang, Nanoscale, 2019, 11, 9698.
7. T. Jian, X. N. Chen, S. D. Li, A. I. Boldyrev, J. Li and L. S. Wang, Chem. Soc. Rev., 2019, 48, 3550.
8. H. Bai, T. T. Chen, Q. Chen, X. Y. Zhao, Y. Y. Zhang, W. J. Chen, W. L. Li, L. F. Cheung, B. Bai, J. Cavanagh, W. Huang, S. D. Li, J. Li and L. S. Wang, Nanoscale, 2019, 11, 23286–23295.
9. H. J. Zhai, Y. F. Zhao, W. L. Li, Q. Chen, H. Bai, H. S. Hu, Z. A. Piazza, W. J. Tian, H. G. Lu, Y. B. Wu, Y. W. Mu, G. F. Wei, Z. P. Liu, J. Li, S. D. Li and L. S. Wang, Nat. Chem., 2014, 6, 727.
10. Q. Chen, W. L. Li, Y. F. Zhao, S. Y. Zhang, H. S. Hu, H. Bai, H. R. Li, W. J. Tian, H. G. Lu, H. J. Zhai, S. D. Li, J. Li and L. S. Wang, ACS Nano, 2015, 9, 754.
11. Y. J. Wang, Y. F. Zhao, W. L. Li, T. Jian, Q. Chen, X. R. You, T. Ou, X. Y. Zhao, H. J. Zhai, S. D. Li, J. Li and L. S. Wang, J. Chem. Phys., 2016, 144, 064307.
12. H. R. Li, T. Jian, W. L. Li, C. Q. Miao, Y. J. Wang, Q. Chen, X. M. Luo, K. Wang, H. J. Zhai, S. D. Li and L. S. Wang, Phys. Chem. Chem. Phys., 2016, 18, 29147.
13. Q. Chen, S. Y. Zhang, H. Bai, W. J. Tian, T. Gao, H. R. Li, C. Q. Miao, Y. W. Mu, H. G. Lu, H. J. Zhai and S. D. Li, Angew. Chem., Int. Ed., 2015, 54, 8160.
14. Q. Chen, H. R. Li, C. Q. Miao, Y. J. Wang, H. G. Lu, Y. W. Mu, G. M. Ren, H. J. Zhai and S. D. Li, Phys. Chem. Chem. Phys., 2016, 18, 11610.
15. W. J. Tian, Q. Chen, H. R. Li, M. Yan, Y. W. Mu, H. G. Lu, H. J. Zhai and S. D. Li, Phys. Chem. Chem. Phys., 2016, 18, 9922.
16. Q. Chen, H. R. Li, W. J. Tian, H. G. Lu, H. J. Zhai and S. D. Li, Phys. Chem. Chem. Phys., 2016, 18, 14186.
17. L. W. Sai, X. Wu, N. Gao, J. J. Zhao and R. B. King, Nanoscale, 2017, 9, 13905–13909.
18. L. Pei, Y.-Y. Ma, M. Yan, M. Zhang, R.-N. Yuan, Q. Chen, W.-Y. Zan, Y.-W. Mu and S. D. Li, Eur. J. Inorg. Chem., 2020, 3296–3301.
19. E. Oger, N. R. M. Crawford, R. Kelting, P. Weis and M. M. K. R. Ahlrichs, Angew. Chem., Int. Ed., 2007, 46, 8503.
20. T. R. Galeev, C. Romanescu, W. L. Li, L. S. Wang and A. I. Boldyrev, Angew. Chem., Int. Ed., 2012, 51, 2101–2105.
21. C. Romanescu, T. R. Galeev, W. L. Li, A. I. Boldyrev and L. S. Wang, J. Chem. Phys., 2013, 138, 134315.
22. C. Romanescu, T. R. Galeev, W. L. Li, A. I. Boldyrev and L. S. Wang, Acc. Chem. Res., 2013, 46, 350–358.
23. I. A. Popov, W. L. Li, Z. A. Piazza, A. I. Boldyrev and L. S. Wang, J. Phys. Chem. A, 2014, 118, 8098–8105.
24. I. A. Popov, T. Jian, G. V. Lopez, A. I. Boldyrev and L. S. Wang, Nat. Commun., 2015, 6, 8654.
25. T. Jian, W. L. Li, X. Chen, T. T. Chen, G. V. Lopez, J. Li and L. S. Wang, Chem. Sci., 2016, 7, 7020–7027.
26. T. T. Chen, W. L. Li, J. Li and L. S. Wang, Chem. Sci., 2019, 10, 2534–2542.
27. W. L. Li, T. T. Chen, D. H. Xing, X. Chen, J. Li and L. S. Wang, PNAS, 2018, 115, E6972–E6977.
28. T. T. Chen, W. L. Li, W. J. Chen, J. Li and L. S. Wang, Chem. Commun., 2019, 55, 7864–7867.
29. T. T. Chen, W. L. Li, W. J. Chen, X. H. Yu, X. R. Dong, J. Li and L. S. Wang, Nat. Commun., 2020, 11, 2766.
30. H. Bai, Q. Chen, H. J. Zhai and S. D. Li, Angew. Chem., Int. Ed., 2015, 54, 941.
31. H. R. Li, X. X. Tian, X. M. Luo, M. Yan, Y. W. Mu, H. G. Lu and S. D. Li, Sci. Rep., 2017, 7, 5701.
32. Y. Zhang, X. Y. Zhao, M. Yan and S. D. Li, RSC Adv., 2020, 10, 29320.
33. Y. F. Zhao, X. Chen and J. Li, Nano Res., 2017, 10, 3407–3420.
34. X. Chen, Y. F. Zhao, L. S. Wang and J. Li, Comput. Theor. Chem., 2017, 1107, 57–65.
35. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158.
36. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
37. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650.
38. D. Feller, J. Comput. Chem., 1996, 17, 1571.
39. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045.
40. M. J. Frisch, et al., Gaussian 09, Revision D.01, Gaussian Inc., Wallingford, CT, 2009.
41. J. Čížek, Adv. Chem. Phys., 1969, 14, 35.
42. G. D. Purvis III and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910.
43. K. Raghavachari, G. W. Trucks, J. A. People and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479.
44. H. J. Werner, et al., Molpro, version 2012.1.
45. N. V. Tkachenko and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2019, 21, 9590.
46. T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580.
47. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103.
48. S. Klod and E. Kleinpeter, J. Chem. Soc., Perkin Trans. 2, 2001, 1893.
49. E. Kleinpeter, S. Klod and A. Koch, J. Mol. Struct., 2007, 811, 45.
50. T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580.
51. T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1–10.
52. M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962–975.
53. M. Mitoraj and A. Michalak, Organometallics, 2007, 26, 6576–6580.
54. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
55. C. Chang, M. Pelissier and P. Durand, Phys. Scr., 1986, 34, 394–404.
56. J. L. Heully, I. Lindgren, E. Lindroth, S. Lundqvist and A. M. Martensson-Pendrill, J. Phys. B: At. Mol. Phys., 1986, 19, 2799–2815.
57. E. v. Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610.
58. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899.
59. L. Zhao, S. Pan, M. Zhou and G. Frenking, Science, 2019, 365, eaay5021.
60. G. Frenking and N. Holzmann, Science, 2012, 336, 1394–1395.
61. H. Braunschweig, R. D. Dewhurst, K. Hammond, J. Mies, K. Radacki and A. Vargas, Science, 2012, 336, 1420–1422.
62. M. Zhou, N. Tsumori, Z. Li, K. Fan, L. Andrews and Q. Xu, J. Am. Chem. Soc., 2002, 124, 12936–12937.
63. S. D. Li, H. J. Zhai and L. S. Wang, J. Am. Chem. Soc., 2008, 130, 2573–2579.
64. N. Holzmann, M. Hermann and G. Frenking, Chem. Sci., 2015, 6, 4089–4094.
65. H. Zhang, Z. Cao, W. Wu and Y. Mo, Angew. Chem., Int. Ed., 2018, 57, 13076–13081.
66. P. v. R. Schleyer and C. Maerker, J. Am. Chem. Soc., 1996, 118, 6317–6318.
67. D. Ciuparu, R. F. Klie, Y. M. Zhu and L. Pfefferle, J. Phys. Chem. B, 2004, 108, 3967–3699.
68. X. Q. Lu, Q. Chen, X. X. Tian, Y. W. Mu, H. G. Lu and S. D. Li, Nanoscale, 2019, 11, 21311–21316.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra06769e

---