Open Access Article
Open Access ArticleConformational dynamics of amyloid-β (16–22) peptide in aqueous ionic liquids†
Sathish Dasari and
Bhabani S. Mallik
and
Bhabani S. Mallik *
*
Department of Chemistry, Indian Institute of Technology Hyderabad, Sangareddy-502285, Telangana, India. E-mail: bhabani@chy.iith.ac.in; Tel: +91 4023016258
First published on 8th September 2020
Abstract
Molecular dynamics simulations of amyloid-β (16–22) peptide dimer in water as well as at two different experimentally studied concentrations of hydrated ionic liquids (ILs), ethylammonium mesylate (EAM), ethylammonium nitrate (EAN), and triethylammonium mesylate (TEAM), were carried out employing an umbrella sampling method. We used the average Ψ angle of the peptide backbone as the reaction coordinate to observe the conformational changes of a peptide dimer. Secondary structural element values were calculated for the peptide dimer along the reaction coordinate to see the transition of the peptide dimer between β-sheet and α-helix conformations. We observe the β-sheet conformation as the global minimum on the free energy surfaces in both EAM and EAN ILs at both the concentrations and at a low concentration of TEAM. However, we observe α-helix conformation as the global minimum at a high concentration of TEAM. Our results are in good correlation with the experimental findings. We calculated the average number of intramolecular and intermolecular hydrogen bonds of α-helix and β-sheet conformations in all solutions, and they are in correlation with the secondary structure element values. To understand the peptide–IL interactions, atom–atom radial distribution functions of cation, anion, and water around amide oxygen and hydrogen atoms were calculated. The solvent-accessible surface area of the peptide dimer was calculated to understand the exposure of the peptide towards the solvent during conformational changes. Finally, van der Waals (vdW) and Coulomb interaction energies were calculated between peptide–cation, peptide–anion, and peptide–water to understand the stability of conformations in different concentrations. We find that the TEA cation has more vdW interaction energy compared to Coulomb interaction energy with peptide in 70% (w/w) TEAM, which mimics a membrane-like environment to induce α-helix conformation rather than β-sheet conformation.
1. Introduction
The self-assembly of denatured proteins forms amyloid fibrils due to acidic conditions, N-terminal truncation, and high temperatures. The formation of amyloid has gained attention because of its role in causing diseases such as Alzheimer's, Huntington's, Parkinson's, Type II diabetes and mad cow disease.1–5 On the other hand, amyloid fibrils have applications in biomaterials due to their remarkable stability, elasticity, and strength. They have high mechanical moduli6 compared to that of beta-sheet silk.7 The understanding of amyloid formation from proteins and its control is essential in both biomedical and materials sciences. The treatment of the disease requires inhibitors, and a promoter is needed to form an amyloid that can be used as a biomaterial. Several experiments8–11 and simulation studies12–16 have been carried out to understand the mechanism of protein aggregation. Ionic liquids (ILs) have remarkable use in biological applications because of their excellent solvating properties towards bio-relevant molecules, variable polarity range, nonvolatility, and recyclability. ILs are shown to stabilize and solvate proteins, enzymes and DNA.17–20 The use of ILs as amyloid-forming solvents have been studied to understand the mechanism of amyloid formation to discover drugs for diseases related to amyloids. The first study to the formation of amyloid fibrils in ammonium-based ILs involves protein hen egg-white lysozyme (HEWL). It was observed that at low concentrations of IL, HEWL formed amyloid fibrils, and the dissolution of amyloids in ILs restored the bioactivity of enzyme up to 72%.21 The restoration of bioactivity from amyloid fibrils could offer a novel approach to long term storage of proteins. ILs can be used as a stimulator for the amyloid formation of α-synuclein, which otherwise takes several months to form amyloids in aqueous buffer solution.22 Amyloid formation of apo-α-lactalbumin, a small calcium-binding protein, was studied in the presence of 5% 1-butyl-3-methyl imidazolium-based ILs, and it was found that they were highly effective in forming amyloid fibrils.23 The fibril formation of Amyloid β protein (16–22) (Aβ16–22) peptide followed reverse Hofmeister trend of anions with triethylammonium cation, which showed that fast fibril formation kinetics could be achieved in seconds.24 Using primary ammonium-based ILs at low concentration resulted in the large conversion of Alzheimer's peptide (16–22) into amyloid fibrils.25On the other hand, ILs can also be used as amyloid inhibitors. Tetramethyl-guanidinium acetate showed the inhibition of amyloid formation of HEWL, and it was observed that the inhibitory effect was related to IL itself and not the solvated ions.26 Tertiary ammonium-based ILs at high concentrations inhibited the formation of amyloid fibrils of Aβ16–22.25 Ethylammonium nitrate (EAN) induced the α-helical structure of β-rich protein β-lactoglobulin.27 In another study, it was showed that helix forming ability of the alkylammonium based nitrate ILs, which can be used for the cryopreservation of proteins.28 Suppression effect of ammonium-based nitrate ILs on the formation of insulin amyloid was observed.29 1-Butyl-3-methyl imidazolium bromide was shown to mitigate the formation of lysozyme fibrils significantly.30 Imidazolium based ILs showed higher dissolution ability of amyloid aggregates of insulin compared to ammonium-based ILs.31 A recent study showed that the aggregation of Aβ1–11 peptide is selective to hydrated 1-butyl-3-methylimidazolium thiocyanate compared to EAN, which did not show aggregation, however, it formed alpha-helix structure from the disordered peptide. It was shown that the aggregation selectivity was due to the denaturation ability of anionic species.
Previous studies proved that Aβ16–22 peptide sequence is responsible for the fibril formation of the full-length Abeta peptide in Alzheimer's disease.32,33 Mechanism of oligomerization of this peptide fragment was studied by various groups using molecular dynamics simulations.34–37 The inhibitory effect of caffeine, choline-o-sulfate and adenosine triphosphate on fibril formation of this peptide fragment was studied using molecular dynamics simulations.38–40 The fibril formation of this peptide fragment was studied experimentally using triethylammonium cation with several anions at high concentrations and found that the fast fibril formation can be achieved in seconds.24 In another study, a similar fibril formation analysis was carried out with changing the concentration of protic IL containing primary, secondary, and tertiary ethylammonium cations with mesylate anion.25 However, the peptide–IL interactions that can happen during the fibril formation were not appropriately understood. Recently, we studied the transition of Aβ33–42 peptide dimer from α-helix to β-sheet in three different aqueous ILs at two different concentrations.41 In the current study, we investigated the mechanism of transition of Aβ16–22 peptide from alpha-helix to beta-sheet in the aqueous solution of three different experimentally studied ionic liquids, ethylammonium mesylate (EAM), ethylammonium nitrate (EAN) and triethylammonium mesylate (TEAM), at two different concentrations [10% (w/w) and 70% (w/w)] using umbrella sampling molecular dynamics simulation. Ammonium-based ILs are found to be less toxic and easily biodegradable as compared to other cation-based ILs.42–44
2. Computational methods
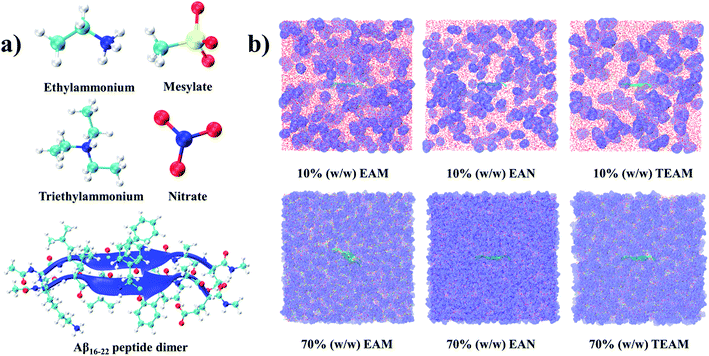
The starting coordinates for the dimer of the amyloid peptide 16–22 with sequence KLVFFAQ were extracted from the protofibril (PDB id 2BEG).45 We do not have coordinates for the lysine residue (K) in the crystal structure. We have modeled this lysine with the coordinates of the other lysine (residue number 28) from the crystal structure. We capped the ends of the peptides with acetyl and N-methyl groups to avoid charge accumulation in the terminals. We carried out three sets of calculations (i) dimer (16–22) of amyloid peptide in aqueous solution (ii) dimer (16–22) of the amyloid peptide in 10% (w/w) of aqueous solutions of EAM, EAN, and TEAM IL (iii) dimer (16–22) of the amyloid peptide in 70% (w/w) of aqueous solutions of EAM, EAN, and TEAM IL. Amber99sb46 and GAFF47 force-field parameters were used for the peptides and ILs, respectively. The IL ions were optimized along with the Merz–Kollman charge calculation48 using the density functional theory method employing B3LYP49–51 exchange–correlation functional and 6-311+G (2d, p) basis set using Gaussian 09 software package.52 The ball and stick models of the optimized IL ions and peptide dimers were shown in Fig. 1(a).The point charges for atoms of IL ions were calculated using the restrained electrostatic potential method53 using the Antechamber module of AMBERTools.54 The point charges of atoms of IL ions were scaled to 0.8, which provides enhanced dynamics during the simulation. It was proved in a previous study that scaling point charges to 0.8 would improve dynamic properties of the ILs.55 Recently, we calculated the solvation free energy of the methylated nucleobases in hydrated IL by scaling charges of IL to 0.8 with changing the concentration of IL.56 The results are found to be in correlation with the experiment qualitatively. There are other studies where charge scaling has been used for ILs in mixtures with water and other solvents to calculate structure and thermodynamic properties.57,58 Water was modeled with an extended simple point charge model (SPC/E).59 The peptides were solvated in a cubic box with water in the case of the aqueous solution, both water, and IL in the case of aqueous IL using PACKMOL software.60 The number of water, ILs, and density, the volume of the simulation box of the studied systems are given in Table 1. The systems were minimized initially using the steepest descent algorithm for 2000 steps freezing the peptide backbone atoms. Later, the systems were heated at 600 K temperature for 5 ns and cooled down to room temperature, 298.15 K, to get good mixing of water and ions. The systems were simulated under the NpT ensemble for 15 ns, followed by the 5 ns NVT ensemble. Finally, the systems were simulated for 50 ns under the NVE ensemble to get good solvation around peptide. The temperature and total energy of the system along the simulation time are given in the ESI (Fig. S1 and S2),† and we observe no drift in these quantities. Mean squared displacements (MSD) of the water, cation, and anion were calculated in 10 and 70% (w/w) in EAM, EAN, and TEAM ILs and are given in ESI (Fig. S3)† to see that the molecules are diffusing enough. We also calculated COM–COM radial distribution functions (RDFs) of anion around cation and are given in ESI (Fig. S4).† It is evident from the MSD and RDFs that the cation and anion escape from their first solvation shell frequently.
| System | Water | IL | Density (kg m−3) | Box length (nm) |
|---|---|---|---|---|
| Water | 6883 | — | 1002.6 | 5.93 |
| 10% (w/w) EAM | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
250 | 1022.77 | 8.30 |
| 70% (w/w) EAM | 5900 | 1750 | 1185.08 | 7.92 |
| 10% (w/w) EAN | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
250 | 1020.37 | 7.62 |
| 70% (w/w) EAN | 4500 | 1750 | 1164.57 | 7.29 |
| 10% (w/w) TEAM | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 770 770 |
150 | 1009.72 | 7.88 |
| 70% (w/w) TEAM | 4700 | 1000 | 1085.36 | 7.57 |
The atoms of the peptide backbone were frozen during equilibration of the system to retain the peptide dimer in β-sheet conformation to start within umbrella sampling simulations. Newton's equations of motion were integrated by using a velocity-Verlet algorithm with a time step of 2 fs. The cut-off distances for nonbonded interactions were 12 Å, and the long-range electrostatic interactions were calculated using particle mesh Ewald method.61 The temperature was controlled using velocity rescaling method62 with a coupling time of 0.1 ps. The pressure was controlled by the Berendsen barostat63 for the first 10 ns of NpT and by Parrinello–Rahman barostat64 for the last 5 ns of the NpT with a coupling time of 2 ps. Periodic boundary conditions were used in all three directions. The bonds between hydrogen and heavy atoms were constrained using the LINCS algorithm.65 The equilibrated simulation boxes of hydrated ILs are shown in Fig. 1(b). All the simulations were performed using the GROMACS-5.0.4 software package.66 The optimized coordinates and force-field parameters of the IL ions are given in the ESI.†
Calculating free energy surface with minima separated by significant energy barriers is difficult using unbiased molecular dynamics simulations as it requires long simulation time. An alternate route to construct the free energy landscape is to perform biased molecular dynamics simulations. Umbrella sampling is one of the biased molecular dynamics simulation technique which provides free energy change along the defined reaction coordinate. We used umbrella sampling simulations to see the transition from the β-sheet structure to α-helix with the help of the average Ψ angle as the reaction coordinate.67,68 The average Ψ angle can be used as a reaction coordinate in umbrella sampling simulations to perform this transition. The final configuration from the NVE simulation was used as the initial configuration for the subsequent umbrella sampling simulations. Peptide (16–22) dimer has 10 different Ψ angles. We constrained each of these Ψ angles to a particular value to get the average Ψ angle. The average Ψ angle in the starting conformation was observed to be 140°. We increased the average Ψ angle to 180° with an increment of 10° and decreased to −180° with an increment of −10°. Each window of the average Ψ angle was simulated for 10 ns, and we have 37 independent simulations corresponding to average Ψ angles from −180° to 180° accumulating 370 ns for one system. The input configuration for each simulation has been chosen from the final configuration from the previous simulation so that the system gets equilibrated quickly. Each Ψ angle was restrained using a harmonic spring constant of 150 kJ mol−1 rad−2. The average Ψ angles, along with the simulation time for all systems, are shown in ESI (Fig. S5–S8).† All umbrella sampling simulations were performed using GROMACS-5.0.4 software package with PLUMED-2.2.0 plug-in.69 Weighted histogram analysis method70 was employed to construct the free energy profiles from the umbrella sampling simulations. The convergence of the free energy profiles with simulation time is shown in the ESI (Fig. S9 and S10).† The dictionary of protein secondary structure (DSSP) tool71 was used to investigate the probability of the secondary structure elements of the peptide dimer in water and hydrated ILs with changing the average Ψ angle. Atom–atom radial distribution functions (RDFs) of cation, anion, and water around amide hydrogen and amide oxygen atoms of peptide backbone were calculated. The average number of intramolecular and intermolecular hydrogen bonds were calculated for α-helix and β-sheet conformations. Solvent accessible surface area (SASA) of the peptide dimer was calculated to know the exposure to the solvent during the transition. We have used a probe radius of 0.14 ns to calculate the SASA of the dipeptide considering water and IL acting as the solvent. In the end, we calculated the van der Waals and Coulomb interactions energies between peptide–cation, peptide–anion, and peptide–water pairs to explain the stability of peptide conformations.
3. Results and discussion
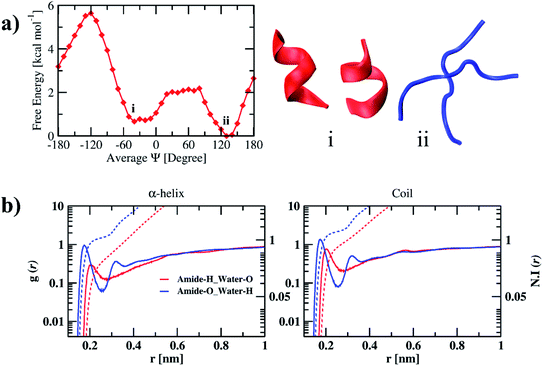
The free energy profile of the peptide dimer with the average Ψ angle in water along with the conformations of the corresponding minima are shown in Fig. 2(a). The free energy profile has two minima separated with a free energy barrier. Average secondary structure elements for conformations corresponding to each average Ψ angle are calculated to understand the structural changes that can happen during the transition and are shown in the ESI (Table S1).† The DSSP values corresponding to minimum energy conformations are shown in Table 2. The global minimum was observed at an average Ψ angle of 130° corresponding to the coil conformation. It has 81% of coil conformation on average. As we move from an average Ψ angle 130° to 60°, the coil conformation increases to 93%. The β-sheet conformation was observed at an average Ψ angle of 140°, with 47% of the β-sheet and 46% of the coil secondary structure. The coil and β-sheet conformations have similar free energy. The helix formation occurs at the average Ψ angle value of −20° and continues to increase till −60°. The minimum is observed at −40° average Ψ angle has 58% of helical conformation and 28% coil conformation on average. The coil and helix conformations are separated with a free energy barrier of 2 kcal mol−1. The transition from the coil to helix needs to cross this energy barrier, while the helix to coil transition requires only 1.5 kcal mol−1. The average number of intramolecular and intermolecular hydrogen bonds of the conformations corresponding to minima are tabulated in Table 3. The average number of intermolecular hydrogen bonds (1.76) between individual peptides is less compared to the average number of intramolecular hydrogen bonds (3.5, 3.2) of helical conformations of individual peptides. Semi-log RDFs of water hydrogen and oxygen atoms around amide oxygen and hydrogen atoms of the peptide along with the number integral calculated and are shown in Fig. 2(b). The corresponding coordination numbers of water oxygen and hydrogen atoms are shown in the ESI (Table S8).† The probability of water hydrogen atoms around amide oxygen atoms is larger than the probability of water oxygen around amide hydrogen atoms in both α-helix and coil conformations. It is also evident from the coordination numbers, where 1.12 water hydrogens coordinate with each amide oxygen atom and 0.4 water oxygens coordinate with each amide hydrogen atom in α-helix conformation. The coordination numbers are found to be more in coil conformation as compared to α-helix conformation. 1.6 water hydrogen atoms are coordinated with each amide oxygen atom, and 0.9 water hydrogen atom are coordinated with each amide hydrogen atom in coil conformation. The coordination numbers are in correlation with the average number of intra and intermolecular hydrogen bonds observed in dipeptide. We also calculated the average interaction energies between dipeptide and solvent for α-helix and coil conformations and are tabulated in Table 4. We observe that both Coulomb and LJ interaction energies and total interaction energies are more negative for coil conformation compared to α-helix conformation. It is evident from the number of hydrogen bonds, RDFs, and peptide–solvent interaction energies that the stabilization of coil conformation is due to the hydrogen bonding of peptides with water molecules and the entropy of the peptide chain due to the large conformational freedom. However, the stabilization of helix conformation is due to the intramolecular hydrogen bonding within the peptide.| System | Conformation | Coil | Bend | Turn | α-Helix | 310-Helix | 5-Helix | β-Sheet | β-Bridge |
|---|---|---|---|---|---|---|---|---|---|
| Water | α-Helix | 0.28 | 0.01 | 0.06 | 0.58 | 0.01 | |||
| Coil | 0.81 | 0.04 | 0.08 | ||||||
| 10% (w/w) EAM | α-Helix | 0.29 | 0.11 | 0.52 | 0.02 | ||||
| β-Sheet | 0.30 | 0.63 | |||||||
| 70% (w/w) EAM | α-Helix | 0.31 | 0.23 | 0.30 | 0.08 | ||||
| β-Sheet | 0.30 | 0.62 | |||||||
| 10% (w/w) EAN | α-Helix | 0.36 | 0.11 | 0.13 | 0.32 | 0.01 | |||
| β-Sheet | 0.39 | 0.54 | |||||||
| 70% (w/w) EAN | α-Helix | 0.48 | 0.35 | 0.10 | 0.08 | ||||
| β-Sheet | 0.28 | 0.65 | |||||||
| 10% (w/w) TEAM | α-Helix | 0.42 | 0.13 | 0.12 | 0.23 | 0.03 | |||
| β-Sheet | 0.31 | 0.62 | |||||||
| 70% (w/w) TEAM | α-Helix | 0.40 | 0.01 | 0.24 | 0.29 | ||||
| β-Sheet | 0.27 | 0.66 |
| System | Alpha helix (intramolecular) | Beta sheet (intermolecular) | |
|---|---|---|---|
| Helix 1 | Helix 2 | ||
| Water | 3.5 | 3.22 | 1.76 |
| 10% (w/w) EAM | 3.33 | 3.56 | 5.34 |
| 70% (w/w) EAM | 3.02 | 3.06 | 5.4 |
| 10% (w/w) EAN | 3.27 | 2.8 | 4.8 |
| 70% (w/w) EAN | 2.18 | 2.03 | 5.8 |
| 10% (w/w) TEAM | 2.41 | 3.41 | 5.48 |
| 70% (w/w) TEAM | 2.54 | 3.31 | 5.78 |
| System | Average Ψ | Cation | Anion | Water | Total | ||||
|---|---|---|---|---|---|---|---|---|---|
| vdW | Coul | vdW | Coul | vdW | Coul | vdW | Coul | ||
| Water | α-Helix | — | — | — | — | −281.62 | −1941.11 | −281.62 | −1941.11 |
| Coil | — | — | — | — | −309.23 | −2231.3 | −309.23 | −2231.3 | |
| 10% (w/w) EAM | α-Helix | −40.08 | −118.03 | −165.16 | −307.70 | −233.25 | −1699.74 | −438.49 | −2125.47 |
| β-Sheet | −33.18 | −76.31 | −112.9 | −159.8 | −213.12 | −1727.33 | −359.2 | −1963.44 | |
| 70% (w/w) EAM | α-Helix | −192.33 | −277.7 | −345.83 | −545.64 | −45.3 | −1021.94 | −583.46 | −1845.28 |
| β-Sheet | −204.42 | −341.52 | −363.4 | −524.14 | −25.21 | −937.27 | −593.03 | −1802.93 | |
| 10% (w/w) EAN | α-Helix | −44.45 | −113.77 | −131.15 | −274.07 | −206.95 | −1688.82 | −382.55 | −2076.66 |
| β-Sheet | −37.24 | −58.06 | −102.73 | −265.01 | −219.63 | −1681.53 | −359.6 | −2004.6 | |
| 70% (w/w) EAN | α-Helix | −273.95 | −393.98 | −314.44 | −769.26 | −46.61 | −904.11 | −634.99 | −2067.35 |
| β-Sheet | −253.99 | −371.21 | −285.95 | −595.3 | −47.3 | −858.33 | −587.24 | −1824.82 | |
| 10% (w/w) TEAM | α-Helix | −89.54 | −33.41 | −150.95 | −266.62 | −217.43 | −1694.9 | −457.92 | −1994.93 |
| β-Sheet | −45.91 | −21.54 | −77.6 | −105.3 | −213.48 | −1833.4 | −336.69 | −1960.24 | |
| 70% (w/w) TEAM | α-Helix | −333.15 | −109.1 | −268.74 | −511.2 | 8.87 | −1107.12 | −593.02 | −1727.42 |
| β-Sheet | −265.2 | −98.9 | −242.3 | −376.3 | −9.72 | −1246 | −517.22 | −1721.2 | |
The free energy profiles of the peptide dimer in 10% and 70% (w/w) of EAM IL in water are shown in Fig. 3(a and b) along with the corresponding conformations of the minima observed. The DSSP values of the peptide with the average Ψ angle are given in the ESI (Tables S2 and S3).† In both the solutions, the global minimum is observed at an average Ψ angle of 140°, corresponding to the β-sheet conformation. The second-lowest minimum was observed at an average Ψ angle of −40° corresponding to α-helix conformation. The secondary structural elements of the peptide dimer corresponding to minima are shown in Table 2. The peptide dimer at the global minimum is having ∼60% of the β-sheet conformation and 30% of coil conformation in both concentrations. However, the peptide shows 52% helical, 29% coil, and 11% of turn secondary structure elements in 10% (w/w) IL, and 30% helical, 31% coil, and 23% of turn secondary structure elements in 70% (w/w) IL for the second-lowest minimum free energy conformation. During the transition of the β-sheet to α-helix, we observe a local minimum corresponding to coil conformation at an average Ψ angle of 50° in 70% IL. However, we do not observe proper local minimum in 10% (w/w) IL. The β-sheet and α-helix conformations are separated with a free energy barrier of 3.6 and 4.8 kcal mol−1, respectively, in 10 and 70% IL solutions. The transition from β-sheet to α-helix needs to cross these energy barriers, while the helix to sheet transition requires 2 kcal mol−1 in both the solutions. The free energy difference observed between the two minima is 1.6 kcal mol−1 in 10% IL, and it increases to 2.8 kcal mol−1 in 70% IL. The average number of intramolecular and intermolecular hydrogen bonds calculated within the individual peptides and between the peptide dimer is given in Table 3. The β-sheet conformation is having an average 5.4 intermolecular hydrogen bonds in both the solutions, which is consistent with the similar β-sheet secondary structural element values of this conformation. Individual helix conformations have an average 3.3 and 3.6 intramolecular hydrogen bonds in 10% IL. However, the helix conformations have on average 3 hydrogen bonds in 70% IL, which are in correlation with the α-helix secondary structural element values.
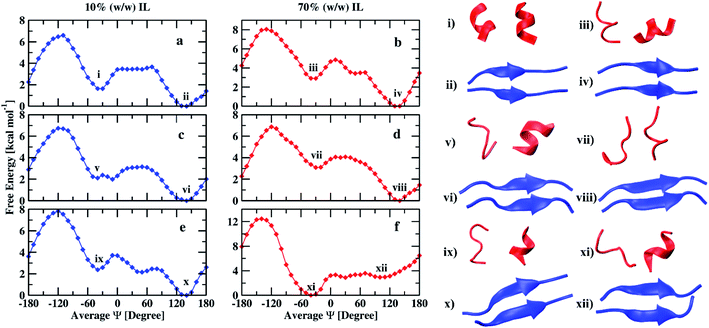 | ||
| Fig. 3 Free energy profiles of peptide (16–22) dimer in 10% and 70% (w/w) EAM (a and b), EAN (c and d), and TEAM (e and f) ILs and corresponding conformations of minima. | ||
In Fig. 3(c and d), we show the free energy landscapes of the peptide dimer in 10 and 70% (w/w) EAN IL with the conformations corresponding to the minima. In this IL, the global minimum also corresponds to β-sheet conformation, which was observed to be at an average Ψ angle of 140° in both the solutions. The second-lowest minimum observed at average Ψ angle of −40° and −30° corresponding to α-helix in 10% and 70% IL solutions, respectively. The DSSP values of the peptide dimer with the average Ψ angle are given in ESI (Tables S4 and S5).† The secondary structure elements corresponding to minima are shown in Table 2. The peptide at the global minimum is having 54, 65% of β-sheet and 39, 28% coil secondary structure elements in 10, 70% IL solutions, respectively. The second minimum corresponding to helical conformation is having 32, 10% of α-helix, 36, 48% of coil conformation and, 13, 35% of turn secondary structure elements in 10, 70% IL solutions, respectively. The coil and turn secondary structure elements are more compared to the α-helix element in 70% of the IL representing the minimum corresponding to coil conformation. However, α-helix and coil secondary structure elements are in equal proportion in 10% IL. The average number of inter and intramolecular hydrogen bonds are given in Table 3, which are in correlation with the secondary structure elements observed. The β-sheet conformations have average values of 4.8 and 5.8 intermolecular hydrogen bonds in 10% and 70% ILs, respectively. Individual peptides corresponding to the other minimum have an average of 2.8, 3.3, and 2.0, 2.2 intramolecular hydrogen bonds in 10%, and 70% ILs, respectively. The β-sheet and α-helix (coil) conformations are separated by a free energy barrier of 3.0 and 4.0 kcal mol−1 in 10% and 70% IL solutions, respectively. The helix to sheet transition requires 1 kcal mol−1 in both the solutions. The free energy difference between two minima is observed to be 2.0 kcal mol−1 in 10% IL and increases to 3.0 kcal mol−1 in 70% IL as observed in EAM IL.
Fig. 3(e and f) depicts the free energy profiles of peptide dimer in 10 and 70% (w/w) TEAM IL with the corresponding conformation representing the minima. The average DSSP values of the peptide dimer with the average Ψ angle are given in ESI (Tables S6 and S7).† We find the global minimum at an average Ψ angle of 140° corresponding to β-sheet conformation and the second-lowest minimum at −40° representing α-helix conformation in 10% IL similar to EAM and EAN ILs. A local minimum corresponding to coil conformation is also observed at an average Ψ angle of −50° in 10% IL. However, the global minimum in 70% IL was observed at an average Ψ angle of −40° representing α-helix conformation. The second-lowest minimum corresponds to coil conformation at an average Ψ angle of 30°, and β-sheet conformation has a minimum at 100°. The minimum of β-sheet conformation is shallow and spread over a range of average Ψ angle from 90° to 150°. DSSP values of conformations of minima are shown in Table 2. The global minimum has 62% of the β-sheet and 32% of coil secondary structure elements in 10% IL. The second-lowest minimum has 47% of the coil, 30% helix, and 10% bend secondary structure elements. In 70% IL, the global minimum has 40% coil, 25% turn, 17% of α-helix, and 11% of 310-helix secondary structure elements. The minimum corresponding to the β-sheet has 40% coil and 53% β-sheet secondary structure elements. The average number of intramolecular hydrogen bonds are similar for individual helix conformations in both the solutions, whereas the β-sheet conformations have intermolecular hydrogen bonds on average 5.5 and 5.8 in 10 and 70% IL, respectively. The free energy difference between two minima is found to be 2.3 kcal mol−1 in 10% IL and the transition from β-sheet to α-helix needs to cross energy barrier of 3.7 kcal mol−1, whereas the transition from α-helix to β-sheet requires only 2.3 kcal mol−1 energy. In 70% IL, the free energy difference between the α-helix and β-sheet conformations is 2.7 kcal mol−1, and the transition requires 3.4 kcal mol−1 energy, whereas the transition from β-sheet to α-helix requires only 0.7 kcal mol−1. Experimentally, it was observed that the Aβ16–22 peptide was forming fibrils at low as well as at high concentrations of EAM, whereas TEAM formed fibrils only at low concentrations. At high concentrations of TEAM, the peptide did not show any fibril formation.25 It was also hypothesized that the EAN also behaved similarly to EAM as it was equally structured.72 Our results are in agreement with the experimental results, where we observe the β-sheet conformation is found to be the global minimum at low as well as at high concentrations of both EAM and EAN ILs and low concentration of TEAM IL. At a high concentration of TEAM, the α-helix conformation is found to be the global minimum, and the well-depth of the minimum for β-sheet conformation is less and spread over a range of reaction coordinate.
We compare our results with the previous experimental results of the same peptide sequence in aqueous ILs at studied concentrations. The details are given in Table 5. The peptide (16–22) was found to form fibrils in 10%, 70% (w/w) EAM, and 10% (w/w) TEAM IL experimentally. Fibrils are primarily the aggregation of β-sheets of the peptide in large quantities. In our simulations, we find that the peptide is energetically more stable in β-sheet conformation in the above mentioned aqueous ILs. The results are in correlation with the experimental findings of fibril formation. However, the peptide was not found to form fibrils from experiments and showed the helical nature in 70% (w/w) TEAM IL. Our simulations are in correlation with the experiment being the peptide is energetically more stable in α-helix conformation in 70% (w/w) TEAM IL. Previous experimental results showed that the aqueous EAN IL behaved similarly as the aqueous EAM IL72 with the evidence of fibril formation of Aβ1–40 peptide. Our simulations show similar results in both the aqueous ILs at two different concentrations.
| System | Experimental25 | Computational |
|---|---|---|
| 10% (w/w) EAM | Fibril formation | More stable β-sheet |
| 10% (w/w) EAN | ||
| 70% (w/w) EAM | Fibril formation | More stable β-sheet |
| 70% (w/w) EAN | ||
| 10% (w/w) TEAM | Fibril formation | More stable β-sheet |
| 70% (w/w) TEAM | No fibril formation | More stable α-helix |
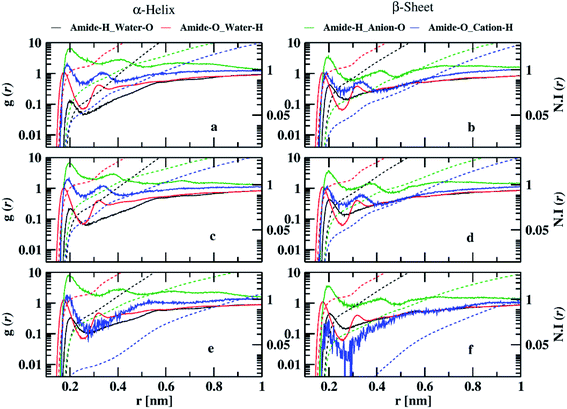
To investigate the interaction of ILs with peptide dimer, we calculated atom–atom RDFs of water, cation, and anion around amide hydrogen and oxygen atoms for corresponding minimum energy conformations in 10 and 70% ILs. Ethylammonium and triethylammonium cations have three and one acidic hydrogen atoms, respectively, which can form hydrogen bonds with amide oxygen atoms. Mesylate and nitrate anions each have three oxygen atoms that can form hydrogen bonds with amide hydrogen atoms. Water acts as both hydrogen bond donor and acceptor. In Fig. 4, we have shown that semi-log RDFs of water, cation, and anion with number integrals for α-helix and β-sheet conformations in 10% ILs. The coordination numbers are given in the ESI (Table S8).† The probability of finding anion oxygen atoms is found to be larger around amide hydrogen atoms of peptide dimer for α-helix conformation in three ILs compared to water oxygen atoms. This is also evident from the coordination numbers of the water and anion oxygen atoms around amide hydrogen atoms. 0.54, 0.52, and 0.34 anion oxygen atoms and 0.03, 0.21, and 0.34 water oxygen atoms coordinate with each amide hydrogen atom in EAM, EAN, and TEAM ILs, respectively. The probability of anion oxygen atoms decreases, and water oxygen atoms increase while going from α-helix to β-sheet conformation as some of the amide hydrogens are involved in intermolecular hydrogen bonding between peptides. 0.13, 0.19, and 0.12 oxygen atoms and 0.42, 0.40, 0.45 water oxygen atoms coordinate with each amide hydrogen atom in β-sheet conformation in EAM, EAN, and TEAM ILs, respectively.
The probability of finding acidic hydrogen atoms of the cation is more around amide oxygen atoms as compared to water hydrogen atoms in α-helix. 0.05, 0.09, and 0.01 cation hydrogen atoms and 1.19, 1.11, and 1.35 water hydrogen atoms coordinate with each amide oxygen atom in EAM, EAN, and TEAM ILs, respectively. This probability decreases for an acidic hydrogen atom of cation, whereas it does not change much for water hydrogen atoms while going from α-helix to β-sheet conformation, and the probability is found to be equal for both cation and water in EAM and EAN ILs. However, the probability of cation hydrogen around amide oxygen is negligible for β-sheet conformation in TEAM IL. 0.03, 0.04, and 0.001 cation hydrogen atoms and 1.13, 1.18, and 1.16 water hydrogen atoms coordinate with each amide oxygen atom in EAM, EAN, and TEAM ILs, respectively. The coordination numbers of water, cation, and anion are in correlation with the average number of intra and intermolecular hydrogen bonds of the dipeptide. We found 3.3 and 3.6 average intramolecular hydrogen bonds for α-helix in EAM IL, which decreases to 3.3, 2.8 and 2.4, 3.4 in EAN and TEAM IL, respectively. This is due to an increase in the coordination number of water oxygen with amide hydrogen in both EAN and TEAM IL and an increase in the coordination number of water hydrogen with amide oxygen in TEAM IL. 5.34, 4.8, and 5.5 average intermolecular hydrogen bonds are found for the β-sheet in EAM, EAN, and TEAM IL, respectively. The decrease in the number of hydrogen bonds in EAN is due to the increase in the coordination number of water hydrogen atoms with amide oxygen and anion oxygen atoms with an amide hydrogen atom as compared to in EAM and TEAM ILs. Semi-log RDFs of cation, anion, and water for α-helix and β-sheet conformations in 70% ILs are shown in Fig. 5.
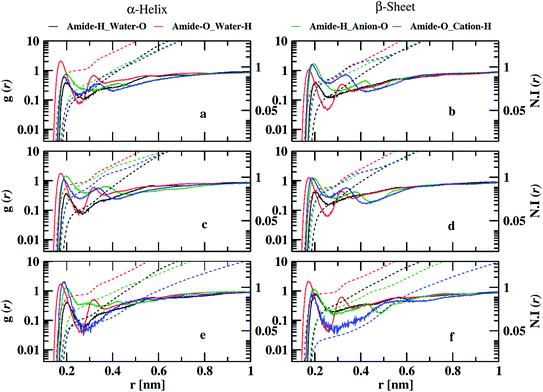
The probability of finding anion oxygen and cation hydrogen atoms around amide hydrogen and oxygen atoms decreases in both α-helix and β-sheet conformations going from 10 to 70% IL. The probability of finding anion oxygen atom around the amide hydrogen atom is larger for α-helix compared to water oxygen atoms, as in the case of 10% ILs which is evident from the coordination numbers. 0.4, 0.73, and 0.25 anion oxygen atoms and 0.15, 0.12, and 0.11 water oxygen atoms are coordinating to each amide hydrogen atom in EAM, EAN, and TEAM IL, respectively. The probability of anion oxygen atom around amide hydrogen increases in EAM decreases in EAN. It remains the same in TEAM IL while going from α-helix to β-sheet conformation. However, the probability of water oxygen atom around amide hydrogen remains the same in EAM, EAN ILs, and increases in TEAM IL during the transition. 0.6, 0.54, and 0.23 anion oxygen atoms and 0.16, 0.15, and 0.27 water oxygen atoms are coordinating with each amide hydrogen atom in EAM, EAN, and TEAM ILs, respectively. The probability of finding water hydrogen atoms around amide oxygen atoms is larger compared to the probability of cation hydrogens for α-helix conformations in EAM and EAN ILs. However, the probability of cation hydrogen atoms is more or less similar to water hydrogens in TEAM IL. 0.8, 0.7, and 0.6 water hydrogen atoms and 0.16, 0.35, and 0.08 cation hydrogen atoms coordinate with each amide oxygen atom in EAM, EAN, and TEAM ILs, respectively. This probability is reversed while going from α-helix to β-sheet conformation, where we observe the probability of finding water around amide oxygen atoms decreases in EAM and EAN, but it increases in TEAM IL. The same is the case with the probability of cation hydrogen around amide oxygen, which increases in the case of EAM, EAN ILs, and decreases in TEAM IL. 0.4, 0.5, and 0.7 water hydrogen and 0.43, 0.42, and 0.04 cation hydrogen atoms coordinate with each amide oxygen atom in EAM, EAN, and TEAM ILs, respectively. The average numbers of intra and intermolecular hydrogen bonds are in correlation with the coordination numbers in 70% IL, also as observed in 10% IL. The decrease in average hydrogen bonds in EAN is due to increased coordination of anion oxygen and cation hydrogen with amide hydrogen and amide oxygen atoms, respectively. 5.4, 5.8, and 5.8 average intermolecular hydrogen bonds are observed in β-sheet conformation in EAM, EAN, and TEAM ILs, respectively. The coordination of anion oxygen and cation hydrogen is high around amide hydrogen and amide oxygen in EAM IL as compared to EAN IL, which leads to less average intermolecular hydrogen bonds in EAM IL.
To further understand the interaction of the solvent with peptide, we calculated SASA. SASA values of the peptide dimer with changing the average Ψ angle in all solutions are shown in ESI (Fig. S11).† The average SASA of the peptide dimer overall solutions is shown in Fig. 6. The SASA is found to be low at average Ψ angle 140° and 80°, which corresponds to the β-sheet conformation of the dipeptide. The value of SASA increases from an average Ψ angle 80° to 10°, which corresponds to the increase in the coil secondary structure element of the dipeptide, exposing the peptide backbone to the solvent. The average SASA decreases from 10° to −30° due to an increase in the helical secondary structure element of the dipeptide, which involves intramolecular hydrogen bonds within individual peptides. From −30° to −180°, the average SASA continuously increases again due to an increase in the coil, bend, and turn secondary structural elements of the dipeptide.
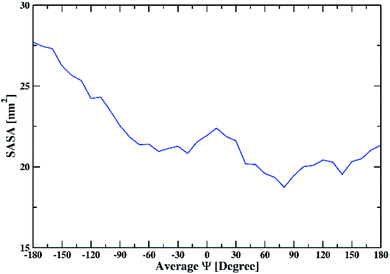 | ||
| Fig. 6 The average solvent-accessible surface area of the peptide dimer overall solutions with changing the average Ψ. | ||
To explain the stability of conformations in different ILs at different concentrations, we calculated the energetic contributions between peptide and solvent molecules. The van der Waals (vdW) and Coulombic energy contributions between peptide–cation, peptide–anion, and peptide–water were calculated for the minimum free energy conformations and are shown in Table 4. The vdW, Coulomb, and total interaction energies between peptide and solvent molecules are plotted with an average Ψ angle and are shown in ESI (Fig. S12).† In all the solutions, the anions and water molecules show more Coulomb interaction with the peptide compared to vdW interaction. The same is the case with the cations in EAM, EAN, and 10% (w/w) TEAM ILs. However, the interaction of cation with the peptide is less in Coulomb energy compared to vdW energy in 70% (w/w) TEAM IL. This resulted in the least Coulomb interaction of solvent with the peptide in 70% (w/w) TEAM IL compared to other ILs at two different concentrations and 10% (w/w) TEAM IL. EAM and EAN have primary ammonium cation with one ethyl chain and are more polar as compared to TEAM, which has tertiary ammonium cation with three ethyl chains. A tight packing between peptides in fibrils was found from using fluorescence spectroscopy.25 This behaviour was observed by replacing the phenylalanine with tryptophan residue at position 19, which shows intrinsic fluorescence. TEA cation shows more hydrophobicity compared to EA cation, which is evident from the van der Waals interaction with the peptide. This hydrophobicity disturbs the internal hydrophobic interactions between peptides in β-sheet conformation and destabilizes at a high concentration of TEAM IL. However, EA cation shows less hydrophobicity and the internal hydrophobic interactions are strong between peptides in β-sheet conformation in EAM and EAN ILs and at low concentration of TEAM that stabilize the β-sheet conformation. As the peptide has mostly amino acids with hydrophobic sidechains, it is observed from free energy profiles and energy contributions that more electrostatic interaction between solvent and peptide promotes β-sheet conformation. Moreover, the least electrostatic interaction promotes α-helix conformation. Recently, we reported a similar transition of Aβ33–42 peptide dimer in three different ILs EAM, EAN, and TEAM at two different concentrations.41 We observed α-helix conformation as the more stable conformation in low concentration of EAM and EAN ILs, and β-sheet conformation as the more stable structure at high concentration of EAM as well as EAN, and at both concentrations of TEAM IL. We also observe more contribution of vdW interactions from TEA cation as compared to EA cation. But the peptide having both the hydrophobic and hydrophilic amino acids result β-sheet conformation as more stable conformation in TEAM IL and α-helix as the more stable structure at low concentration of EAM and EAN ILs. It is evident from this and the previous study that the type of amino acids in the peptide sequence is also responsible for the stability of either α-helix or β-sheet conformation in aqueous ILs. The solvents which create a membrane-like environment all have shown to induce helical conformation of Abeta peptides.72 Triethylammonium cation having three ethyl groups can aggregate, which is evident from the simulation boxes shown in Fig. 1(b). The aggregated TEA cations mimic the membrane-like environment and induce the α-helix conformation of the peptide in 70% (w/w) TEAM IL as compared to 10 and 70% EAM and EAN ILs and 10% (w/w) TEAM IL.
4. Conclusions
We calculated the free energy landscapes of the conformational changes of Abeta (16–22) peptide dimer using average Ψ angle as the reaction coordinate in water, three different concentrations of hydrated ILs. To probe the conformational changes that can happen along with the reaction coordinate, the DSSP values were calculated. Coil conformation was found to be the global minimum, and α-helix conformation was the second-lowest minimum separated with a free energy barrier of 2 kcal mol−1 in pure water. The β-sheet conformation is found to be the global minimum with α-helix conformation, the second-lowest minimum in all solutions except 70% (w/w) TEAM IL. The α-helix conformation is found to be the global minimum with coil conformation, the second-lowest minimum in 70% (w/w) TEAM IL. The transition of the β-sheet to the α-helix conformation of peptide dimer happens through the formation of coil conformation in all the solvents. In some cases, the coil conformation is found to be the intermediate conformation with a minimum on free energy surface. The average number of intramolecular and intermolecular hydrogen bonds were calculated within the individual peptides and between the peptides and are in correlation with the DSSP values. To investigate the peptide–solvent interactions, we calculated atom–atom RDFs and coordination numbers of cation, anion, and water around backbone amide hydrogen and oxygen atoms of the peptides. At low concentrations of IL solutions, the anion strongly interacts with the amide hydrogens of the peptide for both the minimum energy conformations. The interaction of cation and water with the peptide backbone is negligible compared to anion. At a high concentration of IL solutions, anion interaction decreases with peptide backbone compared with low concentration. Water is interacting strongly with amide oxygen atoms for α-helix conformation in EAM and EAN ILs and β-sheet conformation in TEAM IL. The coordination numbers of water, cation, and anion around amide oxygen and amide hydrogen atoms are in correlation with the intra and intermolecular hydrogen bonds observed in peptide dimers. SASA gave information about the exposure of peptide to the solvent during the conformational changes. We observe SASA is less for conformations of α-helix and β-sheet and more for coil and disordered conformations. vdW and Coulomb energies were calculated between peptide and different solvent molecules to explain the stability of conformations on the free energy landscape. We observe that the Coulomb interaction energy is more than the vdW energy for all solvent molecules in all the solvents except in 70% (w/w) TEAM IL. TEA cation with three ethyl chains shows more hydrophobicity as compared to EA cation with one ethyl chain, which is evident from van der Waals interaction energies. In 70% TEAM IL, we observe the cation has more vdW interaction energy with peptide compared to Coulomb energy, which resulted in less total Coulomb interaction energy compared to other solvents. TEA cation mimics the membrane-like environment at high concentrations inducing α-helix formation. Finally, our results are in correlation with the previous experimental results of peptide aggregation with changing IL concentration.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The financial support (EEQ/2018/000494) for this work was provided by the Department of Science and Technology (DST), India. Sathish Dasari likes to thank Council of Scientific and Industrial Research (CSIR), India, for his PhD fellowship.References
- J. Hardy and D. J. Selkoe, The amyloid hypothesis of Alzheimer's disease: progress and problems on the road to therapeutics, Science, 2002, 297, 353–356 CrossRef CAS.
- C. M. Dobson, Protein folding and misfolding, Nature, 2003, 426, 884–890 CrossRef CAS.
- S. S.-S. Wang and T. A. Good, An overview of Alzheimer's disease, J. Chin. Inst. Chem. Eng., 2005, 36, 533–559 CAS.
- D. B. Kell, Towards a unifying, systems biology understanding of large-scale cellular death and destruction caused by poorly liganded iron: Parkinson's, Huntington's, Alzheimer's, prions, bactericides, chemical toxicology, and others as examples, Arch. Toxicol., 2010, 84, 825–889 CrossRef CAS.
- J. W. Wu, K.-N. Liu, S.-C. How, W.-A. Chen, C.-M. Lai, H.-S. Liu, C.-J. Hu and S. S.-S. Wang, Carnosine’s Effect on Amyloid Fibril Formation and Induced Cytotoxicity of Lysozyme, PLoS One, 2018, 8, e81982 CrossRef.
- S. L. Gras, Amyloid Fibrils: From Disease to Design. New Biomaterial Applications for Self-Assembling Cross-β Fibrils, Aust. J. Chem., 2007, 60, 333–342 CrossRef CAS.
- M. E. Greene, Amyloid mechanics reveal disease origins: biomaterials, Mater. Today, 2006, 9, 21 Search PubMed.
- M. R. Nilsson, M. Driscoll and D. P. Raleigh, Low levels of asparagine deamidation can have a dramatic effect on aggregation of amyloidogenic peptides: implications for the study of amyloid formation, Protein Sci., 2002, 11, 342–349 CrossRef CAS.
- J. J. Yerbury, S. Poon, S. Meehan, B. Thompson, J. R. Kumita, C. M. Dobson and M. R. Wilson, The extracellular chaperone clusterin influences amyloid formation and toxicity by interacting with prefibrillar structures, FASEB J., 2007, 21, 2312–2322 CrossRef CAS.
- L. Nagel-Steger, M. C. Owen and B. Strodel, An Account of Amyloid Oligomers: Facts and Figures Obtained from Experiments and Simulations, ChemBioChem, 2016, 17, 657–676 CrossRef CAS.
- F. Chiti and C. M. Dobson, Protein Misfolding, Amyloid Formation, and Human Disease: A Summary of Progress Over the Last Decade, Annu. Rev. Biochem., 2017, 86, 27–68 CrossRef CAS.
- G. Wei, N. Mousseau and P. Derreumaux, Computational Simulations of the Early Steps of Protein Aggregation, Prion, 2007, 1, 3–8 CrossRef.
- A. Morriss-Andrews and J.-E. Shea, Simulations of Protein Aggregation: Insights from Atomistic and Coarse-Grained Models, J. Phys. Chem. Lett., 2014, 5, 1899–1908 CrossRef CAS.
- J. Nasica-Labouze, P. H. Nguyen, F. Sterpone, O. Berthoumieu, N.-V. Buchete, S. Coté, A. De Simone, A. J. Doig, P. Faller, A. Garcia, A. Laio, M. S. Li, S. Melchionna, N. Mousseau, Y. Mu, A. Paravastu, S. Pasquali, D. J. Rosenman, B. Strodel, B. Tarus, J. H. Viles, T. Zhang, C. Wang and P. Derreumaux, Amyloid β Protein and Alzheimer's Disease: When Computer Simulations Complement Experimental Studies, Chem. Rev., 2015, 115, 3518–3563 CrossRef CAS.
- M. Carballo-Pacheco and B. Strodel, Advances in the Simulation of Protein Aggregation at the Atomistic Scale, J. Phys. Chem. B, 2016, 120, 2991–2999 CrossRef CAS.
- I. M. Ilie and A. Caflisch, Simulation Studies of Amyloidogenic Polypeptides and Their Aggregates, Chem. Rev., 2019, 115, 3518–3563 Search PubMed.
- T. L. Greaves and C. J. Drummond, Protic Ionic Liquids: Properties and Applications, Chem. Rev., 2008, 108, 206–237 CrossRef CAS.
- K. Fujita, D. R. MacFarlane and M. Forsyth, Protein solubilising and stabilising ionic liquids, Chem. Commun., 2005, 4804–4806 RSC.
- K. Fujita, M. Forsyth, D. R. MacFarlane, R. W. Reid and G. D. Elliott, Unexpected improvement in stability and utility of cytochrome c by solution in biocompatible ionic liquids, Biotechnol. Bioeng., 2006, 94, 1209–1213 CrossRef CAS.
- R. Vijayaraghavan, A. Izgorodin, V. Ganesh, M. Surianarayanan and D. R. MacFarlane, Long-Term Structural and Chemical Stability of DNA in Hydrated Ionic Liquids, Angew. Chem., Int. Ed., 2010, 49, 1631–1633 CrossRef CAS.
- N. Byrne and C. A. Angell, Formation and dissolution of hen egg white lysozyme amyloid fibrils in protic ionic liquids, Chem. Commun., 2009, 1046–1048 RSC.
- H. Hwang, H. Choi, H. Kim, D. H. Jo and T. D. Kim, Ionic liquids promote amyloid formation from α-synuclein, Anal. Biochem., 2009, 386, 293–295 CrossRef CAS.
- S. Y. Bae, S. Kim, B. Y. Lee, K. K. Kim and T. D. Kim, Amyloid formation using 1-butyl-3-methyl-imidazolium-based ionic liquids, Anal. Biochem., 2011, 419, 354–356 CrossRef CAS.
- N. Debeljuh, C. J. Barrow and N. Byrne, The impact of ionic liquids on amyloid fibrilization of Aβ16–22: tuning the rate of fibrilization using a reverse Hofmeister strategy, Phys. Chem. Chem. Phys., 2011, 13, 16534–16536 RSC.
- N. Debeljuh, S. Varghese, C. J. Barrow and N. Byrne, Role of Cation in Enhancing the Conversion of the Alzheimer's Peptide into Amyloid Fibrils Using Protic Ionic Liquids, Aust. J. Chem., 2012, 65, 1502–1506 CrossRef CAS.
- H. R. Kalhor, M. Kamizi, J. Akbari and A. Heydari, Inhibition of Amyloid Formation by Ionic Liquids: Ionic Liquids Affecting Intermediate Oligomers, Biomacromolecules, 2009, 10, 2468–2475 CrossRef CAS.
- T. Takekiyo, Y. Koyama, K. Yamazaki, H. Abe and Y. Yoshimura, Ionic Liquid-Induced Formation of the α-Helical Structure of β-Lactoglobulin, J. Phys. Chem. B, 2013, 117, 10142–10148 CrossRef CAS.
- T. Takekiyo, K. Yoshida, Y. Funahashi, S. Nagata, H. Abe, T. Yamaguchi and Y. Yoshimura, Helix-forming ability of proteins in alkylammonium nitrate, J. Mol. Liq., 2017, 243, 584–590 CrossRef CAS.
- T. Takekiyo and Y. Yoshimura, Suppression and dissolution of amyloid aggregates using ionic liquids, Biophys. Rev., 2018, 10, 853–860 CrossRef CAS.
- A. Basu, S. C. Bhattacharya and G. S. Kumar, Influence of the ionic liquid 1-butyl-3-methylimidazolium bromide on amyloid fibrillogenesis in lysozyme: evidence from photophysical and imaging studies, Int. J. Biol. Macromol., 2018, 107, 2643–2649 CrossRef CAS.
- T. Takekiyo, Y. Ishikawa, E. Yamaguchi, N. Yamada and Y. Yoshimura, Dissolution of Amyloid Aggregates in Aqueous Ionic Liquid Solutions: A Case Study of Insulin Amyloid, Aust. J. Chem., 2019, 72, 81–86 CrossRef CAS.
- C. Hilbich, B. Kisters-Woike, J. Reed, C. L. Masters and K. Beyreuther, Aggregation and secondary structure of synthetic amyloid beta A4 peptides of Alzheimer's disease, J. Mol. Biol., 1991, 218, 149–163 CrossRef CAS.
- C. Hilbich, B. Kisters-Woike, J. Reed, C. L. Masters and K. Beyreuther, Substitutions of hydrophobic amino acids reduce the amyloidogenicity of Alzheimer's disease beta A4 peptides, J. Mol. Biol., 1992, 228, 460–473 CrossRef CAS.
- D. K. Klimov and D. Thirumalai, Dissecting the assembly of Abeta16–22 amyloid peptides into antiparallel beta sheets, Structure, 2003, 11, 295–307 CrossRef CAS.
- W. Hwang, S. Zhang, R. D. Kamm and M. Karplus, Kinetic control of dimer structure formation in amyloid fibrillogenesis, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 12916–12921 CrossRef CAS.
- G. Favrin, A. Irbäck and S. Mohanty, Oligomerization of amyloid Abeta16–22 peptides using hydrogen bonds and hydrophobicity forces, Biophys. J., 2004, 87, 3657–3664 CrossRef CAS.
- U. F. Röhrig, A. Laio, N. Tantalo, M. Parrinello and R. Petronzio, Stability and structure of oligomers of the Alzheimer peptide Abeta16–22: from the dimer to the 32-mer, Biophys. J., 2006, 91, 3217–3229 CrossRef.
- B. Sharma and S. Paul, Action of Caffeine as an Amyloid Inhibitor in the Aggregation of Aβ16–22 Peptides, J. Phys. Chem. B, 2016, 120, 9019–9033 CrossRef CAS.
- S. Paul and S. Paul, Inhibitory Effect of Choline-O-sulfate on Aβ16–22 Peptide Aggregation: A Molecular Dynamics Simulation Study, J. Phys. Chem. B, 2019, 123, 3475–3489 CrossRef CAS.
- S. Pal and S. Paul, ATP Controls the Aggregation of Aβ16–22 Peptides, J. Phys. Chem. B, 2020, 124, 210–223 CrossRef CAS.
- S. Dasari and B. S. Mallik, Ion-induced free energy landscapes of Aβ33–42 peptide dimer in wet ionic liquids, J. Mol. Liq., 2020, 114026 CrossRef CAS.
- D. J. Couling, R. J. Bernot, K. M. Docherty, J. K. Dixon and E. J. Maginn, Assessing the factors responsible for ionic liquid toxicity to aquatic organisms via quantitative structure–property relationship modeling, Green Chem., 2006, 8, 82–90 RSC.
- K. S. Egorova and V. P. Ananikov, Toxicity of Ionic Liquids: Eco(cyto)activity as Complicated, but Unavoidable Parameter for Task-Specific Optimization, ChemSusChem, 2014, 7, 336–360 CrossRef CAS.
- K. S. Egorova, E. G. Gordeev and V. P. Ananikov, Biological Activity of Ionic Liquids and Their Application in Pharmaceutics and Medicine, Chem. Rev., 2017, 117, 7132–7189 CrossRef CAS.
- T. Lührs, C. Ritter, M. Adrian, D. Riek-Loher, B. Bohrmann, H. Döbeli, D. Schubert and R. Riek, 3D structure of Alzheimer's amyloid-beta(1–42) fibrils, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 17342–17347 CrossRef.
- K. Lindorff-Larsen, S. Piana, K. Palmo, P. Maragakis, J. L. Klepeis, R. O. Dror and D. E. Shaw, Improved side-chain torsion potentials for the Amber ff99SB protein force field, Proteins: Struct., Funct., Bioinf., 2010, 78, 1950–1958 CrossRef CAS.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and testing of a general amber force field, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS.
- B. H. Besler, K. M. Merz and P. A. Kollman, Atomic charges derived from semiempirical methods, J. Comput. Chem., 1990, 11, 431–439 CrossRef CAS.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle–Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B, 1988, 37, 785–789 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, Gaussian 09W Revision C.01, Gaussian, Inc, Wallingford, CT, 2009 Search PubMed.
- W. D. Cornell, P. Cieplak, C. I. Bayly and P. A. Kollmann, Application of RESP charges to calculate conformational energies, hydrogen bond energies, and free energies of solvation, J. Am. Chem. Soc., 1993, 115, 9620–9631 CrossRef CAS.
- D. A. Case, T. E. Cheatham, T. Darden, H. Gohlke, R. Luo, K. M. Merz, A. Onufriev, C. Simmerling, B. Wang and R. J. Woods, The Amber biomolecular simulation programs, J. Comput. Chem., 2005, 26, 1668–1688 CrossRef CAS.
- K. G. Sprenger, V. W. Jaeger and J. Pfaendtner, The General AMBER Force Field (GAFF) Can Accurately Predict Thermodynamic and Transport Properties of Many Ionic Liquids, J. Phys. Chem. B, 2015, 119, 5882–5895 CrossRef CAS.
- S. Dasari and B. S. Mallik, Biosolvation Nature of Ionic Liquids: Molecular Dynamics Simulation of Methylated Nucleobases in Hydrated 1-Ethyl-3-methylimidazolium Acetate, ACS Omega, 2018, 3, 8344–8354 CrossRef CAS.
- M. Chen, R. Pendrill, G. Widmalm, J. W. Brady and J. Wohlert, Molecular Dynamics Simulations of the Ionic Liquid 1-n-Butyl-3-Methylimidazolium Chloride and Its Binary Mixtures with Ethanol, J. Chem. Theory Comput., 2014, 10, 4465–4479 CrossRef CAS.
- P. B. Sánchez, J. García and A. A. H. Pádua, Structural effects on dynamic and energetic properties of mixtures of ionic liquids and water, J. Mol. Liq., 2017, 242, 204–212 CrossRef.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, The missing term in effective pair potentials, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, PACKMOL: a package for building initial configurations for molecular dynamics simulations, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef.
- T. Darden, D. York and L. Pedersen, Particle mesh Ewald: an N·log(N) method for Ewald sums in large systems, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, J. Chem. Phys., 2007, 126, 014101 CrossRef.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, Molecular dynamics with coupling to an external bath, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- M. Parrinello and A. Rahman, Polymorphic transitions in single crystals: a new molecular dynamics method, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, LINCS: a linear constraint solver for molecular simulations, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS.
- R. K. Singh, N. G. Chamachi, S. Chakrabarty and A. Mukherjee, Mechanism of Unfolding of Human Prion Protein, J. Phys. Chem. B, 2017, 121, 550–564 CrossRef CAS.
- S. K. Mudedla, N. A. Murugan and H. Agren, Free Energy Landscape for Alpha-Helix to Beta-Sheet Interconversion in Small Amyloid Forming Peptide under Nanoconfinement, J. Phys. Chem. B, 2018, 122, 9654–9664 CrossRef CAS.
- M. Bonomi, D. Branduardi, G. Bussi, C. Camilloni, D. Provasi, P. Raiteri, D. Donadio, F. Marinelli, F. Pietrucci, R. A. Broglia and M. Parrinello, PLUMED: a portable plugin for free-energy calculations with molecular dynamics, Comput. Phys. Commun., 2009, 180, 1961–1972 CrossRef CAS.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, THE weighted histogram analysis method for free-energy calculations on biomolecules. I. The method, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef CAS.
- W. Kabsch and C. Sander, Dictionary of protein secondary structure: pattern recognition of hydrogen-bonded and geometrical features, Biopolymers, 1983, 22, 2577–2637 CrossRef CAS.
- N. Debeljuh, C. J. Barrow, L. Henderson and N. Byrne, Structure inducing ionic liquids—enhancement of alpha helicity in the Abeta(1–40) peptide from Alzheimer's disease, Chem. Commun., 2011, 47, 6371–6373 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Temperature and total energy of the system along the simulation time of 50 ns in 10% and 70% (w/w) EAM, EAN, and TEAM ILs (Fig. S1 and S2). MSD of water, cation and anion along simulation time of 50 ns in 10% and 70% (w/w) EAM, EAN, and TEAM ILs (Fig. S3). COM–COM RDFs of anion around cation in 10% and 70% EAM, EAN, and TEAM ILs (Fig. S4). Average Ψ angle values of the peptide dimer along the simulation time in the water, 10%, and 70% (w/w) EAM, EAN, and TEAM ILs (Fig. S5–S8). The convergence of the free energy profile with the simulation time for peptide dimer in water, 10% and 70% EAM, EAN, and TEAM ILs (Fig. S9 and S10). SASA of the peptide dimer with changing average Ψ angle in water, 10% and 70% (w/w) EAM, EAN, and TEAM ILs (Fig. S11). vdW, Coulomb, and total interaction energies of the peptide with the solvent with the average Ψ angle (Fig. S12). Secondary structure element values of the peptide with an average Ψ angle in water, 10% and 70% (w/w) EAM, EAN, and TEAM ILs (Tables S1–S7). Coordination numbers of water, cation, and anion atoms around each amide and oxygen atoms (Table S8). Optimized coordinates and force–field parameters of the IL ions. See DOI: 10.1039/d0ra06609e. |
| This journal is © The Royal Society of Chemistry 2020 |