Open Access Article
Open Access ArticlePhotothermal conversion of SiO2@Au nanoparticles mediated by surface morphology of gold cluster layer†
Lulu Yangab,
Zhibin Yan *abc,
Lu Yangab,
Jianxin Yangab,
Mingliang Jinab,
Xiaobo Xingab,
Guofu Zhouab and
Lingling Shui
*abc,
Lu Yangab,
Jianxin Yangab,
Mingliang Jinab,
Xiaobo Xingab,
Guofu Zhouab and
Lingling Shui *abd
*abd
aGuangdong Provincial Key Laboratory of Optical Information Materials and Technology, Institute of Electronic Paper Displays, South China Academy of Advanced Optoelectronics, South China Normal University, Guangzhou 510006, P. R. China. E-mail: zhibin.yan@m.scnu.edu.cn; shuill@m.scnu.edu.cn; Tel: +86-20-3931-4813
bNational Center for International Research on Green Optoelectronics, South China Normal University, Guangzhou 510006, P. R. China
cDefense Key Disciplines Lab of Novel Micro-nano Devices and System Technology, Chongqing University, Chongqing, 400044, P. R. China
dSchool of Information and Optoelectronic Science and Engineering, South China Normal University, Guangzhou 510006, P. R. China
First published on 7th September 2020
Abstract
Photothermal effects in SiO2@Au core–shell nanoparticles have demonstrated great potential in various applications for drug delivery, thermo-photovoltaics and photothermal cancer therapy, etc. However, the photothermal conversion of SiO2@Au nanoparticles partially covered by disconnected gold clusters has rarely been investigated systematically. Here, we control the surface morphology of gold clusters on the photothermal conversion performance of SiO2@Au core–shell nanoparticles by means of chemically adjusting the synthesis parameters, including amounts of gold salts, pH value and reducing agent. The macroscopic variations of the photothermal heating of different nanoparticle dispersions are significantly influenced by the nanoscale differences of gold cluster morphologies on the silica core. The temperature rise can be enhanced by the strong near-field coupling and collective heating among gold clusters with a relatively uniform distribution on the silica core. A numerical model of the simplified photothermal system is formulated to interpret the physical mechanism of the experimental observation, and shows a similar trend of temperature rise implying a reasonably good agreement with experimental data. Our work opens new possibilities for manipulating the light-to-heat conversion performance of SiO2@Au core–shell nanoparticles and potential applications of heat delivery with spatial resolution on the nanoscale.
Introduction
In recent years, noble metal nanoparticles (NPs) have received much attention in nanoscience due to their excellent optical properties.1 Under the irradiation of the light source, the phenomenon that the free electrons on the NPs surface interact with the incident light is called localized surface plasmon resonance (LSPR). In particular, the LSPR of gold nanoparticles (AuNPs) makes it have the remarkable ability to absorb and scatter light in a wide range of visible and near infrared regions. AuNPs can convert the absorbed light energy into heat energy. Thermal energy diffuses into the surrounding environment to raise the temperature, resulting in a nano-scale localized high temperature.2 Based on its unique photothermal effect, AuNPs have been extensively investigated for a variety of applications in photothermal therapy,3–6 nano-surgery,7,8 plasmonic photothermal delivery,9–11 photothermal imaging,12 plasmon enhanced thermophoresis13 and plasmon-assisted optofluidic.14,15The frequency of LSPR depends largely on the morphology, size, and dielectric environment of the AuNPs.16–19 Especially, when a cluster of AuNPs are closely aligned with each other, the coupling between the particles becomes very important such as in surface enhanced Raman scattering (SERS) experiments,20 and the nanogap can significantly enhance the near-field electromagnetic field.21,22 When Su et al. investigated the coupling between pairs of elliptical metal particles by simulations and experiments, they found that the resonant wavelength peak of two interacting particles was red-shifted from that of a single particle because of the near-field coupling and the shift decays approximately exponentially with increasing particle spacing.23 Moreover, researchers found that, in experiments and simulations of nanoparticles, different nanoarrays, incident light irradiation angles, and particle aggregation states could affect the electromagnetic field and temperature field distribution of nanoparticles.24–26 In the process of the light-to-heat conversion, there is a high thermal temperature gradient near the particle surface.13
The coupling and aggregation effects of the particles affect the distribution of the temperature field and the photothermal property of the whole dispersion system.27 From a practical point of view, designing and preparing nanoparticle arrays (clusters) with strong interaction are very important for studying plasmon configurations. There have been many studies on tunable LSPR by varying the gap and size of AuNPs. Top-down methods based on planar lithographic approaches, such as photolithography, electron beam lithography, ion beam lithography, laser interference lithography, nanoimprint lithography and nanosphere lithography,28–33 achieve a variety of nanoscale patterns but are typically expensive and often have a low throughput, which typically limits area coverage. In contrast, bottom-up methods based on chemical assembly offer a cheap, fast and flexible technology for preparing close-packed colloidal particles as LSPR substrate.34–36
Guillermo et al. found that laser irradiation at high energy produced a near-field enhancement at the interparticle gaps, causing the local temperature to increase high enough to melt the tip of the gold nanorod.36 This further proves that the coupling effect brought by the gap between the particles can enhance its photothermal performance. Most of the existing studies focused on the photothermal performances of AuNPs dispersions and nanoparticle array patterned on flat surfaces,37–41 but few reported the heat generation capability of the gold nanoparticle arrays on the surface of other nanospheres for their potential photothermal application.42 For multi-component core–shell gold nanomaterials, more attention has been paid on the photothermal conversion capability of the gold shell.43–46
In this work, we study the effects of the morphology of gold clusters on the surface of SiO2@Au core–shell nanoparticles on their photothermal conversion performance by changing the amount of gold salt, the pH value of the growth solution, and the volume and concentration of the reducing agent used in the chemical synthesis of SiO2@Au. We introduce the equivalent circle diameter to characterize the size of irregular gold clusters on the surface of SiO2 and measure the direct shortest distance between the irregular gold clusters using Image J. These parameters are used to reveal the relationship between the microscale morphology of SiO2@Au particle surface and the macroscale photothermal performance. A numerical model of photothermal conversion is formulated to quantitatively interpret the experimental observations by using a commercial finite element method (FEM) software. The presented results can lead to the development of advanced nanostructures for photothermal applications.
Materials and methods
Materials
Amine-grafted silica nanoparticles (diameter: 100 nm, Nanjing Nanorainbow, China) were used as the core of SiO2@Au nanoparticles. Gold chloride trihydrate (HAuCl4·3H2O, 99.9%, Sigma) was used for deposition process of seeding gold hydroxide (Au(OH)3) and for growing of the gold cluster on the surface of the amine-grafted silica nanoparticle. 0.1 M sodium hydroxide (NaOH, 98%, Sigma-Aldrich, USA) solution was used to control the pH during the Au deposition process. Potassium carbonate (K2CO3, 99.99%, Aladdin, USA) was used to adjust the pH of HAuCl4 for its hydrolysis to form gold hydroxide solution for growing the gold cluster. Sodium borohydride (NaBH4, 99.99%, Fluka, USA) was used as the reducing agent to reduce gold ions to form gold clusters on SiO2 nanoparticles. Sodium citrate dihydrate (C6H5Na3O7·2H2O, 99%, Tianjin Zhiyuan, China) was used in the reduction process of the gold hydroxide to grow gold clusters.Gold seeding on the amine grafted silica core
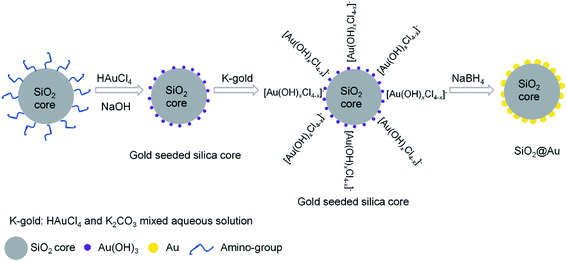
The synthetic procedures of gold-seeded silica nanoparticles were described in previous literatures.47,48 As illustrated in Scheme 1, the gold-seeded silica nanoparticle consists of SiO2 core as a scaffold and the gold nanoparticles loaded on the surface as seeds that can grow into gold shell. In this work, grafting Au(OH)3 on the surface of the amine coated silica nanoparticles was prepared via in situ deposition to form the gold-seeded silica.47,48 4.5 mL of 0.1 M NaOH was added into 20 mL of 6.35 mM HAuCl4 solution, and allowed to stir for about 15 min at room temperature before the solution became light yellow. Then 1 mL of the amine grafted silica dispersion was added to the gold hydroxide solution at pH 6.85, and the solution was heated to 70 °C and was vigorously stirred for 1 h. After successful grafting of Au(OH)3 on the amine grafted silica nanoparticles, the color of the mixture turned from milky white to lemon yellow as an indication. The obtained gold-seeded silica nanoparticle dispersion was then centrifuged at 1000 rpm for 10 minutes, washed 3 times with ethanol and 5 times with water, and dispersed in 40 mL of deionized water. The concentration of the gold-seeded silica nanoparticles was approximated as 9.7 × 1011 particles per mL based on mass calculation.Growth of gold cluster on the surface of gold-seeded silica nanoparticles
The gold cluster was formed via growing the Au(OH)3 nanoparticles as nucleation sites on the gold-seeded SiO2 core surface. Gold was continuously reduced from HAuCl4 by further adding K2CO3–HAuCl4 (K-gold) solution and the Au(OH)3 nanoparticles gradually grew in size until they eventually coalesced to form a complete gold shell around the SiO2 core.47 The K-gold solutions was prepared by addition of 60 mg of K2CO3 to 0.75 g of 0.05 M HAuCl4 diluted in 100 mL of DI water and then stirred for 24 h at room temperature in a dark environment. The pH of the K-gold solution is critical, as K2CO3 content controls ionic speciation of Au3+ and the rate of reduction on the gold-seeded silica surface.48 The pH of the K-gold solution was adjusted by the added amount of K2CO3. The freshly prepared NaBH4 (6.6 mM) was added as the reducing agent at 1 mL for every 10 mL of K-gold. Meanwhile, 1 mL of 10 mM sodium citrate dihydrate per 20 mL of K-gold was also added to slow the reaction and stabilize the gold clusters by acting as a capping agent. Using this synthetic approach, the surface morphology of the gold cluster on the SiO2@Au nanoparticles could be varied by changing the volume ratio of K2CO3–HAuCl4 solution to gold-seeded silica nanoparticle (i.e. K-gold-to-seed ratio), the pH of K-gold solution, and the concentration and volume of NaBH4 solution for reduction reaction, respectively.Experimental setup and procedures
The photothermal measurement apparatus contains three components: the optical system, the fluid system and the data acquisition system as shown in Fig. 1. The optical system consists of a continuous wavelength laser (532 nm, MGL-FN-532, Changchun New Industries Optoelectronics Technology Co, China), a fibre collimation package (F110APC-532-FC/APC, Thorlabs, USA), a threaded manual beam shutter (SM1SH1, Thorlabs, USA) and optical support components. A parallel beam with a spot size of 2.55 mm was generated and focused on a droplet of SiO2@Au dispersion. A laser power meter (PM100, Thorlabs, USA) was used to measure and verify the power of the laser. The fluid system consists of a syringe (1 mL), an injection metal needle (1.2 mm × 31 mm, intradermal bevel needle), a laboratory syringe pump (750N PT-5, Hamilton, USA), a silicone hose (Φ 0.8 × 1.9 mm) and a round glass capillary (Φ 1.0 × 1.5 mm, Sutter, USA). A laboratory syringe pump was used to precisely supply a fixed volume of nanoparticle dispersion droplet on the tip of the glass capillary. In order to reduce heat loss, the silicone hose was used to connect to the metal needle at one end and the glass capillary at the other end. The data collection system consists of a T-type thermocouple, and a data logger (2701, Keithley, USA). The thermocouple was fastened onto the glass capillary. The photos of the droplets were captured and stored by using a digital camera.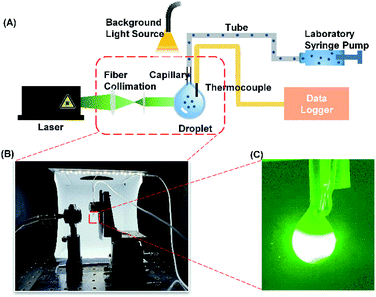 | ||
| Fig. 1 (A) Schematic of the experimental setup for characterizing the photothermal performance. (B) Photo of the experimental setup. (C) An image showing the laser passing through the droplet. | ||
During the experiment, the laser was turned on and allowed to warm up for 10 minutes. The laser output power was fixed at 53.6 mW. The syringe was filled with a SiO2@Au core–shell nanoparticle dispersion (9.7 × 1010 particles per mL). 15 μL of the dispersion was supplied from the syringe by the syringe pump to maintain a stationary hanging droplet on the tip of the glass capillary. The temperature profiles of the droplets under laser irradiation were measured by fully submerging the thermocouple tip inside the hanging droplet. Each experimental condition was repeated three times. The outer diameter of the glass capillary (1.5 mm) was used as scale reference. The micro-displacement platform was implemented to align the laser beam on the droplet to avoid irradiating onto the thermocouple bead. By opening the laser shutter, the temperature began to increase as the laser irradiated the droplet. After 2 minutes, the laser shutter was closed and the droplet temperature was rapidly reduced due to the cooling by the ambient air.
In order to quantify the morphology of the gold clusters, the average equivalent circle diameter (Dave) and the average shortest distance among gold clusters (Lave) on the surface of SiO2@Au were utilized in this study (examples are shown in Fig. S4†). The area of an irregular gold cluster was firstly measured by the software Image J and converted to a circle with the same area as the measured gold cluster. The equivalent circle diameter (Dave) was then calculated according to the area of the circle. Moreover, the ratio of interparticle distance to the particle size has been widely employed to depict the coupling effects among plasmonic nanoparticle assembly.23,49–51 In this study, the ratio of the average shortest distance between the gold clusters to the average equivalent circle diameter (Lave/Dave) was implemented to evaluate the coupling effects.
Results and discussion
Effect of volume ratio of K-gold to precursor seed particles
By varying the volume ratio of K-gold-to-seed (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 20
1, 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 40
1, 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 80
1, 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 160
1, 160![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 200
1, 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 300
1 and 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
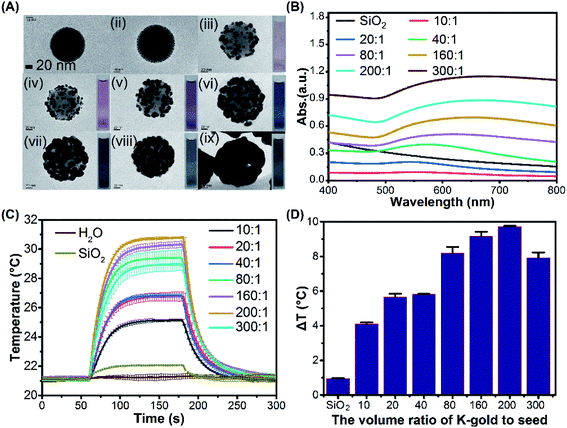
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), various surface morphologies of gold clusters on the gold-seeded silica nanoparticle could be obtained as shown in Fig. 2A(iii–ix), respectively. Fig. 2A(i) and S1† show the TEM and SEM images of the amine grafted silica core with a diameter of 100 nm. A homogeneous distribution of 1.5–4 nm particles was observed on the surface of amine grafted silica under the synthesis conditions (pH 6.85, 70 °C, 1 h) as seen in Fig. 2A(ii) and S2.† As the K-gold-to-seed ratios were increased from 10
1), various surface morphologies of gold clusters on the gold-seeded silica nanoparticle could be obtained as shown in Fig. 2A(iii–ix), respectively. Fig. 2A(i) and S1† show the TEM and SEM images of the amine grafted silica core with a diameter of 100 nm. A homogeneous distribution of 1.5–4 nm particles was observed on the surface of amine grafted silica under the synthesis conditions (pH 6.85, 70 °C, 1 h) as seen in Fig. 2A(ii) and S2.† As the K-gold-to-seed ratios were increased from 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 300
1 to 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the gold clusters gradually grew and eventually coalesced as a complete shell layer. At a ratio of 80
1, the gold clusters gradually grew and eventually coalesced as a complete shell layer. At a ratio of 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, gold clusters grew to an average size of about 40 nm and started to coalesce together. A rough layer of gold shell with many small grooves of 1–4 nm was formed around the silica core at a ratio of 200
1, gold clusters grew to an average size of about 40 nm and started to coalesce together. A rough layer of gold shell with many small grooves of 1–4 nm was formed around the silica core at a ratio of 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. At a higher ratio of 300
1. At a higher ratio of 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
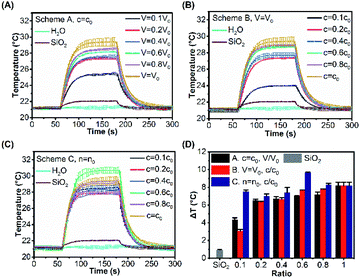
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, a complete shell with a thickness of about 40 nm was formed. The insets in Fig. 2A(iii–ix) show the colors of different SiO2@Au dispersions which mainly depend on the morphology of gold clusters of the SiO2@Au nanoparticles. The UV-Vis absorption spectra of the SiO2@Au dispersions with different gold clusters morphologies were measured as shown in Fig. 2B. As the gold clusters gradually grow till the formation of a fully-covered shell, the peak of the optical absorption response was redshifted from 544 nm to 676 nm and the absorption intensity also increased from 0.093 to 1.148. The temperature evolutions of SiO2@Au dispersions with different gold cluster morphologies under CW laser irradiation are demonstrated in Fig. 2C. The temperature of the SiO2@Au dispersions increased exponentially upon laser irradiation and reached equilibrium after about 110 s, and then returned to the ambient temperature after stopping the laser irradiation. As illustrated in Fig. 2D, no significant temperature change was observed in pure water and SiO2 dispersion under laser irradiation (0.19 °C, 0.94 °C, respectively) but the temperature rise (ΔT) of SiO2@Au dispersion droplets increased from 4.1 °C to 9.71 °C as the volume ratio of K-gold-to-seed solution increased from 10
1, a complete shell with a thickness of about 40 nm was formed. The insets in Fig. 2A(iii–ix) show the colors of different SiO2@Au dispersions which mainly depend on the morphology of gold clusters of the SiO2@Au nanoparticles. The UV-Vis absorption spectra of the SiO2@Au dispersions with different gold clusters morphologies were measured as shown in Fig. 2B. As the gold clusters gradually grow till the formation of a fully-covered shell, the peak of the optical absorption response was redshifted from 544 nm to 676 nm and the absorption intensity also increased from 0.093 to 1.148. The temperature evolutions of SiO2@Au dispersions with different gold cluster morphologies under CW laser irradiation are demonstrated in Fig. 2C. The temperature of the SiO2@Au dispersions increased exponentially upon laser irradiation and reached equilibrium after about 110 s, and then returned to the ambient temperature after stopping the laser irradiation. As illustrated in Fig. 2D, no significant temperature change was observed in pure water and SiO2 dispersion under laser irradiation (0.19 °C, 0.94 °C, respectively) but the temperature rise (ΔT) of SiO2@Au dispersion droplets increased from 4.1 °C to 9.71 °C as the volume ratio of K-gold-to-seed solution increased from 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 200
1 to 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (Fig. 2D). However, ΔT decreased from 9.71 °C to 7.91 °C with further increasing the K-gold-seed ratio to 300
1 (Fig. 2D). However, ΔT decreased from 9.71 °C to 7.91 °C with further increasing the K-gold-seed ratio to 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. This might be explained by the fact that the photothermal effect is mainly induced by the plasmon resonances occurring at the interface between the dielectric silica core and the gold layer. This effect becomes less effective when a thick fully-covered gold shell is formed, because the absorbed light tends to dissipate within the thick gold shell via bulk plasmon, leading to smaller increases in the solution temperature.52 The photothermal conversion efficiency (ηT) was also calculated for different dispersion droplet and the results showed that ηT decreased as the diameter of AuNPs was increased with the K-gold-to-seed volume ratios ranging from 10
1. This might be explained by the fact that the photothermal effect is mainly induced by the plasmon resonances occurring at the interface between the dielectric silica core and the gold layer. This effect becomes less effective when a thick fully-covered gold shell is formed, because the absorbed light tends to dissipate within the thick gold shell via bulk plasmon, leading to smaller increases in the solution temperature.52 The photothermal conversion efficiency (ηT) was also calculated for different dispersion droplet and the results showed that ηT decreased as the diameter of AuNPs was increased with the K-gold-to-seed volume ratios ranging from 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 40
1 to 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (Fig. S3†). According to Mie theory,53 AuNPs with smaller sizes could convert light energy into heat more efficiently compared with larger nanoparticles. It is worth noting that for a single particle, larger nanoparticles would generate more heat due to their higher surface area. Hence, the observed decrease of photothermal efficiency can be attributed primarily to the enhanced scattering as the gold cluster size increased.37
1 (Fig. S3†). According to Mie theory,53 AuNPs with smaller sizes could convert light energy into heat more efficiently compared with larger nanoparticles. It is worth noting that for a single particle, larger nanoparticles would generate more heat due to their higher surface area. Hence, the observed decrease of photothermal efficiency can be attributed primarily to the enhanced scattering as the gold cluster size increased.37
Effect of pH on the formation of gold morphology
By fixing the K-gold-to-seed ratio at 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
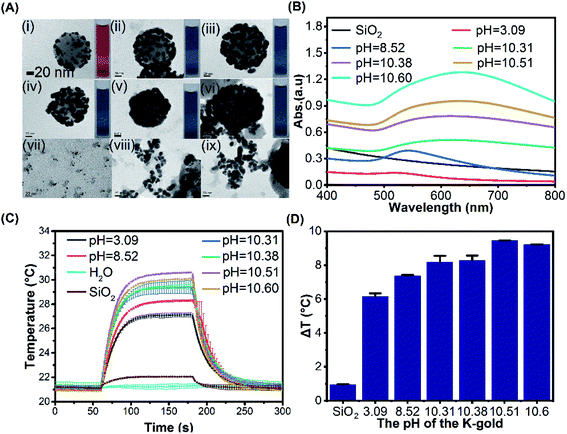
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 4 mL of 6.6 mM NaBH4, six different concentrations of K2CO3 (0, 0.3, 0.6, 1.2, 2.4, 4.8 g L−1) were used to prepare K-gold solution with resulting pH of 3.09, 8.52, 10.31, 10.38, 10.51 and 10.60, respectively, after being stirred overnight at room temperature for 24 h. As the pH was increased, the size of gold clusters on the surface of silica core was increased and the gaps between gold clusters were decreased, gradually forming a complete gold shell (Fig. 3A). The UV-Vis absorption spectra of these products show an increased bathochromic shift from 518 nm (pH = 3.09) to 634 nm (pH = 10.60) with enhanced gold shell perfection (Fig. 3B). The lower pH is unfavourable for gold deposition and leads to form small gold clusters. In the K-gold solution, HAuCl4 is hydrolysed to form [Au(OH)xCl4−x]− (Scheme 1), and the value of x depends on the extent of hydrolysis.54 The extent of hydrolysis in turn depends on the pH value which indicates the amount of OH− available for hydrolysis. It was found that the pH value of the system affected the stability of the primary AuNPs in solution, and ultimately inducing the difference in the surface morphology of SiO2@Au core–shell nanoparticles.55 When pH = 3.09, the neutral AuCl3·H2O is predominant with trace [Au(OH)xCl4−x]−,56 resulting in slow nucleation and growth on the seeds with small gold clusters (Fig. 3A(i)). With the increase of pH value, the form of Au3+ changes, gradually forming Au hydroxylated complex. At pH = 8.52 and 10.31, [Au(OH)3Cl]− is prevalent and optimal for surface nucleation, leading to form gold clusters with larger size and higher dispersion (Fig. 3A(ii and iii)). It was found that higher pH (10.38, 10.51, 10.6) promoted the formation of more gold nanoparticles suspended in solution other than deposition onto the silica core (from 2 to 20 nm, Fig. 3A(vii–ix)) and rough shell (Fig. 3A(iv–vi)). Fig. 3C demonstrates the temperature evolution of SiO2@Au dispersions under the fixed laser irradiation at different pH value of K-gold solution. The ΔT of droplets was increased from 6.14 °C to 9.22 °C as the pH value of K-gold solution increases from 3.09 to 10.6 (Fig. 3D).
1 and 4 mL of 6.6 mM NaBH4, six different concentrations of K2CO3 (0, 0.3, 0.6, 1.2, 2.4, 4.8 g L−1) were used to prepare K-gold solution with resulting pH of 3.09, 8.52, 10.31, 10.38, 10.51 and 10.60, respectively, after being stirred overnight at room temperature for 24 h. As the pH was increased, the size of gold clusters on the surface of silica core was increased and the gaps between gold clusters were decreased, gradually forming a complete gold shell (Fig. 3A). The UV-Vis absorption spectra of these products show an increased bathochromic shift from 518 nm (pH = 3.09) to 634 nm (pH = 10.60) with enhanced gold shell perfection (Fig. 3B). The lower pH is unfavourable for gold deposition and leads to form small gold clusters. In the K-gold solution, HAuCl4 is hydrolysed to form [Au(OH)xCl4−x]− (Scheme 1), and the value of x depends on the extent of hydrolysis.54 The extent of hydrolysis in turn depends on the pH value which indicates the amount of OH− available for hydrolysis. It was found that the pH value of the system affected the stability of the primary AuNPs in solution, and ultimately inducing the difference in the surface morphology of SiO2@Au core–shell nanoparticles.55 When pH = 3.09, the neutral AuCl3·H2O is predominant with trace [Au(OH)xCl4−x]−,56 resulting in slow nucleation and growth on the seeds with small gold clusters (Fig. 3A(i)). With the increase of pH value, the form of Au3+ changes, gradually forming Au hydroxylated complex. At pH = 8.52 and 10.31, [Au(OH)3Cl]− is prevalent and optimal for surface nucleation, leading to form gold clusters with larger size and higher dispersion (Fig. 3A(ii and iii)). It was found that higher pH (10.38, 10.51, 10.6) promoted the formation of more gold nanoparticles suspended in solution other than deposition onto the silica core (from 2 to 20 nm, Fig. 3A(vii–ix)) and rough shell (Fig. 3A(iv–vi)). Fig. 3C demonstrates the temperature evolution of SiO2@Au dispersions under the fixed laser irradiation at different pH value of K-gold solution. The ΔT of droplets was increased from 6.14 °C to 9.22 °C as the pH value of K-gold solution increases from 3.09 to 10.6 (Fig. 3D).
Effect of NaBH4 on gold morphology
NaBH4 was used as a reducing agent to reduce HAuCl4 in K-gold solution and trisodium citrate is used as a stabilizer to form smaller AuNPs. According to the aforementioned investigations on the effects of K-gold-to-seed ratio and pH value of K-gold solution, it can be observed that relatively uniform gold clusters were formed on the silica core surface with K-gold-to-seed ratio at 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and pH = 10.31 (shown in Fig. 2A(iv) and Fig. 3A(iii)). Thus, we fixed these synthetic conditions and used the corresponding concentration (c0 = 6.6 mM) and volume (V0 = 4 mL) of NaBH4 as the reference values. The concentration and volume of NaBH4 were then systematically varied to regulate the morphologies of gold clusters on the silica core surface. Three different schemes were implemented to adjust the addition of NaBH4 as shown in Table 1.
1 and pH = 10.31 (shown in Fig. 2A(iv) and Fig. 3A(iii)). Thus, we fixed these synthetic conditions and used the corresponding concentration (c0 = 6.6 mM) and volume (V0 = 4 mL) of NaBH4 as the reference values. The concentration and volume of NaBH4 were then systematically varied to regulate the morphologies of gold clusters on the silica core surface. Three different schemes were implemented to adjust the addition of NaBH4 as shown in Table 1.
| The volume ratio of K-gold to seed | pH | Scheme Aa | Scheme Bb | Scheme Cc | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| VNaBH4 (mL) | cNaBH4 (mM) | nNaBH4 (10−6 mol) | V/V0 | VNaBH4 (mL) | cNaBH4 (mM) | nNaBH4 (10−6 mol) | c/c0 | VNaBH4 (mL) | cNaBH4 (mM) | nNaBH4 (10−6 mol) | ||
| a Scheme A: keep the concentration of NaBH4 (c0), change the volume V = 0.1/0.2/0.4/0.6/0.8/1.0 V0.b Scheme B: keep the volume of NaBH4 (V0), change the concentration c = 0.1/0.2/0.4/0.6/0.8/1.0 c0.c Scheme C: keep the amount of substance NaBH4 (n0) and change the concentration c = 0.1/0.2/0.4/0.6/0.8/1.0 c0, corresponding volume V = 10/5.0/2.5/1.67/1.25/1.0 V0.d c0 = 6.6 mM, V0 = 4 mL. | ||||||||||||
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 80 |
10.31 | 4 | 6.6 | 26.4 | 1 | 4 | 6.6 | 26.4 | 1 | 4 | 6.6 | 26.4d |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 80 |
10.31 | 3.2 | 6.6 | 21.12 | 0.8 | 4 | 5.28 | 21.12 | 0.8 | 5 | 5.28 | 26.4 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 80 |
10.31 | 2.4 | 6.6 | 15.84 | 0.6 | 4 | 3.96 | 15.84 | 0.6 | 6.68 | 3.96 | 26.4 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 80 |
10.31 | 1.6 | 6.6 | 10.56 | 0.4 | 4 | 2.64 | 10.56 | 0.4 | 10 | 2.64 | 26.4 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 80 |
10.31 | 0.8 | 6.6 | 5.28 | 0.2 | 4 | 1.32 | 5.28 | 0.2 | 20 | 1.32 | 26.4 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 80 |
10.31 | 0.4 | 6.6 | 2.64 | 0.1 | 4 | 0.66 | 2.64 | 0.1 | 40 | 0.66 | 26.4 |
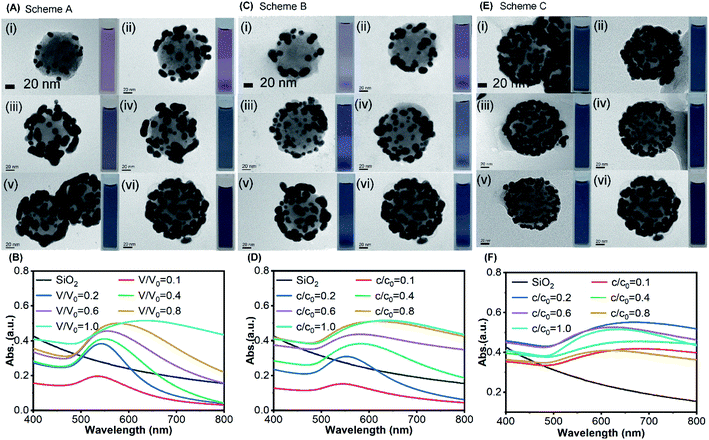
For Scheme A, the concentration (c) of NaBH4 was fixed as the same as the reference value (c = c0 = 6.6 mM) while the volume (V) was proportionally changed according to the volume ratio between the test condition and the reference value (i.e. V/V0). When V = 0.1V0 (Fig. 4A(i)), the spherical AuNPs were formed on the surface of silica core with a relatively large separation distance between each other. The shape of AuNPs gradually changed from spherical to ellipsoidal, until the gold clusters with irregularly shape were formed and coalesced together as the volume of NaBH4 was increased (Fig. 4A(i–vi)). In this process, the UV-Vis absorption spectra show an increasingly bathochromic shift from 542 nm to 632 nm with growing gold cluster sizes (Fig. 4B).
For Scheme B, the volume (V) of NaBH4 was fixed as the same as the reference value (V = V0 = 4 mL) while the concentration (c) was proportionally changed according to the concentration ratio between the test condition and the reference value (i.e. n/n0). The number of AuNPs on the surface of SiO2 was increased as the volume of NaBH4 was increased, and the distance between each other was decreased to form gold clusters (Fig. 4C(i–vi)) with an increasingly bathochromic shift from 544 nm to 632 nm (Fig. 4D). Comparing the resonance wavelength (Fig. S6(a)†) and absorbance (Fig. S6(b)†) of the UV-Vis absorption spectra in Scheme A with that in Scheme B at the same ratio, the resonant wavelength of the product in Scheme A was less red-shifted than those in Scheme B. However, the absorbance in Scheme A was higher than that in Scheme B. When the ratio is the same, the amount of NaBH4 participating in the reaction for both schemes was equal. At the same ratio, the gold clusters with larger size were formed on the silica core surface in Scheme A (Fig. 4A) which made the absorption cross section larger, resulting in higher absorbance. AuNPs with smaller size were formed on the silica core surface in Scheme B (Fig. 4C), which made the coupling effect between them stronger resulting in more red-shift.
For Scheme C, the total amount of NaBH4 was fixed as the same as the reference value (n = n0 = 26.4 × 10−6 mol) while the concentration and the volume were both proportionally changed, respectively. With the same amount of NaBH4 as the reference condition, AuNPs with small size were evenly distributed on the SiO2 surface (Fig. 4E(iv and v)) as the concentration of NaBH4 decreased from n0 to 0.6n0. Further reducing the concentration, the small AuNPs grew larger to coalesce and their distribution became nonuniform (Fig. 4E(i–iii)), and the resonant wavelength red-shifted.
Fig. 5A–C illustrate the temperature evolutions of the SiO2@Au nanoparticle dispersions with different surface morphologies under laser irradiations for three schemes. For Scheme A, as the volume ratio of NaBH4 increased, ΔT showed an increasing trend from 4.34 °C to 8.18 °C (Fig. 5A). Similarly, ΔT increased from 3.05 °C to 8.18 °C when the concentration of NaBH4 increased for Scheme B (Fig. 5B). For the same ratio value in Scheme A and B, the total amount of NaBH4 was actually the same but the surface morphologies of gold cluster were distinct, resulting different photothermal performances. It was observed that the temperature rises of Scheme A and B were close (ΔTA ≈ ΔTB) at the ratio of 0.4. At the ratios above 0.4, ΔTA became smaller than ΔTB, probably because of the more uniform distribution of gold clusters on the surface and stronger coupling effect for Scheme B. With the same ratio value for Scheme A, B and C, the total amount of for Scheme C (n = n0) was higher than Schemes A and B. Thus, ΔT of Scheme C was always the highest (Fig. 5D), because more gold was reduced by NaBH4 resulting in stronger light-to-heat conversion. For Scheme C alone, it can be clearly observed that a more uniform distribution of gold clusters was formed with c/c0 = 0.6 and V/V0 = 1.67 of NaBH4 (Fig. 4E). As a result, the photothermal conversion could be enhanced by the strong coupling effects and the highest ΔT = 9.64 °C was achieved among all tests.
Mechanistic interpretation of the effect of surface morphology of gold cluster layer on photothermal conversion
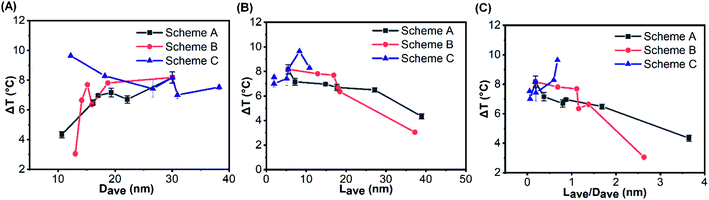
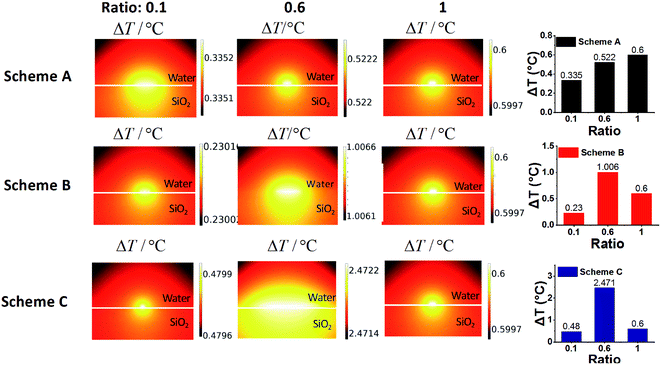
In order to establish the relationship between the surface morphology of the gold clusters and the photothermal performance, ΔT of SiO2@Au nanoparticles with different morphologies of gold clusters for three schemes (Fig. 4A, C and E) are replotted as functions of Dave, Lave and Lave/Dave in Fig. 6. Fig. 6A demonstrates the effects of the gold cluster size (Dave). As the size of the gold cluster was increased up to 20 nm, ΔT was significantly increased for Schemes A and B. When Dave increased above 20 nm, ΔT slightly increased. It is because the scattering cross section was increased with further increasing the gold cluster size, resulting in more the heat loss and lower photothermal conversion. Fig. 6B demonstrates that ΔT was monotonically decreased as the average distance among gold clusters (Lave) was increased for Schemes A and B. Fig. 6C shows that ΔT was decreased as the Lave/Dave was increased for Schemes A and B, because the coupling effects became weak with increase of Lave/Dave. When Lave/Dave was greater than about 1.3, ΔT dramatically decreased, implying the coupling effect became negligible and the photothermal performance mainly depends on the size of the gold cluster. It is worth mentioning that the maximum temperature rise was obtained with c/c0 = 0.6 and V/V0 = 1.67 of NaBH4 in Scheme C in which the Dave and Lave/Dave are 12.21 nm and 0.68, respectively. For a fixed amount of NaBH4, a relatively uniform distribution of gold clusters was formed the SiO2 surface (Fig. 4E) which could induce strong coupling effects and enhance the photothermal effect. Thus, the photothermal effect of SiO2@Au core–shell nanoparticles should not only be affected by the absorption cross section of gold clusters on the SiO2 surface and the coupling effect between them, but also by the uniformity of the distribution of them.In order to quantitatively understand the effects of morphology of gold cluster, a numerical model for electromagnetic adsorption and heat transfer was formulated with a commercial finite element method software COMSOL Multiphysics. Three representative ratios for each scheme were used for simulation, including 0.1, 0.6 and 1.0 as shown in Fig. 4. The model was firstly validated by a comparison with the results in Baffou's work.24 Three key requirements imposed by the experimental results were fulfilled for the cluster geometry: (1) the particle size and interparticle distance were set according to the Dave and Lave, respectively, measured by using ImageJ software in the experiments; (2) the number of AuNPs for each ratio was approximated based on the ratio of the total amount (n) of the reducing reagent (NaBH4), which determined the total mass of the produced gold for each case; (3) the incident laser wavelength and intensity was set as the same as the experimental value. Moreover, a planar SiO2 surface was assumed for simplicity in this study. The details for computing parameters are shown in Table S1.† The thermal field maps of temperature rise at steady state for different cases are plotted in Fig. 7. It can be observed that, the temperature rise is increased from 0.335 to 0.6 with increasing the ratio from 0.1 to 1.0 for Schemes A. It is due to the increased adsorption cross section with more gold reduced by NaBH4 with low ratio value and the coupling effects caused by reduced interparticle distance with high ratio value (Fig. S7†). For Scheme C with fixed amount of gold (n = n0), the maximum temperature rise is achieved with ratio of 0.6 for. It is mainly attributed to the strong coupling effects among small gold nanoparticles (Fig. S7†) and collective heating effects caused the number of AuNPs under laser irradiation. It is also noted that weaker heating effects were observed for all the computed cases compared to the experimental results. This is due to the limited number of gold nanoparticles in the calculations. An appreciable temperature increase can be expected by collective heating effects with presence of more gold nanoparticles under laser irradiation.57,58
 | ||
| Fig. 7 Side view of ΔT map of a chain of gold nanoparticles on SiO2 surface submerged in water. The structure is shined form the top = 532 nm, P = 1.05 × 104 W m−2 with a polarization perpendicular to the nanoparticle chain. The details of gold nanoparticle size, interparticle distance and number for each computing case are shown in Table S2.† | ||
Conclusions
In this study, we have studied the effects of surface morphology of gold cluster on the photothermal conversion performance of SiO2@Au core–shell nanoparticle by means of chemically adjusting the synthesis parameters, including amounts of gold salts, pH value of K-gold solution and reducing agent (NaBH4). To the best of our knowledge, this is the first time to systematically investigate the thermoplasmonics mechanism of various gold clusters on SiO2@Au core–shell nanoparticle. The morphology of gold clusters on the surface of silica core were characterized by calculating the equivalent circular diameter of gold clusters (Dave) and the average distance among gold clusters (Lave) on the silica core surface based on the measurements on TEM image of SiO2@Au using the software ImageJ. Based on the measured temperature rise of the SiO2@Au droplets and the calculated Dave and Lave of the gold cluster, the results show the temperature rise of the SiO2@Au dispersions depends on the size of gold clusters when the ratio of gold clusters' equivalent diameter to average distance among the clusters (Lave/Dave) is greater than 1.3. On the contrary, the strong coupling effect between gold clusters play an important role in photothermal effect when the ratio is less than 1.3. For a given mass of gold clusters, the maximum temperature rise can be achieved with a relatively uniform distribution of gold clusters with which enhanced light-to-heat conversion is obtained via strong coupling effects and collective heating effects. In order to interpret the observed phenomena, a chain of AuNPs distributed in a specific geometry has been simulated by using a commercial FEM software according to measured morphology parameters from the experiment. Obtained results are in reasonably good agreement with experimental results and show different photothermal conversion mechanism with different surface morphologies of gold clusters. Our results demonstrate a potential route to manipulate the heat generation at nanoscale by using SiO2@Au core–shell nanoparticles.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the financial supports from National Key Research and Development Program of China (2016YFB0401502), Guangdong Basic and Applied Basic Research Foundation (2019A1515011631), Science and Technology Program of Guangzhou (No. 2019050001), Foundation for Distinguished Young Talents in Higher Education of Guangdong (2017KQNCX047), the Open Fund of Defense Key Disciplines Lab of Novel Micro-nano Devices and System Technology, the Guangdong Provincial Key Laboratory of Optical Information Materials and Technology (grant number 2017B030301007), the 111 project, and the Research Cultivation Fund for Young Faculty by South China Normal University (SCNU).Notes and references
- M. Pelton, J. Aizpurua and G. Bryant, Laser Photonics Rev., 2008, 2, 136–159 CrossRef CAS.
- A. O. Govorov and H. H. Richardson, Nano Today, 2007, 2, 30–38 CrossRef.
- X. Huang, P. K. Jain, I. H. El-Sayed and M. A. El-Sayed, Lasers Med. Sci., 2008, 23, 217–228 CrossRef.
- R. Ahijado-Guzman, N. Sanchez-Arribas, M. Martinez-Negro, G. Gonzalez-Rubio, M. Santiago-Varela, M. Pardo, A. Pineiro, I. Lopez-Montero, E. Junquera and A. Guerrero-Martinez, Nanomaterials, 2020, 10, 590 CrossRef CAS.
- B. Nasseri, M. Turk, K. Kosemehmetoglu, M. Kaya, E. Piskin, N. Rabiee and T. J. Webster, Int. J. Nanomed., 2020, 15, 2903–2920 CrossRef.
- V. Guerrero-Florez, S. C. Mendez-Sanchez, O. A. Patron-Soberano, V. Rodriguez-Gonzalez, D. Blach and O. F. Martinez, J. Mater. Chem. B, 2020, 8, 2862–2875 RSC.
- M. Berns, J. Aist, J. Edwards, K. Strahs, J. Girton, P. Mcneill, J. Rattner, M. Kitzes, M. Hammer-Wilson and L. Liaw, Science, 1981, 213, 505–513 CrossRef CAS.
- A. S. Urban, T. Pfeiffer, M. Fedoruk, A. A. Lutich and J. Feldmann, ACS Nano, 2011, 5, 3585–3590 CrossRef CAS.
- J. Watanabe and K. Ishihara, NanoBiotechnology, 2008, 3, 76–82 CrossRef.
- P. Ghosh, G. Han, M. De, C. K. Kim and V. M. Rotello, Adv. Drug Delivery Rev., 2008, 60, 1307–1315 CrossRef CAS.
- B. P. Timko, T. Dvir and D. S. Kohane, Adv. Mater., 2010, 22, 4925–4943 CrossRef CAS.
- A. Gaiduk, P. V. Ruijgrok, M. Yorulmaz and M. Orrit, Chem. Sci., 2010, 1, 343–350 RSC.
- L. Lin, X. Peng, M. Wang, L. Scarabelli, Z. Mao, L. M. Liz-Marzan, M. F. Becker and Y. Zheng, ACS Nano, 2016, 10, 9659–9668 CrossRef CAS.
- J. S. Donner, G. Baffou, D. Mccloskey and R. Quidant, ACS Nano, 2011, 5, 5457–5462 CrossRef CAS.
- C. N. Baroud, J. Delville, F. Gallaire and R. Wunenburger, Phys. Rev. E, 2007, 75, 046302 CrossRef.
- S. Eustis and M. A. ElSayed, Chem. Soc. Rev., 2006, 209, 209–217 RSC.
- P. K. Jain, X. Huang, I. H. ElSayed and M. A. EISayed, Acc. Chem. Res., 2008, 41, 1578–1586 CrossRef CAS.
- C. J. Murphy, L. B. Thompson, A. M. Alkilany, P. N. Sisco, S. P. Boulos, S. T. Sivapalan, J. A. Yang, D. J. Chernak and J. Huang, J. Phys. Chem. Lett., 2010, 1, 2867–2875 CrossRef CAS.
- E. Ringe, M. R. Langille, K. Sohn, J. Zhang, J. Huang, C. A. Mirkin, R. P. Van Duyne and L. D. Marks, J. Phys. Chem. Lett., 2012, 3, 1479–1483 CrossRef CAS.
- K. L. Kelly, E. A. Coronado, L. L. Zhao and G. C. Schatz, J. Phys. Chem. B, 2003, 107, 668–677 CrossRef CAS.
- J. P. Kottmann and O. J. F. Martin, Opt. Lett., 2001, 26, 1096–1098 CrossRef CAS.
- J. B. Wagner, P. L. Hansen, A. M. Molenbroek, H. Topsøe, B. S. Clausen and S. Helveg, J. Phys. Chem. B, 2003, 107, 7753–7758 CrossRef CAS.
- K. H. Su, Q. H. Wei, X. Zhang, J. J. Mock, D. R. Smith and S. Schultz, Nano Lett., 2003, 3, 1087–1090 CrossRef CAS.
- G. Baffou, R. Quidant and F. J. García de Abajo, ACS Nano, 2010, 4, 709–716 CrossRef CAS.
- G. Baffou, R. Quidant and C. Girard, Phys. Rev. B, 2010, 82, 165424 CrossRef.
- W. Huang, W. Qian and M. A. ElSayed, J. Phys. Chem. B, 2007, 111, 10751–10757 CAS.
- X. Gu, V. Timchenko, G. Heng Yeoh, L. Dombrovsky and R. Taylor, Appl. Sci., 2018, 8, 1132 CrossRef.
- Y. Chen, Microelectron. Eng., 2015, 135, 57–72 CrossRef CAS.
- F. Watt, A. A. Bettiol, J. A. V. Kan, E. J. Teo and M. B. H. Breese, Int. J. Nanosci., 2008, 04, 269–286 CrossRef.
- C. Lu and R. H. Lipson, Laser Photonics Rev., 2009, 4, 568–580 CrossRef.
- H. Schift, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct., 2008, 26, 458–480 CrossRef CAS.
- A. Horrer, C. Schäfer, K. Broch, D. A. Gollmer and M. Fleischer, Small, 2013, 9, 3987–3992 CrossRef CAS.
- H. Le-The, E. Berenschot, R. M. Tiggelaar, N. R. Tas, A. van den Berg and J. C. T. Eijkel, Adv. Mater. Technol., 2017, 2, 1600238 CrossRef.
- J. Lee, J.-H. Huh, K. Kim and S. Lee, Adv. Funct. Mater., 2018, 28, 1707309 CrossRef.
- M. Zhang, T. H. Ngo, N. I. Rabiah, T. P. Otanicar, P. E. Phelan, R. Swaminathan and L. L. Dai, Langmuir, 2014, 30, 75–82 CrossRef CAS.
- V. A. Turek, S. Cormier, B. Sierra-Martin, U. F. Keyser, T. Ding and J. J. Baumberg, Adv. Opt. Mater., 2018, 6, 1701270 CrossRef.
- K. Jiang, D. A. Smith and A. Pinchuk, J. Phys. Chem. C, 2013, 117, 27073–27080 CrossRef CAS.
- H. H. Richardson, M. T. Carlson, P. J. Tandler, P. Hernandez and A. O. Govorov, Nano Lett., 2009, 9, 1139–1146 CrossRef CAS.
- H. H. Richardson, A. C. Thomas, M. T. Carlson, M. E. Kordesch and A. O. Govorov, J. Electron. Mater., 2007, 36, 1587–1593 CrossRef CAS.
- J. R. Cole, N. A. Mirin, M. W. Knight, G. P. Goodrich and N. J. Halas, J. Phys. Chem. C, 2009, 113, 12090–12094 CrossRef CAS.
- M. Alrahili, R. Peroor, V. Savchuk, K. McNear and A. Pinchuk, J. Phys. Chem. C, 2020, 124, 4755–4763 CrossRef CAS.
- S. E. Park, J. Lee, T. Lee, S. B. Bae, B. Kang, Y. M. Huh, S. W. Lee and S. Haam, Int. J. Nanomed., 2015, 10, 261–271 CAS.
- S. Nouri, E. Mohammadi, B. Mehravi, F. Majidi, K. Ashtari, A. Neshasteh-Riz and S. Einali, Artif. Cells, Nanomed., Biotechnol., 2019, 47, 2316–2324 CrossRef CAS.
- K. Ma, Y. Li, Y. Chen, X. Zhang and Z. Wang, ACS Appl. Mater. Interfaces, 2019, 11, 29630–29640 CrossRef CAS.
- S. H. Kang, Y. K. Lee, I. S. Park, I. K. Park, S. M. Hong, S. Y. Kwon, Y. H. Choi, S. J. Madsen, H. Hirschberg and S. J. Hong, BioMed Res. Int., 2020, 5869235, 1–14 Search PubMed.
- K. Y. Park, H. S. Han, J. Y. Hong, S. J. Seo and S. J. Lee, Dermatol. Ther., 2020, 33, e13189 Search PubMed.
- J. C. Y. Kah, N. Phonthammachai, R. C. Y. Wan, J. Song, T. White, S. Mhaisalkar, I. Ahmad, C. Sheppard and M. Olivo, Gold Bull., 2008, 41, 23–36 CrossRef CAS.
- N. Phonthammachai, J. C. Y. Kah, G. Jun, C. J. R. Sheppard, M. C. Olivo, S. G. Mhaisalkar and T. J. White, Langmuir, 2008, 24, 5109–5112 CrossRef CAS.
- G. Baffou, P. Bon, J. Savatier, J. Polleux, M. Zhu, M. Merlin, H. Rigneault and S. Monneret, ACS Nano, 2012, 6, 2452–2458 CrossRef CAS.
- L. Zhao, K. L. Kelly and G. C. Schatz, J. Phys. Chem. B, 2003, 107, 7343–7350 CrossRef CAS.
- G. Baffou, P. Berto, E. Bermudez Urena, R. Quidant, S. Monneret, J. Polleux and H. Rigneault, ACS Nano, 2013, 7, 6478–6488 CrossRef CAS.
- H. Raether, Surface-Plasmons on Smooth and Rough Surfaces and on Gratings, Springer-Verlag Berlin Heidelberg, Berlin, 1988 Search PubMed.
- X. Ding, C. H. Liow, M. Zhang, R. Huang, C. Li, H. Shen, M. Liu, Y. Zou, N. Gao, Z. Zhang, Y. Li, Q. Wang, S. Li and J. Jiang, J. Am. Chem. Soc., 2014, 136, 15684–15693 CrossRef CAS.
- C. K. Chang, Y. J. Chen and C. T. Yeh, Appl. Catal., A, 1998, 174, 13–23 CrossRef CAS.
- R. Wang, PhD thesis, Jilin University, 2016.
- D. Yin, L. Qin, J. Liu, C. Li and Y. Jin, J. Mol. Catal. A: Chem., 2005, 240, 40–48 CAS.
- A. O. Govorov, W. Zhang, T. Skeini, H. Richardson, J. Lee and N. A. Kotov, Nanoscale Res. Lett., 2006, 1, 84–90 CrossRef.
- G. Palermo, U. Cataldi, A. Condello, R. Caputo, T. Burgi, C. Umeton and A. De Luca, Nanoscale, 2018, 10, 16556–16561 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra06278b |
| This journal is © The Royal Society of Chemistry 2020 |