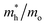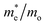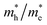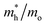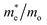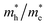Open Access Article
Open Access ArticleUnraveling the relationship between exposed surfaces and the photocatalytic activity of Ag3PO4: an in-depth theoretical investigation
Felipe Lipskya,
Luis Henrique da Silveira Lacerda a,
Sérgio Ricardo de Lazaro
a,
Sérgio Ricardo de Lazaro b,
Elson Longo
b,
Elson Longo c,
Juan Andrés
c,
Juan Andrés d and
Miguel Angel San-Miguel
d and
Miguel Angel San-Miguel *a
*a
aState University of Campinas, Campinas, São Paulo, Brazil. E-mail: smiguel@unicamp.br
bState University of Ponta Grossa, Ponta Grossa, Paraná, Brazil
cCDMF-UFSCAR, Federal University of São Carlos, São Carlos, São Paulo, Brazil
dUniversity Jaume I, Castellón, Spain
First published on 18th August 2020
Abstract
Over the years, the possibility of using solar radiation in photocatalysis or photodegradation processes has attracted remarkable interest from scientists around the world. In such processes, due to its electronic properties, Ag3PO4 is one of the most important semiconductors. This work delves into the photocatalytic activity, stability, and reactivity of Ag3PO4 surfaces by comparing plane waves with projector augmented wave and localized Gaussian basis set simulations, at the atomic level. The results indicate that the (110) surface, in agreement with previous experimental reports, displays the most suitable characteristics for photocatalytic activity due to its high reactivity, i.e. the presence of a large amount of undercoordinated Ag cations and a high value work function. Beyond the innovative results, this work shows a good synergy between both kinds of DFT approaches.
1. Introduction
Yi et al.'s seminal work1 was the first to shed light on the outstanding performance of silver phosphate (Ag3PO4) as a photocatalyst for water splitting. The calculated electronic absorption spectrum showed the material's semiconductor nature, with an indirect bandgap of 2.36 eV and a direct transition of 2.45 eV. This proved that silver phosphate is a very attractive material for visible light absorption applications.1–4 Over the years, several studies focusing on Ag3PO4 were published, revealing more than significant data about this material, its structure and electronic features.5–14The interest in Ag3PO4 increased due to its suitability as a photocatalyst in organic photodegradation processes. This topic has received remarkable attention from the scientific community around the world due to the high contamination of water resources by several kinds of pollutants.15–19 Thus, in this context, Ag3PO4 has been extensively investigated.20–27 It is noteworthy that the highly positive reduction potential observed for the top of the valence band (VB) vs. normal hydrogen electrode (NHE), approximately 2.9 eV, shows that the material is suitable as a photocatalyst for oxygen evolution in the aqueous medium.28 Unfortunately, the positive oxidation potential of the bottom of the conduction band (CB) vs. NHE suggests that the bulk crystal suffers photo corrosion, resulting in the formation of metallic Ag films on the surface, thus undermining its stability and lifespan. Yet, Ag3PO4 displays visible-light-induced antibacterial activity, albeit concomitant with photodegradation.29–31
The measurement of oxygen evolution over time by an Ag3PO4 electrode in a silver nitrate solution under visible-light irradiation attested that Ag3PO4 shows the best performance compared to BiVO4- and WO3-electrodes, which are broadly acknowledged light-sensitive semiconductors for O2 evolution under the same conditions.1 Moreover, Ag3PO4 also presents the highest rate of decomposition of methylene blue under light irradiation in comparison to other materials such as BiVO4 and TiO2−xNx.1 These relevant results increased the interest of the scientific community so as to have a detailed understanding of Ag3PO4's exceptional electronic structure and develop a number of approaches to improve its stability and photocatalytic activity.7,8,28,32–37 Very recently, Li et al.38 have discussed and summarized the progress in the field, namely Ag3PO4 used as a photocatalyst, as well as the barriers that should be overcome prior to practical application.
Exposing specific crystalline surfaces via controlled synthesis leads to enhancing the photoelectric and photocatalytic activities of several known materials.32,39–41 In this context, Raudoniene et al.42 reported a simple chemical solution-based synthesis route to prepare uniform, shape-controllable Ag3PO4 crystals. Guo et al.43 synthetized concave rhombic dodecahedra structures with different morphologies and photocatalytic activity. Bi et al. developed a method to obtain single-crystalline Ag3PO4 with rhombic dodecahedron and cube morphologies.32 The former refers to the predominance of (110) surfaces while favoring the (100) direction results in cube shapes. The results suggest that the rate of photocatalytic degradation of methyl orange and rhodamine B was sensitive to these different morphologies. The rhombic dodecahedron crystals with (110) facets exhibited the highest efficiency on the process and both morphologies led to a fascinating improvement for dye degradation compared to the conventional Ag3PO4 morphology. Other experimental studies also point out the (110) surface as the main responsible for the high catalytic activity of this material.44–47
Although these scientific contributions point out that the geometrical distribution of crystal surfaces plays a critical role in determining photocatalytic activities, adequate theoretical studies on Ag3PO4 surfaces and bulk are still lacking. Thus, this work performs a broad ab initio simulation framed within the density functional theory (DFT) through the combination of the results obtained from plane waves with the projector augmented wave method and localized Gaussian basis set. The results obtained provide new insights, at the atomic level, into the photocatalytic activity, stability, and reactivity of Ag3PO4 surfaces.
The difference in the photocatalytic performance of Ag3PO4 surfaces is rationalized in terms of (i) the surface energy values of the exposed surfaces; (ii) charge separation capability through the comparison of the effective masses of photogenerated electrons and holes; (iii) morphology, wherein an analysis of the coordination of the surface's topmost atoms is used to assess proclivity toward the establishment of new bonds; and (iv) concentration of charge, in which a work function is employed to ascertain the preferential direction for the migration of charge among the crystal's facets. Lastly, a deeper study of the electronic properties of each surface is carried out to provide a deep understanding of the difference in their photocatalytic activity.
2. Computational details and model systems
Ag3PO4 has a body-centered cubic structure (BCC) with space symmetry group number 218,48 in which PO43− groups present regular tetrahedrons with the P5+ located at the vertices and center positions of the unit cell, while the six Ag+ cations are distributed among twelve sites of twofold symmetry.In this work, two different theoretical methodologies based on the DFT were applied in order to describe the electronic and structural properties of bulk Ag3PO4. The first one of them was a plane-wave method. The second one used a non-truncated description of atoms from localized Gaussian functions applied in atomic orbitals linear combination. Both methodologies were based on periodic models constructed according to crystalline data available in the Inorganic Crystallographic Database (ICSD) ID 14000.
The computational simulations based on a plane-wave method were carried out on the Vienna Ab initio Simulation Package (VASP),49,50 using three different approaches for the description of the exchange–correlation interactions: the Perdew–Burke–Ernzerhoff (PBE)51 functional, the PBE revision for solids (PBEsol)52 and the PBE allied to Grimmes's D3 dispersion corrections (PBE+D3).53 In all simulations, the projector augmented wave (PAW) method54 was used to represent the interactions of the core–valence electrons. The valence electrons (Ag 4d105s1, P 3s23p3, and O 2s22p4) were explicitly treated with a plane-wave basis set expansion with a cutoff of 550 eV. The atomic relaxations were carried out through the conjugated-gradient (CG) algorithm. All calculations were deemed fully converged when all the residual forces were below 0.005 eV Å−1 and the total energy difference between successive steps was below 10−5 eV. The Gaussian smearing method20,55 was applied with a smearing width of 0.01 eV. A 5 × 5 × 5 gamma-centered Monkhorst–Pack mesh56 was used to sample the reciprocal space for the bulk calculations (15 × 15 × 15 for the density of states and charge calculations). The PBE functional is well-known to fail to reproduce the exact bandgap for semiconductor materials because of its deficient modeling of the actual exchange–correlation hole, which amounts to an excessive delocalization of the wavefunction.57 To amend that, PBE+U calculations were also performed and an additional on-site Coulomb term (Hubbard U)58 was added to those states which were expected to be more localized—both the Ag 4d states (U = 16.01 eV) and O 2p states (U = 10.93 eV). These values yielded reliable representations of the electronic structures, guaranteeing the agreement between theoretical and experimental data. In particular, for surface models, we adopted a slab model for the description of the most common Ag3PO4 surfaces.32,33 The relaxed bulk unit cell was extended in turn along with the [100], [110], and [111] directions, maintaining the crystal stoichiometry. The cell vectors were shifted accordingly and a vacuum of 15 Å along the z-axis was created in each case. The thickness convergence with the number of layers was achieved using slabs with 8, 10, and 12 formula units for the (100), (110) and (111) surfaces comprising superficial areas of 36.29, 51.32, and 62.86 Å2, respectively. Dipole corrections along the vacuum direction were added to counter the electric dipole resulting from the asymmetrical character of the slabs. Monkhorst–Pack k-point sets of 3 × 3 × 1, 5 × 5 × 1, and 5 × 5 × 1 were used for the (100), (110), and (111) slabs, respectively.
On the other hand, the simulations based on a localized description of atoms were performed on CRYSTAL59,60 software using SCF convergence truncated in 10−8 hartree and Monkhorst–Pack method56,61 for k-points analysis defined as 8 × 8 × 8. This high parameterization guarantees the highest reliability level for our results and keeps the calculation parameter similar to that employed on the plane-wave method. In particular, the Ag, P, and O atoms were described by HAYWSC-311d31G,62 85-21d1G,63 and 8-411 (ref. 64 and 65) basis set, respectively. The exchange–correlation interactions were treated according to PBE, PBE0, and B3LYP functional. Besides, a Grimme correction66 to the description of van der Waals interactions was employed together with the B3LYP hybrid functional, which presents the best description of the system.
The structural features and electronic properties from the density of states (DOS), band structure (BS), and charge carrier mobility for the bulk Ag3PO4 were discussed for all models.
3. Results and discussions
3.1. Ag3PO4: bulk properties
First, the bulk phase of Ag3PO4 was investigated. It has a cubic symmetry (space group 218), in which each Ag cation was fourfold coordinated with oxygen atoms and the P cations are neighboured by four O anions composing a tetrahedral cluster. The unit cell consists of two formula units, amounting to sixteen atoms. The results are presented in Table 1. For the plane-wave approach, the best results were obtained from the addition of dispersion corrections (D3) to the PBE functional, as evidenced by minor relative error. Therefore, long-range interactions between the atoms can be said to play a crucial role in the determination of the Ag3PO4 crystal structures. It is also important to highlight that the PBE+D3 simulation presented the best description among all theoretical levels applied in this study. The structural results for the three-dimensional Gaussian basis set, considering all the applied exchange–correlation functionals, were in agreement with other experimental reports for Ag3PO4. In particular, the PBE0 was more efficient in the description of the lattice parameters. However, the B3LYP functional can better minimize the system's total energy, presenting the best description for optical properties. Therefore, a new structural optimization was performed allying the B3LYP hybrid functional to Grimme's correction, obtaining a better description of the structural parameters. The improvement in lattice parameters points to the B3LYP+Grimme combination as the best option for the three-dimensional Gaussian basis set approach. Therefore, the plane-wave and Gaussian basis sets with dispersion descriptions were the best descriptions to represent the long-range van der Waals interactions. Such representation played a crucial role independent of the DFT approach to determine the Ag3PO4 structure.| Method | Lattice parameter (Å) | Relative error (%) | |
|---|---|---|---|
| Plane-wave | PBE | 6.10 | 1.19 |
| PBEsol | 5.97 | −0.92 | |
| PBE+D3 | 6.02 | −0.022 | |
| PBE+U | 6.10 | 1.19 | |
| Localized Gaussian basis set | PBE | 6.13 | 1.76 |
| PBE0 | 6.08 | 0.97 | |
| B3LYP | 6.16 | 2.31 | |
| B3LYP+Grimme | 6.06 | 0.63 | |
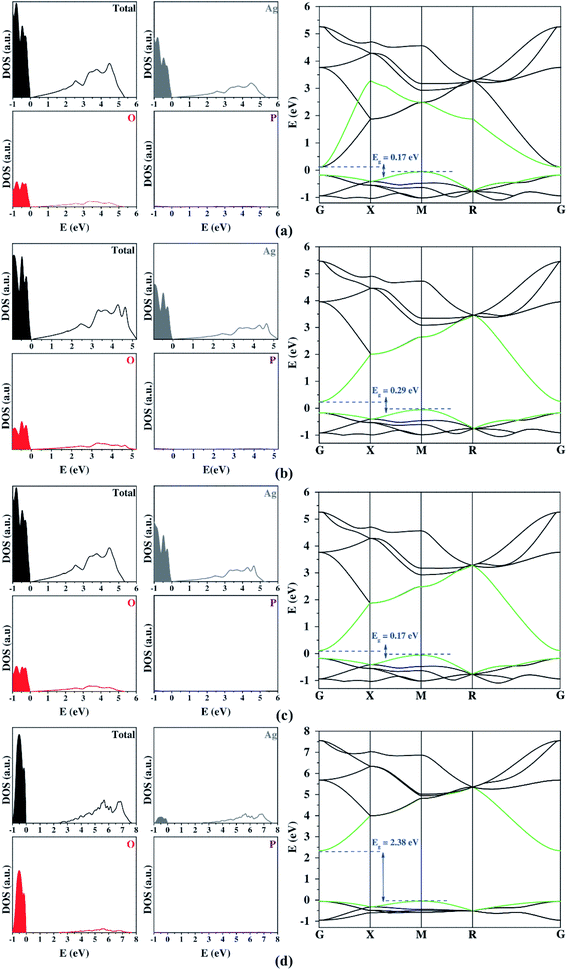
Once the structural properties were predicted, the next steps consisted of the calculations of the electronic properties. The results obtained from the plane-wave approach are presented in Fig. 1. An analysis of the results renders that the PBE functional leads to a thoroughly inadequate description of the bandgap, presenting largely underestimated values. The addition of Hubbard's (U) potential to the Ag 4d and O 2p states improved the bandgap value, making it close to the experimental results. However, the bandgap was still slightly underestimated. In particular, the use of a large Hubbard term displaced most of Ag 4d states at the VB to lower energy values, amounting to O 2p states becoming the main contributors to the VB composition. These results are opposite to those observed in the existing literature34,35 and the other functionals employed in this work (Fig. 1 and 2). The artificial change in the composition of the VB impetrated by the Hubbard U term can be expected to lead to an artificial modification of the band structure's curvature, which should impair the obtaining of accurate effective masses. This downside of using Hubbard's terms has been identified before34 for Ag3PO4 and is further confirmed in this study.
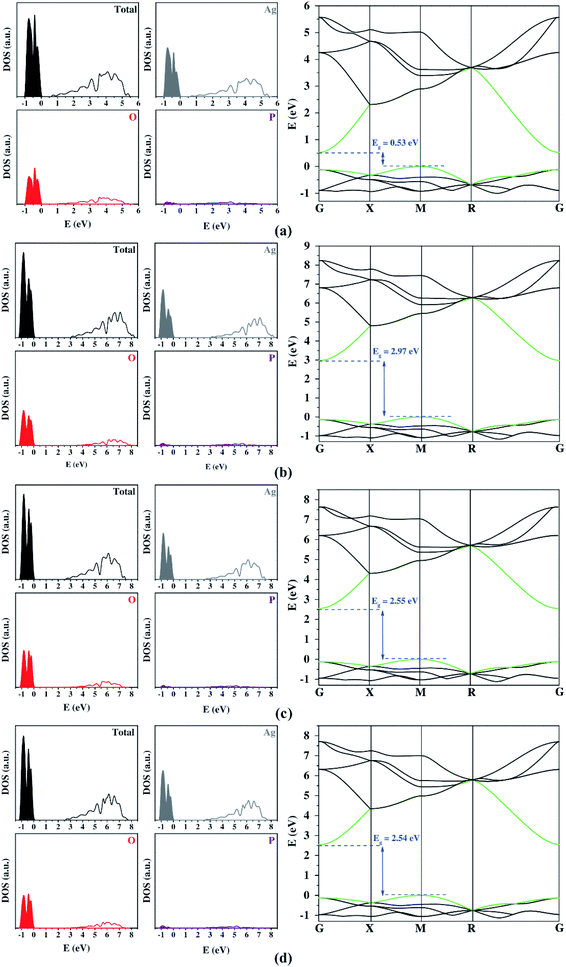
Fig. 2 shows the DOS and BS profiles of Ag3PO4 from the Gaussian basis set. The contribution of Ag, O, and P atoms occurs in the 4d 5s, 2s 2p, and 3s 3p orbitals, respectively. From DOS, the Ag atoms present a higher contribution to VB and CB. The O atoms contribute significantly for VB and CB, while the P atoms exhibit low participation in the band-gap region. In the case of the band structure profiles, a singular bottleneck at the R symmetry point was observed for all functionals. This unexpected behavior was created by the bands' degeneration at this point. All three-dimensional basis set calculations suggest an indirect bandgap between the M and G symmetry points. Yet, only the hybrid functional presents a good description of the bandgap. The best results were the B3LYP and B3LYP+Grimme approaches. The prediction of DOS projection, BS profiles, and bandgaps by localized Gaussian basis sets and functionals were similar.
The optical and photocatalytic properties were also calculated. The optical property shows the possibilities for electronic excitation through bandgap values. The bandgap analyzed the most was the region between VB and CB because it represents the lowest energetic value for electronic excitation. Experimental measurements reported that the bandgap for Ag3PO4 was in the visible range (1.6 eV to 3.3 eV).28 The PBE functional underestimated the bandgap expressively, while other functionals overestimated this quantity either slightly (B3LYP and B3LYP+Grimme) or remarkably (PBE0). Such results show the high influence of the correlation factor included in the PBE0, B3LYP, and B3LYP+Grimme to describe the bandgap adequately.
The valence (VB) and conduction band (CB) edge potentials for Ag3PO4 were calculated for all functionals tested in this work and presented in Table 2. The values were computed using well-known equations8 and they agree with theoretical8 and experimental28 results. Thus, all calculated VB edge potentials are more positive than O2/H2O (1.23 V), being the driving force for oxidizing H2O to produce O2 or to oxidize pollutants. At the same time, the values for CBM potential of Ag3PO4 indicate that the material cannot reduce H+ to H2 (0 V).
| Method | VB edge potential (V) | CB edge potential (V) | VB edge potentiala (V) | CB edge potentiala (V) | VB edge potentialb (V) | |
|---|---|---|---|---|---|---|
| a Theoretical results obtained from DFT/PBE0 approaches using plane-wave methods.8b Experimental results for VB vs. normal hydrogen electrode (NHE).28 | ||||||
| Plane-wave | PBE | 1.54 | 1.37 | 2.67 | 0.24 | 2.90 |
| PBEsol | 1.60 | 1.31 | ||||
| PBE+D3 | 1.54 | 1.37 | ||||
| PBE+U | 2.65 | 0.27 | ||||
| Localized Gaussian basis sets | PBE | 1.72 | 1.20 | |||
| PBE0 | 2.94 | −0.02 | ||||
| B3LYP | 2.73 | 0.18 | ||||
| B3LYP+Grimme | 2.72 | 0.19 | ||||
The photocatalytic activity was discussed in terms of the recombination ratio for the charge carriers obtained through the effective mass method. Such analysis is based on the ratio between the electron (e−) and hole (h+) masses, mathematically represented in eqn (1), where m* is the effective mass of the charge carrier, k is the wave vector, ℏ is the reduced Planck constant, and ν is the transfer rate of photogenerated electrons and holes. Thus, the effective mass for electrons 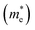 and holes
and holes 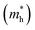 was investigated. The ratio between both values
was investigated. The ratio between both values 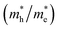 is connected to the charge carriers recombination rate, since values higher than 1.5 or minor than 0.5 indicate that the charge carrier recombination is inhibited, increasing the potential of the material to redox reactions. Meanwhile, values near 1 are related to highly unstable charge carriers.67–71 Moreover, the individual values of effective mass must be evaluated as well, since overly high values hamper the charge mobility, decreasing its ability to migrate from bulk to surface and take part in redox reactions.69 The effective masses (m*) between holes and electrons were determined through a parabolic fitting of the band structure around the immediate vicinity in the reciprocal space (maximum distance of 0.1 Å) of the valence band maximum (VBM) and conduction band minimum (CBM), respectively72 (eqn (2)).
is connected to the charge carriers recombination rate, since values higher than 1.5 or minor than 0.5 indicate that the charge carrier recombination is inhibited, increasing the potential of the material to redox reactions. Meanwhile, values near 1 are related to highly unstable charge carriers.67–71 Moreover, the individual values of effective mass must be evaluated as well, since overly high values hamper the charge mobility, decreasing its ability to migrate from bulk to surface and take part in redox reactions.69 The effective masses (m*) between holes and electrons were determined through a parabolic fitting of the band structure around the immediate vicinity in the reciprocal space (maximum distance of 0.1 Å) of the valence band maximum (VBM) and conduction band minimum (CBM), respectively72 (eqn (2)).
| ν = ℏk/m* | (1) |
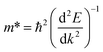 | (2) |
Both plane-wave and localized Gaussian basis set results (Table 3) indicate that there is a considerable difference between the hole and electron effective masses. This feature is fundamental in order to calculate an efficient separation of photogenerated charge carriers for a successful photocatalyst. Firstly, it is important to highlight that all methods employed yielded consistent results for effective masses. The addition of the Hubbard term in the plane-wave method ensured bandgap values closer to the experimental one. However, it also represented the band's curvature inadequately, so the high values for the Hubbard term on Ag 4d states can be considered an artificial result causing a decrease in these electronic states. The large contribution showed on top of the VB is opposite to other functionals (Fig. 2). This change in the VB composition resulted in a deep modification on the band's curvature, clarifying the discrepancy of the calculated effective mass from Hubbard term and other functionals.
| Method | Bandgap (eV) | ||||
|---|---|---|---|---|---|
| Plane-wave | PBE | 0.17 (M–G) | 1.98 | 0.39 | 5.08 |
| PBEsol | 0.29 (M–G) | 2.05 | 0.41 | 5.02 | |
| PBE+D3 | 0.17 (M–G) | 1.98 | 0.39 | 5.08 | |
| PBE+U | 2.38 (M–G) | 2.77 | 0.46 | 6.02 | |
| Localized Gaussian basis sets | PBE | 0.52 (M–G) | 0.31 | 0.10 | 3.10 |
| PBE0 | 2.97 (M–G) | 0.29 | 0.11 | 2.64 | |
| B3LYP | 2.55 (M–G) | 0.30 | 0.11 | 2.73 | |
| B3LYP+Grimme | 2.53 (M–G) | 0.29 | 0.11 | 2.64 | |
Consequently, the effective mass values obtained by the PBE+U method were not reliable, which is consistent with the poor electronic description of Ag3PO4 highlighted by Kahk et al.34 The results for optical and photocatalytic properties indicate that the PBE0, B3LYP, and B3LYP+Grimme functionals represent the bulk phase of Ag3PO4 adequately. In general, the results suggest that Ag3PO4 material in bulk form presents good optical and photocatalytic properties for its application in several electronic and optoelectronic devices.73–76
Regarding the structural features from the plane-wave, it is noteworthy that the best representation was given by the PBE+D3 approach. However, this functional provided a poor description of the bandgap, as previously mentioned. The localized Gaussian basis sets using the B3LYP+Grimme approach rendered an adequate description of the structural properties. As evidenced by the results described in the previous section, Grimme's correction including van der Waals interactions played a fundamental role in the description of the structural features of Ag3PO4.
3.2. Ag3PO4: surface investigation
In order to provide a better understanding of the behavior observed through experimental efforts, a theoretical study on the surfaces of Ag3PO4 was required, especially since the structural stability of each surface is strongly related to its photocatalytic activity. Therefore, in this work, the surfaces were evaluated from DFT calculations using plane-wave basis sets as implemented in VASP. Thus, the surface stability was directly determined from the surface energy (Eisurf) calculated for each termination (i = Z+ or Z−) of the slab (eqn (3)). The cleavage energy (Eicleav) is the energy connected to the cleavage of the solid when the surface is created; the relaxed energy (Eirelax) is the relaxed slab energy. Since the surface investigation was performed in two different quantum codes, some differences were observed in the calculation. For VASP surfaces, the macroscopic dipole was canceled by dipole correction (DIPOL and LDIPOL options) and the structural relaxation was carried out considering only the first two layers of Z+ (up termination) and the last two terminations of Z− (down termination). The other layers fixed represented the bulk effect. Meanwhile, the simulations performed in CRYSTAL canceled the macroscopic dipole through a simple methodology based on slab size increase followed by the relaxation of both terminations, assuming that only the outer layers can relax, while the core layers reproduce the bulk positions.77,78| Eisurf = Eclv + Eirlx | (3) |
As reported by Kahk et al.,34 Ag3PO4 suffers photocorrosion when it acts as a photocatalyst. In this context, the exposure of the most stable termination can be expected to prolong the overall photocatalytic lifespan of the material. Likewise, the terminations with high surface energy are harder to be exposed in crystal morphologies because the crystal reconstruction impairs the photocatalytic lifespan. The values of surface energy (Esurf) and coordination number for the polarized terminations (Z+, Z−) from plane-wave are reported in Table 4. The calculated surface energies indicate that the Z+ termination of the (110) surface presents the lowest energy, while the (100) surfaces present high-energy values for both Z+ and Z− terminations, followed by the Z− termination of the (111) surface. The Z+ termination is the most stable among the surfaces evaluated. Therefore, it can be expected that the Z+ termination of the (110) surface should be more easily exposed in the crystal morphology, showing high resistance to the reconstruction process. This result highlights the fact that the (110) facet overall might be a promising one.
| Termination | Eisurf (J m−2) | Coordination number | |||
|---|---|---|---|---|---|
| Ag | P | VO | |||
| (100) | Z+ | 1.85 | 4 | 4 | — |
| Z− | 2.67 | 2 | 2 | 2 | |
| (110) | Z+ | 0.36 | 2 | 4 | 2 |
| Z− | 1.32 | 4 | 3 | 1 | |
| (111) | Z+ | 1.21 | 4 | 4 | — |
| Z− | 2.28 | 2 | 1 | 3 | |
In order to connect the high energy surface with the crystal reconstruction effect, we analyzed the local coordination of the atoms at the exposed layers of the surface. Such miss-coordination is a molecular region with high photocatalytic potential for the activation of adsorbate molecules.32,79 The low coordination numbers indicate a higher tendency of the miss-coordinated atoms to interact with approaching molecules aiming to complete the coordination number and, consequently, balance such deficiency (presence of O vacancies). Thus, the full-relaxed structure of all surfaces can be analyzed to determine the surface availability for the activation of general reactions. In Table 4, the Ag atoms in the Z+ termination of the (110) surface are in two-coordinated sites with two O vacancies (VO), that is, they are grouped in [AgO2] clusters. The Z+ terminations of the (111) and (100) surfaces, on the other hand, [AgO3] and [AgO4] clusters, respectively. In the latter, the coordination of Ag atoms is complete as in the bulk. The Z+ (110) termination, in turn, can be said to be the most promising one because of the combination of high stability and high reactive potential.
Given the fact that this study focuses on the photocatalytic potential of Ag3PO4, the electronic properties of surfaces are an important aspect to delve into. The results from the plane-wave methodology show conductor-type bandgaps for the (100), (110), and (111) surfaces. Such results have a low connection with the behavior reported experimentally. Similarly, the localized Gaussian basis set approach was not able to obtain converged models due to the high macroscopic moment on the surfaces. Thus, in order to present some valuable information about the photocatalytic potential of Ag3PO4 in different directions, we performed effective mass calculations for charge carriers considering the k-points along the [100], [110] and [111] directions in the bulk. The results are reported in Table 5 and they show the [110] orientation as the preferable one due to its effective masses, which presented the lowest results.
A comparative analysis of the electrostatic potential of the different surfaces of a crystal was employed to estimate the charge carrier transfer and elucidate the tendencies of the carriers' concentration throughout the crystalline structure, making it possible to state which facets are the most indicated to act as oxidative and reductive centers.80 The work function (ϕ) can be calculated as the difference between the potential converged at the vacuum (Evac) and the Fermi level (Ef) (eqn (4)).
| ϕ = Evac − Ef | (4) |
The calculated ϕ for the Z+ terminations suggests that the (100) surface presents the highest work function (7.679 eV), while the (110) and (111) surfaces have similar values (5.412 eV and 5.570 eV, respectively). Thus, it can be expected that the photogenerated electrons migrate preferentially to the (110) and (111) surfaces, becoming promising reductive centers throughout the crystal. On the other hand, the holes can be expected to be found in the (100) facet, which is an oxidative center. Hence, the work function analyses suggested the occurrence of a charge gradient throughout the crystal, promoting the migration of the hole (positive) and electron (negative) carriers to distinct facets. Such migration activates some chemical reactivity on specific surfaces. Over time, this should give rise to an internal electric field after electronic excitation, which contributes to the charge separation.
Finally, we notice that the results of this work may serve as a starting point to rationalize the formation of metallic Ag nanostructures81 and thick film82 on Ag3PO4 surfaces induced by electron beam and femtosecond laser irradiation.
4. Conclusions
This study depicts a broad ab initio simulation within the framework of the density functional theory using a combination of results obtained from both a plane-waves basis set with projector augmented wave method and localized Gaussian basis sets. In summary, both methodologies represent the properties of Ag3PO4 in the bulk phase adequately. The structural features were better represented by PBE+D3 (PAW approach) and by the B3LYP hybrid functional including the Grimme correction (localized Gaussian basis sets). The electronic properties were better represented by B3LYP and PBE+U simulations. In particular, the results evidence that the Hubbard addition in PBE simulations carried out through the PAW method did not successfully represent the bands' curvature. Finally, all analyses for Ag3PO4 bulk on charge carriers' stability suggest a good photocatalytic activity.For Ag3PO4 surfaces, the calculated surface energies indicate that the Z+ termination of the (110) surface presents the lowest energy. The (100) surfaces present high-energy values for both Z+ and Z− terminations, followed by the (111) surface cut. In particular, the Z+ termination is the most stable among the surfaces evaluated. Therefore, the Z+ termination of the (110) surface can be expected to be more easily exposed in the crystal morphology, showing high resistance to the reconstruction process. From the coordination number of cations in the surface, the Z+ (110) termination can be said to be the most promising one because of the combination of high stability and high reactive potential together with good values of work functions.
Finally, the combination of two different methods in the description of atoms in DFT may prove to be very useful, offering good reliability of results at a very exciting computational cost. In this context, we highlight the low cost of localized Gaussian basis set to investigate the bulk properties and the high efficiency of plane-wave methods in VASP code to evaluate high polar surfaces, as that observed in Ag3PO4.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge support from CAPES (PNPD Program), CNPq, Fundação Araucária (Financing Project 009/2017), and the LCAD (High-Performance Computing Laboratory) from Ponta Grossa State University and their computational facilities acquired by FINEP CT-INFRA/2013 support; the Sao Paulo Research Foundation (FAPESP) for grants 2013/07296-2, 2016/23891-6 and 2020/03780-0. This work used computational resources from Centro Nacional de Processamento de Alto Desempenho em São Paulo (CENAPAD-SP), Centro de Computação John David Rogers (CCJDR-UNICAMP), and CENAPAD-RJ (SDumont). J. Andres acknowledges Universitat Jaume I for the project UJI-B2019-30 and Ministerio de Ciencia, Innovación y Universidades (Spain) project PGC2018-094417-B-I00 for supporting this work financially.References
- Z. Yi, J. Ye, N. Kikugawa, T. Kako, S. Ouyang, H. Stuart-Williams, H. Yang, J. Cao, W. Luo, Z. Li, Y. Liu and R. L. Withers, Nat. Mater., 2010, 9, 559–564 CrossRef CAS PubMed.
- T. Yan, W. Guan, Y. Xiao, J. Tian, Z. Qiao, H. Zhai, W. Li and J. You, Appl. Surf. Sci., 2017, 391, 592–600 CrossRef CAS.
- D. J. Martin, G. Liu, S. J. A. Moniz, Y. Bi, A. M. Beale, J. Ye and J. Tang, Chem. Soc. Rev., 2015, 44, 7808–7828 RSC.
- B. Liu, Y. Fang, Z. Li and S. Xu, J. Nanosci. Nanotechnol., 2015, 15, 889–920 CrossRef CAS PubMed.
- A. Durif, I. Tordjmax and R. Masse, Z. Kristallogr.–Cryst. Mater., 1976, 144, 76–81 Search PubMed.
- X. Ma, J. Yan, N. Liu, L. Zhu, B. Wang, C. Huang and H. Lü, J. Semicond., 2016, 37, 033001 CrossRef.
- A. B. Trench, T. R. Machado, A. F. Gouveia, M. Assis, L. G. da Trindade, C. Santos, A. Perrin, C. Perrin, M. Oliva, J. Andrés and E. Longo, Appl. Catal., B, 2018, 238, 198–211 CrossRef CAS.
- J. J. Liu, X. L. Fu, S. F. Chen and Y. F. Zhu, Appl. Phys. Lett., 2011, 99, 191903 CrossRef.
- Y. Huang, T. Ma, Q.-y. Chen, C. Cao and Y. He, Sci. Rep., 2015, 5, 12750 CrossRef CAS PubMed.
- C.-N. He, W.-Q. Huang, L. Xu, Y.-C. Yang, B.-X. Zhou, G.-F. Huang, P. Peng and W.-M. Liu, Sci. Rep., 2016, 6, 22267 CrossRef CAS PubMed.
- P. Reunchan and N. Umezawa, J. Phys. Chem. C, 2015, 119, 2284–2289 CAS.
- Z. Ma, Z. Yi, J. Sun and K. Wu, J. Phys. Chem. C, 2012, 116, 25074–25080 CrossRef CAS.
- J. F. Cruz-Filho, T. M. S. Costa, M. S. Lima, L. J. Silva, R. S. Santos, L. S. Cavalcante, E. Longo and G. E. Luz, J. Photochem. Photobiol., A, 2019, 377, 14–25 CrossRef CAS.
- Q. Liu, N. Li, Z. Qiao, W. Li, L. Wang, S. Zhu, Z. Jing and T. Yan, Front. Chem., 2019, 7, 866 CrossRef CAS PubMed.
- F. Opoku, K. K. Govender, C. G. C. E. van Sittert and P. P. Govender, Adv. Sustainable Syst., 2017, 1, 1700006 CrossRef.
- V. Geissen, H. Mol, E. Klumpp, G. Umlauf, M. Nadal, M. van der Ploeg, S. E. A. T. M. van de Zee and C. J. Ritsema, Int. Soil Water Conserv. Res., 2015, 3, 57–65 CrossRef.
- M. Xie and T. Zhang, J. Mater. Sci., 2019, 55, 3974–3990 CrossRef.
- W. Lin, S. Zhang, D. Wang, C. Zhang and D. Sun, Ceram. Int., 2015, 41, 8956–8963 CrossRef CAS.
- T. Hisatomi and K. Domen, Nat. Catal., 2019, 2, 387–399 CrossRef CAS.
- H. Zhang, H. Huang, H. Ming, H. Li, L. Zhang, Y. Liu and Z. Kang, J. Mater. Chem., 2012, 22, 10501–10506 RSC.
- P. Dong, Y. Wang, H. Li, H. Li, X. Ma and L. Han, J. Mater. Chem. A, 2013, 1, 4651–4656 RSC.
- G.-F. Huang, Z.-L. Ma, W.-Q. Huang, Y. Tian, C. Jiao, Z.-M. Yang, Z. Wan and A. Pan, J. Nanomater., 2013, 2013, 371356 Search PubMed.
- M. Ge, N. Zhu, Y. Zhao, J. Li and L. Liu, Ind. Eng. Chem. Res., 2012, 51, 5167–5173 CrossRef CAS.
- W. Wang, B. Cheng, J. Yu, G. Liu and W. Fan, Chem.–Asian J., 2012, 7, 1902–1908 CrossRef CAS PubMed.
- Y. Bi, S. Ouyang, J. Cao and J. Ye, Phys. Chem. Chem. Phys., 2011, 13, 10071–10075 RSC.
- Y. Bi, H. Hu, S. Ouyang, G. Lu, J. Cao and J. Ye, Chem. Commun., 2012, 48, 3748–3750 RSC.
- D. J. Martin, N. Umezawa, X. Chen, J. Ye and J. Tang, Energy Environ. Sci., 2013, 6, 3380–3386 RSC.
- X. Chen, Y. Dai and X. Wang, J. Alloys Compd., 2015, 649, 910–932 CrossRef CAS.
- S. Podder, S. Halder, A. Roychowdhury, D. Das and C. K. Ghosh, J. Nanopart. Res., 2016, 18, 294 CrossRef.
- L. Liu, J. Liu and D. D. Sun, Catal. Sci. Technol., 2012, 2, 2525–2532 RSC.
- R. Panigrahi, S. Panda, P. K. Behera, S. K. Sahu and L. Rout, New J. Chem., 2019, 43, 19274–19278 RSC.
- Y. Bi, S. Ouyang, N. Umezawa, J. Cao and J. Ye, J. Am. Chem. Soc., 2011, 133, 6490–6492 CrossRef CAS PubMed.
- G. Botelho, J. Andres, L. Gracia, L. S. Matos and E. Longo, ChemPlusChem, 2016, 81, 202–212 CrossRef CAS PubMed.
- J. M. Kahk, D. L. Sheridan, A. B. Kehoe, D. O. Scanlon, B. J. Morgan, G. W. Watson and D. J. Payne, J. Mater. Chem. A, 2014, 2, 6092–6099 RSC.
- N. Umezawa, O. Shuxin and J. Ye, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 035202 CrossRef.
- H. Zhai, T. Yan, P. Wang, Y. Yu, W. Li, J. You and B. Huang, Appl. Catal., A, 2016, 528, 104–112 CrossRef CAS.
- X. Cao, X. Zhang, R. Sinha, S. Tao and A. Bieberle-Hütter, Phys. Chem. Chem. Phys., 2019, 21, 9531–9537 RSC.
- X. Li, P. Xu, M. Chen, G. Zeng, D. Wang, F. Chen, W. Tang, C. Chen, C. Zhang and X. Tan, Chem. Eng. J., 2019, 366, 339–357 CrossRef CAS.
- A. McLaren, T. Valdes-Solis, G. Li and S. C. Tsang, J. Am. Chem. Soc., 2009, 131, 12540–12541 CrossRef CAS PubMed.
- F. Seker, K. Meeker, T. F. Kuech and A. B. Ellis, Chem. Rev., 2000, 100, 2505–2536 CrossRef CAS PubMed.
- X. Han, Q. Kuang, M. Jin, Z. Xie and L. Zheng, J. Am. Chem. Soc., 2009, 131, 3152–3153 CrossRef CAS PubMed.
- J. Raudoniene, R. Skaudzius, A. Zarkov, A. Selskis, O. Karlsson, A. Kareiva and E. Garskaite, Powder Technol., 2019, 345, 26–34 CrossRef CAS.
- R. Guo, Y. Fan and Y. Tang, RSC Adv., 2017, 7, 23977–23981 RSC.
- H. Wang, L. He, L. Wang, P. Hu, L. Guo, X. Han and J. Li, CrystEngComm, 2012, 14, 8342–8344 RSC.
- J. Wang, F. Teng, M. Chen, J. Xu, Y. Song and X. Zhou, CrystEngComm, 2013, 15, 39–42 RSC.
- M. Li, M. Chen, J. Wang and F. Teng, CrystEngComm, 2014, 16, 1237–1240 RSC.
- M. Batvandi, A. Haghighatzadeh and B. Mazinani, Appl. Phys. A: Mater. Sci. Process., 2020, 126, 571 CrossRef CAS.
- H. N. Ng, C. Calvo and R. Faggiani, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1978, 34, 898–899 CrossRef.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- C. L. Fu and K. M. Ho, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 5480–5486 CrossRef CAS.
- J. D. Pack and H. J. Monkhorst, Phys. Rev. B: Solid State, 1977, 16, 1748–1749 CrossRef.
- J. P. Perdew, Int. J. Quantum Chem., 1985, 28, 497–523 CrossRef.
- B. Himmetoglu, A. Floris, S. de Gironcoli and M. Cococcioni, Int. J. Quantum Chem., 2014, 114, 14–49 CrossRef CAS.
- R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D'Arco and M. Llunell, CRYSTAL09 User's Manual, University of Torino, Torino, 2009 Search PubMed.
- R. Dovesi, R. Orlando, B. Civalleri, C. Roetti, V. R. Saunders and C.-M. Zicovich-Wilson, Z. Kristallogr., 2005, 220, 571–573 CAS.
- C. Pisani, R. Dovesi and C. Roetti, Hartree-Fock ab initio Treatment of Crystalline Systems, Springer Berlin Heidelberg, 1988 Search PubMed.
- E. Aprà, E. Stefanovich, R. Dovesi and C. Roetti, Chem. Phys. Lett., 1991, 186, 329–335 CrossRef.
- C. M. Zicovich-Wilson, A. Bert, C. Roetti, R. Dovesi and V. R. Saunders, J. Chem. Phys., 2001, 116, 1120–1127 CrossRef.
- M. D. Towler, N. L. Allan, N. M. Harrison, V. R. Saunders, W. C. Mackrodt and E. Aprà, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 5041–5054 CrossRef CAS PubMed.
- A. M. Ferrari and C. Pisani, J. Phys. Chem. B, 2006, 110, 7909–7917 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- J. Yu, P. Zhou and Q. Li, Phys. Chem. Chem. Phys., 2013, 15, 12040–12047 RSC.
- P. Zhou, J. Yu and Y. Wang, Appl. Catal., B, 2013, 142–143, 45–53 CrossRef CAS.
- X. Ma, Y. Dai, M. Guo and B. Huang, ChemPhysChem, 2012, 13, 2304–2309 CrossRef CAS PubMed.
- G. B. Soares, R. A. P. Ribeiro, S. R. de Lazaro and C. Ribeiro, RSC Adv., 2016, 6, 89687–89698 RSC.
- L. H. S. Lacerda and S. R. de Lazaro, J. Photochem. Photobiol., A, 2020, 400, 112656 CrossRef CAS.
- P. Reunchan, A. Boonchun and N. Umezawa, Phys. Chem. Chem. Phys., 2016, 18, 23407–23411 RSC.
- J. Jian, G. Jiang, R. van de Krol, B. Wei and H. Wang, Nano Energy, 2018, 51, 457–480 CrossRef CAS.
- X. Li and J. Yang, Natl. Sci. Rev., 2016, 3, 365–381 CrossRef CAS.
- H. Pan, Renewable Sustainable Energy Rev., 2016, 57, 584–601 CrossRef CAS.
- T. L. Bahers, M. Rérat, P. Sautet, U. D. Lyon, U. Claude, B. Lyon, E. N. S. Lyon, C. N. De, R. Scientifique and L. Cedex, J. Phys. Chem. C, 2014, 118, 5997–6008 CrossRef CAS.
- Y. Dai, Q. Gao, C. Cui, L. Yang, C. Li and X. Li, Mater. Res. Bull., 2018, 99, 424–428 CrossRef CAS.
- J.-Q. Dai, J.-W. Xu and J.-H. Zhu, ACS Appl. Mater. Interfaces, 2017, 9, 3168–3177 CrossRef CAS PubMed.
- M. R. D. Bomio, R. L. Tranquilin, F. V. Motta, C. A. Paskocimas, R. M. Nascimento, L. Gracia, J. Andres and E. Longo, J. Phys. Chem. C, 2013, 117, 21382–21395 CrossRef CAS.
- S. Bai, J. Jiang, Q. Zhang and Y. Xiong, Chem. Soc. Rev., 2015, 44, 2893–2939 RSC.
- C. C. dos Santos, M. de Assis, T. R. Machado, P. F. dos Santos Pereira, G. Minguez-Vega, E. Cordoncillo, H. Beltran-Mir, C. Doñate-Buendía, J. Andrés and E. Longo, Part. Part. Syst. Charact., 2019, 36, 1800533 CrossRef.
- J. P. d. C. d. Costa, M. Assis, V. Teodoro, A. Rodrigues, C. Cristina de Foggi, M. A. San-Miguel, J. P. Pereira do Carmo, J. Andrés and E. Longo, RSC Adv., 2020, 10, 21745–21753 RSC.
| This journal is © The Royal Society of Chemistry 2020 |