Searching for double σ- and π-aromaticity in borazine derivatives

Abstract

Inspired by the double-aromatic (σ and π) C₆H₃⁺, C₆I₆²⁺, and C₆(SePh)₆²⁺ ring-shaped compounds, herein we theoretically study their borazine derivative analogues. The systems studied are the cation and dications with formulas B₃N₃H₃⁺, B₃N₃Br₆²⁺, B₃N₃I₆²⁺, B₃N₃(SeH)₆²⁺, and B₃N₃(TeH)₆²⁺. Our DFT calculations indicate that the ring-shaped planar structures of B₃N₃H₃⁺, B₃N₃I₆²⁺, and B₃N₃(TeH)₆²⁺ are more stable in the singlet state, while those of B₃N₃Br₆²⁺ and B₃N₃(SeH)₆²⁺ prefer the triplet state. Besides, exploration of the potential energy surface shows that the ring-shaped structure is the putative global minimum only for B₃N₃I₆²⁺. According to chemical bonding analysis, B₃N₃H₃⁺, B₃N₃I₆²⁺, and B₃N₃(TeH)₆²⁺ have σ and π delocalized bonds. The number of delocalized σ/π electrons is 2/6 for the first, and 10/6 for the second and third, similar to what their carbon analogs exhibit. Finally, the analysis of the magnetically induced current density allows B₃N₃H₃⁺, B₃N₃I₆²⁺, and B₃N₃(TeH)₆²⁺ to be classified as strongly σ aromatic, and poorly π aromatic compounds.

---

Introduction

In 1979, Schleyer and co-workers introduced the concept of double aromaticity. They showed that the 3,5-dehydrophenyl cation (1, Scheme 1) exhibits two orthogonal Hückel frameworks, consisting of 6π and 2σ electrons.¹ Since then, many compounds exhibiting double aromaticity have been predicted theoretically,^2–11 with some even being experimentally characterized.^12–17 For instance, in 1988, Martin and Sagl¹⁵ reported the synthesis of the hexaiodobenzene dication, C₆I₆²⁺ (2, Scheme 1), a double-aromatic compound with two concentric delocalization circuits, consisting of 6π electrons delocalized around the C₆ ring, and 10σ electrons delocalized around the I₆ ring. This finding paved the way to synthesize and characterize, by X-ray diffraction, the first double-aromatic “bench-stable” molecule, the hexakis(phenylselenyl)benzene dication¹⁶ (3, Scheme 1).

Scheme 1 Structures of double-aromatic benzene derivatives (1–3) and their borazine derivative analogues. Dashed lines represent the σ delocalization circuits.

Here we evaluate the structure, stability, chemical bonding, and magnetic response properties of B₃N₃H₃⁺, B₃N₃Br₆²⁺, B₃N₃I₆²⁺, B₃N₃(SeH)₆²⁺ and B₃N₃(TeH)₆²⁺ (4, 5, 6, 7 and 8, Scheme 1) systems in pursuit of expanding the family of double-aromatic compounds.

As we can see in Scheme 1, compounds 4–8 are analogues to the double-aromatic benzene derivatives referred above (1, 2 and 3, Scheme 1), where C₆ is replaced by the B₃N₃ ring. It is important to note that the aromatic character of borazine has been a much-debated topic in the past with contrasting conclusions.^18–27 There is even disagreement among studies based on the same criteria, i.e. magnetic. For instance, various studies have evaluated current density maps, both global and dissected (σ and π), and concluded that borazine does not support a net diatropic current (aromaticity indicator) around the B₃N₃ ring. Instead, it displays three local π delocalization pathways (around the N atoms).^18–20 Given the large difference in electronegativity between the two participating elements, Δχ(N,C) = 1.0,²⁸ it sounds reasonable that the π electrons are more polarized to the N atoms. However, analysis of both the induced magnetic field^26,27 and the intensity of the ring current strengths (RCS)^23,24,26 suggests that borazine does sustain a net diatropic ring current (less intense than that of benzene). Given these discrepancies, why would we assume that the compounds 4–8, in this work, would have a double aromatic character? Our answer is based on the quantitative analyses on the aromaticity of borazine available in the literature. The most modern analyses, based on the energetic criteria (aromatic stabilization energy, ASE), agree that the aromaticity of borazine is at least 20% benzene's.^21,22,26 For instance, Baranac-Stojanović et al. reported extra cyclic resonance energy (ECRE) values, at B3LYP/6-311+G(d,p) level, of 89.35 and 20.18 kcal mol⁻¹ for benzene and borazine, respectively.²² Furthermore, in 2013, our group estimated that the aromaticity of borazine is about 30% benzene's, according to the energetic and magnetic criteria.²⁶ The first one, using isodesmic reactions to estimate ASEs, and the second one, through the analysis of three properties: the induced magnetic field, the nucleus independent chemical shift (NICS) and the RCS. These results contrast slightly with RCSs of benzene and borazine (12.8 and 2.1 nA T⁻¹), calculated at RHF level, by Monaco et al.²⁹ However, they agree with both RCS values for benzene and borazine reported most recently by Monaco et al. (11.8 and 3.0 nA T⁻¹)²³ and with our current calculations (11.8 and 3.6 nA T⁻¹). Under this energetic and magnetic evidences, we consider that the B₃N₃ ring, of the systems studied here, should sustain at least a slight π-aromatic character. The latter, together with the fact that the chemistry of borazine, and its derivatives, is well established,^30–32 supports our proposal of compounds 4–8, as potential aromatic derivatives of borazine.

Computational details

In order to evaluate the stability, chemical bonding and aromatic character of the proposed systems, we used the following methodologies:

(a) The potential energy surface (PES) of systems, 4, 6 and 8, was explored via the AUTOMATON program.³³ This program uses a probabilistic automaton method to generate an initial population that evolves to the best individual (global minimum, GM) through genetic operations. The searches were performed via the PBE0 ³⁴ functional in conjunction with the SDDALL^35,36 basis. The low-lying structures were subsequently re-minimized at the PBE0-D3 ³⁷/def2-TZVP³⁸ level. We used an initial population of 5X (X = number of atoms of the system), this small population showed to be enough to successfully identify the lowest energy structures of many clusters and molecules.^39–43 Additionally, we evaluated the dynamic behavior of compounds 4, 6 and 8 (for an insight into their kinetic stability), employing Born–Oppenheimer molecular dynamic (BOMD) simulations.⁴⁴ Geometry optimizations, vibrational frequency and BOMD calculations were carried out using the Gaussian 16 program.⁴⁵

(b) Chemical bonding was analyzed through the adaptive natural density partitioning (AdNDP) method,^46,47 which is an extension of the natural bond orbital (NBO) analysis.^48–50 AdNDP allows for electronic density partitioning of a molecular system in terms of n-center two-electron (nc-2e) bonds, with n ranging from one to the total number of atoms in the molecule. Thus, AdNDP recovers the Lewis elements (lone pairs, and 2c-2e bonds), as well as the delocalized nc-2e bonds. Therefore, the number of nc-2e (n > 2) delocalized bonds allows to classify a system as aromatic (4N + 2) or anti-aromatic (4N), following Hückel's rule.^51–53

(c) The aromatic character was also assessed through the magnetic criteria. Current density maps, induced by an external magnetic field, were calculated for this purpose. These maps allowed us to easily observe the diatropicity/paratropicity of the examined systems, and to correlate these magnetic patterns with their aromatic/antiaromatic character.^54–56 Additionally, the ring current flow was integrated to estimate the ring current strength (RCS) and to use it as a quantitative criterion for aromaticity.^57–59 In general, a positive and a negative RCS value indicate an aromatic and an anti-aromatic character, respectively. Similarly, the larger the absolute value of the RCS, the higher the (anti) aromatic character of the studied molecule. However, it is more difficult to establish an exact RCS value for nonaromatic systems. The value must be close to zero, but how close? To answer this, we need to compare them with suitable references. In this paper, we have calculated the RCSs of a series of five-member C₄XH₄ rings, for which Mo and Schleyer reported their “extra cyclic resonance energy” (ECRE) to characterize and measure the extra stabilization (aromaticity).⁶⁰ ECRE was computed using block-localized wave function (BLW) method⁶¹ and adequate isodesmic reactions. The simple linear correlation of the RCSs vs. ECREs is excellent (r² = 0.97). Furthermore, using the linear equation of this correlation, a value of 0 kcal mol⁻¹ ECRS (nonaromatic) would correspond to an RCS value of 0.88 nA T⁻¹ (see Table S1 and Scheme S1 in the ESI†). This analysis allows us to consider RCS values higher than 1.5 nA T⁻¹ here, as indicative of aromatic character. In addition, our group has shown that RCS correlates very well with NICS, when the latter are measured properly.^62–65

Results and discussion

We began by analyzing compound 4, which is not the global minimum on the B₃N₃H₃⁺ PES, but it lies at 49.3 kcal mol⁻¹ above the lowest singlet state energy structure at PBE0 ³⁴-D3 ³⁷/def2TZVP level.³⁸ However, 4 is a true minimum on its PES since all its vibrational frequencies are positive. The 22 lowest singlet state energy structures of B₃N₃H₃⁺, identified by the AUTOMATON program, are reported in Fig. S1.† It is important to note that AUTOMATON did not identify structure 4, since this program focuses on identifying the GM structure. However, AUTOMATON allowed discarding 4 as the putative GM.

Interestingly, the structure of 4 is similar to that of its analog 1. As with the carbon angles bearing no hydrogens at 1, the angle widens in the boron of compound 4. The optimized structure at PBE0-D3/def2TZVP level shows angles NBN to be 167°. The B–B Wiberg bond index (WBI)^66,67 (0.45|e| at PBE0-D3/def2TZVP level) is similar, to that obtained for the dehydrogenated carbon atoms in 1, which according to Schleyer, has a σ 3c-2e delocalized bond. This result supports a possible in-plane 3c-2e σ-bonding interaction involving the B₃ ring.

According to the AdNDP results reported in Fig. 1, the 26 valence electrons (13 pairs) are distributed in 6 classical B–N σ-bonds (2c-2e) and 3 classical N–H σ-bonds. All other bonds are delocalized. There are three 6c-2e π-bonds (involving the B₃N₃ ring), and one 3c-2e σ-bond (involving the B₃ ring). These results agree with the WBI predictions. Note that 6π/2σ electron counting all conform to the (4n + 2) Hückel rule, providing further support for the double-aromatic character of 4. Interestingly, AdNDP predicts that chemical bonding in compound 4 is similar to that in 1, the 3,5 dehydrophenyl cation (C₆H₃⁺; Fig. 1b).

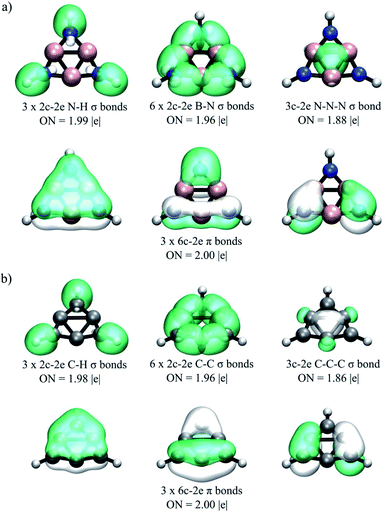Fig. 1 AdNDP bonding pattern of (a) B₃N₃H₃⁺ (4) as compared to that of (b) C₆H₃⁺ (1). Occupation numbers (ONs) are shown.

Fig. 2 depicts the magnetically induced current densities calculated in planes located at 1 a₀ (1 bohr) above the molecular plane of 4 (1 is also included for comparison). The ring current strength (RCS) was computed by integrating the ring current flux that passes along interatomic surfaces defined by the quantum theory of atoms in molecules (QTAIM).^58,59 Diatropic currents are assumed to circle clockwise, and the paratropic ones to circle anticlockwise. The current density map of 4 exhibits two diatropic ring currents (one σ and one π) distributed around the molecular ring (Fig. 2a and b). As expected, compound 1 also exhibits diatropic σ and π ring currents (Fig. 2c and d) with a σ-current flow distribution pattern similar to 4. However, π ring current flow patterns are different for 1 and 4: the ring current is continuous and clearly noticeable at 1, but at 4, there are two types of current, the diatropic local one on each nitrogen atom, and the ring current. Since the local is stronger than the ring current, the pattern for 4 does not exhibit the same continuity as in 1. How intense are these current flows, and therefore, how aromatic is system 4? The σ-RCS/π-RCS value of 5.4/1.5 nA T⁻¹ predicts system 4 to be a σ-aromatic/poorly π-aromatic compound; whereas σ-RCS/π-RCS value of 11.1/9.9 nA T⁻¹ predicts system 1 to be a σ-aromatic/π-aromatic compound. This assignment is made on the basis of the reference σ-RCS/π-RCS values of 0.5/11.7 nA T⁻¹ for benzene, which is a σ-nonaromatic/strongly π-aromatic system. It is important to note that 1 is the global minimum structure for the C₆H₃⁺ combination (at the CCSD(T)-F12b/cc-pVTZ + ZPE(B3LYP/cc-pVTZ)//CCSD(T)/cc-pVTZ level).⁶⁸ Thus, in the light of our current density analysis, it is possible to suggest that the high σ and π aromatic character must be contributing to ring shaped stabilization of C₆H₃⁺. Whereas system 4, despite its substantial σ-diatropic character, is not an energetically competitive isomer.

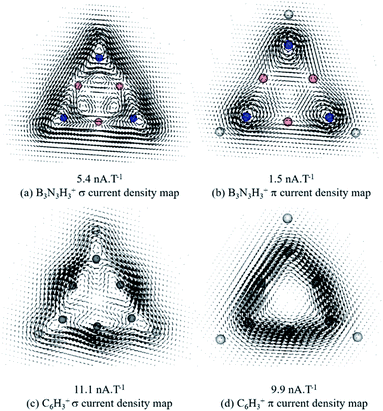Fig. 2 Vector maps of dissected magnetically induced current density (MICD) at 1 a₀ above the molecular plane of (4) B₃N₃H₃⁺ (top) and (1) C₆H₃⁺ (bottom).

We now focus on discussing our results for the set of persubstituted borazine dications, B₃N₃Br₆²⁺ (5), B₃N₃I₆²⁺ (6), B₃N₃(SeH)₆²⁺ (7) and B₃N₃(TeH)₆²⁺ (8). From this series, only structures 6 and 8 are more stable in the singlet state, while structures 5 and 7 prefer the triplet state (at PBE0-D3/def2TZVP level). Therefore, 5 and 7 are discarded as suitable candidates for double-aromatic systems.

After exploring its PES, AUTOMATON predicts 6 as the lowest energy structure for the B₃N₃I₆²⁺ combination, whereas 8 lies 68.7 kcal mol⁻¹ above the lowest energy singlet-state structure for B₃N₃(TeH)₆²⁺ combination (all structures identified by AUTOMATON within 70 kcal mol⁻¹ above the global minimum for B₃N₃(TeH)₆²⁺ are reported in Fig. S2†). It is important to note that canonical AUTOMATON procedure provided dissociated structures as the lowest energy isomers for these systems. Thus, we performed a guided search, which consists in replacing the H by I or by the Te–H fragment in the 60 lowest energy structures identified by AUTOMATON for borazine, subsequently the resulting structures were used as initial population in the AUTOMATON's PES exploration of B₃N₃I₆²⁺ and B₃N₃(TeH)₆²⁺. The second isomer of B₃N₃I₆²⁺ is the triplet-state ring shaped C_2v structure and lies 2.0 kcal mol⁻¹ above 6. Singlet and triplet isomers under 30 kcal mol⁻¹ identified by AUTOMATON for B₃N₃I₆²⁺ combination are reported in Fig. S3 and S4 in the ESI,† respectively.

At the optimized structures (at PBE0-D3/def2TZVP level) of 6 and 8, the B–N distances are 1.42 and 1.43 Å respectively, whereas I–I, and Te–Te distances are 3.49 and 3.55 Å, respectively. The WBI value for B–N in compound 6 and 8 are 0.94, very similar to the B–N WBI value in borazine, 1.02, suggesting that B₃N₃ ring in compound 6 and 8 is bonded in a similar way to the B₃N₃ ring of the borazine. On the other hand, WBI values for I–I and Te–Te bonds are both 0.13, suggesting a covalent bonding interaction between these atoms.

According to AdNDP, the bonding pattern of 6 is composed of localized and delocalized elements (Fig. 3a). The localized part is found as twelve lone pairs in the I atoms (two LPs on each one), six classical B–N 2c-2e σ-bonds, three 2c-2e B–I σ-bonds, and three 2c-2e N–I σ-bonds. The delocalized elements are found as three 6c-2e π-bonds (around the B₃N₃ ring), and five 6c-2e σ-bonds (around the I₆ ring). Thus, AdNDP analysis classifies 6 as a 6π/10σ electron system, doubly satisfying the (4n + 2) Hückel's rule, providing further support for its double-aromatic character. Note that AdNDP predicts that chemical bonding in compound 6 is similar to that in 2 (C₆I₆²⁺; Fig. 3b). Moreover, under the same analysis scheme, system 8 shows a very similar chemical bonding pattern to the one shown for system 6, as can be seen in Fig. S5 in the ESI.†

Fig. 3 AdNDP bonding pattern of (a) B₃N₃I₆²⁺ (6) as compared to that of (b) C₆I₆²⁺ (2). Occupation numbers (ONs) are shown.

Fig. 4 depicts the magnetically induced current densities calculated in planes located at 1 a₀ (1 bohr) above the molecular plane of 6 (2 is also included for comparison). The ring current strength (RCS) was computed by integrating the ring current flux that passes along C–C, B–N and I–I interatomic surfaces, defined by the quantum theory of atoms in molecules (QTAIM). The current density maps of 6 exhibit two diatropic ring currents, one outer-σ (o-σ) and intense distributed around I₆ ring, and the other inner-π (i-π) and weak distributed around B₃N₃ ring (Fig. 4a and b). Compound 2 exhibits a similar o-σ-ring current flow pattern to 6 but a different i-π ring current flow pattern, which is strong in 2. Moreover, the o-σ-RCS/i-π-RCS value of 14.3/3.4 nA T⁻¹ predicts system 6 to be a σ-aromatic/poorly π-aromatic compound, whereas o-σ-RCS/i-π-RCS value of 14.9/10.5 nA T⁻¹ predicts system 2 as a σ-aromatic/π-aromatic compound. For compound 8, a similar pattern to 6 is found, with o-σ-RCS/i-π-RCS value of 8.5/3.6 nA T⁻¹ (see Fig. S6 in the ESI†). Thus, according to ring currents, the borazine derivatives 6 and 8 are σ-aromatic and weakly π-aromatic systems.

Fig. 4 Vector maps of dissected magnetically induced current density (MICD) at 1 a₀ above the molecular plane of B₃N₃I₆²⁺ (top) and C₆I₆²⁺ (bottom).

Finally, BOMD simulations were performed to evaluate the dynamic behavior of compounds 4, 6 and 8 (Movies S1, S2 and S3 in ESI†). The corresponding movies are available in the ESI.† We found that a cyclic arrangement persists over the period of time considered for the dynamics (30 ps), at 900 K. Interestingly, the GM for the combination B₃N₃(TeH)₆²⁺ is not kinetically stable, dissociating in the first steps of the BOMD at 900 K (see Movie S4 in the ESI†). These results suggest good kinetic stability for these compounds, which in conjunction with the evidence that 6 is the putative global minimum for the B₃N₃I₆²⁺ combination, hold promise for its experimental realization.

Conclusions

In summary, we examined five double σ and π aromatic candidates with ring-shaped structures, B₃N₃H₃⁺ (4), B₃N₃Br₆²⁺(5), B₃N₃I₆²⁺(6), B₃N₃(SeH)₆²⁺ (7) and B₃N₃(TeH)₆²⁺ (8), derived by isoelectronic substitution of the C₆ ring of the parent species, C₆H₃⁺, C₆Br₆²⁺, C₆I₆²⁺ C₆(SeH)₆²⁺, and C₆(TeH)₆²⁺. From this series, only 4, 6, and 8 structures are more stable in singlet state, whereas 5 and 7 prefer the triplet state. However, the energy of 4 and 8 is 63.2 kcal mol⁻¹ and 68.7 kcal mol⁻¹ higher than that of the corresponding lowest energy singlet state structure respectively, but structure 6 is the putative global minima on its PES. Moreover, the ab initio BOMD simulations revealed that 6 and 8 structures are rather rigid, persisting over the period of time considered for the dynamics (30 ps), at 900 K. Hence, these results suggest that it might be possible to detect 6 as the thermodynamically and kinetically viable structures in the gas phase. Another promising approach would be to replace TeH by TeR ligands, to include steric protection by using bulky R-groups, considering that 8 shows reasonable kinetic stability (according to the BOMD simulations).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors are grateful for the financial support of the Fondecyt Grant No. 1181165 and Fondecyt postdoctorado No. 3180119. Powered@NLHPC: this research was partially supported by the supercomputing infrastructure of the NLHPC (ECM-02).

References

1. J. Chandrasekhar, E. D. Jemmis and P. v. R. Schleyer, Double aromaticity: aromaticity in orthogonal planes. The 3,5-dehydrophenyl cation, Tetrahedron Lett., 1979, 20, 3707–3710.
2. P. v. R. Schleyer, H. Jiao, M. N. Glukhovtsev, J. Chandrasekhar and E. Kraka, Double aromaticity in the 3,5-dehydrophenyl cation and in cyclo[6] carbon, J. Am. Chem. Soc., 1994, 116, 10129–10134.
3. S. Martín-Santamaría and H. S. Rzepa, Double aromaticity and anti-aromaticity in small carbon rings, Chem. Commun., 2000, 1503–1504.
4. M. Hofmann and A. Berndt, (π + σ)-double aromatic and π,σ-mixed aromatic boron compounds with two electrons delocalized over three centers, Heteroat. Chem., 2006, 17, 224–237.
5. M. D. Wodrich, C. Corminboeuf, S. S. Park and P. v. R. Schleyer, Double aromaticity in monocyclic carbon, boron, and borocarbon rings based on magnetic criteria, Chem.–Eur. J., 2007, 13, 4582–4593.
6. D. Y. Zubarev, B. B. Averkiev, H.-J. Zhai, L.-S. Wang and A. I. Boldyrev, Aromaticity and antiaromaticity in transition-metal systems, Phys. Chem. Chem. Phys., 2008, 10, 257–267.
7. P. W. Fowler, N. Mizoguchi, D. E. Bean and R. W. A. Havenith, Double Aromaticity and Ring Currents in All-Carbon Rings, Chem.–Eur. J., 2009, 15, 6964–6972.
8. C. Romanescu, T. R. Galeev, W. Li, A. I. Boldyrev and L. S. Wang, Aromatic Metal-Centered Monocyclic Boron Rings: Co©B8- and Ru©B9-, Angew. Chem., Int. Ed., 2011, 50, 9334–9337.
9. F. Feixas, E. Matito, J. Poater and M. Solà, Metalloaromaticity, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 105–122.
10. C. Romanescu, T. R. Galeev, W.-L. Li, A. I. Boldyrev and L.-S. Wang, Transition-metal-centered monocyclic boron wheel clusters (M©B_n): a new class of aromatic borometallic compounds, Acc. Chem. Res., 2013, 46, 350–358.
11. T. Ou, W. J. Tian, X. R. You, Y. J. Wang, K. Wang and H. J. Zhai, On the structure and bonding in the B₄O₄⁺ cluster: a boron oxide analogue of the 3,5-dehydrophenyl cation with π and σ double aromaticity, Phys. Chem. Chem. Phys., 2015, 17, 29697–29706.
12. H.-J. Zhai, B. Kiran, J. Li and L.-S. Wang, Hydrocarbon analogues of boron clusters—planarity, aromaticity and antiaromaticity, Nat. Mater., 2003, 2, 827–833.
13. A. N. Alexandrova, H.-J. Zhai, L.-S. Wang and A. I. Boldyrev, Molecular Wheel B₈²⁻ as a New Inorganic Ligand. Photoelectron Spectroscopy and ab Initio Characterization of LiB₈⁻, Inorg. Chem., 2004, 43, 3552–3554.
14. A. Van Orden and R. J. Saykally, Small carbon clusters: spectroscopy, structure, and energetics, Chem. Rev., 1998, 98, 2313–2358.
15. D. J. Sagl and J. C. Martin, The stable singlet ground state dication of hexaiodobenzene: possibly a sigma-delocalized dication, J. Am. Chem. Soc., 1988, 110, 5827–5833.
16. S. Furukawa, M. Fujita, Y. Kanatomi, M. Minoura, M. Hatanaka, K. Morokuma, K. Ishimura and M. Saito, Double aromaticity arising from σ- and π-rings, Commun. Chem., 2018, 1, 1–7.
17. A. I. Boldyrev and L.-S. Wang, All-Metal Aromaticity and Antiaromaticity, Chem. Rev., 2005, 105, 3716–3757.
18. A. Soncini, P. W. Fowler and L. W. Jenneskens, in Intermolecular Forces and Clusters I, Springer, 2005, pp. 57–79.
19. E. Steiner, P. W. Fowler and R. W. A. Havenith, Current Densities of Localized and Delocalized Electrons in Molecules, J. Phys. Chem. A, 2002, 106, 7048–7056.
20. A. Soncini and P. W. Fowler, Ipsocentric and allocentric methods of mapping induced current density, Chem. Phys. Lett., 2004, 396, 174–181.
21. I. Fernandez and G. Frenking, Direct estimate of conjugation and aromaticity in cyclic compounds with the EDA method, Faraday Discuss., 2007, 135, 403–421.
22. M. Baranac-Stojanović and M. Stojanović, Substituent effects on cyclic electron delocalization in symmetric B- and N-trisubstituted borazine derivatives, RSC Adv., 2013, 3, 24108–24117.
23. G. Monaco and R. Zanasi, The making of ring currents, Phys. Chem. Chem. Phys., 2016, 18, 11800–11812.
24. G. Monaco, R. Zanasi, S. Pelloni and P. Lazzeretti, Relative weights of σ and π ring currents in a few simple monocycles, J. Chem. Theory Comput., 2010, 6, 3343–3351.
25. R. Carion, V. Liégeois, B. Champagne, D. Bonifazi, S. Pelloni and P. Lazzeretti, On the Aromatic Character of 1,2-Dihydro-1,2-azaborine According to Magnetic Criteria, J. Phys. Chem. Lett., 2010, 1, 1563–1568.
26. J. J. Torres-Vega, A. Vásquez-Espinal, J. Caballero, M. L. Valenzuela, L. Alvarez-Thon, E. Osorio and W. Tiznado, Minimizing the Risk of Reporting False Aromaticity and Antiaromaticity in Inorganic Heterocycles Following Magnetic Criteria, Inorg. Chem., 2014, 53, 3579–3585.
27. R. Islas, E. Chamorro, J. Robles, T. Heine, J. C. Santos and G. Merino, Borazine: to be or not to be aromatic, Struct. Chem., 2007, 18, 833–839.
28. L. Pauling, The Nature of the Chemical Bond, Cornell University Press, Ithaca, NY, 1960, vol. 260.
29. M. R. Hoare and P. Pal, Physical cluster mechanics: Statics and energy surfaces for monatomic systems, Adv. Phys., 1971, 20, 161–196.
30. A. Stock and E. Pohland, Borwasserstoffe, IX.: B3N3H6, Ber. Dtsch. Chem. Ges. A, 1926, 59, 2215–2223.
31. T. Wideman and L. G. Sneddon, Convenient procedures for the laboratory preparation of borazine, Inorg. Chem., 1995, 34, 1002–1003.
32. A. H. Cowley, H. H. Sisler and G. E. Ryschkewitsch, THE CHEMISTRY OF BORAZINE. III. B-SILYL BORAZINES, J. Am. Chem. Soc., 1960, 82, 501–502.
33. O. Yañez, R. Báez-Grez, D. Inostroza, W. A. Rabanal-León, R. Pino-Rios, J. Garza and W. Tiznado, AUTOMATON: a program that combines a probabilistic cellular automata and a genetic algorithm for global minimum search of clusters and molecules, J. Chem. Theory Comput., 2019, 15, 1463–1475.
34. C. Adamo and V. Barone, Toward Reliable Density Functional Methods Without Ajustable Parameters: The PBE0 Model, J. Chem. Phys., 1999, 110, 6158.
35. A. Bergner, M. Dolg, W. Kuchle, H. Stoll and H. Preuss, Ab-Initio Energy-Adjusted Pseudopotentials for Elements of Groups 13–17, Mol. Phys., 1993, 80, 1431–1441.
36. G. Igel-Mann, H. Stoll and H. Preuss, Pseudopotentials for main group elements (IIIa through VIIa), Mol. Phys., 1988, 65, 1321–1328.
37. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H–Pu, J. Chem. Phys., 2010, 132, 154104.
38. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
39. O. Yañez, A. Vásquez-Espinal, R. Báez-Grez, W. A. Rabanal-León, E. Osorio, L. Ruiz and W. Tiznado, Carbon rings decorated with group 14 elements: new aromatic clusters containing planar tetracoordinate carbon, New J. Chem., 2019, 43, 6781–6785.
40. O. Yañez, V. García, J. Garza, W. Orellana, A. Vásquez-Espinal and W. Tiznado, (Li₆Si₅)_2–5: The Smallest Cluster-Assembled Materials based on Aromatic Si₅⁶⁻ Rings, Chem.–Eur. J., 2019, 25, 2467–2471.
41. O. Yañez, D. Inostroza, B. Usuga-Acevedo, A. Vásquez-Espinal, R. Pino-Rios, M. Tabilo-Sepulveda, J. Garza, J. Barroso, G. Merino and W. Tiznado, Evaluation of restricted probabilistic cellular automata on the exploration of the potential energy surface of Be₆B₁₁⁻, Theor. Chem. Acc., 2020, 139, 41.
42. O. Yañez, R. Báez-Grez, J. Garza, S. Pan, J. Barroso, A. Vásquez-Espinal, G. Merino and W. Tiznado, Embedding a Planar Hypercoordinate Carbon Atom into a [4n + 2] π-System, ChemPhysChem, 2020, 21, 145–148.
43. R. Báez-Grez, J. Garza, A. Vásquez-Espinal, E. Osorio, W. A. Rabanal-León, O. Yañez and W. Tiznado, Exploring the Potential Energy Surface of Trimetallic Deltahedral Zintl Ions: Lowest-Energy [Sn₆Ge₂Bi₆Ge₂Bi]³⁻ and [(Sn₆Ge₂Bi)₂] Structures, Inorg. Chem., 2019, 58, 10057–10064.
44. J. M. Millam, V. Bakken, W. Chen, W. L. Hase and H. B. Schlegel, Ab initio classical trajectories on the Born–Oppenheimer surface: Hessian-based integrators using fifth-order polynomial and rational function fits, J. Chem. Phys., 1999, 111, 3800–3805.
45. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven,K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016.
46. D. Y. Zubarev and A. I. Boldyrev, Developing paradigms of chemical bonding: adaptive natural density partitioning, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217.
47. D. Y. Zubarev and A. I. Boldyrev, Revealing intuitively assessable chemical bonding patterns in organic aromatic molecules via adaptive natural density partitioning, J. Org. Chem., 2008, 73, 9251–9258.
48. E. D. Glendening and F. Weinhold, Natural resonance theory: I. General formalism, J. Comput. Chem., 1998, 19, 593–609.
49. A. E. Reed, R. B. Weinstock and F. Weinhold, Natural population analysis, J. Chem. Phys., 1985, 83, 735–746.
50. J. P. Foster and F. Weinhold, Natural hybrid orbitals, J. Am. Chem. Soc., 1980, 102, 7211–7218.
51. E. Hückel, Quantentheoretische Beiträge zum Benzolproblem, Zeitschrift für Phys., 1931, 70, 204–286.
52. E. Hückel, Zur Quantentheorie der Doppelbindung, Zeitschrift für Phys., 1930, 60, 423–456.
53. E. Hückel, Quanstentheoretische Beiträge zum Benzolproblem, Zeitschrift für Phys., 1931, 72, 310–337.
54. J. Jusélius, D. Sundholm and J. Gauss, Calculation of current densities using gauge-including atomic orbitals, J. Chem. Phys., 2004, 121, 3952–3963.
55. D. Sundholm, H. Fliegl and R. J. F. Berger, Calculations of magnetically induced current densities: theory and applications, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 639–678.
56. J. Jusélius and D. Sundholm, Ab initio determination of the induced ring current in aromatic molecules, Phys. Chem. Chem. Phys., 1999, 1, 3429–3435.
57. T. A. Keith and R. F. W. Bader, Calculation of magnetic response properties using a continuous set of gauge transformations, Chem. Phys. Lett., 1993, 210, 223–231.
58. R. F. W. Bader and T. A. Keith, Properties of atoms in molecules: magnetic susceptibilities, J. Chem. Phys., 1993, 99, 3683–3693.
59. T. A. Keith and R. F. W. Bader, Topological analysis of magnetically induced molecular current distributions, J. Chem. Phys., 1993, 99, 3669–3682.
60. Y. Mo and P. v. R. Schleyer, An energetic measure of aromaticity and antiaromaticity based on the Pauling–Wheland resonance energies, Chem.–Eur. J., 2006, 12, 2009–2020.
61. Y. Mo and S. D. Peyerimhoff, Theoretical analysis of electronic delocalization, J. Chem. Phys., 1998, 109, 1687–1697.
62. J. J. Torres-Vega, A. Vásquez-Espinal, L. Ruiz, M. A. Fernández-Herrera, L. Alvarez-Thon, G. Merino and W. Tiznado, Revisiting Aromaticity and Chemical Bonding of Fluorinated Benzene Derivatives, ChemistryOpen, 2015, 4, 302–307.
63. A. Vásquez-Espinal, R. Pino-Rios, L. Alvarez-Thon, W. A. Rabanal-León, J. J. Torres-Vega, R. Arratia-Perez and W. Tiznado, New Insights into Re₃(μ-Cl)₃Cl₆ Aromaticity. Evidence of σ- and π-Diatropicity, J. Phys. Chem. Lett., 2015, 6, 4326–4330.
64. R. Báez-Grez, L. Ruiz, R. Pino-Rios and W. Tiznado, Which NICS method is most consistent with ring current analysis? Assessment in simple monocycles, RSC Adv., 2018, 8, 13446–13453.
65. R. Báez-Grez, D. Inostroza, V. García, A. Vásquez-Espinal, K. J. Donald and W. Tiznado, Aromatic ouroboroi: heterocycles involving a σ- donor–acceptor bond and 4n + 2π-electrons, Phys. Chem. Chem. Phys., 2020, 22, 1826–1832.
66. E. D. Glendening and F. Weinhold, Natural resonance theory: II. Natural bond order and valency, J. Comput. Chem., 1998, 19, 610–627.
67. K. B. Wiberg, Application of the Pople-Santry-Segal CNDO method to the cyclopropylcarbinyl and cyclobutyl cation and to bicyclobutane, Tetrahedron, 1968, 24, 1083–1096.
68. R. Peverati, P. P. Bera, T. J. Lee and M. Head-Gordon, Formation and Stability of C₆H₃⁺ Isomers, J. Phys. Chem. A, 2014, 118, 10109–10116.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra05939k

---