Understanding the crystal structure-dependent electrochemical capacitance of spinel and rock-salt Ni–Co oxides via density function theory calculations

Abstract

The spinel NiCo₂O₄ and rock-salt NiCoO₂ have been well established as attractive electrodes for supercapacitors. However, what is the intrinsic role of the congenital aspect, i.e., crystal structure and the surface and/or near-surface controlled electrochemical redox behaviors, if the acquired features (i.e., morphology, specific surface area, pore structure, and so on) are wholly ignored? Herein, we purposefully elucidated the underlying influences of unique crystal structures of NiCo₂O₄ and NiCoO₂ on their pseudocapacitance from mechanism analysis through the density function theory based first-principles calculations, along with the experimental validation. Systematic theoretical calculation and analysis revealed that more charge carriers near the Fermi-level, stronger affinity with OH⁻ in the electrolyte, easier deprotonation process, and the site-enriched characteristic for low-index surfaces of NiCoO₂ enable its faster redox reaction kinetics and greater charge transfer, when compared to the spinel NiCo₂O₄. The in-depth understanding of crystal structure–property relationship here will guide rational optimization and selection of appropriate electrodes for advanced supercapacitors.

---

1 Introduction

To date, supercapacitors have shown great potential for electrochemical energy storage due to their higher power density and longer lifespan than rechargeable batteries.¹ From the intrinsic energy storage mechanism point of view, supercapacitors are typically categorized into electric double-layer capacitors (EDLCs) depending upon fast ad/desorption of ions on the electrode surface, and pseudocapacitors originating from rapid faradaic redox reactions on/near the surface of the electrodes.^2,3 However, the low specific capacitances (SCs) of EDLCs, to a great extent, limit their utilization in high energy applications. As a result, enormous amounts of research have been greatly stimulated to develop high-performance electrode materials with pseudocapacitive characteristics.^4,5

Binary transition metal oxides (BTMOs) have been intensively investigated as active materials for supercapacitors due to their easy availability, environmental friendliness, and multiple oxidation states for efficient charge storage.^6,7 Especially, spinel NiCo₂O₄ and rock-salt NiCoO₂, stand out from others, owing to their more than two orders of magnitude higher electrical conductivity than their parent cobalt oxides.^8,9 In general, inherent electronic conductivity and ionic adsorption capability of abundant active sites are key points influencing electrochemical performance of pseudocapacitive electrodes, except for the acquired aspects including specific surface area (SSA) and pore structure.^10,11 Although extensive investigations into structural and/or compositional designs towards enhancing electrochemical properties of NiCo₂O₄ and/or NiCoO₂ electrodes have already been made,^6,12–17 no any reports can be retrieved to figure out which one possesses even better electrochemical activities. In fact, it is yet difficult to draw a definitive conclusion according to the previous contributions about the two for supercapacitors, since all the reported electrochemical properties are based on their different acquired characteristics (i.e., morphology/SSA/pore structure).^6,9,12–17 In this regard, a thought-provoking question comes to the fore: what is the role of the congenital aspect, i.e., crystal structures of spinel NiCo₂O₄ and rock-salt NiCoO₂, in their surface and/or near-surface controlled electrochemical redox behaviors if the aforementioned acquired features are wholly ignored? There is no doubt that the in-depth understanding of crystal structure–property relationship will render instructive insights into future optimal choice of appropriate electrodes for advanced supercapacitors.

With comprehensive considerations above in mind, herein, we elucidated the underlying influences of unique crystal structures of NiCo₂O₄ and NiCoO₂ on their pseudocapacitances from mechanism analysis through the density function theory (DFT) based first-principles calculations, along with the experimental validation. Systematic theoretical calculation and analysis revealed that more charge carriers near the Fermi-level, stronger affinity with hydroxyls in the electrolyte, easier deprotonation process, and the site-enriched characteristic for low-index surfaces of NiCoO₂ enable its faster redox reaction kinetics and more charge transfer, when compared to the spinel NiCo₂O₄. As expected, the NiCoO₂ exhibited enhanced electrochemical behaviors especially at high rates.

2 Computational methods

Spin-polarized density functional theory calculations were carried out based on the Cambridge Sequential Total Energy Package known as CASTEP,¹⁸ using the projector augmented wave (PAW) potentials.¹⁹ we used the Perdew–Burke–Ernzerhof with Hubbard U (PBE + U) form within the generalized gradient approximation (GGA) for exchange–correlation energy.^19,20 Notably, different values between U = 0 and 8 have been used in the Ni/Co compounds in the literature. Herein, we have chosen U values of 5.5 for Ni ions, and 4.5/3.3 eV for Co ions at tetrahedral/octahedral sites, respectively, to obtain the correct electronic and magnetic state of bulk NiCoO₂ and NiCo₂O₄. The number of plane wave was collected by a 500 eV. The Brillouin zones were represented by a Monkhorst–Pack mesh of 7 × 7 × 7 k-points for crystals and 3 × 3 × 1 k-points for studied surface slabs.²¹ The stoichiometric surfaces were modeled by a (1 × 1) unit cell for NiCo₂O₄ and (2 × 2) for NiCoO₂, which were separated in the z-direction by a 15 Å vacuum. The convergence criterion of Hellmann–Feynman forces and total energy were 0.015 eV Å⁻¹ and 10⁻⁵ eV, respectively. For accurate results, we compared band structures between NiCo₂O₄ and NiCoO₂ using HSE06 hybrid functional.²² To model the magnetic state of NiCo₂O₄ and NiCoO₂, we used antiparallel spins for Co and Ni atoms in NiCoO₂ due to its high Néel temperature according to Du et al.²³ In addition, the Co atoms at tetrahedral sites have antiparallel state with Ni atoms for NiCo₂O₄, where the Co ions at octahedral sites have no spin polarization due to the fully occupied t_2g states.²⁴

The surface energy (γ), was computed as γ = (E_slab − nE_bulk)/2A, where E_slab, E_bulk, n and A were the energy of the slab supercell, the bulk energy per unit cell, the number of bulk cells contained in the surface slab, and the surface area of each side for the slab, respectively. For the surface with different hydroxyl coverage, the average adsorption energy could be defined as E_ads = [E_(nOH/slab) − E_(slab) − nE_(OH)]/n.^25,26 The deprotonation energy was calculated by E_de = [E_(O/slab) − E_(nOH/slab) + 0.5nE_(H2)]/n, where E_(nOH/slab), E_(O/slab), E_(slab), E_(OH)/E_(H2) and n were the energies of the adsorbed systems, the energy of the deprotonation system, the energy of the clean surface, the energies for an isolated hydroxyl/H₂ molecules, and the number of adsorbed hydroxyls or desorbed protons, respectively. To have a profound understanding about charge transfer, the Bader charge method, where an amount of each charge was considered in the region separated by the minimum of electronic charge density between each atom, was used.^27,28

3 Results and discussion

3.1 Crystal structures

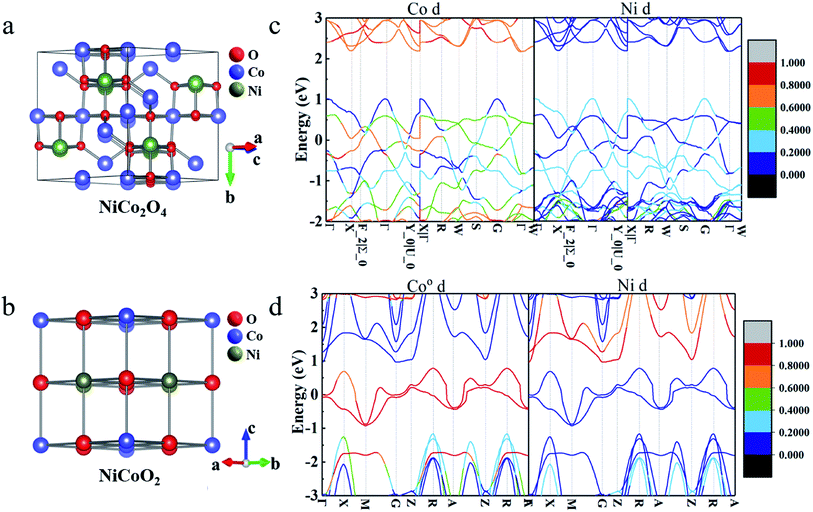
As schematically shown in Fig. 1a and b, the crystal structures of NiCo₂O₄ and NiCoO₂, typically contain 56 and 8 atoms in the unit cells, respectively. According to the site performance theory, the crystal structure of NiCo₂O₄ and NiCoO₂ can be constructed by substituting cobalt atoms located at octahedral sites in spinel Co₃O₄ and rock-salt CoO unit cells with elemental nickel, respectively.^7,24,29 Evidently, the spinel NiCo₂O₄ contains two kinds of Co atoms located at octahedrally coordinated sites (Co^o) and tetrahedrally coordinated sites (Co^t), respectively, coupled with alternating layers of –Co^o–O– and –Ni–O– along the z direction,²⁴ as described in Fig. 1a. The rock-salt NiCoO₂, as shown in Fig. 1b, only possesses the octahedral sites both for Co and Ni atoms. The optimized lattice constant values of NiCo₂O₄ and NiCoO₂ (Table S1, ESI†) are 8.22 and 4.26 Å, just with ∼1.4% and ∼0.5% error, respectively, when compared to their standard files. In addition, the computed magnetic moments of Co^t and Ni are 2.77 and −1.43 μ_B in spinel NiCo₂O₄, respectively, and 2.74 and −1.80 μ_B for Co and Ni in rock-salt NiCoO₂, which are in good agreement with the reported calculational and/or experimental values.^24,30

Fig. 1 Optimized crystallographic constructions of (a) NiCo₂O₄ and (b) NiCoO₂. Red, blue and green represent the oxygen, cobalt and nickel atoms. The contributions of d-orbital of all Co/Ni atoms to the band structure in (c) NiCo₂O₄ and (d) NiCoO₂. The energy zero is set at the Fermi-level.

3.2 Electronic properties

According to the pseudocapacitive system, the electrolyte ions diffuse from the electrolyte to the electrode/electrolyte interface under the effect of external circuit in the charging process, and then, the redox reaction occurs. Thus, the states near the Fermi-level, especially the contribution of d-orbital of metal ions, are considered to be related with the charge storage ability.^31,32 As discerned from the total band structures of NiCo₂O₄ (Fig. 1c) and NiCoO₂ (Fig. 1d), the occupied and unoccupied electronic states are visualized near the Fermi-level, favoring for their rapid electronic transport. To gain more insights into specific electronic structure around the Fermi-level, the projected band structures of d-orbital from the active Ni/Co atoms were calculated. Clearly, the bands near the Fermi-level are mainly contributed by the d-orbital of Co atoms, in which the Ni atoms contribute little. In addition, for spinel NiCo₂O₄, two kinds of atoms, i.e., Co^o and Co^t both contribute the bands near the Fermi-level (Fig. S1, ESI†), where the contribution of Co^t can be wholly negligible. One thing worth noting is that the contributions of d-orbital near the Fermi-level are greatly conducive to the enhanced electron mobility for rapid redox process of pseudocapacitive electrodes.^33,34 On account of more contributions from d-orbital of metal atoms to the bands near the Fermi-level of rock-salt NiCoO₂, it can be rationally anticipated that the NiCoO₂ will exhibit higher electroactivities than spinel NiCo₂O₄.³⁵

3.3 Charge-storage mechanism analysis

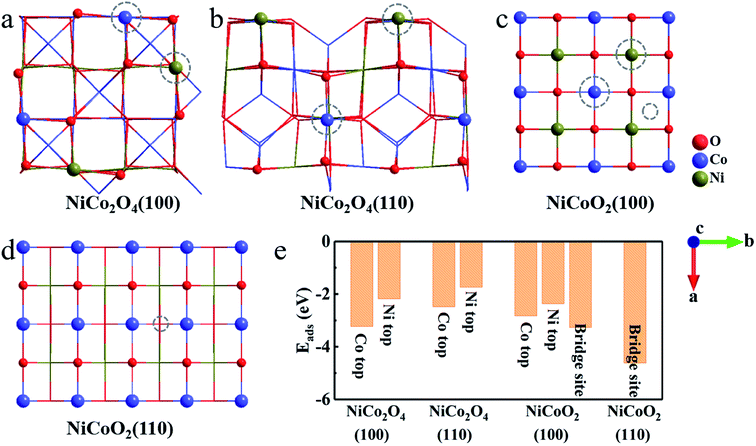
As for the surface modeling, we here consider three low-index, (100), (110) and (111), planes of NiCo₂O₄ and NiCoO₂ with the largest interplanar spacing, as they are predicted to be the most stable in the cubic crystals.^36,37 Among the three surfaces, the (111) plane, both for spinel and rock salt structure, is not truly stable surfaces, which can be expected to undergo surface reconstruction.^36,38 Therefore, we finally study the (100) and (110) surfaces. The surface energy values of (100)/(110) for NiCo₂O₄ and NiCoO₂ are 1.03/1.25 and 0.95/1.99 J m⁻², respectively. Notably, the (110) surface, both for NiCo₂O₄ and NiCoO₂, has two different stable non-polar surface configurations (Fig. 2). Accordingly, we choose the Oh(top) (Fig. 2a) of the NiCo₂O₄(110) for further calculation, since its total energy is 0.23 eV, lower than those of Th/Oh(top) (Fig. 2b) according to the DFT calculation. And the Co(top) (Fig. 2c), whose total energy is 0.66 eV, lower than that of Ni(top) (Fig. 2d), is chosen for the NiCoO₂(110). Corresponding surface lattice constants are summarized as well (Table S1, ESI†).

Fig. 2 Side views for the two kinds of (110) slabs of NiCo₂O₄: (a) Oh(top), (b) Th/Oh(top), and (110) slabs of NiCoO₂: (c) Co(top), (d) Ni(top). The Oh(top) contains only octahedral metal ions while Th/Oh(top) contains both tetrahedral and octahedral metal ions on the top surface. Co(top) and Ni(top) are Co atoms and Ni atoms on the top surface.

According to the established charge-storage mechanism of NiCo₂O₄ and NiCoO₂ in alkaline KOH solution, the pseudocapacitance always takes place as following two steps.^10,14,39,40 First, the redox reaction occurring on the exposed surface generally starts from the OH⁻ adsorption, thus leading to the formation of *OH species. And then, the reaction of adsorbed *OH with the OH⁻ in the solution partially forms the adsorbed *O species, and releases a H₂O molecule meanwhile, which is generally ascribed as a deprotonation process. Since the pseudocapacitance originates from the fast redox reactions through the chemisorption of electrolyte ions, the binding energy can act as one of the descriptors for evaluating electrochemical performance. After simple analysis, there are two kinds of stable adsorbed sites, that is, the top sites of Co and Ni atoms both in (100) and (110) surfaces of NiCo₂O₄ (Fig. 3a and b). For the case of NiCoO₂(100), the OH⁻ can be adsorbed stably both on the top sites of Ni/Co and bridge site between them (Fig. 3c). In contrast, the OH⁻ adsorbs only on the bridge site of two Co atoms in NiCoO₂(110) (Fig. 3d). As collected in Fig. 3e, the binding energy between hydroxyls and active surfaces of NiCo₂O₄/NiCoO₂ is an exothermic and spontaneous process, due to their negative adsorption energy. The Co sites in NiCo₂O₄ display stronger absorption capacity for OH⁻ on both two surfaces, as indicated by even more negative E_ads for (100) (−3.23 eV) and (110) (−2.48 eV) than those of Ni sites (−2.18 and −1.74 eV) (Fig. S2a–d, ESI†). As regards the NiCoO₂(100), the bridge site between Co and Ni (Fig. S2e, ESI†) is a more preferred site, which shows the E_ads of −3.26 eV for OH⁻, lower than those at the top of single Co (−2.83 eV) and Ni (−2.37 eV) ions (Fig. S2f and g, ESI†). The NiCoO₂(110) shows the most negative E_ads of −4.62 eV when adsorbed on the bridge site between two Co atoms (Fig. S2h, ESI†). Clearly, compared with those of NiCo₂O₄, the (100) and (110) surfaces of NiCoO₂ both exhibit more negative E_ads in the case of low coverage (Fig. 3e), which indeed favors for high faradaic reaction kinetics, thanks to the fast and stable OH⁻ adsorption on the two surfaces.

Fig. 3 Top view of the (a) NiCo₂O₄(100); (b) NiCo₂O₄(110); (c) NiCoO₂(100) and (d) NiCoO₂(110). The dotted circles represent the stable adsorbed sites for hydroxyl. (e) Corresponding energy analysis for hydroxyl adsorption at different sites.

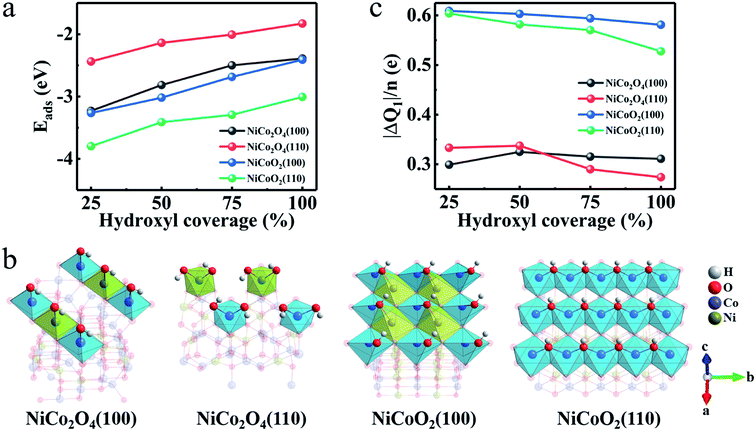
Then, we investigate how OH⁻ pattern varies when its coverage is changed. Fig. 4a presents the E_ads as function of hydroxyl coverage for the most stable adsorption sites of the NiCo₂O₄ and NiCoO₂. It's clear that the E_ads decreases as the hydroxyl coverage increases for both the (100) and (110) surfaces due to the gradual saturation of the surface. The E_ads values of the (100)/(110) surfaces for NiCoO₂ are larger than those of NiCo₂O₄ at all values of hydroxyls coverage. Corresponding relaxation configurations (Fig. S3a–d, ESI†) are summarized as well. According to the coordination configurations of the surface atoms, the Ni/Co atoms display octahedral coordination geometry when the OH⁻ coverage is full (Fig. 4b). Evidently, two hydroxyls are adsorbed on each Ni and Co sites in NiCo₂O₄(110) due to two oxygen atoms loss in the coordination of octahedral Ni and Co.

Fig. 4 (a) Hydroxyl adsorbed energy (E_ads) at different hydroxyl coverage. (b) Coordination configurations at full coverage of all studied surfaces. (c) Charge transfer (ΔQ₁) at different hydroxyl coverage.

Besides the binding ability between electrode surfaces and electrolyte ions, a superior electrode material fundamentally requires rich active sites and high electron-donating capability,³⁵ which are always related to the charge transfer originating from the hydroxyl adsorption. From the lattice constants aforementioned (Table S1, ESI†), the exposed surfaces of NiCoO₂ own higher concentration of active atoms (CAAs) of Ni and Co, which will bond directly to the hydroxyls in the reaction process. The CAAs are calculated as ∼11.02 and ∼7.57 atoms per nm for (100) and (110) surfaces of NiCoO₂, respectively, approximately twice of those for (100) (5.92 atoms per nm) and (110) (4.19 atoms per nm) of NiCo₂O₄ (Fig. S4a, ESI†). Therefore, the preponderant reaction surface of NiCoO₂ promotes a greater proportion of Ni and Co atoms involved in electrochemical reactions, which would provide high electron-donating capability. By performing the calculations on charge density difference (Fig. S4b–e, ESI†), we can deduce that most electrons tend to transfer from electrodes to hydroxyls when the Ni/Co TMOs are charged, indicating that the adsorption process is an oxidation process of surface metal atoms. We further explore the charge transfer (ΔQ₁) versus the hydroxyl coverage according to the Bader charge analysis (Fig. 4c). The average charge values (ΔQ₁/n), that is the adsorbed OH⁻, obtained on the NiCoO₂(100) and (110) surfaces are larger than those in the NiCo₂O₄(100) and NiCo₂O₄(110) at any hydroxyl coverage. It confirms a tendency that a better electron donation of surface Ni/Co atoms ensures their higher oxidation states. All analysis above therefore can deduce the exceptionally high pseudocapacitance of the rock-salt NiCoO₂ in alkaline KOH electrolyte.

The deprotonation process can be described as MOOH + OH⁻ ↔ MO₂ + H₂O (M is Co or Ni). However, the general observation is that the deprotonation process cannot occur at octahedral coordinate Ni ions, at the limited work potential window for supercapacitors, due to the higher transition potential than that of Co ions.^40,41 As shown in Fig. 5, the deprotonation, is a relatively unfavorable process compared to adsorption process due to the high deprotonation energy values (E_de), which means that the reaction involved in the second step needs even higher driving force. The DFT calculation also authenticates that the E_de values on (100) (1.72 eV) and (110) (1.70 eV) surfaces of NiCoO₂ are lower than those of NiCo₂O₄, i.e., 2.65/2.22 eV for the (100)/(110) surfaces (Fig. 5b). Hence, the formed *OH has much more opportunities to desorb protons from the surfaces of NiCoO₂ than the NiCo₂O₄ to form *O. While, there are more electrons transfer from electrodes to adsorbed molecules due to the deprotonation process, which demonstrates that the surface/subsurface metal atoms are further oxidized. But for NiCoO₂(100), the number of charge transfer decreases after hydrogen desorption, which is related to the fact that the adsorption sites deviate from the bridge sites to the top of cobalt, decreasing the charge donation of nickel atoms (Fig. 5c).

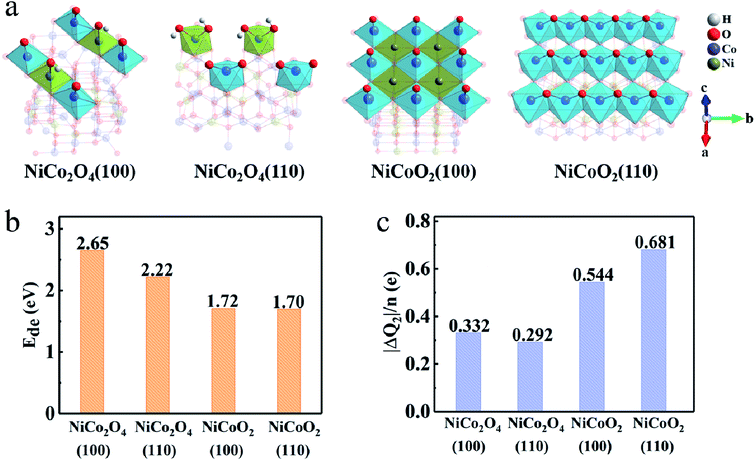Fig. 5 (a) Surface configuration, (b) average deprotonation energy (E_de) and (c) charge transfer (ΔQ₂) after the complete deprotonation.

The first-principles calculation results, as discussed above, corroborate more attractive innate merits of NiCoO₂ serving as the electrode material for supercapacitors as follows. First, the large electronic state contribution from Co atoms of NiCoO₂ near the Fermi-level provides more charge carriers for faradaic redox reactions, thus enhancing the redox activities. Second, the much easier OH⁻ adsorption and deprotonation processes will accelerate the surface reaction dynamics. The two aspects synergistically facilitate the rate behaviors of the NiCoO₂ electrode. Third, the surfaces of NiCoO₂ show high concentration of redox active sites and higher electron donation capability than NiCo₂O₄, realizing a large degree of oxidation after reaction, which is helpful to obtain large SCs. It is thanks to these appealing congenital advantages that the rock-salt NiCoO₂ can be reasonably anticipated with even better electrochemical performance than the spinel NiCo₂O₄.

3.4 Electrochemical properties

To experimentally support the above viewpoint, we purposefully chose our synthesized two Ni–Co binary oxides, i.e., flower-shaped NiCoO₂ (ref. 14) and NiCo₂O₄ (Fig. S5 and S6, ESI†), and comparatively study their capacitive performance. The distinct redox peaks in cyclic voltammetry (CV) curves of both NiCo₂O₄ (Fig. 6a) and NiCoO₂ (ref. 14) verify their typical pseudocapacitance mainly, which typically results from fast and reversible redox processes of Co²⁺/Co³⁺/Co⁴⁺ and Ni²⁺/Ni³⁺ in 2 M KOH aqueous solution.^{9,14,15,42,43} As derived from the chronopotentiometry (CP) plots (Fig. 6b), the spinel NiCo₂O₄ electrode with a mass loading 5 mg cm⁻² exhibits reversible SCs of ∼262, ∼260, ∼258, ∼256, ∼222 and ∼133 F g⁻¹ at the current densities of 2, 3, 4, 5, 10 and 20 A g⁻¹, respectively. By sharp contrast, the rock-salt NiCoO₂ obtains ultrahigh SCs of ∼836 and ∼415 F g⁻¹ at 2 and 20 A g⁻¹, respectively,¹⁴ which are both higher than three times those of the NiCo₂O₄ electrode, as plotted in Fig. 6c.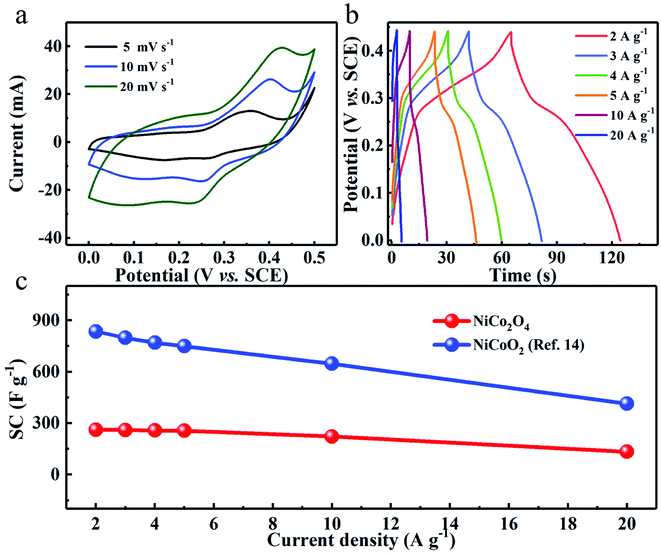

Fig. 6 (a) CV and (b) CP curves of the NiCo₂O₄ electrode. (c) Comparison of SCs between NiCo₂O₄ and NiCoO₂ electrodes at various current densities.

4 Conclusions

In summary, we have comprehensively conducted the first-principle DFT calculations to shed light on the distinguished advantages of rock-salt NiCoO₂ from its crystal structure. The faster hydroxyls adsorption/deprotonation kinetics and higher electron donation capability enable the rock-salt NiCoO₂ as a more competitive electrode for supercapacitors when compared to its spinel counterpart of NiCo₂O₄. Furthermore, electrochemical evaluation experimentally authenticated the theoretical simulation and calculation. The contribution here will guide rational optimization and selection of pseudocapacitive electrodes for advanced supercapacitors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We appreciate the financial support from National Natural Science Foundation of China (Grant No. 51772127 and 51772131), Major Program of Shandong Province Natural Science Foundation (Grant No. ZR2018ZB0317), Taishan Scholars (Grant No. ts201712050), and Collaborative Innovation Center of Technology and Equipment for Biological Diagnosis and Therapy in Universities of Shandong.

References

1. J. Sun, C. Wu, X. Sun, H. Hu, C. Zhi, L. Hou and C. Yuan, J. Mater. Chem. A, 2017, 5, 9443–9464.
2. J. Chen, Y. Han, X. Kong, X. Deng, H. J. Park, Y. Guo, S. Jin, Z. Qi, Z. Lee, Z. Qiao, R. S. Ruoff and H. Ji, Angew. Chem., Int. Ed., 2016, 55, 13822–13827.
3. L. Liu, H. P. Zhao and Y. Lei, InfoMat, 2019, 1, 74–84.
4. H. S. Kim, J. B. Cook, H. Lin, J. S. Ko, S. H. Tolbert, V. Ozolins and B. Dunn, Nat. Mater., 2017, 16, 454–460.
5. R. Wang, M. Yao and Z. Niu, InfoMat, 2020, 2, 113–125.
6. X. Li, L. Jiang, C. Zhou, J. Liu and H. Zeng, NPG Asia Mater., 2015, 7, e165.
7. S. Liu, D. Ni, H.-F. Li, K. N. Hui, C.-Y. Ouyang and S. C. Jun, J. Mater. Chem. A, 2018, 6, 10674–10685.
8. C. Yuan, H. B. Wu, Y. Xie and X. Lou, Angew. Chem., Int. Ed., 2014, 53, 1488–1504.
9. B. B. Liu, J. G. Liu, T. T. Zhang, C. X. Xu and H. Liu, J. Mater. Chem. A, 2019, 7, 16222–16230.
10. J. Li, Z. Liu, Q. Zhang, Y. Cheng, B. Zhao, S. Dai, H.-H. Wu, K. Zhang, D. Ding, Y. Wu, M. Liu and M.-S. Wang, Nano Energy, 2019, 57, 22–33.
11. X. Li, L. Jiang, C. Zhou, J. Liu and H. Zeng, NPG Asia Mater., 2015, 7, e165.
12. D. P. Dubal, P. Gomez-Romero, B. R. Sankapal and R. Holze, Nano Energy, 2015, 11, 377–399.
13. X. Xu, H. Zhou, S. Ding, J. Li, B. Li and D. Yu, J. Power Sources, 2014, 267, 641–647.
14. Z. Wang, Z. Zhao, Y. Zhang, G. Pang, X. Sun, J. Zhang, L. Hou and C. Yuan, J. Alloys Compd., 2019, 779, 81–90.
15. Y. Zhu, H. Huang, G. Li, X. Liang, W. Zhou, J. Guo, W. Wei and S. Tang, Electrochim. Acta, 2017, 248, 562–569.
16. J. Xiao and S. Yang, J. Mater. Chem., 2012, 22, 12253–12262.
17. H. W. Wang, Z. A. Hu, Y. Q. Chang, Y. L. Chen, H. Y. Wu, Z. Y. Zhang and Y. Y. Yang, J. Mater. Chem., 2011, 21, 10504–10511.
18. M. C. Payne, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045–1097.
19. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
20. S. L. Dudarev, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
21. H. J. Monkhorst, Phys. Rev. B: Solid State, 1977, 16, 1748–1749.
22. J. Heyd, G. E. Scuseria and M. J. Ernzerhof, Chem. Phys., 2003, 118, 8207–8215.
23. Y.-Z. Jin, Z. Li, J.-Q. Wang, R. Li, Z.-Q. Li, H. Liu, J. Mao, C.-K. Dong, J. Yang, S.-Z. Qiao and X.-W. Du, Adv. Energy Mater., 2018, 8, 1703469.
24. X. Shi, S. L. Bernasek and A. Selloni, J. Phys. Chem. C, 2016, 120, 14892–14898.
25. X. Yu, Y. Li, Y.-W. Li, J. Wang and H. Jiao, J. Phys. Chem. C, 2013, 117, 7648–7655.
26. K. Shojaee, A. Montoya and B. S. Haynes, Comput. Mater. Sci., 2013, 72, 15–25.
27. E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908.
28. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
29. J. Wu, P. Guo, R. Mi, X. Liu, H. Zhang, J. Mei, H. Liu, W. M. Lau and L.-M. Liu, J. Mater. Chem. A, 2015, 3, 15331–15338.
30. K. Fominykh, G. C. Tok, P. Zeller, H. Hajiyani, T. Miller, M. Dblinger, R. Pentcheva, T. Bein and D. Fattakhova-Rohlfing, Adv. Funct. Mater., 2017, 27, 1605121.
31. Y. F. Zhang, F. Vines, Y. J. Xu, Y. Li, J. Q. Li and F. Illas, J. Phys. Chem. B, 2006, 110, 15454–15458.
32. L. Zhang, J. Fischer, Y. Jia, X. Yan, W. Xu, X. Wang, J. Chen, D. Yang, H. Liu, L. Zhuang, M. Hankel, D. J. Searles, K. Huang, S. Feng, C. L. Brown and X. Yao, J. Am. Chem. Soc., 2018, 140, 10757–10763.
33. C. Xiang, Y. Liu, Y. Yin, P. Huang, Y. Zou, M. Fehse, Z. She, F. Xu, D. Banerjee, D. Hermida Merino, A. Longo, H.-B. Kraatz, D. F. Brougham, B. Wu and L. Sun, ACS Appl. Energy Mater., 2019, 2, 3389–3399.
34. Y. F. Zhang, F. Vines, Y. J. Xu, Y. Li, J. Q. Li and F. Illas, J. Phys. Chem. B, 2006, 110, 15454–15458.
35. Z. Zhang, L. Wang, W. Wang, J. Liu, Z. Hong, K. Cho and W. Wang, J. Mater. Chem. A, 2019, 7, 16231–16238.
36. F. Zasada, J. Gryboś, P. Indyka, W. Piskorz, J. Kaczmarczyk and Z. Sojka, J. Phys. Chem. C, 2014, 118, 19085–19097.
37. S. C. Parker, P. M. Oliver, N. H. De Leeuw, J. O. Titiloye and G. W. Watson, Phase Transitions, 1997, 61, 83–107.
38. W. Zhao, M. Bajdich, S. Carey, A. Vojvodic, J. K. Nørskov and C. T. Campbell, ACS Catal., 2016, 6, 7377–7384.
39. Q. Zhang, Z. Liu, B. Zhao, Y. Cheng, L. Zhang, H.-H. Wu, M.-S. Wang, S. Dai, K. Zhang, D. Ding, Y. Wu and M. Liu, Energy Storage Materials, 2019, 16, 632–645.
40. Z. Wu, Y. Zhu and X. Ji, J. Mater. Chem. A, 2014, 2, 14759–14772.
41. P. Rasiyah, A. C. C. Tseung and D. B. Hibbert, J. Electrochem. Soc., 1982, 129, 1724–1727.
42. T. Y. Wei, C. H. Chen, H. C. Chien, S. Y. Lu and C. C. Hu, Adv. Mater., 2010, 22, 347–351.
43. R. Wang, M. Yao and Z. Niu, InfoMat, 2020, 2, 113–125.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra05578f

---