Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electronic structure and thermoelectric properties of full Heusler compounds Ca2YZ (Y = Au, Hg; Z = As, Sb, Bi, Sn and Pb)†
Yang Hua,
Yurong Jinac,
Guangbiao Zhangab and
Yuli Yan *ab
*ab
aInstitute for Computational Materials Science, School of Physics and Electronics, Henan University, Kaifeng 475004, China. E-mail: yanyl@henu.edu.cn
bInternational Joint Research Laboratory of New Energy Materials and Devices of Henan Province, China
cChongqing Institute of Engineering, Chongqing 402360, China
First published on 3rd August 2020
Abstract
We investigate the transport properties of bulk Ca2YZ (Y = Au, Hg; Z = As, Sb, Bi, Sn and Pb) by a combination method of first-principles and Boltzmann transport theory. The focus of this article is the systematic study of the thermoelectric properties under the effect of a spin–orbit coupling. The highest dimensionless figure of merit (ZT) of Ca2AuAs at optimum carrier concentration are 1.23 at 700 K. Interestingly enough, for n-type Ca2HgPb, the maximum ZT are close to each other from 500 K to 900 K and these values are close to 1, which suggests that semimetallic material can also be used as an excellent candidate for thermoelectric materials. From another viewpoint, at room temperature, the maximum PF for Ca2YZ are greater than 3 mW m−1 K−2, which is very close to that of ∼3 mW m−1 K−2 for Bi2Te3 and ∼4 mW m−1 K−2 for Fe2VAl. However, the room temperature theoretical κl of Ca2YZ is only about 0.85–1.6 W m−1 K−1, which is comparing to 1.4 W m−1 K−1 for Bi2Te3 and remarkably lower than 28 W m−1 K−1 for Fe2VAl at same temperature. So Ca2YZ should be a new type of promising thermoelectric material at room temperature.
I. Introduction
Thermoelectric (TE) materials, which can generate electricity from waste heat or be used as solid-state Peltier coolers, are considered for a variety of energy harvesting and thermal management applications.1–3 The efficiency of TE materials is described by the dimensionless figure of merit ZT, which is defined as ZT = S2σT/(κe + κl), where S is the Seebeck coefficient, σ is the electrical conductivity (S2σ also known as the power factor, PF), T is the absolute temperature, and κe and κl are the electronic and lattice contributions to the thermal conductivity, respectively. Therefore, high thermoelectric performance requires both a high PF and a low thermal conductivity (κ = κe + κl). There are two ways to improve the ZT of thermoelectric materials: one way is to enhance the PF, the other one is to suppress the thermal conductivity. Due to the strongly coupled electrical properties among S, σ, and κe, tuning one of these parameters usually leads to a compensation in the others, resulting in the difficulty for enhancing ZT.Heusler compounds have attracted renewed scientific interest because they have been expected to be new candidates for thermoelectric applications.4–8 Previous studies have shown that although Heusler compounds have high PF, high κl leads to a very low ZT. For example, the S2σ of Fe2VAl is as high as 4–6 mW m−1 K−2 (ref. 9–11) in the temperature range of 300 K to 400 K,16 the S2σT of TiIrAs, ZrIrSb, and ZrCoSb are more than 6 W m−1 K−1 at 800 K,12 but the higher κl seriously restricts the improvement of their ZT values.9–13 In recent years, more and more effects have been focused on lowering the κl to increase the ZT value by alloying, doping, and nono-structuring.13–15 However, these approaches may adversely affect the electronic transport properties. It is extremely expectant to find new thermoelectric materials with both the high PF and intrinsic low thermal conductivity. Excitedly, He et al. discovered a new family of FH compounds X2YZ (X = Ca, Sr, and Ba; Y = Au and Hg; Z = As, Sb, Bi, Sn and Pb) with ultralow κl by employing a high-throughput thermodynamic stability screening based on ab initio calculations. By comparing the PF of X2AuBi (X = Ba and Sr) with that of the well-studied thermoelectric compound Fe2VAl.17–19 They found that the maximum power factor of X2AuBi (X = Ba and Sr) is much larger than that of Fe2YZ.17 These findings suggest that FH X2YZ are very promising TE materials. Now we wonder why the author did not compare the PF of Ca2YZ (Y = Au and Hg; Z = As, Sb, Bi, Sn and Pb) with that of Fe2VAl.17 Could it be said that the PF of Ca2YZ is very low?
Considering that Ca is a earth-abundant, cheap and environmental friendly element, so in this article, we perform a comprehensive study on the electronic structure and the thermoelectric properties of Ca2YZ (Y = Au and Hg; Z = As, Sb, Bi, Sn and Pb) by a combination of first-principles calculations and the semiclassical Boltzmann theory. We compared the calculated PFS of Ca2YZ with that of Bi2Te3 (ref. 20) and Fe2VAl.9–11 The most significant thing is that at room temperature, the maximum value of PFS for Ca2YZ is PF ≧ 3 mW m−1 K−2, which is similar to that of ∼3 mW m−1 K−2 for Bi2Te3 (ref. 20) and ∼4 mW m−1 K−2 for Fe2VAl.9–11 And at room temperature, the theoretical κl of Ca2YZ is estimated to be about 0.85–1.6 W m−1 K−1.17 At the same temperature, the value is comparable to those of known thermoelectric materials i.e., 1.4 W m−1 K−1 for Bi2Te3 (ref. 21) and 28 W m−1 K−1 for Fe2VAl16 at 300 K. So Ca2YZ should be a new promising material for thermoelectric applications.
II. Computational detail
The crystal structures of X2YZ were fully relaxed using the Vienna Ab initio Simulation Package (VASP).22 The pseudopotential based on the projector-augmented-wave (PAW) method was used to describe the interaction between ionic cores and valence electrons, which is very accurate and efficient.23–25 The generalized-gradient approximation (GGA), as parameterized by Perdew, Burke, and Emzerhof,26 was used to describe the exchange–correlation interaction of electron. The cut-off energy of plane-wave basis sets is set at 500 eV, and the energy convergence criterion was chosen to be 10−6 eV. The Brillouin zone was sampled by the Monkhorst–Pack special k-point scheme with 14 × 14 × 14 grid meshes for Ca2YZ. All atoms are relaxed until the residual forces on each of them is smaller than 0.02 eV Å−1.The electronic structures of Ca2YZ were calculated by the full potential-linearized augmented plane wave (FP-LAPW) methods27 based on the density functional theory (DFT),28,29 as implemented in the WIEN2k code.30–32 The muffin-tin radii (RMT) ware chosen 2.5 a.u. for all atoms. The calculations were performed with an energy cut-off such that RMT × Kmax = 7 and a k sampling with 14 × 14 × 14 Monkhorst–Pack mesh. Further increase in the cut-off value and the k-points number, the eigenvalues showed no significant change. The self-consistent cycles were stopped when the total energy difference between the cycles was less than 0.0001 eV. Since these compounds contains heavy atoms and so the scalar relativistic effect and spin–orbit coupling (SOC) effect are taken into account in the computations. Tran and Blaha-modified Becke–Johnson potential (TB-mBJ)33,34 with Perdew–Burke–Ernzerhof generalized-gradient approximation (PBEGGA)35 are used to obtain a more accurate value of the band gap.
The electrical transport coefficients are derived from the DFT electronic structure by using the Boltzmann theory within the constant scattering time approximation,36–38 as implemented in the BoltzTrap code.39 This approximation, which is commonly applied for metals and degenerately doped semiconductors,40 is based on the assumption that the scattering time determining the electrical conductivity does not vary strongly with energy on the scale of kT. It does not involve any assumption about the possibly strong doping and temperature dependence of τ. This method has been wildly used to calculate the transport coefficients of thermoelectric materials.38,41,42
III. Results and discussion
A. Crystal structure
The main focus of this study is a new family of intermetallic compounds with ten valence electrons Ca2YZ (Y = Au and Hg; Z = As, Sb, Bi, Sn and Pb), which was discovered through high-throughput ab initio screening.17 Most these compounds crystallize in the FH structure,17 which is a cubic lattice with space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (no. 225). The Ca atom occupies the Wyckoff position 8c (1/4, 1/4, 1/4), Y and the Z atoms are located at 4a (0, 0, 0) and 4b (1/2, 1/2, 1/2), respectively. The FH structure can also be understood as the interpenetration of YZ face-center-cubic (FCC) and X2 simple cubic (SC) sublattices, as shown in Fig. 1. The conventional cell contains 16 atoms with eight equivalent calcium atoms. The Heusler structure exhibits high symmetry and large isotropy, indicating the same transport properties along the three principal axes of the crystal, so we calculated transport coefficient by averaging over three principal crystal axes.
m (no. 225). The Ca atom occupies the Wyckoff position 8c (1/4, 1/4, 1/4), Y and the Z atoms are located at 4a (0, 0, 0) and 4b (1/2, 1/2, 1/2), respectively. The FH structure can also be understood as the interpenetration of YZ face-center-cubic (FCC) and X2 simple cubic (SC) sublattices, as shown in Fig. 1. The conventional cell contains 16 atoms with eight equivalent calcium atoms. The Heusler structure exhibits high symmetry and large isotropy, indicating the same transport properties along the three principal axes of the crystal, so we calculated transport coefficient by averaging over three principal crystal axes.
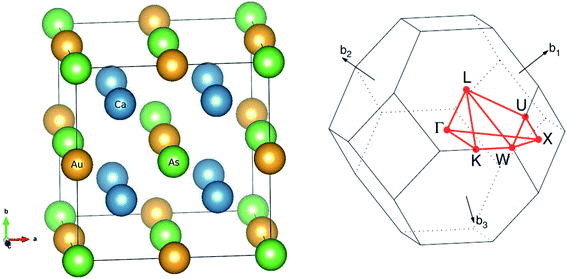 | ||
Fig. 1 The optimized crystal structure of Ca2YZ (Y = Au, Hg; Z = As, Sb, Bi, Sn and Pb) in space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and Brillouin zone. m and Brillouin zone. | ||
B. Electronic structure
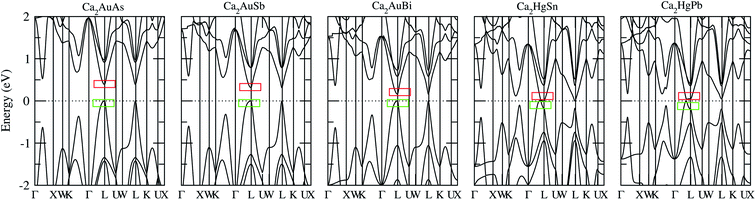
To calculate electrical transport properties, an accurate electronic structure is required. The electronic structures of these FH compounds are calculated with FP-LAPW, TB-mBJ exchange potential, and spin–orbit coupling (SOC). Fig. 2 shows the calculated band structures of Ca2YZ (Y = Au and Hg; Z= Sn, Pb, As, Sb, and Bi). The band gaps of these compounds are 0.389, 0.313, 0.160, 0.00 and 0.00 eV for Ca2AuAs, Ca2AuSb, Ca2AuBi, Ca2HgSn and Ca2HgPb, respectively. Of particular note is that Ca2HgSn have metallic characteristic with very small cross band between the bottom of the conduction band and the top of the valence band. An overlap between hole and electron pockets gives rise to a semimetallic character for Ca2HgPb. All these band gaps are quite different from previous study,17 which is due to the different exchange-correction functionals and the contribution of SOC. We also note that both the valence band maximum (VBM) and conduction band minimum (CBM) of Ca2AuAs, Ca2AuSb, and Ca2AuBi are located at the L point, which has orbital degeneracy is 1. Considering the symmetry of the Brillouin zone, so the valley degenerate is 4. Interestingly enough, the VBM of Ca2HgSn and Ca2HgPb are also located at the L point and is flat along L–Γ direction, which possesses band degeneracy of Nv = 4, and CBM of Ca2HgSn and Ca2HgPb are located along Γ–L (Λ) line, which possesses band degeneracy of Nv = 8. A larger band degeneracy is favorable for large PF. In order to confirm the results, we calculated the isoenergy surface for a Fermi level 0.12 eV below the valence band maximum and above the conduction band minimum and shown in Fig. 3. As is clearly shown in Fig. 3, for Ca2AuZ (Z = As, Sb and Bi), the doped carrier arise from holes or electrons are located in small pockets centered at L, and associated with four fold degenerate valleys. While for n-type Ca2HgZ (Z = Sn and Pb), eight triangular cones along Γ–L connected by bottom angles exhibiting metallic behavior have a high degeneracy with 8. For p-type Ca2HgZ (Z = Sn and Pb), the center of the irregular isoenergetic surface exhibiting semiconductor behaviors is located at L point with larger pockets, which yields a four fold degenerate valence band edge. The number results are in good agreement with those obtained from band structures. We further show the total density of states (TDOS) and partial density of states (PDOS) of these compounds in Fig. 4. The TDOSs show that the conduction band of the these five compounds rises from the band edge much more rapidly than that of the valence band, which suggests that the absolute value of the Seebeck coefficient for electron doping should be significantly greater than that of hole doping. The top of valence band rises faster for Ca2HgZ (Z = Sn and Pb) than the other three compounds, which means the Seebeck coefficient for hole doping for Ca2HgZ (Z = Sn and Pb) is larger than that of the other three compounds. In fact, there are many factors affecting the Seebeck coefficient, such as the band gap, temperature, and carrier concentration. The analysis of PDOS further reveals the top of valence band is formed mainly by the Y s and Z p orbitals and the conduction band is composed of the Ca d and Y p orbitals. The two most electropositive atoms Ca donate their four 5 s electrons to the electronegative Y and Z atoms. The s states of the Z atom are extremely localized and far below the Fermi level, so it does not have contributions. These results can provide guidance for further investigating the doping effect on Ca2YZ with the appropriate atoms.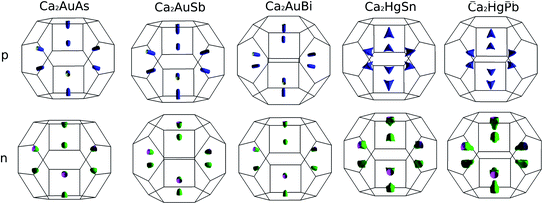 | ||
| Fig. 3 Fermi surface for a Fermi level 0.12 eV below the valence band maximum and above the conduction band minimum. | ||
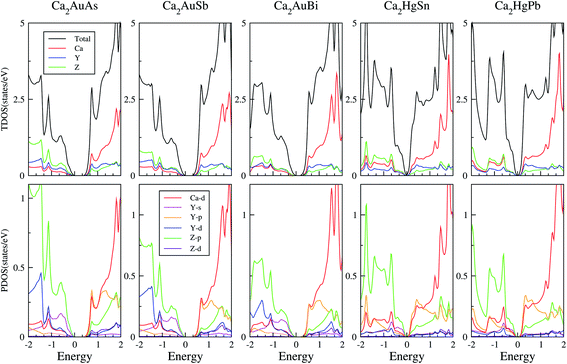 | ||
| Fig. 4 Calculated total, X-total DOS, Y-total and Z-total of Ca2YZ; the projected DOS of Ca2YZ. The Fermi level is at 0 eV. | ||
In order to have a deeper understanding of the electronic structure of Ca2YZ, we provide more detailed study in the following aspects. Firstly, we researched the differences in electronegativity between elements (as shown in Table 1). We can see that a large electronegativity difference between Ca and the Y/Z cite elements. It is expected, therefore, there is considerable charge transfer from the electropositive element Ca to the electronegativity Au(Hg) and As(Sb/Bi), indicating Ca2YZ are incline to be ionic compounds. However, the difference between Au and As(Sb/Bi) or Hg and Sn(Pb) is much smaller. So the type of chemical bond between Y and Z should be a polar covalent bond.
| Comp. | |χX| | |χY| | |χZ| | |χXY| | |χXZ| | |χYZ| | |χX2YZ| | QX | QY | QZ |
|---|---|---|---|---|---|---|---|---|---|---|
| Ca2AuAs | 1.00 | 2.54 | 2.18 | 1.54 | 1.18 | 0.36 | 1.9067 | 1.404 | −1.122 | −1.687 |
| Ca2AuSb | 1.00 | 2.54 | 2.05 | 1.54 | 1.05 | 0.49 | 1.863 | 1.385 | −1.123 | −1.645 |
| Ca2AuBi | 1.00 | 2.54 | 2.02 | 1.54 | 1.02 | 0.52 | 1.8533 | 1.363 | −1.185 | −1.539 |
| Ca2HgSn | 1.00 | 2.00 | 1.96 | 1.00 | 0.96 | 0.04 | 1.6533 | 1.300 | −0.917 | −1.682 |
| Ca2HgPb | 1.00 | 2.00 | 1.87 | 1.00 | 0.87 | 0.13 | 1.6233 | 1.306 | −0.972 | −1.637 |
To further understand the mechanisms, we used Bader charge analysis43 to monitor changes in the charges on each atom of Ca2YZ compounds. As shown in Table 1, Ca apparently loses the charge, while both Y and Z gain electron, and the difference in charge obtained from X atom is not hug between the Y atom and Z atom: from 0.354 for Ca2AuBi to 0.765 for Ca2HgSn, which is consistent with the above analysis of electronegativity.
C. Electrical transport properties
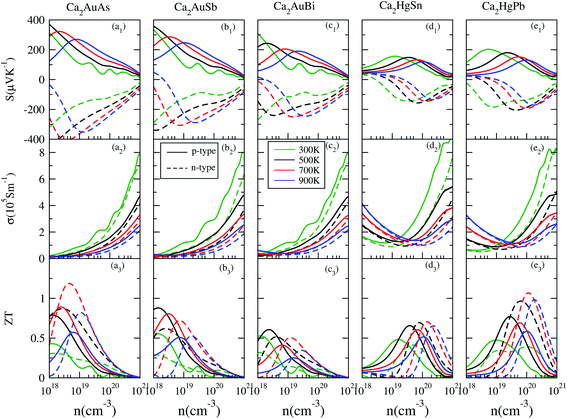
Based on the calculated electronic structures, the electrical transport properties of Ca2YZ (Y = Au and Hg; Z = As, Sb, Bi, Sn and Pb) are evaluated by using the semiclassical Boltzmann transport theory and the rigid-band model. The calculated results show that the absolute value and variation trend for the transport coefficient along the three main directions are almost identical, which is in accordance with the above discussion of crystal symmetry. Thus, in this paper, we only study the electrical transport properties along the x direction.Fig. 5 (a1–e1) show the calculated S as a function of carrier concentration at different temperature (300, 500, 700, and 900 K). We find that the S for Ca2AuZ (Z = As, Sb and Bi) is larger than that of Ca2HgZ (Z = Sn and Pb), which is mainly due to the metallicity of the latter, as we mentioned in the band structure analysis. It is worth mentioning that all the compounds have the maximal value of the absolute S greater than 200 μV K−1 except for that of Ca2HgSn. In further analysis, we found S decreases with the increasing of carrier concentration when at 300 K and 500 K, but increases at first and then decreases with the increasing of carrier concentration at 700 K and 900 K. It is worth noting that, the variation trend of S with temperature and carrier concentration for Ca2HgZ (Z = Sn and Pb) in the whole temperature range under study is quite similar with that of Ca2AuZ (Z = As, Sb and Bi) at 700 K and 900 K, which will be explained in the following. For a semiconductor with carriers including hole and electron, known as bipolar effect, the effective Seebeck coefficient (SE) is defined as:44
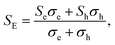 | (1) |
Interestingly, the absolute value of the S for p-type and n-type Ca2HgPb are larger than that of Ca2HgSn, which is mainly due to the larger degeneracy in the second and third conduction bands at the L-point for Ca2HgPb than for Ca2HgSn. Hence, it is very important to optimize carrier concentration, engineer band gap, and align band edge to achieve the largest S.
Here, we discuss S from a different view, taking Ca2AuAs as an example. As Fig. 5 (a1) shows that at the same temperature, the maximum of |S| (absolute value of Seebeck coefficient) for n-type doping is greater than that of p-type, which can be explained as follows: the S of metals or degenerate semiconductors (parabolic band, energy-independent scattering approximation) is defined as:45
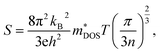 | (2) |
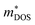 is the density-of-states effective mass, which is defined as Nv2/3 (mb(x)mb(y)mb(z))1/3. For an isotropic material with a same band masses of mb (mb(x) = mb(y) = mb(z) = mb) along three principle directions,
is the density-of-states effective mass, which is defined as Nv2/3 (mb(x)mb(y)mb(z))1/3. For an isotropic material with a same band masses of mb (mb(x) = mb(y) = mb(z) = mb) along three principle directions, 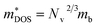 , where Nv is the band degeneracy of an energy band near the Fermi level. The above equation implies that S increases with the increasing of the slope of
, where Nv is the band degeneracy of an energy band near the Fermi level. The above equation implies that S increases with the increasing of the slope of 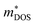 under certain conditions of temperature and carrier concentration. In general,
under certain conditions of temperature and carrier concentration. In general, 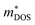 is positively correlated to the steepness of the Fermi–Dirac distribution near the Fermi energy. And Fig. 4 just tells us that the steepness of the total DOS of the valence band near the Fermi energy level is larger than that of the conduction band, which could be another reason that the maximum |S| of electron doping is greater than that of hole doping.
is positively correlated to the steepness of the Fermi–Dirac distribution near the Fermi energy. And Fig. 4 just tells us that the steepness of the total DOS of the valence band near the Fermi energy level is larger than that of the conduction band, which could be another reason that the maximum |S| of electron doping is greater than that of hole doping.
In this section, we discuss the carrier concentration and temperature dependence of the electrical conductivity (σ). It is impossible to obtain σ solely using the electronic structure information since the relaxation time τ is unknown. To solve this question, we use the method of Ong and coworkers46 to eliminate the effects of τ. By comparing the experimental σ with our calculated σ/τ values at the same temperature and carrier concentration, we can obtain τ. However, there is little experimental research on Ca2YZ (Y = Au, Hg; Z = As, Sb, Bi, Sn and Pb), we are having to replace them with Fe2VAl.47 In ref. 47, the electrical resistivity to the experimental value of 0.65 mΩ cm for Fe2VAl1xMx (M = Si, Ge) systems at doping x = 0.03 and 300 K, which combined with the calculated σ/τ yields τ = 3.62 × 10−15 s for Fe2V1−xAlx at 300 K. Near the temperature, the experimental data for this sample and others follow an approximate electron–phonon temperature dependence 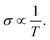 On the other hand, we take into account the impact of doping on electric–phonon form. This yields τ = 8.73 × 10−6 T−1 n−1/3. We then estimate σ as
On the other hand, we take into account the impact of doping on electric–phonon form. This yields τ = 8.73 × 10−6 T−1 n−1/3. We then estimate σ as 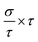 . Fig. 5 (a2–e2) show the relationship between the σ and the carrier concentration. At higher carrier concentration, regardless of n-type or p-type doping, electrical conductivities increase with increasing carrier concentration, which is in agreement with electrical conductivity proportional to the carrier concentration. These figures also shows that at the same doping concentration, the conductivity decreases with the increasing of temperature, which is due to the carrier mobility decreasing with the increase of temperature. However, at low carrier concentration, the electrical conductivities of Ca2HgZ (Z = Sn and Pb) increase with the increasing of temperature and the decreasing of carrier concentration, which may be due to the influence of minority carrier. It is worth noting that for the same carrier concentration and temperature, the electrical conductivities of Ca2HgZ (Z = Sn and Pb) are generally larger than that of Ca2AuZ (Z = As, Sb and Bi). This is a result of the semimetallic properties of Ca2HgZ (Z = Sn and Pb). Therefore, it is possible for semimetal materials to be good thermoelectric materials. It should be noted that we have calculated the electron transport properties by the method used in this paper, and the results show that good agreement is obtained between calculated and experimental values, which proves the reliability of our calculation.
. Fig. 5 (a2–e2) show the relationship between the σ and the carrier concentration. At higher carrier concentration, regardless of n-type or p-type doping, electrical conductivities increase with increasing carrier concentration, which is in agreement with electrical conductivity proportional to the carrier concentration. These figures also shows that at the same doping concentration, the conductivity decreases with the increasing of temperature, which is due to the carrier mobility decreasing with the increase of temperature. However, at low carrier concentration, the electrical conductivities of Ca2HgZ (Z = Sn and Pb) increase with the increasing of temperature and the decreasing of carrier concentration, which may be due to the influence of minority carrier. It is worth noting that for the same carrier concentration and temperature, the electrical conductivities of Ca2HgZ (Z = Sn and Pb) are generally larger than that of Ca2AuZ (Z = As, Sb and Bi). This is a result of the semimetallic properties of Ca2HgZ (Z = Sn and Pb). Therefore, it is possible for semimetal materials to be good thermoelectric materials. It should be noted that we have calculated the electron transport properties by the method used in this paper, and the results show that good agreement is obtained between calculated and experimental values, which proves the reliability of our calculation.
We also calculated the PF of these materials. Results show that the maximum PFs at an optimal carrier concentration are more than 3 mW m−1 K−2, which is very close to that of ∼3 mW m−1 K−2 for Bi2Te3 (ref. 20) and ∼4 mW m−1 K−2 for Fe2VAl.9–11 On the other hand, the theoretical κl of Ca2YZ (Y = Au and Hg; Z = As, Sb, Bi, Sn and Pb) is estimated to be about 0.85–1.6 W m−1 K−1 (ref. 17) at 300 K. The value is comparable to those of known thermoelectric materials i.e., 1.4 W m−1 K−1 for Bi2Te3 (ref. 21) and 28 W m−1 K−1 for Fe2VAl16 at the same temperature. So Ca2YZ should be a very promising material for thermoelectric applications.
D. Thermal conductivity
A valid theoretical approach to compute the thermal conductivity in thermoelectrics is of tremendous importance in material optimization for efficient thermoelectric refrigeration and power generation. As mentioned above, thermal conductivity in materials comes from two sources: (1) phonons travelling by the vibrating lattice (κl); (2) electrons and holes transporting heat (κe):| κ = κl + κe. | (3) |
We adopt κl of Ca2YZ (Y = Au and Hg; Z = As, Sb, Bi, Sn and Pb) from ref. 17. The electronic thermal conductivity κe is calculated through the Wiedemann–Franz law:48
| κe = LσT = neμLT | (4) |
E. Optimized ZT value
With all of the transport coefficients available, we calculated the ZT values of Ca2YZ for different carrier-concentration at 300, 500, 700, and 900 K and shown in Fig. 5 (a3–e3). From these figures, we can see that the optimal ZT values of n-type Ca2YZ are larger than that of p-type except 300 K, although the electrical conductivities of p-type Ca2YZ are larger than that of n-type. The optimal carrier concentration for Ca2HgZ (Z = Sn and Pb) are larger than that of Ca2AuZ (Z = As, Sb and Bi). We also found that the magnitude of the optimal ZT values reduces firstly and increases afterward with the decrease of the energy gap. Very interestingly, the optimal ZT value for n-type Ca2HgPb is much larger than that of Ca2HgSn, which is mainly due to the absolute value of the Seebeck coefficient for n-type Ca2HgPb are larger than that of Ca2HgSn. It is noteworthy that the optimal ZT value for n-type Ca2HgPb is comparable with those of Ca2AuAs. And the values of maximum ZTs are close to each other at different temperatures and carrier concentrations, which provides ideal conditions for the application of Ca2HgPb in the thermoelectric material field. It's remarkable that the maximum ZT value of Ca2AuAs and Ca2HgPb at optimum carrier concentration are 1.23 and 1.1 respectively at 700 K.IV. Conclusion
In summary, we studied a new class of thermo-dynamically stable FH compound with excellent thermoelectric properties using the first principles calculations and semi-classical Boltzmann theory. Our calculation results show that the band gap decreases with the decreasing of the average electronegativity. The analysis of the band structure shows that Ca2AuZ (Z = As, Sb and Bi) exhibit semiconductor properties, however, Ca2HgSn and Ca2HgPb exhibit metallic and semimetallic characteristic, respectively. The thermally activated behavior has been clearly observed for Ca2HgSn and Ca2HgPb at low carrier concentration, pointing out the existence of a pseudogap at around the Fermi level, which has been confirmed by the analysis of the TDOS. It is worth noting that for the same carrier concentration and temperature, the electrical conductivities of Ca2HgZ (Z = Sn and Pb) are generally larger than that of Ca2AuZ (Z = As, Sb and Bi), which then lead to the close proximity of the thermoelectric conversion efficiency for n-type Ca2HgPb and Ca2AuAs. What's interesting is, for Ca2HgPb, the maximum ZT and the corresponding optimal n-type doping concentration are close to each other from 500 K to 900 K, which suggests that semimetallic material can also be used as an excellent candidate for thermoelectric materials. It is noteworthy that the maximum ZT value of Ca2AuAs and Ca2HgPb at optimum carrier concentration are 1.23 and 1.1 respectively at 700 K. On the other hand, at room temperature, the maximum value of PFS for Ca2YZ are greater than 3 mW m−1 K−2, which is equivalent to ∼3 mW m−1 K−2 for Bi2Te3 and ∼4 mW m−1 K−2 for Fe2VAl. And at room temperature, the theoretical κl of Ca2YZ is only about 0.85–1.6 W m−1 K−1, which is comparable to those of known thermoelectric materials i.e., 1.4 W m−1 K−1 for Bi2Te3 and 28 W m−1 K−1 for Fe2VAl at 300 K. As a conclusion, it is reasonable to believe that Ca2YZ (Y = Au and Hg; Z = As, Sb, Bi, Sn and Pb) should be a very promising thermoelectric material.Author contributions
Yuli Yan carried out the calculations and is responsible for organizing the manuscript. Yang Hu and Yurong Jin contributed equally to this work. All authors participated in the discussion.Conflicts of interest
There are no conflicts of interest to declear.Acknowledgements
This research was sponsored by the Henan Province Scientific and Technological Cooperation Project (No. 182106000023); the National Natural Science Fundation of China (No. 11674083).References
- J. D. Lei, D. Zhang, W. D. Guan, Z. Ma, Z. X. Cheng, C. Wang and Y. X. Wang, Enhancement of Thermoelectric Figure of Merit by the Insertion of Multi-Walled Carbon Nanotubes in MgAgSb, Appl. Phys. Lett., 2018, 113, 083901 CrossRef.
- J. F. Yang, J. Y. Li, C. Zhang, Z. Z. Feng, B. B. Shi, W. Y. Zhai, Y. L. Yan and Y. X. Wang, Excellent thermoelectric performance of BaMgSi driven by low lattice thermal conductivity: a promising thermoelectric material, J. Alloys Compd., 2020, 827, 154342 CrossRef CAS.
- Z. Z. Feng, X. L. Zhang, Y. X. Wang, J. H. Zhang, T. T. Jia, B. Q. Cao and Y. S. Zhang, Thermoelectric optimization of AgBiSe2 by defect engineering for room-temperature applications, Phys. Rev. B, 2019, 99, 155203 CrossRef CAS.
- Z. Z. Feng, Y. H. Fu, Y. S. Zhang and D. J. Sing, Characterization of rattling in relation to thermal conductivity: ordered half-Heusler semiconductor, Phys. Rev. B, 2020, 101, 064301 CrossRef CAS.
- S. Sk, P. Devi, S. Singh and S. K. Pandey, Exploring the best scenario for understanding the high temperature thermoelectric behaviour of Fe(2)VAI, Mater. Res. Express, 2019, 6, 026302 CrossRef.
- N. V. Du, J. U. Rahman, E. J. Meang, C. H. Lim, W. H. Shin and W. S. Seo, et al., Synthesis and thermoelectric properties of Ti-substituted (Hf0.5Zr0.5)(1−x)TixNiSn0.998Sb0.002 half-Heusler compounds, J. Alloys Compd., 2019, 773, 1141 CrossRef.
- Y. Huang, H. Nagai, K. Hayashi and Y. Miyazaki, Preparation and thermoelectric properties of pseudogap intermetallic (Ti1−xVx) NiSi solid solutions, J. Alloys Compd., 2019, 771, 111 CrossRef CAS.
- M. J. Alrahamneh, A. A. Mousa and J. M. Khalifeh, First principles study of the structural, electronic, magnetic and thermoelectric properties of Zr2RhAl, Phys. B, 2019, 552, 227 CrossRef CAS.
- E. J. Skoug, C. Zhou, Y. Pei and D. T. Morelli, High thermoelectric power factor near room temperature in full-Heusler alloys, J. Electron. Mater., 2009, 38, 1221 CrossRef CAS.
- C. S. Lue, C. F. Chen, J. Y. Lin and Y. K. Kuo, Thermoelectric properties of quaternary Heusler alloys Fe2VAl1−xSix, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 064204 CrossRef.
- M. Mikami, M. Inukai, H. Miyazaki and Y. Nishino, Thermoelectric Properties of Heusler-Type Fe2VAl Sintered Alloys, J. Electron. Mater., 2016, 45, 1284 CrossRef CAS.
- K. Berland, N. Shulumba, O. Hellman, C. Persson and O. Martin Lvvik, Thermoelectric transport trends in group 4 half-Heusler alloys, J. Appl. Phys., 2019, 126, 145102 CrossRef.
- H. Zhu, J. Mao, Y. Li, J. Sun, Y. Wang, Q. Zhu, G. Li, Q. Song, J. Zhou, Y. Fu, R. He, T. Tong, Z. Liu, W. Ren, L. You, Z. Wang, J. Luo, A. Sotnikov, J. Bao, K. Nielsch, G. Chen, D. J. Singh and Z. F. Ren, Nat. Commun., 2019, 10, 270 CrossRef PubMed.
- H. Tarkhanyan Roland and G. Niarchos Dimitris, Effect of hierarchically distributed nano-to microscale skutterudite inclusions on the lattice thermal conductivity of TiNiSn-based half-Heusler alloys, J. Alloys Compd., 2018, 732, 928 CrossRef.
- A. Karati, V. S. Hariharan, S. Ghosh, A. Prasad, M. Nagini, K. Guruvidyathri, R. Chandra Mallik, R. Shabadi, L. Bichler, B. S. Murty and U. V. Varadaraju, Thermoelectric properties of half-Heusler high-entropy Ti2NiCoSn1−xSb1+x (x = 0.5, 1) alloys with VEC18, Scr. Mater., 2020, 186, 375 CrossRef CAS.
- Y. Nishino, S. Deguchi and U. Mizutani, Thermal and transport properties of the Heusler-type Fe2VAl1−xGex (0 ≦ x ≦ 0.20) alloys: effect of doping on lattice thermal conductivity, electrical resistivity, and Seebeck coefficient, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 115115 CrossRef.
- J. He, M. Amsler, Y. Xia, S. S. Naghavi, V. I. Hegde and S. Hao, et al., Ultralow thermal conductivity in full Heusler semiconductors, Phys. Rev. Lett., 2016, 117, 046602 CrossRef PubMed.
- D. I. Bilc, G. Hautier, D. Waroquiers, G. M. Rignanese and P. Ghosez, Low-dimensional transport and large thermoelectric power factors in bulk semiconductors by band engineering of highly directional electronic states, Phys. Rev. Lett., 2015, 114, 136601 CrossRef PubMed.
- Y. Terazawa, M. Mikami, T. Itoh and T. Takeuchi, Effects of heavy element substitution on electronic structure and lattice thermal conductivity of Fe2VAl thermoelectric material, J. Electron. Mater., 2012, 41, 1348 CrossRef CAS.
- L. Cheng, H. J. Liu, J. Zhang, J. Wei, J. H. Ling and J. Shi, et al., Effects of van der Waals interactions and quasiparticle corrections on the electronic and transport properties of Bi2Te3, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 085118 CrossRef.
- B. Qiu and X. Ruan, Molecular dynamics simulations of lattice thermal conductivity of bismuth telluride using two-body interatomic potentials, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 165203 CrossRef.
- G. Kresse and J. Hafner, Norm-conserving and ultrasoft pseudopotentials for first-row and transition elements, J. Phys.: Condens. Matter, 1994, 6, 8245 CrossRef CAS.
- P. E. Böchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- H. B. Yin, C. Liu, G. P. Zheng, Y. X. Wang and F. Z. Ren, Ab initio simulation studies on the room-temperature ferroelectricity in two-dimensional-phase GeS, Appl. Phys. Lett., 2019, 114, 192903 CrossRef.
- B. Wang, X. W. Zhang, Y. H. Zhang, S. J. Yuan, Y. L. Guo, S. Dong and J. L. Wang, Prediction of a two-dimensional high-Tc f-electron ferromagnetic semiconductor, Mater. Horiz., 2020, 7, 1623 RSC.
- D. M. Ceperley and B. Alder, Ground state of the electron gas by a stochastic method, Phys. Rev. Lett., 1980, 45, 566 CrossRef CAS.
- D. J. Singh and W. E. Pickett, Skutterudite antimonides: quasilinear bands and unusual transport, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 11235 CrossRef CAS PubMed.
- V. Marinca and R. D. Ene, Analytical approximate solutions to the Thomas-Fermi equation, Cent. Eur. J. Phys., 2014, 12, 503 Search PubMed.
- E. Z. Fermi, Statistical method to determine some properties of atoms, Z. Phys., 1927, 48, 73 CrossRef.
- P. Blaha, K. Schwarz, G. Madsen, D. Kvasnicka and J. Luitz, An augmented plane wave local orbitals program for calculating crystal properties, 2001 Search PubMed.
- P. Hohenberg and W. Kohn, Inhomogeneous electron gas, Phys. Rev., 1964, 136, B864 CrossRef.
- D. Koelling and B. Harmon, A technique for relativistic spin-polarised calculations, J. Phys. C: Solid State Phys., 1977, 10, 3107 CrossRef CAS.
- F. Tran and P. Blaha, Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential, Phys. Rev. Lett., 2009, 102, 226401 CrossRef PubMed.
- E. Engel and S. H. Vosko, Exact exchange-only potentials and the virial relation as microscopic criteria for generalized gradient approximations, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 13164 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. M. Ziman, Electrons and phonons: the theory of transport phenomena in solids, Oxford University Press, 1960 Search PubMed.
- W. Jone and N. H. March, Theoretical Solid State Physics, Courier Dover, New York, 1973 Search PubMed.
- M. J. Alrahamneh, A. A. Mous and J. M. Khalifeh, First principles study of the structural, electronic, magnetic and thermoelectric properties of Zr2RhAl, Phys. B, 2019, 552, 227 CrossRef CAS.
- G. K. H. Madsen and D. J. Singh, BoltzTraP. A code for calculating band-structure dependent quantities, Comput. Phys. Commun., 2006, 175, 67 CrossRef CAS.
- Y. L. Yan, G. B. Zhang, C. Wang, C. X. Peng, P. H. Zhang and Y. X. Wang, et al., Optimizing the Dopant and Carrier Concentration of Ca5Al2Sb6 for High Thermoelectric Efficiency, Sci. Rep., 2016, 6, 29550 CrossRef CAS PubMed.
- C. Y. WuL, S. H. R. Gong and S. F. Zhou, Influence of internal displacement on band structure, phase transition, and thermoelectric properties of bismuth, J. Mater. Sci., 2019, 54, 6347 CrossRef.
- B. Ul Haq, S. AlFaify and A. Laref, Design and characterization of novel polymorphs of single-layered tin-sulfide for direction-dependent thermoelectric applications using first-principles approaches, Phys. Chem. Chem. Phys., 2019, 21, 4624–4632 RSC.
- G. Henkelamn, A. Arnaldsson and H. Jonsson, A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- M. Chen, A quick thermoelectric technique for typing HgCdTe at liquid nitrogen temperature, J. Appl. Phys., 1992, 71, 3636 CrossRef CAS.
- N. Wang, H. Li, Y. Ba, Y. Wang, C. Wan and K. Fujinami, et al., Effects of YSZ Additions on Thermoelectric Properties of Nb-Doped Strontium Titanate, J. Electron. Mater., 2010, 39, 1777 CrossRef CAS.
- K. P. Ong, D. J. Singh and P. Wu, Analysis of the thermoelectric properties of n-type ZnO, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 115110 CrossRef.
- M. Vasundhara, V. Srinivas and V. V. Rao, Electronic transport in Heusler-type Fe2Val(1−x)Mx alloys (M = B, In, Si), Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 224415 CrossRef.
- G. J. Snyder and E. S. Toberer, Complex thermoelectric materials, Nat. Mater., 2008, 7, 105 CrossRef CAS PubMed.
- J. K. Lee, S. D. Park, B. S. Kim, M. W. Oh and S. H. Cho, et al., Control of thermoelectric properties through the addition of Ag in the Bi0.5Sb1.5Te3 Alloy, Electron. Mater. Lett., 2010, 6, 201 CrossRef CAS.
- X. J. Tan, W. Liu, H. J. Liu, J. Shi, X. F. Tang and C. Uher, Multiscale calculations of thermoelectric properties of n-type Mg2Si(1−x)Snx solid solutions, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 1992 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra04984k |
| This journal is © The Royal Society of Chemistry 2020 |