Open Access Article
Open Access ArticleComputational prediction of the spin-polarized semiconductor equiatomic quaternary Heusler compound MnVZrP as a spin-filter
D. M. Hoat *ab,
Duc-Quang Hoang
*ab,
Duc-Quang Hoang c,
Mosayeb Naseri
c,
Mosayeb Naseri d,
J. F. Rivas-Silvae,
A. I. Kartamyshevfg and
Gregorio H. Cocoletzie
d,
J. F. Rivas-Silvae,
A. I. Kartamyshevfg and
Gregorio H. Cocoletzie
aComputational Laboratory for Advanced Materials and Structures, Advanced Institute of Materials Science, Ton Duc Thang University, Ho Chi Minh City, Vietnam. E-mail: dominhhoat@tdtu.edu.vn
bFaculty of Applied Sciences, Ton Duc Thang University, Ho Chi Minh City, Vietnam
cApplied Computational Civil and Structural Engineering Research Group, Faculty of Civil Engineering, Ton Duc Thang University, Ho Chi Minh City, Vietnam. E-mail: hoangducquang@tdtu.edu.vn
dDepartment of Physics, Islamic Azad University, Kermanshah Branch, P.O. Box 6718997551, Kermanshah, Iran. E-mail: m.naseri@iauksh.ac.ir
eBenemérita Universidad Autónoma de Puebla, Instituto de Física, Apartado Postal J-48, Puebla 72570, Mexico. E-mail: rivas@ifuap.buap.mx
fDivision of Computational Physics, Institute for Computational Science, Ton Duc Thang University, Ho Chi Minh City, Vietnam. E-mail: kartamyshevandrey@tdtu.edu.vn
gFaculty of Electrical and Electronics Engineering, Ton Duc Thang University, Ho Chi Minh City, Vietnam
First published on 7th July 2020
Abstract
In this work, a new equiatomic quaternary Heusler (EQH) compound, MnVZrP, is predicted using first principles calculations. Simulations show the good stability of the material, suggesting experimental realization. Results show that MnVZrP is a magnetic semiconductor material, exhibiting semiconductor characteristics in both spin channels, however, with strong spin-polarization. Electronic band gaps of 0.97 and 0.47 eV are obtained in the spin-up and spin-dn states, respectively. Mainly the d–d coupling regulates the electronic band structure around the Fermi level. Strain effects on the electronic properties of the proposed compound are also investigated. Simulations give the total magnetic moment of 3 μB satisfying the Slate-Pauling rule. The main magnetic contributions are given by the Mn and V constituents. The results presented here suggest the promising applicability of EQH MnVZrP as a spin-filter. Additionally, the elastic property calculations indicate the mechanical stability and elastic anisotropy. The work may be useful in the magnetic Heusler alloys field, introducing a new member to the small group of magnetic semiconductor EQH compounds for spin-filter applications.
1 Introduction
Recently, with the continuously increasing development of spintronic technology,1,2 numerous studies have focused on Heusler compounds due to their extremely intriguing physical and mechanical properties. Many members of this class of materials have been successfully applied in spintronic devices, such as spin filters,3,4 spin valves,5,6 magnetic tunnel junctions7,8 and spin injectors.9,10 It appears that the half-metallicity in the NiMnSb half-Heusler discovered by Groot et al.11 has motivated extensive investigations into Heusler compounds of varying chemical composition. Besides the half-metallicity, novel electronic properties have been obtained. So far, a large variety of Heusler alloys have been investigated, and they can be classified based on either chemical composition or electronic properties. Specifically,(1) Chemical composition:
• Full-Heusler (FH) with stoichiometry 2-1-1, forming the chemical formula X2YZ.12–14
• Half-Heusler (HH) with stoichiometry 1-1-1, generating the chemical formula XYZ.15–17
• Equiatomic quaternary Heusler (EQH) with stoichiometry 1-1-1-1, giving place to the chemical formula XX′YZ.13,18,19
Herein, in most cases, X, X′ and Y are transition metals or rare earth elements, however, interesting electronic and magnetic properties have been found even in those containing only sp elements.20–23
(2) Electronic properties:
• Metal: both spin channels show the metallic nature (Fig. 1a).24
• Half-metal: one of the spin states is metallic and the other exhibits semiconducting behavior (Fig. 1b).25–27
• Semiconductor: both spin configurations are semiconductors with total symmetry, showing no magnetism (Fig. 1c).28,29
• Spin-gapless semiconductor: the valence band maximum or conduction band minimum of one spin channel touches the Fermi level, and the remaining spin channel displays semiconducting characteristics (Fig. 1d).30,31
• Magnetic semiconductor: the two spin states are semiconductors, however they differ from the semiconductor case by the spin-polarization, inducing important magnetic properties in the materials (Fig. 1e).32
 | ||
| Fig. 1 Scheme of density of states of (a) metal, (b) half-metal, (c) semiconductor, (d) spin-gapless semiconductor and (e) spin-polarized semiconductor behavior. | ||
EQH compounds exhibit some advantageous features including small additional disorder scattering and low power dissipation.33 These materials have been prepared and characterized experimentally. For example, the CrVTiAl with a small-moment has been successfully synthesized and characterized by Stephen et al.34 to demonstrate its potential spin-filter applicability at room temperature. Two alloys, CoFeTiSn and CoFeTiGa, were prepared using arc-melting by Chatterjee et al.,35 and CoFeVSi films have been grown by Yamada et al.36 via molecular beam epitaxy. All of them possess extremely interesting magnetic and transport properties. Recently, CoFeV1−xMnxSi films with positive linear magnetoresistance (PLMR) effects at low temperatures, have been prepared and characterized by Yamada et al.37 Theoretically, EQH compounds have also been the subject of many studies, and most of them are found to have the half-metallicity feature, demonstrating the suitability for spintronic technology. Otherwise, not many EQH compounds have been reported to be magnetic spin-polarized semiconductors.
In order to search for more members and provide new information for the big Heusler alloys field, we have carried out first principles calculations to predict a new EQH compound, namely MnVZrP. To the best of our knowledge, no previous studies treating this compound have been performed. Herein, our main aim is to design the structure, examine the stability, as well as investigate the electronic, magnetic and elastic properties of the proposed material. It is expected that the material designed here will be experimentally prepared soon for applications in spintronic devices. We anticipate that MnVZrP exhibits magnetic semiconducting behavior, which makes it suitable for spin-filter devices.
2 Computational details
Density functional theory (DFT)38 is an efficient approach to calculate and predict properties of materials. In this work, the study of the structural, electronic, magnetic and elastic properties of the new equiatomic quaternary Heusler compound, MnVZrP, has been carried out using the all-electron full-potential linearized augmented plane-wave (FP-LAPW) method, which is executed in the WIEN2k package.39 The revised version of the Perdew–Burke–Ernzerhof generalized gradient approximation (GGA-PBESol) is adopted for the exchange–correlation. It is well known that the band structure, electron density and magnetic properties of solids, including the highly correlated systems, are accurately described by the mBJ potential,40–43 which has been successfully applied to study the EQH compounds.44,45 In addition, a much more balanced description of the band gaps can be achieved using a reparametrization of the coefficients proposed by Koller et al.46 (mBJK). Therefore, the mBJK potential is also included in the calculation of electronic and magnetic properties of the compound studied here. A k-mesh size of 10 × 10 × 10 is used in the Brillouin zone integrations. Electronic states are expanded in plane wave basis functions up to RMTKmax = 8, RMT and Kmax indicate the magnitude of the smallest muffin-tin radius and largest wave vector in the cell. The largest quantum number of the spherical harmonics is lmax = 10. An energy tolerance of 10−4 Ryd is selected for the self-consistent iterations.3 Results and discussion
3.1 Structural properties
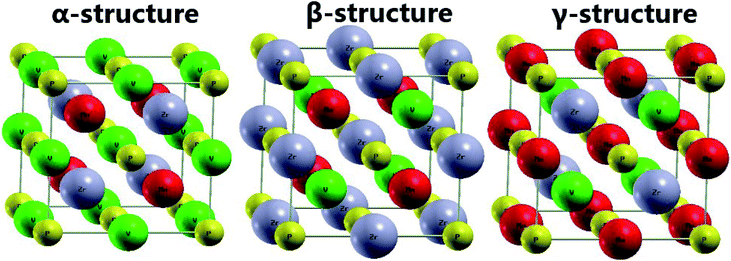
The EQH compound MnVZrP crystallizes in a face-centered cubic (FCC) structure ascribed to the F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m space group, in which there are four unit formulae with Wyckoff positions at A(0; 0; 0), B(0.5; 0.5; 0.5), C(0.25; 0.25; 0.25) and D(0.75; 0.75; 0.75). By fixing the P atom at the A(0; 0; 0) position, three possible atomic arrangements can be formed as listed in Table 1, and each of them forms a different structure, namely, the α-, β- and γ-structure. In Fig. 2 these structures are displayed. In order to determine the most favorable structure, we calculate the energy of the non-magnetic (NM) and ferromagnetic (FM) states for all three structures varying the cell volume. Fig. 3 shows the energy difference ΔE = E − Eβ-FM. Note that in all cases ΔE takes a positive value, indicating that the ferromagnetic β-structure is the most stable in terms of the energy provided, it possesses the lowest energy at a given volume. The ground state structural parameters are determined using the Birch–Murnaghan equation of state:47
3m space group, in which there are four unit formulae with Wyckoff positions at A(0; 0; 0), B(0.5; 0.5; 0.5), C(0.25; 0.25; 0.25) and D(0.75; 0.75; 0.75). By fixing the P atom at the A(0; 0; 0) position, three possible atomic arrangements can be formed as listed in Table 1, and each of them forms a different structure, namely, the α-, β- and γ-structure. In Fig. 2 these structures are displayed. In order to determine the most favorable structure, we calculate the energy of the non-magnetic (NM) and ferromagnetic (FM) states for all three structures varying the cell volume. Fig. 3 shows the energy difference ΔE = E − Eβ-FM. Note that in all cases ΔE takes a positive value, indicating that the ferromagnetic β-structure is the most stable in terms of the energy provided, it possesses the lowest energy at a given volume. The ground state structural parameters are determined using the Birch–Murnaghan equation of state:47
 | (1) |
| Mn | V | Zr | P | |
|---|---|---|---|---|
| α-Structure | (0.25; 0.25; 0.25) | (0.5; 0.5; 0.5) | (0.75; 0.75; 0.75) | (0; 0; 0) |
| β-Structure | (0.25; 0.25; 0.25) | (0.75; 0.75; 0.75) | (0.5; 0.5; 0.5) | (0; 0; 0) |
| γ-Structure | (0.5; 0.5; 0.5) | (0.75; 0.75; 0.75) | (0.25; 0.25; 0.25) | (0; 0; 0) |
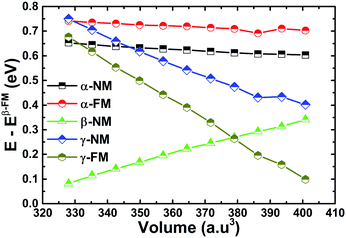 | ||
| Fig. 3 Energy difference versus volume of the equiatomic quaternary Heusler compound MnVZrP (energy of the β-structure in the ferromagnetic state is set as the reference). | ||
In theoretical work, calculations of the formation energy Ef and cohesive energy Ec are frequently carried out using the following expressions:
 | (2) |
 | (3) |
3.2 Electronic properties
The spin-resolved band structure of EQH compound MnVZrP within its optimized lattice parameter has been calculated using the PBESol and mBJK potentials, as illustrated in Fig. 5. Both theories predict that the valence band maximum (VBM) touches the Fermi level at Γ point in the case of the spin-up channel, while the conduction band minimum (CBM) occurs at the Γ point and along ΓX direction as determined by the PBESol and mBJK potential, respectively. The direct and indirect band gap values are 0.33 and 0.97 eV, respectively. At the same time, the PBESol functional finds the metallic nature for the spin-dn channel provided that the CBM along the WL direction takes place at an energy of 0.09 eV below the Fermi level. However, this spin-dn CBM point is located above the Fermi level as determined by the mBJK potential, giving rise to a clear semiconductor nature. It is worth recalling that the PBESol functional may underestimate the electronic band gap of solids and inefficiently treats the highly correlated electrons as those in transition metals, however, these issues are considerably overcome using the mBJK potential. Therefore, we believe that the mBJK potential results are more reliable, that is, the EQH compound MnVZrP exhibits semiconductor behavior in both of its spin configurations. The spin-dn band gap is 0.47 eV resulting from the VBM at −0.31 eV and CBM at 0.16 eV, and both of them are situated along the WL direction. Moreover, significant magnetism can be expected in the material studied here as its band structure shows strong asymmetry between the spin-up and spin-dn states. Results show clearly the magnetic semiconducting characteristics of the studied compound, and show that prospectively it could be used as a spin-filter material in spintronic devices. | ||
| Fig. 5 Spin-resolved band structure of the equiatomic quaternary Heusler compound MnVZrP, calculated with PBESol and mBJK potentials. | ||
The total density of states (TDOS) and projected density of states (PDOS) yield additional information to describe electronic properties. Fig. 6 shows the TDOS and PDOS of the EQH compound MnVZrP, in which the positive DOS values represent the spin-up state, and negative DOS values indicate the spin-dn state. Note that in the energy range from −2 to 2 eV, the Mn-3d, V-3d and Zr-4d states are the most populated, while the contribution from the s and p orbitals of all four constituent atoms is quite small. It can be seen that in the spin-up channel, the Mn-dt2g and V-dt2g state make the most important contributions to the upper part of the valence band, whereas the Mn-deg and V-deg state are the main contributors to the lower part of the conduction band. Sub-bands nearest to the Fermi level are formed by the Mn-dt2g, V-dt2g and Zr-dt2g electrons. Results suggest that the spin-polarized semiconductor behavior of the EQH compound MnVZrP is governed mainly by the bonding and anti-bonding states generated by the d–d interactions of the transition metals. Based on the DOS profiles, the mechanism of the d–d interaction, as well as d-electrons distribution in the considered compound, are indicated in Fig. 7. Specifically, the interaction of double-degenerated states Mn-deg and V-deg, generates the two-fold bonding state 2eg and two-fold antibonding state 2eu, while the three-fold bonding state 3t2g and three-fold antibonding state 3tu are induced by the Mn-dt2g and V-dt2g states. Eight 3d electrons (5 of Mn and 3 of V) fill the spin-up channel of the 2eg, 3t2g and 3tu states, leaving the 2eu state totally unoccupied in the lower conduction band part. At the same time, the 3t2g state hybridizes with the Zr-dt2g state yielding the formation of the three-fold 3tt2g bonding state and 3ttu anti-bonding state. While the interaction between the 2eg state with the Zr-deg gives place to the formation of the two-fold 2eeg bonding state and 2eeu anti-bonding state. 7 electrons coming from the 2eg, 3t2g and Zr-deg, occupy the last two mentioned bonding states. From the presented analysis, we can conclude that the 3tu and 2eu states formed the valence band upper part and conduction band lower part in the spin-up channel, while the spin-dn channel band gap is generated by the separation of the 3tt2g and 3tu states.
 | ||
| Fig. 6 Total and projected density of states of the equiatomic quaternary Heusler compound MnVZrP calculated with mBJK potential. | ||
 | ||
| Fig. 7 Mechanism of d–d interactions and d-electrons distribution in the equiatomic quaternary Heusler compound MnVZrP. | ||
In the next step, we examine the strain effect on the MnVZrP compound’s electronic structure. The strain is defined by means of a small lattice distortion as follows:  , the equilibrium and strained states are represented by their corresponding lattice parameter a and a0, respectively. The VBM and CBM positions calculated at different strains from −6% to 6% are listed in Table 2, and the results are plotted in Fig. 8 for visualization. In the case of the spin-dn channel, both VBM and CBM increase in terms of energy in most of the considered strain range when switching the strain from compressive to tensile, with exception of the CBM from a tension strength of 4%. Clearly, the MnVZrP spin-dn state retains the semiconductor nature for the strain ranging from −4% to 5% with the band gap increasing from compressive to tensile strain, beyond this it becomes metallic as either the CBM is found below the Fermi level or the VBM is above the Fermi level. Passing to the spin-up channel, the CBM approaches the Fermi level once the strain is applied to the lattice, it appears that the CBM is more sensitive to the tensile strains than to the compressive strain. Negligible variation is observed for the VBM, which is found at 0 eV in the strain range −4% to 4%. From a compression and tension strength of ±5%, the studied material exhibits a metallic spin-up channel. It is worth mentioning that the half-metallicity is achieved at a tensile strain of 5%, at the same time the spin-dn and spin-up configurations show metallic and semiconductor behavior, respectively.
, the equilibrium and strained states are represented by their corresponding lattice parameter a and a0, respectively. The VBM and CBM positions calculated at different strains from −6% to 6% are listed in Table 2, and the results are plotted in Fig. 8 for visualization. In the case of the spin-dn channel, both VBM and CBM increase in terms of energy in most of the considered strain range when switching the strain from compressive to tensile, with exception of the CBM from a tension strength of 4%. Clearly, the MnVZrP spin-dn state retains the semiconductor nature for the strain ranging from −4% to 5% with the band gap increasing from compressive to tensile strain, beyond this it becomes metallic as either the CBM is found below the Fermi level or the VBM is above the Fermi level. Passing to the spin-up channel, the CBM approaches the Fermi level once the strain is applied to the lattice, it appears that the CBM is more sensitive to the tensile strains than to the compressive strain. Negligible variation is observed for the VBM, which is found at 0 eV in the strain range −4% to 4%. From a compression and tension strength of ±5%, the studied material exhibits a metallic spin-up channel. It is worth mentioning that the half-metallicity is achieved at a tensile strain of 5%, at the same time the spin-dn and spin-up configurations show metallic and semiconductor behavior, respectively.
| Band edges | Magnetic moments | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| dn-VBM | dn-CBM | up-VBM | up-CBM | Total | Mn | V | Zr | P | |
| −6% | −0.84 | −0.20 | 0.03 | 0.49 | 2.85 | 1.10 | 1.58 | −0.03 | 0.00 |
| −5% | −0.70 | −0.10 | 0.01 | 0.55 | 2.91 | 1.13 | 1.62 | −0.03 | 0.00 |
| −4% | −0.57 | 0.01 | 0.00 | 0.70 | 2.95 | 1.14 | 1.67 | −0.04 | −0.01 |
| −3% | −0.50 | 0.06 | 0.00 | 0.79 | 2.96 | 1.11 | 1.69 | −0.03 | −0.01 |
| −2% | −0.42 | 0.11 | 0.00 | 0.87 | 2.99 | 1.15 | 1.73 | −0.05 | −0.01 |
| −1% | −0.38 | 0.12 | 0.00 | 0.93 | 3.00 | 1.16 | 1.74 | −0.06 | −0.02 |
| 0% | −0.31 | 0.16 | 0.00 | 0.97 | 3.00 | 1.18 | 1.76 | −0.08 | −0.03 |
| 1% | −0.25 | 0.18 | 0.00 | 0.80 | 3.00 | 1.22 | 1.77 | −0.11 | −0.03 |
| 2% | −0.21 | 0.19 | 0.00 | 0.55 | 3.00 | 1.33 | 1.77 | −0.17 | −0.04 |
| 3% | −0.16 | 0.21 | 0.00 | 0.33 | 3.00 | 1.27 | 1.80 | −0.14 | −0.04 |
| 4% | −0.11 | 0.23 | 0.00 | 0.12 | 3.00 | 1.29 | 1.81 | −0.16 | −0.05 |
| 5% | −0.08 | 0.05 | 0.00(1) | −0.10 | 3.00 | 1.29 | 1.82 | −0.17 | −0.05 |
| 6% | 0.01 | −0.11 | 0.02 | −0.02 | 3.00 | 1.37 | 1.79 | −0.21 | −0.06 |
3.3 Magnetic properties
As analyzed above, the asymmetric spin-resolved band structure may lead to significant magnetism in the MnVZrP compound. Since the MnVZrP has 21 valence electrons Zt (7 of Mn atom, 5 of V atom, 4 of Zr atom and 5 of P atom), a total spin magnetic moment Mt of 3 μB can be expected when using the Slater–Pauling rule:49| Mt = Zt − 18 | (4) |
At equilibrium, FP-LAPW results do obey eqn (4), that is, a total magnetic moment of 3 μB. The magnetism is produced mainly by the 3d transition metals with the atomic magnetic moments of Mn and V being 1.18 and 1.76 μB, respectively. It is important to clarify that these positive values evidence the ferromagnetic coupling between Mn and V atoms in the studied EQH compound. Moreover, the Zr- and P-contribution is quite small, with local atomic moments of −0.08 and −0.03 μB, respectively.
Total and atomic spin magnetic moments at different strains are listed in Table 2 and are plotted for visualization in Fig. 8c. Note that the integer total magnetic moment of 3 μB is retained in the strain range from −1% to 6%, in contrast stronger compressive strains induce a slight reduction of this parameter. The local atomic moment of the 3d transition metals increases when switching from lattice compression to tension. However, the opposite behavior is observed for Zr and P atoms. It is well known that a magnetic moment is the difference of the spin-up charge and spin-dn charge. Results suggest that the total spin-dn charge increases slightly with compressive strain, which can be attributed mainly to the stronger interaction of the d–d orbitals in the considered material being favored by the interatomic distance.
3.4 Elastic properties
In practical applications, materials suffer stress frequently which may generate structural deformations, and their ability to return to their original form after removing the stress is measured using elastic constants. Therefore, these constants are also indicative of the materials mechanical and physical properties. In this work, we calculate three different elastic constants C11, C12 and C44 of MnVZrP, which are sufficient to investigate the elastic properties of materials adopting a cubic structure. To achieve this goal, the energy is calculated when small orthorhombic, cubic and tetragonal strains are applied to the lattice, and the elastic constants are determined by the second derivative of the energy with respect to strain (see Appendix). Our calculated elastic constants are: C11 = 253.01 GPa, C12 = 143.88 GPa and C44 = 94.53 GPa.Mechanical stability Born criteria:50 C11 > C12; C11 > 0; C44 > 0 and C11 + 2C12 > 0 have been widely employed for solids, here we adopt these criteria. Note that for the EQH compound MnVZrP, elastic constants satisfy all the mentioned criteria, indicating that the material is mechanically stable. Moreover, greater resistance to the longitudinal deformation in comparison to that of the shear deformation is also demonstrated provided that the C11 is considerably larger than C44. Further, various important mechanical parameters including bulk modulus, shear modulus, and Young’s modulus can be calculated from elastic constants (see Appendix). In general, bulk modulus and shear modulus provide important information on the hardness of materials, while their stiffness is characterized by the Young’s modulus. Calculations give the values of the bulk modulus, shear modulus, and Young’s modulus as 180.26, 75.83 and 199.51 GPa, respectively.
Another important property that shall be examined is the ductile and brittle character of materials. The Pugh’s index (B/G) and Poisson’s ratio (see Appendix) with values larger than their critical points of 1.75 and 0.26, respectively, are indicative of the ductility, and otherwise the brittleness is suggested. In the case of MnVZrP, these parameters take values of 2.38 and 0.32, respectively. These results in combination with the positive Cauchy pressure (C12–C44) indicate that the considered EQH compound is mechanically ductile.
The crack formation and intrinsic defects distribution within materials are linked to the elastic anisotropy, an important parameter that should be taken into account during material design. An elastically isotropic material will have a unity value of the elastic anisotropy. the calculated value of the MnVZrP compound is 1.73, significantly deviating from unity, indicating that the material studied here is elastically anisotropic. Additionally, we also examine the elastic anisotropy by calculating the directional dependent Young’s modulus and shear modulus, their 3D surface construction and corresponding 2D projections are visualized by ELATE code,51 and are exhibited in Fig. 9 and 10. The totally spherical surfaces indicate the elastic isotropy, while the greater the deviation from a sphere form, the more anisotropic the material. Clearly, MnVZrP is classified as an elastically anisotropic material provided that non-spherical surfaces are obtained, in particular, stronger deviation is observed in the shear modulus.
 | ||
| Fig. 9 Directional dependence of Young’s modulus of the equiatomic quaternary Heusler compound MnVZrP. | ||
 | ||
| Fig. 10 Directional dependence of the shear modulus of the equiatomic quaternary Heusler compound MnVZrP. | ||
4 Conclusions
In conclusion, the structural, electronic, magnetic and elastic properties of the new EQH compound MnVZrP have been comprehensively investigated using first principles calculations based on DFT. The most significant results of the work are:• MnVZrP crystallizes in the FCC structure (space group F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m), where Mn, V, Zr and P are located at the 4c, 4d, 4b and 4a Wyckoff positions, respectively.
3m), where Mn, V, Zr and P are located at the 4c, 4d, 4b and 4a Wyckoff positions, respectively.
• Thermodynamic and structural stability are confirmed by the negative formation and cohesive energies, respectively, suggesting the experimental realization of the material at hand.
• Semiconductor behavior is found in both spin channels, and is generated by the partially occupied hybridized states resulting from the d–d interactions of the transition metals.
• At equilibrium, Mn and V are the main contributors to the magnetism with atomic spin moments of 1.18 and 1.76 μB, respectively.
• Study of the strain effect shows that the material retains magnetic semiconductor characteristics in the range from −4% to 4%, in contrast the half-metal is induced with a tensile strain of 5%.
• The MnVZrP compound is mechanically stable with greater resistance to longitudinal deformation than to shear deformation. The elastic ductility and anisotropy of the material are also demonstrated.
We hope that these results motivate experimental work to synthesize and characterize the MnVZrP compound for spin-filter applications, proving that spin-polarized semiconductor characteristics are found in this material making it suitable for practical applications.
Appendices
The energy is expressed according to Hooke’s law as follows:
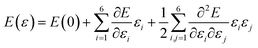 | (5) |
Elastic constants are calculated through the second derivative of energy:
 | (6) |
Derivation of related parameters from the calculated C11, C12 and C44 constants of the cubic structure:
Bulk modulus B:
 | (7) |
Shear modulus G:
 | (8) |
 | (9) |
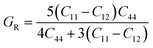 | (10) |
Young’s modulus:
 | (11) |
Elastic anisotropy A:
 | (12) |
Poisson’s ratio:
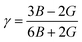 | (13) |
Conflicts of interest
No conflicts of interest to declare.Acknowledgements
This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 103.01-2019.348.Notes and references
- I. Žutić, J. Fabian and S. D. Sarma, Rev. Mod. Phys., 2004, 76, 323 CrossRef.
- V. K. Joshi, Eng. Sci. Technol., 2016, 19, 1503–1513 Search PubMed.
- I. Galanakis, K. Özdoğan and E. Şaşıogglu, J. Phys.: Condens. Matter, 2014, 26, 086003 CrossRef CAS PubMed.
- I. Galanakis, K. Özdoğan and E. Şaşıoğlu, AIP Adv., 2016, 6, 055606 CrossRef.
- H. Sukegawa, S. Kasai, T. Furubayashi, S. Mitani and K. Inomata, Appl. Phys. Lett., 2010, 96, 042508 CrossRef.
- K. Kodama, T. Furubayashi, H. Sukegawa, T. Nakatani, K. Inomata and K. Hono, J. Appl. Phys., 2009, 105, 07E905 CrossRef.
- T. Ishikawa, T. Marukame, H. Kijima, K.-I. Matsuda, T. Uemura, M. Arita and M. Yamamoto, Appl. Phys. Lett., 2006, 89, 192505 CrossRef.
- Z. Gercsi, A. Rajanikanth, Y. Takahashi, K. Hono, M. Kikuchi, N. Tezuka and K. Inomata, Appl. Phys. Lett., 2006, 89, 082512 CrossRef.
- S. Chadov, T. Graf, K. Chadova, X. Dai, F. Casper, G. H. Fecher and C. Felser, Phys. Rev. Lett., 2011, 107, 047202 CrossRef PubMed.
- R. Farshchi and M. Ramsteiner, J. Appl. Phys., 2013, 113, 7_1 CrossRef.
- R. De Groot, F. Mueller, P. Van Engen and K. Buschow, Phys. Rev. Lett., 1983, 50, 2024 CrossRef CAS.
- F. Dahmane, Y. Mogulkoc, B. Doumi, A. Tadjer, R. Khenata, S. B. Omran, D. Rai, G. Murtaza and D. Varshney, J. Magn. Magn. Mater., 2016, 407, 167–174 CrossRef CAS.
- D. Hoat, J. Rivas-Silva and A. M. Blas, J. Comput. Electron., 2018, 17, 1470–1477 CrossRef CAS.
- A. O. Oliynyk, E. Antono, T. D. Sparks, L. Ghadbeigi, M. W. Gaultois, B. Meredig and A. Mar, Chem. Mater., 2016, 28, 7324–7331 CrossRef CAS.
- C. S. Birkel, W. G. Zeier, J. E. Douglas, B. R. Lettiere, C. E. Mills, G. Seward, A. Birkel, M. L. Snedaker, Y. Zhang and G. J. Snyder, et al., Chem. Mater., 2012, 24, 2558–2565 CrossRef CAS.
- D. Hoat, Comput. Mater. Sci., 2019, 159, 470–477 CrossRef CAS.
- T. Djaafri, A. Djaafri, A. Elias, G. Murtaza, R. Khenata, R. Ahmed, S. B. Omran and D. Rached, Chin. Phys. B, 2014, 23, 087103 CrossRef.
- D. Hoat and M. Naseri, Phys. B, 2020, 583, 412058 CrossRef CAS.
- Y. Han, Y. Wu, T. Li, R. Khenata, T. Yang and X. Wang, Materials, 2018, 11, 797 CrossRef PubMed.
- G. Gao, K. Yao, E. Şaşıoğlu, L. Sandratskii, Z. Liu and J. Jiang, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 174442 CrossRef.
- G. Gao, K. Yao, Z. Liu, J. Jiang, L. Yu and Y. Shi, J. Phys.: Condens. Matter, 2007, 19, 315222 CrossRef CAS PubMed.
- D. Hoat, J. Rivas-Silva and A. M. Blas, Chin. J. Phys., 2018, 56, 3078–3084 CrossRef CAS.
- K. Kenmochi, V. Ann Dinh, K. Sato, A. Yanase and H. Katayama-Yoshida, J. Phys. Soc. Jpn., 2004, 73, 2952–2954 CrossRef CAS.
- M. Ilkhani, A. Boochani, M. Amiri, M. Asshabi and D. P. Rai, Solid State Commun., 2020, 308, 113838 CrossRef CAS.
- V. Alijani, J. Winterlik, G. H. Fecher, S. S. Naghavi and C. Felser, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 184428 CrossRef.
- E. Şaşıoğlu, L. Sandratskii and P. Bruno, J. Appl. Phys., 2005, 98, 063523 CrossRef.
- M. Meinert, C. Friedrich, G. Reiss and S. Blügel, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 245115 CrossRef.
- S. A. Khandy, I. Islam, D. C. Gupta, R. Khenata and A. Laref, Sci. Rep., 2019, 9, 1–8 CrossRef CAS PubMed.
- I. H. Bhat, T. M. Bhat and D. C. Gupta, J. Phys. Chem. Solids, 2018, 119, 251–257 CrossRef CAS.
- I. Galanakis, K. Özdoğan, E. Şaşıoğlu and S. Blügel, J. Appl. Phys., 2014, 115, 093908 CrossRef.
- G. Xu, E. Liu, Y. Du, G. Li, G. Liu, W. Wang and G. Wu, EPL, 2013, 102, 17007 CrossRef.
- X. Wang, Z. Cheng, G. Liu, X. Dai, R. Khenata, L. Wang and A. Bouhemadou, IUCrJ, 2017, 4, 758–768 CrossRef CAS PubMed.
- L. Bainsla and K. Suresh, Appl. Phys. Rev., 2016, 3, 031101 Search PubMed.
- G. M. Stephen, I. McDonald, B. Lejeune, L. H. Lewis and D. Heiman, Appl. Phys. Lett., 2016, 109, 242401 CrossRef.
- S. Chatterjee, S. Das, S. Pramanick, S. Chatterjee, S. Giri, A. Banerjee and S. Majumdar, J. Magn. Magn. Mater., 2019, 478, 155–160 CrossRef CAS.
- S. Yamada, S. Kobayashi, F. Kuroda, K. Kudo, S. Abo, T. Fukushima, T. Oguchi and K. Hamaya, Phys. Rev. Mater., 2018, 2, 124403 CrossRef CAS.
- S. Yamada, S. Kobayashi, A. Masago, L. Kumara, H. Tajiri, T. Fukushima, S. Abo, Y. Sakuraba, K. Hono and T. Oguchi, et al., Phys. Rev. B, 2019, 100, 195137 CrossRef CAS.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- K. Schwarz and P. Blaha, Comput. Mater. Sci., 2003, 28, 259–273 CrossRef CAS.
- A. Becke and E. Johnson, J. Chem. Phys., 2006, 124, 221101 CrossRef PubMed.
- F. Tran, P. Blaha and K. Schwarz, J. Phys.: Condens. Matter, 2007, 19, 196208 CrossRef.
- F. Tran and P. Blaha, Phys. Rev. Lett., 2009, 102, 226401 CrossRef PubMed.
- D. Koller, F. Tran and P. Blaha, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195134 CrossRef.
- H. Kara, M. U. Kahaly and K. Özdoğan, J. Alloys Compd., 2018, 735, 950–958 CrossRef CAS.
- S. A. Khandy and J.-D. Chai, J. Appl. Phys., 2020, 127, 165102 CrossRef.
- D. Koller, F. Tran and P. Blaha, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 155109 CrossRef.
- F. Birch, J. Geophys. Res.: Solid Earth, 1978, 83, 1257–1268 CrossRef CAS.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. Probert, K. Refson and M. C. Payne, Z. Kristallogr. - Cryst. Mater., 2005, 220, 567–570 CAS.
- S. Skaftouros, K. Özdoğan, E. Şaşıoğlu and I. Galanakis, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 024420 CrossRef.
- F. Mouhat and F.-X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef.
- R. Gaillac, P. Pullumbi and F.-X. Coudert, J. Phys.: Condens. Matter, 2016, 28, 275201 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2020 |