New refractory MAB phases and their 2D derivatives: insight into the effects of valence electron concentration and chemical composition

Abstract

Since MAB (where M is a transition metal, A is an groups 13–16 element, and B is boron) phases possess good electrical conductivity, high-temperature oxidation and shock resistance, it is meaningful to develop a database to help us figure out optimal compositions and further promote their applications. In this paper, we screened and studied all the available MABs with the M-site being one of the 3d, 4d, or 5d transition metals by using an ab initio method. Among them, 23 MAB phases of M₂Al₂B₂ (222-MAB phases with M = Ti, V, Nb, Ta, Cr, Mo, W, Mn, and Tc) and M₂AlB₂ (212-MAB phases with M = Sc, Ti, Zr, Hf, V, Nb, Cr, Mo, W, Mn, Tc, Fe, Co, and Ni) stand out in terms of structural stability and their electronic, mechanical, optical and thermodynamic properties have been investigated. For both types of MAB phases early transition elements are more feasible to synthesize than post transition elements, because of the lower number of valence electrons and lower formation energy. The effect of valence electron concentration and composition of MAB compounds could also enable fine tuning of their mechanical properties. The bulk modulus, shear modulus, and Young's modulus of the 222-MAB phases are in the range of 145–233 GPa, 101–145 GPa, and 252–361 GPa, respectively, while they are 152–262 GPa, 91–177 GPa, and 237–422 GPa for the 212-MAB phases, respectively. Their mechanical ductilities also show strong valence electron number dependency, with their maximum value occurring at Ni₂AlB₂ and Co₂AlB₂, respectively. More interestingly, a low thermal expansion coefficient and good high temperature strength have also been found in those MAB phases, which are favorable for their potential applications as refractory materials. In addition, the possibility of forming new two-dimensional (2D) materials from layered MAB phases, termed MBenes, is predicted by investigating the interplay of the tensile strain, complex chemical bonding and exfoliation energy.

---

1. Introduction

“MAX phases”, originally studied in the 1960s,^1–4 are a family of 80+ ternary carbides and nitrides that share a common type of layered structure. They are named “MAX” because of their chemical formula: M_n+1AX_n, where n = 1, 2, or 3, M is a transition metal, A is an A-group element (specifically, the subset of group 13–16 elements), and X is either carbon or nitrogen. MAX phases have some outstanding properties and behave like both metals and ceramics.⁵ Like metals, they have good thermal and electrical conductivity, thermal shock resistance, machinability, and damage tolerance. Like ceramics, they are light weight, stiff, refractory, and oxidation resistant. Owing to this unique combination of properties, MAX phases are well developed as high temperature foil bearings, heating elements, and sputtering targets for electrical contact deposition.

Another group of compounds, MAB phases, as boron analog of MAX phases, contain stacked M–B blocks and interleaved with A-atom planes. The first MAB-type phase, MoAlB, was synthesized in 1942 by Halla and Thury.⁶ Soon afterward, the Mo–Al–B ternary phase diagram has been determined using cold compress and weld. In experiment at 1000 °C, MoAlB is indeed stable with a relatively narrow stoichiometric range.⁷ Meanwhile, X-ray diffraction data indicated that this MoAlB compound crystallized with an orthorhombic structure (Cmcm space group).⁸ Although MoAlB has been successfully synthesized, MAB phases as a class of compounds were not widely investigated until recently. Benefited from the development of synthesis technique, MAB phases have recovered to be an interesting topic now. The number of pure MAB phases as well as their solid solutions continues to expand. For example, an isostructural member of MoAlB with transition metal element W has been reported.^9,10 A new series competing phase, 212-MAB phases have been successfully prepared, such as Fe₂AlB₂ and Cr₂AlB₂.^10,11 In addition, solid-solution single-crystals, (Mo_x, M_1−x)AlB with M = Cr and W¹² and (Fe₂, M_2−x)AlB₂ with M = Cr and Mn, have been also synthesized recently.¹³

The discovery of the versatile structures endows MAB phases many interesting properties, such as near room-temperature (RT) magnetocaloric properties,¹⁴ high-temperature oxidation resistance,¹⁵ shock resistance,¹⁶ and electrocatalytic properties.^17,18 Ke et al. investigated the intrinsic magnetic properties of Fe₂AlB₂-related compounds and their alloys.¹⁹ They found Mn₂AlB₂ to be ferromagnetic within the basal ab plane and antiferromagnetic along the c axis. All 3d transition metal doping will decrease the magnetization and Curie temperature in Fe₂AlB₂. At ground-states and high temperatures, the mechanical and thermal properties of MAB (M = Mo and W) were thoroughly calculated by Xiang et al.,²⁰ which confirm their high-temperature stability. The nature of bonding and mechanical properties in some MAB (M = Cr, W, Mo) compounds has been studied.^21–23 Bai et al.²¹ found that, similar to Mo₂AlC, MoAlB also have good mechanic properties for the potential engineering applications. Dai et al.²² and Zhou et al.²³ discussed the potential impacts of strong B–B/M–B bonds and the weaker Al–Al/M–Al bonds on high elastic modulus and damage tolerance of MAlB. The optical conductivity of MoAlB has been further investigated by Li et al., and they found high reflectivity in the visible-ultraviolet region up to ∼19 eV region,²⁴ which make it possible to use as coating material. By combining theory with experiments, Kádas et al.¹¹ studied the mechanical properties of AlM₂B₂ (M = Cr, Mn, Fe, Co and Ni) and predicted their brittle or ductile behavior with different M metals. They further presented evidences of delamination phenomena and discussed the mechanism.

It is expected that the growing family of MAB phases and their properties would have significant applications like MAX phases. However, a large number of MAB compounds are still unexplored by considering the diverse elements combinations. As for just 211-M₂AX compounds, the possible stable phases have 1080 candidate structures. Moreover, the constructed structure maps will help us understand the stability trends and give the guideline to experimental synthesis of new MAB phases. Therefore, in this paper, we mainly focus on constructing a structure map for MAB compounds with compositions of 2 : 2 : 2 and 2 : 1 : 2, respectively. We start from the possible compositions of MAB phases with the M-site metal being one of the 3d, 4d and 5d transition metals and A site being generally accepted Al element. By high-throughput DFT calculations, 23 stable MAB phases: nine 222-MAB phases (M = Ti, V, Nb, Ta, Cr, Mo, W, Mn, and Tc) and fourteen 212-MAB phases (M = Sc, Ti, Zr, Hf, V, Nb, Cr, Mo, W, Mn, Tc, Fe, Co and Ni) have been identified by rigorous structural stability analysis. Along with the calculations of electronic structure, mechanical properties, chemical bonding, delamination properties, thermal and optical conductivities, the effects of valence electron number and compositions have been further discussed. Although the sparse data of electronic structure and mechanical properties have already reported for few MAB phases,^{11,13,14,19,21} a comprehensive study using an unified computational method would be helpful for deep understanding of the overall trend relationship between stability/properties and chemical compositions.

2. Theoretical methods

The electronic structures of the MAB phases were calculated using density functional theory (DFT)²⁵ implemented in the VASP code.^26,27 We employed the projected augmented wave (PAW) method^28,29 to treat outermost electrons as valence electrons for atoms in MAB phases, respectively. The Perdew–Burke–Ernzerh of (PBE) parameterization³⁰ within the generalized gradient approximation (GGA) was adopted to describe the exchange and correlation interactions. Integrations over the Brillouin zone were performed using Monkhorst–Pack grids³¹ with uniform spacing of 2π × 0.03 Å⁻¹. The plane-wave cutoff energy was set to 500 eV. The optical conductivities were calculated by using CASTEP program.³² The dynamic stability of the constructed structures was assessed by phonon dispersion, which were computed using a supercell approach as implemented in the PHONOPY code.³³

For the equilibrium crystal structure, its second-order elastic constants (C_ij) were determined using a finite strain technique,³⁴ and bulk and shear moduli were thus derived from the elastic constants using the Voigt–Reuss–Hill averaging scheme.³⁵ The calculations of stress–strain relations were performed using the method in ref. 36. This approach with a relaxed loading path has been successfully applied to the calculation of the strength of several strong solids. Hardness were estimated based on the empirical formula developed by Jiang et al.³⁷ The quasi-harmonic Debye model³⁸ implemented in the Gibbs2 program³⁸ was employed to determine the thermodynamic properties at ambient conditions and elevated temperatures and pressures.

3. Results and discussions

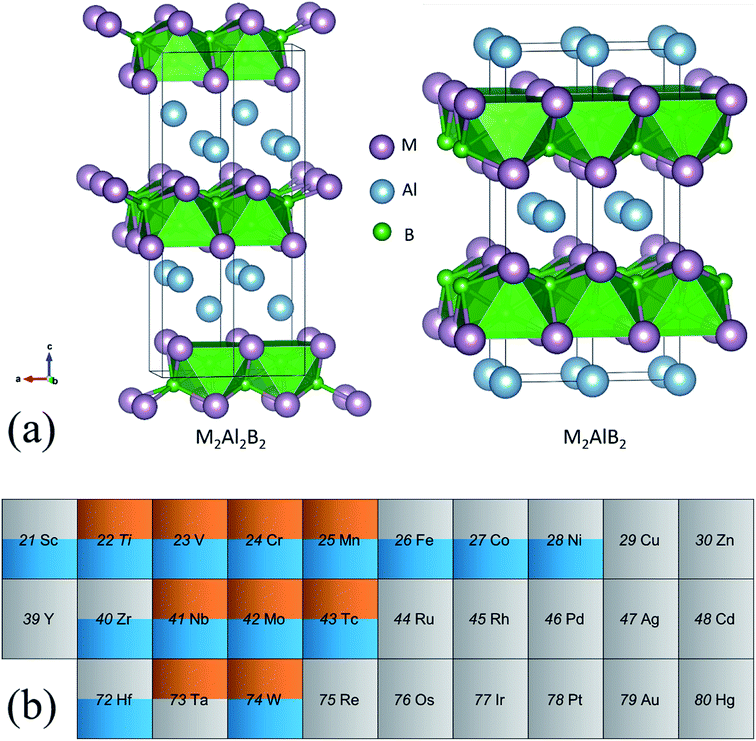
Based on experimental confirmations,^8,10,39 the crystal structures of two types of MAB phases with stoichiometry of 2 : 2 : 2 and 2 : 1 : 2 are displayed in Fig. 1(a). According to the compositions, they are named as 222-MAB and 212-MAB phases, respectively. Here, we only focus on the generally accepted Al containing MAB phases. On one hand, the number of MAB phases is much smaller in comparison to that of the MAX-phases. The reason is that the variation of the transition metal and especially the main group metal “A” is much more restricted. Up to now, mostly MAB-phases are characterized only for A = Al.¹⁰ On the other hand, only the Al containing MAX-phases and MAB-phases are identified experimentally as the likely precursors to achieve a high-yield synthesis of two-dimensional MXene⁴⁰ and MBene.^41–44 As seen from the Fig. 1(a), the difference between 222-MAB and 212-MAB phases is the thickness of the Al layers, that is, the binary M–B boride are separated by single and double Al layers, respectively. In addition, both types of MAB phases are crystallized in orthorhombic lattices but with different atomic arrangements, i.e., space group of Cmcm for 222-MAB phases and space group of Cmmm for 222-MAB. To obtain the potentially unreported MAB phases, transition metals in 3d (Ti, V, Cr, Mn, Fe, Co, Ni, Cu and Zn), 4d (Zr, Nb, Mo, Tc, Ru, Rh, Pd, Ag and Cd) and 5d (Hf, Ta, W, Re, Os, Ir, Pt, Au and Hg) series are systematically investigated by first-principles calculations.

Fig. 1 (a) Crystal structure of (left) 222-MAB compounds and (right) 212-MAB compounds. (b) Transition metal element table of the structure stabilities in MAB, the orange/blue color means stable and the grey color means unstable, while the upper and lower parts in an element grid are correspond to 222-MAB type and 212-MAB typed phases, respectively.

We first assess the dynamic, thermodynamically, and mechanical stabilities of totally 58 MAB phases in terms of the phonon dispersions, formation energy, and elastic constants. Among them, nine 222-MAB phases (M = Ti, V, Nb, Ta, Cr, Mo, W, Mn, and Tc) and fourteen 212-MAB phases (M = Sc, Ti, Zr, Hf, V, Nb, Cr, Mo, W, Mn, Tc, Fe, Co, and Ni) stand out (Fig. 1(b)). The lattice parameters, mass densities per formula unit obtained for those MAB phases are listed in Tables 1 and 2. For comparison, the previous experimental and theoretical results of 222-MABs with M = Mo, W and 212-MABs with M = Cr, Mn, Fe, Co and Ni are also presented in this paper.^10,11,21 The current lattice parameters and cell volumes for the MAB compounds are in good agreement with previous experimental and theoretical values,^10,11,21 validating our methodology of DFT calculations. Generally, as the valence electron number increases in one row of periodic table, the atomic radius decreases. Thus, for 222-MABs with M = Ti, V and Cr, and 212-MABs with M = Sc, Ti, V, Cr and Mn, the increasing valence electron number directly reduce the lattice parameters and cell volumes.

Table 1 Theoretical and experimental unit cell parameters a, b, and c (in Å), mass density ρ (in gcm⁻³) and formation energy ΔE (in eV) of nine stable 222-MAB typed phases

M2Al2B	a (Å)	b (Å)	c (Å)	ρ (g cm^−3)	ΔE (eV)
Ti2Al2B2	3.049	3.297	14.641	3.87	−1.933
V2Al2B2	3.009	3.084	14.235	4.46	−1.649
Nb2Al2B2	3.124	3.359	14.675	5.64	−1.486
Ta2Al2B2	3.107	3.351	14.576	9.57	−1.453
Cr2Al2B2	2.968	3.001	13.886	4.82	−1.183
Mo2Al2B2	3.109	3.217	14.040	6.33	−1.357
Mo2Al2B2, expt.^10	3.094	3.199	13.922	6.45	—
W2Al2B2	3.118	3.217	13.985	10.50	−0.929
W2Al2B2, expt.^10	3.102	3.202	13.906	10.66	—
Mn2Al2B2	3.011	2.821	14.137	5.13	−0.937
Tc2Al2B2	3.162	3.024	14.111	6.73	−1.089

---

Table 2 Theoretical and experimental unit cell parameters a, b, and c (in Å), mass density ρ (in g cm⁻³) and formation energy ΔE (in eV) of fourteen stable 212-MAB typed phases

M2AlB2	a (Å)	b (Å)	c (Å)	ρ (g cm^−3)	ΔE (eV)
Sc2AlB2	3.185	3.613	11.745	3.40	−3.410
Ti2AlB2	3.046	3.308	11.3203	4.20	−4.034
Zr2AlB2	3.190	3.572	12.067	5.58	−3.674
Hf2AlB2	3.165	3.549	11.819	10.15	−3.441
V2AlB2	3.009	3.084	11.141	4.46	−3.043
Nb2AlB2	3.161	3.341	11.626	6.34	−2.471
Cr2AlB2	2.923	2.932	11.042	5.36	−2.447
Cr2AlB2, expt.^10	2.937	2.968	11.051	5.26	—
Mo2AlB2	3.076	3.147	11.538	7.15	−2.333
W2AlB2	3.088	3.139	11.566	12.33	−1.466
Mn2AlB2	2.893	2.821	11.063	5.83	−2.373
Mn2AlB2, expt.^10	2.918	2.893	11.038	5.65	—
Tc2AlB2	3.048	3.021	11.519	7.72	−2.316
Fe2AlB2	2.913	2.847	11.021	5.82	−2.064
Fe2AlB2, expt.^10	2.923	2.870	11.034	5.75	—
Co2AlB2	2.959	2.694	11.323	6.13	−2.178
Ni2AlB2	3.000	2.784	11.107	5.94	−1.284

---

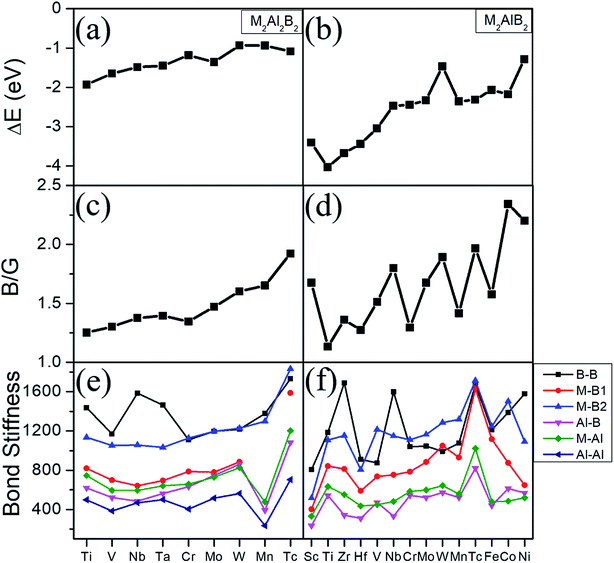
Phonon dispersions, formation energy and elastic constants are shown in Fig. S1,† Tables 3 and 4. There are no negative frequencies throughout the entire Brillouin zone for these MAB phases, and all independent elastic constants satisfy the well-known Born stability criteria.³⁵ These results confirm that the studied structures are dynamically and mechanically stable at ambient conditions. Considering the specific experimental reactants and products,¹⁰ the formation energies (ΔE) are further computed by ΔE = E(MAB) − E(M) − E(B) − E(Al). Among them, E(MAB) is the per MAB formula total energy of MAB crystal compound, where E(M), E(B) and E(Al) are the total energies of M, B and Al crystal, respectively. By definition, a negative ΔE means that the formation of this system is exothermic. Noted from Fig. 2(a) and (b) that the formation energies are negative and decrease with valence electron number of M atom increasing. For example, first-principles calculations show that formation energy of 212-MABs with M = Cr, Mn, Fe, Co and Ni are −2.447 eV, −2.373 eV, −2.064 eV, −2.178 eV and −1.284 eV, respectively. Such tendency is in accordance with the results of previous work,¹¹ which show that MAB compounds are indeed more feasible to crystallize in lower valence electron number of M metal component. The 212-MABs with M = Cr, Mn, Fe, Co and Ni and 222-MABs with M = Mo and W have already been produced in the laboratory now.^10,11 Based on the favorable formation energy, we can infer that Ti₂Al₂B₂, V₂Al₂B₂, Sc₂AlB₂, Ti₂AlB₂, Zr₂AlB₂, Hf₂AlB₂ are most likely to be identified in experiments.

Table 3 Calculated elastic constants (C_ij), bulk modulus (B), shear modulus (G), Young modulus (E), Poisson's ratio (ν) and ratio of B/G of 9 stable 222-MAB typed phases

M2Al2B2	C11	C12	C13	C23	C22	C33	C44	C55	C66	B	G	E	ν	B/G
Ti2Al2B2	352	74	83	92	273	202	122	130	158	145	116	274	0.18	1.25
V2Al2B2	354	102	118	110	310	244	181	145	179	173	133	317	0.19	1.30
Nb2Al2B2	352	125	104	123	298	271	173	152	165	180	130	315	0.21	1.38
Ta2Al2B2	369	131	116	138	321	278	187	163	181	192	138	333	0.21	1.39
Cr2Al2B2	395	112	119	131	339	262	173	192	160	189	140	338	0.20	1.35
Mo2Al2B2	390	146	129	142	349	326	168	191	162	210	143	350	0.22	1.47
W2Al2B2	405	189	143	160	365	349	183	195	171	233	145	361	0.24	1.60
Mn2Al2B2	318	108	143	125	292	181	145	159	132	167	101	252	0.25	1.65
Tc2Al2B2	349	154	172	162	375	287	169	111	144	220	114	292	0.28	1.92

---

Table 4 Calculated elastic constants (C_ij), bulk modulus (B), shear modulus (G), Young modulus (E), Poisson's ratio (ν) and ratio of B/G of 14 stable 212-MAB typed phases

M2AlB2	C11	C12	C13	C23	C22	C33	C44	C55	C66	B	G	E	ν	B/G
Sc2AlB2	497	147	122	146	453	380	129	118	168	238	142	356	0.25	1.67
Ti2AlB2	406	91	80	108	307	270	176	165	204	170	150	347	0.16	1.13
Zr2AlB2	344	99	84	124	267	185	144	134	178	152	112	270	0.20	1.36
Hf2AlB2	371	109	87	113	294	246	160	140	190	168	132	314	0.19	1.27
V2AlB2	414	102	116	128	336	315	115	110	200	195	129	317	0.23	1.51
Nb2AlB2	366	160	136	139	292	276	125	116	168	199	110	279	0.27	1.80
Cr2AlB2	521	118	107	113	444	428	165	160	215	229	177	422	0.19	1.29
Mo2AlB2	497	147	122	146	453	380	129	118	168	238	142	356	0.25	1.67
W2AlB2	511	187	154	179	474	365	147	115	163	262	139	354	0.28	1.89
Mn2AlB2	488	102	173	120	504	381	160	174	200	239	169	411	0.21	1.42
Tc2AlB2	473	135	203	187	505	333	130	129	163	260	132	339	0.28	1.97
Fe2AlB2	421	116	147	129	323	369	131	132	168	209	133	329	0.24	1.58
Co2AlB2	374	173	182	165	268	292	111	83	157	216	92	242	0.31	2.34
Ni2AlB2	362	157	140	162	241	296	107	114	110	200	91	237	0.30	2.20

---

Fig. 2 (a) and (b) Formation energies, (c) and (d) ratio of B/G, (e) and (f) bond stiffness versus increasing valence electron filings of M atom for 222-MAB compounds (left) and 212-MAB (right) compounds, respectively.

To further evaluate the stabilities and examine the electronic structure, Fig. S2† shows the total and partial density of state (DOS) of the predicted 23 MAB phases. The finite DOS at the Fermi energy for all those MABs reveal their metallic character. The total density of states near the Fermi level are dominated by transition metal atoms, while the lower lying states are dominated by B and Al atoms. As the valence electron number of M metal increases, the number of states lower than Fermi level increases because of valance electron filling, which push the total density of states to lower energy and are mainly responsible for the stability. As suggested in pervious literature,¹¹ the stability of the metallic materials is roughly relative to the pseudogap formation. That is to say, a local minimum (dip) at Fermi energy level (E_f) for metals implies higher structural stability, while a local maximum E_f is usually a sign of structural instability. Among our predicted 23 MABs, Cr₂Al₂B₂, Mo₂Al₂B₂ and W₂Al₂B₂ have their E_f located at a local minimum in the total density of state (TDOS), suggesting their higher level of stability. These results are indirectly supported by the experimental findings of Mo₂Al₂B₂ and W₂Al₂B₂ phases. Meanwhile, we demonstrated again that Cr₂Al₂B₂ is a very promising candidate for experimental synthesis. In addition, V₂Al₂B₂, V₂AlB₂ and Nb₂AlB₂ show a peak in the TDOS at the Fermi level, suggesting a relative lower stability than Cr₂Al₂B₂, Mo₂Al₂B₂ and W₂Al₂B₂. However, they might show better conductive performance than the other MABs systems reported here (Fig. S2†).

To promote their practical engineering applications, we have also investigated the mechanical properties of 222-MAB and 212-MAB phases. The theoretical single crystal elastic constants C_ij are shown in Tables 3 and 4. The corresponding bulk modulus (B), shear modulus (G), Young modulus (E), and Poisson's ratio (ν) are also obtained on basis of the Voigt–Reuss–Hill approximation.³⁵ Clearly, our present elastic constants coincide with the previous theoretical values.^11,21 As the Al concentration decreases, the modulus of MABs are strengthened. For instance, the theoretical bulk modulus, shear modulus, and Young modulus of 222-MAB phases are in the range of 145–233 GPa, 101–145 GPa, and 252–361 GPa, while those values of 212-MAB phases are 152–262 GPa, 91–177 GPa, and 237–422 GPa, respectively. It is noticeable that these values of MAB phases are comparable to or even higher than the corresponding MAX compounds.⁴⁵ We further predict the Vickers hardness (H_v) of those MAB phases. The average H_v from the empirical formula developed by ourselves³⁷ are 12–26 GPa (Tables S1 and S2†), which is consistent with experimental value of 7.0–21.7 GPa.⁴⁶ Among them, Ta₂Al₂B₂, Cr₂Al₂B₂, Mo₂Al₂B₂, W₂Al₂B₂, Sc₂AlB₂, Cr₂AlB₂, Mo₂AlB₂, W₂AlB₂, Mn₂AlB₂ possess higher modulus and hardness than other MAB phases. Moreover, we examined the universal anisotropy index, A_u.⁴⁷ A_u accounts for both compressibility and shear contributions and it can be positive or zero, zero A_u value represents an isotropic crystal. In Tables S1 and S2,† it is seen that most MAB compounds have high elastic anisotropies, except Cr₂AlB₂, Mo₂AlB₂ W₂AlB₂ and Fe₂AlB₂, which have notably low anisotropies (A_u = 0.08, 0.13, 0.15 and 0.12, respectively) than the other compounds. Thus, Cr₂AlB₂, Mo₂AlB₂ W₂AlB₂ with high modulus, high hardness and low elastic anisotropies are highly anticipated for future material applications.

The bulk modulus to shear modulus ratio, B/G, is an important measure of elasticity of a material. Materials with a B/G < 1.75 are expected to be brittle, while materials with B/G > 1.75 are ductile. The ratios B/G are also summarized in Tables 3, 4, Fig. 2(c) and (d). It can be seen that the ratio of B/G for most 222-MAB compounds are in the range from 1.30 to 1.65, implying that they are brittle-like ceramics. For the 212-MAB compounds, the values of B/G are in the range from 1.27 to 2.34. The ductile materials are predicted for Tc₂Al₂B₂, Nb₂AlB₂, W₂AlB₂, Tc₂AlB₂, Co₂AlB₂ and Ni₂AlB₂ with B/G values of 1.92, 1.79, 1.89, 1.97, 2.34 and 2.20, respectively. In orthorhombic materials, the Cauchy pressure can be defined for the three different crystal directions: P_a = C₂₃–C₄₄, P_b = C₁₃–C₅₅, and P_c = C₁₂–C₆₆, while is also an indicator of ductile behavior. As listed in Tables S1 and S2,† the Cauchy pressure of W₂AlB₂, Co₂AlB₂ and Ni₂AlB₂ are positive in all the three directions. In short, a strong dependence of the elasticity with valence electron number is observed from Fig. 2(c) and (d). The B/G ratio of MABs increases with the increasing valence electron number. By substitute different M element, these MAB phases can be tune from inductile to ductile. For example, the ductility of 212-MAB compounds can be improved by alloying it with Tc, W, Co and Ni, or a combination of them.

The mechanical properties can be understood by their bond stiffness, tensile–stress curve, the work of separation, and the effective charge, respectively. Based on the bond stiffness values listed in Fig. 2(e), (f) and Table S3,† we can summarize several findings. Firstly, the bond stiffness values show the trend as B–B > M–B > M–Al > Al–B > Al–Al. That is to say, the bond stiffnesses for intralayer B–B and B–M bonds are much larger than those for interlayer Al–M (Al–B/Al–Al) bonds. Secondly, the high bond stiffnesses of B–B and B–M bonds mainly determine their mechanical properties. One can observe relation of intralayer B–B, B–M bond stiffness as Mo₂Al₂B₂ < W₂Al₂B₂, which coincide with the tendency of experimental hardness value H_v (13.6 GPa¹⁰) of W₂Al₂B₂ being lower than H_v (21.7 GPa¹⁰) of Mo₂Al₂B₂. Moreover, there is relation of intralayer B–B, B–M bond stiffness as Cr₂AlB₂ < Mn₂AlB₂ < Fe₂AlB₂, which also agrees with the relation of experimental H_v of three 212-MAB phases Cr₂AlB₂ (7.0 GPa) < Mn₂AlB₂ (9.6 GPa) < Fe₂AlB₂ (14.7 GPa).¹⁰ Analogously, some hypothetical compounds of Tc₂Al₂B₂, Tc₂AlB₂ and W₂AlB₂ probably possess higher H_v value due to their higher bond stiffness of B–B and B–M bonds. Thirdly, the mechanical properties of MAB phases are also affected by the ratio of the bond stiffness of the weakest bond to that of the strongest bond. As listed in Tables S3 and S4,† Mn₂Al₂B₂, Sc₂AlB₂, Zr₂AlB₂ and Nb₂AlB₂ have lower ratios, suggesting the contributions from interlayer weak M–Al, Al–B, Al–Al bonds to mechanical properties are also important, which will weaken the modulus and hardness to some extent.

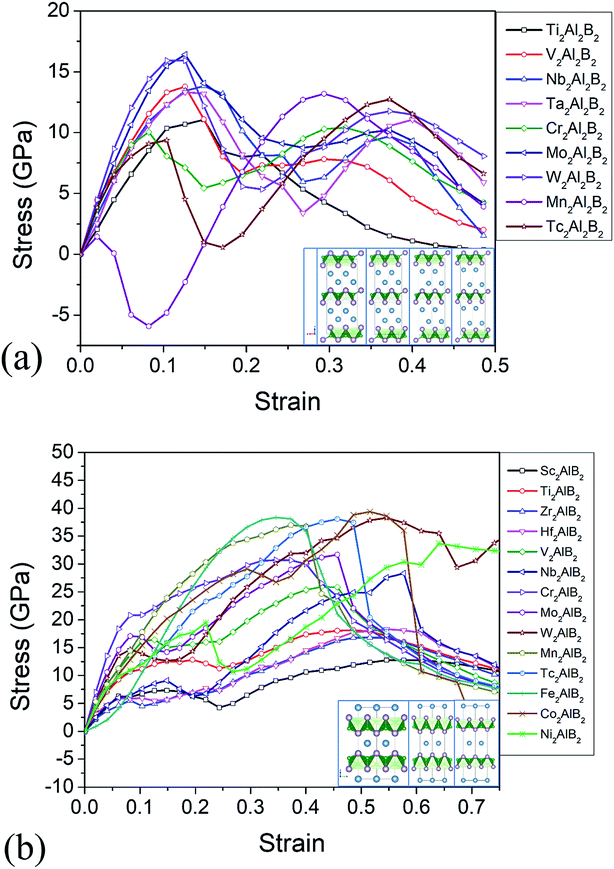
The relatively weak bond stiffness of the M–Al and Al–B bonds can be related to the delamination properties and the production mechanism of 2D derivatives. The tensile–strain relationships along the [001] stacking direction are illustrated in Fig. 3. The highest points on the stress–strain curves can be defined as ideal tensile strengths at the critical fractural strain. The ideal tensile strength for 222-MAB are about 11–16 GPa from c axis, and the ideal tensile strength of 212-MAB compounds are 13–39 GPa, respectively. Such big difference in ideal strength is mainly attributed to their atomic arrangements. The failure of 212-MAB is characterized by an abrupt stretch of the M–Al bonds, which is very similar to that of MAX phases.⁴⁸ However, the failure of 222-MAB is characterized by an abrupt stretching of the Al–Al bonds (Fig. 3).

Fig. 3 (a) Calculated stress versus tensile strain along c axis for (a) 222-MAB compounds and (b) 212-MAB compounds. The inset photograph shows the deformation at free strain, at critical fractural strains and at strain after critical point, respectively.

Large ideal strengths are observed in the Mo₂Al₂B₂, W₂Al₂B₂, W₂AlB₂, Mn₂AlB₂, Tc₂AlB₂ and Co₂AlB₂ phases, which means that those compounds have strong delamination resistance. While for Mn₂Al₂B₂, Sc₂AlB₂, Zr₂AlB₂, and Hf₂AlB₂, the ideal tensile strengths are less than 15 GPa due to the weak Al–Al or Al–B bond, which suggest the corresponding 2D derivatives could be synthesized through mechanical exfoliation. In those compounds, Al atoms donate less electrons (0.5–1.2e) to B atoms forming weaker Al–B and Al–Al bonds (Fig. 4). Indeed, the corresponding 2D Hf₂B₂, V₂B₂, Nb₂B₂, Cr₂B₂, Mn₂B₂ and Co₂B₂ sheets are dynamically stable by our phonon calculations (Fig. S3†). Interestingly, 2D MBenes, such as MoB, CrB, FeB, TiB have already been synthesized by chemical stepwise etching.^41–44 The works of separation of them are further studied and shown in Fig. 5. The corresponding works of separation of Hf₂AlB₂, V₂AlB₂, Nb₂AlB₂, Cr₂AlB₂, Mn₂AlB₂ and Co₂AlB₂ are 3.148 J m⁻², 3.929 J m⁻², 3.509 J m⁻², 5.095 J m⁻², 4.861 J m⁻² and 3.986 J m⁻², respectively, which are comparable to the value of monolayer Ti₂C MXene (∼5 J m⁻²).⁴⁹

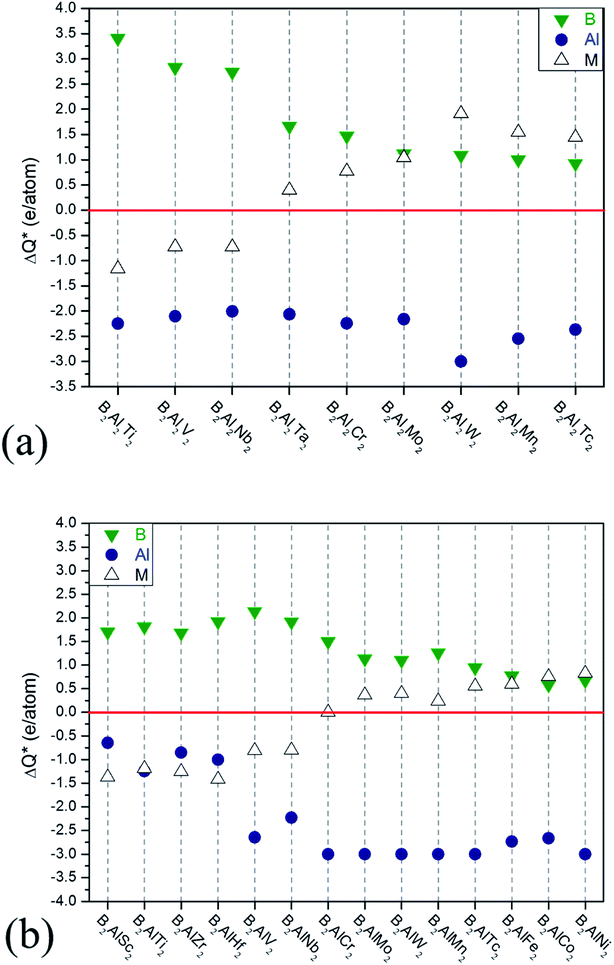Fig. 4 Charge transfers versus increasing valence electron filings of M atoms for (a) 222-MAB compounds and (b) 212-MAB compounds.

Fig. 5 Work of separation for 222-MAB compounds and 212-MAB compounds.

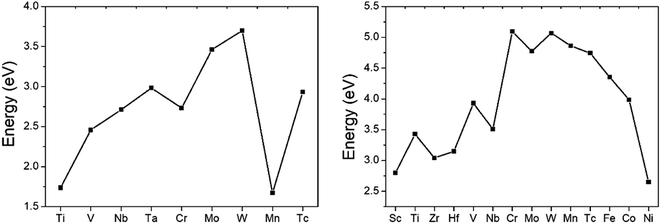
We have also calculated the interband dielectric function ε(ω) for the MAB phases in the frequency range from 0 to 30 eV using CASTEP code. Then, the optical conductivities and reflectivity are extracted from the obtained dielectric function. The optical conductivities resolved into axial components (X, Y, Z) are displayed in Fig. S4(a) and (b).† Several interesting observations can be made from these plots. The X, Y, Z components of optical conductivities show distinctly isotropic property, except in the energy range of 1 eV. For 222-MAB compounds, the conductivity shows a sharp increase to reach the maximum value in the energy in range from 4.5 to 5.0 eV in the ultraviolet region and then decreases to the minimum. While for 212-MAB compounds, the conductivity reaches the maximum value in the energy range from 6 to 8 eV. In generally, both 222-MABs and 212-MABs should be more conductive for the incident photon energy ranges from 4.5 eV to 8.0 eV. The reflectivity is the ratio of the energy of a wave reflected from a surface to the energy of the wave incident on the surface. The reflectivity spectra of MAB as a function of incident light energy are presented in Fig. S5(a) and (b).† For M = Ti, Cr, Mo, W, Mn, Tc of 222-MAB and M = Ti, Zr, W, Mn, Tc of 212-MAB, the reflectivities increase to reach the maximum value of about 80% in the ultraviolet region, i.e., in the range of 15 and 20 eV, then decrease drastically to reach the minimum, which mean optical properties of MAB changes from metallic to dielectric after about 20 eV. For others studied compounds, the values of reflectivity are almost above 44% (in the range of 0 and 20 eV). These MAB compounds will be capable of reducing solar heating if it has reflectivity >44%⁵⁰ in the visible light region. Therefore, we may conclude MAB compounds are also candidate materials for coating to reduce solar heating.

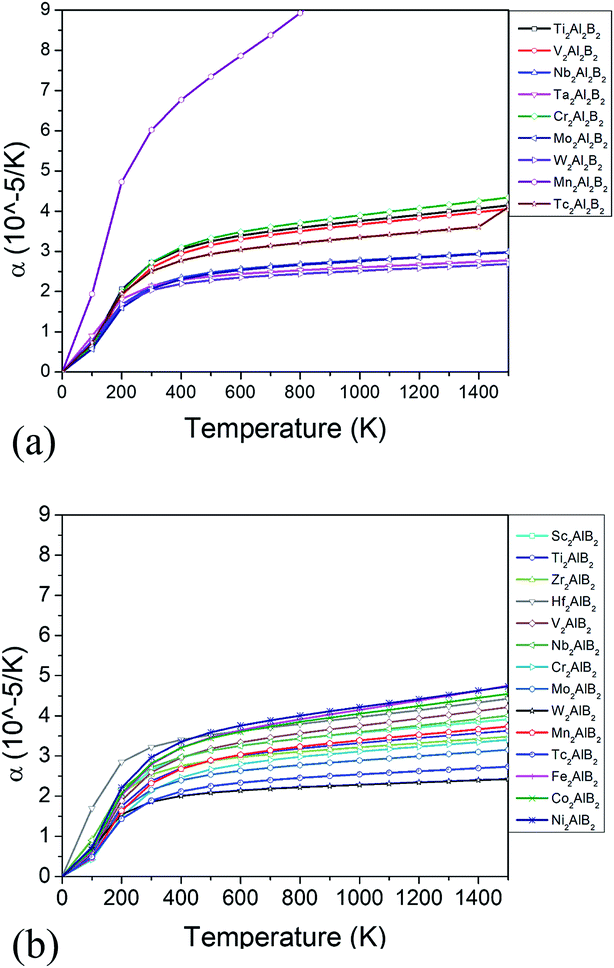
The thermodynamic properties such as thermal expansion coefficient α and bulk modulus are evaluated in the temperature range from 0 to 1500 K (Fig. 6 and 7), where the quasi-harmonic approximate (QHA) remains fully valid. As seen in Fig. 6, the temperature dependence of volume thermal expansion coefficient α can be divided into two regions: in the first region, the α increases sharply with increasing temperature up to 300 K, whereas in the second region (300–1500 K), the α increases slowly with a nearly constant volume thermal expansion coefficient. With the exception of Mn₂Al₂B₂, the values of them are 1.8–4.5 × 10⁻⁵ K⁻¹ in 300–1500 K, which are comparable to α of MAX phases (1.5–3 × 10⁻⁵ K⁻¹ (ref. 46)), and are relatively low as expected for refractory solids.⁵¹ Our predicted thermal expansion coefficient of Mo₂Al₂B₂ is 2.88 × 10⁻⁵ K⁻¹ in 1270 K, which is in good agreement with the experimental value that of 2.85 × 10⁻⁵ K⁻¹ at 1000 °C.¹⁵ The temperature dependent bulk modulus are shown in Fig. 7. One can see that they are nearly a constant (140–260 GPa) in the temperature range of 0 and 100 K. When temperature exceeds 100 K, it starts to decrease linearly with increasing temperature. However, the bulk modulus of most MAB compounds decreases by only 10% (∼20 GPa) from 100 K to 1500 K, showing the temperature driven softening of modulus. In a word, we propose MAB possess temperature insensitive elastic modulus, meanwhile they have low thermal expansion in high temperature region. We propose the good thermodynamic properties MAB compounds make them applicable for potential ultra-high temperature ceramics applications.

Fig. 6 (a) Thermal expansion α for the (a) 222-MAB phases and (b) 212-MAB phase, respectively.

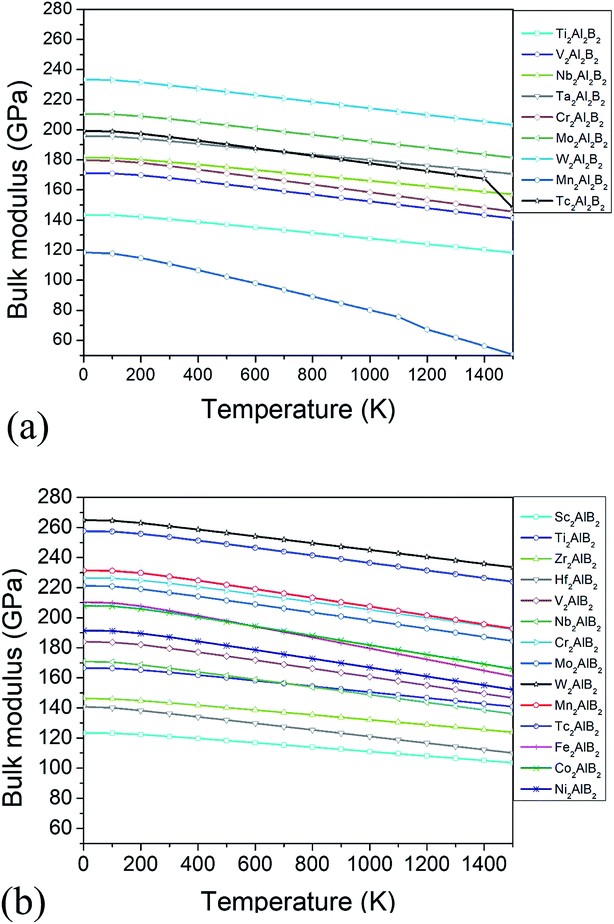Fig. 7 (a) The bulk modulus B versus temperature for studied (a) 222-MAB phases and (b) 212-MAB phases, respectively.

4. Summary

We have performed a systematic first-principles calculation of the 222-MABs and 212-MABs compounds with the M-site being one of 3d, 4d, and 5d transition metal elements. We final assess 23 dynamicaly and mechanically stable MAB phases. According to our calculations, the dynamic stabilities, electronic structure, tendency of hardness and the thermal expansion of Mo₂Al₂B₂, W₂Al₂B₂, Cr₂AlB₂, Mn₂AlB₂, Fe₂AlB₂, Co₂AlB₂ and Ni₂AlB₂ coincide with those reported by previous work. Furthermore, we found many interesting properties in unreported MAB phases. For example, Ti₂Al₂B₂, Sc₂AlB₂, Ti₂AlB₂, Zr₂AlB₂ and Hf₂AlB₂ are energetically more favorable and Cr₂Al₂B₂ is more stable provided by analysis of their formation energy and DOS. V₂Al₂B₂, V₂AlB₂ and Nb₂AlB₂ could show better conductive performance as well. The ductile materials are Tc₂Al₂B₂, Nb₂AlB₂, W₂AlB₂, Tc₂AlB₂, Co₂AlB₂ and Ni₂AlB₂, while high modulus and low elastic anisotropies compounds are Mo₂AlB₂ W₂AlB₂ revealed by elastic modulus exploration. The Tc₂Al₂B₂, Tc₂AlB₂ and W₂AlB₂ could possess high hardness provided by bond stiffness calculation. By correlating with the interlayer strength, work of separation and phonon dispersion curve, 2D structures of Hf₂B₂, V₂B₂, Nb₂B₂, Cr₂B₂, Mn₂B₂ and Co₂B₂ are found to be stable. For M = Ti, Cr, Mo, W, Mn, Tc of 222-MAB and M = Ti, Zr, W, Mn, Tc of 212-MAB, the ultraviolet reflectivities are as high as 90% showing attractive coating applications to reduce solar heating. Finally, the temperature dependence of volume thermal expansion coefficient and bulk modulus are investigated, the results show they have low thermal expansion as transition metal borides in 300–1500 K and the desired bulk modulus decreases by only 10% in 100–1500 K.

With a much enlarged database and comprehensive discussion of electronic structure, mechanical properties, chemical bonding, delamination properties, thermodynamic and optical properties, this study may eventually provide a theoretical fundamental property as guide to experimental work in MAB phases. These results enrich the family of MAB phases, and make the deep understanding of the overall trend relationship between stability/properties and chemical compositions, which are surely more beneficial for future material applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (11874097) and the Fundamental Research Funds for the Central Universities of China (DUT19LK12). We acknowledge the Xinghai Scholar project of Dalian University of Technology and the project of Dalian Youth Science and Technology Star (2017RQ012). We also acknowledge the Supercomputing Center of Dalian University of Technology for providing the computing resource.

References

1. W. Jeitschko, H. Nowotny and F. Benesovsky, Monatshefte für Chemie und verwandte Teile anderer Wissenschaften, 1963, 94, 672–676.
2. W. Jeitschko and H. Nowotny, Monatshefte für Chemie - Chemical Monthly, 1967, 98, 329–337.
3. H. Wolfsgruber, H. Nowotny and F. Benesovsky, Monatshefte für Chemie und verwandte Teile anderer Wissenschaften, 1967, 98, 2403–2405.
4. O. Beckmann, H. Boller, H. Nowotny and F. Benesovsky, Monatshefte für Chemie/Chemical Monthly, 1969, 100, 1465–1470.
5. M. W. Barsoum, Prog. Solid State Chem., 2000, 28, 201–281.
6. F. Halla and W. Thury, Z. Anorg. Allg. Chem., 1942, 249, 229–237.
7. W. Rieger, H. Nowotny and F. Benesovsky, Monatshefte für Chemie und verwandte Teile anderer Wissenschaften, 1965, 96, 844–851.
8. W. Jeitschko, Monatshefte für Chemie und verwandte Teile anderer Wissenschaften, 1966, 97, 1472–1476.
9. Y. Zhang, S. Okada, T. Atoda, T. Yamabe and I. Yasumori, J. Ceram. Soc. Jpn., 1987, 95, 374–380.
10. M. Ade and H. Hillebrecht, Inorg. Chem., 2015, 54, 6122–6135.
11. K. Kádas, D. Iuşan, J. Hellsvik, J. Cedervall, P. Berastegui, M. Sahlberg, U. Jansson and O. Eriksson, J. Phys.: Condens. Matter, 2017, 29, 155402.
12. S. Okada, K. Iizumi, K. Kudaka, K. Kudou, M. Miyamoto, Y. Yu and T. Lundström, J. Solid State Chem., 1997, 133, 36–43.
13. P. Chai, S. A. Stoian, X. Tan, P. A. Dube and M. Shatruk, J. Solid State Chem., 2015, 224, 52–61.
14. X. Tan, P. Chai, C. M. Thompson and M. Shatruk, J. Am. Chem. Soc., 2013, 135, 9553–9557.
15. S. Kota, E. Zapata-Solvas, A. Ly, J. Lu, O. Elkassabany, A. Huon, W. E. Lee, L. Hultman, S. J. May and M. W. Barsoum, Sci. Rep., 2016, 6, 26475.
16. J. Liu, S. Li, B. Yao, J. Zhang, X. Lu and Y. Zhou, Ceram. Int., 2018, 44, 16035–16039.
17. D. K. Mann, J. Xu, N. E. Mordvinova, V. Yannello, Y. Ziouani, N. González-Ballesteros, J. P. S. Sousa, O. I. Lebedev, Y. V. Kolen'ko and M. Shatruk, Chem. Sci., 2019, 10, 2796–2804.
18. L. T. Alameda, C. F. Holder, J. L. Fenton and R. E. Schaak, Chem. Mater., 2017, 29, 8953–8957.
19. L. Ke, B. N. Harmon and M. J. Kramer, Phys. Rev. B, 2017, 95, 104427.
20. H. Xiang, Z. Feng, Z. Li and Y. Zhou, J. Alloys Compd., 2018, 738, 461–472.
21. Y. Bai, X. Qi, A. Duff, N. Li, F. Kong, X. He, R. Wang and W. E. Lee, Acta Mater., 2017, 132, 69–81.
22. F.-Z. Dai, Z. Feng and Y. Zhou, Comput. Mater. Sci., 2018, 147, 331–337.
23. Y. Zhou, H. Xiang, F.-Z. Dai and Z. Feng, Mater. Res. Lett., 2017, 5, 440–448.
24. X. Li, H. Cui and R. Zhang, Sci. Rep., 2016, 6, 39790.
25. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
26. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
27. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
28. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
29. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
30. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
31. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
32. J. Clark Stewart, D. Segall Matthew, J. Pickard Chris, J. Hasnip Phil, I. J. Probert Matt, K. Refson and C. Payne Mike, Z. Kristallogr. – Cryst. Mater., 2005, 220(5–6) DOI: 10.1524/zkri.220.5.567.65075.
33. K. Parlinski, Z. Q. Li and Y. Kawazoe, Phys. Rev. Lett., 1997, 78, 4063–4066.
34. Y. Le Page and P. Saxe, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 104104.
35. Z.-j. Wu, E.-j. Zhao, H.-p. Xiang, X.-f. Hao, X.-j. Liu and J. Meng, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 054115.
36. D. Roundy and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 212103.
37. X. Jiang, J. Zhao and X. Jiang, Comput. Mater. Sci., 2011, 50, 2287–2290.
38. A. Otero-de-la-Roza and V. Luaña, Comput. Phys. Commun., 2011, 182, 1708–1720.
39. W. Jeitschko, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1969, 25, 163–165.
40. J.-C. Lei, X. Zhang and Z. Zhou, Front. Phys., 2015, 10, 276–286.
41. L. T. Alameda, P. Moradifar, Z. P. Metzger, N. Alem and R. E. Schaak, J. Am. Chem. Soc., 2018, 140, 8833–8840.
42. H. Zhang, F.-Z. Dai, H. Xiang, X. Wang, Z. Zhang and Y. Zhou, J. Mater. Sci. Nanotechnol., 2019, 35, 1593–1600.
43. L. T. Alameda, R. W. Lord, J. A. Barr, P. Moradifar, Z. P. Metzger, B. C. Steimle, C. F. Holder, N. Alem, S. B. Sinnott and R. E. Schaak, J. Am. Chem. Soc., 2019, 141, 10852–10861.
44. J. Wang, T.-N. Ye, Y. Gong, J. Wu, N. Miao, T. Tada and H. Hosono, Nat. Commun., 2019, 10, 2284.
45. W.-Y. Ching, Y. Mo, S. Aryal and P. Rulis, J. Am. Ceram. Soc., 2013, 96, 2292–2297.
46. S. Kota, M. Sokol and M. W. Barsoum, Int. Mater. Rev., 2019, 1–30,  DOI:10.1080/09506608.2019.1637090.
47. S. I. Ranganathan and M. Ostoja-Starzewski, Phys. Rev. Lett., 2008, 101, 055504.
48. Z. Guo, L. Zhu, J. Zhou and Z. Sun, RSC Adv., 2015, 5, 25403–25408.
49. T. Hu, M. Hu, Z. Li, H. Zhang, C. Zhang, J. Wang and X. Wang, Phys. Chem. Chem. Phys., 2016, 18, 20256–20260.
50. S. Li, R. Ahuja, M. W. Barsoum, P. Jena and B. Johansson, Appl. Phys. Lett., 2008, 92, 221907.
51. M. Radovic and M. W. Barsoum, American Ceramics Society Bulletin, 2013, 92, 20–27.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra04385k

---