Open Access Article
Open Access ArticleMicrobial-induced calcium carbonate precipitation: an experimental toolbox for in situ and real time investigation of micro-scale pH evolution†
Jennifer Zehner *a,
Anja Røyne
*a,
Anja Røyne b,
Alexander Wentzelc and
Pawel Sikorski
b,
Alexander Wentzelc and
Pawel Sikorski *a
*a
aDepartment of Physics, Norwegian University of Science and Technology (NTNU), Trondheim, Norway. E-mail: jennifer.s.zehner@ntnu.no; pawel.sikorski@ntnu.no
bThe Njord Centre, Department of Physics, University of Oslo (UiO), Oslo, Norway
cDepartment of Biotechnology and Nanomedicine, SINTEF Industry, Trondheim, Norway
First published on 28th May 2020
Abstract
Concrete is the second most consumed product by humans, after water. However, the production of conventional concrete causes more than 5% of anthropogenic CO2 emissions and therefore there is a need for emission-reduced construction materials. One method to produce a solid, concrete-like construction material is microbial-induced calcium carbonate precipitation (MICP). To get a better understanding of MICP it is important to be able to follow local pH changes in dissolution and precipitation processes of CaCO3. In this work we present a new method to study processes of MICP at the micro-scale in situ and in real time. We present two different methods to monitor the pH changes during the precipitation process of CaCO3. In the first method, the average pH of small sample volumes is measured in real time, and pH changes are subsequently correlated with processes in the sample by comparing to optical microscope results. The second method is introduced to follow local pH changes at a grain scale in situ and in real time. Furthermore, local pH changes during the dissolution of CaCO3 crystals are monitored. We demonstrate that these two methods are powerful tools to investigate the pH changes for both MICP precipitation and CaCO3 dissolution for knowledge-based improvement of MICP-based material properties.
1 Introduction
The concrete industry is a major contributor to human-made CO2 emissions. The production of cement as a binder in concrete for construction purposes accounts for more than 5% of all anthropogenic CO2 emissions.1Due to increasing awareness of the climate impact of anthropogenic CO2, there is a large interest in reducing the global CO2 emissions, including the carbon footprint of the construction industry. Approaches such as alternative raw materials, alternative fuels, and carbon capturing techniques have the potential of energy savings and CO2 reduction in cement production.2–4 An alternative approach could be based on replacing conventional concrete in some applications with a material based on biomineralization, so-called bio-cement. The production procedure of bio-cement utilizes bacteria to achieve biomineralization within a granular material to form a solid, concrete-like material. The most researched mechanism for producing bio-cement is microbially induced calcium carbonate precipitation (MICP).5–8 Ureolytic bacteria, such as Sporosarcina pasteurii have been studied extensively in MICP.9–11 The process of MICP is based on urea hydrolysis,9,12 where the enzyme urease catalyzes the hydrolysis reaction:
 | (1) |
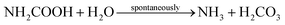 | (2) |
Ammonia and carbonic acid equilibrate further to form ammonium and bicarbonate (eqn (3) and (4)):
| 2NH3 + 2H2O ↔ 2NH4+ + 2OH− | (3) |
| H2CO3 ↔ HCO3− + H+ | (4) |
Eqn (3) lead to an increase in the pH and a shift in the bicarbonate equilibrium (eqn (4)). In the presence of sufficient concentration of calcium ions this can result in CaCO3 precipitation:
| Ca2+ + HCO3− + OH− → CaCO3↓ + H2O | (5) |
The MICP process is controlled by four key-factors: (1) availability of nucleation sites, (2) pH value, (3) concentration of dissolved inorganic carbon (DIC), and (4) the concentration of free calcium ions in the crystallization solution.12 In a MICP process, both the granular medium and the microorganisms can act as nucleation sites for CaCO3 precipitation.13 The remaining three factors influence the saturation state S of the solution. The solution is supersaturated, once the ion activity product of Ca+ and CO3− exceeds the solubility product of the nucleating polymorph. This results in a driving force of the system towards crystallization. Large S leads to fast, spontaneous crystallization, where nucleation and crystal growth occurs. Once crystals nucleate, there is a reduction in solution supersaturation S. Below a critical supersaturation level, no new crystal nucleate and crystal growth is responsible for relaxation of the supersaturated system.14
CaCO3 can crystallize in different polymorphs: calcite, vaterite and aragonite as well as hydrated crystalline phases such as monohydrocalcite and ikaite.15 Calcite has the lowest solubility in water, followed by aragonite and vaterite. Vaterite is the least thermodynamically stable polymorph and transforms rapidly in aqueous solutions into calcite or aragonite. According to Ostwald's rule of stages, metastable polymorphs form first and subsequently transform into the thermodynamically more stable polymorph.14 Additionally, amorphous calcium carbonate (ACC) can be formed, which rapidly transforms to calcite via vaterite.16 It has been shown that vaterite preferably crystallizes at high supersaturation levels.17
The precipitation process for MICP is schematically shown in Fig. S1, ESI.† The pH is increased due to urea hydrolysis. Once the solution is supersaturated, spontaneous crystallization occurs. For high supersaturation values, calcite is precipitated via ACC and vaterite, while lower supersaturation levels lead to direct calcite precipitation.18,19
The pH value of a MICP process is controlled by the urea hydrolysis reaction. During the ammonium formation the pH increases (eqn (3)). The pH increase leads to an increase of the amount of dissolved inorganic carbon (DIC). Depending on the experimental conditions, two cases can be considered. In a closed system, the amount of DIC is controlled only by urea hydrolysis. In case of an open system, additionally CO2 can be exchanged with the atmosphere:20
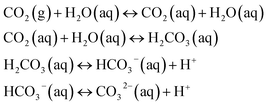 | (6) |
The saturation state of the crystallization solution is also influenced by the calcium concentration. CaCl2 is the most frequent used calcium source in MICP,21,22 however, it is expensive and not environmentally friendly, since Cl−-ions react fast to form chloride salts and pollute water and can lead to steel corrosion of steel-reinforcement in concrete. The effect of other calcium sources, such as calcium lactate23,24 and calcium acetate24,25 on the properties of the consolidated material has been investigated. Recently, an environmentally friendly and inexpensive alternative based on crushed limestone dissolved with lactic acid was used in a MICP process. In this approach, it is possible to conduct the dissolution process by lactic acid producing bacteria, making both dissolution and precipitation rely on bacterial processes:26
| CaCO3 + 2CH3CH(OH)COOH → Ca2+ + CH3CH(OH)COO− + H2O + CO2 | (7) |
For acidic conditions the dissolution process can in general be described with the following equations:
| CaCO3(s) ↔ Ca2+ + CO32− | (8) |
| CO32− + 2H+ ↔ HCO3− + OH− | (9) |
Bicarbonate can react further at very low pH values to gaseous CO2:
| HCO3− + H+ → CO2(g) + H2O | (10) |
The dissolution reaction consists of several steps, including diffusion and surface reactions. The slowest process will be the rate limiting process for the dissolution reaction.27 For pH values below 4 it has been reported that the dissolution is controlled by the diffusion of protons to the calcite surface28 and is therefore limited by mass transport. For pH values in the range from pH 4 to pH 5.5 surface reactions are influencing the dissolution, limited by mass transfer.
Previous research in MICP has been focused on macro-scale properties of the consolidated material. Scanning electron microscopy (SEM) is a commonly used technique to investigate characteristics of the precipitated CaCO3 minerals (e.g. ref. 29). Even if the properties of the consolidated material, in terms of crystal shape and polymorphism, can be characterized well by imaging methods such as SEM, this method fails to provide information about the precipitation process. Microfluidic chips have been developed to observe the formation of CaCO3 crystals in real time and in situ.30 Furthermore, nucleation and crystal growth have been investigated with direct optical microscope observation.19 However, those micro-scale studies do not give information about pH changes during the crystallization processes.
In this contribution, we introduce two experimental methods to monitor pH changes in real time and in situ in small volumes and at the grain scale. In the first method, the average pH in small volumes (200 μL) is measured in real time using absorption spectroscopy, and precipitation processes are correlated to pH changes with the help of optical microscopy. The second method allows monitoring of local pH changes at the grain scale with the help of confocal laser scanning microscopy (CLSM).
Both methods can also be applied to investigate the pH changes during the dissolution of CaCO3 crystals, for example using lactic acid or acid producing bacteria. The usability of both methods is demonstrated by investigating CaCO3 precipitation at high supersaturation induced by Sporosarcina pasteurii and CaCO3 dissolution with lactic acid.
2 Materials and methods
2.1 Materials
All chemicals were purchased at SigmaAldrich (Norway) unless otherwise stated. Solutions were prepared with deionized water (DI) and filtered with 0.22 μm polycarbonate syringe-filter before use.Immediately before use in experiments, the bacterial culture was centrifuged at 5200 × g for 8 min and the cells subsequently washed twice with pre-warmed 0.01 M PBS (phosphate buffered saline) to remove the growth medium. The cells were re-suspended and diluted in 0.01 M PBS. Cell concentrations were determined by optical density measurement of 150 μL dilutions in a 96-well plate at 600 nm (OD600 nm).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10. As an indication for the bacterial cell concentration of the bacteria suspension the optical density was measured before adding it to the crystallization solution (for the presented experiments: OD600 nm = 1.260).
10. As an indication for the bacterial cell concentration of the bacteria suspension the optical density was measured before adding it to the crystallization solution (for the presented experiments: OD600 nm = 1.260).2.2 pH monitoring
Fig. 1(b) shows a schematic illustration of the local pH monitoring principle. A CLSM is used to scan the area surrounding crystallization or dissolution processes, using a modified technique reported elsewhere.33 The two fluorescent dyes were excited with an argon laser (excitation wavelength: 514 nm) and a diode pumped solid state laser (excitation wavelength: 561 nm). For spatiotemporal pH measurements the images were scanned sequentially line-by-line to avoid crosstalk between the two fluorescent dyes. The fluorescent signal was detected with two Leica HyD detectors in photon counting mode. R6G-EDA and SR101 were detected separately by setting the emission filter to 525 nm to 554 nm and 578 nm to 625 nm, respectively. The scan speed was set to 100 Hz, and image resolution was 512 × 512 pixel. The bit depth was set to 12 bit. All measurements were performed with a pinhole size of 1 Airy. After the measurements, images were processed using a 3 × 3 median filter, and the intensity ratio between R6G-EDA and SR101 was calculated pixel-by-pixel. Two standard curves were generated in order to convert the ratio of fluorescent intensities to pH values. For the standard curve, images were taken for 13 pH values in a range from 3.1 to 9.5. The curves were used to convert intensity ratios into pH values. For precipitation processes the ratio between SR101 to R6G-EDA was used (ratio 1, see Fig. S6, ESI†). For dissolution the ratio of fluorescent intensities of R6G-EDA to SR101 was used (ratio 2, see Fig. S7, ESI†). Additionally, a mask was applied to the local pH map images, rendering forming and dissolving crystals gray in the presented pH maps.
2.3 Raman microspectroscopy
For the sample preparation Jack Bean urease (plant derived) was used for catalyzing the urea hydrolysis reaction. The precipitation was stopped at different time-points with ethanol, and the CaCO3 precipitate was filtered out of the crystallization solution and dried before further characterization. Raman microspectroscopy was employed to characterize the polymorph phase of the precipitated CaCO3 using a Renishaw InVia Reflex Spectrometer equipped with a 532 nm laser and a Leica 50× 0.75 NA lens.3 Results
3.1 CaCO3 precipitation
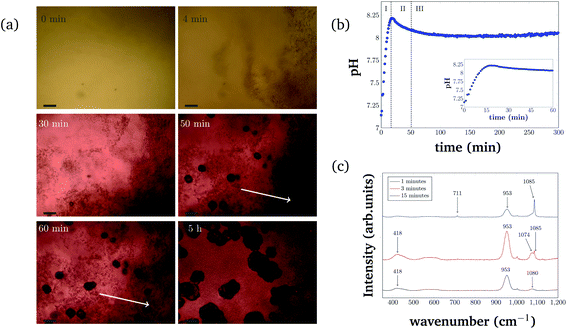
For consistency purposes, all presented experiments were performed with the same batch of S. pasteurii. The rate of urea hydrolysis will depend on both bacteria concentration and in some extent the time-point of the experiment within the growth curve of S. pasteurii. Therefore, in the following precipitation experiments, nucleation time-points are specific for the used bacteria cell concentration and growth time.The precipitation process in a 96-well plate was monitored with optical microscopy to identify different stages of the bacterial-induced precipitation of CaCO3. Optical microscopy was initiated approximately 30 s after the reagents were added. Selected time-points of the crystallization process are shown in Fig. 2(a). Note that the time-labels refer to the start of measurements and are characteristic for the used bacteria concentration.
Parallel to the optical microscope experiment, the pH evolution of the crystallization solution in multiple samples was monitored using absorption spectroscopy. With the method applied here, the average, i.e. global pH of the solution is measured. This measurements will also serve as a reference for the pH evolution at the grain scale described below.
The pH evolution corresponding to the precipitation process of Fig. 2(a) is shown in Fig. 2(b). Both figures cover the initial 5 h of the reaction.
The pH measurements were started approximately 1 min after adding the bacteria cells. For the precipitation process, three distinct stages can be identified. Stage I starts shortly after the start of the reaction and is characterized by the appearance of small particles in the solution. The small particles first float freely in the solution, before settling at the bottom of the well. Fig. 2(a) (4 min) represents an example for Stage I, 4 min after starting the reaction. The crystallization solution is changing color from yellow to red, indicating a pH increase, as also observed in direct pH measurements (Fig. 2(b)). The pH in the starting phase is increasing rapidly up to a value of 8.2.
For the chosen experimental conditions, Stage II starts after approximately 25 min, when the pH of the crystallization solution starts to decrease. As can be seen in Fig. 2(a) (30 min), this stage is characterized by nucleation and crystal growth occurring simultaneously with the dissolution of the precipitates formed in Stage I (see Fig. 2(a) (4 min)). During Stage II, pH of the solution drops by 0.1 to pH 8.1. Two time-points representing Stage II are shown in Fig. 2(a) (50 min), and (60 min), which illustrate the nucleation, the crystal growth as well as the start of the dissolution of initial precipitated particles (indicated by two white arrows in Fig. 2(a) (60 min) and (5 h)).
In Stage III, which starts in the presented experiment after about 50 min, crystal growth is the dominating process. The initial precipitate continues to dissolve. Correlating this to the global pH evolution measurement (Fig. 2(b)) shows, that in this phase, the pH is stable around a value of 8.0. After 200 min the pH of the crystallization solution starts to increase slowly again, which is probably a consequence of slow urea hydrolysis in the absence of free calcium ions, as all calcium is bound in already formed precipitates.
The different polymorphs of the precipitation process have been investigated and identified with Raman microspectroscopy in a separate experiment (Fig. 2(c)). In this experiment, plant derived urease was used to catalyze the reaction, and the reaction was stopped by adding ethanol at different time-points (after 1 min, 3 min, and 15 min). Characteristic Raman peaks for CaCO3 can be found at approximately 1085 cm−1. It can be seen that the small precipitates that appear initially are consistent with ACC (broad peak at 1080 cm−1). ACC quickly transforms into vaterite (characteristic double peak at 1074 cm−1 and 1085 cm−1). At later time-points (15 min), a Raman signal at 1085 cm−1 and 711 cm−1 that is characteristic of calcite crystals is observed. Further appearing Raman peaks at 953 cm−1 and 418 cm−1 could be caused by intermediate products of the urea hydrolysis reaction as well as by impurities in the formed CaCO3. However, the peaks could not be identified with absolute certainty. Despite this, the different polymorph stages during the precipitation process can still be identified as amorphous calcium carbonate (Fig. 2(c) (black curve)), vaterite (Fig. 2(c) (red curve)), and calcite (Fig. 2(c) (blue curve)).
Additionally, pH evolution was also monitored at the grain scale using CLSM microscopy. 2D local pH changes during the precipitation process close to the precipitating crystals could be documented, using the same concentration of urea, calcium and bacterial cells.
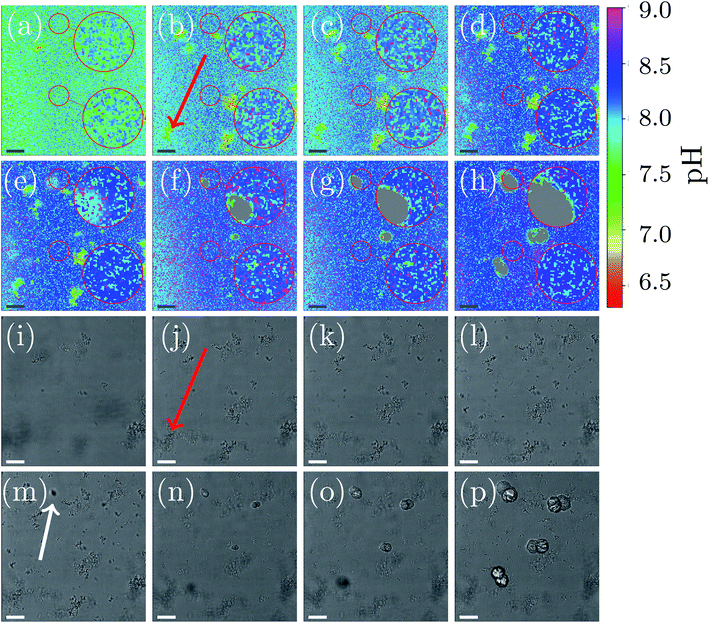
A representative example of spatial and temporal pH mapping is shown in Fig. 3. The pH evolution on the scale of individual crystals is shown in Fig. 3(a)–(h), with the corresponding brightfield images in Fig. 3(i)–(p). Data acquisition started approximately 2 min after mixing the reactants.
For easier identification of local pH differences, two selected areas in each of the images are highlighted and magnified. The upper area corresponds to a location in the sample where a calcite crystal appears after 14 min. The lower area shows pH evolution in a region in which no calcite nucleation occurs during the course of the experiment.
As in the global precipitation experiments, three distinct stages of precipitation can be observed. Note that the timescale is not exactly the same as in the experiments at the global scale (Fig. 2(a)). This is due to differences between the experimental setups that affect factors such as gas exchange with the environment, local variations in temperature, and different crystallization conditions.
Fig. 3 shows the spatial and temporal pH evolution during the precipitation process. In Stage I, during the first 12 min, the color changes from light green to blue, corresponding to a continuous pH change from around 7.7 to 8.2. In good agreement with the global-scale experiments, small particles of ACC and vaterite precipitate and float in the liquid. In areas where ACC and vaterite appears, the local pH decreases (to around pH 7.0) compared to the rest of the sample. An example of this is indicated by a red arrow in Fig. 3(b) and (j). The first calcite crystal can be observed after 14 min, which marks the beginning of Stage II of the crystallization process. Calcite crystals first appear as dark spots in the optical image (Fig. 3(m); marked with a white arrow). Simultaneously, it can be observed (Fig. 3(e)) that the pH around the growing crystal is lowered by approximately 0.5 compared with the rest of the sample (pH 7.9).
The nucleation process is shown in more detail in the ESI document (see Fig. S8, ESI†). The highlighted and magnified part emphasizes the area where nucleation occurs. The crystals start to appear after 12 min in the brightfield image. Simultaneously, the spatial pH mapping shows a pH drop in the same area. This can be clearer seen in (see Fig. S8(c) and (d), ESI†) when the nucleating crystal moves into the focus of the CLSM. A color change to cyan can be observed in the area where the crystal appears. This corresponds to a pH drop from 8.2 to 7.9. During crystal growth (Fig. 3(f)–(h)), a color change to green/cyan can be observed in the area close to the growing crystal. This is equivalent to a pH in a range between 7.5 to 8.0. The pH of the rest of the sample is above 8.2 (blue color Fig. 3(e)–(h)). The crystal growth corresponds to the Stage III of the precipitation process. Additionally, it can be observed that the ACC and vaterite formed in Stage I and visible as small particles in the brightfield images, as well as local pH changes in the pH mapping, is starting to dissolve, and the nucleated crystals increase in size. The dissolution of vaterite can be observed after crystallization has started. This also coincides with a more uniform pH map in areas without growing crystals (Fig. 3(h); lower magnified area).
3.2 Dissolution of CaCO3 crystals
Spatial and temporal evolution of the pH at the scale of single CaCO3 crystals was investigated in dissolution experiments. Our goal is to employ bacteria to produce acid for the dissolution of CaCO3, and therefore a method was developed to study the local pH variations during calcite dissolution. For the presented experiments calcite crystals were grown on a polymer microscope slide and then dissolved using 10 mM aqueous solution of lactic acid. Experiments were conducted in a flow cell as shown in Fig. 1(b) under stagnant (no flow) conditions. The addition of the acid leads to slow dissolution of the calcite crystals was observed by decreasing crystal size (see Fig. S9, ESI†) and leads to changes in the solution pH (Fig. 4).The dissolution of calcite crystals was investigated with CLSM using the same approach as used to monitor local pH changes in bacteria induced precipitation described above. Measurements were started approximately 30 s after the addition of the acid. The results of the microscale pH mapping are shown in Fig. 4.
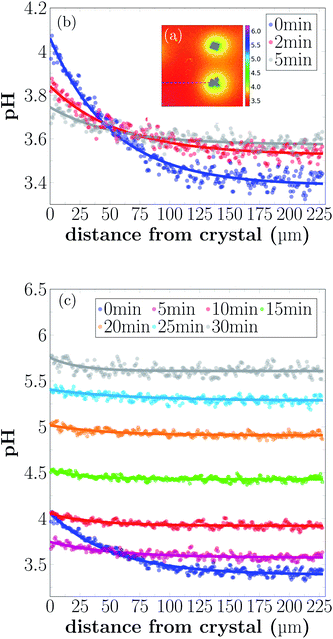
Shortly after the acid is injected into the flow cell, clearly observable local pH gradients are established in the proximity of dissolving crystals. Regions with increased pH can be recognized by the bright yellow color in Fig. 4(a). The pH value close to the crystal is around 4.1, while the pH further away from the crystals is around 3.4. During the first 5 min of the experiment, the area with higher pH is decreasing, while the pH of the entire sample increases.
During the dissolution process, two phases can be observed. In the starting phase of the dissolution, the main observed process is the pH change in close proximity of the calcite crystal. The pH close to the crystal is decreasing, while the pH of points distant to the crystals is increasing. Once a uniform pH in the sample is established (after approximately 5 min), the main observed process in local pH monitoring experiments is the increase of the pH of the entire sample.
The pH profiles have been plotted along the dashed line shown in Fig. 5(a) for 7 different time-points.
Local pH differences are largest at the beginning of the dissolution process (0 min). The pH value close to the crystal is around 4.1, while the pH further away is around 3.4. During the initial 0 min to 5 min, the local differences in pH become smaller, until after 5 min the pH is nearly uniform in the sample. A higher pH near the dissolving crystals can only be detected within a distance of 40 μm from the crystal surfaces for longer reaction times.
4 Discussion
4.1 CaCO3 precipitation
During CaCO3 precipitation, we observed the formation of different CaCO3 polymorphs (Fig. 2(a) and 3). In the initial stage of the reaction, ACC and vaterite was observed, while at later time-points of the experiment calcite was the dominating polymorph (Fig. 2(c)). It has been previously reported that during CaCO3 precipitation at high supersaturation conditions, hydrated ACC is formed first.16 This phase subsequently transforms into vaterite, which dissolves once the supersaturation with respect to vaterite approaches S = 1 and re-precipitates according to Ostwald's rule of stages, as calcite. This has also been reported for MICP processes.18 The precipitation and dissolution of small CaCO3 particles in MICP have previously been observed in microscale experiments.19 In our experiments, the previously reported precipitation pathway could be confirmed using Raman microspectroscopy (Fig. 2(c)).The presented global pH monitoring method provides the average pH evolution of the crystallization solution. The expected pH evolution is a rapid pH increase due to urea hydrolysis followed by a pH decrease due to crystallization of CaCO3 (eqn (5)), which was confirmed by our measurements (Fig. 2(c)). This also agrees with previously reported pH evolution's in bulk experiments. In the work of Dupraz et al.,34 the influence of gas exchange with the environment on the pH evolution in larger volumes (30 mL and 60 mL) was investigated. In systems with limited gas exchange, the pH increase and carbonate precipitation was faster than in systems with gas exchange with the environment (eqn (6)). In addition, the pH value before nucleation was reported to be higher for closed systems. This is due to limitation of CO2 during the hydrolysis reaction. CO2 exchange with the environments is more pronounced when the surface to volume ratio of the sample is high, which is the case in our global pH monitoring experiments. This explains why the global pH values we detect are low compared with previously reported MICP experiments.9,34
In our observations of local pH on the grain scale, we found that both the appearance of the initial precipitation (ACC and vaterite), as well as the crystallization of calcite, gave rise to a local decrease in pH. The pH decrease due to ACC and vaterite precipitation could not be detected in the global pH measurements, because its average effect was smaller than the global pH increase due to urea hydrolysis.
The precipitation processes in global and local pH monitoring experiments show the same trend, however crystallization occurs at different time-points, despite using of the same bacteria cell concentrations. This can be explained by several experimental factors. Perhaps the most important is that the flow cell (Fig. 1(b)) can be considered a closed system, because only a very small fraction of the solution is in equilibrium with the atmosphere. In the global pH monitoring experiments, gas exchange was limited, however, gas exchange cannot be neglected for those measurements. The closed conditions of the flow cell experiments lead to a faster pH increase and as a consequence faster precipitation of CaCO3.
Furthermore, the influence of the surface morphology of the substrate on precipitation and morphology of precipitated crystals in MICP has been reported earlier.35 This shows that precipitation depends on the surface chemistry of the substrate, and can contribute to the different time-points at which precipitation starts in global and local pH monitoring experiments.
4.2 Dissolution of CaCO3 crystals
In our dissolution experiments, we observed a slow dissolution of calcite crystals (see Fig. S9, ESI†). H+ ions are consumed in the dissolution process (eqn (9)), and the resulting diffusion of protons from the bulk solution towards the dissolving surfaces can be seen as a pH gradient between the surface and the bulk solution. After a reaction time of 5 min, a pH profile with nearly constant shape is reached (Fig. 4).At low pH values, it is expected that the bicarbonate from the dissolution reaction further reacts to produce CO2. This could not be observed in the presented experiments due to the fast diffusion of the reaction products and low concentration of dissolved carbon.
As shown in Fig. 5, the pH close to the crystal is observed to decrease after a fast increase from bulk pH conditions, during the first 5 min of the experiment. This somewhat counterintuitive observation can probably be explained by an initial fast dissolution rate of the calcite crystal, caused by the large availability of active reaction sites on the fresh calcite surface.36 As the density of reactive sites decreases and the dissolution rate slows down, the diffusion of H+ and reaction products cause a temporary drop in local pH. This previously unobserved dynamic may have implications for biogeochemical reactions in the vicinity of dissolving calcite surfaces.
5 Conclusions
We have presented two novel methods for monitoring the pH evolution of MICP processes at the micro-scale. The global pH evolution in small volumes was measured with absorption spectroscopy. Furthermore, a method was introduced for monitoring local pH changes using CLSM.With the presented methods we were able to achieve detailed, in situ pH monitoring, which allows us to learn more about the reactions during MICP. This allows us to gain more control when designing and optimizing the process on the micro-scale.
Local pH monitoring revealed details about local pH changes, which have not been observed in bulk measurements. We were able to demonstrate that the appearance of metastable phases during the initial pH increase causes a local pH decrease. Furthermore, for dissolution experiments local and temporal pH variations around the dissolving calcite crystals have been observed, which may have implications for other biochemical reactions taking place in close proximity of the dissolving crystals.
The methods introduced in this work allow the detailed, micro-scale evaluation of MICP processes and represent a valuable tool for improving material properties in MICP-based materials, with prospects for becoming more sustainable alternatives for conventional concrete in a wider range of applications in the construction industry.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Research Council of Norway under project 269084/O70. Additional support was provided by Norwegian Micro- and Nano-Fabrication Facility, NorFab under the Research Council of Norway project 245963/F50. The authors thank Simone Balzer Le and Sidsel Markussen from SINTEF Industry, Trondheim, Norway for providing the bacteria cultures for this work.Notes and references
- C. Le Quéré, R. Moriarty, R. M. Andrew, J. G. Canadell, S. Sitch, J. I. Korsbakken, P. Friedlingstein, G. P. Peters, R. J. Andres and T. A. Boden, et al., Earth System Science Data, 2015, 7, 349–396 CrossRef.
- A. Naqi and J. G. Jang, Sustainability, 2019, 11, 537 CrossRef CAS.
- A. Bosoaga, O. Masek and J. E. Oakey, Energy Procedia, 2009, 1, 133–140 CrossRef CAS.
- K. Vatopoulos and E. Tzimas, J. Cleaner Prod., 2012, 32, 251–261 CrossRef CAS.
- V. Achal and A. Mukherjee, Constr. Build. Mater., 2015, 93, 1224–1235 CrossRef.
- W. De Muynck, N. De Belie and W. Verstraete, Ecol. Eng., 2010, 36, 118–136 CrossRef.
- V. Stabnikov, M. Naeimi, V. Ivanov and J. Chu, Cem. Concr. Res., 2011, 41, 1143–1149 CrossRef CAS.
- L. S. Wong, J. Cleaner Prod., 2015, 93, 5–17 CrossRef CAS.
- S. Stocks-Fischer, J. K. Galinat and S. S. Bang, Soil Biol. Biochem., 1999, 31, 1563–1571 CrossRef CAS.
- V. Achal, A. Mukherjee, P. C. Basu and M. S. Reddy, J. Ind. Microbiol. Biotechnol., 2009, 36, 981–988 CrossRef CAS PubMed.
- D. Sarda, H. S. Choonia, D. D. Sarode and S. S. Lele, J. Ind. Microbiol. Biotechnol., 2009, 36, 1111–1115 CrossRef CAS PubMed.
- F. Hammes and W. Verstraete, Reviews in Environmental Science and Biotechnology, 2002, 1, 3–7 CrossRef CAS.
- T. Ghosh, S. Bhaduri, C. Montemagno and A. Kumar, PLoS One, 2019, 14, e0210339 CrossRef CAS PubMed.
- J. Mullin, Crystallization, Elsevier Science, 2001 Search PubMed.
- H. Cölfen, M. Fricke, S. Harry, H. Imai, R. Kniep, K. Sato, S. Sewell, P. Simon, D. Volkmer and D. Wright, Biomineralization I: Crystallization and Self-Organization Process, Springer Science & Business Media, 2007, vol. 1 Search PubMed.
- J. D. Rodriguez-Blanco, S. Shaw and L. G. Benning, Nanoscale, 2011, 3, 265–271 RSC.
- Y. S. Han, G. Hadiko, M. Fuji and M. Takahashi, J. Cryst. Growth, 2006, 289, 269–274 CrossRef CAS.
- L. van Paassen, PhD thesis, Delft Univ. of Technology, Delft, The Nethelands, 2009.
- W. Zhang, Y. Ju, Y. Zong, H. Qi and K. Zhao, Environ. Sci. Technol., 2018, 52, 9266–9276 CrossRef CAS PubMed.
- W. Stumm and J. Morgan, Aquatic chemistry: an introduction emphasizing chemical equilibria in natural waters, Wiley, 1981 Search PubMed.
- J. T. DeJong, M. B. Fritzges and K. Nüsslein, J. Geotech. Geoenviron. Eng., 2006, 132, 1381–1392 CrossRef CAS.
- M. Burbank, T. Weaver, R. Lewis, T. Williams, B. Williams and R. Crawford, J. Geotech. Geoenviron. Eng., 2013, 139, 928–936 CrossRef CAS.
- J. Xu, Y. Du, Z. Jiang and A. She, Front. Microbiol., 2015, 6, 1366 Search PubMed.
- C. M. Gorospe, S. H. Han, S. G. Kim, J. Y. Park, C. H. Kang, J. H. Jeong and J. S. So, Biotechnol. Bioprocess Eng., 2013, 18, 903–908 CrossRef CAS.
- Y. Zhang, H. X. Guo and X. H. Cheng, Constr. Build. Mater., 2015, 77, 160–167 CrossRef.
- A. Røyne, Y. J. Phua, S. B. Le, I. G. Eikjeland, K. D. Josefsen, S. Markussen, A. Myhr, H. Throne-Holst, P. Sikorski and A. Wentzel, PLoS One, 2019, 14, e0212990 CrossRef PubMed.
- J. W. Morse and R. S. Arvidson, Earth-Sci. Rev., 2002, 58, 51–84 CrossRef CAS.
- E. L. Sjöberg and D. T. Rickard, Chem. Geol., 1984, 42, 119–136 CrossRef.
- J. T. DeJong, B. M. Mortensen, B. C. Martinez and D. C. Nelson, Ecol. Eng., 2010, 36, 197–210 CrossRef.
- Y. Wang, K. Soga, J. T. Dejong and A. J. Kabla, Géotechnique, 2019, 69, 1086–1094 CrossRef.
- Z. Li, S. Wu, J. Han and S. Han, Analyst, 2011, 136, 3698–3706 RSC.
- J.-S. Wu, I.-C. Hwang, K. S. Kim and J. S. Kim, Org. Lett., 2007, 9, 907–910 CrossRef CAS PubMed.
- S. H. Bjørnøy, S. Mandaric, D. C. Bassett, A. K. Åslund, S. Ucar, J.-P. Andreassen, B. L. Strand and P. Sikorski, Acta Biomater., 2016, 44, 243–253 CrossRef PubMed.
- S. Dupraz, M. Parmentier, B. Ménez and F. Guyot, Chem. Geol., 2009, 265, 44–53 CrossRef CAS.
- C. Rodriguez-Navarro, F. Jroundi, M. Schiro, E. Ruiz-Agudo and M. T. González-Muñoz, Appl. Environ. Microbiol., 2012, 78, 4017–4029 CrossRef CAS PubMed.
- I. Bibi, R. S. Arvidson, C. Fischer and A. Lüttge, Minerals, 2018, 8, 256 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Fig. S1 and S2 illustrate schematically the precipitation process and the dissolution process. Fig. S3 shows the absorption spectra of phenol red, Fig. S4 shows the calibration curve for global pH monitoring experiments, and Fig. S5 illustrates the data processing for global pH monitoring experiments. Fig. S6 and S7 show the calibration curves for local pH monitoring experiments. Fig. S8 shows the nucleation process for the precipitation experiments in more detail. The brightfield images of dissolution of calcite crystals are shown in Fig. S9. Table S1 contains information about the growth medium for the bacteria culture. See DOI: 10.1039/d0ra03897k |
| This journal is © The Royal Society of Chemistry 2020 |