Open Access Article
Open Access ArticleInfluence of liquid bridge formation process on its stability in nonparallel plates†
Xiongheng Bian ,
Haibo Huang‡
* and
Liguo Chen‡*
,
Haibo Huang‡
* and
Liguo Chen‡*
Robotics & Microsystem Center, Collaborative Innovation Center of Suzhou Nano Science and Technology, Soochow University, Suzhou 215123, China. E-mail: hbhuang@suda.edu.cn; chenliguo@suda.edu.cn
First published on 27th May 2020
Abstract
The formation of a liquid bridge in non-parallel plates is very common and the stability (whether or not it can move spontaneously) of such liquid bridges has been studied a lot for industry, e.g. in printing applications. It is generally considered that the liquid bridge stability is determined by Contact Angle (CA), Contact Angle Hysteresis (CAH), the position of the liquid bridge (represented as P) and the dihedral angle (θ) between non-parallel plates. The stability equation is θ = f(CA, CAH, P). Since P is a process quantity, which is difficult to determine, so it is also difficult to obtain the critical equation for the stability of the liquid bridge. In the previous study (J. Colloid Interface Sci., 2017, 492, 207–217), based on the fitting simulation results, the critical equation about CA, CAH and θ is obtained, as θ = f(CA, CAH). However, in some special cases, the results are still biased (e.g. the weak hydrophilic situation). In this paper, unlike simulation, we get the critical equation θ = f(CA, CAH) from a theoretical point of view. For the first time, by in-depth analysis of the process of liquid bridge formation, the theoretical calculation equation of P is obtained as P = f(CA, CAH, θ). And then, combining the equations θ = f(CA, CAH, P) and P = f(CA, CAH, θ), the theoretical equation is obtained. A lot of simulations and experiments were performed to verify our theoretical equation. Furthermore, comparing our equation with the previous equation, it was found that our equation is more consistent with the experimental results (error less than 0.2°). Finally, the importance of considering the liquid bridging process (the function of P) for stability analysis is illustrated by comparing the results with those not considered (the difference is more than 20% in some cases). The outputs of this paper provide in-depth theoretical support for the analysis and application of liquid bridges.
1. Introduction
The formation of a liquid bridge is a common phenomenon of droplets, and is widespread in various industrial applications.1–5 As a common type, the liquid bridge in non-parallel plates has been widely used in droplet collection,6 oil–water separation7 and other microfluidics applications8–10 due to its directional spontaneous motion. In the last few decades, the stability of this kind of liquid bridge (whether it can move spontaneously) has been discussed a lot.11–13 The different Contact Angles (CAs) generated by the hydrophilic non-parallel plate structure lead to the different Laplace pressure on the opposite side of the liquid bridge, which propels the liquid bridge to move. Meanwhile, the Contact Angle Hysteresis (CAH) provides the hysteresis for the change of CAs, which prevents the motion of the liquid bridge, so as to maintain the stability of the liquid bridge.14 Therefore, it is generally believed that the stability of the bridge is mainly determined by the properties of the surface (CA and CAH), the structure of nonparallel plates (the dihedral angle θ). In addition, Ataei et al.15 proposed that the stability of the liquid bridge was also affected by the bridge position. Therefore, the critical equation should be θ = f(CA, CAH, P). Since P is a process quantity, which is mainly determined by the bridge formation process and difficult to determine. Then, it is also difficult to obtain the critical equation for the stability of the liquid bridge. In the previous study, Luo et al.14 analyzed the equation θ = f(CA, CAH, P) and gave a rough estimate of the stability of the liquid bridge by ignoring the influence of the parameter P. By fitting the experimental and simulation results, Ataei et al. obtained the critical equation as θ = f(CA, CAH) instead of θ = f(CA, CAH, P), to judge the stability of the liquid bridge in the hydrophilic nonparallel plates. The existing methods all choose to avoid the calculation of P.However, there are still three shortcomings in the current research. Firstly, since the critical equation θ = f(CA, CAH)16 is obtained by fitting the experimental and simulation results, and the influence of P is ignored, the equation works well in most cases, but there are still deviations in some special cases (for example, the weak hydrophilic situation). Secondly, since P is decided by the liquid bridge formation process, then, how to calculate the value of P by analyzing the process of liquid bridge formation is still unknown. Third, the importance of considering the process of liquid bridge formation is still unknown.
In this paper, based on equation θ = f(CA, CAH, P), we try to find a theoretical method to calculate P, so as to obtain a theoretical equation about θ = f(CA, CAH). First, from a geometric perspective, the critical equation about θ = f(CA, CAH, P) was given out. Then, through theoretical analysis, the influence of bridge formation process on its post-bridge position is studied, and the theoretical calculation equation P = f(CA, CAH, θ) is obtained, and verified by simulations. Furthermore, the theoretical curves, as θ = f(CA, CAH), for judging the stability of the liquid bridge are obtained for the first time. After that, the theoretical curves are compared with the existing fitting equation,16 and found it more consistent with the experimental results in the weak hydrophilic situation. Finally, the situation where the formation process needs to be considered are identified. The outputs of this paper provide a new theoretical support for the analysis and application of the liquid bridge.
2. Theoretical analysis of liquid bridge in nonparallel plates
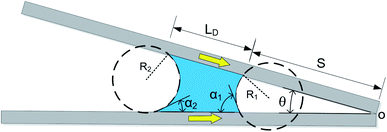
According to the geometric structure of Fig. 1, the equations about CAs can be obtained (the CA near the cusp α1 and the CA away from the cusp α2):
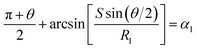 | (1) |
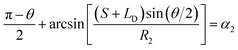 | (2) |
• For the case of inward motion: eqn (1) and (2) can be transformed into the equations about R, as 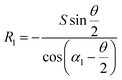 and
and 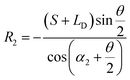 . According to Laplace equation, |R1| < |R2| is necessary to make the spontaneous inward motion. Besides that, CAs also have to satisfy α1 = αa and α2 = αr (subscripts a and r represent the advancing and receding angles of the droplets on the surface, respectively). Therefore, it can be found that when
. According to Laplace equation, |R1| < |R2| is necessary to make the spontaneous inward motion. Besides that, CAs also have to satisfy α1 = αa and α2 = αr (subscripts a and r represent the advancing and receding angles of the droplets on the surface, respectively). Therefore, it can be found that when 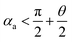 and θ > αCAH, the requirements can be met. More precisely, the conditions of inward motion can be written as:
and θ > αCAH, the requirements can be met. More precisely, the conditions of inward motion can be written as:
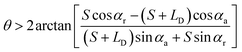 | (3) |
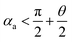 (the details are offered in the ESI 1†). From eqn (3), it can be inferred that the stability conditions of the liquid bridge on the hydrophilic surface are mainly determined by αa, αCAH and LD/S. Here, LD/S is used to represent the position of liquid bridge (value of P).
(the details are offered in the ESI 1†). From eqn (3), it can be inferred that the stability conditions of the liquid bridge on the hydrophilic surface are mainly determined by αa, αCAH and LD/S. Here, LD/S is used to represent the position of liquid bridge (value of P).
• For the case of outward motion: to achieve the spontaneous outward motion, CAs have to satisfy α1 = αr and α2 = αa. Therefore, the conditions of θ is:
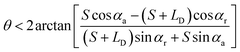 | (4) |
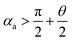 needs to be satisfied. From these inequations, it can be found that:
needs to be satisfied. From these inequations, it can be found that:
(1) Only on the hydrophobic surface can the liquid bridge move outwards spontaneously.
(2) θ will be smaller and approaching to zero with the decreasing of LD/S. However, with the spontaneous outward motion, LD/S has to be smaller, so the liquid bridge cannot exit nonparallel plates completely.
In conclusion, the critical condition for the liquid bridge to move inward is 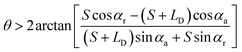 , and the critical condition for the liquid bridge to move outward is
, and the critical condition for the liquid bridge to move outward is 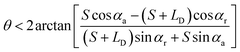 . It shows that the conditions for stable liquid bridges should be associated with the coupling of CA, CAH, θ and LD/S. Among them, CA, CAH and θ are determined by the surface properties and structural properties of nonparallel plates. LD/S is determined by the formation process of the liquid bridge. Then, in next sections, the influence of liquid bridge formation on LD/S is discussed.
. It shows that the conditions for stable liquid bridges should be associated with the coupling of CA, CAH, θ and LD/S. Among them, CA, CAH and θ are determined by the surface properties and structural properties of nonparallel plates. LD/S is determined by the formation process of the liquid bridge. Then, in next sections, the influence of liquid bridge formation on LD/S is discussed.
3. The improved simulation process of liquid bridge formation
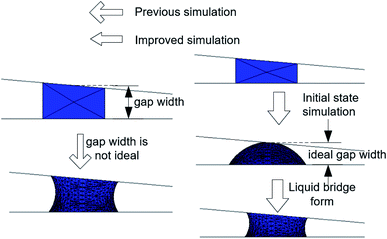
In order to study the influence of liquid bridge formation on LD/S, the formation process of liquid bridge was simulated through surface evolver. A friction model based on Santos and White19 was used to implement CAH. By this method, the contact lines will only move if the CA is greater than the advancing angle or less than the receding angle. Different from previous simulation method,16 as shown in Fig. 2, the simulation process was improved to make it more in line with the actual liquid bridge forming process. The improved simulation is composed of two steps: initial state simulation and liquid bridge formation simulation. The first step is the initial state simulation, which aims to simulate the instantaneous state of the droplet when it just touches the upper plate. In this process, the wetting angle of the upper plate is set to 70° and the wetting angle of the upper plate is set to nearly 180° to ensure that droplets will not adhere to the upper plate. In addition, the initial droplet is ensured to be spherical by setting CAH = 0. By doing this, the gap width is similar to the ideal width (where the droplet just touches the upper plate). The second step is the liquid bridge formation simulation, which was carried out by resetting the CA of the upper plate to the same as the bottom plate (70°).4. The influence of bridge forming process on LD/S
In order to better understand the influence of bridge forming process on LD/S, the formation process is theoretically discussed and verified by simulations and experiments.4.1 Analysis of the influence of the formation of liquid bridge on LD/S
As shown in Fig. 3b, geometrically, the initial value of the LD/S can be written as eqn (5) (the calculation process is offered in the ESI 2†).
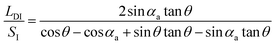 | (5) |
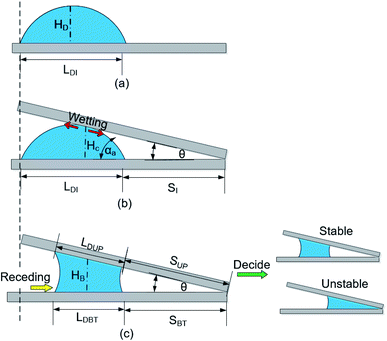 | ||
| Fig. 3 The model of liquid bridge forming process (a) before bridge forming process (b) at the beginning of bridge forming process (c) after bridge forming process (which decide the later stability). | ||
During the bridge forming process, with the droplet wetting along the up-plate and receding on the bottom plate, as shown in Fig. 3b and c, LDI goes down to LDBT, and SI goes up to SBT (here, subscripts I, BT and UP represent the initial state, bottom plate and upper plate respectively). Since the exist of CAH, LDBT is larger than LDUP and SBT is smaller than SUP, but these difference are very small and negligible when calculating the value of LD/S (the details is demonstrated in Section 4.1.2). Therefore, it can be found that 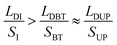 . LD/S after bridge forming can be calculated by:
. LD/S after bridge forming can be calculated by:
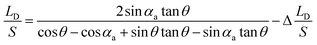 | (6) |
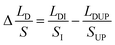 ,
, 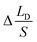 represents the change of
represents the change of 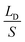 induced by the bridge formation process and is mainly affected by the corner angle θ, CA and CAH. Then, how can Δ(LD/S) be calculated in terms of θ, αa, CAH is discussed.
induced by the bridge formation process and is mainly affected by the corner angle θ, CA and CAH. Then, how can Δ(LD/S) be calculated in terms of θ, αa, CAH is discussed.
In fact, the process of liquid bridge formation is also the process that liquid droplets wetting along the upper plate. Since α1 is always greater than α2 when in the hydrophilic nonparallel plates (according to eqn (1) and (2)), the inner contact line stays still while the outer contact line recedes, that is, SI ≈ SUP. In addition, in order to simplify the calculation, the liquid bridge can be seen as cylindrical in shape after its formation, and its average height is HB (as shown in Fig. 3c). Such height is similar to the height of the contact point (marked as HC, as shown in Fig. 3b) when the upper plate contacts the droplets and is also the height of the droplets in the initial state (marked as HD, as shown in Fig. 3a). Then, the average height and volume after the formation of the liquid bridge can be written as:
HB ≈ (SUP + LDUP/2)tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ
| (7) |
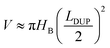 | (8) |
Meanwhile, for the initial droplet, the average height and volume before the formation of the liquid bridge can be written as (the calculation process is offered in the ESI 3†):
HD = LDI/(2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αa)(1 − cos αa)(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αa) αa)
| (9) |
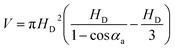 | (10) |
According eqn (7)–(10), HB ≈ HD and SI ≈ SUP, eliminate the variables (HB, HD, V) in them and substitute into the equation 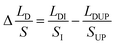 , the expression of
, the expression of 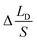 without considering CAH can be written as:
without considering CAH can be written as:
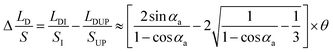 | (11) |
To verify the relationship between Δ(LD/S), θ and αa in eqn (11), verification simulations by surface evolver are carried out. In these simulations, CAHs are ignored, αa has different values (varying from 60° to 80°) and θ also has different values (varying from 1° to 6°). According to the simulation results shown in Fig. 4b, the curves are approximately linear. The approximate lines with different αa are 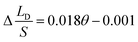 ,
, 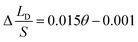 and
and 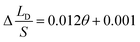 respectively. Compared with the theoretical results obtained from eqn (11), as shown in Fig. 4a (the approximate lines are
respectively. Compared with the theoretical results obtained from eqn (11), as shown in Fig. 4a (the approximate lines are 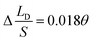 ,
, 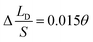 and
and 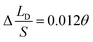 respectively), the theoretical curves and the simulation curves are basically the same.
respectively), the theoretical curves and the simulation curves are basically the same.
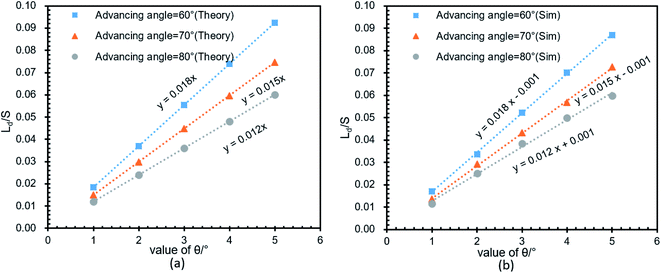 | ||
| Fig. 4 Verify the relationship between Δ(LD/S), θ and αa in eqn (11). (a) The theoretical relationship between Δ(LD/S) and θ with different αa. (b) The simulation results between Δ(LD/S) and θ with different αa. | ||
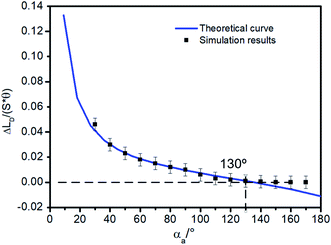
In addition, more simulations were carried out to verify the correctness of the eqn (11) for a larger range of αa (varying from 30° to 170°). Simulation results are shown in Fig. 5. The solid line is the theoretical curve obtained by the eqn (11) and the points are the simulations results. The theory and simulation results are consistent. When αa is greater than 130°, Δ(LD/S) is approximately 0, so in this case, the bridge formation process does not need to be considered.
ΔLCAH ≈ H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan(αCAH/2) tan(αCAH/2)
| (12) |
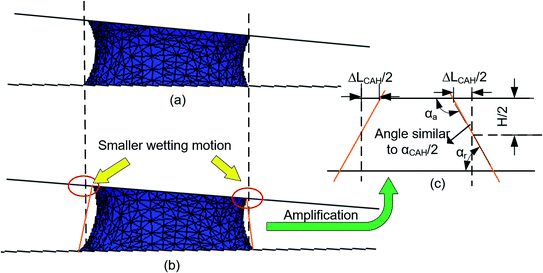 | ||
| Fig. 6 Analysis about the CAH effect based on simulation (a) simulation result without CAH (b) simulation result with αCAH = 30° (c) theoretical analysis model about the effect of αCAH. | ||
According to the structural equation (H ≈ Sθ), it can be found 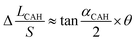 . Combining the eqn (11), the equation of Δ(LD/S) considering CAH can be obtained as:
. Combining the eqn (11), the equation of Δ(LD/S) considering CAH can be obtained as:
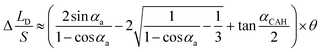 | (13) |
The relationship between Δ(LD/S) and αCAH is further analyzed by eqn (13) and simulations (obtained by surface evolver). The theoretical curves in Fig. 7 are obtained by eqn (13) and the points in Fig. 7 are obtained through simulations. In these simulations, θ is set to 1° and αCAH has three different values (varying from 10° to 30°). The following two points can be obtained:
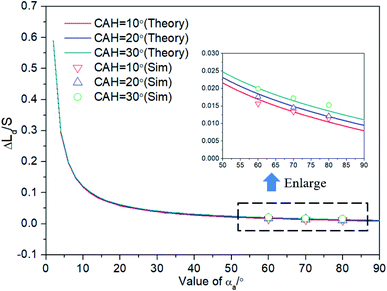 | ||
| Fig. 7 Verify the relationship between Δ(LD/S) and αCAH in eqn (13) and demonstrate that the effect of αCAH on Δ(LD/S) is negligible. | ||
(1) The curves almost coincide with each other at different αCAH, indicating that the influence of αCAH on Δ(LD/S) is almost negligible.
(2) Considering the effect of αCAH, as shown in the local enlarged image, the greater αCAH, the greater Δ(LD/S). The simulation results are also consistent with the prediction of eqn (13) (the maximum error is less than 0.002). The correctness of the equation is verified.
In conclusion, the influence of CAH on Δ(LD/S) is so small and can be ignored, which explains why the theoretical model in the third section and eqn (6) and (7) can be used in this paper.
4.2 Verification about our critical equations by simulations and experiments
Substitute eqn (13) into eqn (6), and eqn (6) into eqn (4), and the theoretical curves for the stability determination of the liquid bridge in the hydrophilic nonparallel plates can be obtained (as shown in Fig. 8).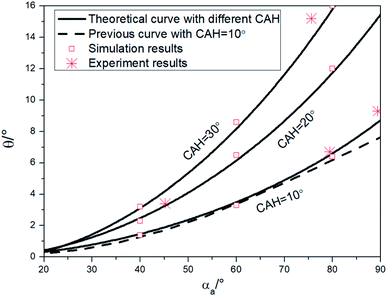 | ||
| Fig. 8 Verify the theoretical curves with the simulations, experiment results and compare with previous study. | ||
In order to verify these theoretical curves, simulations and experiments were carried out. Based on the simulation model of the third section, the simulation results are also obtained in the Fig. 8, which are found to be basically consistent with the theoretical curves (error less than 0.5°). In the experimental part, polystyrene (PS, αa ≈ 89.5°, CAH ≈ 10.2°), poly(ethyl methacrylate) (PEMA, αa ≈ 79.4°, CAH ≈ 10.5°), silicon (αa ≈ 44.5°, CAH ≈ 21.2°) and glass (αa ≈ 75.6°, CAH ≈ 29.2°) surfaces are adopted. The CAs and CAHs were measured using the sessile drop method and obtained by programming based on OpenCV. Measurements was repeated for five times for each surface. The experiments were carried out on the platform built in our previous study.20 The bottom plate was placed horizontally, and then the downward movement of the upper plate was controlled by a micro motor. As soon as the upper plate came into contact with droplets at a low speed (0.01 mm s−1), it stopped moving immediately. The critical angle of the stable liquid bridge was obtained by repeatedly locating θ when the liquid bridge was stable and unstable, and all the experiments were repeated five times and averaged for each case. The experimental results are shown in Fig. 8 (the asterisk marked), which also in line with the theoretical curves (the error was less than 0.5°). Comparing with the existing simulation fitting curve obtained by Alidad (the dotted line in Fig. 8),16 the two have a good fit (the difference is less than 0.2°) in most situations, but slightly different when αa is larger than 60°. It can be found that the critical angle of PS surface is about 9.2° by experiment (the asterisk marked), 8.8° by our theoretical curve (the solid line) and 7.5° by the previous study (the dotted line). It means that when αa was greater than 60°, our curves are more consistent with the experimental results and has a better performance.
In conclusion, comparing our method with the previous methods, Table 1 can be obtained:
4.3 The situation where the process of liquid bridge formation needs to be considered
To illustrate the importance of considering the liquid bridging process, more research has been done. According to Fig. 5, when αa is large than 130°, Δ(LD/S) will goes down to zero, the change of Δ(LD/S) can be neglected. But the importance of considering the process of liquid bridge formation in analyzing the stability of a liquid bridge when αa is smaller than 130° is still unknow. Then, the situation of considering and without considering bridge forming was compared.As shown in the Fig. 9, the theoretical curves (consider the process of liquid bridge formation) are obtained with different CAHs (the dotted line) by using the eqn (4), (6) and (13). Compared with the case that the formation process of liquid bridge is not considered (without consider the eqn (13)), it can be found that the difference between these two curves increases first and then decreases as αa increases. If αa is greater than 110°, the influence of the formation process of the liquid bridge on the stability can be ignored. But according to the research in Section 2, to achieve the inward motion, αa also should smaller than 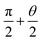 (at the right part the red dotted line in Fig. 9). In this region, the results with and without considering the process of bridge formation are quite different (in some cases, the difference is more than 20%). Therefore, the process of bridge formation should be considered for inwards motion.
(at the right part the red dotted line in Fig. 9). In this region, the results with and without considering the process of bridge formation are quite different (in some cases, the difference is more than 20%). Therefore, the process of bridge formation should be considered for inwards motion.
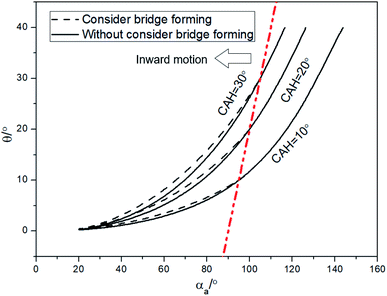 | ||
| Fig. 9 Comparisons of results between considering and without considering bridge forming by theoretical analysis. | ||
5. Summary and conclusion
In summary, experimental and numerical approaches as well as a theoretical analysis were employed to study the stability and formation process of a liquid bridge.Compared with previous studies,10,15,21–23 the paper provided the following new research progress.
(a) This research conclusion points out that the formation process of liquid bridge has influence on its later stability for the first time.
(b) The theoretical equation about the influence of formation process on bridge position is presented as P = f(CA, CAH, θ), and then, the theoretical curves for the stability determination of the liquid bridge are obtained as. The theoretical curves are verified by simulations and experiments.
(c) For inward motion, the process of bridge formation should be considered in all the cases.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Authors acknowledge financial support from National Key R&D Program of China (2018YFB1304905), Natural Science Foundation of the Jiangsu Higher Education Institutions of China (17KJA460008) and Natural Science Foundation of Jiangsu Province of China (BK20171215).References
- S. Collignon, J. Friend and L. Yeo, Planar microfluidic drop splitting and merging, Lab Chip, 2015, 15(8), 1942–1951 RSC
.
- L. Wang, M. Qiu, Q. Yang, Y. Li, G. Huang, M. Lin, T. J. Lu and F. Xu, Fabrication of Microscale Hydrogels with Tailored Microstructures based on Liquid Bridge Phenomenon, ACS Appl. Mater. Interfaces, 2015, 7(21), 11134–11140 CrossRef PubMed
.
- S. Kumar, Liquid Transfer in Printing Processes: Liquid Bridges with Moving Contact Lines, in Annu Rev Fluid Mech, ed. S. H. Davis and P. Moin, 2015, vol. 47, pp. 67–94 Search PubMed
.
- H. Chen, T. Tang and A. Amirfazli, Liquid transfer mechanism between two surfaces and the role of contact angles, Soft Matter, 2014, 10(15), 2503–2507 RSC
.
- D. J. Broesch and J. Frechette, From Concave to Convex: Capillary Bridges in Slit Pore Geometry, Langmuir, 2012, 28(44), 15548–15554 CrossRef CAS PubMed
.
- X. Heng and C. Luo, Bioinspired Plate-Based Fog Collectors, ACS Appl. Mater. Interfaces, 2014, 6(18), 16257–16266 CrossRef CAS PubMed
.
- C. Luo and X. Heng, Separation of oil from a water/oil mixed drop using two nonparallel plates, Langmuir, 2014, 30(33), 10002–10010 CrossRef CAS PubMed
.
- D. Baratian, A. Cavalli, D. van den Ende and F. Mugele, On the shape of a droplet in a wedge: new insight from electrowetting, Soft Matter, 2015, 11(39), 7717–7721 RSC
.
- J. Hong, J. K. Park, B. Koo, K. H. Kang and Y. K. Suh, Drop transport between two non-parallel plates via AC electrowetting-driven oscillation, Sens. Actuators, B, 2013, 188, 637–643 CrossRef CAS
.
- Y. Huang, L. Hu, W. Chen, X. Fu, X. Ruan and H. Xie, Directional Transport of a Liquid Drop between Parallel-Nonparallel Combinative Plates, Langmuir, 2018, 34(15), 4484–4493 CrossRef CAS PubMed
.
- P. Concus and R. Finn, Discontinuous behavior of liquids between parallel and tilted plates, Phys. Fluids, 1998, 10, 39–43 CrossRef CAS
.
- T. Y. Chen, J. A. Tsamopoulos and R. J. Good, Capillary Bridges between Parallel and Nonparallel Surfaces and their Stability, J. Colloid Interface Sci., 1992, 151(1), 49–69 CrossRef CAS
.
- W. Xu, Z. Lan, B. Peng, R. Wen, Y. Chen and X. Ma, Directional Movement of Droplets in Grooves: Suspended or Immersed?, Sci. Rep., 2016, 6, 18836 CrossRef CAS PubMed
.
- C. Luo, X. Heng and M. Xiang, Behavior of a liquid drop between two nonparallel plates, Langmuir, 2014, 30(28), 8373–8380 CrossRef CAS PubMed
.
- M. Ataei, H. Chen and A. Amirfazli, Behavior of a Liquid Bridge between Nonparallel Hydrophobic Surfaces, Langmuir, 2017, 33(51), 14674–14683 CrossRef CAS PubMed
.
- M. Ataei, H. Chen, T. Tang and A. Amirfazli, Stability of a liquid bridge between nonparallel hydrophilic surfaces, J. Colloid Interface Sci., 2017, 492, 207–217 CrossRef CAS PubMed
.
- J. W. Bush, F. Peaudecerf, M. Prakash and D. Quere, On a tweezer for droplets, Adv. Colloid Interface Sci., 2010, 161(1–2), 10–14 CrossRef CAS PubMed
.
- L. Wang, H. Wu and F. Wang, Efficient transport of droplet sandwiched between saw-tooth plates, J. Colloid Interface Sci., 2016, 462, 280–287 CrossRef CAS PubMed
.
- M. J. Santos and J. A. White, Theory and Simulation of Angular Hysteresis on Planar Surfaces, Langmuir, 2011, 27(24), 14868–14875 CrossRef CAS PubMed
.
- X. Bian, H. Huang and L. Chen, Motion of droplets into hydrophobic parallel plates, RSC Adv., 2019, 9(55), 32278–32287 RSC
.
- M. Ataei, T. Tang and A. Amirfazli, Motion of a liquid bridge between nonparallel surfaces, J. Colloid Interface Sci., 2017, 492, 218–228 CrossRef CAS PubMed
.
- W. Wang and T. B. Jones, Moving droplets between closed and open microfluidic systems, Lab Chip, 2015, 15(10), 2201–2212 RSC
.
- J. Berthier, Microdrops and Digital Microfluidics, 2008 Search PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra03438j |
| ‡ Present addresses: Robotics & Microsystem Center & Collaborative Innovation Center of Suzhou Nano Science and Technology, Soochow University Suzhou 215123, China. |
| This journal is © The Royal Society of Chemistry 2020 |