Reverse shape selectivity of hexane isomer in ligand inserted MOF-74

Abstract

Separation of linear, mono-branched, and di-branched isomers is critically important in the petrochemical industry. In this computational study, we demonstrate that the ligand inserted Mg-MOF-74 structure leads to a reverse selectivity effect (i.e. phenomenon that preferentially allows larger species molecules to permeate in a gas mixture) of hexane isomers in the resulting material. Molecular dynamics simulations suggest that strong confinement of the di-branched hydrocarbons in the small pores lead to reverse selectivity. Over a magnitude difference in diffusivity between linear alkanes and their di-branched isomers was observed, clearly showing the steric effects imposed by the pore structure.

---

In the petrochemical industry, separation of the hexane isomers is an important process that removes impurities for fuel purification and the isolation of mixtures for applied further reaction.^1,2 The sieving of n-hexane and its branched isomers is particularly interesting research because of the varying octane numbers in the isomers affecting the gasoline production,^3–5 and as such, it is imperative to facilitate separation of these isomers. Unfortunately, this separation is particularly challenging due to the similar polarizabilities and chemical inertness of the molecules, leading one to resort to highly energy expensive distillation processes.^1,6

The presently used methods such as molecular sieving using zeolites and the conventional distillation processes still include mixtures of the isomers that lowers the overall octane number^7,8 compared to the pure di-branched molecule composition. To discover the adsorbent materials that can completely separate the isomers into their individual components, many researchers have investigated adsorbent materials with an appropriate pore size and shape.^9–12 Recently, metal–organic frameworks (MOFs) have attracted great deal of attention from the researchers due to their potential applications in gas separations,^13–20 CO₂ capture,^21,22 catalysis,^23–26 water harvesting^27–29 and several other applications.^30–32 MOFs are crystalline microporous materials composed of inorganic metal nodes and organic linkers^33–35 and via combining various metal clusters and organic linkers, MOFs can be tuned specifically to ideal shapes and pore chemical environment for targeted gas separations.^36–38 This tunability allows one to potentially design MOFs that are ideal for hexane isomers. Bárcia et al.³⁹ firstly used MOFs called Zn(BDC)(DABCO)_0.5 (MOF-1) to separate hexane isomers, although this MOF showed low adsorption capacities. Also, Herm et al.¹² synthesized a MOF named Fe₂(BDP)₃ (BDP²⁻ = 1,4-benzenedipyrazolate), which contain triangular pore channels that can discriminate hexane isomers better than the commercial standard. More recently, Lv et al.⁴⁰ demonstrated that [Fe₃(μ3-O)(COO)₆] and 2,2-bis(4-carboxyphenyl)-hexafluoropropane (6FDCA) have strong capability to separate n-hexane from its branched isomers on the basis of a kinetically controlled molecular sieve separation.

Overall, conventional wisdom dictates that one would seek to design materials whose pore limiting diameter can separate the molecules of interest within the mixture. With that being said, there have been few observances where the ordering based on kinetic diameters is reversed (in what is called reverse selectivity).⁴¹ Previous study by Bárcia et al.⁴² used the concept of “length entropy” to describe the adsorption and separation behavior in UiO-66(Zr). They showed that UiO-66(Zr) preferentially adsorb branched alkanes over their linear isomer, in what they called “reverse selectivity”. Moreover, Pan et al.⁴³ described the unusual reverse selective separation of n-butane from normal hydrocarbons above C₄ in a fluorinated MOF with 1D channels. Additionally, reverse selectivity has also been mentioned in recent works with IRMOF-8 (ref. 44) and UiO-66@SiO₂ (ref. 45) with regards to linear and iso-alkane separation.

In our previous computational work, we designed the ligand inserted MOF frameworks using the ligand insertion strategy. Using computational analysis, these structures showed increase in the working capacity of CO₂ under humid flue gas conditions,²² utility as a catalyst for enhanced ethane oxidation²⁵ and potential usage in water harvesting material.²⁹ In the current work, the dpt ligand inserted Mg-MOF-74 structures with 1-D channel was used to examine the reverse selectivity of hexane isomer and separation properties by considering mixtures of n-hexane and its branched isomers (2,2-dimethylbutane, 2,3-dimethylbutane, 2-methylpentane and 3-methylpentane). In the context of the hexane isomer separation, the inserted ligand finely tuned the shape and the size of the pores within the MOF such that branched isomer can reverse selectively pass through the MOF channel.

Optimization of the MOFs and the hexane isomer binding energy calculations were conducted using the first-principles calculations through the density functional theory (DFT) as implemented by the plane-wave pseudopotential approach in Quantum Espresso.⁴⁶ The second version of a van der Waals dispersion-corrected density functional (vdW-DF2)⁴⁷ was used to describe the dispersion interactions. Ultrasoft pseudopotentials were used for GGA and vdW-DF2 calculations. A 2 × 2 × 2 k-point mesh was used for the Brillouin zone sampling in the reciprocal space. The kinetic energy and charge density planewave cutoff were set to 30 Ry and 240 Ry, respectively.

All molecular dynamics simulations were carried out using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) program.⁴⁸ In the simulations, the MOF structures are set to be fixed with the dpt ligand and the hexane isomers considered to be flexible, incorporating all intramolecular motions such as bond vibrations, bond angle bending, and torsional motions. All non-bonded interactions between the atoms were calculated using the Lennard-Jones (LJ) potential. Adsorbate–adsorbate and adsorbate–MOF interactions were truncated at 14 Å and at 12.8 Å with analytical tail-corrections applied for interactions beyond this cutoff distance, respectively. The LJ parameters for the atoms of the MOF were taken from the UFF⁴⁹ and The TraPPE force field were employed to model the inter- and intramolecular interactions of the hexane isomers as previous studies reported that these models accurately model the adsorption and diffusion properties of alkanes⁵⁰ and nHEX⁵¹ in the MOFs. Initially, all systems were equilibrated for 2 ns in an NVT ensemble, and afterwards, another 10 ns of simulation was performed in the NVT ensemble during which the equilibrated phase space trajectories were stored at every 10 ps. These trajectories were then used to analyze the diffusion behavior of the hexane isomers with the diffusion coefficients calculated from the mean square displacements (MSD) of the molecules using the Einstein's relation.

The ligand insertion strategy within the MOF-74 structure can be used to reconfigure the pore space to enhance the separation performance. To demonstrate this, a size-matching regulated ligand (2,4-di(4-pyridinyl)-1,3,5-triazine (dpt)) was inserted as shown in Fig. 1(a).

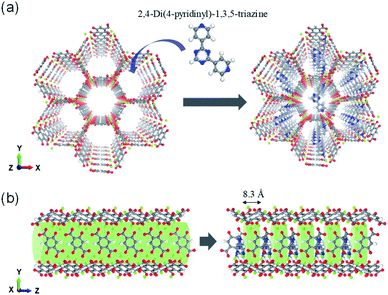Fig. 1 Illustration of pore space partitioned Mg-MOF-74 using ligands 2,4-di(4-pyridinyl)-1,3,5-triazine. (a) Viewed along z axis and (b) side view of the channels showing the cylindrical channel.

The insertion of 2,4-di(4-pyridinyl)-1,3,5-triazine (dpt) ligands into the hexagonal channels of Mg-MOF-74 was demonstrated in our previous theoretical study on catalyst for ethane oxidation.²⁵ In the previous work, the computed DFT binding energy of the dpt ligand was −198.3 kJ mol⁻¹ in the Mg-MOF-74 structures, providing evidence that the ligands would stay intact and not wash away, post synthesis. The dpt ligands were inserted such that the distance between the two dpt ligands is 8.3 Å along the channel direction in the z-axis (Fig. 1(b)). In the alkane separations, configurational and length entropy effects may act in a completely different manner. These effects plays a bigger role for separating linear and branched alkanes in materials such as AFI⁵² and MOF-74 that have cylindrical channels. Hence, it is important to consider both the maximum diameter (i.e. molecular length)⁵³ of the molecules as well as kinetic diameter. As can be seen from Table 1, the kinetic diameter of the hexane isomers increases with branching. However, the maximum diameter is inversely correlated (for example, nHEX has the largest maximum diameter despite having the smallest kinetic diameter).

Table 1 Kinetic diameters and maximum diameter of all hexane isomers^53,54

Name	Kinetic diameter (Å)	Maximum diameter (Å)
n-Hexane (nHEX)	4.3	10.3
2-Methylpentane (2MP)	5.0	9.4
3-Methylpentane (3MP)	5.0	9.4
2,3-Dimethylbutane (23DMB)	5.8	8.1
2,2-Dimethylbutane (22DMB)	6.2	8.1

---

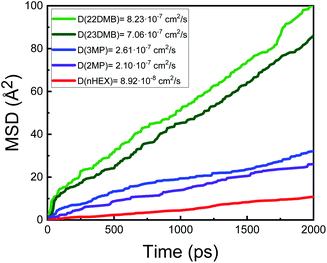
The mean squared displacement (MSD) analysis is a general method to characterize mobility as it can help determine whether a molecule is freely diffusing or bound and limited in its movement. To demonstrate the gas molecule diffusivity, MSD analysis was used for the hexane isomers (Fig. 2).

Fig. 2 Mean-squared displacement (MSD) of hexane isomer at 300 K for 2 ns. Linear hexane (nHEX, red), 2-methylpentane (2MP, purple), 3-methylpentane (3MP, blue), 2,3-dimethylpentane (23DMB, dark green), and 2,2-dimethylpentane (22DMB, green) are shown respectively.

The mobility of the five isomers in the 100% ligand inserted MOF (where there is a ligand per every 6 metal sites in the hexagonal plane of the channel) is largely dominated by the isomer shapes. In general, the MSD (and the resulting self diffusion coefficient) has an inverse relationship with the kinetic diameter as molecules with the smallest kinetic diameters tend to diffuse the slowest (Fig. 2). It turns out that the distance between two neighbouring ligands (Fig. 1(b), along the z-axis, measured to be D = 8.3 Å) significantly influences the mobility of hexane isomers. As noted in Table 1, nHEX is the longest molecule (d_nHex = 10.3 Å), and 22DMB is the shortest one (d_22DMB = 8.1 Å). When passing through the channel, nHEX suffer from the hindrance because of configurational penalty as d_nHex > D. On the other hand, 22DMB can be packed more efficiently in each space between the ligands within the channels as d_22DMB < D. Due to the discrepancy in the maximum diameter values for the hexane isomers, the ligand inserted MOF has an unusual behavior in which the di-branched hexane (2,2-dimethylbutane, 2,3-dimethylbutane) show higher diffusivity than mono-branched hexane (3-methylpentane, 2-meythylpentane) and linear hexane (nHEX). Finally, the results at a different temperature of T = 433 K are shown in the ESI† and qualitatively, the simulated data show similar trends compared to the T = 300 K case (Fig. S1†).

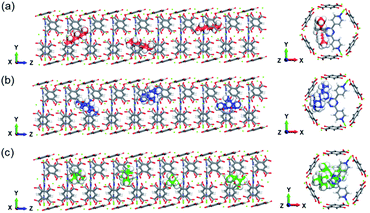
To visualize the trajectory of the hexane isomers, MD snapshots are presented in Fig. 3. The reverse selectivity largely comes from nHEX (Fig. 3(a)) being “stuck” inside the cage created between the two neighbouring ligands. With increasing number of branches, it becomes easier for these branched isomers to rotate vertically and diffuse through the channels (Fig. 3(b) and (c)). The double branched isomer has the shortest length and thus can freely rotate, leading to relative fast diffusion despite having the largest kinetic diameter (Fig. 3(c)).

Fig. 3 (a) Snapshot of nHEX in dpt-Mg-MOF-74 at 300 K. (b) Snapshot of 3MP in dpt-Mg-MOF-74 at 300 K. (c) Snapshot of 22DMB in dpt-Mg-MOF-74. C (nHEX), C (3MP), C (22DMB), and H are shown in red, blue, green and white colors, respectively. To better illustrate the diffuse configurations, the cluster was zoomed in and exterior atoms were omitted.

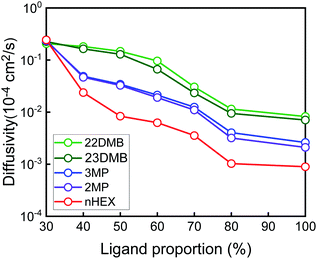
Thus far, the computational simulations assumed that all of the available metal sites within the MOF-74 structure were filled with the ligands. Most likely, during experimental synthesis of this material, it might be difficult to populate dpt ligands for all of the metal sites within the MOF. As such, the proportion of all available occupied sites was varied from 30 to 100% to see its effect on the diffusion properties of the hexane isomers (Fig. 4, and see Fig. S2–S5† for individual ligand proportion data).

Fig. 4 Diffusivity versus inserted dpt ligand proportion in Mg-MOF-74. The linear hexane (nHEX, red), 2-methylpentane (2MP, purple), 3-methylpentane (3MP, blue), 2,3-dimethylpentane (23DMB, dark green), and 2,2-dimethylpentane (22DMB, green), respectively.

Fig. 4 shows that the diffusivity of all of the hexane isomers reduces with increasing proportion of the ligands. However, the behavior for each of the isomers is different as at 30% (representing low occupancy of dpt ligand), the diffusion coefficient values are pretty much the same for all the isomers as relatively ample amount of space within the MOF materials lead to similar diffusivity values. For materials with more than 40% or more occupancy of the ligands, the gap in diffusivity between the isomers become pronounced due to the hindrance effects described earlier. From Fig. 4, one can see that the proportion of the ligands plays a crucial role in maintaining the high reverse selectivity and as such, dense occupancy of the ligands is preferred.

Finally, diffusivity of pentane and heptane isomers were also computed as a comparison with the hexane data to better understand the role of the molecule size in the reverse selectivity effect (see Fig. S6 and S7 in ESI†). Since pentane isomers are smaller compared to the hexane isomers, linear pentane was not affected by steric hindrance and the length entropy when passing through the dpt-MOF channel, resulting in the diffusivity ordering based on the kinetic diameter. For the heptane isomers, the molecular size of the isomers is so large that all of them have difficulty passing through the dpt-MOF channel, which results in overall poor diffusivity.

In this work, we applied a ligand insertion strategy to modify the MOF-74 structure and to introduce reverse selectivity of the hexane isomers. Specifically, we revealed that inclusion of ligands in dpt-Mg-MOF-74 leads to reversed hierarchy (22DMB > 23DMB > 3MP > nHEX) due to the steric effects of the molecules that becomes prominent in passing through the straight cylindrical channel. The findings here illustrate the importance of rational materials design in separating gas molecules that are relevant to the petroleum industry.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Mid-Career Researcher Program (NRF-2017R1A2B4004029) through the NRF (National Research Foundation of Korea) funded by the Ministry of Science and ICT.

References

1. J. G. Speight, Handbook of Petroleum Refining, CRC Press, 2016.
2. S. A. Treese, P. R. Pujadó and D. S. J. Jones, Handbook of Petroleum Processing, SpringerReference, 2015, pp. 53–124.
3. R. A. Myers, Handbook of Petroleum Refining Processes, McGraw-Hill, NewYork, 2004.
4. Z. R. Herm, E. D. Bloch and J. R. Long, Chem. Mater., 2014, 26, 323–338.
5. M. Schenk, S. L. Vidal, T. J. H. Vlugt, B. Smit and R. Krishna, Langmuir, 2001, 17, 1558–1570.
6. Z. Zhang, Q. Yang, X. Cui, L. Yang, Z. Bao, Q. Ren and H. Xing, Angew. Chem., Int. Ed., 2017, 56, 16282–16287.
7. P. S. Bárcia, J. A. C. Silva and A. E. Rodrigues, Microporous Mesoporous Mater., 2005, 79, 145–163.
8. R. Krishna and J. M. van Baten, Sep. Purif. Technol., 2007, 55, 246–255.
9. N. Chang, Z. Y. Gu and X. P. Yan, J. Am. Chem. Soc., 2010, 132, 13645–13647.
10. D. Peralta, G. Chaplais, A. Simon-Masseron, K. Barthelet and G. D. Pirngruber, Ind. Eng. Chem. Res., 2012, 51, 4692–4702.
11. P. A. P. Mendes, A. E. Rodrigues, P. Horcajada, C. Serre and J. A. C. Silva, Microporous Mesoporous Mater., 2014, 194, 146–156.
12. Z. R. Herm, B. M. Wiers, J. A. Mason, J. M. Van Baten, M. R. Hudson, P. Zajdel, C. M. Brown, N. Masciocchi, R. Krishna and J. R. Long, Science, 2013, 340, 960–964.
13. Z. Bao, S. Alnemrat, L. Yu, I. Vasiliev, Q. Ren, X. Lu and S. Deng, Langmuir, 2011, 27, 13554–13562.
14. E. D. Bloch, W. L. Queen, R. Krishna, J. M. Zadrozny, C. M. Brown and J. R. Long, Science, 2012, 335, 1606–1610.
15. J. R. Li, J. Sculley and H. C. Zhou, Chem. Rev., 2012, 112, 869–932.
16. P. A. P. Mendes, P. Horcajada, S. Rives, H. Ren, A. E. Rodrigues, T. Devic, E. Magnier, P. Trens, H. Jobic, J. Ollivier, G. Maurin, C. Serre and J. A. C. Silva, Adv. Funct. Mater., 2014, 24, 7666–7673.
17. Y. G. Chung, P. Bai, M. Haranczyk, K. T. Leperi, P. Li, H. Zhang, T. C. Wang, T. Duerinck, F. You, J. T. Hupp, O. K. Farha, J. I. Siepmann and R. Q. Snurr, Chem. Mater., 2017, 29, 6315–6328.
18. R. B. Lin, S. Xiang, H. Xing, W. Zhou and B. Chen, Coord. Chem. Rev., 2019, 378, 87–103.
19. X. Zhao, Y. Wang, D. S. Li, X. Bu and P. Feng, Adv. Mater., 2018, 30, 1705189.
20. M. L. Gao, W. J. Wang, L. Liu, Z. B. Han, N. Wei, X. M. Cao and D. Q. Yuan, Inorg. Chem., 2017, 56, 511–517.
21. K. Sumida, D. L. Rogow, J. A. Mason, T. M. McDonald, E. D. Bloch, Z. R. Herm, T. H. Bae and J. R. Long, Chem. Rev., 2012, 112, 724–781.
22. B. L. Suh, S. Lee and J. Kim, J. Phys. Chem. C, 2017, 121, 24444–24451.
23. D. J. Xiao, E. D. Bloch, J. A. Mason, W. L. Queen, M. R. Hudson, N. Planas, J. Borycz, A. L. Dzubak, P. Verma, K. Lee, F. Bonino, V. Crocellà, J. Yano, S. Bordiga, D. G. Truhlar, L. Gagliardi, C. M. Brown and J. R. Long, Nat. Chem., 2014, 6, 590–595.
24. P. Verma, K. D. Vogiatzis, N. Planas, J. Borycz, D. J. Xiao, J. R. Long, L. Gagliardi and D. G. Truhlar, J. Am. Chem. Soc., 2015, 137, 5770–5781.
25. B. L. Suh and J. Kim, J. Phys. Chem. C, 2018, 122, 23078–23083.
26. N. Wei, R. X. Zuo, Y. Y. Zhang, Z. B. Han and X. J. Gu, Chem. Commun., 2017, 53, 3224–3227.
27. H. Kim, S. Yang, S. R. Rao, S. Narayanan, E. A. Kapustin, H. Furukawa, A. S. Umans, O. M. Yaghi and E. N. Wang, Science, 2017, 356, 430–434.
28. M. J. Kalmutzki, C. S. Diercks and O. M. Yaghi, Adv. Mater., 2018, 30, 1704304.
29. B. L. Suh, S. Chong and J. Kim, ACS Sustainable Chem. Eng., 2019, 7, 15854–15859.
30. M. P. Suh, H. J. Park, T. K. Prasad and D. W. Lim, Chem. Rev., 2012, 112, 782–835.
31. X. Fang, B. Zong and S. Mao, Nano-Micro Lett., 2018, 10, 64.
32. S. Bai, X. Liu, K. Zhu, S. Wu and H. Zhou, Nat. Energy, 2016, 1, 16094.
33. M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Wachter, M. O'Keeffe and O. M. Yaghi, Science, 2002, 295, 469–472.
34. B. Chen, N. W. Ockwig, A. R. Millward, D. S. Contreras and O. M. Yaghi, Angew. Chem., Int. Ed., 2005, 44, 4745–4749.
35. O. M. Yaghi, M. J. Kalmutzki and C. S. Diercks, Introduction to Reticular Chemistry, John Wiley & Sons, 2019.
36. C. Y. Lee, Y. S. Bae, N. C. Jeong, O. K. Farha, A. A. Sarjeant, C. L. Stern, P. Nickias, R. Q. Snurr, J. T. Hupp and S. T. Nguyen, J. Am. Chem. Soc., 2011, 133, 5228–5231.
37. B. Valizadeh, T. N. Nguyen and K. C. Stylianou, Polyhedron, 2018, 145, 1–15.
38. G. Han, Y. Gong, H. Huang, D. Cao, X. Chen, D. Liu and C. Zhong, ACS Appl. Mater. Interfaces, 2018, 10, 32128–32132.
39. P. S. Bárcia, F. Zapata, J. A. C. Silva, A. E. Rodrigues and B. Chen, J. Phys. Chem. B, 2007, 111, 6101–6103.
40. D. Lv, H. Wang, Y. Chen, F. Xu, R. Shi, Z. Liu, X. Wang, S. J. Teat, Q. Xia, Z. Li and J. Li, ACS Appl. Mater. Interfaces, 2018, 10, 6031–6038.
41. T. C. Merkel, B. D. Freeman, R. J. Spontak, Z. He, I. Pinnau, P. Meakin and A. J. Hill, Science, 2002, 296, 519–522.
42. P. S. Bárcia, D. Guimarães, P. A. P. Mendes, J. A. C. Silva, V. Guillerm, H. Chevreau, C. Serre and A. E. Rodrigues, Microporous Mesoporous Mater., 2011, 139, 67–73.
43. L. Pan, D. H. Olson, L. R. Ciemnolonski, R. Heady and J. Li, Angew. Chem., Int. Ed., 2006, 45, 616–619.
44. J. Pires, J. Fernandes, A. C. Fernandes and M. Pinto, Sep. Sci. Technol., 2017, 52, 51–57.
45. X. Zhang, Q. Han and M. Ding, RSC Adv., 2015, 5, 1043.
46. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. De Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 39.
47. K. Lee, É. D. Murray, L. Kong, B. I. Lundqvist and D. C. Langreth, Phys. Rev. B, 2019, 82, 081101.
48. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
49. A. K. Rappé, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035.
50. H. Zhang, P. Deria, O. K. Farha, J. T. Hupp and R. Q. Snurr, Energy Environ. Sci., 2015, 8, 1501.
51. N. A. Ramsahye, P. Trens, C. Shepherd, P. Gonzalez, T. K. Trung, F. Ragon and C. Serre, Microporous Mesoporous Mater., 2014, 189, 222–231.
52. R. Krishna, B. Smit and S. Calero, Chem. Soc. Rev., 2002, 31, 185–194.
53. V. A. Solanki and B. Borah, Ind. Eng. Chem. Res., 2019, 58, 20047–20065.
54. A. F. P. Ferreira, M. C. Mittelmeijer-Hazeleger, M. A. Granato, V. F. D. Martins, A. E. Rodrigues and G. Rothenberg, Phys. Chem. Chem. Phys., 2013, 15, 8795–8804.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra03377d

---