Open Access Article
Open Access ArticleDetection of L-band electron paramagnetic resonance in the DPPH molecule using impedance measurements
Ushnish Chaudhuri and
R. Mahendiran *
*
Department of Physics, National University of Singapore, 2 Science Drive 3, Singapore-117551, Republic of Singapore. E-mail: phyrm@nus.edu.sg
First published on 5th May 2020
Abstract
Detection of electron paramagnetic resonance (EPR) using a microwave cavity resonating at a fixed frequency (between 9 and 10 GHz) remains the most popular method to date. Here, we report a cavity-less technique which makes use of only an impedance analyzer and a copper strip coil to detect L-band EPR (f = 1–3 GHz) in the standard EPR marker 2,2-diphenyl-1-picrylhydrazyl (DPPH). Our method relies on measuring the magnetoimpedance (MI) response of DPPH through a copper strip coil that encloses DPPH. In contrast to commercial EPR which measures only the field derivative of power absorption, our method enables us to deduce both absorption and dispersion. Changes in resistance (R) and reactance (X) of the copper strip while sweeping an external dc magnetic field, were measured for different frequencies (f = 0.9 to 2.5 GHz) of radio frequency current in the coil. R exhibits a sharp peak at a critical value of the dc magnetic field, which is identified as the resonance field and X shows a dispersion at the same frequency. The data were analyzed to obtain line width and resonance field parameters. The resonance field increased linearly with frequency and the obtained Landé g factor of 1.999 ± 0.0197 is close to the accepted value of 2.0036, measured in the X-band. The simplicity of this technique can be exploited to study paramagnetic centers in catalysis and other materials.
Introduction
The first electron paramagnetic resonance (EPR) spectrum was recorded by Evgeny Konstantinovich Zavoisky almost 70 years ago using a simple home-built spectrometer.1 Over the years, EPR has evolved into a sophisticated instrument and become an essential tool to detect unpaired electrons in solids which in turn provides information about electronic structure of the paramagnetic centers and their chemical environments.2 EPR is also used to probe local defects in Si/SiO2,3 to study structural phase transitions,4 kinetics of chemical reactions,5,6 electron and spin transfer in catalysis,7,8 structure of proteins, organic free radicals, etc.7 Thus, applications of EPR span all the branches of science. To date, the most popular method to detect EPR makes use of a fixed frequency microwave cavity resonator in the X band (∼9 GHz) or Q band (∼35 GHz) frequency regime.9 However, metallic samples with high conductive losses as well as aqueous biological/chemical samples with large dielectric losses prove to be limiting for commercial EPR spectrometers operating in X band since they cause frequency shift due to dispersion of permeability.10 Recently, coplanar waveguides (CPW)11–14 and microstripline resonators (MSR)15–18 have been exploited to investigate smaller sized lossy samples over a broad frequency range. These methods take advantage of advances in microwave synthesizers working in a broad frequency range (∼50 MHz to ∼50 GHz) to deliver microwave power to CPW/MSR to create intense local microwave magnetic field on the surfaces of CPW or MSR upon which a paramagnetic metallic sample is placed. However, with increasing frequency of the microwave signal, penetration of electromagnetic field inside a conducting sample also decreases due to skin effect. An EPR spectrometer working L-band (1–3 GHz) or still lower frequencies is preferable to ensure a deeper penetration of electromagnetic waves into a conducting or a biological sample. The EPR spectra at low frequencies can exhibit better resolution in certain cases, e.g. the EPR spectra of Cu2+ complexes such as Cu(DOPA)2 and Cu(carnosine)4 were better resolved at 2.62 GHz than at 9.30 GHz.19 Eaton and Eaton have given an overview of spectrometers developed for frequencies below X-band.20 In this paper we describe a previously unreported technique for free radical compounds which can aid researchers investigate EPR from a fresh perspective.In this article, we present a simple method to detect EPR in the L-band frequency region, which makes use of only an impedance analyzer and a copper strip coil. In a closely related work, Kitagawa studied EPR of DPPH placed above a 50 ohm impedance matched microinductor fabricated with CMOS-25 nanotechnology and used a vector network analyzer to extract EPR signal in frequency sweep mode.21 A vector network analyzer measures the ratio of a transmitted or reflected power to the incident power from a device under test. Impedance is calculated from scattering parameter S12 and S11.21 In contrast, the instrument used in the current work (Agilent E4991 RF impedance analyzer) measures impedance of a copper strip based on the radio frequency current–voltage technique and does not require 50 ohm impedance matching or CMOS technology. The copper strip is prepared manually by cutting and folding a copper foil to desired shape. Our method is compact, requires very less instrumentation and does not require multistep device fabrication therefore, it can be easily incorporated in teaching and research laboratories. Our technique provides additional information pertaining to the absorptive and dispersive components of the high frequency magnetic susceptibility whereas conventional EPR spectrometers are designed to provide information about the field derivative of the power absorbed by the sample. Using our simple setup, we demonstrate the detection of EPR due to free radicals in a standard sample of 2,2-diphenyl-1-picrylhydrazyl (DPPH). As a stable and well-characterized solid radical source, DPPH is the most popular reference sample with Landé g-factor of 2.0036.22 The intensity of EPR signals depends on the number of radicals for a freshly prepared sample and can be determined by weighing the DPPH sample. DPPH exhibits a single response line in X-band with a small linewidth ∼1.5–4.7 Oe due to the presence of only one unpaired spin per 41 atoms.
Experimental details
To detect EPR in DPPH sample we measure the magnetoimpedance (MI) of a copper strip surrounding the sample. MI refers to the variation of electrical impedance (Z(f,H) = R(f,H) + iX(f,H)) of a material in presence of an applied dc magnetic field (Hdc) at different frequencies of alternating current (f). It consists of measuring the magnetic field dependence of the magnitude of impedance (Z) alone or resistance (R) and reactance (X) of the sample i.e., magnetoresistance and magnetoreactance, respectively.23 Magnetoimpedance in soft ferromagnetic metallic conductors has been investigated many researchers using either an inductance–capacitance–resistance (LCR) meter in the frequency range (10 kHz to few tens of MHz) by two/four probe methods or vector network analyzers in the frequency range 10 MHz to 20 GHz.24–26 For the later case, a microstripline is photolithographically fabricated on a dielectric substrate.27,28 On the other hand, we have recently have discovered that MI measured by passing microwave (MW) current directly through some electrically conducting Mn-based perovskite oxides can detect not only paramagnetic but also ferromagnetic resonance of exchange coupled t2g spins of Mn3+:t32ge1g and Mn4+:t32ge0g ions.29,30 In manganites, short-range correlation between localized t2g core spins (S =![[/]](https://www.rsc.org/images/entities/char_e0ee.gif) ) mediated by hopping of eg electron (S = ½) leads to intense ESR signal in the paramagnetic state. Resistivity of a manganite shows semiconducting like behavior in the paramagnetic and its value is of the order few milliohm cm at room temperature. However, DPPH is an insulator and hence an indirect method is employed in the present work to measure the MI of DPPH.
) mediated by hopping of eg electron (S = ½) leads to intense ESR signal in the paramagnetic state. Resistivity of a manganite shows semiconducting like behavior in the paramagnetic and its value is of the order few milliohm cm at room temperature. However, DPPH is an insulator and hence an indirect method is employed in the present work to measure the MI of DPPH.
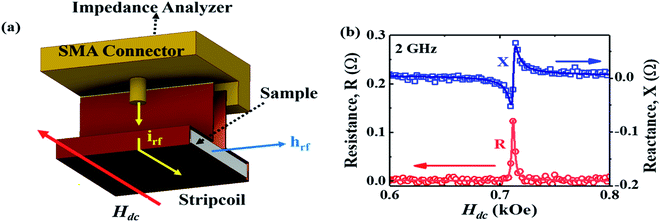
Our technique involves using a copper strip coil as an antenna and a radio frequency impedance analyzer (Agilent model E4991A) as a microwave signal source and detector. DPPH powder obtained from Sigma-Aldrich™ was pressed into a disc shaped pellet at room temperature using a hydraulic press (pressure 5 ton per in2). Then, the disc was cut into a rectangular bar of dimension (4.5 mm × 3.5 mm × 0.5 mm). A 0.2 mm thick copper strip was folded in the shape of a cuboidal coil of the same dimension as that of the sample. The sample was tightly fixed inside the coil whose inner surface was covered with a Kapton tape to electrically insulate the sample from the copper strip. One end of the copper strip coil was soldered to the signal line while the other end was soldered to the ground of a subminiature A type (SMA) coaxial connector. The radio frequency (rf) current from the impedance analyzer flows through the strip coil and terminates at the ground of the SMA connector creating an rf magnetic field in the interior of the strip coil along the axial direction as shown in Fig. 1. Hence, the DPPH sample experiences an rf axial magnetic field. An electromagnet is used to apply dc magnetic field perpendicular to the axial rf field. The resistance (R) and reactive (X) components of the electrical impedance of the copper strip were simultaneous measured at different frequencies of rf current while sweeping the dc magnetic field. The electrical impedance of the copper strip is 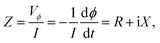 where ϕ is the rf magnetic flux passing through the strip coil given by ϕ = μ0μrHrfA. Here, Hrf is the magnetic field inside the strip-coil and A is the cross-sectional area of the strip coil. Since the high frequency permeability is μ = μ′ − iμ′′ where μ′ is the in-phase and μ′′ is the out-of phase of the permeability which describe dispersion and absorption or loss in the sample, respectively. By substituting the complex permeability, we obtain
where ϕ is the rf magnetic flux passing through the strip coil given by ϕ = μ0μrHrfA. Here, Hrf is the magnetic field inside the strip-coil and A is the cross-sectional area of the strip coil. Since the high frequency permeability is μ = μ′ − iμ′′ where μ′ is the in-phase and μ′′ is the out-of phase of the permeability which describe dispersion and absorption or loss in the sample, respectively. By substituting the complex permeability, we obtain 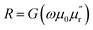 and
and 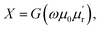 where G is a constant depending on the geometry of the strip coil. Since the high frequency permeability of the paramagnetic DPPH sample is affected by the application of dc bias magnetic field, resistance and reactance of the strip coil also changes. R and X were recorded without and with the sample inside the strip coil and data for each frequency and magnetic field were subtracted to obtain only the sample contribution. As the impedance analyzer measures the radio-frequency current–voltage characteristics of the strip coil, there is no need extra analysis to extract the impedance from scattering “S” parameters as in a network analyzer.
where G is a constant depending on the geometry of the strip coil. Since the high frequency permeability of the paramagnetic DPPH sample is affected by the application of dc bias magnetic field, resistance and reactance of the strip coil also changes. R and X were recorded without and with the sample inside the strip coil and data for each frequency and magnetic field were subtracted to obtain only the sample contribution. As the impedance analyzer measures the radio-frequency current–voltage characteristics of the strip coil, there is no need extra analysis to extract the impedance from scattering “S” parameters as in a network analyzer.
Results and discussions
Fig. 1(b) shows the magnetic field dependence of R and X for an rf current excitation of frequency 2 GHz in the strip coil. As Hdc is swept from Hdc = 1 kOe to Hdc = 0 Oe, R rapidly increases in a narrow field range and exhibits a sharp peak at 712 Oe whereas X shows a sudden jump around the same field. These features reflect the absorption and dispersion of the complex susceptibility, i.e., χ′′ and χ′, respectively, in the vicinity of electron–spin resonance.31 Conventional EPR spectroscopy with lock-in detection technique measures the field derivative of the rf power absorbed, dP/dH, which is proportional to dχ′′/dH. The dispersive signal is rarely reported except in a few experiments32–34 even though it offers a better understanding of the spin dynamics in a material. The R and X responses were fitted to eqn (1) and are shown as solid lines in Fig. 1(b) which contains both a symmetric Lorentzian term (first component) and a dispersive antisymmetric term (second component).
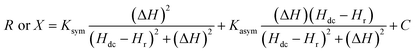 | (1) |
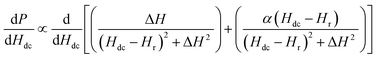 | (2) |
The first term in the above equation describes the absorption while the second term represents the dispersion. α denotes the dispersion-to-absorption ratio. The asymmetricity is prominent in conducting samples since the electric and magnetic rf components in conducting samples become out of phase with each other leading to an admixture of the dispersion into the absorption spectra. α = 0 when the skin effect is negligible as in insulating samples while α = 1 for highly conducting samples where the skin depth is very small compared to the sample size. In this case the absorption and dispersion are of equal strength. So, a dP/dH measurement alone cannot isolate the absorption and dispersion effect whereas, the R and X responses from the magnetoimpedance measurements can provide this information and enable accurate analysis of the physical parameters.
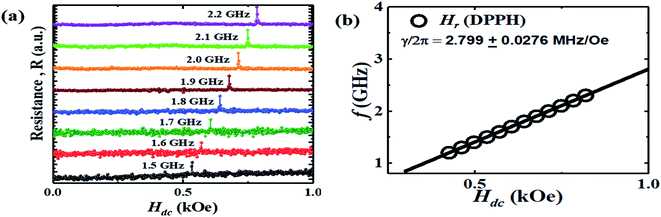
In Fig. 2(a), the field dependence of R for various frequencies from 1.5 GHz to 2.2 GHz are shown. The peak in R shifts towards a higher magnetic field with increasing frequency of current. We performed the line shape analysis for all the frequencies and extracted the frequency dependent line widths (ΔH) as well as the resonance fields (Hr) using eqn (1). It is known that the resonance frequency (fr) for EPR is proportional to the dc magnetic field and follows the relation 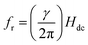 where γ is the gyromagnetic ratio (γ = gμB/ℏ, where g is the Landé g factor, μB is the Bohr magneton and ℏ is the reduced Planck's constant). Therefore, with increasing Hdc the resonance frequency increases linearly. This linear behavior was observed in the plot of fr vs. Hdc presented in Fig. 2(b) and we obtain γ/2π = 2.799 ± 0.0276 MHz Oe−1. This γ/2π value corresponds to a Landé g value of 1.999 ± 0.0197 which is well within the reported value of 2.0036. The small error in the g value is possibly due to inhomogeneity in dc magnetic field or determination of the magnetic field. The line width in this frequency range was about 2 Oe which is consistent with the dilute nature of paramagnetic species (free radicals) in DPPH.36
where γ is the gyromagnetic ratio (γ = gμB/ℏ, where g is the Landé g factor, μB is the Bohr magneton and ℏ is the reduced Planck's constant). Therefore, with increasing Hdc the resonance frequency increases linearly. This linear behavior was observed in the plot of fr vs. Hdc presented in Fig. 2(b) and we obtain γ/2π = 2.799 ± 0.0276 MHz Oe−1. This γ/2π value corresponds to a Landé g value of 1.999 ± 0.0197 which is well within the reported value of 2.0036. The small error in the g value is possibly due to inhomogeneity in dc magnetic field or determination of the magnetic field. The line width in this frequency range was about 2 Oe which is consistent with the dilute nature of paramagnetic species (free radicals) in DPPH.36
To verify the results obtained through the MI method, we measured the EPR spectra with a broad band ferromagnetic resonance spectrometer (Cryo-FMR by NanoOsc™ from Quantum Design Inc. USA). This spectrometer makes use of the lock-in technique and records the derivative of power absorbed (dP/dH) by the DPPH sample placed on top of a wave guide while Hdc is swept for fixed rf excitations of 2 GHz, 4 GHz, 10 GHz and 12 GHz as shown in Fig. 3(a). We can see that the resonance field (Hr) which corresponds to the zero crossing point and amplitude of dP/dH increase with increasing frequency. The inset in Fig. 3(b) shows Hr increasing linearly with frequency and γ/2π = 2.801 GHz kOe−1, which is close to the value observed in the MI measurement. The dP/dH line shape was fitted to eqn (3):
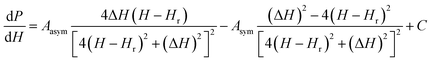 | (3) |
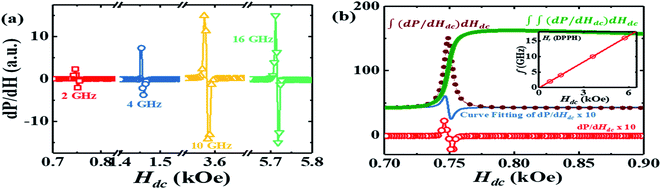 | ||
| Fig. 3 (a) The EPR spectroscopic signal (dP/dH) for the DPPH sample measured using the Cryo-FMR spectrometer for excitation frequencies of 2 GHz (squares), 4 GHz (circles), 10 GHz (upward triangle) and 16 GHz (downward triangle). (b) dP/dH curve at 2 GHz along with the line shape fit using eqn (3), the single integrated signal: ∫(dP/dH)dHdc and the double integrated signal: ∫∫(dP/dH)dHdc of the curve fitted dP/dH curve. Inset: plot of f vs. Hdc with open circles used to depict the resonance fields (Hr) obtained using the dP/dH data. | ||
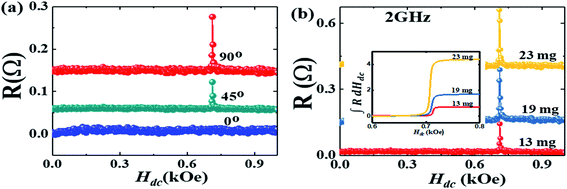
In Fig. 4(a) R is presented for various angles which Hdc makes with hrf. When Hdc is perpendicular to hrf the signal is the most intense while it disappears when Hdc is parallel to hrf. The R response for different masses of DPPH is also presented in Fig. 4(b). The signal strength is proportional to the mass of the DPPH with 23 mg of DPPH exhibiting the largest response. Since R is proportional to χ′′, a single integration of the R response can be used to estimate the number of spins in the sample. The single integration of R is presented in the inset of Fig. 4(b) which provides the EPR intensity of absorption by the DPPH samples and increases with increase in number of spins. For 13 mg, 19 mg and 23 mg of DPPH, we obtain 1.9853 × 1019, 2.9017 × 1019 and 3.5125 × 1019 spins, respectively.
Although the presented strip coil method does not need microfabrication, use of this method is constrained by the natural frequency of the strip coil and maximum frequency of the signal sourced (f = 3 GHz) by the impedance analyzer. In this study, natural resonance of the strip coil was around 2.6 GHz. However, one can prepare a cylindrical coil or a cuboidal coil depending on the shape and physical state (thin film/bulk sample/powder) of the sample and it can be extended to study liquid samples as well. We had successfully tested for ferrofluids (not shown here). These limitations should be taken into consideration.
Conclusions
In summary, we have presented a simple technique to probe EPR in the standard DPPH sample by passing high frequency currents in a copper strip coil which surrounds the sample while measuring the magnetic field dependence of electrical impedance. We analyzed the line shapes using symmetric and asymmetric Lorentzian functions and the g-value was extracted. The electrical detection of EPR signal using an impedance analyzer which is traditionally used to characterize dielectric samples could aid the broad scientific community to probe EPR and understand the spin dynamics in the low frequency regime of the microwave spectrum.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
R. M. acknowledges the Ministry of Education, Singapore (Grant number: R144-000-381-112).References
- E. K. Zavoisky, Zhur. Eksperiment. i Theoret. Fiz., vol. 15, 1945, pp. 344–350 Search PubMedFor historical perspective, see G. R. Eaton, S. S. Eaton and K. M. Salikhov, Foundations of modern EPR, World Scientific, Singapore, 1998, pp. 45–50 Search PubMed.
- M. M. Roessler and E. Salvadori, Chem. Soc. Rev., 2018, 47, 2534 RSC.
- K. L. Bower, Rev. Sci. Instrum., 1977, 48, 135 CrossRef CAS; P. M. Lenhan and J. F. Conley Jr, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct., 1998, 16, 2134 CrossRef; F. Jelezko and J. Wrachtrup, Phys. Status Solidi A, 2006, 203, 3207 CrossRef.
- K. A. Muller, W. Berlinger and F. Waldner, Phys. Rev. Lett., 1968, 21, 814 CrossRef.
- K. L. Brower and S. M. Myers, Appl. Phys. Lett., 1990, 57, 162 CrossRef CAS.
- V. V. Khramstov, A. A. Bobkov, M. Tseytlin and B. Driesschaert, Anal. Chem., 2017, 89, 4758 CrossRef PubMed.
- S. Van Doorslaer and D. M. Murphy, EPR Spectroscopy: Applications in Chemistry and Biology, ed. M. Drescher and G. Jeschke, Springer-verlag, Berlin, 2012, pp. 1–29 Search PubMed.
- M. Che and E. Giamello, Catalyst Characterization, ed. B. Imelik and J. C. Vedrine, Springer, Berlin, 1994, p. 131 Search PubMed.
- E. Reijerse and A. Savitsky, Electron Paramagnetic Resonance Instrumentation in eMagRes, ed. R. K. Harris and R. L. Wasylishen, 2017, DOI:10.1002/9780470034590.emrstm1511.
- G. R. Eaton, EPR Imaging and In-vivo EPR, CRC Press, London, 2018 Search PubMed.
- C. Clauss, M. Dressel and M. Scheffler, J. Phys.: Conf. Ser., 2015, 592, 012146 CrossRef.
- Y. Wiemann, J. Simmendinger, C. Clauss, L. Bogani, D. Bothner, D. Koelle, R. Kleiner, M. Dressel and M. Scheffler, Appl. Phys. Lett., 2015, 106, 193505 CrossRef.
- K. Jing, Z. Lan, Z. Shi, S. Mu, X. Qin, X. Rong and J. Du, Rev. Sci. Instrum., 2019, 90, 125109 CrossRef PubMed.
- H. Malissa, D. I. Schuster, A. M. Tryshkin, A. A. Houck and S. A. Lyon, Rev. Sci. Instrum., 2013, 84, 025115 CrossRef PubMed.
- B. Johansson, S. Haraldson, L. Pettersson and O. Beckman, Rev. Sci. Instrum., 1974, 45, 1445 CrossRef CAS.
- E. D. Dahlberg and S. A. Dodds, Rev. Sci. Instrum., 1981, 52, 472 CrossRef CAS.
- A. C. Torrezan, T. P. M. Alegre and G. Medeiros-Ribeiro, Rev. Sci. Instrum., 2009, 80, 075111 CrossRef CAS PubMed.
- A. Ghirri, C. Bonizzoni, M. Righi, F. Fedele, G. Timco, R. Winpenny and M. Affronte, Appl. Magn. Reson., 2015, 46, 749 CrossRef CAS.
- S. K. Misra, Multifrequency electron paramagnetic resonance: theory and applications, John Wiley & Sons, 2011 Search PubMed.
- G. R. Eaton and S. R. Eaton, EPR: Instrumental Methods, ed. L. J. Berliner and C. J. Bender, Springer, New York, 2004, pp. 59–114 Search PubMed.
- A. Kitagawa, J. Sens., 2011, 2011, 813636 Search PubMed.
- H. Ueda, Z. Kuri and S. Shida, J. Chem. Phys., 1962, 36, 1676 CrossRef CAS.
- L. V. Panina, K. Mohri, K. Bushida and M. Noda, J. Appl. Phys., 1994, 76, 6198 CrossRef CAS.
- A. E. P. De Araujo, F. L. A. Machado, F. M. De Aguiar and S. M. Rezende, J. Magn. Magn. Mater., 2001, 226, 724 CrossRef.
- M. A. Corrêa, F. Bohn, A. D. C. Viegas, M. A. Carara, L. F. Schelp and R. L. Sommer, J. Magn. Magn. Mater., 2008, 320, 25 CrossRef.
- J. M. Gonzalez, A. Garcia-Arribas, S. V. Shcherbinin, V. N. Lepalovkij, J. M. Collantes and G. V. Kurlyandskaya, Measurement, 2018, 126, 215 CrossRef.
- G. V. Kurlyandskaya, S. V. Shcherbinin, S. O. Volchkov, S. M. Bhagat, E. Calle, R. Perez and M. Vasquez, J. Magn. Magn. Mater., 2019, 459, 154 CrossRef.
- N. A. Buznikov, A. P. Safronov, I. Orue, E. V. Golubeva, V. N. Lepalovskij, A. V. Svalov, A. A. Chlenova and G. V. Kurlyandskaya, Biosens. Bioelectron., 2018, 117, 366 CrossRef CAS PubMed.
- U. Chaudhuri and R. Mahendiran, Appl. Phys. Lett., 2019, 115, 092405 CrossRef.
- U. Chaudhuri and R. Mahendiran, J. Magn. Magn. Mater., 2018, 488, 165377 CrossRef.
- A. G. Marshall and D. C. Roe, Anal. Chem., 1978, 50, 756 CrossRef CAS.
- P. Fajer and D. Marsh, J. Magn. Reson., 1983, 55, 205 CAS.
- C. Mailer, H. Thomann, B. H. Robinson and L. R. Dalton, Rev. Sci. Instrum., 1980, 51, 1714 CrossRef CAS.
- J. S. Hyde, W. Froncisz and A. Kusumi, Rev. Sci. Instrum., 1982, 53, 1934 CrossRef.
- V. A. Ivanshin, J. Deisenhofer, H.-A. Krug Von Nidda, A. Loidl, A. A. Mukhin, A. M. Balbashov and M. V. Eremin, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 6213 CrossRef CAS.
- W. R. Hagen, J. Phys. Chem. A, 2019, 123, 6986 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2020 |