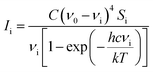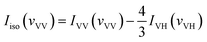Open Access Article
Open Access ArticleThe noncoincidence phenomenon of acetonylacetone C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h2_char_e001.gif) O stretching in a binary mixture and the aggregation-induced split theory†
O stretching in a binary mixture and the aggregation-induced split theory†
Huigang Wang *,
Hang Xu,
Qiuna Liu and
Xuming Zheng
*,
Hang Xu,
Qiuna Liu and
Xuming Zheng
Department of Chemistry, Key Laboratory of Advanced Textiles Materials and Manufacture Technology of the Ministry of Education, Engineering Research Center for Eco-Dyeing and Finishing of Textiles of the Ministry of Education, Zhejiang Sci-Tech University, Hangzhou 310018, P. R. China. E-mail: zdwhg@163.com; hugwang@ucdavis.edu; Tel: +86-571-8684-3627
First published on 21st August 2020
Abstract
This article aims to correlate the noncoincidence effect phenomenon with the aggregation state of acetylacetone C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching in a binary mixture. C
O stretching in a binary mixture. C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching noncoincidence effect (NCE) was observed not only between IR and Raman spectra but also between the isotropic and anisotropic Raman spectra of acetonylacetone. The difference in C
O stretching noncoincidence effect (NCE) was observed not only between IR and Raman spectra but also between the isotropic and anisotropic Raman spectra of acetonylacetone. The difference in C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching wavenumbers of the isotropic and anisotropic Raman spectra (NCE value) in a binary mixture at different concentrations has been calculated. We found that both isotropic and anisotropic Raman wavenumbers of C
O stretching wavenumbers of the isotropic and anisotropic Raman spectra (NCE value) in a binary mixture at different concentrations has been calculated. We found that both isotropic and anisotropic Raman wavenumbers of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching increase with the dilution of acetonylacetone by CCl4 while the NCE value decreases. These noncoincidence and concentration effect phenomena seem to go against the quantum theory. Herein, we proposed an aggregation-induced split (AIS) model to explain the NCE phenomenon and concentration effect. The experimental data were consistent with the DFT calculations performed at the B3LYP-D3/6-311++G (d,p) levels based on the proposed model. The dynamics of transformation from monomers to an aggregated structure can be easily controlled by tuning the concentration. Solvent dependent experiments show that the value of NCE decreased with the increase of the solvent dielectric constant at the same concentration, which is in accordance with Logan's theory.
O stretching increase with the dilution of acetonylacetone by CCl4 while the NCE value decreases. These noncoincidence and concentration effect phenomena seem to go against the quantum theory. Herein, we proposed an aggregation-induced split (AIS) model to explain the NCE phenomenon and concentration effect. The experimental data were consistent with the DFT calculations performed at the B3LYP-D3/6-311++G (d,p) levels based on the proposed model. The dynamics of transformation from monomers to an aggregated structure can be easily controlled by tuning the concentration. Solvent dependent experiments show that the value of NCE decreased with the increase of the solvent dielectric constant at the same concentration, which is in accordance with Logan's theory.
I. Introduction
Vibrational spectroscopy is an excellent technique for probing the nature of bonding and identifying chemical structures or phases in the analysis of chemical substances.1–4 It has been commonly applied in industrial processes, geochemistry, and health-related chemistry fields.5–7 Experiments have demonstrated that some polar vibrational modes present their vibration wavenumber at different positions in IR and Raman spectroscopy.8–10 Moreover, their frequencies in isotropic and anisotropic components of Raman spectra are not in coincidence; scientists refer to these phenomena as noncoincidence effects (NCEs).11–20 They ascribe these phenomena to transition dipole-transition dipole (TD–TD) interactions.11–20Our group concentrated on these phenomena for several years. First, we discovered NCEs in C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S vibrational modes.21,22 The difference between the isotropic and anisotropic peak frequencies of C
S vibrational modes.21,22 The difference between the isotropic and anisotropic peak frequencies of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretching for ethylene trithiocarbonate was determined to be 4.60 cm−1.21 This difference decreased upon dilution. These NCEs and concentration effects made us believe that C
S stretching for ethylene trithiocarbonate was determined to be 4.60 cm−1.21 This difference decreased upon dilution. These NCEs and concentration effects made us believe that C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretching is not a single vibrational mode, but a complex vibrational mode that is beyond spectroscopic resolution.22
S stretching is not a single vibrational mode, but a complex vibrational mode that is beyond spectroscopic resolution.22
Matrix isolation is a powerful technique for the enhancement of spectroscopic resolution because the translational and rotational motions can freeze below 6 K.23,24 We applied this technique to study the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching NCE behavior of acetone, the most investigated model molecule for NCE phenomena.25,26 Acetone was isolated in an argon matrix and the Raman spectra were collected at different annealing temperatures. Single, double, and triple peaks were detected separately at different temperatures for the C
O stretching NCE behavior of acetone, the most investigated model molecule for NCE phenomena.25,26 Acetone was isolated in an argon matrix and the Raman spectra were collected at different annealing temperatures. Single, double, and triple peaks were detected separately at different temperatures for the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vibration, and the isotropic and anisotropic spectra for each wavenumber overlapped fairly well with no NCE.26 Thus, an aggregation-induced split (AIS) model has been proposed to explain the acetone C
O vibration, and the isotropic and anisotropic spectra for each wavenumber overlapped fairly well with no NCE.26 Thus, an aggregation-induced split (AIS) model has been proposed to explain the acetone C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vibration NCE phenomenon and its concentration effect.25,26 The polar bond vibration coupling tends to align the molecules to reduce the potential energy and increase the attraction. The alignment and reorganization stabilized the aggregation structure to form dimers, trimers or clusters. Polar bonds such as C
O vibration NCE phenomenon and its concentration effect.25,26 The polar bond vibration coupling tends to align the molecules to reduce the potential energy and increase the attraction. The alignment and reorganization stabilized the aggregation structure to form dimers, trimers or clusters. Polar bonds such as C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, C
O, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S, S
S, S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, C–N, and C–O especially play an important role in these interactions. The vibration coupling between adjacent polar bonds split the degenerate vibrations to two vibrational modes: in phase vibration and out of phase vibration. The pairs with prominent vibrational wavenumber difference and depolarization ratio difference produced “NCE effects” with the limited spectroscopic resolution; however, in high-resolution spectroscopy, they were well separated.25,26 Acetylacetone is the simplest β-diketone that bears two tautomeric forms (keto and enol). Due to the existence of intramolecular hydrogen bonds,27,28 the enol form is more stable in the gas phase or in weak polar solvents, while the keto form is more stable in polar solvents, especially protic solvents. The keto structure will form intermolecular hydrogen bonds with protic solvents. Acetylacetone is a good molecule for studying solvent effects. This article aims to investigate the solvent polarity influence on its aggregation state.
O, C–N, and C–O especially play an important role in these interactions. The vibration coupling between adjacent polar bonds split the degenerate vibrations to two vibrational modes: in phase vibration and out of phase vibration. The pairs with prominent vibrational wavenumber difference and depolarization ratio difference produced “NCE effects” with the limited spectroscopic resolution; however, in high-resolution spectroscopy, they were well separated.25,26 Acetylacetone is the simplest β-diketone that bears two tautomeric forms (keto and enol). Due to the existence of intramolecular hydrogen bonds,27,28 the enol form is more stable in the gas phase or in weak polar solvents, while the keto form is more stable in polar solvents, especially protic solvents. The keto structure will form intermolecular hydrogen bonds with protic solvents. Acetylacetone is a good molecule for studying solvent effects. This article aims to investigate the solvent polarity influence on its aggregation state.
The AIS model can explain most of the NCE phenomena.25,26,29–31 In this work, 2,5-hexanedione was chosen to investigate the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O coupling behavior and the NCE phenomenon. 2,5-Hexanedione contains two carbonyl groups, and there are two possible C
O coupling behavior and the NCE phenomenon. 2,5-Hexanedione contains two carbonyl groups, and there are two possible C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O interactions,.intramolecular and intermolecular. Intramolecular C
O interactions,.intramolecular and intermolecular. Intramolecular C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O interactions have no relation to their neighboring molecules, and do not show concentration effects, while intermolecular C
O interactions have no relation to their neighboring molecules, and do not show concentration effects, while intermolecular C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O interactions show both NCE phenomena and concentration effects. In this work, the isotropic and anisotropic Raman bands of 2,5-hexanedione has been recorded and their concentration dependent behavior has been investigated to know the exact molecular interaction structure.
O interactions show both NCE phenomena and concentration effects. In this work, the isotropic and anisotropic Raman bands of 2,5-hexanedione has been recorded and their concentration dependent behavior has been investigated to know the exact molecular interaction structure.
II. Methods
A. Materials
Acetonylacetone (CH3COCH2CH2COCH3, TCL, >99.0%); chloroform (AR, shanghai San Ying chemical reagent company).B. Experimental setup
The experimental setup for Raman spectroscopy has been used with minor modifications.21 The experimental apparatus consists of a triple monochromator (TriVista TR557, Princeton Instruments) equipped with an argon ion laser (Coherent, CVI MELLES GRIOT) as a source of exciting light at 488 nm (75 mW output) and with a liquid nitrogen cooled CCD array (manufacturer, Princeton Instruments Inc.) allowing the wavenumber coverage of 1089 cm−1 and a spectral resolution (the instrumental apparatus function, FWHM) of 2.0 cm−1. The accuracy in the measurement (the physical matrix pixel of the CCD camera) of band positions was 0.45 cm−1. A polarization scrambler was placed between the polarizer and the spectrometer entrance slit. All measurements were carried out at room temperature (293 K) and atmospheric pressure.The Fourier transform (FT)-Raman and FT-IR spectra were obtained with 2 cm−1 resolution using a FT-Raman spectrometer at 1064 nm excitation (Thermo Nicolet 960, Thermo Fisher Nicolet, USA) and a FT-IR spectrometer (Thermo Nicolet avatar 370, Thermo Fisher Nicolet, USA).
C. Computational methods
Computational chemists often pay attention to specific technologies associated with computer memory, data, storage, processor speed, and program development software, which help to understand the photophysical and photochemical characteristics of molecules. Herein, density functional (DFT) calculations and the polarizable continuum model (PCM) were used to study the vibration wavenumber of acetonyl acetone in CCl4 and its linear dimer at B3LYP levels of theory with the 6-311++G(d,p) basis set using the Gaussian 09 program.32 The influence of the solvent was included using the PCM and optimized geometry and the corresponding vibrational frequencies were obtained to verify the reasonable dimer structure.We converted Raman intensity from scattering activities using the Multiwfn software (http://multiwfn.codeplex.com/releases). Multiwfn is an extremely powerful wavefunction analysis program and supports almost all of the most important wavefunction analysis methods.33 In our case, the excitation wavenumber is 20491.80 cm−1 (corresponding to 488 nm) and the conversion relationship is shown as34
With the parallel and perpendicular polarized Raman spectra we get the isotropic and anisotropic components of Raman spectra using the equation:27
| Ianiso(vVH) = IVH(vVH) |
With the DFT calculated Gaussian Output File of acetonylacetone, we also get the isotropic and anisotropic spectrum theoretically from the dimer model DFT calculations. Gaussview or Multiwfn can transform the dimer frequencies into Raman spectra. The original output file can be regarded as IVV(vVV). Since we were interested in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vibration, we focused our attention on the C
O vibration, we focused our attention on the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O frequency and their depolarization ratio. With the depolarization ratio band corresponding to the Raman activity of C
O frequency and their depolarization ratio. With the depolarization ratio band corresponding to the Raman activity of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vibration, we can get the depolarized Raman activity of C
O vibration, we can get the depolarized Raman activity of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vibration. With Gaussview, we can transform the frequencies to the depolarized Raman spectra, IVH of the C
O vibration. With Gaussview, we can transform the frequencies to the depolarized Raman spectra, IVH of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vibration. Finally, with
O vibration. Finally, with 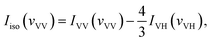 we can get the isotropic Raman activity, Iisospectra (see ESI† for more demonstrations).
we can get the isotropic Raman activity, Iisospectra (see ESI† for more demonstrations).
III. Results and discussion
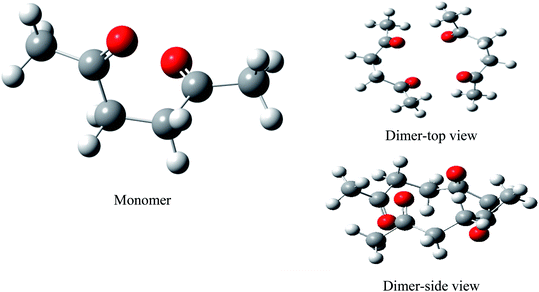
We performed full geometry optimization of the monomer and dimer structures of acetonylacetone. In order to establish the most stable conformation as the initial point for further calculations, the molecule was submitted to rigorous conformation analysis with all bonds having free rotation. Fig. 1 shows the optimized monomer and dimer structure of acetonylacetone. No imaginary vibrational frequencies were found in the further calculations. The dimer assembled in a head to tail antiparallel manner through weak intermolecular interactions. All DFT calculated vibrational frequencies, depolarization ratio, and the ZPE corrected total free energy for the acetonylacetone monomer and dimer are given in Table 1. The total free energy of the dimer is lower than the monomer by approximately 3.164 cal mol−1. Thus, the dimer is the thermodynamically favored structure. Table 1 lists a comparison of the B3LYP-D3/6-311++G(d,p) calculated vibrational wavenumber with the experimental FT-Raman and FT-IR values. It is worthy to emphasize that C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching in the monomer has two modes, ν11 and ν12; ν11 is Raman active but ν12 is IR active. These two modes split individually into two pairs of frequencies after the formation of the dimer structure (ν11 at 1770 cm−1 split into 1768/1760 cm−1, ν12 at 1759 cm−1 split into 1756/1750 cm−1). The peaks at 1768 cm−1 and 1760 cm−1 are Raman active, andcan be assigned to the experimental anisotropic Raman frequency at 1718.4 cm−1 and isotropic peak at 1710.7 cm−1, respectively (Fig. 3). From the calculations, we can imagine that when the dimer is broken into the monomer, the C
O stretching in the monomer has two modes, ν11 and ν12; ν11 is Raman active but ν12 is IR active. These two modes split individually into two pairs of frequencies after the formation of the dimer structure (ν11 at 1770 cm−1 split into 1768/1760 cm−1, ν12 at 1759 cm−1 split into 1756/1750 cm−1). The peaks at 1768 cm−1 and 1760 cm−1 are Raman active, andcan be assigned to the experimental anisotropic Raman frequency at 1718.4 cm−1 and isotropic peak at 1710.7 cm−1, respectively (Fig. 3). From the calculations, we can imagine that when the dimer is broken into the monomer, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching should blue shift to a higher frequency.
O stretching should blue shift to a higher frequency.
| Modes | Computed/cm−1 | Experiment/cm−1 | Descriptions | ||||
|---|---|---|---|---|---|---|---|
| Monomer freq. | Dimer | Raman | IR | ||||
| cis | anti | Freq. | D radio | ||||
| ν1 | 3144 | 3138 | 3141/3138 | 0.71/0.72 | C–H stretch | ||
| ν2 | 3139 | 3138 | 3137/3134 | 0.68/0.71 | C–H stretch | ||
| ν3 | 3107 | 3085 | 3106/3104 | 0.32/0.72 | C–H stretch | ||
| ν4 | 3094 | 3085 | 3097/3095 | 0.72/0.55 | C–H stretch | ||
| ν5 | 3087 | 3064 | 3090/3088 | 0.75/0.65 | C–H stretch | ||
| ν6 | 3053 | 3064 | 3083/3075 | 0.46/0.74 | C–H stretch | ||
| ν7 | 3033 | 3034 | 3044/3038 | 0.03/0.04 | C–H stretch | ||
| ν8 | 3030 | 3030 | 3035/3032 | 0.25/0.07 | C–H stretch | ||
| ν9 | 3027 | 3024 | 3031/3027 | 0.08/0.07 | C–H stretch | ||
| ν10 | 3017 | 3023 | 3027/3017 | 0.03/0.50 | C–H stretch | ||
| ν11 | 1770 | 1781 | 1768/1760 | 0.41/0.32 | 1714S | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e001.gif) C stretch C stretch |
|
| ν12 | 1759 | 1775 | 1756/1750 | 0.38/0.18 | 1712vs | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e001.gif) C stretch C stretch |
|
| ν13 | 1476 | 1478 | 1478/1474 | 0.45/0.75 | H–C–H bend | ||
| ν14 | 1472 | 1478 | 1472/1470 | 0.74/0.65 | H–C–H bend | ||
| ν15 | 1467 | 1468 | 1466/1465 | 0.70/0.45 | H–C–H bend | ||
| ν16 | 1458 | 1466 | 1464/1463 | 0.74/0.68 | H–C–H bend | ||
| ν17 | 1457 | 1458 | 1460/1456 | 0.71/0.74 | 1455vs | 1400w | H–C–H bend + H–C–C–C tors |
| ν18 | 1452 | 1454 | 1445/1430 | 0.75/0.74 | H–C–H bend | ||
| ν19 | 1390 | 1401 | 1401/1394 | 0.31/0.63 | H–C–H bend | ||
| ν20 | 1388 | 1388 | 1392/1390 | 0.69/0.70 | 1353vw | 1365s | H–C–H bend |
| ν21 | 1374 | 1384 | 1383/1375 | 0.63/0.72 | H–C–H bend | ||
| ν22 | 1355 | 1333 | 1373/1370 | 0.71/0.64 | H–C–C bend | ||
| ν23 | 1284 | 1301 | 1262/1244 | 0.60/0.36 | H–C–C bend + H–C–C–C tors | ||
| ν24 | 1215 | 1198 | 1224/1221 | 0.70/0.73 | H–C–C bend | ||
| ν25 | 1208 | 1188 | 1203/1197 | 0.68/0.63 | H–C–C bend | ||
| ν26 | 1175 | 1172 | 1183/1182 | 0.70/0.74 | C–C stretch | ||
| ν27 | 1094 | 1098 | 1096/1090 | 0.10/0.05 | O=C–C–C out-of-plane bend | ||
| ν28 | 1055 | 1096 | 1059/1050 | 0.29/0.72 | C–C stretch | ||
| ν29 | 1021 | 993 | 1033/1026 | 0.75/0.59 | H–C–C–C tors | ||
| ν30 | 995 | 968 | 984/973 | 0.33/0.71 | C–C stretch + H–C–C–C tors | ||
| ν31 | 966 | 956 | 966/958 | 0.19/0.17 | C–C stretch | ||
| ν32 | 891 | 872 | 908/894 | 0.42/0.28 | H–C–C bend + H–C–C–C tors + C–C–C–C tors | ||
| ν33 | 835 | 869 | 862/862 | 0.68/0.44 | C–C stretch | ||
| ν34 | 768 | 799 | 761/752 | 0.74/0.08 | 829vs | C–C stretch | |
| ν35 | 734 | 729 | 749/749 | 0.58/0.02 | H–C–C–C tors | ||
| ν36 | 621 | 602 | 639/637 | 0.60/0.73 | C–C stretch + O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C bend C–C bend |
||
| ν37 | 556 | 588 | 576/574 | 0.43/0.47 | O=C–C bend + C–C–C bend | ||
| ν38 | 530 | 479 | 505/485 | 0.75/0.75 | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C bend + H–C–C–C tors + O C–C bend + H–C–C–C tors + O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C–C out-of-plane bend C–C–C out-of-plane bend |
||
| ν39 | 467 | 477 | 473/455 | 0.68/0.71 | H–C–C–C tors + C–C–C–C tors + O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C–C out-of-plane bend C–C–C out-of-plane bend |
||
| ν40 | 439 | 448 | 452/429 | 0.74/0.71 | C–C–C bend + O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C–C out-of-plane bend C–C–C out-of-plane bend |
||
| ν41 | 348 | 316 | 360/343 | 0.24/0.34 | C–C–C bend | ||
| ν42 | 262 | 260 | 271/270 | 0.27/0.74 | C–C–C bend | ||
| ν43 | 234 | 130 | 246/232 | 0.57/0.70 | C–C–C bend | ||
| ν44 | 188 | 109 | 163/150 | 0.55/0.66 | C–C–C bend | ||
| ν45 | 120 | 107 | 139/126 | 0.70/0.54 | H–C–C–C tors | ||
| ν46 | 102 | 89 | 114/113 | 0.71/0.68 | H–C–C–C tors + C–C–C–C tors | ||
| ν47 | 56 | 61 | 108/97 | 0.65/0.73 | C–C–C–C tors | ||
| ν48 | 45 | 28 | 87/81 | 0.75/0.74 | C–C–C–C tors | ||
| ν49 | 72/62 | 0.69/0.70 | Relative rotation | ||||
| ν50 | 51/36 | 0.63/0.75 | Relative rotation | ||||
| ν51 | 33/26 | 0.56/0.71 | Relative rotation | ||||
| Sum of electronic and thermal free energies (Kcal mol−1) | Momomer | G = −385.130890 | |||||
| Dimer | G = −770.264944 | ΔG = G(dimer) − 2G(momomer) = −0.003164 | |||||
| Remarks | In the dimer, there are in-phase and out-of-phase vibrational modes, in-phase vibrational frequency is lower than the out-of-phase vibrational frequency | ||||||
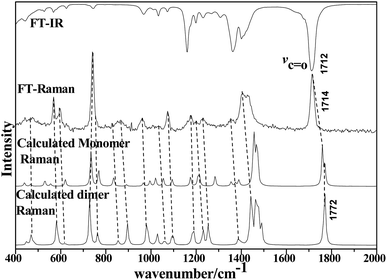 | ||
| Fig. 2 Comparison of FT-IR and LCM-Raman spectra with calculated Raman and IR spectra of acetonylacetone. | ||
The 36 atoms of the acetonylacetone dimer give rise to 102 normal modes of vibration. The overall 102 normal modes of vibration for this dimer are considered to comprise 96 normal modes arising from the in-phase and out-of-phase coupling of these two acetonylacetone molecules and 6 modes associated with the relative translation and rotation of two acetonylacetone molecules. A detailed description is listed in Table 1. The converted calculated Raman spectra using Multiwfn software are shown in Fig. 2. The corresponding in-phase and out-of-phase vibrational modes may differ in wavenumbers and depolarization ratios and the magnitude of these splitting will depend on the strength of interactions between different parts of the neighboring molecules. The overall agreement between the DFT calculated vibrational wavenumbers and the experimental values is good for acetonylacetone. Fig. 2 displays a comparison of the calculated monomer and dimer Raman spectra with the FT-Raman spectrum and FT-IR spectrum of acetonylacetone. The dashed lines in Fig. 2 indicate the correlation between the vibrational modes of acetonylacetone in the calculated Raman spectra and those corresponding to the fundamental modes of acetonylacetone in the FT-Raman and IR spectrum, respectively. The 1712 cm−1 band is assigned to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch. The wavenumber difference between the FT-Raman spectrum and FT-IR spectrum is 2.3 cm−1. This wavenumber difference is a key characteristic of the noncoincidence effect; other experimental proofs including the isotropic and anisotropic Raman spectra at different concentrations will be presented later. The largest difference between the calculated monomer and dimer lies in the C
O stretch. The wavenumber difference between the FT-Raman spectrum and FT-IR spectrum is 2.3 cm−1. This wavenumber difference is a key characteristic of the noncoincidence effect; other experimental proofs including the isotropic and anisotropic Raman spectra at different concentrations will be presented later. The largest difference between the calculated monomer and dimer lies in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching wavenumber. The wavenumber of the monomer is higher than that of the dimer. Other modes are similar with the calculated monomer and dimer structures. The calculation results show that when acetonylacetone transforms from the dimer to the monomer, the frequency of the C
O stretching wavenumber. The wavenumber of the monomer is higher than that of the dimer. Other modes are similar with the calculated monomer and dimer structures. The calculation results show that when acetonylacetone transforms from the dimer to the monomer, the frequency of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching increases while other modes remain consistent. From the spectral comparison between the FT-Raman and the calculated monomer and dimer, the spectral pattern of the dimer describes more accurately the liquid acetonylacetone. It needs to be stressed that the listed calculated wavenumbers describe the vibrational frequencies of the molecule in its gaseous phase. Hence, the experimentally observed spectrum of the liquid phase may differ to some extent from the calculated spectrum. In the DFT calculation, the B3LYP function tends to overestimate the wavenumbers of the fundamental modes compared to the experimentally observed values due to the combination of electron correlation effects and basis set deficiencies. By comprehensively considering the calculated and experimental FT-Raman spectra, acetonylacetone is prone to present a short dimer order induced by C
O stretching increases while other modes remain consistent. From the spectral comparison between the FT-Raman and the calculated monomer and dimer, the spectral pattern of the dimer describes more accurately the liquid acetonylacetone. It needs to be stressed that the listed calculated wavenumbers describe the vibrational frequencies of the molecule in its gaseous phase. Hence, the experimentally observed spectrum of the liquid phase may differ to some extent from the calculated spectrum. In the DFT calculation, the B3LYP function tends to overestimate the wavenumbers of the fundamental modes compared to the experimentally observed values due to the combination of electron correlation effects and basis set deficiencies. By comprehensively considering the calculated and experimental FT-Raman spectra, acetonylacetone is prone to present a short dimer order induced by C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vibrational td–td interactions. While in dilute solution, due to solvation effects and cage effects, where solvent molecules are surrounded by solute molecules that stabilize the solvate, acetonylacetone may present the monomer formation. Thus, the frequency of C
O vibrational td–td interactions. While in dilute solution, due to solvation effects and cage effects, where solvent molecules are surrounded by solute molecules that stabilize the solvate, acetonylacetone may present the monomer formation. Thus, the frequency of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching is influenced by concentration effects.
O stretching is influenced by concentration effects.
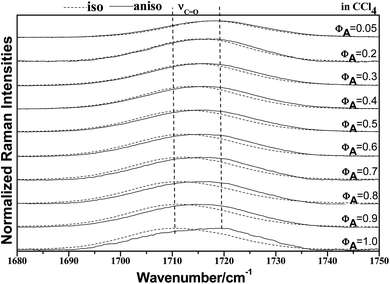
To characterize the concentration effects, we collected the isotropic and anisotropic spectra of acetonylacetone in a variety of volume fractions, as shown in Fig. 3. They are assigned to the ν11(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) stretching mode. The isotropic peak frequencies at 1710.7 cm−1 and the anisotropic peak at 1718.4 cm−1 were assigned to the calculated wavenumbers at 1760 cm−1 and 1768 cm−1, respectively. The corresponding depolarization ratios are 0.32 and 0.41. The dimer model calculations are in good agreement with the experimental non-coincident isotropic and anisotropic Raman data. The isotropic and anisotropic spectra, at a variety of volume fractions of acetonylacetone in CCl4, are shown in Fig. 3. Fig. 3 demonstrates that both isotropic and anisotropic Raman wavenumbers of the C
O) stretching mode. The isotropic peak frequencies at 1710.7 cm−1 and the anisotropic peak at 1718.4 cm−1 were assigned to the calculated wavenumbers at 1760 cm−1 and 1768 cm−1, respectively. The corresponding depolarization ratios are 0.32 and 0.41. The dimer model calculations are in good agreement with the experimental non-coincident isotropic and anisotropic Raman data. The isotropic and anisotropic spectra, at a variety of volume fractions of acetonylacetone in CCl4, are shown in Fig. 3. Fig. 3 demonstrates that both isotropic and anisotropic Raman wavenumbers of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch increase with the dilution of acetonylacetone by CCl4, while the separation between isotropic and anisotropic Raman wavenumbers decrease from 7.66 cm−1 in neat acetonylacetone to 1 cm−1 at χm = 0.05. The FWHM (full width at half maxima) of the C
O stretch increase with the dilution of acetonylacetone by CCl4, while the separation between isotropic and anisotropic Raman wavenumbers decrease from 7.66 cm−1 in neat acetonylacetone to 1 cm−1 at χm = 0.05. The FWHM (full width at half maxima) of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching modes also gets smaller and the peak gets sharper with decreasing acetonylacetone concentrations. The peak frequencies abstracted from Fig. 3 for isotropic (Iiso) and anisotropic (Ianiso) C
O stretching modes also gets smaller and the peak gets sharper with decreasing acetonylacetone concentrations. The peak frequencies abstracted from Fig. 3 for isotropic (Iiso) and anisotropic (Ianiso) C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching Raman spectra are shown in Fig. 4. The Raman peak frequencies of both components show an increase in wavenumber with decreasing solute concentrations. The difference between isotropic (Iiso) and anisotropic (Ianiso) C
O stretching Raman spectra are shown in Fig. 4. The Raman peak frequencies of both components show an increase in wavenumber with decreasing solute concentrations. The difference between isotropic (Iiso) and anisotropic (Ianiso) C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching wavenumbers ΔυNCE decreases upon dilution with CCl4 and reduces to 1.00 cm−1 at χm = 0.05, as shown in Fig. 5. This experimental data can be explained with our aggregation-induced split theory. Normally, acetonylacetone presents a dimer pattern. The dilution of the solute alters the short-range order of the C
O stretching wavenumbers ΔυNCE decreases upon dilution with CCl4 and reduces to 1.00 cm−1 at χm = 0.05, as shown in Fig. 5. This experimental data can be explained with our aggregation-induced split theory. Normally, acetonylacetone presents a dimer pattern. The dilution of the solute alters the short-range order of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching normal coordinate and the relative alignment of the dimer structure. The solvent molecules diffuse towards the reference molecule and break its structure, thereby weakening the dipole–dipole interactions of solute molecules. Thus, this leads to a decrease in the non-coincidence effect. The breaking of the dimer structure also makes the C
O stretching normal coordinate and the relative alignment of the dimer structure. The solvent molecules diffuse towards the reference molecule and break its structure, thereby weakening the dipole–dipole interactions of solute molecules. Thus, this leads to a decrease in the non-coincidence effect. The breaking of the dimer structure also makes the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vibrational wavenumber shift to a higher wavenumber because the calculation shows that the C
O vibrational wavenumber shift to a higher wavenumber because the calculation shows that the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching of the monomer lies at a higher wavenumber than that of dimers. This is in accordance with the concentration effect observed in experiments shown in Fig. 3 and 4.
O stretching of the monomer lies at a higher wavenumber than that of dimers. This is in accordance with the concentration effect observed in experiments shown in Fig. 3 and 4.
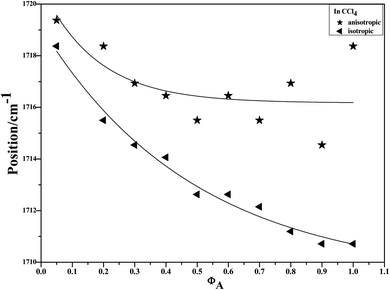 | ||
Fig. 4 Variation of isotropic and anisotropic Raman peak frequencies of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching mode of acetonylacetone as a function of the solute concentration. O stretching mode of acetonylacetone as a function of the solute concentration. | ||
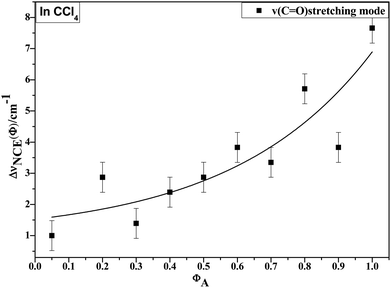 | ||
Fig. 5 Variation in NCE of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching mode of acetonylacetone as a function of solute volume fraction. O stretching mode of acetonylacetone as a function of solute volume fraction. | ||
In our study, the NCE of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching mode of acetonylacetone is positive, and may be due to the antiparallel C
O stretching mode of acetonylacetone is positive, and may be due to the antiparallel C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O side-by-side organization. The antiparallel C
O side-by-side organization. The antiparallel C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O coupling split the C
O coupling split the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vibrational wavenumber to two. It has been widely known that the NCE represents a spectroscopic manifestation of resonant intermolecular interactions between nearby IR-active oscillators through the transition dipole–transition dipole interaction mechanism.8–10 The cis and trans forms of acetonylacetone have C
O vibrational wavenumber to two. It has been widely known that the NCE represents a spectroscopic manifestation of resonant intermolecular interactions between nearby IR-active oscillators through the transition dipole–transition dipole interaction mechanism.8–10 The cis and trans forms of acetonylacetone have C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O Raman activity vibrational frequencies at 1770 cm−1 and 1781 cm−1, respectively. We also carried out IRC/path scan for the cis to trans transformation, as shown in Fig. S1.† This is a barrierless process. In the solution, normally, we believe that acetonylacetone predominantly bears the anti-form but this is not the case for the Raman spectra. Fig. 3 shows a split in the isotropic and anisotropic parts in most of the concentrated solutions. The concentration effect demonstrates that the aggregated structure is formed by intermolecular interactions, instead of intramolecular.
O Raman activity vibrational frequencies at 1770 cm−1 and 1781 cm−1, respectively. We also carried out IRC/path scan for the cis to trans transformation, as shown in Fig. S1.† This is a barrierless process. In the solution, normally, we believe that acetonylacetone predominantly bears the anti-form but this is not the case for the Raman spectra. Fig. 3 shows a split in the isotropic and anisotropic parts in most of the concentrated solutions. The concentration effect demonstrates that the aggregated structure is formed by intermolecular interactions, instead of intramolecular.
To study the influence of dipole moment of the solvent upon NCE, we collected the isotropic and anisotropic Raman spectra of acetonylacetone in a series of solvents with different static dielectric constant, as shown in Fig. 6. The corresponding NCEs were calculated and are illustrated in Fig. 7. Generally, the value of the NCE declined with an increase in the solvent dielectric constant with the same concentration. This rule is consistent with Logan's theory.11,35 Especially in water, as shown in Fig. 6, the value of the NCE is nearly equal to zero. From ref. 27 and 28, we speculate that it may be due to the formation of intermolecular hydrogen bonds between protons of water and the carbonyl groups of acetonylacetone, which hinder the dimerization of acetonylacetone molecules, thus making the NCE disappear.
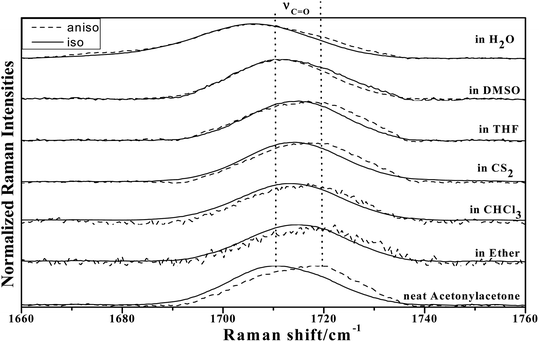 | ||
Fig. 6 The isotropic and anisotropic parts of ν12(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) vibrational Raman spectra of acetonylacetone in the binary mixture with different solvents (φA = 0.500). O) vibrational Raman spectra of acetonylacetone in the binary mixture with different solvents (φA = 0.500). | ||
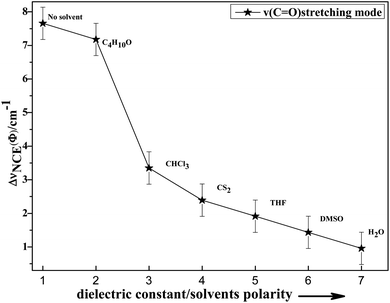 | ||
Fig. 7 Variation in NCE of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching mode of acetonylacetone as a function of the solvent dielectric constant. O stretching mode of acetonylacetone as a function of the solvent dielectric constant. | ||
To investigate NCE solvent polarity dependent properties and demonstrate the rationality of the dimer model, the polarizable continuum model (PCM) was applied to calculate the dimer structure at the hybrid B3LYP-D3 levels of theory with the 6-311++G(d,p) basis set using the Gaussian 09 program. The solvent polarity influence, the optimized geometry, and the corresponding vibrational frequencies were obtained. Table S1† shows the DFT/PCM calculated C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vibrational frequencies, depolarization ratios, dielectric constants (ε), dipole moments (μ)/D, and ΔνNCE in a variety of solvents. With a decrease in the solvent dielectric constant, the two monomers of the acetonylacetone dimer became closer and the value of the NCE increased. These results are consistent with the experimental results shown in Fig. 7. Simultaneously, this verifies that a strong polar solvent will weaken the dimer structure of acetonylacetone in the mixture while a nonpolar solvent can reinforce the dimer structure. All results that are obtained from experiments, the theoretical dimer model, and DFT calculations demonstrate a consistent picture of the relationship between the NCE behavior, a spectroscopic feature of vibrational Raman bands, and the effect of dipolar interactions in liquid mixtures at molecular level.
O vibrational frequencies, depolarization ratios, dielectric constants (ε), dipole moments (μ)/D, and ΔνNCE in a variety of solvents. With a decrease in the solvent dielectric constant, the two monomers of the acetonylacetone dimer became closer and the value of the NCE increased. These results are consistent with the experimental results shown in Fig. 7. Simultaneously, this verifies that a strong polar solvent will weaken the dimer structure of acetonylacetone in the mixture while a nonpolar solvent can reinforce the dimer structure. All results that are obtained from experiments, the theoretical dimer model, and DFT calculations demonstrate a consistent picture of the relationship between the NCE behavior, a spectroscopic feature of vibrational Raman bands, and the effect of dipolar interactions in liquid mixtures at molecular level.
IV. Conclusion
The Raman spectroscopic noncoincidence effect of the ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) band of acetonylacetone in a binary mixture has been reported and Δυnce has been measured for different concentrations. The monomer (cis and trans forms) and dimer of acetonylacetone were calculated at the B3LYP-D3/6-311++G (d,p) level of theory, which makes it easy to accurately investigate the molecular interactions through observation of concentration dependent and NCE properties. During the dilution process, the solute–solvent interactions weaken the dipole–dipole interactions, which results in the Raman spectra gradually transforming from dimer to monomer character, indicated by a blueshift in the C
O) band of acetonylacetone in a binary mixture has been reported and Δυnce has been measured for different concentrations. The monomer (cis and trans forms) and dimer of acetonylacetone were calculated at the B3LYP-D3/6-311++G (d,p) level of theory, which makes it easy to accurately investigate the molecular interactions through observation of concentration dependent and NCE properties. During the dilution process, the solute–solvent interactions weaken the dipole–dipole interactions, which results in the Raman spectra gradually transforming from dimer to monomer character, indicated by a blueshift in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching. Density functional theory (DFT) calculations based on the aggregation model provide satisfactory results and fit well with the experimental findings while the cis and trans forms cannot explain the Raman behavior; on the other hand, this model and experimental data verified the rationality of the aggregation-induced split theory. Solvent dependent experiments show that the value of NCE decreased with an increase in the dielectric constant of the solvent, for the same concentration.
O stretching. Density functional theory (DFT) calculations based on the aggregation model provide satisfactory results and fit well with the experimental findings while the cis and trans forms cannot explain the Raman behavior; on the other hand, this model and experimental data verified the rationality of the aggregation-induced split theory. Solvent dependent experiments show that the value of NCE decreased with an increase in the dielectric constant of the solvent, for the same concentration.
Author's contributions
All authors contributed equally to this work.Data availablity
The data that supports the findings of this study are available within the article and its ESI.†Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by grants from the National Natural Science Foundation of China (No. 21873084 and 21473161), Zhejiang Provincial Natural Science Foundation of China (LZ17B030001), Alexander von Humboldt Foundation (No. 1141172), and Zhejiang SCI-TECH University for 521 distinguished scholar's scheme.References
- J. H. Baraban, P. B. Changala, G. C. Mellau, J. F. Stanton, A. J. Merer and R. W. Field, Spectroscopic characterization of isomerization transition states, Science, 2015, 350(6266), 1338–1342 CrossRef PubMed.
- J.-X. Cheng and X. S. Xie, Vibrational spectroscopic imaging of living systems: An emerging platform for biology and medicine, Science, 2015, 350(6264), aaa8870 CrossRef PubMed.
- V. H. Paschoal, L. F. O. Faria and M. C. C. Ribeiro, Vibrational Spectroscopy of Ionic Liquids, Chem. Rev., 2017, 117(10), 7053–7112 CrossRef PubMed.
- F. Billes, I. Mohammed-Ziegler and H. Mikosch, Methanol in its own gravy. A PCM study for simulation of vibrational spectra, Phys. Chem. Chem. Phys., 2011, 13(17), 7760–7772 RSC.
- W.-H. Su and D.-W. Sun, Fourier Transform Infrared and Raman and Hyperspectral Imaging Techniques for Quality Determinations of Powdery Foods: A Review, Compr. Rev. Food Sci. Food Saf., 2018, 17(1), 104–122 CrossRef.
- J.-B. Wu, M.-L. Lin, X. Cong, H.-N. Liu and P.-H. Tan, Raman spectroscopy of graphene-based materials and its applications in related devices, Chem. Soc. Rev., 2018, 47(5), 1822–1873 RSC.
- Y. Cai, Z. Wei, C. Song, C. Tang, W. Han and X. Dong, Optical nano-agents in the second near-infrared window for biomedical applications, Chem. Soc. Rev., 2019, 48(1), 22–37 RSC.
- H. Y. Juan, W. C. Lin, Y. L. Wu and J. H. Perng, Substituent effects in porphyrin dimer complexes studied by IR spectroscopy, Polyhedron, 2008, 27(16), 3377–3382 CrossRef.
- S. Shigeto, C. F. Chang and H. Hiramatsu, Directly Probing Intermolecular Structural Change of a Core Fragment of beta(2)-Microglobulin Amyloid Fibrils with Low-Frequency Raman Spectroscopy, J. Phys. Chem. B, 2017, 121(3), 490–496 CrossRef PubMed.
- G. Fini, P. Mirone and B. Fortunat, Evidence for Short-Range Orientation Effects in Dipolar Aprotic Liquids from Vibrational Spectroscopy 1. Ethylene and Propylene Carbonates, J. Chem. Soc., Faraday Trans., 1973, 69(8), 1243–1248 RSC.
- D. E. Logan, THE RAMAN NONCOINCIDENCE EFFECT IN DIPOLAR BINARY-MIXTURES, Chem. Phys., 1989, 131(2–3), 199–207 CrossRef CAS.
- M. G. Giorgini, Raman noncoincidence effect: A spectroscopic manifestation of the intermolecular vibrational coupling in dipolar molecular liquids, Pure Appl. Chem., 2004, 76(1), 157–169 CAS.
- M. G. Giorgini, M. Musso and H. Torii, Concentration-dependent frequency shifts and Raman spectroscopic noncoincidence effect of the C=O stretching mode in dipolar mixtures of acetone/dimethyl sulfoxide. Experimental, theoretical, and simulation results, J. Phys. Chem. A, 2005, 109(26), 5846–5854 CrossRef CAS PubMed.
- H. Torii, Effects of intermolecular vibrational coupling and liquid dynamics on the polarized Raman and two-dimensional infrared spectral profiles of liquid N,N-dimethylformamide analyzed with a time-domain computational method, J. Phys. Chem. A, 2006, 110(14), 4822–4832 CrossRef CAS PubMed.
- M. G. Giorgini, H. Torii, M. Musso and G. Venditti, Influence of ions on the structural organization of dipolar liquids probed by the noncoincidence effect: Experimental and quantum chemical results, J. Phys. Chem. B, 2008, 112(25), 7506–7514 CrossRef CAS PubMed.
- H. Torii, Y. Osada and M. Iwami, Merged and separate band profiles arising from resonantly coupled vibrational modes of liquid mixtures: theoretical study, J. Raman Spectrosc., 2008, 39(11), 1592–1599 CrossRef CAS.
- M. G. Giorgini, H. Torii and M. Musso, The influence of alkaline earth ions on the structural organization of acetone probed by the noncoincidence effect of the nu(C=O) band: experimental and quantum chemical results, Phys. Chem. Chem. Phys., 2010, 12(1), 183–192 RSC.
- H. Torii, Intermolecular Electron Density Modulations in Water and Their Effects on the Far-Infrared Spectral Profiles at 6 THz, J. Phys. Chem. B, 2011, 115(20), 6636–6643 CrossRef CAS PubMed.
- G. Upadhyay, T. G. Devi, R. K. Singh, A. Singh and P. R. Alapati, Solvent dependent frequency shift and Raman noncoincidence effect of S=O stretching mode of Dimethyl sulfoxide in liquid binary mixtures, Spectrochim. Acta, Part A, 2013, 109, 239–246 CrossRef CAS PubMed.
- H. Torii, Amide I Vibrational Properties Affected by Hydrogen Bonding Out-of-Plane of the Peptide Group, J. Phys. Chem. Lett., 2015, 6(4), 727–733 CrossRef CAS PubMed.
- F. Wu, H. Wang and X. Zheng, Concentration-dependent frequency shifts of the CS stretching modes in ethylene trithiocarbonate studied by Raman spectroscopy, J. Raman Spectrosc., 2015, 46(6), 591–596 CrossRef CAS.
- R. Zhou, F. Wu, X. Zhou, H. Wang and X. Zheng, The structural configurations of Ethylene Trithiocarbonate in the binary mixture (SCS2CH2CH2+CFICl3) investigated by polarized Raman: Experimental and quantum chemical results, J. Mol. Struct., 2017, 1129, 205–210 CrossRef CAS.
- Y. Gong, M. Zhou and L. Andrews, Spectroscopic and Theoretical Studies of Transition Metal Oxides and Dioxygen Complexes, Chem. Rev., 2009, 109(12), 6765–6808 CrossRef CAS PubMed.
- Q. Wang, S. Pan, S. Lei, J. Jin, G. Deng, G. Wang, L. Zhao, M. Zhou and G. Frenking, Octa-coordinated alkaline earth metal-dinitrogen complexes M(N-2)(8) (M=Ca, Sr, Ba), Nat. Commun., 2019, 10, 3375 CrossRef PubMed.
- M. Liu, Y. Zhao, F. Wu, H. Wang and X. Zheng, Argon matrix Raman spectroscopic and aggregation model density function theoretical study of methyl isothiocyanate, J. Raman Spectrosc., 2019, 50(8), 1217–1225 CrossRef CAS.
- W. W. Xu, F. Q. Wu, Y. Y. Zhao, R. Zhou, H. G. Wang, X. M. Zheng and B. K. Ni, Study on the noncoincidence effect phenomenon using matrix isolated Raman spectra and the proposed structural organization model of acetone in condense phase, Sci. Rep., 2017, 7, 43835 CrossRef PubMed.
- R. Srinivasan, J. S. Feenstra, S. T. Park, S. Xu and A. H. Zewail, Direct determination of hydrogen-bonded structures in resonant and tautomeric reactions using ultrafast electron diffraction, J. Am. Chem. Soc., 2004, 126(8), 2266–2267 CrossRef PubMed.
- J. Emsley and N. J. Freeman, β-diketone interactions: Part 5. Solvent effects on the keto = enol equilibrium, J. Mol. Struct., 1987, 161(c), 193–204 CrossRef.
- W. Xu, Y. Sun, X. Dong, S. Li, H. Wang, J. Xue and X. Zheng, Local order and vibrational coupling of the C=O Stretching Mode of gamma-Caprolactone in liquid binary mixtures, Sci. Rep., 2017, 7, 12182 CrossRef PubMed.
- W. Xu, H. Wang, Y. Tao and X. Zheng, The structural organization of N-methyl-2-pyrrolidinone in binary mixtures probed by Raman spectroscopy: Experimental and quantum chemical results, J. Raman Spectrosc., 2018, 49(2), 362–371 CrossRef.
- H. Ouyang, M. Liu, Y. Zhao, H. Wang and X. Zheng, Noncoincidence Effects of Dimethyl Carbonate in Binary Mixtures Probed by Raman Spectroscopy: Experimental and DFT Calculations, ACS Omega, 2019, 4(6), 11074–11081 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Lui, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03(1), Revision C.02, Gaussian 03, Revision B.02, Gaussian, Inc., Pittsburgh, PA, 2003 Search PubMed.
- T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33(5), 580–592 CrossRef.
- G. Keresztury, S. Holly, G. Besenyei, J. Varga, A. Wang and J. Durig, Vibrational spectra of monothiocarbamates-II. IR and Raman spectra, vibrational assignment, conformational analysis and ab initio calculations of S-methyl-N, N-dimethylthiocarbamate, Spectrochim. Acta, Part A, 1993, 49(13–14), 20072019–20172026 Search PubMed.
- D. E. Logan, The Non-Coincidence Effect in the Raman-Spectra of Polar Liquids, Chem. Phys., 1986, 103(2–3), 215–225 CrossRef.
Footnote |
† Electronic supplementary information (ESI) available: Additional FT-Raman spectra for acetonylacetone, DFT/PCM calculation of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vibrational frequencies, depolarization ratios, dielectric constant (ε), dipole moments (μ)/D, and ΔνNCE for acetonylacetone. See DOI: 10.1039/d0ra02932g O vibrational frequencies, depolarization ratios, dielectric constant (ε), dipole moments (μ)/D, and ΔνNCE for acetonylacetone. See DOI: 10.1039/d0ra02932g |
| This journal is © The Royal Society of Chemistry 2020 |