Electronic structure and lattice dynamics of Ba₂CuTeO₆ single crystals

Abstract

The electronic structure and lattice dynamics of Ba₂CuTeO₆ single crystals were investigated through spectroscopic ellipsometry and Raman scattering measurements. The room-temperature optical absorption spectrum of Ba₂CuTeO₆ presented a direct optical band gap at approximately 1.04 eV and exhibited four bands at approximately 1.45, 3.43, 4.65, and 5.79 eV. The optical absorption band at 1.45 eV was attributed to on-site Cu²⁺ d–d transition. The other bands were attributed to charge-transfer transitions between the O 2p and Cu 3d or Te 5p states. The room-temperature Raman scattering spectrum of Ba₂CuTeO₆ exhibited 16 phonon modes at approximately 85, 97, 104, 119, 160, 194, 380, 396, 404, 409, 492, 568, 574, 606, 679, and 751 cm⁻¹. When the temperature decreased to less than 287 K, which is the temperature at which structural phase transition occurs from the monoclinic phase to the triclinic phase, additional phonon modes appeared at approximately 124, 128, 152, and 601 cm⁻¹. On further cooling to lower than 75 and 15 K, which are the temperatures at which short- and long-range antiferromagnetic phase transitions occur, respectively, the phonon modes at approximately 97, 104, 124, 128, 152, 160, 194, 380, 396, 409, 568, 574, 606, and 679 cm⁻¹ exhibited softening, which indicates a coupling between the magnetic and lattice degrees of freedom. The stretching vibration of CuO₆ octahedra located at 679 cm⁻¹ had the largest spin–phonon coupling constant (1.67 mRy Å⁻²).

---

I. Introduction

Double perovskite Ba₂CuTeO₆ has attracted considerable research interest because of its complex physical properties, such as structural phase transition,^1,2 low-dimensional magnetism with S = 1/2 Cu²⁺ ions accompanied by magnetic phase transitions,³ and quantum criticality.⁴ It consists of CuO₆ octahedra that are linked with corner-shared and face-shared TeO₆.^1,2,4–6 The room-temperature crystal structure of Ba₂CuTeO₆ is monoclinic. Ba₂CuTeO₆ undergoes a structural phase transition to the triclinic structure at approximately 287 K (ref. 4, 7 and 8) and exhibits magnetic phase transitions at approximately 75 and 15 K.¹ When the temperature decreases to 75 K, the S = 1/2 Cu²⁺ ions form complex-couple Cu–O–Te–O–Cu superexchange paths. Ba₂CuTeO₆ exhibits short-range antiferromagnetic (AF) correlations.¹ A long-range AF ordering is observed at 15–16 K. The two-leg ladders have strong interladder couplings, which render the Néel-ordered ground state stable.⁷ The crystal and magnetic phase transitions of Ba₂CuTeO₆ are presented in Fig. 1.

Fig. 1 Crystal structure of Ba₂CuTeO₆ at low temperatures. Schematic depicting the electric, structural, and magnetic properties of Ba₂CuTeO₆ (AFM: antiferromagnetic and PM: paramagnetic).

Although considerable research has been conducted on Ba₂CuTeO₆, its optical and phonon properties have remained relatively unexplored. Rao et al.¹ performed the first-principles calculations and predicted a direct band gap energy of 1.0 eV for Ba₂CuTeO₆. Glamazda et al.⁸ examined the polarized Raman scattering spectra of Ba₂CuTeO₆ as a function of temperature. They found that the two-magnon Raman response of Ba₂CuTeO₆ exhibits linear temperature dependence in its peak energy, linewidth, and intensity over a wide range of temperatures. This scaling behavior suggests that Ba₂CuTeO₆ is close to a quantum-critical point from an ordered side. In this study, we used spectroscopic ellipsometry and Raman scattering measurements to investigate the electronic structure and lattice dynamics of Ba₂CuTeO₆. We observed a direct optical band gap near 1.04 eV at room temperature and four optical excitations at approximately 1.45, 3.43, 4.65, and 5.79 eV. Furthermore, we noted 16 Raman-active phonon modes. When the temperature was decreased, anomalous results were observed at temperatures lower than 75 K for the position and strength of the phonon modes at approximately 97, 104, 124, 128, 152, 160, 194, 380, 396, 409, 568, 574, 606, and 679 cm⁻¹, which can be attributed to spin–phonon coupling-induced phonon renormalization.

II. Experiment

Single-crystal Ba₂CuTeO₆ samples were grown through the flux method by using BaCl₂ as the flux. A mixture of the polycrystalline sample of Ba₂CuTeO₆ and the flux of BaCl₂ (molar ratio, 1 : 3) was melted in an alumina crucible at 1150 °C for 24 h. The furnace was slowly cooled to 850 °C at a rate of 3 °C h⁻¹ and then cooled to room temperature at a rate of 80 °C h⁻¹. Dark green crystals (1–3 mm) were mechanically separated from the crucible and then washed with hot water.¹ The crystal structure and phase purity of the samples were examined through synchrotron X-ray powder diffraction.¹ Spectroscopic ellipsometry measurements were conducted at an incidence angle of 75° by using a Woollam M-2000U ellipsometer over a spectral range of 0.73–6.42 eV. The experimental data were measured reproducibly at three spots (100 × 100 μm²) on the sample surface by using a specially designed focusing optics system coupled with an ellipsometer. Lorentz approximation was used to fit the raw ellipsometry data and calculate the dielectric function. Micro-Raman scattering experiments were conducted with a backscattering geometry by using a diode-pumped solid-state laser at an excitation wavelength of 532 nm. We focused linearly polarized light on the sample through a 50× optical microscope objective (numerical aperture: 0.75) with a spatial resolution of 3 μm. To avoid heating effects, the laser power used was less than 1 mW. The scattered light, which was not subject to polarization analysis, was collected and dispersed using a SENTERRA spectrometer equipped with a 1024-pixel-wide charge-coupled detector. The spectral resolution with this spectrometer is typically less than 0.5 cm⁻¹. The polarized Raman scattering spectra were obtained in backscattering geometry from four scattering configurations, namely Z(Y, Y)Z̄, Z(Y, X)Z̄, Z(Y′, Y′)Z̄, and Z(Y′, X′)Z̄. In this Porto notation, the first and last letter represent the directions of the incident and scattered light, whereas the letters in parentheses indicate the polarizations of the incident and scattered light, respectively. X, Y, and Z are parallel to the orthorhombic [100], [010], and [001] crystal directions, whereas X′ and Y′ are along [110] and [1̄10] crystal directions, respectively. The sample was placed in a continuous helium flow cryostat, which allowed measurements to be conducted in the temperature range of 10–300 K.

III. Results and discussion

Fig. 2(a) presents the real (ε₁) and imaginary (ε₂) parts of the dielectric function ε(ω) of Ba₂CuTeO₆, which was obtained through spectroscopic ellipsometry analysis at room temperature. The dispersive response of ε₁ had a positive value, which was similar to the typical behavior of a semiconductor. The peak of ε₂ at approximately 4.0 eV leveled off at higher energies, which revealed that electromagnetic radiation was absorbed by Ba₂CuTeO₆ near 4.0 eV. Fig. 2(b) illustrates the optical absorption coefficient spectrum of Ba₂CuTeO₆ measured at room temperature. We fitted this absorption spectrum by using standard Lorentzian functions.⁹ With an increase in photon energy, absorption increased progressively and four absorption bands were observed at approximately 1.45, 3.43, 4.65, and 5.79 eV. According to the previous first-principles calculations, the first absorption peak (the inset of Fig. 2(b)) was attributed to the on-site Cu²⁺ d–d transition. The other peaks were attributed to charge-transfer transitions from the oxygen 2p states to the copper 3d or tellurium 5p states.¹

Fig. 2 (a) Dielectric function of Ba₂CuTeO₆ estimated at room temperature. (b) The optical absorption coefficient of Ba₂CuTeO₆ estimated at room temperature. The dashed lines show the optimal fit from the Lorentzian model. The inset illustrates the optical absorption coefficient in the low-energy region (0.5–3.5 eV) and the direct band gap analysis of Ba₂CuTeO₆.

In a typical solid, the absorption coefficient includes contributions from the direct and indirect band gap transitions and is expressed as follows:^10,11

where E_g,dir and E_g,ind are the magnitudes of the direct and indirect band gaps, respectively, E_ph is the absorbed (emitted) phonon energy, and A and B are constants. The aforementioned model, which assumes a simple band shape, enables the extraction of the direct energy gap when (αE)² is plotted as a function of the photon energy. The inset of Fig. 2(b) presents a direct band gap of 1.04 ± 0.01 eV at 300 K. Plotting (αE)^0.5 as a function of photon energy led to an indirect band gap of about 0.24 eV (see ESI Fig. 1†). Our experimental result in the direct band gap analysis is in good agreement with the theoretical band structure calculations of Ba₂CuTeO₆, which yield a direct band gap energy of 1.0 eV.¹

Fig. 3 depicts the room-temperature Raman scattering spectrum of Ba₂CuTeO₆. The spectrum comprises 16 first-order Raman phonon modes. We fitted these phonon peaks using standard Lorentzian functions.⁹ We observed a total of 16 Raman-active phonon modes at room temperature at approximately 85, 97, 104, 119, 160, 194, 380, 396, 404, 409, 492, 568, 574, 606, 679, and 751 cm⁻¹. The inset illustrates the polarized Raman scattering spectra of Ba₂CuTeO₆ at room temperature in four configurations. The modes at 85, 97, 104, 119, 160, 194, 380, 396, 404, 409, 492, 568, 574, 606, 679, and 751 cm⁻¹ exhibited a higher intensity in the parallel configuration (YY) than in the cross configuration (YX). This satisfies the selection rule for C2/m in which A_1g and B_1g modes should appear in the YY configuration and no peaks are expected for the YX configuration. On the other hand, the primed spectra Y′Y′ was different from its unprimed counterpart YY, which shows that the sample is a single crystal. The Y′Y′ spectrum showed the suppressed intensity of the modes approximately 160 and 606 cm⁻¹. We deduced that the 85, 97, 104, 119, 194, 380, 396, 404, 409, 492, 568, 574, 679, and 751 cm⁻¹ phonon modes exhibited A_1g symmetry, whereas the 160 and 606 cm⁻¹ phonon modes exhibited B_1g symmetry. According to factor group analysis, Ba₂CuTeO₆ has a monoclinic structure (space group C2/m)⁸ that contains one formula unit per primitive cell at room temperature. The irreducible representation of the phonon modes at the center of the Brillouin zone is presented as follows: Γ = 16A_g + 11B_g.⁸ In accordance with previous report,⁸ the phonon peaks at approximately 85, 97, 104, 119, 160 and 194 cm⁻¹ were assigned to the displacement of Ba atoms and the rotations of CuO₆ and the TeO₆ octahedra. The phonon peaks at approximately 380, 396, 404, 409, and 492 cm⁻¹ were associated with the bending vibrations of CuO₆ and TeO₆ octahedra. The phonon peaks at approximately 568, 574, 606, 679, and 751 cm⁻¹ were attributed to the stretching vibration of TeO₆ and CuO₆ octahedra.

Fig. 3 Unpolarized Raman scattering spectrum of Ba₂CuTeO₆ measured at room temperature. The dashed line shows the fitting results of the spectrum obtained using the Lorentzian model. The inset illustrates the polarized Raman scattering spectra and the optical image of Ba₂CuTeO₆ single crystal. The notations used for the crystallographic directions are also given.

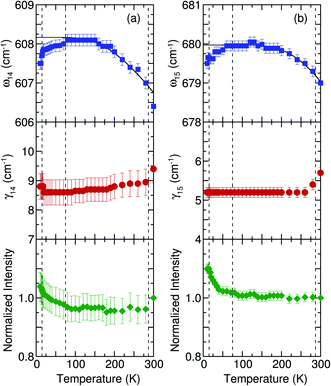
The temperature-dependent Raman scattering spectra of Ba₂CuTeO₆ are depicted in Fig. 4. The inset illustrates the Raman scattering spectra between 75 and 150 cm⁻¹. At low temperatures, the irreducible representation of the phonon modes at the center of the Brillouin zone is presented as Γ = 27A_g. In our investigation, we observed 20 phonon modes. New peaks appeared at approximately 124, 128, 152, and 601 cm⁻¹ at low temperatures. Fig. 5 illustrates the new peaks that appeared between 120 and 130 cm⁻¹ at low temperatures. The new peaks indicate that a weak crystal phase change occurred from the monoclinic state to the triclinic state.^2,8 With a decrease in temperature, these new phonon modes exhibited softening at temperatures lower than 75 K. Fig. 6 displays the temperature-dependent parameters (frequency, linewidth, and normalized intensity) of the phonon modes at 606 and 679 cm⁻¹. The temperature-dependent parameters of other phonon modes are provided in ESI Fig. 2.† The stretching vibrations of TeO₆ and CuO₆ octahedra near 606 and 679 cm⁻¹ exhibited a blueshift when the temperature decreased to 200 K. When the temperature decreased to 75 K, which is the short-range AF phase transition temperature, the redshift and normalized intensities of the phonon modes increased. Our results differed from those of previous measurements.⁸ Glamazda et al. did not observe the phonon anomalies at temperatures lower than the magnetic phase transition temperatures. One possibility that could account for this difference is due to the different growth processes,^1,8 resulting in different quality of single crystals.

Fig. 4 Temperature dependence of Raman scattering spectra of Ba₂CuTeO₆. The inset indicates the Raman scattering spectra between 75 and 150 cm⁻¹.

Fig. 5 Temperature dependence of phonon frequency near 119, 124, and 128 cm⁻¹.

Fig. 6 Temperature dependence of frequency, linewidth, and normalized intensity of (a) 606 and (b) 679 cm⁻¹ phonon modes. The vertical dashed lines indicate the magnetic phase transition temperatures at 15 K, 75 K and structure phase transition at 287 K. The thin solid line denotes the result of the fitting obtained using the anharmonic model.

The temperature dependence of the phonon frequency can be expressed as follows:¹²

where ω₀ is the intrinsic frequency of the optical phonon mode, parameter A is the anharmonic coefficient, and corresponds to the thermal population factor of acoustic modes. For the analysis of anharmonic contributions to the 606 cm⁻¹ phonon modes, the values of ω₀ (approximately 615 cm⁻¹) and parameter A (approximately −6.8 cm⁻¹) were determined. For the 679 cm⁻¹ phonon mode, the values of ω₀ (approximately 690 cm⁻¹) and parameter A (approximately −10 cm⁻¹) were determined. The thin solid lines in Fig. 6(a) and (b) represent the theoretical predictions based on eqn (2). The frequency of the stretching vibrations of the TeO₆ and CuO₆ octahedra deviated from the theoretical predictions at temperatures lower than 75 K. This phenomenon occurred because of a spin–phonon coupling in the AF state of Ba₂CuTeO₆.

In a magnetic material, the temperature-dependent frequency change of the phonon mode can be expressed as follows:¹³

ω(T) = ω₀ + Δω_latt(T) + Δω_anh(T) + Δω_e-ph(T) + Δω_s-ph(T), (3)

where ω₀ is the harmonic frequency of the phonon; Δω_latt(T) is the contribution of lattice expansion and contraction to the phonon frequency; Δω_anh(T) is the intrinsic anharmonic contribution; Δω_e-ph(T) is the contribution due to the renormalization effect of the phonon frequency that results from electron–phonon coupling, which could be negligible in Ba₂CuTeO₆; and Δω_s-ph(T) is the spin–phonon coupling contribution caused by lattice vibrations due to the modulation of the exchange integral. The magnetic coupling among Cu spins is expected to be established through the Cu–O–Te–O–Cu superexchange path. Spin correlations develop when the temperature decreases to 75 K. We calculated Δω_s-ph from the frequency-shift data by using the following expression:¹⁴where λ_eff is the spin–phonon coupling constant and M_sub(T) is the sublattice magnetic susceptibility. We used the magnetic susceptibility¹ to estimate the spin–phonon coupling constant for all redshifted phonon modes. The spin–phonon coupling constants are listed in Table 1. These values were one order of magnitude lower than those obtained for perovskite oxides,^15–20 thus reflecting a weak spin-phonon coupling in Ba₂CuTeO₆.

Table 1 Spin–phonon coupling constants for 14 phonon modes

Mode frequency (cm^−1)	Spin–phonon coupling constant (mRy Å^−2)
97	0.39
104	0.76
124	0.40
128	0.38
152	0.37
160	0.56
194	0.51
380	0.56
396	1.27
409	0.60
568	0.56
574	0.88
606	1.49
679	1.67

---

IV. Summary

We used spectroscopic ellipsometry and Raman scattering spectroscopy to investigate the electronic and phononic excitations of Ba₂CuTeO₆. The direct optical band gap was found to be 1.04 eV. The optical absorption band at approximately 1.45 eV was attributed to on-site Cu²⁺ d–d transition. The other bands at approximately 3.43, 4.65, and 5.79 eV were attributed to charge-transfer transitions between the O 2p and Cu 3d or Te 5p states. Anomalies in the phonon frequency and intensity were detected at approximately 75 K, which indicated a spin–phonon coupling in Ba₂CuTeO₆. The stretching vibration of CuO₆ octahedra located at 679 cm⁻¹ exhibited the largest spin–phonon coupling constant (1.67 mRy Å⁻²).

Author contributions

H. L. L. conceived the idea and designed the experiments. Y. C. C. performed the experiments. S. K. K. and F. C. C. prepared the samples. Y. C. C. and H. L. L. wrote the paper. All the authors discussed the results and commented on the manuscript.

Data availability statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

H. L. L. thanks financial support from the Ministry of Science and Technology of Republic of China under Grants No. MOST 108-2112-M-003-013. F. C. C. thanks financial support from the Ministry of Science and Technology of Republic of China under Grants No. MOST 104-2119-M-002-028-MY2.

References

1. G. N. Rao, R. Sankar, A. Singh, I. P. Muthuselvam, W. T. Chen, V. N. Singh, G.-Y. Guo and F. C. Chou, Tellurium-bridged two-leg spin ladder in Ba₂CuTeO₆, Phys. Rev. B, 2016, 93, 104401.
2. V. P. Köhl and D. Reinen, Strukturelle und spektroskopische Untersuchungen am Ba₂CuTeO₆, Z. Anorg. Allg. Chem., 1974, 409, 257.
3. V. P. Köhl, U. Müller and D. Reinen, Ba₂NiTeO₆ – eine neue Verbindung in der Reihe der hexagonalen Perowskite, Z. Anorg. Allg. Chem., 1972, 392, 124.
4. A. S. Gibbs, A. Yamamoto, A. N. Yaresko, K. S. Knight, H. Yasuoka, M. Majumder, M. Baenitz, P. J. Saines, J. R. Hester, D. Hashizume, A. Kondo, K. Kindo and H. Takagi, S = 1/2 quantum critical spin ladders produced by orbital ordering in Ba₂CuTeO₆, Phys. Rev. B, 2017, 95, 104428.
5. R. L. Moreira, R. P. S. M. Lobo, S. L. L. M. Ramos, M. T. Sebastian, F. M. Matinaga, A. Righi and A. Dias, Raman and infrared spectroscopic investigations of a ferroelastic phase transition in Ba₂ZnTeO₆ double perovskite, Phys. Rev. Mater., 2018, 2, 054406.
6. D. Iwanaga, Y. Inaguma and M. Itoh, Crystal structure and magnetic properties of B′-site ordered perovskite-type oxides A₂CuB′O₆ (A = Ba, Sr; B′ = W, Te), J. Solid State Chem., 1999, 147, 291.
7. D. Macdougal, A. S. Gibbs, T. Ying, S. Wessel, H. C. Walker, D. Voneshen, F. Mila, H. Takagi and R. Coldea, Spin dynamics of coupled spin ladders near quantum criticality in Ba₂CuTeO₆, Phys. Rev. B, 2018, 98, 174410.
8. A. Glamazda, Y. S. Choi, S.-H. Do, S. Lee, P. Lemmens, A. N. Ponomaryov, S. A. Zvyagin, J. Wosnitza, D. P. Sari, I. Watanabe and K.-Y. Choi, Quantum criticality in the coupled two-leg spin ladder Ba₂CuTeO₆, Phys. Rev. B, 2017, 95, 184430.
9. F. Wooten, Optical Properties of Solids, Ann. Phys., 1935, 24, 636.
10. J. I. Pankove, Optical Processes in Semiconductors, Dover, New York, 1971.
11. H. L. Liu, C. R. Huang, G. F. Luo and W. N. Mei, Optical properties of antiferroelectric Cs₂Nb₄O₁₁: Absorption spectra and first-principles calculations, J. Appl. Phys., 2011, 110, 103515.
12. J. Menéndez and M. Cardona, Temperature dependence of the first-order Raman scattering by phonons in Si, Ge, and α−Sn: Anharmonic effects, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 2051.
13. J. Xu, J. H. Park and H. M. Jang, Orbital-spin-phonon coupling in Jahn-Teller-distorted LaMnO₃: Softening of the 490 and 610 cm⁻¹ Raman-active modes, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 012409.
14. W. Baltensperger and J. S. Helman, Influence of magnetic order in insulators on the optical phonon frequency, Helv. Phys. Acta, 1968, 41, 668.
15. J. Vermette, S. Jandl and M. M. Gospodinov, Raman study of spin–phonon coupling in ErMnO₃, J. Phys.: Condens. Matter, 2008, 20, 425219.
16. E. Granado, A. García, J. A. Sanjurjo, C. Rettori, I. Torriani, F. Prado, R. D. Sánchez, A. Caneiro and S. B. Oseroff, Magnetic ordering effects in the Raman spectra of La_1-xMn_1-xO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 11879.
17. J. Laverdiere, S. Jandl, A. A. Mukhin, V. Y. Ivanov, V. G. Ivanov and M. N. Illiev, Spin-phonon coupling in orthorhombic RMnO₃ (R = Pr, Nd, Sm, Eu, Gd, Tb, Dy, Ho, Y): A Raman study, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 214301.
18. H. S. Hsu, F. C. Chou, K. Koyama, K. Watanabe and H. L. Liu, Spin-phonon coupling in antiferromagnetic Bi₂Sr₂CoO_6+δ: An infrared reflectance study, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 155109.
19. S. Issing, A. Pimenov, V. Yu. Ivanov, A. A. Mukhin and J. Geurts, Composition-dependent spin-phonon coupling in mixed crystals of the multiferriuc manganite Eu_1-xY_xMnO₃ (0 ≤ x ≤ 0.5) studied by Raman spectroscopy, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 024304.
20. H. W. Chen, Y.-W. Chen, J.-L. Kuo, Y. C. Lai, F. C. Chou, C. H. Du and H. L. Liu, Spin-charge-lattice coupling in YBaCuFeO₅: Optical properties and first-principles calculations, Sci. Rep., 2019, 9, 3223.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra02314k

‡ PACS numbers: 71.27.+a, 71.35.Cc, 78.30.-j.

---