Open Access Article
Open Access ArticleSwitching Xe/Kr adsorption selectivity in modified SBMOF-1: a theoretical study†
Jiao-jiao Qian a,
Guang-hui Chen
a,
Guang-hui Chen *a,
Song-tao Xiaob,
Hui-bo Lib,
Ying-gen Ouyang*b and
Qiang Wang
*a,
Song-tao Xiaob,
Hui-bo Lib,
Ying-gen Ouyang*b and
Qiang Wang c
c
aDepartment of Chemistry, Key Laboratory for Preparation and Application of Ordered Structural Materials of Guangdong Province, Shantou University, Guangdong 515063, China. E-mail: ghchen@stu.edu.cn
bInstitute of Radiochemistry, China Institute of Atomic Energy (CIAE), Beijing, 102413, People's Republic of China. E-mail: 13911262687@139.com
cDepartment of Applied Chemistry, College of Science, Nanjing Tech University, Nanjing 211816, People's Republic of China
First published on 1st May 2020
Abstract
The separation of Xe/Kr mixtures in used nuclear fuel (UNF) has attracted lots of attention, but no report on the adsorption and separation of Kr from mixed Kr/Xe at room temperature can be found. From grand canonical Monte Carlo (GCMC) simulation, it is found that by replacing the metal center Ca of SBMOF-1 with Mg, due to the appropriate pore size, the adsorption selectivity (SKr/Xe) was extremely high (250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) and the adsorption capacity for Kr on Mg–SBMOF-1 modified with –NH2 was increased by 300% to 1.020 from 0.248 mmol g−1. Based on the calculations of density functional theory (DFT), we found that the stronger electron-donating ability of a functional group will increase the polarizability of the ligand, and thus increase the adsorption capacity to Kr. In addition, the analysis of electronic structures with independent gradient model (IGM) and energy decomposition analysis (EDA) indicates that van der Waals forces will be responsible for the interaction of Mg–SBMOF-1 and Kr gas. Among them, the interaction of Mg–SBMOF-1 and Kr gas is mainly an induction force, while that of modifications with –CH3 and –NH2 is mainly a dispersion force. The present theoretical study represents the first report of the separation of Kr from Xe with MOF adsorption at room temperature. We hope this work may promote the experimental synthesis of Mg–SBMOF-1 for efficient separation of Kr and Xe.
000) and the adsorption capacity for Kr on Mg–SBMOF-1 modified with –NH2 was increased by 300% to 1.020 from 0.248 mmol g−1. Based on the calculations of density functional theory (DFT), we found that the stronger electron-donating ability of a functional group will increase the polarizability of the ligand, and thus increase the adsorption capacity to Kr. In addition, the analysis of electronic structures with independent gradient model (IGM) and energy decomposition analysis (EDA) indicates that van der Waals forces will be responsible for the interaction of Mg–SBMOF-1 and Kr gas. Among them, the interaction of Mg–SBMOF-1 and Kr gas is mainly an induction force, while that of modifications with –CH3 and –NH2 is mainly a dispersion force. The present theoretical study represents the first report of the separation of Kr from Xe with MOF adsorption at room temperature. We hope this work may promote the experimental synthesis of Mg–SBMOF-1 for efficient separation of Kr and Xe.
1. Introduction
The world we are living in is experiencing an energy crisis, more and more scientists are paying attention to the development and utilization of nuclear energy.1 However, radioactive, used nuclear fuel (UNF) from energy generation in nuclear power plants requires an economically viable process to recover precious isotopes and reduce the pollution of radionuclides to the atmosphere.2 There are large amounts of 127Xe and 85Kr in UNF, and the content of 127Xe is ten times of 85Kr. Note that Xe is useful in commercial lighting, imaging, anesthesia, as a propellant in ion propulsion engines, and so on.3 At the same time, krypton is widely used in electric light sources, gas lasers and plasma flows4,5 due to its special physical and chemical properties. Radioactive krypton (85Kr) can be used to make gas radiation source, thickness gauge, densitometer, electron capture tester and aerosol neutralizer, etc. 85Kr also plays an important role in the ‘deuteration’ technology, i.e., 85Kr gas can be used to detect engine surface defects, and whose sensitivity is one thousand times higher than the general non-destructive testing method.6 Most importantly, 85Kr can also be used as one of the important nuclides to track nuclear explosion. The extraction for pure krypton is of great strategic significance for its application in military and civil fields. The traditional method of separation these two gases is cryogenic distillation, however, which is energy consuming.7 Separation of Kr from Xe is an important step in removing radioactive Kr during the reprocessing of irradiated nuclear fuel.8 Therefore, discovery of new materials and new processes for separating Kr and Xe at room temperature is a very valuable subject.9,10In recent years, metal–organic frameworks (MOFs) have attracted more and more attention due to their large specific surface area and porosity, high thermal stability, adjustable physical and chemical properties, regular and uniform pore structure and so on, many researches have focused on the separation of Xe from Xe/Kr mixed gases with MOFs.11,12 For example, in 2012, Thallapally et al.9 simulated the real industrial waste gas environment by means of experiment, and found that the adsorption capacity of Ni/DOBDC for xenon is 9.3 mmol kg−1, with the selectivity of Xe/Kr at 7.3 in the air with 400 ppm Xe and 40 ppm Kr; in 2016, Bae et al.13 explored the reason for the difference of adsorption performance between Xe and Kr of MOF-74 (Co, Zn, Cu) in different metal centers theoretically, and found that the MOF materials corresponding to Co center with higher polarizability had stronger adsorption capacity for Xe; in 2018, Wang et al.14 experimentally reported that MOF–Cu–H, has a Henry constant of 39.74 mmol (g bar−1) and a selectivity of 15.8 for Xe/Kr adsorption at room temperature and pressure; in 2016, Simon et al.15 found that SBMOF-1, a MOF with calcium center and 4,4-sulfonyldibenzoate (SDB) with one-dimensional channel, possesses the highest adsorption selectivity 16 for Xe/Kr with Xe adsorption capacity of 1.4 mmol g−1, by screen from synthesized 5000 and simulated 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MOFs databases by Monte Carlo method. Note that SBMOF-1 was formerly synthesized by Banerjee et al.16 in 2015.
000 MOFs databases by Monte Carlo method. Note that SBMOF-1 was formerly synthesized by Banerjee et al.16 in 2015.
However, the above works just focus on the separation of Xe from Xe/Kr mixture, although the importance of krypton, only one work reported in 2012 on the separation of Kr and Xe experimentally and theoretically, i.e., Thallapally et al.17 found that FMOF–Cu can achieve Xe/Kr adsorption reversal at low temperature of 203 K and 0.1 bar, with Kr/Xe selectivity at 36. But no work about Kr/Xe adsorption and separation by MOF to get pure Kr gas at the normal temperature and pressure was reported so far.
In 2013, Thonhauser et al.18 demonstrated the possibility of replacing the metal center of MOF by means of theoretical simulation, and investigated the adsorption behaviors of MOF-74 of 25 different metal centers for H2, CO2, CH4, and H2O theoretically. Subsequently, Yaghi et al.19 successfully synthesized microcrystalline MOF-74 [M2(DOT);DOT = dioxidoterephthalate] with 2 (Mg and Co), 4 (Mg, Co, Ni, and Zn), 6 (Mg, Sr, Mn, Co, Ni, and Zn), 8 (Mg, Ca, Sr, Mn, Fe, Co, Ni, and Zn), and 10 (Mg, Ca, Sr, Ba, Mn, Fe, Co, Ni, Zn, and Cd) different kinds of divalent metals in 2014. The different metal centers and isomorphic MOF-74 confirmed the accuracy of the previous theoretical calculations and lay the foundation for the experimental synthesis of homomorphic metal centers with different MOFs.
Inspired by the above work, we decide to develop new MOF to separate Kr/Xe mixtures efficiently, which can be used not only for the specific adsorption of Kr in Xe/Kr mixture gas, but also in two-column adsorption experiment, that is, two different columns are packed with MOFs with contrary adsorption selectivity to Kr and Xe. For example, Kr can be adsorbed in the first column while Xe in the second one. Through the strategy of double column adsorption, it is not only possible to achieve high efficiency Kr/Xe separation, but also to obtain pure Kr gas easily.
Naturally, we wonder whether SBMOF-1 can be modified so as to adsorb Kr mainly instead of Xe. Herein, we decide to adopt two ways to modify SBMOF-1 including replace the metal center and functionalization of SDB ligand. By exploring the adsorption isotherms, selectivity, geometrical and electronic structures of Kr and Xe gases adsorbed on modified SBMOF-1, we found that Mg–SBMOF-1 modified by –NH2 group exhibits superiority to Kr adsorption with Kr/Xe selectivity so high as 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 at room temperature and normal pressure.
000 at room temperature and normal pressure.
2. Computational methods
Starting from the crystal structure of SBMOF-1,15 the metal center of Ca is replaced by different metals and modified by various functional groups for SDB, were fully optimized by using DMol3 module incorporated in Materials Studio 8.0,20,21 the LDA/PWC functional combined with the double numerical basis set containing polarization function (DNP) are employed. The relevant MOFs frameworks covered in this work are shown in Fig. S1 and Table S1.† The global cavity diameter (GCD), pore limiting diameter (PLD) and largest cavity diameter (LCD) were calculated by using Zeo++ code.22,23The gas adsorption isotherms were simulated with the Grand Canonical Monte Carlo (GCMC) using RASPA code.24,25 Thallapally et al.15 simulated the adsorption of Xe and Kr on SBMOF-1 by GCMC with rigid force field, and the calculated adsorption capacity is comparable with experiment. So, in this work all structures were regarded as rigid during simulation. Weak interactions between adsorbates and framework atoms were described using 12-6 Lennard-Jones and Coulomb potentials with following eqn (1).26,27
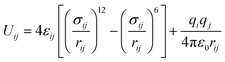 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MC cycles simulations at each pressure, where the first 100
000 MC cycles simulations at each pressure, where the first 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles were used for equilibration and the remaining 100
000 cycles were used for equilibration and the remaining 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles for the computation of the average of thermodynamic properties. The insertion, deletion, translation, rotation, and identity-change MC trial moves were considered in all GCMC calculations. RASPA developers have implemented the fluctuation method to calculate Qst at Monte Carlo level using eqn (2).
000 cycles for the computation of the average of thermodynamic properties. The insertion, deletion, translation, rotation, and identity-change MC trial moves were considered in all GCMC calculations. RASPA developers have implemented the fluctuation method to calculate Qst at Monte Carlo level using eqn (2).
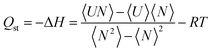 | (2) |
The thermodynamic stability of modified SBMOF-1 is explored in Forcite module34 of Materials Studio package.21 We set up the annealing process from 273 to 5600 K (intermediate temperature is 500 K), the entire annealing process consists of 5 cycles with a total time of 5 ps in NVT ensemble. Besides, the electrostatic potential gradient (EPG) and the adsorption energies (Eads) of every modified framework were also calculated with the GGA/PBE functional exchange-correlation functional including Grimme's D correction in conjunction with the double numerical basis set containing polarization function (DNP) with DMol3 module21 incorporated in Materials Studio package.20 The Eads can be calculated at DFT level according to eqn (3).
| Eads = EMOF+Ng − EMOF − ENg | (3) |
The Mg–SBMOF-1 cluster was cut out in MS visualizer, to obtain the optimized structure of cluster adsorbed by guest molecule at the B3LYP-D3/6-31+G(d)/SDD (Kr) level with Gaussian 16 package, the polarizability of ligand was calculated at the B3LYP-D3/aug-cc-pVDZ level. The IGM (Independent Gradient Model) calculation34 was performed to analyze the weak interaction between Kr/Xe and MOF with Multiwfn35 coming from the calculations of Gaussian program.36,37
To perform the energy decomposition analysis of the adsorption energy, the medium order symmetry-adapted perturbation theory (SAPT) calculations38 were performed at the SAPT2/aug-cc-pVQZ-pp level of theory with PSI4 code39 on the optimized geometries. Note that SAPT is essentially free of BSSE problem,40 no additional correction for BSSE is needed.38,41
During the separation process, the adsorption selectivity (Sads) is an essential parameter to evaluate the separation ability of a porous material. The adsorption selectivity of component i over component j in a mixture is defined as following eqn (4).
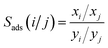 | (4) |
3. Results and discussion
In this section, we mainly organize the discussion as follows: in Section 3.1, the adsorption capacities of Kr and Xe on SBMOF-1 with different metal centers will be investigated; in Section 3.2, the Kr and Xe adsorbed on Mg–SBMOF-1 functionalized with –F, –CH3, –OH, and –NH2 will be explored; in Section 3.3, the intrinsic interaction mechanism between Kr, Xe and Mg–SBMOF-1 will be proposed; in Section 3.4, the effect of temperature, pressure and molar fraction of feed gas on Kr/Xe selectivity during adsorption process will be explored.3.1 The adsorption capacities and selectivities of X–SBMOF-1 (X = Ca, Mg, Ti, Zn, and Cd) for Kr and Xe
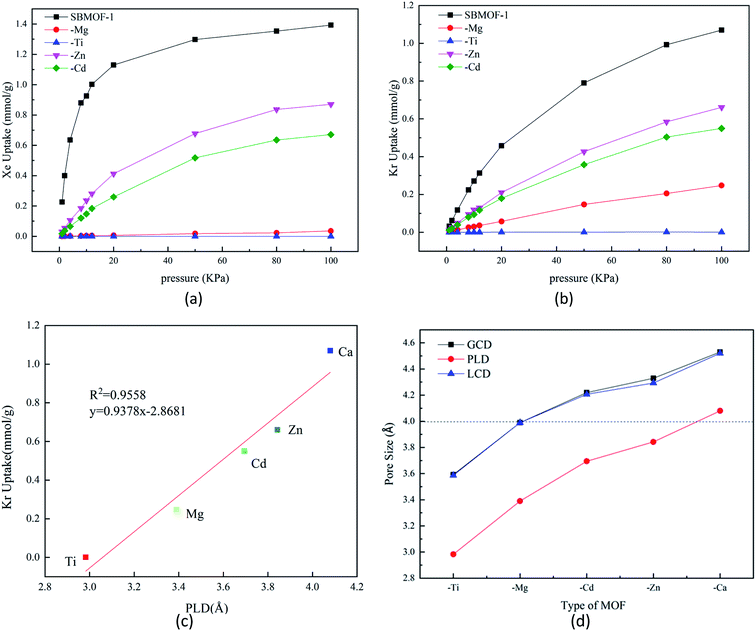
The adsorption isotherms of X–SBMOF-1 (X = Ca, Mg, Ti, Zn, Cd) on Xe and Kr at 298 K are plotted in Fig. 1(a) and (b). In fact, Ti–SBMOF-1 has no adsorption on either Xe or Kr, and the adsorption capacities of Zn–SBMOF-1 and Cd–SBMOF-1 for Xe (0.871 mmol g−1, 0.671 mmol g−1) are larger than those for Kr (0.661 mmol g−1, 0.550 mmol g−1). It should be noted that Mg–SBMOF-1 can adsorb a certain amount of Kr (0.248 mmol g−1), yet hardly adsorb Xe. Although the substitution of metal center makes the adsorption capacity lower than the original SBMOF-1 (Xe: 1.393 mmol g−1, Kr: 1.070 mmol g−1), Mg–SBMOF-1 exhibits huge potential for specific adsorption of Kr in mixed Kr/Xe gases.Mg–SBMOF-1 has two types of pores including pore I and II as shown in Fig. S1(a),† since the pore I is too small (3.39 Å) to accommodate Kr or Xe, so the adsorption mainly occurs in pore II. Based on the aperture distribution analysis of X–SBMOF-1 as plotted in Fig. 1, there is a linear positive correlation between adsorption capacities and PLDs of Kr with R2 = 0.96 as plotted in Fig. 1(c), i.e., the larger of the PLD, the easier for Kr to enter and thus the higher adsorption capacity. As we know that the dynamic diameters of Kr and Xe are 3.60 and 4.00 Å, respectively, it is clear that the LCDs of SBMOF-1, Zn–SBMOF-1, and Cd–SBMOF-1 are larger than 4.00 Å, while Ti–SBMOF-1 has the smallest pore size less than 3.60 Å as plotted in Fig. 1(d), and only Mg–SBMOF-1's LCD (3.90 Å) is right between the dynamic diameters of Xe and Kr, thus specific adsorption of Kr may be achieved. In addition, we also investigated the adsorption heat (Qst) and energy (Eads) of X–SBMOF-1 (X = Ca, Mg, Ti, Zn, Cd) to Kr and Xe, which were calculated at MC and DFT levels, respectively. As listed in Table S3,† it is shown that the Eads are slightly greater than those of Qst, but the result sequences with the two calculation methods are generally consistent. For SBMOF-1, Zn–SBMOF-1 and Cd–SBMOF-1, the binding abilities to Xe are generally larger than Kr. The absolute values of adsorption heat of Ti–SBMOF-1 for Kr and Xe are less than 15 kJ mol−1, basically no adsorption, which is consistent with the previous results of adsorption capacity and pore size analysis. For Mg–SBMOF-1, the absolute value of Qst and Eads for Kr at −24.25 kJ mol−1 and −28.53 kJ mol−1 are larger than those of −22.61 kJ mol−1 and −18.56 kJ mol−1 for Xe. From the calculation results of Qst as listed Table S3,† we can find that for X–SBMOF-1 (X = Ca, Mg, Ti, Zn, Cd), the interaction between the host and guest is dominant, and no guest–guest interaction can be found. Note that although the adsorption capacity of Mg–SBMOF-1 for Kr (0.248 mmol g−1) is not the largest, the adsorption selectivity to Kr/Xe is the highest up to 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.
000.
Experimentally, annealing process is often used to verify the thermal stability of the material structure.42 Theoretically, the influence of temperature on the stability can be verified by molecular simulation. In 2018, Dikshit et al. explored the thermodynamic stability of graphene composite by using the annealing process with Forcite module.43 In 2019, Zhang et al. verified the structural stability of serrated InSe nanobelts (H-ZN(7)-X) using the same method.44 At the same time, the binding energy between metal center Mg and ligand (SDB) calculated at PBE/DNP level is 69.17 kJ mol−1, indicating the large stability of Mg–SBMOF-1. In order to understand the thermal stability of Mg–SBMOF-1, we simulated annealing process with Forcite module45 incorporated in Material Studio package.46 The energy change curve during annealing process and the unit structure of Mg–SBMOF-1 after annealing were plotted in Fig. S3,† respectively. From Fig. S3(a),† it can be found that the energy of system quickly reaches equilibrium after 0.1 ps, the upper and lower amplitudes are not very large, and is converged at 2000 kcal mol−1, lower the kinetic energy more stable is the model which also confirm the thermal stability of the model. After annealing, the geometry of framework just has a slight deformation as plotted in Fig. S3(b),† indicating the large thermal stability of Mg–SBMOF-1.
3.2 The adsorption capacities and selectivity of Mg–SBMOF-1 with various functional groups
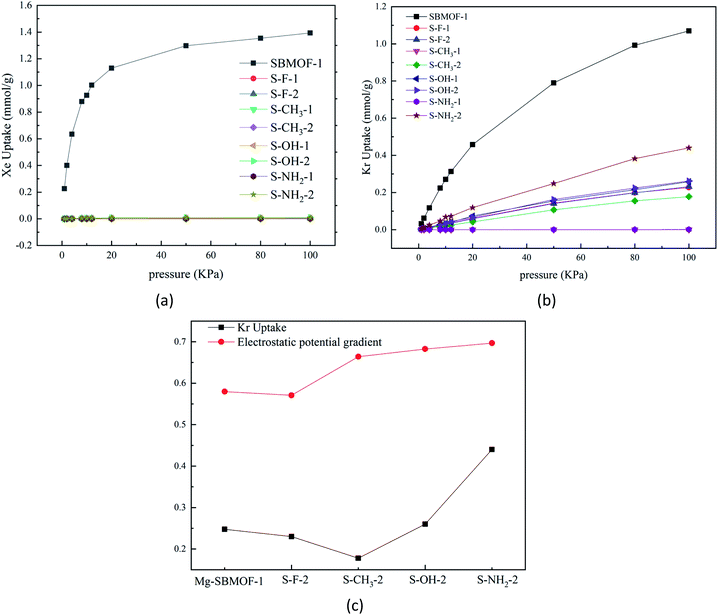
In 2016, Bae et al.47 theoretically proved that the UiO-66 modified with –OCH3, –F, or –NH2 groups at different positions of terephthalic acid can adsorb and separate Xe/Kr efficiently. In view of the large adsorption selectivity to Kr/Xe and high thermal stability, we decide to further modify Mg–SBMOF-1 to investigate the Kr, Xe adsorption with functional groups including –F, –CH3, –OH and –NH2.It is important to understand the influence of pore size of functionalized Mg–SBMOF-1 on the adsorption capacity. So, we calculated their aperture conditions as plotted in Fig. S5,† and it is shown that after the modification on the position 1, the LCDs of the skeleton are shortened greatly, and that of 1-CH3–Mg–SBMOF-1 is even shortened to 2.93 Å, thus no adsorption on Kr and Xe can be found. However, the LCDs of the modified Mg–SBMOF-1 at position 2 are still larger than 3.60 Å which well between 3.60 and 4.00 Å. Obviously, the modification of position 1 has a larger steric hindrance on the pore size of framework than position 2, so modification of position 2 is suitable for the specific adsorption of Kr.
In order to learn the discrepancy in the adsorption capacity on Kr and Xe of Mg–SBMOF-1 modified with above different functional groups with electron-donating capacity of –F < –CH3 < –OH < –NH2, the electrostatic potential and the polarizability of them were investigated also. From the calculated electrostatic potential gradient (EPG) as shown in Fig. S6,† it is clear that after modified with –F, the EPG of the EPG of MOF decreases from 0.58 to 0.57. Obviously, modification with electron-withdrawing groups will reduce the EPG of MOF, while the opposite result is obtained by modifying with electron-rich groups of –NH2, –OH. Comparing the adsorption curve of Kr under the same condition, we can find that, increase of the EPG of the system has a positive effect on the adsorption capacity for Kr as plotted in Fig. 2(c). The only exception is for methyl, the adsorption capacity of Mg–SBMOF-1 on Kr is reduced to just 0.178 mmol g−1, even less than that of adsorption after –F substitution (0.231 mmol g−1), which may result from its large steric hindrance in the pores.
To gain more insight on the effect of modified group on the adsorption capacity, the polarizability of the modified ligands at different positions with different groups were analyzed and compared as listed in Table 1, and it is clear that the modification of the larger group such as –CH3, –NH2, will increase the polarizability evidently. For example, the polarizability of 1-NH2–SDB is about 459.75 a.u., which is much larger than that of SDB by 20.89 a.u. while the polarizability of SDB modified with electron-withdrawing group –F decreased by 0.38 a.u. And we further found that modification of the same group at position 2 has larger effect than position 1, for example, the polarizability of the system modified by –OH at positions 2 is 452.21 a.u., which is larger than that of position 1 by 4.23 a.u.
| ligand category | SDB | S-F-1 | S-CH3-1 | S-OH-1 | S-NH2-1 | S-F-2 | S-CH3-2 | S-OH-2 | S-NH2-2 |
|---|---|---|---|---|---|---|---|---|---|
| Polarizability (a.u.) | 438.86 | 438.48 | 462.07 | 447.98 | 459.75 | 441.55 | 463.64 | 452.21 | 466.93 |
In summary, the modification with the electron-rich –NH2 will favor the adsorption of Kr, because the electron-donating ability of –NH2 group leads to great polarizability of the modified ligand and large EPG of the MOF, it will favor the adsorption of guest molecules. Thus, we selected –NH2 group for the further modification in the following.
In order to explore the influence of different modification schemes on the adsorption capacity, we analyzed it from the aspect of geometry size including GCD, PLD and LCD as plotted in Fig. S8(c).† It is shown that the LCDs of D-NH2-1, D-NH2-3, and D-NH2-6 are all smaller than 3.60 Å, may due to –NH2 within these modification schemes all occupies position 1 close to sulfuryl group, which greatly blocks the pore II and thus difficult to adsorb Kr. So, in the case of multiple substitutions, the –NH2 is always added on the benzene ring except for position 1. From the result of pore size analysis in Fig. S8(c),† we found that the modification schemes including 2, 4, and 5 have minute effect on the size of pore II in Mg–SBMOF-1, which are all around 3.90 Å and well between Xe and Kr dynamic diameters. Due to the confinement effect, Xe cannot enter the pore channel, and only increase the adsorption of Kr.
In the next step, we also explored the electronic structure influence of MOF modified with multiple –NH2 on the adsorption capacity of Kr. Note that when the number of –NH2 group for Mg–SBMOF-1 is increased from 2 to 6, the adsorption capacity for Kr is increased from 0.574 to 1.015 mmol g−1, which may be related to the change in the polarizability of the ligand modified with –NH2. Then, we decide to investigate the relationship between the polarizability and the adsorption capacity for Kr of MOFs decorated with various number of –NH2 as plotted in Fig. S8(d).† It is found that there is a linear positive correlation (R2 = 0.81) between adsorption capacities and polarizabilities of the modified SDB ligands, i.e., the greater polarizability of the ligands, the larger adsorption capacity for framework to Kr.
3.3 The electronic structure comparison of Kr, Xe adsorbed on SBMOF-1 and Mg–SBMOF-1
To further understand the adsorption properties of Kr, Xe on SBMOF-1 and Mg–SBMOF-1, the adsorption sites, adsorption heats were explored, the weak interaction was analyzed with independent gradient model (IGM), and the energy decomposition analyses between MOF and Xe, Kr were also performed with SAPT.36At first, the electronic structures of Xe and Kr adsorbed on SBMOF-1 were analyzed with density functional theory. From adsorption positions of Xe, Kr in the pore of SBMOF-1 as shown in the Fig. S9,† we can find that both have similar adsorption sites, and located in the middle of MOF channel. The calculated adsorption heats of SBMOF-1 with Xe and Kr are −34.46 kJ mol−1, −27.21 kJ mol−1, respectively, both belong to the category of physical adsorption. The IGM analysis was also performed on the SBMOF-1 adsorption of Xe, Kr to determine the weak interaction property as shown in Fig. S10.† Note that the color of the iso-surface is green, indicating the interaction type between them belongs to van der Waals force, and the strength of the iso-surface between SBMOF-1 and Xe is significantly larger than Kr, which coincides with the fact that the binding energies between SBMOF-1 and Xe is stronger than that of Kr.15 From above analysis, it is shown that there are mainly van der Waals interactions between SBMOF-1 and Xe or Kr. To deeply understand the nature of interaction between MOF and guest, we further explore energy decomposition analysis (EDA) by using SAPT calculations. As listed in Table 2, the adsorption energies between SBMOF-1 and Xe is −24.59 kJ mol−1, however, that of Kr is just −16.39 kJ mol−1, which is obviously less than Xe. So, the adsorption of SBMOF-1 takes on Xe/Kr selectivity to some extent. Secondly, from the percents of the three types of adsorption energies including electrostatics, induction and dispersion, the interaction between MOF and Xe is mainly of dispersion force while that of Kr is determinated by induction force.
| SBMOF-1 | Mg–SBMOF-1 | |||
|---|---|---|---|---|
| Kr | Xe | Kr | Xe | |
| a ΔEelec, ΔEexc, ΔEindu, ΔEdisp, ΔEtot represent electrostatic interaction, exchange interaction, induction interaction, dispersion interaction and total interaction respectively. | ||||
| ΔEelec | −0.83 | −3.70 | −0.80 | −0.45 |
| Percentage | 4.6% | 11.9% | 4.5% | 2.8% |
| ΔEexc | 1.81 | 6.48 | 1.79 | 8.01 |
| ΔEindu | −9.46 | −5.99 | −9.15 | −4.56 |
| Percentage | 52.0% | 19.3% | 52.0% | 28.8% |
| ΔEdisp | −7.91 | −21.38 | −7.66 | −10.82 |
| Percentage | 43.4% | 68.8% | 43.5% | 68.4% |
| ΔEtot | −16.39 | −24.59 | −15.82 | −7.82 |
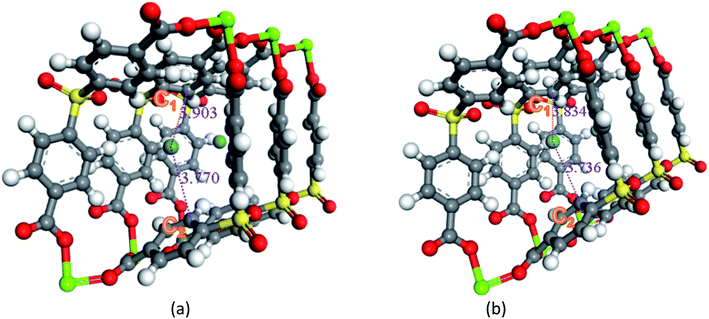
Secondly, the electronic structures of Kr, Xe adsorbed on Mg–SBMOF-1 were also explored with density functional theory. At first, we focus on the difference in adsorption sites between Kr and Xe on Mg–SBMOF-1. From the adsorption position of gas molecules on Fig. 3, it is found that Kr and Xe are all adsorbed in the middle of the pore II in Mg–SBMOF-1, at the same time the distances between Kr and C1, C2 (Kr⋯C: 3.83 Å, 3.74 Å) are smaller than those between Xe and C1, C2 (Xe⋯C: 3.90 Å, 3.77 Å), so Kr is closer to the skeleton. The adsorption heats of Mg–SBMOF-1 with Kr and Xe were calculated as −24.25, −22.61 kJ mol−1, respectively, suggesting that the binding ability of framework with Kr is larger than Xe. Therefore, both in terms of geometry and energy, Mg–SBMOF-1 is more likely to combine with Kr instead of Xe, thereby achieving adsorption reversal. At the same time, the adsorption isoline and IGM were applied to analyze the host-guest and the guest–guest interaction during the adsorption process, where IGM analysis is based on DFT at the B3LYP/6-31+G(d)/SDD (Kr) level. Fig. 4 shows the adsorption isosteres of Kr in Mg–SBMOF-1 and amino-modified Mg–SBMOF-1, we can find that with more –NH2 groups added to MOF, the adsorption heat is larger, for example, the adsorption heat of 3NH2–Mg–SBMOF-1 and 6NH2–Mg–SBMOF-1 were 29.41 kJ mol−1, 30.60 kJ mol−1, respectively. In addition, all the adsorption heat decreases with the increase of adsorption amount, which is in accordance with the change rule of traditional equivalent adsorption heat curve, i.e., there is no interaction between guest molecules. From the optimized structure of Fig. 5(a), it is clear that there are weak interaction between Kr and framework, and the green iso-surface denotes there is van der Waals force between them as we supposed. The IGM analysis between the cluster of 6NH2–Mg–SBMOF-1 and Kr are plotted in Fig. 5(b). Compared with the adsorption in Mg–SBMOF-1, Kr is no longer located in the middle of the channel, but close to the benzene ring (a) with a red iso-surface, indicating a certain steric effect. Note that there is another green iso-surface between Kr and the parallel benzene ring (b), indicating the van der Waals force.
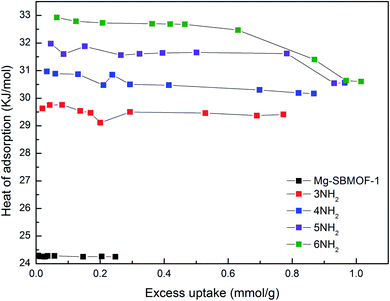 | ||
| Fig. 4 The adsorption heats of Kr in Mg–SBMOF-1 and different amounts of amino-modified Mg–SBMOF-1 at 298 K. | ||
In Table 2, the EDA of interactions between Mg–SBMOF-1 and Xe or Kr are listed. It is shown that the interaction between Mg–SBMOF-1 and Xe is very small just at −7.82 kJ mol−1, which is not beneficial to the binding of Xe. From the energy decomposition analysis (EDA), it is shown that just like the adsorption of Xe, Kr by SBMOF-1, the interactions between Mg–SBMOF-1 and Xe or Kr are dominated by dispersion and induction, respectively. In Table S4,† the EDA of interactions between functionalize Mg–SBMOF-1 and Kr are listed. From the comparison with EDA of Kr adsorbed on Mg–SBMOF-1 functionalized four groups including –F, –CH3, –OH and –NH2 at the same position of Mg–SBMOF-1, respectively, it is found that accompanied by the increase of electron-donating ability of group, the absolute value of the adsorption energy of host-guest is increased also, i.e., S-NH2-2 (−16.76 kJ mol−1) > S-OH-2 (−16.03 kJ mol−1) > S-F-2 (−14.86 kJ mol−1) > S-CH3-2 (−14.41 kJ mol−1), and the main interaction between MOF and Kr has been changed from the induction of predecessor to the dispersion of predominance. After functionalized with –CH3 or –NH2 with large steric hindrance, the exchange energy will be improved with increase the dispersion interaction which is not beneficial the binding of MOF and Kr.
For SBMOF-1, both IGM and EDA show that the interaction intensity between framework and Xe is higher than Kr, while Mg–SBMOF-1 is in the opposite. In addition to confinement factor, Mg–SBMOF-1 also benefit the Kr adsorption from the perspective of electronic structure. And there is just the interaction between the host and the guest while no guest-guest can be found for the Kr adsorption in Mg–SBMOF-1.
3.4 The effects of different temperature, pressure, and molar fraction on Kr, Xe selectivity of Mg–SBMOF-1
For the gas adsorption separation process, selectivity is a key parameter to characterize the performance of adsorbent materials. So, we decide to investigate the effects of temperature, pressure and molar fraction of raw gas on the adsorption selectivity of Kr/Xe.At first, we will pay attention to the effect of temperature on the selectivity of Kr/Xe in Mg–SBMOF-1. From Fig. 6(a), it is shown that SKr/Xe decreases with increased temperature, especially in the range of 243–263 K, and corresponds to a minute decrease after 273 K. Because Mg–SBMOF-1 is rigid, compared with low temperature, the molecular motion is more intense at high temperature, and the adsorption capacity of Mg–SBMOF-1 to Kr is reduced, which leads to the decrease of selectivity.
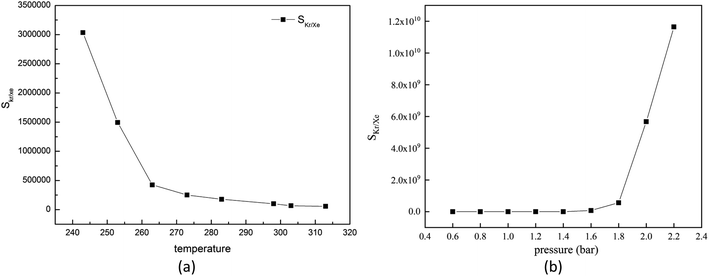 | ||
| Fig. 6 (a) Simulated selectivity of krypton toward xenon for 0.5 krypton and 0.5 xenon composition with GCMC; (b) adsorption selectivity of Mg–SBMOF-1 for Kr/Xe at different pressure. | ||
Next, we will explore the pressure effect on SKr/Xe as plotted in Fig. 6(b). And we can observe that the SKr/Xe increases with increased pressure. The increase slope of selectivity in the range of 0.6–1.6 bar is less than that over 1.6 bar. Snurr et al.48 have theoretically studied the adsorption properties of MOF-505 and HKUST-1 to Kr and Xe in the pressure range of 0–10 bar. Bunzen et al.49 also explored the adsorption of Xe by MFU-4 at 30 bar. The pressure in a certain range does not affect the stability of MOF material. Therefore, in order to obtain high purity Kr gas in practical application, it is necessary to increase the adsorption pressure properly on the premise of considering the production cost.
In addition, we also explored the Kr/Xe adsorption selectivity at three different molar ratios (Kr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Xe = 0.4
Xe = 0.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.6, 0.5
0.6, 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5, 0.6
0.5, 0.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.4) with GCMC simulation as shown in Fig. S11(a).† Note that the selectivity of Kr and Xe at different molar ratios is almost the same at above 273 K. However, in the low temperature region from 263 to 243 K, when the mixture ratio of Kr
0.4) with GCMC simulation as shown in Fig. S11(a).† Note that the selectivity of Kr and Xe at different molar ratios is almost the same at above 273 K. However, in the low temperature region from 263 to 243 K, when the mixture ratio of Kr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Xe is 0.5
Xe is 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5, the selectivity is increased; when the Kr: Xe ratio is 0.6
0.5, the selectivity is increased; when the Kr: Xe ratio is 0.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.4, its selectivity takes 253 K as the node, showing a bottom-up trend; while when the ratio is 0.4
0.4, its selectivity takes 253 K as the node, showing a bottom-up trend; while when the ratio is 0.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.6, the situation is different, the selectivity takes 253 K as the central point, shows rising first and then decreasing trend. In addition, we also simulated the adsorption isotherms of binary mixtures (Kr, Xe) with different molar fraction at 243, 263, 298 and 313 K, respectively, as shown in Fig. S11(b)–(e).† Through comparative analysis, it can be found that the different molar fraction of adsorbate has little effect on the adsorption selectivity at room temperature or higher, due to the intense molecular movement in this case, and the framework is difficult to capture more adsorbate. For example, the difference is only 0.03 mmol g−1 for Kr of molar fraction Kr
0.6, the situation is different, the selectivity takes 253 K as the central point, shows rising first and then decreasing trend. In addition, we also simulated the adsorption isotherms of binary mixtures (Kr, Xe) with different molar fraction at 243, 263, 298 and 313 K, respectively, as shown in Fig. S11(b)–(e).† Through comparative analysis, it can be found that the different molar fraction of adsorbate has little effect on the adsorption selectivity at room temperature or higher, due to the intense molecular movement in this case, and the framework is difficult to capture more adsorbate. For example, the difference is only 0.03 mmol g−1 for Kr of molar fraction Kr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Xe of 0.6
Xe of 0.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.4 and 0.4
0.4 and 0.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.6 at 313 K. Therefore, above 298 K the change of proportion of Kr in mixture will not change the adsorption selectivity too much according to eqn (4), while below 253 K, the proportion of 0.5
0.6 at 313 K. Therefore, above 298 K the change of proportion of Kr in mixture will not change the adsorption selectivity too much according to eqn (4), while below 253 K, the proportion of 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 will benefit the adsorption selectivity of Kr.
0.5 will benefit the adsorption selectivity of Kr.
In summary, when the temperature is lower than 298 K with pressure higher than 1.7 bar, the adsorption selectivity of Mg–SBMOF-1 to Kr will be larger. The molar fraction of the feed gas at room temperature or higher has minute effect on selectivity, but at low temperature, the high homogeneity of the mixed feed gas may be conducive to the selective adsorption of Kr.
4. Conclusions
In this work, the adsorption capacity and selectivity of modified SBMOF-1 for Kr/Xe mixture in used nuclear fuel (UNF) was investigated theoretically at GCMC and DFT levels. By replacing Ca with Mg atoms on SBMOF-1, the pore size of MOF was shortened to achieve the Kr/Xe selective adsorption. And we mainly draw conclusion as follows:After the metal center atom Ca of SBMOF-1 was replaced by different metals including Mg, Ti, Zn, and Cd, it is found that Mg–SBMOF-1 can realize Xe and Kr adsorption reversal at 298 K and 100 kPa, exhibit ultra-high adsorption selectivity to Kr with SKr/Xe at 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. Moreover, based on Mg–SBMOF-1, the ligand SDB (4,4-sulfonyldibenzoate) was modified with different types of groups including –F, –CH3, –OH, and –NH2, it is found that modification with –NH2 is most beneficial for the Kr adsorption with the capacity increased from 0.248 to 1.020 mmol g−1 further.
000. Moreover, based on Mg–SBMOF-1, the ligand SDB (4,4-sulfonyldibenzoate) was modified with different types of groups including –F, –CH3, –OH, and –NH2, it is found that modification with –NH2 is most beneficial for the Kr adsorption with the capacity increased from 0.248 to 1.020 mmol g−1 further.
Mg–SBMOF-1 can separate Kr and Xe mainly due to its pore size of 3.90 Å is exactly between the kinetic diameters of Kr and Xe atoms. Meanwhile, as a result of modification, it is the strong electron-donating ability of –NH2 increases the polarizability of the ligand and the electrostatic potential gradient of MOF, thereby increases the weak interaction between the framework and Kr.
The interaction between Mg–SBMOF-1 and Kr is mainly of van der Waals force, and no interaction of guest–guest molecules can be found. From the results of EDA, it is shown that the interaction between Mg–SBMOF-1 and Kr is mainly induction force, while after the modification of electron-rich group, it is mainly of dispersion force.
In conclusion, the present investigation represents the first report on reversal adsorption of Xe/Kr mixture on MOF at room temperature and normal pressure, with the Kr/Xe selectivity as high as 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, which is much larger than those of FMOF–Cu (SKr/Xe = 0.6 at room temperature, 1 bar; SKr/Xe = 36 at 203 K, 0.1 bar) reported previously. We hope that the present investigation may provide a basis for the synthesis of advanced MOFs and utilized for Kr/Xe, Xe/Kr two-column adsorption experiment to achieve Kr extraction at a low price.
000, which is much larger than those of FMOF–Cu (SKr/Xe = 0.6 at room temperature, 1 bar; SKr/Xe = 36 at 203 K, 0.1 bar) reported previously. We hope that the present investigation may provide a basis for the synthesis of advanced MOFs and utilized for Kr/Xe, Xe/Kr two-column adsorption experiment to achieve Kr extraction at a low price.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Thanks to the Guangdong Provincial Key Laboratory for financial support, and to scientific researchers and institutions that have been cooperating.References
- W. A. Gamson and A. Modigliani, Am. J. Sociol., 1989, 95, 1–37 CrossRef.
- D. Banerjee, A. J. Cairns, J. Liu, R. K. Motkuri, S. K. Nune, C. A. Fernandez, R. Krishna, D. M. Strachan and P. K. Thallapally, Acc. Chem. Res., 2014, 48, 211–219 CrossRef PubMed.
- E. Santos, B. Edwards, V. Chepel, H. M. Araujo, D. Akimov, E. J. Barnes, V. A. Belov, A. Burenkov, A. Currie and L. Deviveiros, J. High Energy Phys., 2011, 115 CrossRef.
- M. Auer, T. Kumberg, H. Sartorius, B. Wernsperger and C. Schlosser, Pure Appl. Geophys., 2010, 167, 471–486 CrossRef.
- A. Bogaerts, E. Neyts, R. Gijbels and J. van der Mullen, Spectrochim. Acta, Part B, 2002, 57, 609–658 CrossRef.
- T. Matsumura, A. Sasahara, Y. Nauchi and T. Saegusa, Nucl. Eng. Des., 2008, 238, 1260–1263 CrossRef CAS.
- F. G. Kerry, Industrial gas handbook: gas separation and purification, CRC Press, 2007 Search PubMed.
- J. Duhayon, J.-P. Goumondy, A. Leudet and J.-C. Rousseau, Method for processing a mixture of air and rare gases, especially xenon and krypton, US Pat., 4 277 363, United States Commissariat, L'energie Atomique A., Paris, FR, 1981.
- J. Liu, P. K. Thallapally and D. Strachan, Langmuir, 2012, 28, 11584–11589 CrossRef CAS PubMed.
- D. Banerjee, C. M. Simon, S. K. Elsaidi, M. Haranczyk and P. K. Thallapally, Chem, 2018, 4, 466–494 CAS.
- L. Li, L. Guo, Z. Zhang, Q. Yang, Y. Yang, Z. Bao, Q. Ren and J. Li, J. Am. Chem. Soc., 2019, 141, 9358–9364 CrossRef PubMed.
- H. Bunzen, F. Kolbe, A. Kalytta-Mewes, G. Sastre, E. Brunner and D. Volkmer, J. Am. Chem. Soc., 2018, 140, 10191–10197 CrossRef CAS PubMed.
- S.-J. Lee, K. C. Kim, T.-U. Yoon, M.-B. Kim and Y.-S. Bae, Microporous Mesoporous Mater., 2016, 236, 284–291 CrossRef CAS.
- S. Xiong, Y. Gong, S. Hu, X. Wu, W. Li, Y. He, B. Chen and X. Wang, J. Mater. Chem. A, 2018, 6, 4752–4758 RSC.
- D. Banerjee, C. M. Simon, A. M. Plonka, R. K. Motkuri, J. Liu, X. Chen, B. Smit, J. B. Parise, M. Haranczyk and P. K. Thallapally, Nat. Commun., 2016, 7, ncomms11831 CrossRef CAS PubMed.
- D. Banerjee, Z. Zhang, A. M. Plonka, J. Li and J. B. Parise, Cryst. Growth Des., 2012, 12, 2162–2165 CrossRef CAS.
- C. A. Fernandez, J. Liu, P. K. Thallapally and D. M. Strachan, J. Am. Chem. Soc., 2012, 134, 9046–9049 CrossRef CAS PubMed.
- P. Canepa, C. A. Arter, E. M. Conwill, D. H. Johnson, B. A. Shoemaker, K. Z. Soliman and T. Thonhauser, J. Mater. Chem. A, 2013, 1, 13597–13604 RSC.
- L. J. Wang, H. Deng, H. Furukawa, F. Gándara, K. E. Cordova, D. Peri and O. M. Yaghi, Inorg. Chem., 2014, 53, 5881–5883 CrossRef CAS PubMed.
- B. Delley, J. Chem. Phys., 1990, 92, 508–517 CrossRef CAS.
- B. Delley, J. Chem. Phys., 2000, 113, 7756–7764 CrossRef CAS.
- T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Microporous Mesoporous Mater., 2012, 149, 134–141 CrossRef CAS.
- R. L. Martin, B. Smit and M. Haranczyk, J. Chem. Inf. Model., 2011, 52, 308–318 CrossRef PubMed.
- D. Dubbeldam, S. Calero, D. E. Ellis and R. Q. Snurr, Mol. Simul., 2016, 42, 81–101 CrossRef CAS.
- D. Dubbeldam, S. Calero and T. J. Vlugt, Mol. Simul., 2018, 44, 653–676 CrossRef CAS.
- D. Frenkel and B. Smit, Phys. Today, 2002, 1, 1–638 Search PubMed.
- M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Oxford University Press, 2017 Search PubMed.
- C. E. Wilmer and R. Q. Snurr, Chem. Eng. J., 2011, 171, 775–781 CrossRef CAS.
- A. K. Rappé, C. J. Casewit, K. Colwell, W. A. Goddard III and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897–8909 CrossRef CAS.
- J. J. Potoff and J. I. Siepmann, AIChE J., 2001, 47, 1676–1682 CrossRef CAS.
- L. Zhang and J. I. Siepmann, Theor. Chem. Acc., 2006, 115, 391–397 Search PubMed.
- T. Vazhappilly, T. K. Ghanty and B. N. Jagatap, J. Phys. Chem. C, 2016, 120, 10968–10974 CrossRef CAS.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- P. Li, Y. Shen, D. Wang, Y. Chen and Y. Zhao, Molecules, 2019, 24, 1822–1831 CrossRef CAS PubMed.
- M. Xiao and T. Lu, J. Adv. Phys. Chem., 2015, 4, 111–124 CrossRef CAS.
- K. Szalewicz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 254–272 CAS.
- R. M. Parrish, L. A. Burns, D. G. Smith, A. C. Simmonett, A. E. De Prince III, E. G. Hohenstein, U. Bozkaya, A. Y. Sokolov, R. Di Remigio and R. M. Richard, J. Chem. Theory Comput., 2017, 13, 3185–3197 CrossRef CAS PubMed.
- K. E. Riley and P. Hobza, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 3–17 CAS.
- S. Emamian, T. Lu, H. Kruse and H. Emamian, J. Comput. Chem., 2019, 40, 2868–2881 CrossRef CAS PubMed.
- Z. Ju, C.-X. Shan, C. Yang, J. Zhang, B. Yao, D. Zhao, D. Shen and X. Fan, Appl. Phys. Lett., 2009, 94, 101902 CrossRef.
- M. Dikshit, G. Nair, K. Pathak and A. Srivastava, Mater. Phys. Mech., 2019, 42, 224–233 Search PubMed.
- Y. Li, Z. Fang and Z. Zhang, J. Phys., 2019, 68, 19–29 Search PubMed.
- B. Rai and Pradip, Mol. Simul., 2008, 34, 1209–1214 CrossRef CAS.
- 10188 T. Court, San Diego 92121, 2010.
- S.-J. Lee, S. Kim, E.-J. Kim, M. Kim and Y.-S. Bae, Chem. Eng. J., 2018, 335, 345–351 CrossRef CAS.
- Y.-S. Bae, B. G. Hauser, Y. J. Colón, J. T. Hupp, O. K. Farha and R. Q. Snurr, Microporous Mesoporous Mater., 2013, 169, 176–179 CrossRef CAS.
- H. Bunzen, F. Kolbe, A. Kalytta-Mewes, G. Sastre, E. Brunner and D. Volkmer, J. Am. Chem. Soc., 2018, 140, 10191–10197 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra02212h |
| This journal is © The Royal Society of Chemistry 2020 |