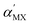Open Access Article
Open Access ArticleTunable Rashba spin splitting in Janus transition-metal dichalcogenide monolayers via charge doping†
Jiajia Chen,
Kai Wu,
Huanhuan Ma,
Wei Hu * and
Jinlong Yang
* and
Jinlong Yang *
*
Department of Chemical Physics, Hefei National Laboratory for Physical Sciences at Microscale, Synergetic Innovation Center of Quantum Information and Quantum Physics, University of Science and Technology of China, Hefei, Anhui 230026, China. E-mail: whuustc@ustc.edu.cn; jlyang@ustc.edu.cn
First published on 11th February 2020
Abstract
Two-dimensional (2D) Janus transition-metal dichalcogenides (TMDs) (MXY, M = Mo, W; X, Y = S, Se, Te; X ≠ Y) have desirable energy gaps and high stability in ambient conditions, similar to traditional 2D TMDs with potential applications in electronics. But different from traditional 2D TMDs, 2D Janus TMDs possess intrinsic Rashba spin splitting due to out-of-plane mirror symmetry breaking, with promising applications in spintronics. Here we demonstrate a new and effective way to manipulate the Rashba effect in 2D Janus TMDs, that is, charge doping, by using first-principles density functional theory (DFT) calculations. We find that electron doping can effectively strengthen the Rashba spin splitting at the valence band maximum (VBM) and conduction band minimum (CBM) in 2D Janus TMDs without constant energy consumption, superior to traditional techniques (electric fields and strain engineering), but hole doping would weaken the Rashba effect in 2D Janus TMDs. By combining the DFT calculations with the electric-triple-layer model, we also reveal the intrinsic mechanism of tuning the Rashba effect in 2D Janus TMDs by charge doping, and find that the charge transfer plays an important role in tuning the Rashba spin splitting in 2D polar semiconductors. In particular, the Rashba constants are linearly dependent on the charge transfer between X (or Y) and M atoms in 2D Janus TMDs. These results enrich the fundamental understanding of the Rashba effect in 2D semiconductors, which can be promising candidates for spin field-effect transistors (FETs) in experiments.
1 Introduction
The interaction of an electron’s spin with its motion inside an electric field is called spin–orbit coupling (SOC),1 which provides a bridge between the orbital motion and the spin degree of freedom. Among various kinds of SOC, one representative example is the Rashba spin splitting,2 which is a direct result of structure inversion asymmetry (SIA). The Rashba effect attracts considerable attention due to its tunability by an external electric field.3 A giant Rashba spin splitting is desirable for practical spintronic applications, such as spin field-effect transistors (FETs), because it can decrease the precession time of the spin to be even smaller than the spin relaxation time.4An ideal Rashba material in spintronics should meet two key conditions: on the one hand, there is a desirable Rashba spin splitting, that is, the Rashba constant should be larger than 0.1 eV Å; refer to the InGaAs/InAlAs heterostructure3 or the LaAlO3/SrTiO3 heterostructure.5–7 On the other hand, the Rashba spin splitting can be effectively tuned by some external conditions and experimental techniques, such as electric fields, with potential applications in spin FETs in experiments. Furthermore, metals have too small dielectric constants to make a big difference in electric potential. The Rashba effect is on account of the built-in electric field. Hence, metals are not good Rashba materials, and Rashba materials should be dielectric semiconductors. When considering practical applications, two dimensional (2D) materials attract more attention than bulk (interfaces or 3D heterostructures), resulting from the merit in manipulating spin carriers in spintronics.8–10 Therefore, we expect to find desirable 2D dielectric semiconductors with large and tunable Rashba spin splitting effect. But common 2D semiconductors, e.g., transition-metal dichalcogenides (TMDs)11 and phosphorene,12,13 are nonpolar and don’t possess an intrinsic Rashba effect. In 2D nonpolar TMDs, the Rashba effect can be induced by breaking the out-of-plane symmetry, which is often achieved by electric fields11 or interfacial effects.14–16
Recently, a polar TMD monolayer, MoSSe, has been successfully synthesized in experiments,17,18 and is a Janus TMD. 2D Janus TMD monolayers MXY (M = Mo, W; X, Y = S, Se, Te; X ≠ Y) show desirable energy gaps (1.0–2.0 eV)19,20 and high stability17–20 in ambient conditions, similar to traditional 2D TMDs21–23 with potential applications in electronics. In particular, the Janus TMD monolayers show intrinsic Rashba spin splitting due to the built-in electric field perpendicular to the monolayer plane induced by out-of-plane mirror symmetry breaking.11,19,20,24
Furthermore, the Rashba effect in 2D Janus TMDs can also be effectively manipulated by traditional experimental techniques (electric fields and strain engineering)11,20 but with constant energy consumption, showing potential applications in spin FETs in experiments. Theoretically, the Rashba effect can be effectively characterized by the Rashba constant, which can be calculated according to the electronic band structure and shows a linear dependence on electric field20 and a nonlinear dependence on the strain engineering.11,20 Nevertheless, the intrinsic mechanism of manipulating the Rashba effect in 2D semiconductors has not been revealed yet.
In this work, we demonstrate a new and effective way to tune the Rashba effect in 2D Janus TMDs, that is, charge doping, which can be realized by the gate voltage of FETs in experiments.25 In particular, we find that electron doping can effectively strengthen the Rashba spin splitting in 2D Janus TMDs without constant energy consumption, which is better than traditional experimental techniques (electric fields and strain engineering). By combining the DFT calculations with the electric-triple-layer model, we also reveal the intrinsic mechanism of tuning the Rashba effect in 2D Janus TMDs by charge doping, and find that charge transfer plays an important role in manipulating the Rashba spin splitting in 2D polar semiconductors.
2 Computational models and methods
2.1 Rashba model
The spin-chirality-induced Rashba effect (Fig. 1(a)) can be described by the Bychkov–Rashba Hamiltonian2,26
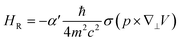 | (1) |
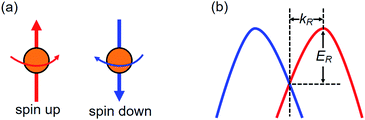 | ||
| Fig. 1 (a) Spin up (red arrow) and down (blue arrow) chiral states. (b) A magnified schematic illustration of the Rashba spin splitting with Rashba energy ER and momentum offset kR. | ||
In accordance with the scalar and cross product construction rules and the electric field (Ez) expression, the Rashba Hamiltonian in 2D structures can be written as
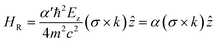 | (2) |
 | (3) |
Thus, the dispersion law for the Rashba spin splitting is11,26
 | (4) |
Thus, the Rashba energy ER at momentum offset kR determines the α constant as shown in Fig. 1(b)24
 | (5) |
2.2 Electric-triple-layer model
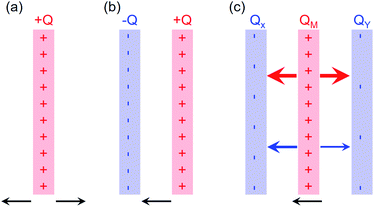
For 2D materials, the Rashba constant α is proportional to the electric field perpendicular to the surfaces. The electric-double-layer model has been used to study the built-in electric field in polar surfaces and 2D materials.27–29 In particular, a one-atom structure can be considered as an electric-single-layer model with an electric field perpendicular to the monolayer plane as shown in Fig. 2(a). In both directions, the built-in electric field equals
 | (6) |
Fig. 2(b) shows that a two-atom structure can be regarded as an electric-double-layer model,27,29 whose built-in electric field is also dependent on the charge density:
 | (7) |
A Janus MXY monolayer, which has three atoms in a unit cell, can be considered as an electric-triple-layer model as shown in Fig. 2(c). The local electric fields are proportional to the charges of the W, X and Y atoms:
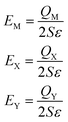 | (8) |
As shown in Fig. 2(c), the net electric field Ez consists of EM, EX and EY, whose respective contributions are inconclusive. Combined with eqn (3), the Rashba constant can be written as
| α = kMQM + kXQX + kYQY | (9) |
 | (10) |
2.3 Computational methods
We perform the density functional theory (DFT)30 calculations through the Vienna Ab initio Simulation Package (VASP).31 Structure relaxations and self-consistent total energy calculations are treated by the projector augmented wave (PAW)32 and generalized gradient approximations using the Perdew–Burke–Ernzerhof functional (GGA-PBE).33 The optB86b-vdW functional34,35 is used to describe the van der Waals interactions in 2D layered structures17,18,20,36,37 (see ESI†). Spin–orbit coupling (SOC) calculations are performed to investigate the Rashba effect. The charge doping is implemented by applying an additional neutralizing background charge.38 The charge transfer is computed with the Bader analysis.39 The kinetic energy cutoff of the plane wave and the Γ-centered k-point meshes of the Brillouin zone (BZ) are set to 600 eV and 15 × 15 × 1, respectively. The MXY monolayer is placed in the x–y plane with the z direction perpendicular to the layer plane, and a vacuum slab of 20 Å is introduced in the z direction to avoid the periodic interaction. The geometric convergence criteria for the energy and forces acting on each atom are set at 10−8 eV and 0.001 eV Å−1, respectively. According to the crystal symmetry, the band structures of the Janus MXY monolayers are calculated along the special lines connecting the following high-symmetry points in the k space: M (0.5, 0, 0), Γ (0, 0, 0) and K (1/3, 1/3, 0).3 Results and discussion
3.1 Geometrical structures
We consider the WSeTe monolayer as a representative of six Janus MXY monolayers, whose atomic structure is shown in Fig. 3(a). Compared to the space group D3h of MX2, the space group of monolayer MXY is changed to C3v due to the out-of-plane mirror symmetry breaking. The structural constants of the MXY monolayers are presented in Table S1.† As the XY atomic number sum increases (SSe → STe → SeTe), the lattice constants of the MXY monolayers increase. The atomic number of X is smaller than that of Y in each MXY monolayer, so that lM–X < lM–Y and dM–X < dM–Y. The structural constants of the six Janus MXY monolayers are listed in the ESI.†Fig. 3(a) also shows the charge of the WSeTe monolayer calculated by Bader charge analysis. The different electronegativity values of the X and Y atoms (S(2.58), Se(2.55) and Te(2.10)) result in the M atom having a positive charge, and the X and Y atoms having a negative charge. Furthermore, it is clear that the X atom gets more electrons than the Y atom, leading to a built-in electric field pointing from the Y atom to the X atom in MXY monolayers. The greater electron accumulation on the Se side leads to larger potential energy and work function on the Se side than the Te side as shown in Fig. 3(b). The work function difference, namely Δϕ, is 0.338 eV in the WSeTe monolayer. On account of the large electronegativity difference between S and Te atoms, MSTe structures have the largest Δϕ values, which are nearly double those of MSSe and MSeTe structures (see ESI†).
3.2 Electronic structures and Rashba effect
To clearly demonstrate the Rashba effect, we compute the band structures of the WSeTe monolayer without and with SOC as shown in Fig. 4(a) and (b), respectively. When the SOC effect is not included, the WSeTe monolayer is a semiconductor with a direct band gap of 1.42 eV, which is larger than that of WTe2 (1.13 eV) and smaller than that of WSe2 (1.62 eV), with the valence band maximum (VBM) and conduction band minimum (CBM) at the K point. Some MXY monolayers have direct band gaps, while others have indirect band gaps, which is consistent with previous research.20 There is a special energy valley marked as Γ, whose three dimensional view is shown in Fig. 4(g).Due to SOC, the WSeTe monolayer becomes an indirect band semiconductor with the VBM at the K point and the CBM along the K–Γ direction as shown in Fig. 4(b). With SOC, the spin degeneracies at the VBM and CBM are removed. The Rashba spin splitting effect at the VBM is much stronger than at the CBM. In particular, the Rashba spin splitting occurring at the Γ point of the VBM is remarkable. The red and blue lines are used to highlight the splitting bands, and the corresponding three dimensional view is shown in Fig. 4(h). The other five systems have similar spin splitting with smaller magnitude.
In this case, the VBM mainly comprises the dx2–y2, dxy and dz2 orbitals of the W atom at the K point, as shown in Fig. 4(c). The projected band structures of the WSeTe monolayer are shown in Fig. 4(d–f). It is shown that different energy bands such as the Γ point are composed of various atomic orbitals, while the dz2 orbital of the W atom makes an enormous contribution to the Γ point and the Se atomic orbitals make a greater contribution to the Γ point than the Te orbitals.
All the bands in Rashba semiconductors are used in spintronics experiments. The bands close to the Fermi level, such as the VBM and CBM, can be manipulated easily in experiments. In Janus TMD monolayers, the Rashba VBM around the Γ point and the Rashba CBM around the M point show Rashba spin splitting. However, the Rashba constant around the M point in the M–Γ direction at the CBM is too small to be manipulated in experiments (see ESI†). Thus, the Rashba VBM around the Γ point is further discussed in this work. Fig. 4(i and j) show the spin arrows around the Γ point forming clockwise and anticlockwise rotations, which elucidates the existence of the Rashba effect. It has been found that Rashba constants are not sensitive to the directions selected in the Brillouin zone for Janus TMD monolayers.20 Therefore, the Rashba constant α at the Γ point along the Γ–K direction of the VBM is selected to illustrate the Rashba effect. ER, kR and α of the WSeTe monolayer are calculated to be 35.584 meV, 0.149 Å−1 and 0.479 eV Å, respectively. The α value at the M point along the M–Γ direction of the VBM is only 0.241 eV Å, and α of the WSeTe monolayer is the largest one among the six Janus TMD monolayers. The Rashba constant α for the WSeTe monolayer is larger than those of the Au(111) surface,40 the InGaAs/InAlAs heterostructure3 and the LaAlO3/SrTiO3 heterostructure,5–7 but smaller than those of the Bi(111) surface,41 the MoS2/Bi(111) heterostructure14 and BiTeX (X = Br, I) monolayers.42 Compared to other Rashba materials, ER and kR of the WSeTe monolayer are considerable.
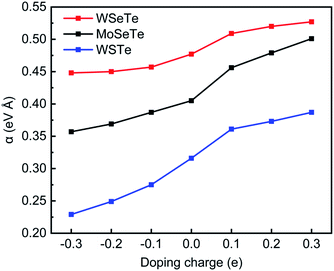
3.3 Tunable Rashba effect via charge doping
In general, there are two traditional techniques (electric fields and strain engineering)11,20 to regulate the Rashba effect in 2D Janus TMDs. Here, we demonstrate that charge doping can also effectively manipulate the Rashba effect in 2D Janus TMDs. In order to prove it, we dope charge from −0.3e to +0.3e in the Janus MXY monolayers and examine the corresponding α. Positive doping charge means electron doping and negative doping charge means hole doping. All calculated α are shown in the ESI.† The calculated α values as a function of doping charge of WSeTe, MoSeTe and WSTe, which have considerable Rashba constants among the six Janus TMDs, are presented in Fig. 5.We find that charge doping can manipulate the Rashba effect at both the VBM and the CBM. In particular, electron doping (+0.1 ∼ +0.3e) can strengthen the Rashba effect at the Γ point of the VBM and the M point of the CBM, both of which are positively correlated. Taking the Rashba spin splitting around the Γ point of the VBM as an example, with electron doping (+0.3e), the positive charge of the W atom decreases and the negative charges of the Se and Te atoms increase compared to the neutral WSeTe monolayer, as shown in Fig. 6(a). Meanwhile, the band structure in Fig. 6(c) indicates that the Fermi level rises and the Rashba spin splitting becomes larger, with the Rashba constant increasing by 10.5% compared with the neutral structures. The corresponding spin textures shown in Fig. 6(e) and (g) elucidate the existence of Rashba spin splitting.
It is also found that hole doping (−0.3 ∼ −0.1e) can weaken the Rashba effect at the VBM and CBM. With hole doping (−0.3e) in the WSeTe monolayer, the positive charge of the W atom increases and the negative charges of the Se and Te atoms decrease in comparison with the neutral WSeTe monolayer. In the meantime, Fig. 6(d) shows that the Fermi level falls and the Rashba constant decreases by 6.1% compared with the neutral case at the Γ point of the VBM. The existence of the Rashba effect is also proved by the spin textures as shown in Fig. 6(f) and (h).
These results demonstrate that charge doping can effectively tune the Rashba effect, and that the Rashba effect can be enhanced by electron doping. It should be noted that charge doping still cannot produce Rashba spin splitting in nonpolar TMDs, different from the traditional technique, namely out-of-plane electric fields.11
3.4 Intrinsic mechanism of tuning the Rashba effect via charge doping
We reveal the intrinsic mechanism of the tunable Rashba effect via charge doping in 2D Janus TMDs. As discussed in Section 2, Janus TMD monolayers can be considered as electric-triple-layer models. We compute the charges of the M, X and Y atoms of six Janus MXY monolayers by using the Bader charge analysis39 (see ESI†). Fig. 7 shows the charges of the W, Se and Te atoms, as well as the charge differences between the W, Se and Te atoms in the WSeTe monolayer. We find that the Rashba effect is strengthened as the charges of the three atoms decrease. Moreover, the charges of three atoms are linearly dependent on the doping charge. | ||
| Fig. 7 (a) The charge of W, Se and Te atom, as well as (b) the charge difference between W, Se and Te atoms in WSeTe monolayer. | ||
In particular, we find that the Rashba effect is strengthened as the charge difference between the W atom and the Se (Te) atom increases in the Janus WSeTe monolayer. Thus, the Rashba effect is positively correlated with the charge transfer between the W atom and the Se or Te atom. As shown in Fig. 2(b), the net electric field Ez is related to the charge difference. Their respective contributions to the net electric field are still inconclusive. Combined with eqn (9), the Rashba constant can be written as
| α = kMX(QM − QX) + kMY(QM − QY) + kYX(QY − QX) | (11) |
In order to solve the non-homogeneous linear equation, we use the singular value decomposition (SVD) algorithm43 implemented in the MATLAB software.44 Calculation details are provided in the ESI.† Thus, kMX, kMY and kYX are calculated to be −8.330 V Å, 8.755 V Å and 8.541 V Å, respectively. The coefficients for the six MXY monolayers are listed in Table 1.
 ,
,  and
and  ) (10−14 C)
) (10−14 C)
| Structure | kMX | kMY | kYX | m | S | ε∞ | |||
|---|---|---|---|---|---|---|---|---|---|
| MoSSe | −0.035 | 0.115 | 0.150 | −4.587 | 9.036 | 4.93 | −1.561 | 5.128 | 6.688 |
| MoSTe | −8.046 | 8.279 | 7.763 | −3.222 | 9.683 | 5.73 | −220.427 | 226.824 | 212.683 |
| MoSeTe | −11.134 | 11.609 | 11.051 | −1.714 | 10.077 | 5.78 | −90.577 | 94.439 | 89.902 |
| WSSe | −14.290 | 14.408 | 14.164 | −2.608 | 9.041 | 4.54 | −189.808 | 191.373 | 188.143 |
| WSTe | −31.397 | 31.766 | 31.076 | −1.724 | 9.682 | 5.25 | −225.624 | 228.281 | 223.322 |
| WSeTe | −8.330 | 8.755 | 8.541 | −1.600 | 10.082 | 5.38 | −55.000 | 57.808 | 56.394 |
Thus, coefficients α′ can be calculated by the following equations
 | (12) |
In the Janus TMD monolayers, the calculated  and
and  have positive signs, while
have positive signs, while 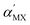 has a negative sign.
has a negative sign. 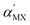 and
and  have opposite signs and approximately equal absolute values, which is consistent with the fact that nonpolar TMDs possess neither built-in electric nor intrinsic Rashba spin splitting around the Γ point. Although
have opposite signs and approximately equal absolute values, which is consistent with the fact that nonpolar TMDs possess neither built-in electric nor intrinsic Rashba spin splitting around the Γ point. Although 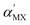 is smaller than
is smaller than  , the contribution of the charge transfer between M and X atoms (kMX(QM − QX)) is larger than that between M and Y atoms (kMY(QM − QY)), which is in agreement with the projected band structures of MXY structures.
, the contribution of the charge transfer between M and X atoms (kMX(QM − QX)) is larger than that between M and Y atoms (kMY(QM − QY)), which is in agreement with the projected band structures of MXY structures.
The dependence of the built-in electric field on the doping charge provides a potential strategy for manipulating the Rashba effect in Janus TMD monolayers by applying a gate voltage. It is known that a negative gate voltage injects electrons into the structure and produces electron doping, while a positive gate voltage extracts electrons from the material and leads to hole doping. Thus, it is feasible to enhance the Rashba effect in Janus TMD monolayers by using a negative gate voltage in experiments. Furthermore, this mechanism can also be used to improve the traditional techniques (electric fields and strain engineering) for tuning the Rashba effect in 2D materials.
4 Conclusions
Janus transition-metal dichalcogenide monolayers (MXY, M = Mo, W; X = Y = S, Se, Te; X ≠ Y) are two-dimensional polar materials possessing out-of-plane mirror symmetry breaking and intrinsic Rashba spin splitting at the VBM and CBM. In this work, the geometries and electronic structures of MXY monolayers are systematically researched. The Rashba spin splitting can be effectively manipulated by charge doping. Especially, negative charge doping can effectively strengthen the Rashba effect and consumes less energy compared to the traditional techniques (electric fields and strain engineering), which may make a contribution to semiconductor spintronics. The Rashba VBM around the Γ point is discussed in detail. Using the electric-triple-layer model, we also find that charge transfer plays an important role in manipulating the Rashba spin splitting in 2D Janus TMDs, which reveals the intrinsic mechanism of tuning the Rashba effect in 2D Janus TMDs by charge doping and enriches the fundamental understanding of the Rashba effect in 2D polar semiconductors as promising candidates in spintronics.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (21688102, 21803066), the National Key Research and Development Program of China (2016YFA0200604), Anhui Initiative in Quantum Information Technologies (AHY090400), the Strategic Priority Research Program of Chinese Academy of Sciences (XDC01040100), Research Start-Up Grants (KY2340000094) and the Academic Leading Talents Training Program (KY2340000103) from University of Science and Technology of China, and the Chinese Academy of Sciences Pioneer Hundred Talents Program. The authors thank USTC, CAS, Tianjin, and Shanghai Supercomputer Centers for the computational resources.References
- G. Dresselhaus, Phys. Rev., 1955, 100, 580–586 CrossRef CAS.
- Y. A. Bychkov and E. I. Rashba, JETP Lett., 1984, 39, 78–81 Search PubMed.
- J. Nitta, T. Akazaki, H. Takayanagi and T. Enoki, Phys. Rev. Lett., 1997, 78, 1335–1338 CrossRef CAS.
- S. Datta and B. Das, Appl. Phys. Lett., 1990, 56, 665–667 CrossRef CAS.
- A. Caviglia, M. Gabay, S. Gariglio, N. Reyren, C. Cancellieri and J.-M. Triscone, Phys. Rev. Lett., 2010, 104, 126803 CrossRef CAS PubMed.
- A. Fête, S. Gariglio, A. Caviglia, J.-M. Triscone and M. Gabay, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 201105 CrossRef.
- Z. Zhong, A. Tóth and K. Held, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 161102 CrossRef.
- S. Huang, A. Badrutdinov, L. Serra, T. Kodera, T. Nakaoka, N. Kumagai, Y. Arakawa, D. Tayurskii, K. Kono and K. Ono, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 085325 CrossRef.
- J. Park, S. W. Jung, M.-C. Jung, H. Yamane, N. Kosugi and H. W. Yeom, Phys. Rev. Lett., 2013, 110, 036801 CrossRef PubMed.
- Q. Liu, Y. Guo and A. J. Freeman, Nano Lett., 2013, 13, 5264–5270 CrossRef CAS PubMed.
- Q.-F. Yao, J. Cai, W.-Y. Tong, S.-J. Gong, J.-Q. Wang, X. Wan, C.-G. Duan and J. Chu, Phys. Rev. B, 2017, 95, 165401 CrossRef.
- L. Yang, Y. Song, W. Mi and X. Wang, RSC Adv., 2016, 6, 66140–66146 RSC.
- Y. Li, X. Li, Q. Wan, R. Bai and Z. Wen, Phys. E Low-dimens. Syst. Nanostruct., 2018, 98, 33–38 CrossRef.
- K. Lee, W. S. Yun and J. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 125420 CrossRef.
- T.-H. Wang and H.-T. Jeng, npj Comput. Mater., 2017, 3, 5 CrossRef.
- Y. Wang, W. Wei, B. Huang and Y. Dai, J. Phys.: Condens. Matter, 2019, 31, 125003 CrossRef PubMed.
- J. Zhang, S. Jia, I. Kholmanov, L. Dong, D. Er, W. Chen, H. Guo, Z. Jin, V. B. Shenoy and L. Shi, et al., ACS Nano, 2017, 11, 8192–8198 CrossRef CAS PubMed.
- A.-Y. Lu, H. Zhu, J. Xiao, C.-P. Chuu, Y. Han, M.-H. Chiu, C.-C. Cheng, C.-W. Yang, K.-H. Wei and Y. Yang, et al., Nat. Nanotechnol., 2017, 12, 744–749 CrossRef CAS PubMed.
- C. Xia, W. Xiong, J. Du, T. Wang, Y. Peng and J. Li, Phys. Rev. B, 2018, 98, 165424 CrossRef CAS.
- T. Hu, F. Jia, G. Zhao, J. Wu, A. Stroppa and W. Ren, Phys. Rev. B, 2018, 97, 235404 CrossRef CAS.
- W. S. Yun, S. Han, S. C. Hong, I. G. Kim and J. Lee, Phys. Rev. B:Condens. Matter Mater. Phys., 2012, 85, 033305 CrossRef.
- A. Kuc and T. Heine, Chem. Soc. Rev., 2015, 44, 2603–2614 RSC.
- X. Zhang, X.-F. Qiao, W. Shi, J.-B. Wu, D.-S. Jiang and P.-H. Tan, Chem. Soc. Rev., 2015, 44, 2757–2785 RSC.
- W. Zhou, J. Chen, Z. Yang, J. Liu and F. Ouyang, Phys. Rev. B, 2019, 99, 075160 CrossRef.
- Y. Sun, Z. Shuai and D. Wang, Nanoscale, 2018, 10, 21629–21633 RSC.
- T. Etienne, E. Mosconi and F. De Angelis, J. Phys. Chem. Lett., 2016, 7, 1638–1645 CrossRef CAS PubMed.
- W. Hu, Z. Li, J. Yang and J. Hou, J. Chem. Phys., 2013, 138, 034702 CrossRef PubMed.
- W. Hu, Z. Li and J. Yang, Comput. Theor. Chem., 2013, 1021, 49–53 CrossRef CAS.
- X. Li, Z. Li and J. Yang, Phys. Rev. Lett., 2014, 112, 018301 CrossRef PubMed.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. Klimeš, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2010, 22, 022201 CrossRef PubMed.
- J. Klimeš, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131 CrossRef.
- W. Hu and J. Yang, Comput. Mater. Sci., 2016, 112, 518–526 CrossRef CAS.
- X. Qin, W. Hu and J. Yang, Phys. Chem. Chem. Phys., 2019, 21, 23611–23619 RSC.
- R. Hughes, Perspect. Sci., 2006, 14, 457–524 CrossRef.
- R. Bader, Atoms in Molecules, A Quantum Theory, 1990, vol. 22 Search PubMed.
- S. LaShell, B. McDougall and E. Jensen, Phys. Rev. Lett., 1996, 77, 3419 CrossRef CAS.
- Y. M. Koroteev, G. Bihlmayer, J. Gayone, E. Chulkov, S. Blügel, P. M. Echenique and P. Hofmann, Phys. Rev. Lett., 2004, 93, 046403 CrossRef PubMed.
- Y. Ma, Y. Dai, W. Wei, X. Li and B. Huang, Phys. Chem. Chem. Phys., 2014, 16, 17603–17609 RSC.
- G. Golub and C. Reinsch, Numer. Math., 1970, 14, 403–420 CrossRef.
- MATLAB, version 9.4.0.813654 (R2018a), The MathWorks Inc Natick, MA, 2018 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra00674b |
| This journal is © The Royal Society of Chemistry 2020 |