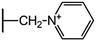Open Access Article
Open Access ArticleRevealing electronic features governing hydrolysis of cephalosporins in the active site of the L1 metallo-β-lactamase†
Elena O. Levina ab,
Maria G. Khrenova
ab,
Maria G. Khrenova *ac,
Andrey A. Astakhovad and
Vladimir G. Tsirelson
*ac,
Andrey A. Astakhovad and
Vladimir G. Tsirelson ae
ae
aFederal Research Centre “Fundamentals of Biotechnology” of the Russian Academy of Sciences, Moscow, Russia. E-mail: khrenova.maria@gmail.com
bMoscow Institute of Physics and Technology, Dolgoprudny, Russia
cLomonosov Moscow State University, Moscow, Russia
dJoint Institute for Nuclear Research, Dubna, Russia
eMendeleev University of Chemical Technology of Russia, Moscow, Russia
First published on 27th February 2020
Abstract
The QM/MM simulations followed by electron density feature analysis are carried out to deepen the understanding of the reaction mechanism of cephalosporin hydrolysis in the active site of the L1 metallo-β-lactamase. The differences in reactivity of ten similar cephalosporin compounds are explained by using an extended set of bonding descriptors. The limiting step of the reaction is characterized by the proton transfer to the nitrogen atom of the cephalosporin thiazine ring accompanied with formation of the C4![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C3 double bond in its N–C4–C3 fragment. The temporary N⋯H–Ow hydrogen bond, which is formed in the transition state of the limiting step of the reaction was recognized as a key atomic interaction governing the reactivity of various cephalosporins. Non-local real-space bonding descriptors show that different extent of localization of electron lone pair at N atom in the transition state affect the reactivity of compounds: smaller electron localization is typical for the less reactive species. In particular, the Fermi hole analysis shows how exchange electron correlation in the N⋯H–Ow fragment control electron lone pair localization. Delocalization tensor, linear response kernel and source function indicate that features of electron delocalization in the N–C4–C3 fragment of cephalosporins in the transition state complexes determine the differences in C4–C3 bond for substrates with high and low rate constants. The C4–C3 bond of the N–C4–C3 fragment at the transition state is similar to that of the preceding intermediate for the less reactive species and resembles the features of the enzyme–product complex for more reactive compounds. The power and limitations of the descriptors applied for solving the problem are discussed and the generality of approach is stressed.
C3 double bond in its N–C4–C3 fragment. The temporary N⋯H–Ow hydrogen bond, which is formed in the transition state of the limiting step of the reaction was recognized as a key atomic interaction governing the reactivity of various cephalosporins. Non-local real-space bonding descriptors show that different extent of localization of electron lone pair at N atom in the transition state affect the reactivity of compounds: smaller electron localization is typical for the less reactive species. In particular, the Fermi hole analysis shows how exchange electron correlation in the N⋯H–Ow fragment control electron lone pair localization. Delocalization tensor, linear response kernel and source function indicate that features of electron delocalization in the N–C4–C3 fragment of cephalosporins in the transition state complexes determine the differences in C4–C3 bond for substrates with high and low rate constants. The C4–C3 bond of the N–C4–C3 fragment at the transition state is similar to that of the preceding intermediate for the less reactive species and resembles the features of the enzyme–product complex for more reactive compounds. The power and limitations of the descriptors applied for solving the problem are discussed and the generality of approach is stressed.
1. Introduction
Enzymes are complex finely tuned machines that efficiently perform certain chemical reactions.1 The rate constants may vary dramatically depending on the particular substrate involved in enzymatic reaction. It is still an open question, what particular features of the substrates govern their reactivity in the active site of an enzyme.1–4 Existing experimental techniques are able to register the difference in reactivity of a series of similar compounds although they cannot explain its origin. The molecular modeling and quantum chemistry are the proper tools that shed light on this point. Analysis of electron density5 is able to locate specific inter- and intramolecular interactions in the chemical systems while various bonding descriptors allow one to analyze and quantify the features of particular chemical interactions.6–23 Recently we have demonstrated24–26 that there are certain key interactions among a great number of all interatomic interactions in the active site of enzyme that mainly determine the observed macroscopic property, the steady-state rate constant. We pointed out that these key interactions can be defined at the stationary points of the reaction path on the potential energy surface (PES) from quantum mechanics/molecular mechanic (QM/MM) approach27,28 combined with subsequent electron-density analysis.Molecular modeling in combination with electron-density analysis is already used for organic reaction studies. Equilibrium geometry configurations and corresponding calculated electron densities of reagents, intermediates, transition states and products of chemical reactions are analyzed by various approaches as QTAIM (Quantum Theory of Atoms in Molecules)29–41 or conceptual DFT (Density Functional Theory)23,36,42–44 as well as diverse bonding descriptors.33–37,45,46 Current studies of enzymatic reactions47–49 also demonstrate an enhanced interest in the application of such combined methods in biochemistry. For example, the Fukui function interpreted the residue–residue interactions in biomolecular systems simulated by QM/MM method,47 electrostatic potential allowed to identify regions of electrophilic/nucleophilic attack in the QM/MM structural models,48,49 etc. Thus, here we aim to systematically examine the applicability of various available bonding descriptors in the QM/MM models of enzymatic reactions.
We focus on the following issues: (i) what electronic features of key interactions are responsible for different reactivity of similar substrates in the active site of a particular enzyme? (ii) What electronic features and related bonding descriptors allow to quantitatively characterize the progress of such reactions?
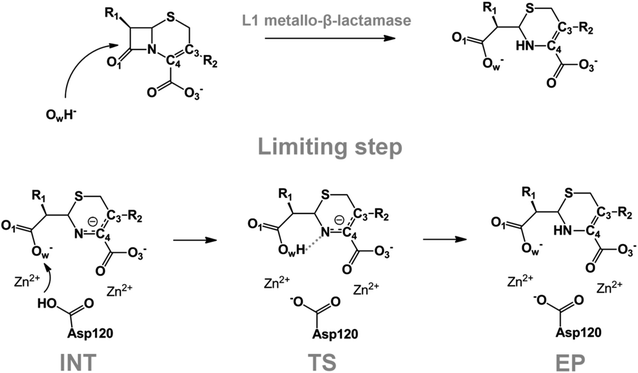
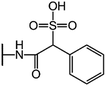
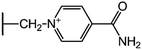
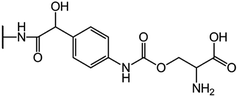
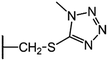
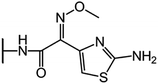
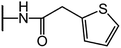
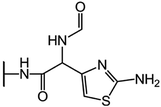
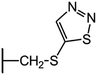
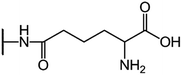
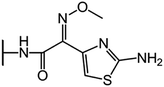
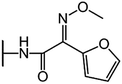
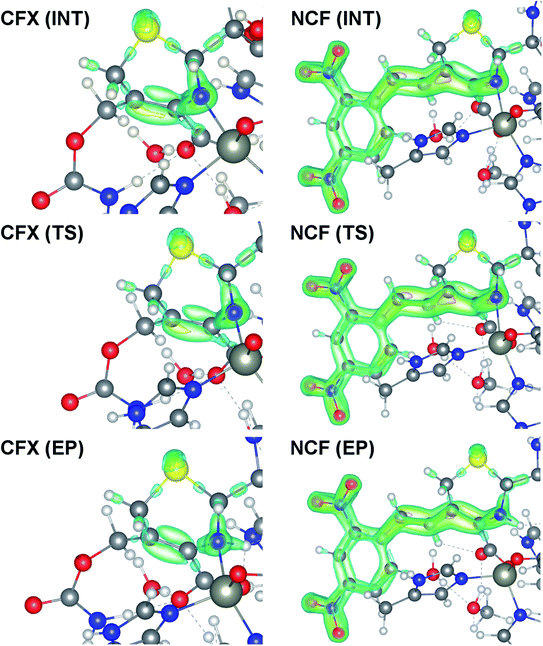
We examine below cephalosporin hydrolysis induced by L1 metallo-β-lactamase (L1 MβL). This bacterial enzyme is responsible for destruction of β-lactam antibiotics50,51 that is one of the known reasons of bacterial resistance.52,53 This chemical reaction exhibits outstanding mechanism (Fig. 1).54–56 Typically, proton transfer happens with low energy barrier along the hydrogen bond in enzymatic reactions.57,58 Here, the proton is transferred from the carboxylate group of catalytic aspartate to the nitrogen atom of the substrate forming temporary O–H covalent bond at the transition state of the limiting step (Fig. 1).54
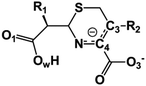
We utilize molecular models obtained via QM/MM approach together with the detailed electron density study to follow the progress of this reaction in a set of 10 similar systems. Those are composed of the L1 MβL and various cephalosporin compounds differing in their reactivity in the active site of the selected enzyme.59,60 We focus on the limiting stage of the reaction and discriminate the electronic features determining the reactivity of compounds. We analyze the key interaction (the temporary hydrogen bond formed in the transition state suggested in ref. 24) and electronic features in the N–C4–C3 fragment of cephalosporins to establish the influence of conjugated system (Fig. 1) on this interaction. Finally, we formulate how these features are related to each other and affect the observed reaction rate constant.
2. Methodology
We utilize the two-step methodology to study electronic features governing the reactivity of 10 cephalosporins in the active site of L1 MβL. First, the QM/MM approach is utilized to obtain equilibrium geometry configurations on the potential energy surface corresponding to the reaction intermediates (minima) and transitions states (saddle points). Second, we explicitly reveal the electronic features in the active sites of the complexes. We apply the QTAIM5,61 and other advanced bonding descriptors: source function,11,62 Fermi hole,15,63 electron delocalization indices,16 delocalization tensor,64 condensed linear response kernel23 to analyze the QM part of each system, i.e. its active site. The basic information about these bonding descriptors is summarized in Table 2; more information is given in the ESI.†We consider cephalosporin antibiotics with rate constants from 1.1 to 80 s−1 (Table 1).59,60 The electronic structure analysis is carried out for stationary points on PES obtained in the QM/MM simulations. The structures of intermediates, transition states and products at the limiting step were taken from our previous study.24 Each QM subsystem included cephalosporin, two Zn2+ ions and amino acid residues (Tyr32, His116, His118, Asp120, His121, His196, Ser221, His263) in the active site of L1 MβL, atoms of catalytic OwH− ion, performing the nucleophilic attack, and two water molecules (see Fig. S1†). The QM subsystems were described at the PBE0-D3/6-31G** level of DFT using the NWChem program package,65–67 while the MM parts (included protein and solvation water shell) were modeled with AMBER force field parameters.68 The electronic embedding scheme was applied assuming contributions of the partial charges from all MM atoms to one-electron part of QM Hamiltonian. Other details of QM/MM computational protocol are presented in ref. 54.
The electron densities in the QM subsystems were calculated at stationary points on the PES obtained in the QM/MM calculations. The environmental effects of the MM subsystem were included explicitly by adding terms to the one-electron part of the QM Hamiltonian corresponding to the interactions of the partial atomic charge of the MM atoms with the QM subsystem. The QTAIM analysis5 and the bonding descriptor calculations were performed using Multiwfn program.69 More computational details can be found in the ESI.†
3. Results and discussion
The role of electronic features in the active sites of 10 cephalosporin – L1 MβL complexes and influence of the immediate and distant surrounding on the bonding picture along the limiting step of reaction (INT → TS → EP) (Fig. 1) is examined below in detail. The non-covalent atomic interactions in the INT, TS and EP systems were located using the QTAIM criteria, namely the existence of the bond path, i.e. bond critical point (bcp) and two corresponding gradient lines, between atoms.6 Characteristics of main atomic interactions in the enzyme–substrate complexes are collected and discussed in the ESI.† We focus further on the two pivotal processes happening at the limiting step: proton transfer, which occur with formation of the key atomic interaction, temporary N⋯H–Ow hydrogen bond in the TS, and bond transformations in the N–C4–C3 fragment of the substrate (Fig. 1). The complexity of these processes assumes usage of diverse bonding descriptors to reveal the impact of electronic structure features and effects of surrounding on the chemical bonding and the rate constants of cephalosporin hydrolysis by the L1 MβL.3.1. The proton transfer in terms of bonding characteristics
The significance of TS intramolecular N⋯H–Ow hydrogen bond (see Fig. 1) in the cephalosporin hydrolysis is established in our recent studies.24–26 We found that electron density, kinetic and potential energy densities, atomic source function and other electron-density based descriptors calculated at bcp of this H-bond correlate with the experimental hydrolysis rate constants, kcat.24–26 It allows us to consider this H-bond as a key atomic interaction responsible for reactivity of the substrates. At that, atomic source function, SF, and its relative form, SF%,11 calculated at the N⋯H–Ow bcp in TS complexes show the best correlation with kcat values among other studied descriptors.24 Therefore, we study more deeply the influence of atomic surrounding on the N⋯H–Ow hydrogen bond by the analysis of atomic source function contributions to the ρ(rb)N⋯H from the entire active site in the TS complexes, see Table 3. The SF% contribution from all atoms of the substrate is being larger than 70%. The core of cephalosporin (all atoms in a cephalosporin molecule excluding R1 and R2 substituting groups) contributes to ρ(rb)N⋯H 55–62% depending on the particular compound (Table 3) and the other part comes from the substituents R1 and R2 (Fig. 1). The impacts of the neighboring amino acids, water molecules and zinc cations are much lower and do not exceed 15% for each of these species. The atomic source contributions to ρ(rb)N⋯H for the same substituents (R1 or R2) are similar for the compounds with different properties (Table S1†). This is in line with the idea of chemical transferability of the atomic groups: we may expect that similar groups will give similar electron density contributions to the ρ(rb)N⋯H.62,70| Descriptor | Expression | Meaning |
|---|---|---|
| Ellipticity of electron density (ε) | 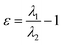 , where λ1 and λ2 are negative eigenvalues of the Hesse matrix of electron density (|λ2| < |λ1|) , where λ1 and λ2 are negative eigenvalues of the Hesse matrix of electron density (|λ2| < |λ1|) |
It is a measure of the axial symmetry deviation of electron density along the bond path; indicates existence of the π component of chemical bonds61 |
| Source/influence function (SF) | 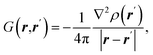 where ρ(r) is electron density at point r and ∇2ρ(r) is its Laplacian where ρ(r) is electron density at point r and ∇2ρ(r) is its Laplacian |
SF represents the influence of electron density curvature in point r′ on electron density at point r11,62 |
| Atomic source function | 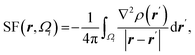 where Ωi is i-th QTAIM zero-flux atomic basin where Ωi is i-th QTAIM zero-flux atomic basin |
Atomic SF measures total influence of i atom on the electron density at point r.11 The percentage form of SF70 is 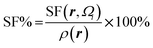 |
| Fermi hole | 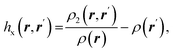 where ρ2(r,r′) is the electron pair density where ρ2(r,r′) is the electron pair density |
Fermi hole71,72 expresses the decrease in probability of finding electron with spin σ at a point r′ while the reference electron of the same spin is at a position r. It measures spatial localization of the electron of given spin σ |
| Electron delocalization index | 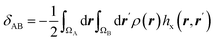 |
Electron delocalization index shows the number of electron pairs spreading out between basins of A and B atoms16,17 |
| Delocalization tensor density (DTD) | 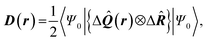 where Ψ0 is the ground-state many-electron wave function of a system; where Ψ0 is the ground-state many-electron wave function of a system; 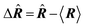 is the fluctuations of the total electron position operator, is the fluctuations of the total electron position operator, 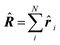 , relative to its mean value 〈R〉; , relative to its mean value 〈R〉; 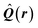 is a local analog of is a local analog of 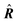 (local electron position operator)64 (local electron position operator)64 |
DTD evaluates the contribution of spatial fluctuations of Q(r) at the point r to the total fluctuations of the center of masses R of electron subsystem. DTD expresses the contribution of small space volume near r to the total electron delocalization resulting from various physical effects (position quantum uncertainty of each particle; mutual correlations in electron motion, etc) |
| Condensed linear response kernel (CLRK) | 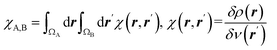 is the linear response of electron density at point r to variation of external potential at point r′; ΩA and ΩB are atomic basins of A and B atoms, respectively23 is the linear response of electron density at point r to variation of external potential at point r′; ΩA and ΩB are atomic basins of A and B atoms, respectively23 |
It measures propensity of electron density in the atomic basin, ΩA, to flow towards atomic basin, ΩB, induced by the difference in the electric potential between these basins.73 CLRK reflects influence of the changes of the nuclei configuration in molecular systems to changes in electron density |
| SF(core)% | SF(R1)% | SF(R2)% | SF(Ai)% | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| S | C3 | C4 | N | H | Ow | O1 | O3 | ||||
| CFX | 61.8 | 11.6 | 3.7 | 5.8 | 3.7 | 5.1 | 0.2 | −11.4 | 31.4 | 15.2 | 6.9 |
| CFS | 67.5 | 6.9 | 2.8 | 6.0 | 2.6 | 5.0 | 0.8 | −10.6 | 34.3 | 13.6 | 5.6 |
| CF0 | 67.1 | 6.8 | 3.2 | 6.2 | 3.2 | 4.9 | −0.8 | −10.2 | 32.7 | 14.5 | 6.1 |
| CFP | 65.4 | 8.0 | 2.2 | 6.2 | 3.4 | 4.9 | −0.1 | −13.1 | 34.9 | 15.5 | 6.2 |
| NCF | 67.5 | 8.5 | 3.5 | 6.0 | 2.8 | 7.9 | −2.1 | −12.2 | 32.5 | 16.6 | 8.3 |
| CFR | 62.6 | 8.9 | 3.3 | 6.7 | 4.7 | 5.6 | −6.0 | −17.0 | 36.6 | 16.4 | 8.8 |
| CF3 | 60.3 | 9.4 | 3.7 | 6.7 | 4.0 | 4.9 | −6.8 | −12.8 | 31.0 | 17.5 | 7.2 |
| CFL | 60.4 | 8.6 | 3.8 | 6.7 | 4.9 | 5.0 | −8.6 | −16.2 | 34.6 | 17.2 | 8.7 |
| CFT | 56.5 | 10.6 | 4.3 | 7.6 | 5.3 | 5.4 | −14.8 | −15.4 | 30.7 | 20.3 | 9.5 |
| CFU | 55.9 | 10.8 | 4.5 | 7.9 | 4.9 | 6.1 | −16.0 | −12.2 | 26.5 | 21.2 | 9.8 |
However, the N and OwH atomic fragments, which form the N⋯H–Ow bond in TS complexes, are not chemically transferable, as is usually observed for hydrogen bonds of close length.11 The electron density contributions to the ρ(rb)N⋯H from the N and OwH groups vary significantly for the substrates with different reactivity in spite of close N⋯H–Ow bond lengths (ΔRN⋯H = 0.2 Å, ΔRN–Ow = 0.2 Å). The difference between the highest and the lowest SF(OwH)% values amounted to 9.4%, the range for the SF(N)% is even larger and reaches 16.8%, see Table 3. This difference in SF values highlights the dissimilarities in the N⋯H–Ow bond nature in the TS complexes of cephalosporins despite close N⋯H bond lengths.
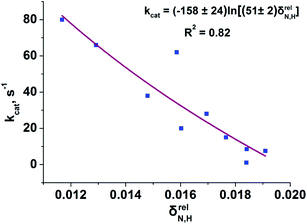
To reveal the influence of delocalization of the lone pair of N atom (see Fig. 1) on the features of N⋯H–Ow bonds in TS complexes and reactivity of the cephalosporins, we analyzed relative delocalization indices, 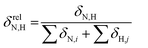 (see ESI† for definition) (Fig. 2). The δrelN,H expresses the ratio of number of electrons delocalized between N and H atoms and all other atomic basins in the TS complexes. The higher δrelN,H value the more electrons are delocalized between N and H atoms. It was found, that δrelN,H indices in TS complexes correlate with the kcat values (Fig. 2): cephalosporins with high kcat values have less delocalized electrons along the N⋯H–Ow bond than those with low kcat. This indicates the role of N electron lone pair delocalization in the N⋯H fragment in the transition state on the rate of hydrolysis.
(see ESI† for definition) (Fig. 2). The δrelN,H expresses the ratio of number of electrons delocalized between N and H atoms and all other atomic basins in the TS complexes. The higher δrelN,H value the more electrons are delocalized between N and H atoms. It was found, that δrelN,H indices in TS complexes correlate with the kcat values (Fig. 2): cephalosporins with high kcat values have less delocalized electrons along the N⋯H–Ow bond than those with low kcat. This indicates the role of N electron lone pair delocalization in the N⋯H fragment in the transition state on the rate of hydrolysis.
The interrelation of SF(N)% and δrelN,H with kcat values originates from the internal link between these descriptors:11 the atomic source function and delocalization indices values are complied with each other for similar systems. Other essential fact is that delocalization indices for some molecules correlate with the Lewis basicity constants.74 From chemical viewpoint, correlation of δrelN,H with kcat means that in the transition state of the limiting step substrates with low kcat values (and high δrelN,H values) shows higher Lewis basicity than substrates with high kcat values. Recalling the definition of basicity as capability of electron pair donation,75 we conclude that interpretation in terms of Lewis basicity supports the observed features of N⋯H bonding.
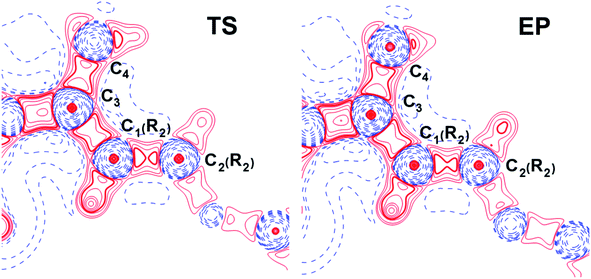
Fermi hole (see Table 2) originates in Pauli exclusion principle and measures spatial localization of the electron with given spin relatively to a reference same-spin electron. Electron delocalization indices are expressed through the electron Fermi hole (see eqn (6) in ESI†).76 Therefore, it is fruitful to compare the spatial details of the Fermi hole distribution in the region of the N⋯H–Ow bond for the reference electron placed at the N⋯H bcp. Fig. 3 compares two substrates with high kcat values (CFT and CFU), two substrates with low kcat values (CFP and CFX) and two substrates with high and low kcat values (CFU and CFX). The almost identical Fermi hole distribution near N atoms for substrates with close catalytic rate constants is remarkable. Isolines around N atom are close to each other both in CFU–CFT and CFP–CFX pairs (Fig. 3a and b). Fig. 3c demonstrates that the Fermi hole is more compact and locates around N atom for substrate with high kcat value and is more extended along hydrogen bond for substrate with low kcat values (Fig. 3c). Moreover, this behavior is also observed for all other considered complexes.
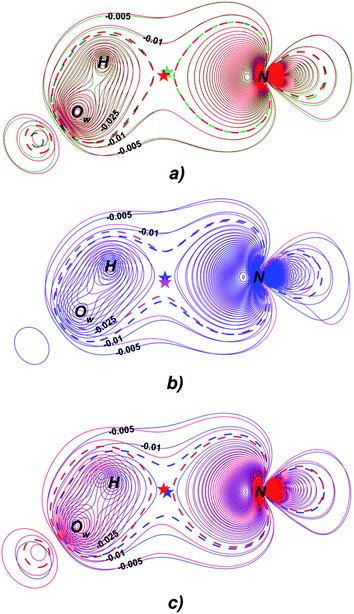 | ||
| Fig. 3 Distribution of the Fermi holes pairwise laid one on another in the plane of N⋯H–Ow bond for substrates with (a) high kcat – CFU (red) and CFT (green); (b) low kcat – CFP (pink) and CFX (blue); (c) high and low kcat – CFU (red) and CFX (blue). In each case the reference electron is placed at N⋯H bcp (bcp positions are marked by stars). Isolines are in interval −0.4 ÷ 0.0 a.u. with a 0.005 a.u. step. Bold dashed isolines correspond to the −0.015 a.u. Distribution of the Fermi holes for the other cephalosporins is given in the ESI (Fig. S3†). | ||
Fermi hole also provides information about electron pair localization. Expanded Fermi hole distribution in the N⋯H–Ow bond for TS complexes of substrates with low kcat values shows that electron lone pair of N atom stronger delocalize along N⋯H bond comparing with cephalosporins with high rate constants. One can say that proton transfer process is slow insofar as electron lone pair of N atom spreads towards H–Ow fragment.
Thus, the reactivity of cephalosporins is controlled by the N electron lone pair delocalization in the N⋯H–Ow fragment in the transition state of the limiting reaction step. The high delocalization of N electron lone pair towards H–Ow group in the N⋯H–Ow fragment makes hydrolysis of cephalosporins by L1 MβL slow. The Fermi hole analysis showed how electronic exchange in the N⋯H–Ow fragment is responsible for different reactivity of cephalosporins when hydrolyzing by the L1 MβL.
3.2. Analysis of the C3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e001.gif) C4 double bond formation
C4 double bond formation
The double bond formation between the C4 and C3 atoms is another significant phenomenon that occurs in the cephalosporins at the limiting stage (Fig. 1). To study the π character of C4–C3 bond in the INT, TS and EP complexes, the QTAIM bond ellipticity indices, ε, along the C4–C3 bond path were computed (see Fig. 4, 5 and S4†). Their remarkable asymmetry in case of INT complexes reflects the existence of carbanion,77 caused by the delocalized electron lone pair between the N and C3 atoms. This feature is preserved for TS structures of cephalosporins with low kcat values. For substrates with high rate constants nearly bell-shaped ε profiles are observed (Fig. 4). In the EP complexes the bond ellipticity maxima (εmax) are close to the C4 atoms. This shift in εmax position signals about completion of double bond formation. The asymmetry of ε profiles for EP complexes are caused by chemically non-equivalent substituting groups at the C3 and C4 atoms. The electron-withdrawing carboxylate group at the C4 atom provides the charge transfer to the C4 atomic basin.
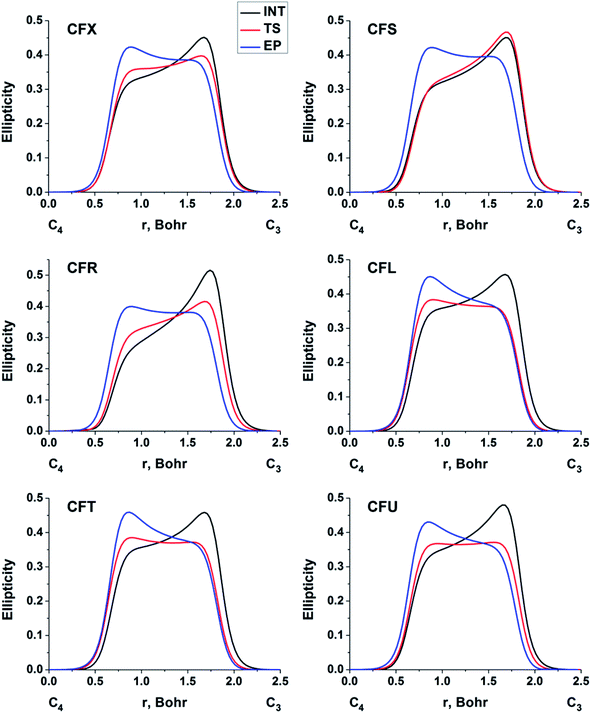 | ||
| Fig. 4 The bond ellipticity index profiles along the C4–C3 bond path for the INT, TS and EP structures in case of substrates with low (CFX, CFS), medium (CFR) and high (CFL, CFT, CFU) rate constants. Profiles for the other cephalosporins are given in ESI (Fig. S4†). | ||
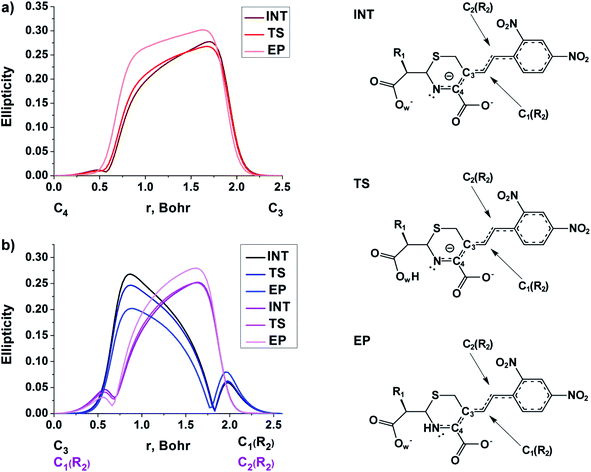 | ||
| Fig. 5 The bond ellipticity profiles along the (a) C4–C3, C3–C1(R2) and C1(R2)–C2(R2), (b) bond paths for the INT, TS and EP structures in case of NCF. | ||
We conclude that the significant feature of C4![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C3 bond formation for cephalosporins with high kcat values is similarity of the bonds between C3 and C4 atoms in the TS and EP complexes. The opposite is true for substrates with low kcat values: C4–C3 bond in the TS structures is similar to that in the INT complexes.
C3 bond formation for cephalosporins with high kcat values is similarity of the bonds between C3 and C4 atoms in the TS and EP complexes. The opposite is true for substrates with low kcat values: C4–C3 bond in the TS structures is similar to that in the INT complexes.
At the same time, the ε profiles in NCF considerably differ from the ε profiles of other considered compounds (Fig. 5a). NCF has long conjugated π-system in the R2 substituting group, see Table 1, Fig. 5b. This suggests dissimilar type of electron delocalization in the N–C4–C3 fragment for NCF and other cephalosporins. Nevertheless, due to the semi-local nature of the ellipticity index, its profiles fail to manifest effects of extensive electron delocalization in chemical bond picture. Therefore, to study electron delocalization in the N–C4–C3 fragment in more detail and to reveal the influence of the conjugated bonds in R2 on the C4–C3 bond in the NCF complexes, we applied the electron delocalization tensor D (see the ESI,† eqn (7)–(9)),64 which is a quantitative measure of uncertainty in electrons' positions and reflects various physical effects: from quantum uncertainty in position of each particle to mutual correlations in electron motion. The major eigenvalue of delocalization tensor density D(r), λ1(r), expresses delocalization magnitude along the direction of maximum electron delocalization in a system. A continuous domain in the distribution of λ1(r) in the N–C4–C3 area is the typical feature of INT and TS structures (at least at one side of 6-membered ring), see Fig. 6. EP complexes of substrates without conjugated bonds in R2 exhibit isolated domains in the C4–C3 and N–C4 bond regions (Fig. 6, left panel). It signals about completion of double bond formation. In the EP structure of NCF the isolated domains in the distribution of λ1(r) along conjugated system are absent. Delocalization of electrons gradually increases in the transition from INT to EP complexes (Fig. 6b). This feature may be compared to the changes in the bond ellipticity along the C4–C3 bond paths for INT, TS and EP structures of NCF (Fig. 5a).
The influence of conjugated bonds in R2 in the NCF complexes on the C4–C3 bond features was studied by the source function, G(r,r′) (see ESI† for definition).11 The C4–C3 bcp was treated as a reference point. The source function local maxima at the C1(R2)–C2(R2) bond become higher for the EP structure (Fig. 7) in comparison with the TS complex. It illustrates increased influence of C1(R2)–C2(R2) chemical bond on the ρ(rb)C4–C3 value. Therefore, the SF analysis in combination with delocalization tensor study of NCF complexes implies, that changes in electron delocalization in the C1(R2)–C2(R2) fragment predominantly affect features of C4![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C3 bond formation during the INT → EP reaction step.
C3 bond formation during the INT → EP reaction step.
 | ||
| Fig. 7 The source function G(r,r′) (see ESI† for definition) for TS and EP complexes of NCF plotted in the plane of C3–C1(R2)–C2(R2) atoms. The C4–C3 bcp was regarded as a reference point. The solid red and broken blue lines represent positive and negative contours, correspondingly. The contour lines range from −500 to 1200 a.u. All contour lines are drawn at intervals of ±100 a.u., except the additional 24 contours in range from −10 to 10 a.u. (each new value is equal to the half of the previous one). The changes in the C1(R2)–C2(R2) bond region are marked by a bold line. | ||
We conclude, that features of electron delocalization in the N–C4–C3 fragment in cephalosporins plays pivotal role in the double C4![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C3 bond formation at the limiting step of reaction. They lead to differences in C4–C3 bonds in the TS complexes for substrates with high and low kcat values. First of all, these differences are reflected in the bond ellipticity profiles along C4–C3 bond path. However, correct interpretation of ε profiles demands the non-local bonding description. Delocalization tensor and source function revealed how electron delocalization in the conjugated bond system of cephalosporins in the TS structures influences the reactivity of these compounds in the active site of the L1 MβL.
C3 bond formation at the limiting step of reaction. They lead to differences in C4–C3 bonds in the TS complexes for substrates with high and low kcat values. First of all, these differences are reflected in the bond ellipticity profiles along C4–C3 bond path. However, correct interpretation of ε profiles demands the non-local bonding description. Delocalization tensor and source function revealed how electron delocalization in the conjugated bond system of cephalosporins in the TS structures influences the reactivity of these compounds in the active site of the L1 MβL.
3.3. Relationship between the proton transfer and the double bond formation
The linear response kernel (CLRK) χN,B (where B = C3, C4, see eqn (11) in ESI†) for the N–C4–C3 fragment in the TS complexes of cephalosporins allows to have a close look of the cumulative impact of the close and distant effects in the proton transfer and C4![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C3 double bond formation on the rate constants of cephalosporin hydrolysis by L1 MβL. The CLRK matrix elements χN,B (Fig. 8) reflect the response of electron density of N atom upon a perturbation in the external potential δν (i.e. infinitesimal nucleus shift) at one of the atoms of C4–C3–R2 fragment (i.e. B = C4, C3 and atoms of the R2 substituting group) of cephalosporins in TS structures. The χN,C3 and χN,C4 values are higher for cephalosporins with low catalytic rate constants in comparison with the substrates with high kcat values (Fig. 8a). Since linear response function is associated with electron delocalization in the molecular system,73 one can conclude that higher χN,C3 and χN,C4 values indicate higher delocalization in the N–C4–C3 fragment. In other words, high electron delocalization in the N–C4–C3 fragment in the TS complexes leads to lower reactivity of cephalosporins. Recall that the N electron lone pair delocalization in the H⋯N fragment also influences the rate constants of cephalosporin hydrolysis (see Section 3.2): the faster the proton transfer and double bond formation are, the smaller delocalization in the H⋯N–C4–C3 fragment in TS complexes of cephalosporins is.
C3 double bond formation on the rate constants of cephalosporin hydrolysis by L1 MβL. The CLRK matrix elements χN,B (Fig. 8) reflect the response of electron density of N atom upon a perturbation in the external potential δν (i.e. infinitesimal nucleus shift) at one of the atoms of C4–C3–R2 fragment (i.e. B = C4, C3 and atoms of the R2 substituting group) of cephalosporins in TS structures. The χN,C3 and χN,C4 values are higher for cephalosporins with low catalytic rate constants in comparison with the substrates with high kcat values (Fig. 8a). Since linear response function is associated with electron delocalization in the molecular system,73 one can conclude that higher χN,C3 and χN,C4 values indicate higher delocalization in the N–C4–C3 fragment. In other words, high electron delocalization in the N–C4–C3 fragment in the TS complexes leads to lower reactivity of cephalosporins. Recall that the N electron lone pair delocalization in the H⋯N fragment also influences the rate constants of cephalosporin hydrolysis (see Section 3.2): the faster the proton transfer and double bond formation are, the smaller delocalization in the H⋯N–C4–C3 fragment in TS complexes of cephalosporins is.
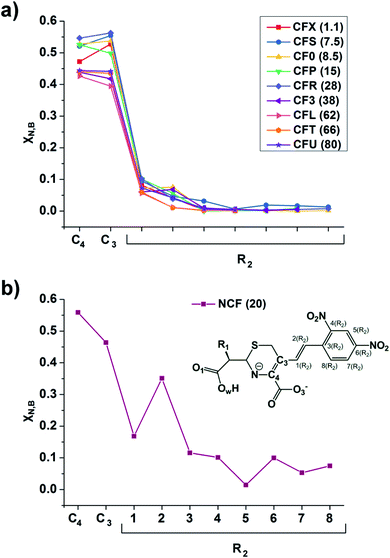 | ||
| Fig. 8 The linear response elements χN,B (see the ESI,† eqn (11)) between the proton and various atoms of C4–C3–R2 fragment (see Fig. 1 and Table 1) of cephalosporins except NCF (a) and NCF (b) in the TS structures. The kcat values for each of substrates are given in parenthesis. | ||
Additionally, the CLRK analysis of the TS structure of NCF reveals influence of long conjugated bond system in the R2 substituting group on the delocalization of lone pair electrons of N atom. The maxima and minima positions at R2 correspond to the mesomeric active and passive atoms, respectively (Fig. 8b). This result supports conclusions obtained through delocalization tensor and source function analysis (Section 3.2).
To summarize, the delocalization of N atom electron lone pair along H⋯N–C4–C3 fragment governs the process of proton transfer in cephalosporin hydrolysis at the limiting step of reaction. The more lone pair localizes at N atom in TS complexes, the faster hydrolysis reaction is. On the contrary, high delocalization of lone electron pair of N atom in the H⋯N–C4–C3 fragment of transition state structures leads to the low rate constants of cephalosporin hydrolysis by L1 MβL.
4. Conclusions
We demonstrated that the reaction mechanism in the active site of enzyme and the origin of different reactivity of a set of similar compounds can be deeply studied and interpreted using the QM/MM simulations followed by modern electron-density based bonding analysis. We considered the practically important reaction mechanism of hydrolysis of cephalosporin compounds by L1 metallo-β-lactamase. The set of considered compounds has the same core and different substituents that affect their reactivity. We have already showed24 that the temporary N⋯H–Ow hydrogen bond formed in the transition state of limiting step of reaction in these enzymatic complexes acts as a key atomic interaction governing the reactivity of cephalosporins. Here we deepen the understanding of the reaction mechanism by analysis of the non-local real-space distributed bonding descriptors.Fermi hole and delocalization indices analysis demonstrate that exchange electron correlation in the N⋯H–Ow fragment influence greatly the different reactivity of cephalosporins in the reaction with L1 MβL. It is determined by different localization of electron lone pair at N atom for cephalosporins with high and low reaction rate constants. The less lone pair localizes at the N atom in transition state complexes, the slower hydrolysis reaction is. This is in line with the previously found dependency between the reactivity of compounds and the atomic influence to the electron density at the bond critical point of the N⋯H–Ow hydrogen bond24 as the source/influence function and delocalization indices are related descriptors.11
Analysis of the alternation of the N–C4–C3 fragment along the limiting stage demonstrate the following features. The C3–C4 bond at the transition state is similar to that of the preceding intermediate for the less reactive species and resembles the features of the enzyme–product complex for more reactive compounds. Bond critical point characteristics for thiazine ring of cephalosporins do not show correlation with kcat values. At the same time, the electron delocalization in the N–C4–C3 fragment of thiazine ring strongly affects hydrolytic activity of cephalosporins. It was established by delocalization tensor analysis combined with condensed linear response kernel study. We suppose that the applied protocol of bonding analysis has the general character and it is applicable to other enzymatic reactions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Russian Science Foundation (project #18-74-10056). The research is carried out using the equipment of the shared research facilities of HPC computing resources at Lomonosov Moscow State University.78References
- R. Wolfenden and M. J. Snider, The depth of chemical time and the power of enzymes as catalysts, Acc. Chem. Res., 2001, 34, 938 CrossRef CAS PubMed.
- V. Vaissier Welborn and T. Head-Gordon, Computational design of synthetic enzymes, Chem. Rev., 2018, 119, 6613 CrossRef PubMed.
- P. Dušan and K. S. C. Lynn, Molecular modeling of conformational dynamics and its role in enzyme evolution, Curr. Opin. Struct. Biol., 2018, 52, 50 CrossRef PubMed.
- J. P. Richard, Protein flexibility and stiffness enable efficient enzymatic catalysis, J. Am. Chem. Soc., 2019, 141, 3320 CrossRef CAS PubMed.
- R. F. W. Bader, Atoms in molecules. Quantum Theory, Clarington Press, Oxford, 1994 Search PubMed.
- S. A. Glover, Comment on “Penicillin's catalytic mechanism revealed by inelastic neutrons and quantum chemical theory” by Z. Mucsi, G. A. Chass, P. Ábrányi-Balogh, B. Jójárt, D.-C. Fang, A. J. Ramirez-Cuesta, B. Viskolczc and I. G. Csizmadia, Phys. Chem. Chem. Phys., 2013, 15, 20447, Phys. Chem. Chem. Phys., 2019, 21, 18012 RSC.
- M. K. Thomsen, C. Gatti and J. Overgaard, Probing cyclic π-electron delocalization in an imidazol-2-ylidene and a corresponding imidazolium salt, Chem.–Eur. J., 2018, 24, 4973 CrossRef CAS PubMed.
- W. Scherer, P. Sirsch, D. Shorokhov, M. Tafipolsky, G. S. McGrady and E. Gullo, Valence charge concentrations, electron delocalization and β-agostic bonding in d0 metal alkyl complexes, Chem.–Eur. J., 2003, 9, 6057 CrossRef CAS PubMed.
- A. D. Becke and K. E. Edgecombe, A simple measure of electron localization in atomic and molecular systems, J. Chem. Phys., 1990, 92, 5397 CrossRef CAS.
- A. Savin, The electron localization function (ELF) and its relatives: interpretations and difficulties, J. Mol. Struct.: THEOCHEM, 2005, 727, 127 CrossRef CAS.
- C. Gatti, The Source function descriptor as a tool to extract chemical information from theoretical and experimental electron densities, in Electron Density and Chemical Bonding II. Structure and Bonding, ed. D. Stakle, Springer, Berlin, Heidelberg, 2012, pp. 1–93 Search PubMed.
- C. Gatti and L. Bertini, The local form of the source function as a fingerprint of strong and weak intra-and intermolecular interactions, Acta Crystallogr. A, 2004, 60, 438 CrossRef PubMed.
- J. Overgaard, B. Schiøtt, F. K. Larsen and B. B. Iversen, The charge density distribution in a model compound of the catalytic triad in serine proteases, Chem.–Eur. J., 2001, 7, 3756 CrossRef CAS.
- C. Gatti, G. Macetti, R. J. Boyd and C. F. Matta, An electron density source-function study of DNA base pairs in their neutral and ionized ground states, J. Comput. Chem., 2018, 39, 1112 CrossRef CAS PubMed.
- R. F. W. Bader, A. Streitwieser, A. Neuhaus, K. E. Laidig and P. Speers, Electron delocalization and the Fermi hole, J. Am. Chem. Soc., 1996, 118, 4959 CrossRef CAS.
- R. F. W. Bader and M. E. Stephens, Spatial localization of the electronic pair and number distributions in molecules, J. Am. Chem. Soc., 1975, 97, 7391 CrossRef CAS.
- X. Fradera, M. A. Austen and R. F. W. Bader, The Lewis model and beyond, J. Phys. Chem. A, 1999, 103, 304 CrossRef CAS.
- J. Geier, Spatial shape of electron delocalization: structure of the laplacian of the negative exchange−correlation density, J. Phys. Chem. A, 2006, 110, 9273 CrossRef CAS PubMed.
- F. R. Wagner, M. Kohout and Y. Grin, Direct space decomposition of ELI-D: interplay of charge density and pair-volume function for different bonding situations, J. Phys. Chem. A, 2008, 112, 9814 CrossRef CAS PubMed.
- M. Kohout, K. Pernal, F. R. Wagnerand and Y. Grin, Electron localizability indicator for correlated wavefunctions. I. Parallel-spin pairs, Theor. Chem. Acc., 2004, 112, 453 Search PubMed.
- P. de Silva and C. Corminboeuf, Simultaneous visualization of covalent and noncovalent interactions using regions of density overlap, J. Chem. Theory Comput., 2014, 10, 3745 CrossRef CAS PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-García, A. J. Cohen and W. Yang, Revealing noncovalent interactions, J. Am. Chem. Soc., 2010, 132, 6498 CrossRef CAS PubMed.
- P. Geerlings, S. Fias, Z. Boisdenghien and F. de Proft, Conceptual DFT: chemistry from the linear response function, Chem. Soc. Rev., 2014, 43, 4989 RSC.
- M. G. Khrenova, A. V. Krivitskaya and V. G. Tsirelson, The QM/MM-QTAIM approach reveals the nature of the different reactivity of cephalosporins in the active site of L1 metallo-β-lactamase, New J. Chem., 2019, 43, 7329 RSC.
- M. G. Khrenova and V. G. Tsirelson, The N⋯H hydrogen bond strength in the transition state at the limiting step determines the reactivity of cephalosporins in the active site of L1 metallo-β-lactamase, Mendeleev Commun., 2019, 29, 492 CrossRef CAS.
- M. G. Khrenova, A. V. Tomilko and V. G. Tsirelson, Electronic steric factors in the active site of metallo-β-lactamase and reactivity of cephalosporin antibiotics, Moscow Univ. Chem. Bull., 2019, 74, 106 CrossRef.
- H. M. Senn and W. Thiel, QM/MM methods for biomolecular systems, Angew. Chem. Int. Ed., 2009, 48, 1198 CrossRef CAS PubMed.
- A. Warshel and M. Levitt, Theoretical studies of enzymic reactions: dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme, J. Mol. Biol., 1976, 103, 227 CrossRef CAS PubMed.
- M. Izadyar, M. Gholizadeh, M. Khavani and M. R. Housaindokht, Quantum chemistry aspects of the solvent effects on 3,4-dimethyl-2,5-dihydrothiophen-1,1-dioxide pyrolysis reaction, J. Phys. Chem. A, 2013, 117, 2427 CrossRef CAS PubMed.
- H. Torabifard and A. Fattahi, Mechanisms and kinetics of thiotepa and tepa hydrolysis: DFT study, J. Mol. Model., 2012, 18, 3563 CrossRef CAS PubMed.
- F. Teixeira, R. Mosquera, A. Melo, C. Freire and M. N. D. Cordeiro, Driving forces in the sharpless epoxidation reaction: a coupled AIMD/QTAIM study, Inorg. Chem., 2017, 56, 2124 CrossRef CAS PubMed.
- T. N. Hooper, M. Garçon, A. J. White and M. R. Crimmin, Room temperature catalytic carbon–hydrogen bond alumination of unactivated arenes: mechanism and selectivity, Chem. Sci., 2018, 9, 5435 RSC.
- A. Rey, A. Espinosa Ferao and R. Streubel, Quantum chemical calculations on CHOP derivatives—spanning the chemical space of phosphinidenes, phosphaketenes, oxaphosphirenes, and COP− isomers, Molecules, 2018, 23, 3341 CrossRef PubMed.
- L. Domingo, Molecular electron density theory: a modern view of reactivity in organic chemistry, Molecules, 2016, 21, 1319 CrossRef PubMed.
- Á. Sánchez-González, F. J. Martín-Martínez and J. A. Dobado, The role of weak interactions in lignin polymerization, J. Mol. Model., 2017, 23, 80 CrossRef PubMed.
- V. Tognetti, S. Bouzbouz and L. Joubert, A theoretical study of the diastereoselective allylation of aldehydes with new chiral allylsilanes, J. Mol. Model., 2017, 23, 5 CrossRef PubMed.
- M. R. Ryzhikov, V. A. Slepkov, S. G. Kozlova and S. P. Gabuda, Evolution of chemical bonding and electron density rearrangements during D3h→ D3d reaction in monolayered TiS2: a QTAIM and ELF study, J. Comput. Chem., 2014, 35, 1641 CrossRef CAS PubMed.
- M. R. Nechay, N. M. Gallup, A. Morgenstern, Q. A. Smith, M. E. Eberhart and A. N. Alexandrova, Histone deacetylase 8: characterization of physiological divalent metal catalysis, J. Phys. Chem. B, 2016, 120, 5884 CrossRef CAS PubMed.
- O. H. O. Brovarets’ and D. M. Hovorun, The nature of the transition mismatches with Watson–Crick architecture: the G*·T or G·T* DNA base mispair or both? A QM/QTAIM perspective for the biological problem, J. Biomol. Struct. Dyn., 2015, 33, 925 CrossRef PubMed.
- C. L. Firme, S. J. Garden, N. C. de Lucas, D. E. Nicodem and R. J. Correa, Theoretical study of photochemical hydrogen abstraction by triplet aliphatic carbonyls by using density functional theory, J. Phys. Chem. A, 2013, 117, 439 CrossRef CAS PubMed.
- B. Ośmiałowski, Proton transfer reaction and intermolecular interactions in associates of 2,5-dihydroxy-1,8-naphthyridine, J. Mol. Model., 2012, 18, 1633 CrossRef PubMed.
- P. Geerlings and F. de Proft, Conceptual DFT: the chemical relevance of higher response functions, Phys. Chem. Chem. Phys., 2008, 10, 3028 RSC.
- H. M. T. Nguyen, J. Peeters, M. T. Nguyen and A. K. Chandra, Use of DFT-based reactivity descriptors for rationalizing radical reactions: a critical analysis, J. Phys. Chem. A, 2004, 108, 484 CrossRef CAS.
- A. K. Chandra and M. T. Nguyen, Use of DFT-based reactivity descriptors for rationalizing radical addition reactions: applicability and difficulties, Faraday Discuss., 2007, 135, 191 RSC.
- D. A. Saez, S. Vogt-Geisse, R. Inostroza-Rivera, T. Kubař, M. Elstner, A. Toro-Labbé and E. Vöhringer-Martinez, The effect of the environment on the methyl transfer reaction mechanism between trimethylsulfonium and phenolate, Phys. Chem. Chem. Phys., 2016, 18, 24033 RSC.
- S. Calvo-Losada and J. J. Quirante, Exploring the regioselectivity in the cycloaddition of azides to alkynes catalyzed by dinuclear copper clusters (Cu2AAC reaction) using the topologies of ∇2ρ(r) and ∇∇2ρ(r), J. Mol. Model., 2017, 23, 337 CrossRef CAS PubMed.
- H. W. Qi, M. Karelina and H. J. Kulik, Quantifying Electronic Effects in QM and QM/MM Biomolecular Modeling with the Fukui Function, Acta Phys.-Chim. Sin., 2017, 34, 81 Search PubMed.
- R. N. Devi, M. G. Khrenova, S. Israel, C. Anzline, A. A. Astakhov and V. G. Tsirelson, Testing the ability of rhodanine and 2,4-thiazolidinedione to interact with the human pancreatic alpha-amylase: electron-density descriptors complement molecular docking, QM, and QM/MM dynamics calculations, J. Mol. Model., 2017, 23, 252 CrossRef PubMed.
- C. U. Ibeji, G. F. Tolufashe, T. Ntombela, T. Govender, G. E. Maguire, G. Lamichhane, H. G. Kruger and B. Honarparvar, The catalytic role of water in the binding site of l, d-transpeptidase 2 within acylation mechanism: a QM/MM (ONIOM) modelling, Tuberculosis, 2018, 113, 222 CrossRef CAS PubMed.
- M.-R. Meini, L. I. Llarrull and A. J. Vila, Overcoming differences: the catalytic mechanism of metallo-β-lactamases, FEBS Lett., 2015, 589, 3419 CrossRef CAS PubMed.
- A. I. Karsisiotis, C. F. Damblon and G. C. Roberts, A variety of roles for versatile zinc in metallo-β-lactamases, Metallomics, 2014, 6, 1181 RSC.
- B. Peng, H. Li and X. Peng, Proteomics approach to understand bacterial antibiotic resistance strategies, Expert Rev. Proteomics, 2019, 16, 829 CrossRef CAS PubMed.
- J. L. Anaya-López, J. E. López-Meza and A. Ochoa-Zarzosa, Bacterial resistance to cationic antimicrobial peptides, Crit. Rev. Microbiol., 2013, 39, 180 CrossRef PubMed.
- M. G. Khrenova and A. V. Nemukhin, Modeling the transient kinetics of the L1 metallo-β-lactamase, J. Phys. Chem. B, 2018, 122, 1378 CrossRef CAS PubMed.
- D. Xu, H. Guo and Q. Cui, Antibiotic deactivation by a dizinc β-lactamase: mechanistic insights from QM/MM and DFT studies, J. Am. Chem. Soc., 2007, 129, 10814 CrossRef CAS.
- J. D. Garrity, A. L. Carenbauer, L. R. Herron and M. W. Crowder, Metal binding Asp-120 in metallo-β-lactamase L1 from Stenotrophomonas maltophilia plays a crucial role in catalysis, J. Biol. Chem., 2004, 279, 920 CrossRef CAS PubMed.
- H. Ishikita and K. Saito, Proton transfer reactions and hydrogen-bond networks in protein environments, J. R. Soc. Interface, 2014, 11, 20130518 CrossRef PubMed.
- J. H. Wang, Directional character of proton transfer in enzyme catalysis, Proc. Natl. Acad. Sci. U.S.A., 1970, 66, 874 CrossRef CAS PubMed.
- M. W. Crowder, T. R. Walsh, L. Banovic, M. Pettit and J. Spencer, Overexpression, purification, and characterization of the cloned metallo-β-Lactamase L1 from Stenotrophomonas maltophilia, Antimicrob. Agents Chemother., 1998, 42, 921 CrossRef CAS PubMed.
- A. Felici and G. Amicosante, Kinetic analysis of extension of substrate specificity with Xanthomonas maltophilia, Aeromonas hydrophila, and Bacillus cereus metallo-beta-lactamases, Antimicrob. Agents Chemother., 1995, 39, 192 CrossRef CAS PubMed.
- J. R. Cheeseman, M. T. Carroll and R. F. W. Bader, The mechanics of hydrogen bond formation in conjugated systems, Chem. Phys. Lett., 1988, 143, 450 CrossRef CAS.
- R. F. W. Bader and C. Gatti, A Green's function for the density, Chem. Phys. Lett., 1998, 287, 233 CrossRef CAS.
- R. F. W. Bader, S. Johnson, T.-H. Tang and P. L. A. Popelier, The electron pair, J. Phys. Chem., 1996, 100, 15398 CrossRef CAS.
- A. A. Astakhov and V. G. Tsirelson, Spatially resolved characterization of electron localization and delocalization in molecules: extending the Kohn-Resta approach, Int. J. Quant. Chem., 2018, 118, e25600 CrossRef.
- M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. Van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, NWChem: a comprehensive and scalable open-source solution for large scale molecular simulations, Comput. Phys. Commun., 2010, 181, 1477 CrossRef CAS.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: the PBE0 model, J. Chem. Phys., 1999, 110, 6158 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, A second generation force field for the simulation of proteins, nucleic acids, and organic molecules, J. Am. Chem. Soc., 1995, 117, 5179 CrossRef CAS.
- T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- C. Gatti, F. Cargnoni and L. Bertini, Chemical information from the source function, J. Comput. Chem., 2003, 24, 422 CrossRef CAS PubMed.
- W. L. Luken and J. C. Culberson, Localized orbitals based on the Fermi hole, Theor. Chim. Acta, 1984, 66, 279–293 CrossRef CAS.
- M. Kohout, Electron pairs in position space, in The Chemical Bond II, ed. D. Michael and P. Mingos, Springer, Cambridge, 2015, pp. 119–168 Search PubMed.
- B. Mussard and J. G. Ángyán, Relationships between charge density response functions, exchange holes and localized orbitals, Comput. Theor. Chem., 2015, 1053, 44 CrossRef CAS.
- E. V. Bartashevich, E. A. Troitskaya and V. G. Tsirelson, The N⋯I halogen bond in substituted pyridines as viewed by the source function and delocalization indices, Chem. Phys. Lett., 2014, 601, 144 CrossRef CAS.
- M. B. Smith and J. March, March's advanced organic chemistry: reactions, mechanisms, and structure, John Wiley & Sons, 2007 Search PubMed.
- R. F. W. Bader, C. F. Matta and F. Cortés-Guzmán, Where to draw the line in defining a molecular structure, Organometallics, 2004, 23, 6253 CrossRef CAS.
- W. Scherer, P. Sirsch, D. Shorokhov, G. S. McGrady, S. A. Mason and M. G. Gardiner, Valence-shell charge concentrations and electron delocalization in alkyllithium complexes: negative hyperconjugation and agostic bonding, Chem.–Eur. J., 2002, 8, 2324 CrossRef CAS.
- V. V. Voevodin, A. S. Antonov, D. A. Nikitenko, P. A. Shvets, S. I. Sobolev, I. Y. Sidorov, K. S. Stefanov, V. V. Voevodin and S. A. Zhumatiy, Supercomputer Lomonosov-2: large scale, deep monitoring and fine analytics for the user community, Supercomput. Front. Innov., 2019, 6, 4 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra10649a |
| This journal is © The Royal Society of Chemistry 2020 |