Open Access Article
Open Access ArticleStructural study and large magnetocaloric entropy change at room temperature of La1−x□xMnO3 compounds
C. Henchiri a,
T. Mnasrib,
A. Benaliac,
R. Hamdiad,
E. Dhahri
a,
T. Mnasrib,
A. Benaliac,
R. Hamdiad,
E. Dhahri a,
M. A. Valentec and
B. F. O. Costae
a,
M. A. Valentec and
B. F. O. Costae
aLaboratoire de Physique Appliquée, Faculté des Sciences de Sfax, Université de Sfax, B. P. 802, Sfax 3018, Tunisia
bResearch Unit UPIM, Faculty of Science, University of Gafsa, 2112, Tunisia
cI3N, Physics Department, University of Aveiro, 3810-193 Aveiro, Portugal
dCollege of Health and Life Sciences, Hamad Bin Khalifa University, Doha, Qatar
eCFisUC, Physics Department, University of Coimbra, RuaLarga, 3004-516 Coimbra, Portugal
First published on 26th February 2020
Abstract
In this study, our central focus is to investigate the magnetocaloric characteristics of a La1−x□xMnO3 (x = 0.1, 0.2 and 0.3) series prepared by a sol–gel technique published in Prog. Mater. Sci., 93, 2018, 112–232. The crystallographic study revealed that our compounds crystallize in a rhombohedral structure with R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c. Ferromagnetic (FM) and paramagnetic (PM) characters were detected from the variation in magnetization as a function of magnetic fields at different temperatures. The second order transition was verified from the Arrott plots (M2 vs. (μ0H/M)), where the slopes have a positive value. In order to verify the second order, we traced the variation of magnetization vs. temperature at different magnetic fields for x = 0.2. This revealed a ferromagnetic (FM)–paramagnetic (PM) transition when temperature increases. Relying on the indirect method while using the Maxwell formula, we determined the variation in the entropy (−ΔSM) as a function of temperature for different magnetic fields for the three samples. We note that all the studied systems stand as good candidates for magnetic refrigeration with relative cooling power (RCP) values of around 131.4, 83.38 and 57.26 J kg−1 with magnetic fields below 2 T, respectively. Subsequently, the magnetocaloric effect was investigated by a phenomenological model for x = 0.2. The extracted data confirm that this phenomenological model is appropriate for the prediction of magnetocaloric properties. The study also demonstrated that this La0.8□0.2MnO3 system exhibits a universal behaviour.
c. Ferromagnetic (FM) and paramagnetic (PM) characters were detected from the variation in magnetization as a function of magnetic fields at different temperatures. The second order transition was verified from the Arrott plots (M2 vs. (μ0H/M)), where the slopes have a positive value. In order to verify the second order, we traced the variation of magnetization vs. temperature at different magnetic fields for x = 0.2. This revealed a ferromagnetic (FM)–paramagnetic (PM) transition when temperature increases. Relying on the indirect method while using the Maxwell formula, we determined the variation in the entropy (−ΔSM) as a function of temperature for different magnetic fields for the three samples. We note that all the studied systems stand as good candidates for magnetic refrigeration with relative cooling power (RCP) values of around 131.4, 83.38 and 57.26 J kg−1 with magnetic fields below 2 T, respectively. Subsequently, the magnetocaloric effect was investigated by a phenomenological model for x = 0.2. The extracted data confirm that this phenomenological model is appropriate for the prediction of magnetocaloric properties. The study also demonstrated that this La0.8□0.2MnO3 system exhibits a universal behaviour.
1. Introduction
Today, materials that have better properties have long drawn the interest and attention of researchers.1 For this reason, there is a spate of interest in manganites because of their promising properties such as the colossal magnetoresistance (CMR), magnetocaloric effect of exchange (EME), Griffiths phase.2–8 Perovskite-lanthanum manganites proved to be potential candidates for magnetic refrigeration at different temperature ranges.9–12 Nanomaterials are expected to bring new features to the magnetocaloric effect (MCE) and magnetic properties compared to bulk materials.13,14We note that there are numerous complex physical phenomena of manganites such as the charge ordering (CO). Swain et al. have shown that this phenomenon exists in nanomaterials. This is due to the planar defects and surface spin disorder, i.e., the deformation within a nanomaterial disturbs the AFM arrangement of the spins in the nucleus. Consequently, the state of the charge order is suppressed. However, for a bulk material the deformation is small as compared to a nanomaterial and that it has no impact on the AFM core and therefore, the appearance of the charge ordering (CO). More the suppression of the charge ordering (CO) in the materials can be due to the eruption of the spatial symmetry.15 The charge ordering (CO) can be demonstrated from the electrical measurements. In the system Pr0.5Ca0.5MnO3,16 the suppression of CO is explained by the melting of long-range charge ordering behavior due to surface spin disorder and induced lattice strain effects in PCMO manganite system.
Electric field controlled magnetism is an exciting area of condensed matter physics. It allows the exploration of device applications with ultra-low energy consumption compared to the conventional current-controlled or magnetic field-controlled devices. Numerous studies were performed by Swain et al. to demonstrate the electric field-controlled magnetoresistance (MR) in a three layer structure composed of La0.67Sr0.33MnO3 (LSMO) (40 nm)/SrTiO3 (10 nm)/LSMO (10 nm) grown via the pulsed laser deposition technique on a 500 μm thick BaTiO3 (001) monocrystalline substrate (BTO). The jumps observed in the temperature-dependent magnetization curve around the structural phase transitions of BTO ensure the magnetoelectric coupling mediated by the stress between the LSMO and BTO layers. A significant change in the MR of this structure in the applied electric fields shows no dependence on polarity. Results are linked to magnetoelectric coupling mediated by network constraint in ferromagnetic/ferroelectric LSMO BTO heterostructures.17
Today, a new technology called magnetic cooling offers several advantages, including higher cooling efficiency, lower power consumption, lower noise level, much compactness, and higher safety for the environment. This new technology rests on a phenomenon called “magnetocaloric effect” (MCE). Recent discoveries in materials science disclosed that colossal ECM values can be observed in many materials (manganites, ferrites, amorphous alloys, intermetallic compounds, etc.).18 The magnetocaloric effect (MCE) is a basic character of magnetic materials. It is the response of the material to the application or suppression of magnetic fields. Relying upon the isothermal magnetic data, the magnetic entropy change (ΔSM) can be assessed through the use of the standard Maxwell relation:19
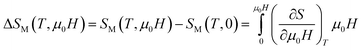 | (1) |
According to Maxwell's relation, we get
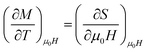 | (2) |
The extremums of the −ΔSM of our compounds are reported in the vicinity of TC, where 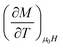 is the experimental value obtained from the M(T) curve for multiple magnetic fields (μ0H). Magnetic entropy change is provided by the following expression:
is the experimental value obtained from the M(T) curve for multiple magnetic fields (μ0H). Magnetic entropy change is provided by the following expression:
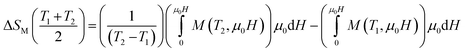 | (3) |
The entropy is connected to the relative cooling power (RCP) by the relation:20
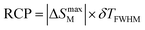 | (4) |
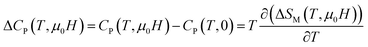 | (5) |
Features of manganites continuously have drawn the attention of multiple researchers specialized in condensed matter physics.21–26 These compounds are known for their close relations between orbital, charge, spin, and lattice degrees of freedom, which results in a diversity of their phase states and physical properties.27–30 Among the wide variety of factors specifying the properties of manganites, the most significant ones are the stoichiometry (the types of ions and their ratio) and crystal structure parameters (the mean 〈Mn–O〉 bond length and the mean 〈Mn–O–Mn〉 bond angle).
It is conventionally known that the magnetic and electronic properties of substituted manganites are specified by the eg electron bandwidth W = cos(1/2[π − 〈Mn–O–Mn〉])/〈Mn–O〉3.5.31 Compounds with a greater bandwidth W display more pronounced ferromagnetic and metallic properties (i.e., higher Curie point (TC), higher metal insulator transition temperature and lower resistivity (ρ)32–34).
This study centers around the magnetocaloric effect and Hamed model for the three compounds, x = 0.1, 0.2 and 0.3.
2. Preparation method
The sol–gel technique is the preparation method of La1−x□xMnO3 (x = 0.1, 0.2 and 0.3) from the precursors lanthanum nitrate (La(NO3)2·6H2O) and manganese nitrate (Mn(NO3)2·4H2O) up to purity 99%. The method of preparation has been well described in ref. 35.3. Results and discussion
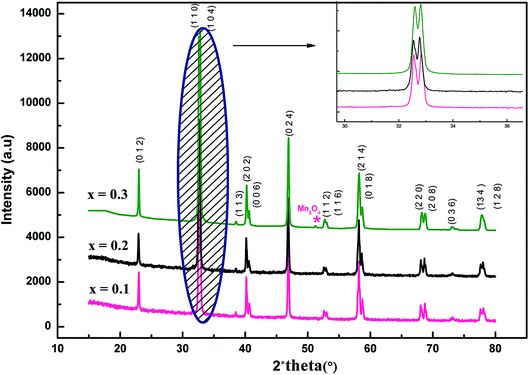
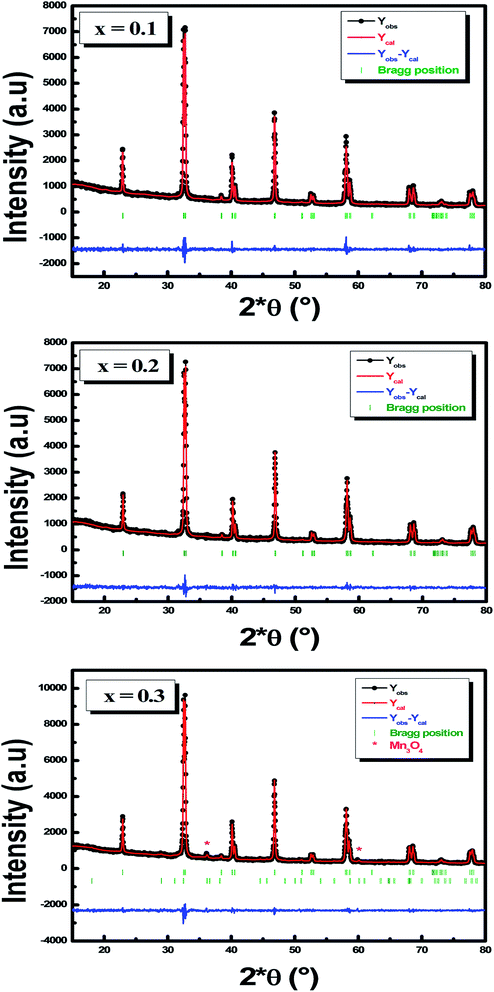
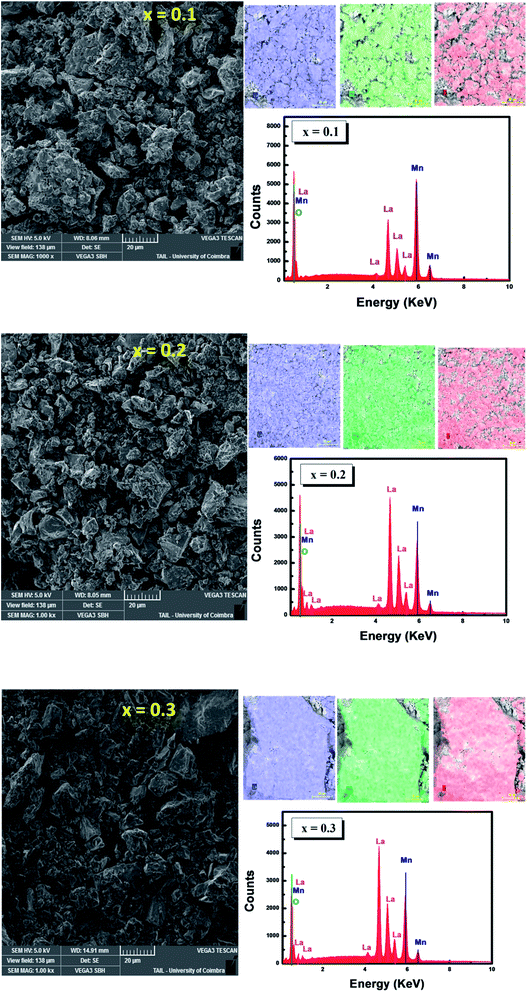
In the first step, we performed XRD analysis to verify the crystal structure of the studied samples. Powder XRD patterns of La1−x□xMnO3 (x = 0.1, 0.2 and 0.3) compounds collected at room temperature are plotted in Fig. 1. We note that our samples are of a single phase with a very small amount of Mn3O4 for x = 0.3, as found in recent studies.35 XRD data were analyzed using Rietveld refinement.36 Fig. 2 illustrates the Rietveld refinement of the XRD profiles for La1−x□xMnO3 (x = 0.1, 0.2 and 0.3) samples, with a good agreement between the observed and the calculated profiles, this is due to the excellent goodness of χ2. The analyzed data showed that our samples crystallize in the rhombohedral system with R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c. The SEM micrographs of Fig. 3 show a non-homogenous microstructure and non-uniform grain size distribution. In order to check the existence of all elements in the compound, EDX was performed. Fig. 3 shows that the energy dispersive analysis of X-ray (EDX) spectra reveals the presence of La, Mn and O elements in La1−x□xMnO3 compounds, confirming that there is no loss of any integrated element. In order to examine the distribution of detected elements, the EDX mapping of La (slate blue), Mn (green) and O (red) is checked and presents non uniform dispersion. All samples reveal the presence of the characteristic peaks of La and Mn and O elements The inset curves in Fig. 4 display the magnetic isotherms of x = 0.1, 0.2 and 0.3 samples measured with a magnetic field change from 0 to 2 T in the temperature interval of 4 K. Here, the maximum magnetization is recorded for x = 0.2 and 0.3 samples, suggesting that adiabatic magnetization and demagnetization result in the maximum order and disorder in these samples. The Arrott plots (Fig. 4) exhibit the variation of M2 vs. μ0H/M for the three compounds (x = 0.1, 0.2 and 0.3) to determine the nature of transition (first order: negative slope and second order: positive slope). We notice that these curves have a positive slope, which indicates that the transition from the FM to the PM state at the Curie temperature (TC) is a second order magnetic phase transition, according to the criteria reported by Banerjee.37
c. The SEM micrographs of Fig. 3 show a non-homogenous microstructure and non-uniform grain size distribution. In order to check the existence of all elements in the compound, EDX was performed. Fig. 3 shows that the energy dispersive analysis of X-ray (EDX) spectra reveals the presence of La, Mn and O elements in La1−x□xMnO3 compounds, confirming that there is no loss of any integrated element. In order to examine the distribution of detected elements, the EDX mapping of La (slate blue), Mn (green) and O (red) is checked and presents non uniform dispersion. All samples reveal the presence of the characteristic peaks of La and Mn and O elements The inset curves in Fig. 4 display the magnetic isotherms of x = 0.1, 0.2 and 0.3 samples measured with a magnetic field change from 0 to 2 T in the temperature interval of 4 K. Here, the maximum magnetization is recorded for x = 0.2 and 0.3 samples, suggesting that adiabatic magnetization and demagnetization result in the maximum order and disorder in these samples. The Arrott plots (Fig. 4) exhibit the variation of M2 vs. μ0H/M for the three compounds (x = 0.1, 0.2 and 0.3) to determine the nature of transition (first order: negative slope and second order: positive slope). We notice that these curves have a positive slope, which indicates that the transition from the FM to the PM state at the Curie temperature (TC) is a second order magnetic phase transition, according to the criteria reported by Banerjee.37
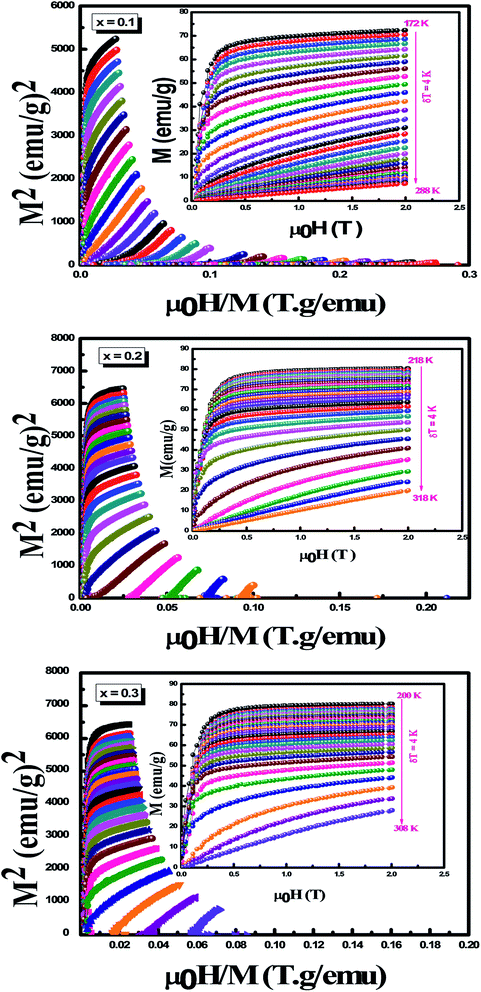 | ||
| Fig. 4 Isothermal magnetization plots M versus H of the La1−x□xMnO3 (x = 0.1, 0.2 and 0.3) series, and the inset is the Standard Arrot. | ||
In order to apply the phenomenological model,38,39 Fig. 3 depicts the variation in the magnetization M as a function of temperature at various magnetic applied fields for x = 0.2. Experimental data (symbols) were modified by the eqn (1)40 (solid line). We find that this equation well portrays the pace of magnetization, which proves the validity of this model in our case. Model parameters are presented in table in the inset Fig. 5. Furthermore, the curves M(H, T) at μ0H unveil the presence of a second order paramagnetic–ferromagnetic transition, where the magnetization varies from continuous way deduced from the increase in TC with the magnetic field.
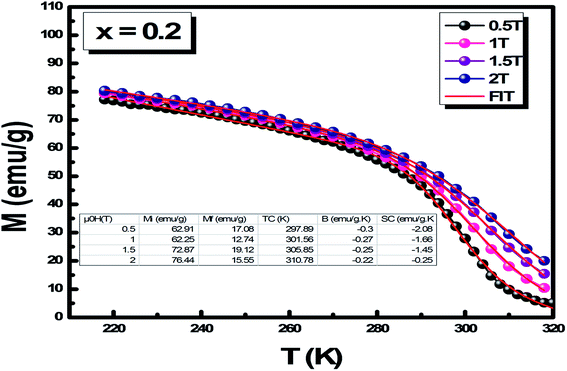 | ||
| Fig. 5 Magnetization versus temperature for La0.8□0.2MnO3. The symbols are the experimental data and the solid lines are the modeled results. | ||
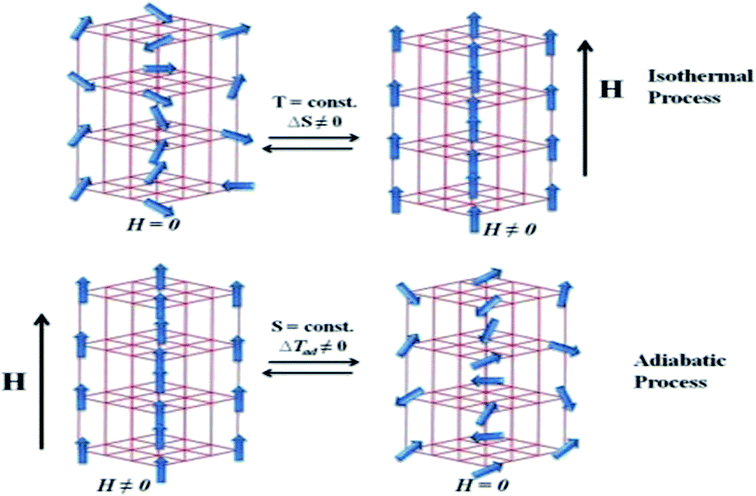
Fig. 6 portrays the schematic representation of the magnetic refrigeration cycle whose value of the change in entropy of a ferromagnetic material depends on both μ0H and T. Fig. 7 illustrates the variation in the magnetic entropy change (−ΔSM) as a function of T for different μ0H using eqn (3) for the three samples x = 0.1, 0.2 and 0.3. It increases by augmenting the value of μ0H and reaches a maximum around TC. For x = 0.2 and using eqn (5),40 we plot the theoretical entropy as a function of magnetic field for x = 0.2. We can assert that the maximum magnetic entropy is obtained around TC. Zener model was appropriate to justify the change to perovskite large magnetic entropy. This model discloses an indirect interaction between Mn3+ and Mn4+ related to the change in their ratio.41 Guo et al.42 assumed that the large magnetic entropy change in perovskite manganites could refer to the spin-lattice coupling in the magnetic ordering process, which plays an intrinsic role in additional magnetic changes.43,44
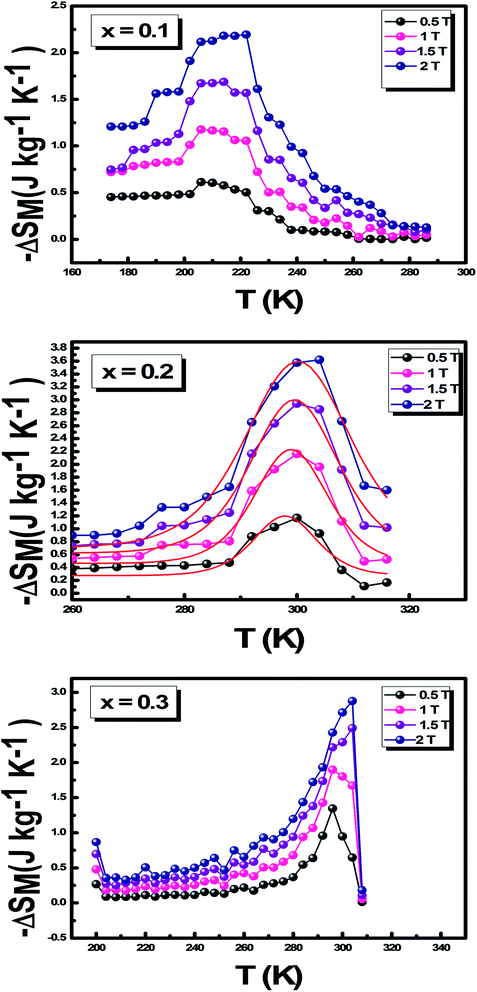 | ||
| Fig. 7 Thermal variation of the magnetic entropy (−ΔSM) of La1−x□xMnO3 (x = 0.1, 0.2 and 0.3) systems under different magnetic fields between 0.5 T and 2 T and modeled for x = 0.2. | ||
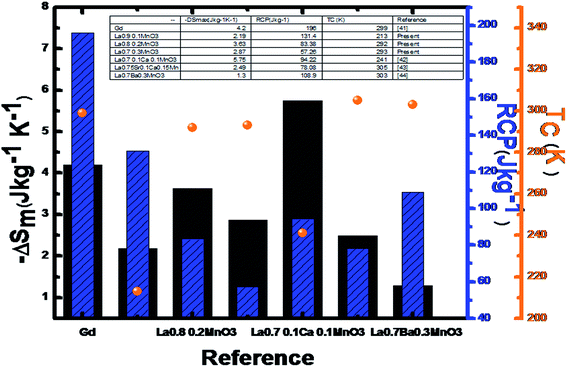
The experimental values of (−ΔSM), RCP and TC for our compound are compared to other references at 2 T, which are listed in the inset table in Fig. 8. We observe that −ΔSM increases and RCP decreases. This is explained by the effect of spin coupling, which became less important when the applied magnetic field increased. We can detect that the proposed compounds exhibit important values. The maximum values of ΔSM and RCP obtained at 2 T were compared to gadolinium Gd45 as well as several other materials reported in literature.46–48 The results are in favor of promising magnetic refrigerants in terms of application. The good value of RCP equal to 131.4 J kg−1 for x = 0.1 is due to the strong magneto-structural coupling.
Using eqn (5), we plot the experimental (−ΔCP) as a function of temperature for x = 0.1 and 0.2 in Fig. 9. Using eqn (6),40 we plot the theoretical variation of (−ΔCP) for x = 0.2 as an example. This figure demonstrates that the intersection of these curves is around TC. It is clear that (−ΔCP) is positive when TC > T and negative when TC < T.
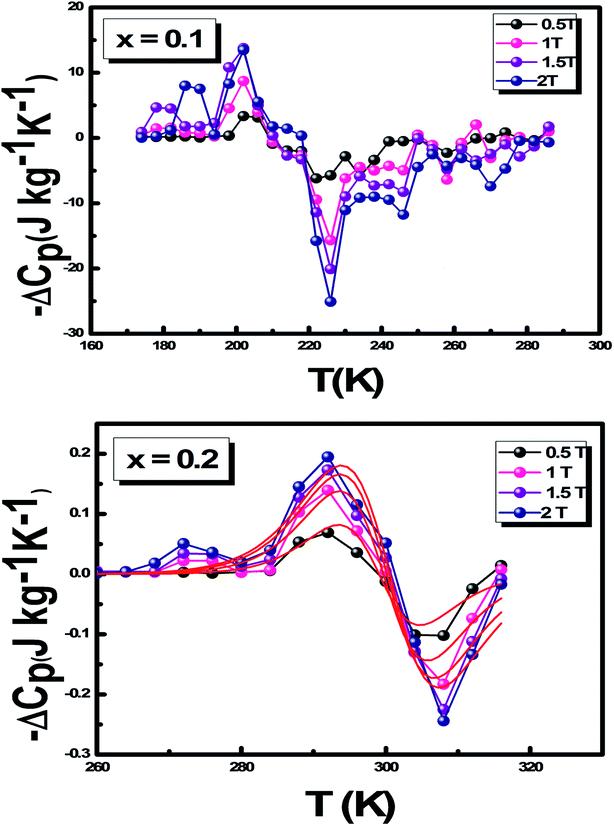 | ||
| Fig. 9 Variation in the specific heat as a function of temperature at different magnetic fields of La1−x□xMnO3 (x = 0.1 and 0.2) and modeled for x = 0.2. | ||
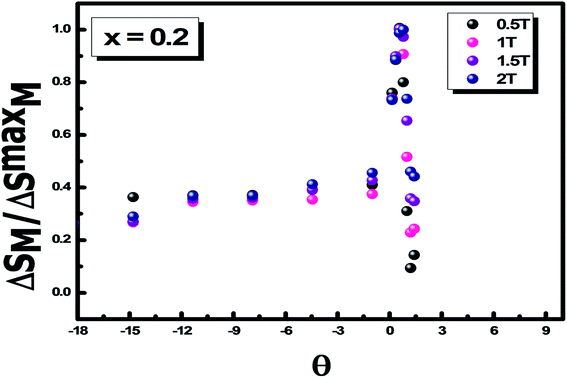
A universal behavior of ΔSM and its dependence on the field in materials with a second order transition have recently been proposed by Franco et al.,49,50 who set forward a universal behavior of −ΔSM. The phenomenological universal curve consists of the collapse of the entropy variation curves after a scaling process, regardless of the applied magnetic field. Therefore, the main hypothesis is based on the fact that if a universal curve exists, then the equivalent points of ΔSM (T) curves measured for different applied magnetic fields should collapse on the same universal curve. It is also demonstrated that these curves are unique for each class of universality.50 MCE data from different materials of the same universality class should overlap on the same curve regardless of the applied magnetic field.
This phenomenological universal curve can be established by normalizing all ΔSM(T) curves by their respective maximum value. ΔSmaxM, as a function of 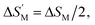 and the temperature axis are rescaled by a new parameter θ = ±1, identified by the expression:
and the temperature axis are rescaled by a new parameter θ = ±1, identified by the expression:
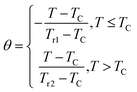 | (6) |
Fig. 10 illustrates the universal curve for x = 0.2 (as an example). We can clearly infer that all the curves collapse on a single universal curve regardless of the magnetic field, which proves the validity of the technique and suggests that the transition is of a second order.
4. Conclusion
In this study, we investigated the magnetocaloric effects of La1−x□xMnO3 (x = 0.1, 0.2 and 0.3) prepared via a sol–gel technique. We demonstrated that our samples displayed a second order transition, as implied from the Arrot plot. In order to verify the second order, we traced the variation of M vs. T at different magnetic fields for x = 0.2. This exhibited an FM–PM transition when the temperature increased. Based upon the Maxwell formula, we determined the variation in the entropy (−ΔSM) as a function of temperature for different magnetic fields for the three samples. It is noteworthy to mention that all studied systems stand as good candidates for magnetic refrigeration at about 131.4, 83.38 and 57.26 J kg−1 with magnetic fields under to 2 T, respectively. The study also proved that this La0.8□0.2MnO3 system presents a universal behaviour. After exploring the magnetocaloric effect by a phenomenological model for x = 0.2, the extracted data confirm that this phenomenological model is convenient for the prediction of magnetocaloric properties.Being a promising compound, in future studies, we aspire to further explore its additional interesting features so as to be invested in technological as well as industrial fields.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the financial support of the research project by the Tunisian Ministry of Higher Education and Scientific Research and the FCT-Portugal within the framework of Tunisian-Portuguese cooperation in the field of scientific research and technology.References
- P. T. Phong, N. V. Dang, L. V. Bau, N. M. An and In-Ja Lee, Landau mean-field analysis and estimation of the spontaneous magnetization from magnetic entropy change in La0.7Sr0.3MnO3 and La0.7Sr0.3Mn0.95Ti0.05O3, J. Alloys Compd., 2017, 698, 451–459 CrossRef CAS.
- K. Y. Wang, C. Sangregorio, J. Wiggins, J. Wiemann and J. Tang, Colossal magnetoresistance and magnetic phase transitions in bulk Nd0.7Ba0.3MnO3, J. Appl. Phys., 2000, 87, 5819–5821 CrossRef CAS.
- F. B. Jemaa, S. H. Mahmood, M. Ellouze, E. K. Hlil and F. Halouani, Structural, magnetic, magnetocaloric, and critical behavior of selected Ti-doped manganites, Ceram. Int., 2015, 41, 8191–8202 CrossRef.
- P. T. Phong, L. V. Bau, L. C. Hoan, D. H. Manh, N. X. Phuc and In-Ja Lee, Effect of B-site Ti doping on the magnetic, low-field magnetocaloric and electrical transport properties of La0.7Sr0.3Mn1−xTixO3 perovskites, J. Alloys Compd., 2016, 656, 920–928 CrossRef CAS.
- S. E. L. Kossi, S. Ghodhbane, S. Mnefgui, J. Dhahri and E. K. Hlil, The impact of disorder on magnetocaloric properties in Ti-doped manganites of La0.7Sr0.25Na0.05Mn(1−x)TixO3 (0 ≤ x ≤ 0.2), J. Magn. Magn. Mater., 2015, 395, 134–142 CrossRef CAS.
- S. Liu, Magnetocaloric effect of electron-doped manganites LaMn1−xTixO3 (0.05 ≤ x ≤ 0.2), Phys. B, 2015, 456, 227–231 CrossRef CAS.
- A. Sendil Kumar and S. Srinath, Exchange bias effect in Ti doped nanocrystalline SrFeO3−δ, AIP Adv., 2014, 4, 087144–087148 CrossRef.
- V. Dayal, V. P. Kumar, R. L. Hadimani and D. C. Jiles, Evolution of Griffith's phase in La0.4Bi0.6Mn1-xTixO3 perovskite oxide, J. Appl. Phys., 2014, 115, 17E111 CrossRef.
- H. Y. Hwang, S. W. Cheong, N. P. Ong and B. Batlogg, Spin-Polarized Intergrain Tunneling in La2/3Sr1/3MnO3, Phys. Rev. Lett., 1996, 77, 2041–2044 CrossRef CAS PubMed.
- C. N. R. Rao, R. Mahesh, A. K. Raychaudhuri and R. Mahendiran, Giant magnetoresistance, charge ordering and other novel properties of perovskite manganates, J. Phys. Chem. Solids, 1998, 59, 487–501 CrossRef CAS.
- B. C. Tofield and W. R. Scott, Oxidative nonstoichiometry in perovskites, an experimental survey; the defect structure of an oxidized lanthanum manganite by powder neutron diffraction, J. Solid State Chem., 1974, 10, 183–194 CrossRef CAS.
- N. Zhang, W. Ding, T. Tanx, W. Zhong and Y. Du, Simultaneous observation of tunnel-type GMR and intrinsic CMR in nanometer perovskite, Sci. China, Ser. A: Math., Phys., Astron., 1998, 41, 967–973 CrossRef CAS.
- L. J. S. R. D. Shull and L. H. Bennett, in Proceedings of the 6th International Cryocoolers Conference, ed. G. G. a. M. Knox, Annapolis, 1991, p. 231 Search PubMed.
- T. A. Yamamoto, M. Tanaka, Y. Misaka, T. Nakagawa, T. Nakayama, K. Niihara and T. Numazawa, Dependence of the magnetocaloric effect in superparamagnetic nanocomposites on the distribution of magnetic moment size, Scr. Mater., 2002, 46, 89–94 CrossRef CAS.
- A. Swain and V. Gorige, Irreversible Meta-Magnetic Transition in Charge Ordered Nd0.5Ca0.5MnO3 Manganite, Phys. Status Solidi B, 2019, 1800707 CrossRef.
- A. Swain, P. S. Anil Kumar and V. Gorige, Electrical conduction mechanism for the investigation of charge ordering in Pr0.5Ca0.5MnO3 manganite system, J. Magn. Magn. Mater., 2019, 485, 358–368 CrossRef CAS.
- A. Swain, K. Komatsu, M. Itoh, T. Taniyama and V. Gorige, Strain-mediated magnetic response in La0.67Sr0.33MnO3/SrTiO3/La0.67Sr0.33MnO3/BaTiO3 structure, AIP Adv., 2018, 8, 055808 CrossRef.
- V. Franco, J. S. Blázquez, J. J. Ipus, J. Y. Law, L. M. Moreno-Ramírez and A. Conde, Magnetocaloric effect: from materials research to refrigeration devices, Prog. Mater. Sci., 2018, 93, 112–232, DOI:10.1016/j.pmatsci.2017.10.005.
- K. Vitalij, V. K. Pecharsky and K. A. Gschneidner Jr, Magnetocaloric effect and magnetic refrigeration, J. Magn. Magn. Mater., 1999, 200, 44–56 CrossRef.
- K. A. Gschneidner Jr, V. K. Pecharsky and A. O. Tsokol, Recent developments in magnetocaloric materials, Rep. Prog. Phys., 2005, 68, 1479–1539 CrossRef.
- S. V. Trukhanov, I. O. Troyanchuk, M. Hervieu, H. Szymczak and K. Bärner, Phys. Rev. B: Condens. Matter, 2002, 66, 184424 CrossRef.
- S. M. Dunaevskii, Fiz. Tverd. Tela, 2004, 46(2), 193 CAS.
- J. B. Goodenough, Rep. Prog. Phys., 2004, 67, 1915 CrossRef CAS.
- E. Dagotto, New J. Phys., 2005, 7, 67 CrossRef.
- K. Dörr, J. Phys. D: Appl. Phys., 2006, 39, R125 CrossRef.
- S. V. Trukhanov, L. S. Lobanovski, A. V. Trukhanov, S. G. Zemskova and A. I. Beskrovniy, Phys. Status Solidi C, 2009, 6, 1001 CrossRef CAS.
- J. M. D. Coey, M. Viret and S. von Molnar, Adv. Phys., 1999, 48, 167 CrossRef CAS.
- E. L. Nagaev, Phys. Rep., 2001, 346, 387 CrossRef CAS.
- S. V. Trukhanov, Zh. Eksp. Teor. Fiz., 2005, 128(3), 597 (J. Exp. Theor. Phys., 2005, 101(3), 513) Search PubMed.
- S. V. Trukhanov, D. P. Kozlenko and A. V. Trukhanov, J. Magn. Magn. Mater., 2008, 320, e88 CrossRef CAS.
- M. Medarde, J. Mesot, P. Lacorre, S. Rosenkranz, P. Fischer and K. Gobrecht, Phys. Rev. B: Condens. Matter, 1995, 52(3), 9248 CrossRef CAS PubMed.
- Y. Moritomo, A. Asamitsu and Y. Tokura, Phys. Rev. B: Condens. Matter, 1995, 51, 16491 CrossRef CAS PubMed.
- Y. Moritomo, A. Asamitsu and Y. Tokura, Phys. Rev. B: Condens. Matter, 1997, 56, 12190 CrossRef CAS.
- H. Y. Hwang, T. T. M. Palstra, S. W. Cheong and B. Batlogg, Phys. Rev. B: Condens. Matter, 1995, 52, 15046 CrossRef CAS PubMed.
- C. Henchiri, R. Hamdi, T. Mnasri, M. AValente, P. R. Prezas and E. Dhahri, Structural and magnetic properties of La1−x□xMnO3 (x = 0.1; 0.2 and 0.3) manganites, 2019, DOI:10.1007/s00339-019-2980-3.
- D. B. Wiles and R. A. Young, J. Appl. Crystallogr., 1981, 14, 149–151 CrossRef CAS.
- S. K. Banerjee, On a generalized approach to first and second order magnetic transition, Phys. Lett., 1964, 12, 16–17 CrossRef.
- M. A. Hamed, Phase Transitions, 2012, 85, 106 CrossRef.
- M. A. Hamed, Mater. Lett., 2012, 82, 181 CrossRef.
- H. Gharsallah, M. Jeddi, M. Bejar, E. Dhahri and E. K. Hlil, Prediction of magnetocaloric effect using a phenomenological model in (x) La0.6Ca0.4MnO3/(1 − x)La0.6Sr0.4MnO3 composites, Appl. Phys., 2019, 125, 541 CAS.
- C. Zener, Interaction between the d shells in the transition metals, Phys. Rev., 1951, 81, 440 CrossRef CAS.
- Z. B. Guo, Y. M. Du, J. S. Zhu, H. Huang, W. P. Ding and D. Feng, Large Magnetic entropy, 1997 Search PubMed.
- P. G. Radaelli, D. E. Cox, M. Marezio, S.-W. Cheong, P. E. Schiffer and A. P. Ramirez, Simultaneous Structural, Magnetic, and Electronic Transitions in La1−xCaxMnO3 with x = 0.25 and 0.50, Phys. Rev. Lett., 1995, 75, 4488–4491 CrossRef CAS PubMed.
- V. Franco, J. S. Blázquez and A. Conde, Field dependence of the magnetocaloric effect in materials with a second order phase transition: a master curve for the magnetic entropy change, Appl. Phys. Lett., 2006, 89, 222512 CrossRef.
- Y. Xu, M. Meier, P. Das, M. R. Koblischka and U. Hartmann, Perovskite manganites: potential materials for magnetic cooling at or near room temperature, Cryst. Eng., 2002, 5, 383–389 CrossRef CAS.
- S. Ridha, D. Essebti and E. K. Hlil, Impact of Annealing Temperature on the Physical Properties of the Lanthanum Deficiency Manganites, Crystals, 2017, 7, 301 CrossRef.
- Ah. Dhahri, M. Jemmali, E. Dhahri and M. A. Valente, Structural characterization, magnetic, magnetocaloric properties and phenomenological model in manganite La0.75Sr0.1Ca0.15MnO3 compound, J. Alloys Compd., 2015, 638, 221–227 CrossRef CAS.
- V. K. Pecharsky and K. A. Gschneidner, Some common misconceptions concerning magnetic refrigerant materials, J. Appl. Phys., 2001, 90, 4614–4622 CrossRef CAS.
- V. Franco, A. Conde, V. Provenzano and R. D. Shull, Scaling analysis of the magnetocaloric effect in Gd5Si2Ge1.9X0.1 (X = Al, Cu, Ga, Mn, Fe, Co, J. Magn. Magn. Mater., 2010, 322, 218–223 CrossRef CAS.
- V. Franco, A. Conde, J. M. Romero-Enrique and J. S. Blázquez, A universal curve for the magnetocaloric effect: an analysis based on scaling relations, J. Phys.: Condens. Matter, 2008, 20, 285207 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |