Photocatalytic properties and energy band offset of a tungsten disulfide/graphitic carbon nitride van der Waals heterojunction

Abstract

Semiconductor heterojunctions have higher photocatalytic performance than a single photocatalytic material. However, the energy band offset and the photocatalytic reaction mechanism of these heterojunctions remain controversial. Here, tungsten disulfide (WS₂)/graphitic carbon nitride (GCN) heterojunction photocatalytic water splitting is investigated with the hybrid density functional method. The band structures and the density of states (DOS) indicate that the WS₂/GCN heterojunction is a type-II heterojunction, and its valence band offset and conduction band offset are 0.27 and 0.04 eV, respectively. The differential charge density distribution and the work function calculation indicate that a built-in electric field is formed in the WS₂/GCN heterojunction. The potential of the built-in electric field is 0.16 V, and its direction is from the GCN surface to the WS₂ surface. The built-in electric field separates the photogenerated electrons and the holes in space, effectively improving the photocatalytic efficiency of the WS₂/GCN heterojunction. Our work provides insights into the electronic properties and the photocatalytic hydrogen evolution mechanism of the WS₂/GCN heterojunction.

---

1. Introduction

Semiconductor photocatalytic materials can absorb solar energy for photocatalytic water splitting. This green technology is considered a promising solution for the current problems of environmental pollution and the energy crisis. TiO₂ is the earliest material used for the photocatalytic water splitting into H₂ and O₂.¹ However, TiO₂ has a wide bandgap (3.2 eV), which indicates that it can only absorb ultraviolet light, and its solar light spectrum utilization rate is only approximately 4%. Searching for a new visible-light photocatalyst has subsequently become a popular topic in the field of solar energy. In recent years, with the discovery of graphene, a large number of two-dimensional semiconductor materials have been used for photocatalytic reactions. These materials have excellent physical properties. For example, graphitic carbon nitride (GCN) not only has a large specific surface area, but it also has a suitable conduction band potential and valence band potential.² Transition metal disulfide, such as tungsten disulfide (WS₂), has a narrow bandgap (approximately 1.8 to 2.1 eV) and high carrier mobility.^3,4 These outstanding advantages enable the material to enhance its photocatalytic performance.^5–7 However, a single two-dimensional semiconductor material cannot effectively overcome the recombination of photogenerated electrons and holes, and the resultant photocatalytic efficiency is relatively low.⁸ At present, an effective solution is to design a heterojunction to reduce the recombination rate of photogenerated carriers and improve the quantum efficiency of photocatalysts.^9,10 A number of studies have reported that photocatalytic properties can be remarkably improved by constructing semiconductor heterostructures, such as phosphorene/g-C₃N₄,¹¹ α-Fe₂O₃/g-C₃N₄,¹² graphdiyne/g-C₃N₄,¹³ WO₃/g-C₃N₄,¹⁴ MoS₂/g-C₃N₄,¹⁵ g-C₃N₄/TiO₂,¹⁶ ZnIn₂S₄/WS₂,¹⁷ TiO₂/WS₂,¹⁸ etc. Recently, a semiconductor heterojunction constructed with WS₂ and GCN is found to have excellent photocatalytic properties.^19–25 Akple et al. prepared WS₂/GCN composites and achieved enhanced photocatalytic activity for H₂ production under visible light.¹⁹ Zhou et al. prepared an optimal WS₂/GCN, with the highest photocatalytic hydrogen evolution at 154 μmol h⁻¹ g⁻¹, a value 34 times higher than that of GCN.²⁰ WS₂/GCN nano heterostructures are also widely studied through experiments, but their photocatalytic water splitting mechanisms remain to be contentious. Ma et al. investigated the electronic structures of triazine-based GCN/WS₂ composites by performing first-principle calculations.²⁶ However, in their experiment, the WS₂/GCN nanocomposites appeared to have a heptazine-based GCN structure instead of a triazine-based GCN structure. Heptazine-based GCNs and triazine-based GCNs completely differ from each other in terms of crystalline and electronic structures. Thus far, no theoretical studies have been conducted on the heptazine-based WS₂/GCN heterojunction photocatalytic mechanism. Therefore, the photocatalytic mechanism of the heptazine-based WS₂/GCN heterojunction needs to be clarified through theoretical research. Building a reasonable heptazine-based WS₂/GCN heterojunction and investigating its theoretical microscopic electronic structure to reveal the photocatalytic water splitting mechanism are highly desirable.

In this study, we built heptazine-based WS₂/GCN heterojunction and calculated its energy bands and density of states (DOS) by using the HSE06 hybrid density functional approach. The charge transfer of the WS₂/GCN heterojunction was analyzed together with its work function and differential charge density. Then, the separation and mobility processes of the photogenerated electrons and the holes were investigated. A type II heterojunction photocatalytic water splitting mechanism was confirmed.

2. Computational methods

All calculations were performed with the Vienna ab initio simulation package (vasp).²⁷ Exchange correction energy was described with the generalized gradient approximation (GGA) of the PBE functional method. The DFT-D3 method with Grimme correction was employed to describe the effect of the vdW interactions.²⁸ The projector augmented wave method was adopted for the ion–electron forces. The energy cutoff was set to 520 eV, and the Monkhorst–Pack k-point mesh was set to 5 × 5 × 1. The structural optimizations converged when the energy and the forces reached 1.0 × 10⁻⁵ eV and 0.02 eV Å⁻¹ on each atom, respectively. The screened hybrid HSE06 functional method was used to obtain the accurate energy band structures.

3. Results and discussion

The 2D/2D WS₂/GCN nano heterojunction is constructed using a monolayer GCN and a monolayer WS₂. The heptazine-structured GCN is orthorhombic and belongs to the Cmc2₁ space group. The lattice constant (a = b = 7.14 Å) of the optimized monolayer GCN is extremely close to the experimental value.^2,29 WS₂ is the trigonal crystal and belongs to the P3̄m1 space group. The lattice constant (a = b = 3.18 Å) of the optimized monolayer WS₂ only has a 0.95% error relative to the experimental value (3.15 Å).³⁰ The monolayer g-C₃N₄ nanosheet of the supercell is placed on the monolayer WS₂ nanosheet of the 4 × 4 supercell as a means to build the WS₂/GCN heterojunction (Fig. 1a–c). The lattice mismatch ratio between the optimized g-C₃N₄ supercell and the WS₂ supercell is only 2.9%. The WS₂/GCN heterojunction contains a total of 90 atoms, including 16 tungsten atoms, 32 sulfur atoms, 18 carbon atoms, and 24 hydrogen atoms. By calculating the minimum value of the energy of the single-layer GCN supercell and the single-layer WS₂ supercell, the optimized lattice constant (12.54 Å) can be obtained. This value corresponds to the lattice constant of the 2D/2D WS₂/GCN heterojunction. The vacuum layer thickness of the WS₂/GCN heterojunction is set to 20 Å to eliminate the periodic influence of the contiguous layers. The calculated minimum distance between the two interfaces of the WS₂/GCN heterojunction is 3.12 Å. The calculated distance between the two interfaces of the WS₂/GCN heterojunction is extremely close to those of the other calculated GCN-based heterostructures.^31–33

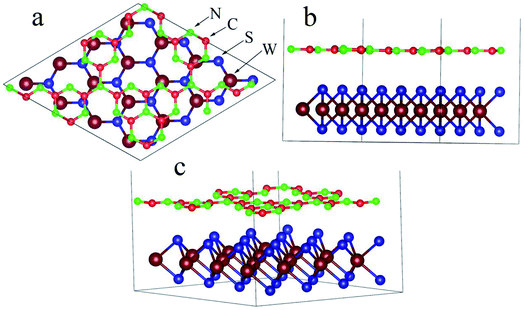Fig. 1 (a) Vertical view, (b) lateral view, and (c) three dimensional optimal WS₂/GCN heterojunction.

The C–N covalent bond lengths at the WS₂/GCN heterojunction are approximately 1.35, 1.36, 1.41, and 1.50 Å, while the W–S covalent bond lengths are 2.40 and 2.41 Å. They hardly differ from the C–N covalent bond lengths (1.33, 1.39, and 1.48 Å) in the single-layer GCN nano-sheet and from the W–S covalent bond lengths (2.41 Å) in the single-layer WS₂ nano-sheet. Therefore, the interaction is very weak between the GCN nano-sheet and the WS₂ nano-sheet.

Interface formation energy is usually used to quantitatively describe the thermodynamic stability of formed heterostructures. The formulaic expression of the formation energy of the interface between GCN and WS₂ is as follows:

E_F = E_WS2/GCN − E_WS2 − E_GCN (1)

where E_WS2/GCN, E_WS2, and E_GCN represent the total energies of the WS₂/GCN heterostructure, the single-layer GCN, and the single-layer WS₂ nanosheet, respectively. The formation energy of the WS₂/GCN heterojunction is −2.15 eV, indicating that the formation of the WS₂/GCN heterojunction is an exothermic process. The WS₂/GCN heterojunction has a stable structure in thermodynamics. The calculated interfacial formation energy per unit area is 15.8 meV Å⁻², and the value is within the interface forming energy range generated by the van der Waals interaction.³⁴ In addition, the distance at the two interfaces of the WS₂/GCN heterojunction is as high as 3.12 Å. In summary, the WS₂/GCN heterojunction is a typical van der Waals heterostructure.

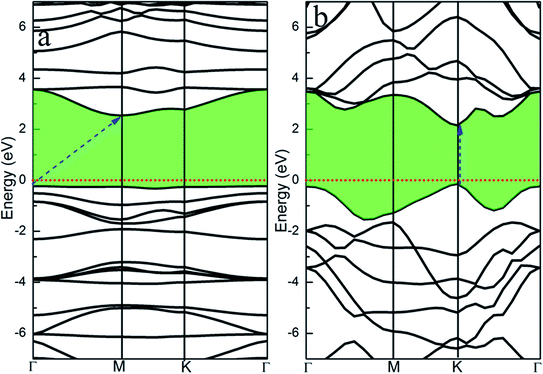
We first calculate the energy band structures of the single-layer GCN and the single-layer WS₂ to further investigate the WS₂/GCN heterojunction (Fig. 2a and b). The single-layer GCN is an indirect bandgap semiconductor with a valence band maximum (VBM) at the Γ high symmetry point and a conduction band minimum (CBM) at the M high symmetry point. The calculated indirect bandgap is 2.76 eV based on the HSE06 hybrid functional theory. The calculated result of the HSE06 hybrid functional theory is closer to the experimental value (2.7 eV) compared with that of the PBE functional method at 1.36 eV. The calculated monolayer WS₂ is a direct bandgap semiconductor, and the CBM and the VBM are both located at the high symmetry point of K. The direct bandgap of the monolayer WS₂ calculated by HSE06 hybrid functional approach is 2.28 eV, while the result calculated by the PBE functional approach is 1.59 eV. The bandgap of the monolayer WS₂ measured experimentally is approximately 2.0 eV.³⁵ The comparison indicates that the monolayer WS₂ bandgap calculated by the HSE06 hybrid functional approach is closer to the experimental value and more precise than that calculated by the PBE functional.

Fig. 2 Energy band structures of monolayer (a) GCN and (b) WS₂ nanosheet.

The project energy band structure of the WS₂/GCN heterojunction is calculated by the HSE06 hybrid functional approach (Fig. 3). The WS₂/GCN heterojunction is a typical indirect bandgap semiconductor structure and its bandgap is 2.34 eV (Fig. 3a). The CBM of the heterojunction is located at the Γ point, by contrast, the VBM is not located at the high-symmetry point, and instead positioned between the high-symmetry points of M and K. Different from the energy band structures of the monolayer GCN and the monolayer WS₂, the energy band structure of the WS₂/GCN heterojunction is not just a simple addition of the energy band structures of GCN and WS₂. The CBM and the VBM of the WS₂/GCN heterojunction have both changed. At this point, the van der Waals interactions between the monolayer GCN and the WS₂ nanosheet are affected by the energy band structure of the WS₂/GCN heterojunction. In the conduction band region, the lowest energy orbitals of the conduction band belong to GCN, whereas the relatively high energy orbitals of the conduction band belong to WS₂. The CBM of the WS₂/GCN heterojunction is composed of the electron orbitals of GCN (Fig. 3b). In the valence band region, the highest energy orbitals of the conduction band are occupied by WS₂, whereas the relatively low energy levels of the valence band are occupied by GCN. The VBM of the WS₂/GCN heterojunction is composed of the electron orbitals of WS₂ (Fig. 3c). The band edges of GCN and WS₂ are shaped similar to a ladder, and the WS₂/GCN heterojunction has a type II structure.

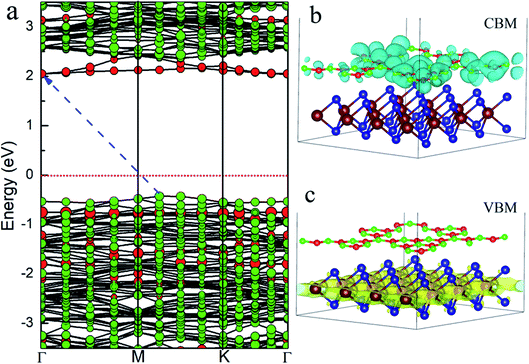Fig. 3 (a) The project energy band structure of WS₂/GCN heterojunction; (b) the electron orbitals in the CBM and (c) VBM of WS₂/GCN heterojunction.

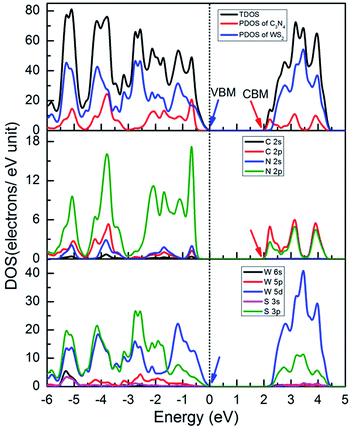
We calculated the total density of states (TDOS) and the partial density of states (PDOS) of WS₂/GCN heterojunction by using HSE06 hybrid functional approach to further study the composition of the microelectronic structure. The VBM of the WS₂/GCN heterojunction is mainly composed of W 5d and S 3p orbits, and also contains a small number of W 6s and W 5p orbits. The ratios were 77%, 19.5%, 1.7% and 1.5%, respectively. While the CBM of the WS₂/GCN heterojunction is mainly occupied by C 2p and N 2p orbits, and also includes a small number of N 2s orbits. The ratios were 65.3%, 34.1% and 0.5%, respectively (Fig. 4). The configuration differs from the orbital composition of the monolayer GCN and the WS₂ nanosheet. The van der Waals force between the GCN nanosheet and the WS₂ nanosheet has changed the distribution of the electrons in the WS₂/GCN heterojunction, and it has a type II heterostructure, which is consistent with the previous band structure's analytical results. The WS₂/GCN heterojunction, as a type II structure, is conducive in promoting the separation of photoexcited electrons and holes, subsequently improving photocatalytic activity effectively.

Fig. 4 The TDOS and PDOS of WS₂/GCN heterojunction.

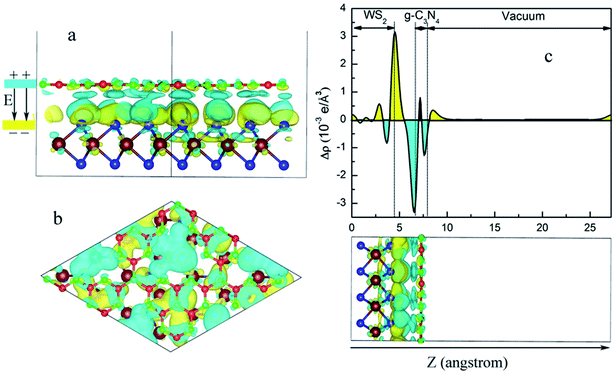
The interaction between the interfaces of the heterostructure will change the charge distribution on the two surfaces. Therefore, a built-in electric field will be formed within the heterostructure. This phenomenon can affect the transfer of photogenerated electrons and holes and further affect the photocatalytic performance of the heterojunction. Thus, an analysis of the charge distribution between the interfaces of the WS₂/GCN heterojunction is extremely important.

First, we investigated the differential charge density distribution of the WS₂/GCN heterojunction. The formula of the differential charge density is as follows:

Δρ = ρ_WS2/GCN − ρ_GCN − ρ_WS2 (2)

where ρ_WS2/GCN, ρ_GCN, and ρ_WS2 are the charge densities of the WS₂/GCN heterojunction, the single-layer GCN, and the WS₂ nanosheet, respectively. The calculated differential charge density distributions of the WS₂/GCN heterojunction are shown in the Fig. 5a and b. In these figures, cyan represents electron loss, while yellow represents electron accumulation. The charge density distribution on the GCN interface is mainly cyan and accompanied by a small amount of yellow. The color plots indicate that electrons are lost at the GCN interface and aggregate holes, and the GCN interface is positively charged. On the contrary, the charge density distribution on the WS₂ interface is mainly yellow and accompanied with some cyan. The color plots indicate that electrons are accumulated at the WS₂ interface, and the WS₂ interface is negatively charged. We further project the differential charge density to the Z axis (Fig. 5c). The figure intuitively implies that the GCN interface is positively charged, and the WS₂ interface in negatively charged. A built-in electric field exists, and its direction is from the GCN interface to the WS₂ interface within the WS₂/GCN heterojunction.

Fig. 5 (a) The lateral view and (b) vertical view of the charge density difference of WS₂/GCN heterojunction. (c) Electron density difference of plane projection along with Z axis for the WS₂/GCN heterojunction.

Second, we calculate the work functions of the monolayer WS₂, the GCN nanosheet, and the WS₂/GCN heterojunction to investigate the charge transfers between the WS₂/GCN interface. The work function represents the minimum energy needed to lift an electron from the Fermi level to the vacuum. The formula of the work function is as follows:

Φ = E_vac − E_Fermi (3)

where Φ, E_vac, and E_Fermi are the work function, the vacuum energy level, and the Fermi energy level, respectively.³³ The calculated work functions of the single-layer WS₂, the GCN nanosheet, and the WS₂/GCN heterojunction are 5.97, 5.81, and 5.86 eV, respectively (Fig. 6a–c). As the GCN nanosheet and the WS₂ nanosheet come into contact, the electrons on the GCN nanosheet flow into the WS₂ nanosheet owing to the Fermi energy level of the former is higher than that of the latter. The charge distribution at the interface will reach a thermal equilibrium when their Fermi energy levels become equal. Then, as parts of the electrons transfer from the GCN nanosheet to the WS₂ nanosheet, the former becomes positively charged, whereas the latter becomes negatively charged. Therefore, a stable built-in electric field (V_D) is formed between the WS₂/GCN heterojunction interfaces. The value of V_D is 0.16 V, and its direction is from the GCN nanosheet to the WS₂ nanosheet. The result of the work function analysis is consistent with that of the differential charge density distribution analysis.

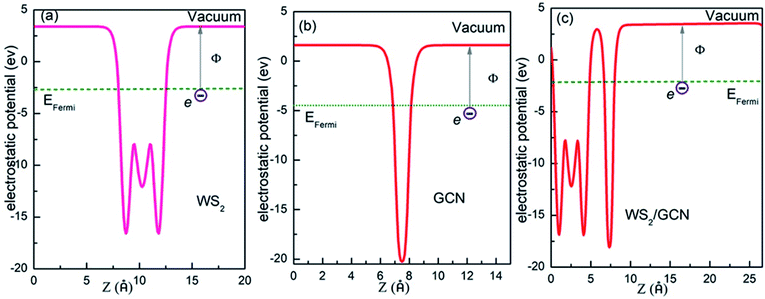Fig. 6 The electrostatic potential of (a) monolayer WS₂, (b) GCN nanosheets and (c) WS₂/GCN heterojunction.

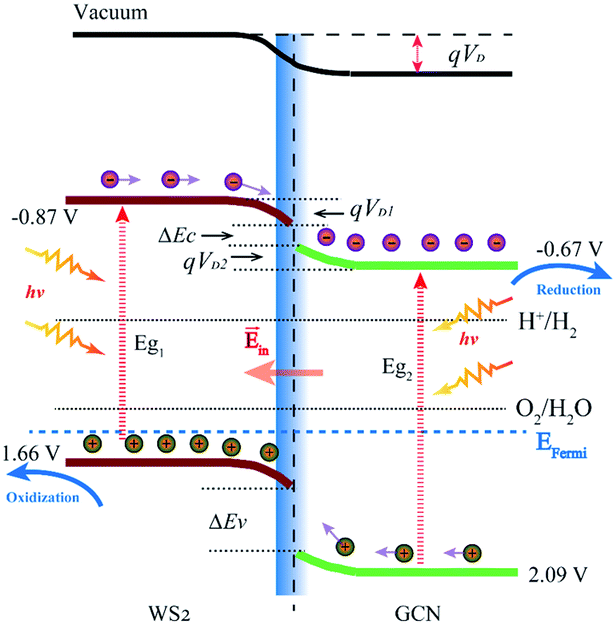
The VBM and CBM potentials of a semiconductor are the main factors of photocatalytic redox capacity. A positive VBM potential means strong oxidation capacity, while a negative CBM potential means strong reduction ability. Combined with the calculation for energy band structure, DOS, and electrostatic potential, we can further study the mechanism of the photocatalytic water splitting in the WS₂/GCN heterojunction. According to the work function calculation, WS₂ and GCN differ in their Fermi energy levels. When WS₂ and GCN form a WS₂/GCN heterojunction, the energy bands of the WS₂ and the GCN will bend. The energy band of WS₂ has a downward bending amount (qV_D2) of 0.11 eV, the energy band of GCN has an upward bending amount (qV_D1) of 0.06 eV, and the total band bending amount (qV_D) is 0.16 eV, where V_D is the potential of the built-in electric field between two interfaces of the WS₂/GCN heterojunction. From the calculated results of the electrostatic potential and the DOS of the WS₂/GCN heterojunction, we can derive the CBM and VBM potentials of the WS₂/GCN heterojunction. The details are shown in Fig. 7. The CBM and VBM potentials of WS₂ are −0.87 and 1.66 V (vs. NHE), respectively. Meanwhile, the CBM and VBM potentials of GCN are −0.67 V and 2.09 V, respectively. The conduction band offset (ΔE_C) and the valence band offset (ΔE_V) of the WS₂/GCN heterojunction are 0.04 and 0.27 eV, respectively. When irradiated with light, the electrons on the valence bands of WS₂ and GCN are excited to the conduction band. Meanwhile, the same number of holes are generated on the valence bands of WS₂ and GCN. Driven by built-in electric field forces, the electrons on the conduction bands of WS₂ transfer to the conduction bands of GCN, while the holes on the valence bands of GCN transfer to the valence bands of WS₂. Consequently, the photoexcited electrons and holes gather in the conduction bands of GCN and the valence bands of WS₂, respectively. These phenomena result in the separation of photoexcited electrons and holes in space, effectively avoiding a large number of recombination of photoexcited electrons and holes, and they extend the lifetime of the photoexcited carriers. Therefore, the photogenerated electrons and the holes can further increase the probability of surface photocatalytic reaction, effectively improving the photocatalytic efficiency of the WS₂/GCN heterojunction. The photoexcited electrons' potential in the CBM of GCN is −0.67 V, which is negative relative to the reduction potential of H⁺/H₂ (0 V), indicating sufficient ability to reduce hydrogen ion to hydrogen. Meanwhile, the photogenerated holes' potential in the VBM of WS₂ is 1.66 V, which is more positive than the potential of O₂/H₂O (1.23 V), suggesting sufficient ability to oxidize water to oxygen. The results of the theoretical analysis are consistent with the experimental study. In summary, the WS₂/GCN heterojunction has a type II photocatalytic structure with staggered energy levels. This configuration can effectively promote the separation of photogenerated electrons and holes in space, and it has enough potential to decompose water to produce hydrogen and oxygen.

Fig. 7 Photocatalytic mechanism of type II WS₂/GCN heterojunction.

4. Conclusion

In this work, the electronic structures and the photocatalytic water decomposition of the WS₂/GCN heterojunction are systematically investigated by using the hybrid density functional approach. The bandgap of the monolayered WS₂, the GCN nanosheet and the WS₂/GCN heterojunction are 2.28, 2.76, and 2.34 eV, respectively. The calculated interfacial formation energy and the interface distance indicate that the interface interaction of the WS₂/GCN heterojunction belong to a van der Waals force. Furthermore, the WS₂/GCN heterojunction has a typical van der Waals heterostructure. The energy band structures and the DOS calculations reveal that the WS₂/GCN heterojunction has a typical type-II heterostructure, and its valence band offset and conduction band offset are 0.27 and 0.04 eV, respectively. The different Fermi energy levels of the monolayer WS₂ and the GCN nanosheet causes the energy band to bend at the interface when they form a heterojunction. The total band bending amount (qV_D) is 0.16 eV, and the potential of the built-in electric field between the interfaces of the WS₂/GCN heterojunction is 0.16 V. The built-in electric field can promote the separation of the photoexcited electrons and the holes in space, and a large number of recombination of photoexcited electrons and holes can be effectively avoided. Therefore, photogenerated electrons and holes can further increase the probability of surface photocatalytic reaction, effectively improving the photocatalytic efficiency of the WS₂/GCN heterojunction. In terms of WS₂/GCN heterojunction photocatalytic water decomposition, the photoexcited electrons' potential in the CBM of GCN is −0.67 V, which is negative relative to the reduction potential of H⁺/H₂ (0 V), indicating sufficient ability to reduce hydrogen ion to hydrogen. Meanwhile, the photogenerated holes' potential in the VBM of WS₂ is 1.66 V, which is more positive than the potential of O₂/H₂O (1.23 V), suggesting sufficient the ability to oxidize water to oxygen. Our work not only elucidates the photocatalytic water decomposition mechanism of the WS₂/GCN heterostructure but also provides a good idea for designing photocatalytic heterojunctions.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by Anhui Provincial Natural Science Foundation (No. 1908085MA23 and 1908085QE222) and Natural Science Foundation of Education Department of Anhui Province (No. KJ2017A385)

Notes and references

1. A. Fujishima and K. Honda, Nature, 1972, 238, 37–38.
2. X. Wang, K. Maeda, A. Thomas, K. Takanabe, G. Xin, J. M. Carlsson, K. Domen and M. Antonietti, Nat. Mater., 2009, 8, 76–80.
3. Y. Sang, Z. Zhao, M. Zhao, P. Hao, Y. Leng and H. Liu, Adv. Mater., 2015, 27, 363–369.
4. V. Q. Bui, T. T. Pham, D. A. Le, C. M. Thi and H. M. Le, J. Phys.: Condens. Matter, 2015, 27, 305005.
5. B. Mahler, V. Hoepfner, K. Liao and G. A. Ozin, J. Am. Chem. Soc., 2014, 136, 14121–14127.
6. C. Tan, X. Cao, X. J. Wu, Q. He, J. Yang, X. Zhang, J. Chen, W. Zhao, S. Han, G. H. Nam, M. Sindoro and H. Zhang, Chem. Rev., 2017, 117, 6225–6331.
7. H. Huang, K. Xiao, N. Tian, F. Dong, T. Zhang, X. Du and Y. Zhang, J. Mater. Chem. A, 2017, 5, 17452–17463.
8. M. Yousefi, M. Faraji, R. Asgari and A. Z. Moshfegh, Phys. Rev. B, 2018, 97, 195428.
9. T. Su, Q. Shao, Z. Qin, Z. Guo and Z. Wu, ACS Catal., 2018, 8, 2253–2276.
10. N. Tian, H. Huang, X. Du, F. Dong and Y. Zhang, J. Mater. Chem. A, 2019, 7, 11584–11612.
11. J. R. Ran, W. W. Guo, H. L. Wang, B. C. Zhu, J. G. Yu and S. Z. Qiao, Adv. Mater., 2018, 30, 6.
12. X. J. She, J. J. Wu, H. Xu, J. Zhong, Y. Wang, Y. H. Song, K. Q. Nie, Y. Liu, Y. C. Yang, M. T. F. Rodrigues, R. Vajtai, J. Lou, D. L. Du, H. M. Li and P. M. Ajayan, Adv. Energy Mater., 2017, 7, 7.
13. Q. L. Xu, B. C. Zhu, B. Cheng, J. G. Yu, M. H. Zhou and W. K. Ho, Appl. Catal., B, 2019, 255, 10.
14. J. W. Fu, Q. L. Xu, J. X. Low, C. J. Jiang and J. G. Yu, Appl. Catal., B, 2019, 243, 556–565.
15. Y. J. Yuan, Z. K. Shen, S. T. Wu, Y. B. Su, L. Pei, Z. G. Ji, M. Y. Ding, W. F. Bai, Y. F. Chen, Z. T. Yu and Z. G. Zou, Appl. Catal., B, 2019, 246, 120–128.
16. J. G. Yu, S. H. Wang, J. X. Low and W. Xiao, Phys. Chem. Chem. Phys., 2013, 15, 16883–16890.
17. W. Pudkon, S. Kaowphong, S. Pattisson, P. J. Miedziak, H. Bahruji, T. E. Davies, D. J. Morgan and G. J. Hutchings, Catal. Sci. Technol., 2019, 9, 5698–5711.
18. Y. C. Wu, Z. M. Liu, Y. R. Li, J. T. Chen, X. X. Zhu and P. Na, Chin. J. Catal., 2019, 40, 60–69.
19. M. S. Akple, J. X. Low, S. Wageh, A. A. Al-Ghamdi, J. G. Yu and J. Zhang, Appl. Surf. Sci., 2015, 358, 196–203.
20. Y. L. Zhou, X. Y. Ye and D. Y. Lin, Int. J. Hydrogen Energy, 2019, 44, 14927–14937.
21. M. M. Shao, W. Z. Chen, S. J. Ding, K. H. Lo, X. W. Zhong, L. M. Yao, W. F. Ip, B. M. Xu, X. S. Wang and H. Pan, ChemSusChem, 2019, 12, 3355–3362.
22. P. Zeng, X. Y. Ji, Z. G. Su and S. P. Zhang, RSC Adv., 2018, 8, 20557–20567.
23. Y. N. Ma, J. Li, E. Z. Liu, J. Wan, X. Y. Hu and J. Fan, Appl. Catal., B, 2017, 219, 467–478.
24. H. H. Tran, D. H. Truong, T. T. Truong, T. Xuan Dieu Nguyen, Y.-S. Jin, S. J. Kim and V. Vo, Bull. Korean Chem. Soc., 2018, 39, 965–971.
25. J. Huang, J. Mei, J. Han, H. Liang, W. Wang, B. Dong and L. Cao, J. Colloid Interface Sci., 2019, 556, 224–231.
26. X. G. Ma, C. Chen, J. S. Hu, M. K. Zheng, H. H. Wang, S. J. Dong, C. Y. Huang and X. B. Chen, J. Alloys Compd., 2019, 788, 1–9.
27. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
28. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
29. J. Gracia and P. Kroll, J. Mater. Chem., 2009, 19, 3013–3019.
30. W. J. Schutte, J. L. De Boer and F. Jellinek, J. Solid State Chem., 1987, 70, 207–209.
31. J. Wang, Z. Guan, J. Huang, Q. Li and J. Yang, J. Mater. Chem. A, 2014, 2, 7960–7966.
32. J. Zhang, F. Ren, M. Deng and Y. Wang, Phys. Chem. Chem. Phys., 2015, 17, 10218–10226.
33. J. Liu, J. Phys. Chem. C, 2015, 119, 28417–28423.
34. T. Björkman, A. Gulans, A. V. Krasheninnikov and R. M. Nieminen, Phys. Rev. Lett., 2012, 108, 235502.
35. Y. Sun, H. Cheng, S. Gao, Z. Sun, Q. Liu, Q. Liu, F. Lei, T. Yao, J. He, S. Wei and Y. Xie, Angew. Chem., Int. Ed., 2012, 51, 8727–8731.

---