Open Access Article
Open Access ArticleTheoretical investigations of a new two-dimensional semiconducting boron–carbon–nitrogen structure†
Yihua Lua,
Xi Zhu*a and
Min Wang *b
*b
aShenzhen Institute of Artificial Intelligence and Robotics for Society (AIRS), 14-15F, Tower G2, Xinghe World, Rd Yabao, Longgang District, Shenzhen, Guangdong 518172, China. E-mail: zhuxi@cuhk.edu.cn
bChongqing Key Laboratory for Advanced Materials and Technologies of Clean Energies, School of Materials and Energy, Southwest University, Chongqing 400715, China. E-mail: minwang@swu.edu.cn
First published on 21st January 2020
Abstract
A new two-dimensional boron–carbon–nitrogen (BCN) structure is predicted and is theoretically investigated based on density functional theory. The BCN structure belongs to the space group C222, and is composed of twelve B, twelve C and twelve N atoms per orthorhombic cell (named oC-B12C12N12). It consists of small hollow spheres with two hexagons per sphere. The dynamical, thermal and mechanical stabilities of oC-B12C12N12 are respectively evaluated by phonon spectroscopy, ab initio molecular dynamics calculations and elastic constant measurements. The simulated in-plane stiffness and Poisson ratio display anisotropic features. The band structure shows that oC-B12C12N12 is a direct semiconductor with a gap of 2.72 eV (GW). oC-B12C12N12 has an absorption range from the visible light spectrum to the ultraviolet. Therefore, due to its small direct band gap and optical absorption, oC-B12C12N12 may be a good candidate for electronic and optical applications.
Introduction
Since its discovery,1 graphene has attracted tremendous interest in its unique features, such as good transparent, thermal conductivity, massless Dirac fermions, near-ballistic transport and high carrier mobility.2,3 Furthermore, other two-dimensional (2D) materials have also been inspired by graphene,4 such as transition metal dichalcogenides,5–7 silicene,8,9 hexagonal boron nitride (h-BN),10–14 phosphorene15,16 and Mxenes.17,18 These 2D materials also display specific properties and have promising applications.19–21Though graphene has many good properties, its zero band gap is a major challenge for electronics. h-BN, as an analogue of graphene, has a wide band gap and always acts as a substrate or a dielectric layer to enhance the performance of electronic devices. The findings of graphene and h-BN stimulate research on hexagonal boron–carbon–nitrogen (h-BCN), that is, boron, carbon and nitrogen atoms occupy the atomic sites of graphene or h-BN. The constructions arising from ternary phase diagram exhibit possible compounds.22,23
Besides graphene, other 2D carbon allotropes are also investigated, such as penta-graphene,24 graphyne,25 graphdiyne,26,27 net W carbon,28 twin graphene,29 hP-C18 carbon30 and hP-C17 carbon.31 Related BCN analogues are also inspired. For example, multiple Dirac cones can be predicted in BN co-doped β-graphyne,32 and different ratios of BN can affect the band gaps of BN co-doped twin-graphene.33
Motivated by recent progresses of BCN materials, a new 2D BCN compound is also predicted and is theoretically investigated. This BCN belongs to the space group C222, and has twelve B, twelve C and twelve N atoms per orthorhombic cell, named as oC-B12C12N12. The calculations reveal that it is dynamically, thermally and mechanically stable. The simulated in-plane stiffness and Poisson ratio display anisotropic features. It is a direct semiconductor with a gap of 2.72 eV (GW). Therefore, oC-B12C12N12 is a good candidate for electronic and optical applications.
Computational details
The theoretical studies were implemented by density-functional-theory based VASP codes34 with projector augmented wave potential.35 The Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional was chosen within generalized gradient approximation (GGA).36,37 2s22p1, 2s22p2 and 2s22p3 for the valence states of boron, carbon and nitrogen atoms were adopted. An energy cutoff is set as 500 eV. The Brillouin zone was sampled by a Monkhorst–Pack k-point grid of 5 × 9 × 1. The respective convergences of 10−3 eV Å−1 and 10−6 eV per atom were adopted for the ion force and the total energy during the optimization. G0W0 approximation38,39 is also considered for a more accurate band gap. Based on GW calculations, the optical absorption is further obtained from the dielectric function, which is calculated by Bethe–Salpeter equation (BSE).40,41 The convergence test for different cutoff energies (450, 500 and 550 eV) and k-point grids (4 × 8 × 1, 5 × 9 × 1 and 6 × 10 × 1) is plotted in Fig. S1 (ESI†). The phonon is obtained by the phonopy code23 based on displacement method. The searching way for a new BCN geometry was following: the traversal searching was explored with the consideration of all of space groups and Wyckoff positions. In this work, one BCN configuration, which consists of 12B, 12C and 12N atoms belonging to C222 space group with different Wyckoff positions, was adopted as the first generation. Then after several generations by performing genetic-algorithm code, some BCN structures may be possibly stable ones. The construction of oC-B12C12N12 was approached after the stable evaluation. However, there is no experimental clue for this BCN.Results and discussion
Structure
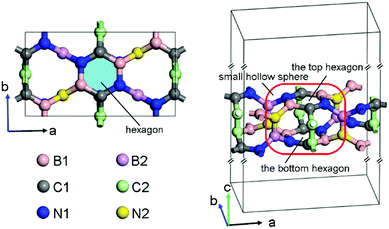
After the successful searching of BCN, the lattice was fully optimized to obtain the lattice parameters. This BCN structure belongs to the space group C222, and it has twelve B, twelve C and twelve N atoms per orthorhombic cell as shown in Fig. 1, thus it is named as oC-B12C12N12. Its crystal parameters are listed as: a = 9.84 Å, b = 5.51 Å, c = 30 Å, α = β = γ = 90°. The parameter c is the length of the simulation box. There are six inequivalent atoms, denoted as B1, B2, C1, C2, N1, and N2 in Fig. 1, occupying the following respective Wyckoff positions: 8l (0.8706, 0.1270, 0.4519), 4k (0.25, 0.25, 0.4795), 8l (0.9946, 0.7392, 0.4538), 4j (0, 0.5, 0.4771), 8l (0.1279, 0.1377, 0.4545) and 4k (0.75, 0.25, 0.4729). The hexagons, which are composited of two B1, two C1, and two N1 atoms (see light blue region in the left panel of Fig. 1), possesses all bond angles of ∼120° and the respective bond lengths LC1–N1, LB1–N1, and LC1–B1 of 1.38 Å, 1.46 Å and 1.52 Å. Each atom of one top hexagon is connected with the corresponding atom of the bottom hexagon via two bridge atoms (C2–C2 or B2–N2). Furthermore, two hexagons and twelve bridge atoms could compose a small hollow sphere (red rounded rectangle in the right panel of Fig. 1). Additionally, in the sphere, the bond lengths LN1–B2, LC1–C2, LB1–N2, LC2–C2 and LB2–N2 are 1.55 Å, 1.49 Å, 1.50 Å, 1.43 Å and 1.37 Å, respectively. And the bond angles ∠B1–N2–B2, ∠N2–B2–N1 and ∠C1–C2–C2 are 115°, 119° and 118°, respectively. In brief, oC-B12C12N12 is composited of small hollow spheres with two hexagons per sphere. Additionally, compared with two experimental synthesized BCN structures (denoted as BCN_v1 and BCN_v3)23, oC-B12C12N12 has a higher energy, as shown in Fig. S2 (ESI†). The energy difference between BCN_v3 and oC-B12C12N12 is 0.4 eV per atom.Stability
The phonon spectra and its phonon density of states (DOS) (see Fig. 2) are investigated not only to analyze the vibration of the materials but also to evaluate its stability. And the k-path is set as Γ(0,0,0)-Y(−1/2,1/2,0)-K(−1/3,2/3,0)-Γ-S(0,1/2,0)-K for its reciprocal primitive cell. No imaginary phonon branch can be seen in the phonon spectra, meeting the requirement of the dynamical stability. The highest frequency is around 1466 cm−1, which is dominated by C2 atoms through the analysis of phonon DOS. Additionally, the quasi-direct vibration gap between 1390 cm−1 and 1466 cm−1 in the phonon spectra reveals that no radiation in the gap range can propagation, extending a promising application of filter.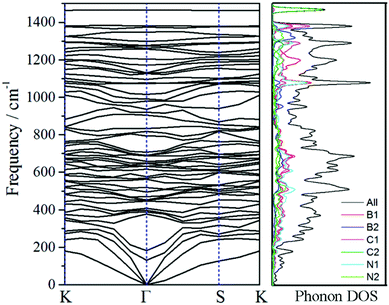 | ||
| Fig. 2 Phonon spectra and its density of states via its reciprocal primitive cell. The k-path is set as K(−1/3,2/3,0)-Γ(0,0,0)-S(0,1/2,0)-K. | ||
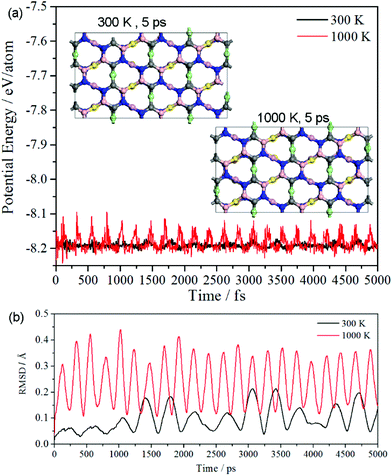
The simulations based on ab initio molecular dynamics (MD) were performed with canonical ensemble. 2 × 2 × 1 supercells with 144 atoms were set as the model. The time step of 1 fs was used. The MD simulations were performed at the temperature of 300 K and 1000 K for 5 ps. The potential energy and the root mean square displacement (RMSD) as a function of time are plotted in Fig. 3(a) and (b), respectively. The potential energy at 300 K has a very weak fluctuation, and the respective snapshot reveals it sustain its configuration well. Additionally, though potential energy at 1000 K has a larger fluctuation than that at 300 K, the snapshot shows that it still has a good configuration without tremendous reconstruction. Thus, oC-B12C12N12 not only has good thermal stability at room temperature, but also it can keep its configuration even at a temperature as high as 1000 K.
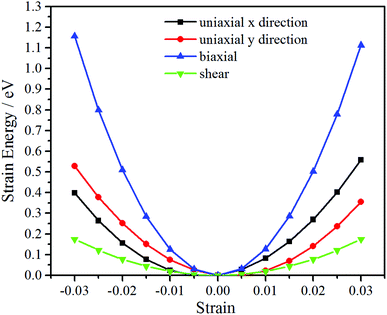
The oC-B12C12N12 shows an orthorhombic symmetry, resulting in an anisotropic linear elastic behavior. The strain energy, which is the energy difference between the strained system (U(ε)) and the unstrained one (U0), can be expressed as42
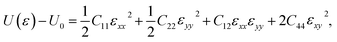 | (1) |
The Cij can be obtained by fitting second-order polynomials to the curves of strain energy with uniaxial x/y direction, biaxial and shear strains, as shown in Fig. 4. The values C11 = 314 N m−1, C22 = 290 N m−1, C12 = 70 N m−1, C44 = 29 N m−1 meet the criteria for 2D crystals (C11C22 − C122 > 0, C44 > 0),43 revealing that it is mechanically stable. Thus, after the structural stability has been determined by phonon spectra, ab initio MD simulations and elastic constants, mechanical, electronic and optical properties are investigated in the following.
Mechanical properties
Moreover, since the elastic constants have been obtained, the in-plane stiffness (C) and Poisson's ratio (ν) can be evaluated for the mechanical properties. Assuming an arbitrary direction has an angle θ relative to the x axis, the in-plane stiffness (C(θ)) and Poisson's ratio (ν(θ)) have the following expressions:34
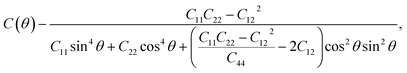 | (2) |
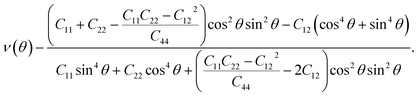 | (3) |
Thus, the θ-dependent C(θ) and ν(θ) can be obtained.
Due to the orthorhombic symmetry of oC-B12C12N12, C(θ) and ν(θ) apparently display anisotropic features. The values of in-plane stiffness C(0°) and C(90°) along x and y direction are 297 N m−1 and 274 N m−1, respectively, while the smallest in-plane stiffness C(θ) is 100 N m−1 when θ equals to 45°, 135°, 225° and 315°. Compared to in-plane stiffness of graphene (344 N m−1),42 the largest in-plane stiffness of oC-B12C12N12 (297 N m−1) is comparable, revealing that it may has some mechanic usages. The values of Poisson ratio ν(0°) and ν(90°) are 0.24 and 0.22, respectively. When θ equals to 45°, 135°, 225° and 315°, Poisson ratio ν(θ) equals to 0.73, which is the largest value.
Electronic properties
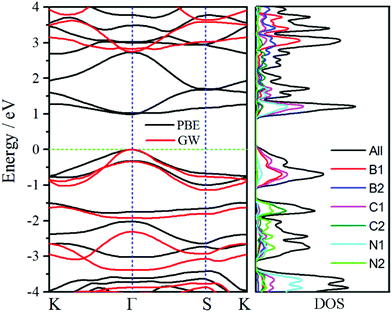
To further obtain insights of electronic properties, the band structure and density of states (DOS) of oC-B12C12N12 are calculated and plotted in Fig. 5. The band structure reveals that oC-B12C12N12 is a direct semiconductor and both valence band maximum and conduction band minimum are at Γ point. The band gap obtained by PBE functional is only 0.98 eV, which is underestimated. With the GW method, a more accurate band gap of around 2.72 eV is obtained. According to the DOS plots, the conduction bands are mainly dominated by C1 and N1 atoms, while the valence bands are mostly contributed by C1 and B1 atoms. Due to the narrow band gap, oC-B12C12N12 may have more usage for electronic and optical devices.Optical properties
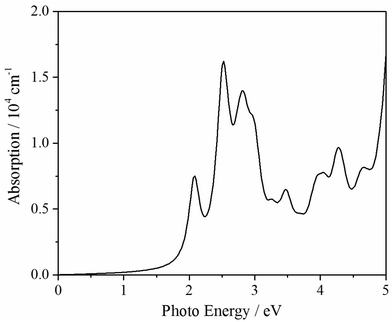
To further extend its applications, we simulate its optical absorption based on GW-BSE method (see Fig. 6). It exhibits that oC-B12C12N12 can absorb the photons with a photon energy larger than 2.10 eV, correspondingly, it has a absorption range from part of visible lights to ultraviolet ones. Thus, oC-B12C12N12 may be a good candidate for optical usage.Conclusions
A new two-dimensional BCN structure, named as oC-B12C12N12, is theoretically predicted and is investigated. It belongs to the space group C222, and has twelve B, twelve C and twelve N atoms per orthorhombic cell. It consists of small hollow spheres with two hexagons per sphere. No imaginary vibration branch is observed in phonon spectra, revealing oC-B12C12N12 is dynamically stable. The thermal stability is confirmed by ab initio molecular dynamics at 300 K and 1000 K, indicating that oC-B12C12N12 not only has good thermal stability at room temperature, but also it can keep its configuration even at a temperature as high as 1000 K. The calculated elastic constants meet the criteria for 2D crystals, revealing that oC-B12C12N12 is mechanically stable. The simulated in-plane stiffness and Poisson ratio display anisotropic features. The values of in-plane stiffness C(0°) and C(90°) along x and y direction are 297 N m−1 and 274 N m−1, respectively, while the smallest in-plane stiffness C(θ) is 100 N m−1 when θ equals to 45°, 135°, 225° and 315°. The values of Poisson ratio ν(0°) and ν(90°) are 0.24 and 0.22, respectively. When θ equals to 45°, 135°, 225° and 315°, Poisson ratio ν(θ) equals to 0.73. The band structure displays that it is a direct semiconductor with a band gap of 2.72 eV (GW). It has an absorption range from part of visible lights to ultraviolet ones. In summary, because of its direct band gap and optical absorption, oC-B12C12N12 may be a good candidate for electronic and optical applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by Shenzhen Fundamental Research Foundation (JCYJ20170818103918295), National Natural Science Foundation of China (Grant No 21805234), President's funds from CUHK-Shenzhen (PF00728), and Chongqing Key Laboratory for Advanced Materials and Technologies of Clean Energies (Grant No. JJNY201902).Notes and references
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed
.
- A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191 CrossRef CAS PubMed
.
- A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109–162 CrossRef CAS
.
- G. R. Bhimanapati, Z. Lin, V. Meunier, Y. Jung, J. Cha, S. Das, D. Xiao, Y. Son, M. S. Strano, V. R. Cooper, L. Liang, S. G. Louie, E. Ringe, W. Zhou, S. S. Kim, R. R. Naik, B. G. Sumpter, H. Terrones, F. Xia, Y. Wang, J. Zhu, D. Akinwande, N. Alem, J. A. Schuller, R. E. Schaak, M. Terrones and J. A. Robinson, ACS Nano, 2015, 9, 11509–11539 CrossRef CAS PubMed
.
- A. Splendiani, L. Sun, Y. Zhang, T. Li, J. Kim, C.-Y. Chim, G. Galli and F. Wang, Nano Lett., 2010, 10, 1271–1275 CrossRef CAS PubMed
.
- M. Chhowalla, H. S. Shin, G. Eda, L.-J. Li, K. P. Loh and H. Zhang, Nat. Chem., 2013, 5, 263–275 CrossRef PubMed
.
- D. Jariwala, V. K. Sangwan, L. J. Lauhon, T. J. Marks and M. C. Hersam, ACS Nano, 2014, 8, 1102–1120 CrossRef CAS PubMed
.
- A. Fleurence, R. Friedlein, T. Ozaki, H. Kawai, Y. Wang and Y. Yamada-Takamura, Phys. Rev. Lett., 2012, 108, 245501 CrossRef PubMed
.
- P. Vogt, P. De Padova, C. Quaresima, J. Avila, E. Frantzeskakis, M. C. Asensio, A. Resta, B. Ealet and G. Le Lay, Phys. Rev. Lett., 2012, 108, 155501 CrossRef PubMed
.
- C. R. Dean, A. F. Young, I. Meric, C. Lee, L. Wang, S. Sorgenfrei, K. Watanabe, T. Taniguchi, P. Kim, K. L. Shepard and J. Hone, Nat. Nanotechnol., 2010, 5, 722–726 CrossRef CAS PubMed
.
- D. Golberg, Y. Bando, Y. Huang, T. Terao, M. Mitome, C. Tang and C. Zhi, ACS Nano, 2010, 4, 2979–2993 CrossRef CAS PubMed
.
- L. Fang, C. Wu, R. Qian, L. Xie, K. Yang and P. Jiang, RSC Adv., 2014, 4, 21010–21017 RSC
.
- J. Hou, G. Li, N. Yang, L. Qin, M. E. Grami, Q. Zhang, N. Wang and X. Qu, RSC Adv., 2014, 4, 44282–44290 RSC
.
- J. Wang, F. Ma and M. Sun, RSC Adv., 2017, 7, 16801–16822 RSC
.
- L. Li, Y. Yu, G. J. Ye, Q. Ge, X. Ou, H. Wu, D. Feng, X. H. Chen and Y. Zhang, Nat. Nanotechnol., 2014, 9, 372–377 CrossRef CAS PubMed
.
- H. Liu, A. T. Neal, Z. Zhu, Z. Luo, X. Xu, D. Tomanek and P. D. Ye, ACS Nano, 2014, 8, 4033–4041 CrossRef CAS PubMed
.
- M. Naguib, V. N. Mochalin, M. W. Barsoum and Y. Gogotsi, Adv. Mater., 2014, 26, 992–1005 CrossRef CAS PubMed
.
- F. Shahzad, M. Alhabeb, C. B. Hatter, B. Anasori, S. M. Hong, C. M. Koo and Y. Gogotsi, Science, 2016, 353, 1137–1140 CrossRef CAS PubMed
.
- A. K. Geim and I. V. Grigorieva, Nature, 2013, 499, 419–425 CrossRef CAS PubMed
.
- S. Das, D. Pandey, J. Thomas and T. Roy, Adv. Mater., 2019, 31, 1802722 CrossRef PubMed
.
- C. Tan, X. Cao, X.-J. Wu, Q. He, J. Yang, X. Zhang, J. Chen, W. Zhao, S. Han, G.-H. Nam, M. Sindoro and H. Zhang, Chem. Rev., 2017, 117, 6225–6331 CrossRef CAS PubMed
.
- L. Song, Z. Liu, A. L. M. Reddy, N. T. Narayanan, J. Taha-Tijerina, J. Peng, G. Gao, J. Lou, R. Vajtai and P. M. Ajayan, Adv. Mater., 2012, 24, 4878–4895 CrossRef CAS PubMed
.
- S. Beniwal, J. Hooper, D. P. Miller, P. S. Costa, G. Chen, S.-Y. Liu, P. A. Dowben, E. C. H. Sykes, E. Zurek and A. Enders, ACS Nano, 2017, 11, 2486–2493 CrossRef CAS PubMed
.
- S. Zhang, J. Zhou, Q. Wang, X. Chen, Y. Kawazoe and P. Jena, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2372–2377 CrossRef CAS PubMed
.
- J. Kang, Z. Wei and J. Li, ACS Appl. Mater. Interfaces, 2019, 11, 2692–2706 CrossRef CAS PubMed
.
- G. Li, Y. Li, H. Liu, Y. Guo, Y. Li and D. Zhu, Chem. Commun., 2010, 46, 3256–3258 RSC
.
- G. Luo, X. Qian, H. Liu, R. Qin, J. Zhou, L. Li, Z. Gao, E. Wang, W.-N. Mei, J. Lu, Y. Li and S. Nagase, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075439 CrossRef
.
- X.-Q. Wang, H.-D. Li and J.-T. Wang, Phys. Chem. Chem. Phys., 2013, 15, 2024–2030 RSC
.
- J.-W. Jiang, J. Leng, J. Li, Z. Guo, T. Chang, X. Guo and T. Zhang, Carbon, 2017, 118, 370–375 CrossRef CAS
.
- S. Wang, J. Li, X. Zhu and M. Wang, Carbon, 2019, 143, 517–522 CrossRef CAS
.
- Y. Lu, X. Zhu and M. Wang, Comput. Mater. Sci., 2019, 167, 8–12 CrossRef CAS
.
- Y. Mu and S.-D. Li, J. Mater. Chem. C, 2016, 4, 7339–7344 RSC
.
- R. Majidi and T. Rabczuk, J. Phys. Chem. Solids, 2019, 135, 109115 CrossRef CAS
.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533–16539 CrossRef CAS PubMed
.
- R. W. Godby, M. Schluter and L. J. Sham, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 10159–10175 CrossRef PubMed
.
- M. S. Hybertsen and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 5390–5413 CrossRef CAS PubMed
.
- S. Albrecht, L. Reining, R. Del Sole and G. Onida, Phys. Rev. Lett., 1998, 80, 4510–4513 CrossRef CAS
.
- M. Rohlfing and S. G. Louie, Phys. Rev. Lett., 1998, 81, 2312–2315 CrossRef CAS
.
- E. Cadelano, P. L. Palla, S. Giordano and L. Colombo, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 235414 CrossRef
.
- Y. Ding and Y. Wang, J. Phys. Chem. C, 2013, 117, 18266–18278 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra09723f |
| This journal is © The Royal Society of Chemistry 2020 |