Open Access Article
Open Access ArticleHalf-metallicity in new Heusler alloys Mn2ScZ (Z = Si, Ge, Sn)
Mahesh Ram ab,
Atul Saxenaa,
Abeer E. Aly
ab,
Atul Saxenaa,
Abeer E. Aly *c and
Amit Shankar
*c and
Amit Shankar b
b
aDepartment of Physics, North-Eastern Hill University, Shillong, India-793022
bCondensed Matter Theory Research Lab, Department of Physics, Kurseong College, Kurseong, Darjeeling, India – 734203. E-mail: amitshan2009@gmail.com
cBasic Science Department, El Salam Institute for Engineering and Technology, Cairo, Egypt. E-mail: abeerresmat782000@yahoo.com
First published on 21st February 2020
Abstract
Study of half-metallicity has been performed in a new series of Mn2ScZ (Z = Si, Ge and Sn) full Heusler alloys using density functional theory with the calculation and implementation of a Hubbard correction term (U). Volume optimization in magnetic and non-magnetic phases for both the Cu2MnAl and Hg2CuTi type structures was done to predict the stable ground state configuration. The stability was determined by calculating their formation energy as well as from elastic constants under ambient conditions. A half-metal is predicted for Mn2ScSi and Mn2ScGe with a narrow band gap in the minority spin whereas Mn2ScSn shows a metallic nature. The magnetic moments of Mn and Sc are coupled in opposite directions with different strengths indicating that the ferrimagnetic order and the total magnetic moment per formula unit for half-metals follows the Slater Pauling rule. And a strong effect was shown by the size of the Z element in the electronic and magnetic properties.
1. Introduction
The current pursuit in the field of materials research is to develop a material for spintronics applications, where the spin degree of freedom of an electron plays a significant role in encoding, faster transfer and processing of data as compared to a charged based equivalent transistor,1,2 as well as low power consumption,3 high circuit density4 and non-volatility.5 The performance of a spintronic device depends on efficiency of spin injection from electrodes to semiconductors and their degree of spin polarization. The spintronic devices mostly consist of a non-magnetic layer sandwiched between two ferromagnetic electrodes like giant-magnetoresistance (GMR),6,7 tunnelling magnetoresistance (TMJ)8 and magnetic tunnel junction (MTJ)9 devices. Half-metallic ferromagnets (HMF) are becoming prominent in this context because of their peculiar electronic structure at the Fermi energy level (EF), with 100% electron spin polarization.10,11The systems like oxides, manganites, pyrites and double perovskites belongs to HMF,12–14 but the Heusler alloys are gaining preferences over them due to their stable half-metallicity with high Curie temperature (TC) (1520 K for Cr2CoZa,15 1100 K for Co2FeSi16) and compatible lattice structure to construct a hetero structure with conventional semiconductor for spintronic devices. The other interesting feature of Heusler alloys is the predictability of their physical properties by simple empirical relation such as Slater-Pauling (SP) rule or by simply knowing the valence electron count, atomic ordering in the lattice, degree of atomic disorder and the strength of exchange interactions.17,18 The diverse applicability of these Heusler alloys also increases as one can easily tune their electronic and magnetic properties by doping.19–21
In previous reports, researchers have predicted half-metallicity in Fe2YSi (Y = Cr, Mn, Fe, Co and Ni), Ti2YAl and Ti2Y′Ga (Y = Co, Fe and Y′ = Cr, Fe) from the theoretical and experimental studies.22–25 The recent development on the experimental studies of HM in thin film structures of Heusler alloys Co2MnSi, Co2FeAl, Fe2CoSi, Cr2CoGa, Co2MnGe and Fe2CrGa26–31 also highlights some novel properties such as perpendicular magnetic anisotropy (PMA) as their intrinsic properties which is a requirement for spin transfer torque-random access memory and for skyrmions-based research.
Among the Heusler alloys, Mn2YZ based members (Y being a 3d or 4d transition element and Z an sp element) are of significant interest due to the presence of Mn3+ ion with d4 electronic configuration that leads to Jahn–Teller tetragonal distortion with partially filled degenerate orbitals.32,33 The interaction of the long range strain due to Jahn–Teller distortion with magnetic degrees of freedom gives way to multifunctional properties such as exchange bias, magnetocaloric effect and magnetic shape memory alloys.34–36 Moreover the parallel or antiparallel alignment of two Mn magnetic moments depending on interaction with the neighbouring atoms results in ferromagnetic or ferrimagnetic ordering, respectively.37,38 Mn2YZ in ferrimagnetic structure are of more interest due to anti-parallel alignment of two Mn magnetic moments that results in low saturation magnetization reducing the stray fields which makes the devices more resistant to external fields. This along with large PMA, high electron-spin polarization with high Tc39,40 and efficient spin-transfer torque41 are responsible for making Mn2YZ Heusler alloys a promising material in future spintronic devices.
Among the Mn2YZ compounds, Mn2VAl is the first half-metallic ferrimagnet (HMFi) that was studied both theoretically and experimentally42,43 followed by Mn2YZ (Y = V, Cr, Cu, Fe, Co, Ni and Z = Al, Ga, Si, Ge, Sb, Sn)44–47 Heusler alloys. In this context Wollmann and co-workers48,49 have reported a tetragonal distortion with reduced electron spin polarization in series of Mn2YZ, with Y belonging to 3d, 4d and 5d transition elements. Also, among X2YZ Heusler alloys there exist limited studies predicting half-metal with Y = Sc based materials such as V2ScP, Cr2ScAl and Fe2ScP/As/Sb.50,51 Likewise, to the best of our knowledge, half-metallic properties in Mn2ScZ (Z = sp elements) Heusler compounds has not been reported so far using experimental or trending density functional theory (DFT). The inefficiency of DFT based conventional exchange correlation functional such as generalized gradient approximation (GGA) and local spin density approximation (LSDA) to predict ground state properties and understand the underlying physics of the strongly correlated d and f transition metals based systems limits to unfold their HM properties.52 Similar anomaly was also observed in Mott insulators where DFT interpreted metallic bands due to ignorance of the effect of localized d and f orbitals53–55 resulting in a self-interaction error.55 This effect is also visible in narrow band oxides56,57 and molecular systems.58 The introduction of on-site Coulomb repulsion term (U) in the Hubbard model (DFT+U)55 corrects the self interaction and consider the effects of localized electrons and removes the inconsistency observed in first principle calculations and experimental results of strongly correlated systems. Heusler alloys are no exception to the inadequacy of DFT and Co2FeSi is a prototype where the experimental findings could be reproduced theoretically only with the inclusion of U.59,60 Bandyopadhyay and Sarma61 have calculated the U values for 3d transition and 5f actinide elements and showed its dependence on the number of electrons. U values for 3d electrons have been calculated experimentally as well.62,63 At present there are large number of studies in case of Heusler alloys in which calculation of U value and its effect on the electronic and magnetic properties are reported.64–66 A clear implication of U calculation and its influence on Heusler alloys to predict exact ground state properties can be found from the studies carried out by Rai et al.67,68
The effect of electron correlation in Heusler alloys are evident from the above literature and it is expected to have significant impact on alloys where highly localized d orbitals based transition metals Mn and Sc are present whose exact ground state properties are yet unexplored. Hence, in view of importance of DFT+U calculation in the material research, an effort have been made to investigate the half metallic behaviour of highly localized Mn and Sc based sample alloys Mn2ScZ (Z = Si, Ge and Sn) by adding U correction for 3d electrons of Mn and Sc. Their stability at ground state fcc phases were verified by calculating formation energy and their mechanical properties are also estimated using elastic constants at ambient condition.
2. Computational method
We have employed a plane wave pseuodopotential (PW-PP)69 and full potential-linearized augmented plane wave (FP-LAPW)70 methods based on density functional theory for the study presented in this manuscript. In FP-LAPW method, the space is divided into a non-overlapping muffin-tin (MT) spheres centred on the atomic sites and in an interstitial region. Inside the MT spheres, the basis set is consist of a linear combination of product of radial functions and the spherical harmonics whereas the basis consist of plane waves in IR region similar to PW-PP method with a cut off value of 50 Ry and charge density cut-off value of 800 Ry were used to expand the kinetic energy to describe the Kohn–Sham orbitals. Whereas, the energy convergence in the FP-LAPW method was achieved by expanding the plane wave functions in the IR with a cut off RMT × Kmax = 8, where RMT denotes the smallest muffin-tin sphere radius and Kmax gives the maximum value of wave vector (K) in the plane wave expansion. The MT sphere radii (RMT) used were 2.42, 2.30, 2.00, 2.22 and 2.50 (in a.u.) for Mn, Sc, Si, Ge and Sn, respectively. The potential inside the MT sphere and the non-spherical contributions to the charge density were expanded up to lmax = 14, whereas the potential and charge density were expanded as a Fourier series with the wave vectors up to Gmax = 14. A uniform grid of 16 × 16 × 16 automatically generated k-points following the convention of Monkhorst and Pack71 centred at Γ-point for integration over the Brillouin zone was considered with energy convergence of 10−6 Ry. We have used the spin polarized Perdew–Burke–Ernzerhof scheme of generalized gradient approximation (PBE-GGA)72 for the exchange correlation functional by treating onsite strong correlation of the 3d electrons by Coulomb repulsion U term (GGA+U).73–76 The system dependent U term is calculated based on Hubbard Hamiltonian model (eqn (1)) for the onsite Coulomb repulsion.55,67,68
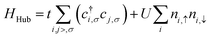 | (1) |
| U = EI − EA = (EN−1 − EN) − (EN − EN+1) | (2) |
3. Results and discussion
3.1 Structural optimization and elastic properties
Full Heusler alloys X2YZ where X and Y are transition elements and Z is an sp element crystallizes in a cubic fcc structure with four atomic basis at 4a (0, 0, 0),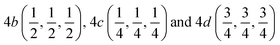 . Depending on the number of valence electrons of X atom being greater than or less than that of Y atom, the alloy can crystallize in either Cu2MnAl type structure (space group Fm
. Depending on the number of valence electrons of X atom being greater than or less than that of Y atom, the alloy can crystallize in either Cu2MnAl type structure (space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) with X in 4a and 4b positions, Y in 4c and Z in 4d position or in Hg2CuTi type structure (space group F
m) with X in 4a and 4b positions, Y in 4c and Z in 4d position or in Hg2CuTi type structure (space group F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m) with X occupying 4a and 4c positions, Y in 4b and Z in 4d positions respectively. The Cu2MnAl structure is also known as L21 structure or regular Heusler alloys whereas the Hg2CuTi structure is known as XA structure or inverse Heusler alloys.
3m) with X occupying 4a and 4c positions, Y in 4b and Z in 4d positions respectively. The Cu2MnAl structure is also known as L21 structure or regular Heusler alloys whereas the Hg2CuTi structure is known as XA structure or inverse Heusler alloys.
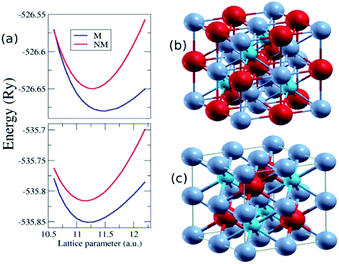
The type of structure depending on the valence electron count rule as described above is generally true for almost all the Heusler alloys however, Galehgirian et al. found Ti2VZ(Z = Al, Ga and In) to be stable in Hg2CuTi type structure,79 against the above rule. Similarly Luo et al.80 studied a series of X2CuAl (X = Sc, Ti, V, Cr, Mn, Fe, Co, Ni) and found that although all should crystallize in XA structure according to above rule, some of the alloys crystallizes in Cu2MnAl type and the others in Hg2CuTi type structure. In this context, an interesting result was reported by Bensiad et al. in series of Mn2RhZ (Z = Si, Ge and Sn), where Mn2RhSi and Mn2RhGe were found to crystallize in Cu2MnAl type structure whereas the Mn2RhSn crystallizes in Hg2CuTi type structure.81 Hence, following the above discrepancies, the sample alloys were optimized for both the structure in magnetic (M) and non magnetic phases in both Cu2MnAl and Hg2CuTi type structure to understand equilibrium structure. The variation of total energy as a function of lattice constant fitted into empirical Murnaghan's equation of state is presented in Fig. 1a. Due to similar nature of the curves, we have presented the curve only for Mn2ScSi (Fig. 1b) and the energy difference ΔE = EFm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m − EF
m − EF![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m between the Cu2MnAl and Hg2CuTi type structure are summarized in Table 1 which depicts, that the magnetic phase of Cu2MnAl type structure are energetically stable and has been used to further explore their physical properties at optimized lattice constant (Table 1). The addition of bigger size atom (Si to Sn) expand the overall size of the crystal in consistent to analogous Fe2MnZ (Z = Si, Ge and Sn)82 and by Mn2RhZ (Z = Si, Ge and Sn).81
3m between the Cu2MnAl and Hg2CuTi type structure are summarized in Table 1 which depicts, that the magnetic phase of Cu2MnAl type structure are energetically stable and has been used to further explore their physical properties at optimized lattice constant (Table 1). The addition of bigger size atom (Si to Sn) expand the overall size of the crystal in consistent to analogous Fe2MnZ (Z = Si, Ge and Sn)82 and by Mn2RhZ (Z = Si, Ge and Sn).81
| Z | a (Å) | ΔE (Ry) | Eo (Ry) | Eform (eV) |
|---|---|---|---|---|
| Si | 5.949 | −9.133 | −535.851 | −3.209 |
| Ge | 6.036 | −5.372 | −701.9321 | −5.105 |
| Sn | 6.396 | −2.028 | −688.582 | −3.188 |
The hypothetical compounds Mn2ScZ (Z = Si, Ge and Sn) are thermodynamically stable and their experimental synthesis is also possible as predicted from formation energy (Eform) (Table 1) obtained from relation83
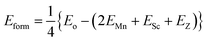 | (3) |
Elastic constants can be used to furnish the critical informations regarding the mechanical stability of a solid structure against the arbitrary deformation and moreover, the physical properties such as propagation of elastic waves in normal mode, specific heat, chemical bonds, hardness and Debye temperature are also related to them. The strain was used to determine the independent elastic constants (Cij) in such a way that the total volume of the system remains constant. The details about the type of strains applied are given in ref. 84. The symmetry of the cubic crystal reduces the total number of independent elastic constants into 3 i.e. C11, C12 and C44 and they are the elements of elastic stiffness matrix of order 6 × 6, with 6 eigen values. However there are only 3 different eigen values; C11 + 2C12 (non-degenerate), C11 − C12 (two fold degenerate) and C44 (threefold degenerate), which corresponds to bulk, the tetragonal shear and the shear moduli of the crystal and the cubic crystals becomes unstable if these values become negative. The listed elastic constants in Table 2 are found to satisfy the above stability criteria as mentioned by Born and Huang.85
| Parameters | Mn2ScSi | Mn2ScGe | Mn2ScSn |
|---|---|---|---|
| C11 | 220.449 | 222.949 | 227.029 |
| C12 | 129.05 | 138.855 | 145.449 |
| C44 | 79.128 | 94.923 | 103.608 |
| C11 − C12 | 91.399 | 84.094 | 81.58 |
| C11 + 2C12 | 478.549 | 500.659 | 517.927 |
| B (GPa) | 159.517 | 166.886 | 172.642 |
| G (GPa) | 63.487 | 68.464 | 71.297 |
| E (GPa) | 168.152 | 180.683 | 188.010 |
| A | 1.731 | 2.258 | 2.540 |
| ν | 0.324 | 0.320 | 0.318 |
| CP | 49.922 | 43.932 | 41.841 |
| (B/G) | 2.5126 | 2.43758 | 2.42145 |
| υl (m s−1) | 13012.672 | 12238.046 | 11753.483 |
| υt (m s−1) | 3335.374 | 6302.145 | 6065.602 |
| υm (m s−1) | 7434.818 | 7057.058 | 6791.246 |
| ΘD (K) | 937.491 | 878.227 | 826.381 |
The bulk modulus (B) and the isotropic shear modulus (G) has been calculated using the Voigt–Reuss and Hill86 approximation as84
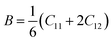 | (4) |
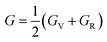 | (5) |
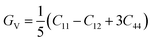 | (6) |
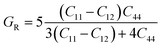 | (7) |
B defines the hardness of the material and characterizes the resistance of the material to fracture whereas G gives the resistant to plastic deformations. One can find from the table that B > G, indicating the prominence of shear modulus in the stability of the sample materials. Also the computed values of B and G are comparable with of Mn2ZrSi (B = 187.015 GPa, G = 80.249 GPa), Mn2ZrGe (B = 175.478 GPa, G = 71.088 GPa)87 and Fe2MnSi (B = 228 GPa, G = 73 GPa).82
Using the above B and G, one can find the Young's modulus (E) and Poisson's ratio (ν) as84
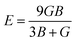 | (8) |
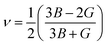 | (9) |
E is the ratio of tensile stress to tensile strain that measures the stiffness of the material and here Mn2ScSn is the stiffest. The ν determines the nature of atomic bonding present in the material and its critical value is 0.26 (ref. 88) separating the covalent and ionic nature. The Pugh's ratio (B/G) with a critical value of 1.75 (ref. 84) predicts their ductile with ionic type of bonding. One can also determine the type of atomic bonding by calculating CP with large negative value for directional covalent bonding whereas a positive value for non-directional metallic bonding and all the materials are found to show non-directional metallic bonding in the present study.
| CP=C12 − C44 | (10) |
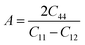 | (11) |
The anisotropy factor A, which is the measure of the degree of anisotropy of the material and the deviation from unity indicates the probability of development of cracks during the crystal growth process. Although it deviates from unity in present case, it is quite less when compared to Fe2MnSi (7.21), Fe2MnGe (8.30) and Fe2MnSn (25.88).82
The Debye temperature (ΘD) is an important elastic parameter which is related to many thermodynamic properties and its estimation from elastic constants is expected to reflect the true value at low temperatures because in such conditions the crystal vibration is of acoustic type. It can be calculated from the average mean velocity (υm) as:84
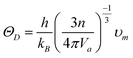 | (12) |
3.2 Electronic structure and magnetic properties
Study of electronic structure in context of half-metallicity have been performed earlier in analogous system like Fe2MnZ, Mn2RhZ, Mn2TiZ, Mn2ZrZ and Co2MnZ (Z= Si, Ge and Sn)81,82,87,89,90 where the decrease in HM gap or even lost of half-metallicity with increase in size of Z atom has been reported. To check similar feature in the sample materials and understand their effect we have calculated spin-polarized electronic band structure along the high-symmetric direction of the Brillouin zone (BZ) (Fig. 2) and corresponding density of states (DOS) (Fig. 3) in the equilibrium configuration. In present study, the total number of valence electron is 21, thus according to Slater Pauling rule (SP) of 24 we have spin down electron as the majority spin and spin up electron as minority spin.91 From the figures one can find both Mn2ScSi and Mn2ScGe shows half metallic structure with continuous bands and DOS crossing the EF for majority spin whereas a gap occurs at EF for minority spin. For Mn2ScSn, the band crosses EF for both the spin channels, showing a metallic nature. Moreover the profile of the DOSs and bands are similar for two HMs whereas, completely different for metallic Mn2ScSn. There are many peaks in the minority DOS around −2 eV below EF for Mn2ScSi and Mn2ScGe which is visible as flat regions in their corresponding bands. These peaks merge to form a more prominent one in magnitude in case of Mn2ScSn as seen from a broader flat band at Γ point. Moreover the minority DOS peaks above EF around 1 eV for Mn2ScSi and Mn2ScGe moves below EF at around −0.8 eV in case of Mn2ScSn, thus destroying the half-metallicity. This feature is again visible as flat regions between 0–1 eV for Mn2ScSi and Mn2ScGe at Γ and L point which are pushed below EF for Mn2ScSn. Moreover the bands between −4 eV to −3 eV in both the spins for Mn2ScSi and Mn2ScGe at Γ are pushed towards the EF in case of Mn2ScSn as seen in their respective DOSs. The DOS also reveals the prominent role of Mn around the EF in comparison to Sc and Z (Si, Ge and Sn) atoms in all the three sample materials. Moreover the asymmetry in the bands and DOS between majority and minority spin of these alloys is mainly due to Mn atoms. For the HMs, the band gaps are indirect with the maximum of valence band and the minimum of conduction bands occurring at Γ and X points of the BZ respectively. The band gaps are very narrow, 0.151 eV and 0.051 eV for Mn2ScSi and Mn2ScGe respectively. And as the size of the Z atom increases from Si to Ge, the band gap decreases and eventually disappears for Sn in consistent analogous Fe2MnZ (Z = Si, Ge and Sn),82 Mn2TiZ (Z = Si, Ge and Sn)89 and Co2MnZ (Z = Ge and Sn).90 This indicate the prominence of size of Z atoms in Mn2YZ compounds for controlling the size of the lattice (Table 1) and eventually determining the strength of interaction between the transition elements and overlap of d orbitals resulting in half-metallicity.40 So, with the addition of bigger atomic radius Z, the lattice constant increases and the overlap of d orbitals reduces and ultimately results in loss of HM in Mn2ScSn.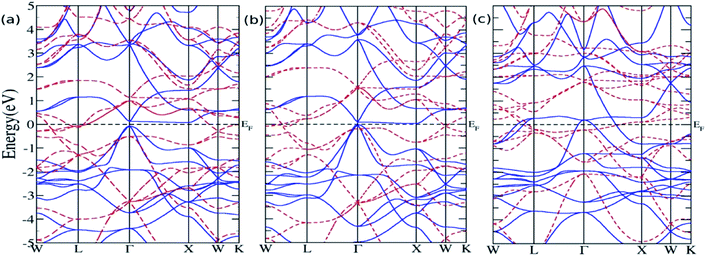 | ||
| Fig. 2 Energy band structure of (a) Mn2ScSi, (b) Mn2ScGe and (c) Mn2ScSn (colour scheme, solid blue lines = minority spin and dash red lines = majority spin). | ||
Further analysis of electronic structure is done by studying their partial density of states (PDOS) as presented in Fig. 4, which gives us insight into the hybridization between atomic orbitals and formation of energy gap in minority spin resulting in HM as explained by Galanakis et al.92 in full Heusler alloys with L21 structure. The sp Z atom forms one s and three p bands fully occupied by electrons. The s state forms band in the core region (not shown in the PDOS) well below from the EF and are well separated from the d bands, whereas on the other hand, the p electrons contribute at around −4 eV and are not completely separated from the d bands. The PDOS clearly shows that around EF, it is the d electrons which play the predominant role and as suggested by Galanakis,92 we shall consider formation of band gap in two steps. The whole crystal has tetrahedral symmetry (Td) but the Mn atoms at 4a and 4b positions obey octahedral symmetry (Oh) with respect to each other and d orbitals splits into doubly degenerate eg and triply degenerate t2g. Therefore, in first step we should consider the interaction of Mn atoms which is schematically shown in Fig. 5. Due to symmetry, eg of Mn at 4a can hybridize only with eg of Mn at 4b and t2g orbitals follow the same trend giving 2 eg and 3 t2g bonding and 2 eu and 3 t1u anti-bonding orbitals (Fig. 5a). The numeral figures before the states give the degeneracy of the orbitals. Now in the second step, these Mn–Mn orbitals again combine with eg and t2g orbitals of Sc atom (Oh) at 4c to give 2 eg and 3 t2g bonding below and 2 eg and 3 t2g anti-bonding orbitals above EF respectively. These anti-bonding eg and t2g orbitals can be seen as peaks in the minority spin PDOS between 3 to 4 eV and the degeneracy of orbitals can be verified by counting the number of bands in the same energy range at Γ point in the bands. The bonding t2g orbitals peaks just below −2 eV in the minority PDOS and which can be seen at Γ point in the bands whereas the eg bonding orbitals peak around −4 eV and is correspondingly appears as doubly degenerate band at Γ point in the band. The 2 eu and 3 t1u orbitals of Mn–Mn hybridization cannot couple with the d orbitals of Sc atom due to their different symmetry and the gap is formed between these non-bonding orbitals as seen from the peaks in the valence band edge and conduction band edge in the PDOS. In the PDOS the representation of eu and t1u remains as eg and t2g respectively and can be seen as doubly degenerate and triply degenerate bands just above and below EF minority spin bands.
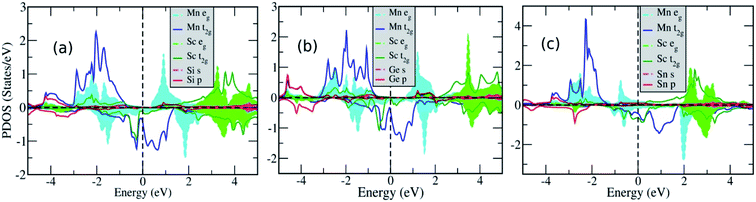 | ||
| Fig. 4 Partial density of states (a) Mn2ScSi (b) Mn2ScGe and (c) Mn2ScSn (dashed lines are filled with same colour). | ||
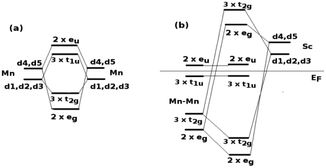 | ||
| Fig. 5 Scheme of d orbitals of Mn2ScZ (Z = Si, Ge and Sn) in Cu2MnAl configuration: (a) Mn–Mn and (b) Mn–Mn–Sc hybridization. | ||
For regular Heusler alloy with L21 structure, the SP rule for total magnetic moment (MT) per formula unit for HMs is MT = (NT − 24) μB, where NT is the total number of valence electron. Thus in the present study with NT = 21, we expect a MT of −3 μB as presented in Table 3. The negative moment comes from the fact that gap occurs in the minority spin states and DOS at EF of majority spin states. The total magnetic moment (MT) per formula unit for Mn2ScSi and Mn2ScGe is almost an integral value of −3.0 μB which also confirms the half-metallic nature in these two compounds. Also, the MT for Mn2ScSn decreases to −5.93 μB deviating from SP rule and clearly indicating the loss of HM and such similar behaviour in magnetic moment was reported by Jain et al.82 in 27 valence electrons system Fe2MnZ (Z = Si, Ge and Sn) with 5.73 μB for Fe2MnSn and 3.0 μB for the rest. Again, Mn predominantly contributes to the MT and determines the magnetic properties of these alloys whereas the contribution from Sc and Z atom to MT is comparatively less as presented by partial magnetic moments in Table 3. Moreover, the magnetic moments of Mn and Sc are aligned in opposite direction with different strength showing the ferrimagnetic ordering of moments. These magnetic behaviours can be understood by examining the DOS (Fig. 3) and PDOS (Fig. 4) of these compounds and this asymmetry in the DOS between majority and minority spins reflects the origin of magnetism. The PDOS explains the opposite alignment of magnetic moment of Mn and Sc atoms in these compounds. The d states of Mn emerge in −2.0 eV below EF in minority spin, whereas around 0.8 eV above EF in majority spin. However, in case of Sc, the d states emerges slightly more in majority spin than in minority spin around −2.0 eV below EF. As a consequence, it is the majority spin of Mn atoms which is predominantly unoccupied giving a large and opposite magnetic moment to Mn in comparison to that of Sc for HMs. This situation is magnified in case of metallic Mn2ScSn, where the asymmetry and occupancy of d states of Mn and Sc in majority and minority states is distinctly visible and results in large magnetic moment of Mn. Here, Table 3 also shows that with increase in the lattice parameter a which increases with the atomic radius of Z atom i.e. on going from Mn2ScSi to Mn2ScSn, the magnetic moment of Mn keeps on decreasing whereas that of Sc increases. This clearly indicates the role of size of Z atom on determining the size of crystal structure and thereby affecting the strength of coupling interaction of moments in these alloys.
| Magnetic moment (in μB) | Mn | Sc | Z | Total (MT) |
|---|---|---|---|---|
| Mn2ScSi | −1.606 | 0.159 | 0.084 | −2.99 |
| Mn2ScGe | −1.646 | 0.213 | 0.073 | −2.98 |
| Mn2ScSn | −3.169 | 0.298 | 0.065 | −5.93 |
4. Conclusions
The ground state electronic and magnetic properties of new Heusler alloys Mn2ScZ (Z = Si, Ge and Sn) have been investigated using density functional theory with the implementation of Hubbard correction term of Coulomb repulsion U to the generalized gradient approximation for exchange correlation functional. All these sample materials were found to crystallize in Cu2MnAl type structure and the stability as well as the possibility of experimental synthesis was determined by calculating the formation energy and from independent elastic constants. The analysis of electronic structure predicted half-metallic character for Mn2ScSi and Mn2ScGe whereas metallic character for Mn2ScSn. The lost of HM in Mn2ScSn is due to the increase in size of crystal which comes from the size of Z atom resulting in lesser overlap of d orbitals consistent to previous reports of analogous alloys. The HM and metallic nature was also confirmed from the study of magnetic properties which showed anti-parallel alignment of magnetic moments of Mn with Sc resulting in ferrimagnetic ordering in these alloys. Moreover, the total magnetic moments per formula unit for half-metals were found to be 3.00 μB which comes from Slating–Pauling rule of 24 and for metal was found to be far more than predicted by above rule, thereby confirming HM in Mn2ScSi and Mn2ScGe whereas metallic nature for Mn2ScSn. Analysis of both electronic and magnetic properties reveals the prominence of size of sp element in these alloys.Conflicts of interest
There are no conflicts to declare.Notes and references
- I. Žutić, J. Fabian and S. D. Sarma, Spintronics: Fundamentals and applications, Rev. Mod. Phys., 2004, 76(2), 323 CrossRef.
- S. A. Wolf, D. D. Awschalom, R. A. Buhrman, J. M. Daughton, S. Von Molnar, M. L. Roukes and D. M. Treger, Spintronics: a spin-based electronics vision for the future, science, 2001, 294(5546), 1488–1495 CrossRef CAS PubMed.
- K. L. Wang, J. G. Alzate and P. K. Amiri, Low-power non-volatile spintronic memory: STT-RAM and beyond, J. Phys. D: Appl. Phys., 2013, 46(7), 074003 CrossRef.
- H. Lee, F. Ebrahimi, P. K. Amiri and K. L. Wang, Low-power, high-density spintronic programmable logic with voltage-gated spin Hall effect in magnetic tunnel junctions, IEEE Magn. Lett., 2016, 7, 1–5 Search PubMed.
- W. Zhao, E. Belhaire, C. Chappert and P. Mazoyer, Spintronic device based non-volatile low standby power SRAM, in 2008 IEEE Computer Society Annual Symposium on VLSI, IEEE, 2008, pp. 40–45 Search PubMed.
- K. Nikolaev, P. Kolbo, T. Pokhil, X. Peng, Y. Chen, T. Ambrose and O. Mryasov, “All-Heusler alloy” current-perpendicular-to-plane giant magnetoresistance, Appl. Phys. Lett., 2009, 94(22), 222501 CrossRef.
- Y. Sakuraba, A. M. Hattori, M. Oogane, Y. Ando, H. Kato, A. Sakuma and H. Kubota, Giant tunneling magnetoresistance in Co2MnSi/AlO/Co2MnSi magnetic tunnel junctions, Appl. Phys. Lett., 2006, 88(19), 192508 CrossRef.
- S. Tsunegi, Y. Sakuraba, M. Oogane, K. Takanashi and Y. Ando, Large tunnel magnetoresistance in magnetic tunnel junctions using a Co2MnSi Heusler alloy electrode and a MgO barrier, Appl. Phys. Lett., 2008, 93(11), 112506 CrossRef.
- T. Ishikawa, T. Marukame, H. Kijima, K. I. Matsuda, T. Uemura, M. Arita and M. Yamamoto, Spin-dependent tunneling characteristics of fully epitaxial magnetic tunneling junctions with a full-Heusler alloy Co2MnSi thin film and a MgO tunnel barrier, Appl. Phys. Lett., 2006, 89(19), 192505 CrossRef.
- Y. Wang, J. Zheng, Z. Ni, R. Fei, Q. Liu, R. Quhe and J. Lu, Half-metallic silicene and germanene nanoribbons: towards high-performance spintronics device, Nano, 2012, 7(05), 1250037 CrossRef.
- H. X. Liu, Y. Honda, T. Taira, K. I. Matsuda, M. Arita, T. Uemura and M. Yamamoto, Giant tunneling magnetoresistance in epitaxial Co2MnSi/MgO/Co2MnSi magnetic tunnel junctions by half-metallicity of Co2MnSi and coherent tunneling, Appl. Phys. Lett., 2012, 101(13), 132418 CrossRef.
- J. Y. T. Wei, N. C. Yeh, R. P. Vasquez and A. Gupta, Tunneling evidence of half-metallicity in epitaxial films of ferromagnetic perovskite manganites and ferrimagnetic magnetite, J. Appl. Phys., 1998, 83(11), 7366–7368 CrossRef CAS.
- K. Ramesha, R. Seshadri, C. Ederer, T. He and M. A. Subramanian, Experimental and computational investigation of structure and magnetism in pyrite Co1−xFexS2: chemical bonding and half-metallicity, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70(21), 214409 CrossRef.
- J. H. Park, S. K. Kwon and B. I. Min, Half-metallic antiferromagnetic double perovskites: LaAVRuO6 (A= Ca, Sr, and Ba), Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65(17), 174401 CrossRef.
- I. Galanakis and E. Şaşıoğlu, High TC half-metallic fully-compensated ferrimagnetic Heusler compounds, Appl. Phys. Lett., 2011, 99(5), 052509 CrossRef.
- S. Wurmehl, G. H. Fecher, H. C. Kandpal, V. Ksenofontov, C. Felser and H. J. Lin, Investigation of Co2FeSi: The Heusler compound with highest Curie temperature and magnetic moment, Appl. Phys. Lett., 2006, 88(3), 032503 CrossRef.
- I. Galanakis, P. Mavropoulos and P. H. Dederichs, Electronic structure and Slater–Pauling behaviour in half-metallic Heusler alloys calculated from first principles, J. Phys. D: Appl. Phys., 2006, 39(5), 765 CrossRef CAS.
- K. Özdoğan, E. Şaşıoğlu and I. Galanakis, Slater-Pauling behavior in LiMgPdSn-type multifunctional quaternary Heusler materials: half-metallicity, spin-gapless and magnetic semiconductors, J. Appl. Phys., 2013, 113(19), 193903 CrossRef.
- S. Chadov, X. Qi, J. Kübler, G. H. Fecher, C. Felser and S. C. Zhang, Tunable multifunctional topological insulators in ternary Heusler compounds, Nat. Mater., 2010, 9(7), 541 CrossRef CAS PubMed.
- T. Graf, S. S. Parkin and C. Felser, Heusler compounds: a material class with exceptional properties, IEEE Trans. Magn., 2011, 47(2), 367–373 CAS.
- A. K. Nayak, M. Nicklas, S. Chadov, P. Khuntia, C. Shekhar, A. Kalache and U. Zeitler, Design of compensated ferrimagnetic Heusler alloys for giant tunable exchange bias, Nat. Mater., 2015, 14(7), 679 CrossRef CAS PubMed.
- S. Fujii, S. Ishida and S. Asano, A half-metallic band structure and Fe2MnZ (Z= Al, Si, P), J. Phys. Soc. Jpn., 1995, 64(1), 185–191 CrossRef CAS.
- S. Ishida, S. Mizutani, S. Fujii and S. Asano, Theoretical prediction of materials to preserve high spin polarization against chemical disorder, Mater. Trans., 2006, 47(1), 31–37 CrossRef CAS.
- L. Hongzhi, Z. Zhiyong, M. Li, X. Shifeng, L. Heyan, Q. Jingping and W. Guangheng, Electronic structure and magnetic properties of Fe2YSi (Y = Cr, Mn, Fe, Co, Ni) Heusler alloys: a theoretical and experimental study, J. Phys. D: Appl. Phys., 2007, 40(22), 7121 CrossRef.
- X. J. Zhang, Z. H. Liu, Y. J. Zhang, H. Y. Liu, G. D. Liu, Y. T. Cui and X. Q. Ma, Theoretical and experimental study of the phase formation for Ti2YAl and Ti2Y′Ga (Y = Co, Fe; Y′= Cr, Fe), Intermetallics, 2016, 73, 26–30 CrossRef CAS.
- W. H. Wang, M. Przybylski, W. Kuch, L. I. Chelaru, J. Wang, Y. F. Lu and J. Kirschner, Magnetic properties and spin polarization of Co2MnSi Heusler alloy thin films epitaxially grown on GaAs (001), Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71(14), 144416 CrossRef.
- S. Mizukami, D. Watanabe, M. Oogane, Y. Ando, Y. Miura, M. Shirai and T. Miyazaki, Low damping constant for Co2FeAl Heusler alloy films and its correlation with density of states, J. Appl. Phys., 2009, 105(7), 07D306 CrossRef.
- V. Asvini, G. Saravanan, R. K. Kalaiezhily, M. M. Raja and K. Ravichandran, Effect of film thickness on soft magnetic behaviour of Fe2CoSi Heusler alloy for spin transfer torque device applications, in AIP Conference Proceedings, AIP Publishing, 2018, p. 130051, Vol. 1942, No. 1 Search PubMed.
- M. P. Geisler, M. Meinert, J. Schmalhorst, G. Reiss and E. Arenholz, Multiple phases in sputtered Cr2CoGa films, J. Alloys Compd., 2014, 598, 213–216 CrossRef CAS.
- R. Knut, P. Svedlindh, O. Mrvasov, K. Gunnarsson, P. Warnicke, D. A. Arena, M. Bjorck, A. J. Dennison, A. Sahoo, S. Mukherjee and D. D. Sarma, Interface characterization of Co2MnGe/Rh2CuSn Heusler multilayers, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88(13), 134407 CrossRef.
- H. G. Zhang, C. Z. Zhang, W. Zhu, E. K. Liu, W. H. Wang, H. W. Zhang, J. L. Cheng, H. Z. Luo and G. H. Wu, Significant disorder-induced enhancement of the magnetization of Fe2CrGa by ball mining, J. Appl. Phys., 2013, 114(1), 013903 CrossRef.
- J. Winterlik, S. Chadov, A. Gupta, V. Alijani, T. Gasi, K. Filsinger and J. Kübler, Design Scheme of New Tetragonal Heusler Compounds for Spin-Transfer Torque Applications and its Experimental Realization, Adv. Mater., 2012, 24(47), 6283–6287 CrossRef CAS PubMed.
- C. Felser, V. Alijani, J. Winterlik, S. Chadov and A. K. Nayak, Tetragonal Heusler compounds for spintronics, IEEE Trans. Magn., 2013, 49(2), 682–685 CAS.
- A. K. Nayak, C. Shekhar, J. Winterlik, A. Gupta and C. Felser, Mn2PtIn: A tetragonal Heusler compound with exchange bias behavior, Appl. Phys. Lett., 2012, 100(15), 152404 CrossRef.
- A. K. Nayak, M. Nicklas, S. Chadov, C. Shekhar, Y. Skourski, J. Winterlik and C. Felser, Large zero-field cooled exchange-bias in bulk Mn2PtGa, Phys. Rev. Lett., 2013, 110(12), 127204 CrossRef CAS PubMed.
- C. Felser, L. Wollmann, S. Chadov, G. H. Fecher and S. S. Parkin, Basics and prospective of magnetic Heusler compounds, APL Mater., 2015, 3(4), 041518 CrossRef.
- G. D. Liu, X. F. Dai, H. Y. Liu, J. L. Chen, Y. X. Li, G. Xiao and G. H. Wu, Mn2CoZ ( Z = Al, Ga, In, Si, Ge, Sn, Sb) compounds: Structural, electronic, and magnetic properties, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77(1), 014424 CrossRef.
- P. Entel, M. Siewert, M. E. Gruner, H. C. Herper, D. Comtesse, R. Arróyave and F. Albertini, Complex magnetic ordering as a driving mechanism of multifunctional properties of Heusler alloys from first principles, Eur. Phys. J. B, 2013, 86(2), 65 CrossRef.
- M. Meinert, J. M. Schmalhorst and G. Reiss, Ab initio prediction of ferrimagnetism, exchange interactions and Curie temperatures in Mn2TiZ Heusler compounds, J. Phys.: Condens. Matter, 2010, 23(3), 036001 CrossRef PubMed.
- M. Meinert, J. M. Schmalhorst and G. Reiss, Exchange interactions and Curie temperatures of Mn2CoZ compounds, J. Phys.: Condens. Matter, 2011, 23(11), 116005 CrossRef PubMed.
- T. Gasi, A. K. Nayak, J. Winterlik, V. Ksenofontov, P. Adler, M. Nicklas and C. Felser, Exchange-spring like magnetic behavior of the tetragonal Heusler compound Mn2FeGa as a candidate for spin-transfer torque, Appl. Phys. Lett., 2013, 102(20), 202402 CrossRef.
- R. Weht and W. E. Pickett, Half-metallic ferrimagnetism in Mn2VAl, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60(18), 13006 CrossRef CAS.
- T. Kubota, K. Kodama, T. Nakamura, Y. Sakuraba, M. Oogane, K. Takanashi and Y. Ando, Ferrimagnetism in epitaxially grown Mn2VAl Heusler alloy investigated by means of soft x-ray magnetic circular dichroism, Appl. Phys. Lett., 2009, 95(22), 222503 CrossRef.
- H. Luo, Z. Zhu, G. Liu, S. Xu, G. Wu, H. Liu and Y. Li, Prediction of half-metallic properties for the Heusler alloys Mn2CrZ (Z = Al, Ga, Si, Ge, Sb): A first-principles study, J. Magn. Magn. Mater., 2008, 320(3–4), 421–428 CrossRef CAS.
- H. Zenasni, H. I. Faraoun and C. Esling, First-principle prediction of half-metallic ferrimagnetism in Mn-based full-Heusler alloys with highly ordered structure, J. Magn. Magn. Mater., 2013, 333, 162–168 CrossRef CAS.
- H. Z. Luo, H. W. Zhang, Z. Y. Zhu, L. Ma, S. F. Xu, G. H. Wu and H. B. Xu, Half-metallic properties for the Mn2FeZ (Z = Al, Ga, Si, Ge, Sb) Heusler alloys: A first-principles study, J. Appl. Phys., 2008, 103(8), 083908 CrossRef.
- V. V. Sokolovskiy, M. A. Zagrebin, Y. A. Sokolovskaya and V. D. Buchelnikov, Structural and Magnetic Properties of Mn2NiZ (Z= Ga, In, Sn, Sb) Heusler Alloys from Ab initio Calculations, in Solid State Phenomena, Trans Tech Publications, 2015, Vol. 233, pp. 229–232 Search PubMed.
- L. Wollmann, S. Chadov, J. Kübler and C. Felser, Magnetism in cubic manganese-rich Heusler compounds, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90(1), 214420 CrossRef.
- L. Wollmann, S. Chadov, J. Kübler and C. Felser, Magnetism in tetragonal manganese-rich Heusler compounds, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92(6), 064417 CrossRef.
- M. Tas, E. Şaşıoğlu, C. Friedrich, S. Blügel and I. Galanakis, Design of L21-type antiferromagnetic semiconducting full-Heusler compounds: A first principles DFT+GW study, J. Appl. Phys., 2017, 121(5), 053903 CrossRef.
- S. S. Shastri and S. K. Pandey, Two functionals approach in DFT for the prediction of thermoelectric properties of Fe2ScX (X= P, As, Sb) full Heusler compounds, arXiv preprint arXiv:1904.04322, 2019.
- J. L. Da Silva, M. V. Ganduglia-Pirovano and J. Sauer, Formation of the cerium orthovanadate CeVO4: DFT+U study, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76(12), 125117 CrossRef.
- M. Derzsi, P. Piekarz, P. T. Jochym, J. Łażewski, M. Sternik, A. M. Oleś and K. Parlinski, Effects of Coulomb interaction on the electronic structure and lattice dynamics of the Mott insulator Fe2SiO4 spinel, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79(20), 205105 CrossRef.
- A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, Density-functional theory and strong interactions: Orbital ordering in Mott-Hubbard insulators, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52(8), R5467 CrossRef CAS PubMed.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Band theory and Mott insulators: Hubbard U instead of Stoner I, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44(3), 943 CrossRef CAS PubMed.
- I. de PR Moreira, F. Illas and R. L. Martin, Effect of Fock exchange on the electronic structure and magnetic coupling in NiO, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65(15), 155102 CrossRef.
- H. Tang, F. Levy, H. Berger and P. E. Schmid, Urbach tail of anatase TiO2, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52(11), 7771 CrossRef CAS PubMed.
- M. Sodupe, J. Bertran, L. Rodríguez-Santiago and E. J. Baerends, Ground State of the (H2O)2+ Radical Cation: DFT versus Post–Hartree−Fock Methods, J. Phys. Chem. A, 1999, 103(1), 166–170 CrossRef CAS.
- S. Wurmehl, G. H. Fecher, H. C. Kandpal, V. Ksenofontov, C. Felser, H. J. Lin and J. Morais, Geometric, electronic, and magnetic structure of Co2FeSi: Curie temperature and magnetic moment measurements and calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72(18), 184434 CrossRef.
- S. Wurmehl, G. H. Fecher, H. C. Kandpal, V. Ksenofontov, C. Felser and H. J. Lin, Investigation of Co2FeSi: The Heusler compound with highest Curie temperature and magnetic moment, Appl. Phys. Lett., 2006, 88(3), 032503 CrossRef.
- T. Bandyopadhyay and D. D. Sarma, Calculation of Coulomb interaction strengths for 3d transition metals and actinides, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39(6), 3517 CrossRef CAS PubMed.
- C. Herring, Magnetism, Academic Press, New York and London, 1966, vol. IV, p. 228 Search PubMed.
- B. N. Cox, M. A. Coulthard and P. Lloyd, A calculation of the Coulomb correlation energy, U, for transition metals in Hubbard's model, J. Phys. F: Met. Phys., 1974, 4(6), 807 CrossRef CAS PubMed.
- D. Do, M. S. Lee and S. D. Mahanti, Effect of onsite Coulomb repulsion on thermoelectric properties of full-Heusler compounds with pseudogaps, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84(12), 125104 CrossRef.
- S. Yousuf and D. C. Gupta, Insight into electronic, mechanical and transport properties of quaternary CoVTiAl: spin-polarized DFT+U approach, J. Mater. Sci. Eng. B, 2017, 221, 73–79 CrossRef CAS.
- A. H. Reshak, Transport properties of Co-based Heusler compounds Co2VAl and Co2VGa: spin-polarized DFT+U, RSC Adv., 2016, 6(59), 54001–54012 RSC.
- D. P. Rai, A. Shankar, M. P. Ghimire and R. K. Thapa, A comparative study of a Heusler alloy Co2FeGe using LSDA and LSDA+U, Phys. B, 2012, 407(18), 3689–3693 CrossRef CAS.
- D. P. Rai and R. K. Thapa, An abinitio study of the half-metallic properties of Co2TGe (T= Sc, Ti, V, Cr, Mn, Fe): LSDA+U method, J. Korean Phys. Soc., 2013, 62(11), 1652–1660 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni and A. Dal Corso, QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21(39), 395502 CrossRef PubMed.
- P. Blaha, K. Schwarz, G. K. Madsen, D. Kvasnicka and J. Luitz, wien2k. An augmented plane wave+ local orbitals program for calculating crystal properties, 2017 Search PubMed.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13(12), 5188 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef CAS PubMed.
- M. Lazzeri, C. Attaccalite, L. Wirtz and F. Mauri, Impact of the electron-electron correlation on phonon dispersion: Failure of LDA and GGA DFT functionals in graphene and graphite, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78(8), 081406 CrossRef.
- N. Zaki, H. Park, R. M. Osgood, A. J. Millis and C. A. Marianetti, Failure of DFT-based computations for a stepped-substrate-supported correlated Co wire, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89(20), 205427 CrossRef.
- B. Barbiellini, E. G. Moroni and T. Jarlborg, Effects of gradient corrections on electronic structure in metals, J. Phys.: Condens. Matter, 1990, 2(37), 7597 CrossRef CAS.
- A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, Density-functional theory and strong interactions: Orbital ordering in Mott-Hubbard insulators, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52(8), R5467 CrossRef CAS PubMed.
- O. Gunnarsson, O. K. Andersen, O. Jepsen and J. Zaanen, Density-functional calculation of the parameters in the Anderson model: Application to Mn in CdTe, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39(3), 1708 CrossRef PubMed.
- J. Van Den Brink, M. B. J. Meinders and G. A. Sawatzky, Influence of screening effects and inter-site Coulomb repulsion on the insulating correlation gap, Phys. B, 1995, 206, 682–684 CrossRef.
- S. Galehgirian and F. Ahmadian, First principles study on half-metallic properties of Heusler compounds Ti2VZ (Z = Al, Ga, and In), Solid State Commun., 2015, 202, 52–57 CrossRef CAS.
- H. Luo, Y. Xin, B. Liu, F. Meng, H. Liu, E. Liu and G. Wu, Competition of L21 and XA structural ordering in Heusler alloys X2CuAl (X = Sc, Ti, V, Cr, Mn, Fe, Co, Ni), J. Alloys Compd., 2016, 665, 180–185 CrossRef CAS.
- D. Bensaid, T. Hellal, M. Ameri, Y. Azzaz, B. Doumi, Y. Al-Douri and F. Benzoudji, First-principle investigation of structural, electronic and magnetic properties in Mn2RhZ(Z= Si, Ge, and Sn) Heusler alloys, J. Supercond. Novel Magn., 2016, 29(7), 1843–1850 CrossRef CAS.
- V. K. Jain, N. Lakshmi, R. Jain and A. R. Chandra, Electronic Structure, Elastic, Magnetic, and Optical Properties of Fe2MnZ (Z = Si, Ge, and Sn) Full Heusler Alloys: First-Principle Calculations, J. Supercond. Novel Magn., 2019, 32(3), 739–749 CrossRef CAS.
- H. Joshi, D. P. Rai, L. Hnamte, A. Laref and R. K. Thapa, A theoretical analysis of elastic and optical properties of half Heusler MCoSb (M= Ti, Zr and Hf), Heliyon, 2019, 5(3), e01155 CrossRef PubMed.
- S. C. Wu, S. S. Naghavi, G. H. Fecher and C. Felser, A critical study of the elastic properties and stability of Heusler compounds: Phase change and tetragonal X2YZ compounds, J. Mod. Phys., 2018, 09(04), 83535 Search PubMed.
- M. Born and K. Huang, Dynamical theory of crystal lattices, Clarendon press, 1954 Search PubMed.
- L. Zuo, M. Humbert and C. Esling, Elastic properties of polycrystals in the Voigt-Reuss-Hill approximation, J. Appl. Crystallogr., 1992, 25(6), 751–755 CrossRef.
- A. Abada, K. Amara, S. Hiadsi and B. Amrani, First principles study of a new half-metallic ferrimagnets Mn2-based full Heusler compounds: Mn2ZrSi and Mn2ZrGe, J. Magn. Magn. Mater., 2015, 388, 59–67 CrossRef CAS.
- I. N. Frantsevich, F. F. Voronov and S. A. Bakuta, Elastic Constants and Elastic Moduli of Metals and Nonmetals, Naukova Dnmka, Kiev, 1982 Search PubMed.
- H. Zenasni, H. I. Faraoun and C. Esling, First-principle prediction of half-metallic ferrimagnetism in Mn-based full-Heusler alloys with highly ordered structure, J. Magn. Magn. Mater., 2013, 333, 162–168 CrossRef CAS.
- S. Ishida, S. Fujii, S. Kashiwagi and S. Asano, Search for half-metallic compounds in Co2MnZ (Z= IIIb, IVb, Vb element), J. Phys. Soc. Jpn., 1995, 64(6), 2152–2157 CrossRef CAS.
- I. Galanakis, K. Özdoğan, E. Şaşıoğlu and B. Aktaş, Doping of Mn 2VAl and Mn2VSi Heusler alloys as a route to half-metallic antiferromagnetism, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75(9), 092407 CrossRef.
- I. Galanakis, P. H. Dederichs and N. Papanikolaou, Slater-Pauling behavior and origin of the half-metallicity of the full-Heusler alloys, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66(17), 174429 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |