Open Access Article
Open Access ArticleCoronary artery decision algorithm trained by two-step machine learning algorithm
Young Woo Kima,
Hee-Jin Yua,
Jung-Sun Kimb,
Jinyong Hac,
Jongeun Choi*a and
Joon Sang Lee *a
*a
aDepartment of Mechanical Engineering, Yonsei University, Korea. E-mail: joonlee@yonsei.ac.kr; jongeunchoi@yonsei.ac.kr
bDivision of Cardiology, Severance Cardiovascular Hospital, Yonsei University College of Medicine, Korea
cDepartment of Electrical Engineering, Sejong University, Korea
First published on 24th January 2020
Abstract
A two-step machine learning (ML) algorithm for estimating both fractional flow reserve (FFR) and decision (DEC) for the coronary artery is introduced in this study. The primary purpose of this model is to suggest the possibility of ML-based FFR to be more accurate than the FFR calculation technique based on a computational fluid dynamics (CFD) method. For this purpose, a two-step ML algorithm that considers the flow characteristics and biometric features as input features of the ML model is designed. The first step of the algorithm is based on the Gaussian progress regression model and is trained by a synthetic model using CFD analysis. The second step of the algorithm is based on a support vector machine with patient data, including flow characteristics and biometric features. Consequently, the accuracy of the FFR estimated from the first step of the algorithm was similar to that of the CFD-based method, while the accuracy of DEC in the second step was improved. This improvement in accuracy was analyzed using flow characteristics and biometric features.
Introduction
Fractional flow reserve (FFR) is known as the gold standard for decision-making in coronary stenosis.1 The primary advantage of FFR measurement is that it helps to avoid unnecessary stent insertion. The importance of FFR was confirmed by the FFR versus angiography for multivessel evaluation study, which demonstrated that an FFR-guided group exhibited significantly lower rates of major adverse effects compared with an angiography-guided group.2 The pressure wire-based FFR, or the experimental FFR (FFREXP), is an original method for invasively measuring FFR. In this method, blood pressure at the proximal lesion and distal lesion of stenosis is directly measured using a wire;3 however, the procedural time and expenses of FFR are not negligible, and there is a risk of complication because of adenosine injection.4To overcome these problems, an FFR calculation technique based on computational fluid dynamics (CFD) has been developed. The CFD-based FFR calculation technique, or CFD-FFR, can avoid some invasive procedures by using geometric information from computed tomography (CT) or optical coherence tomography (OCT) images, along with the estimated or assumed boundary conditions. According to Coenen et al., the accuracy of FFRCFD is ∼80% with a sensitivity of 87.5% and a specificity of 67.5%;5 however, it requires expensive computational resources and a computational time of >8 h.6
Recently, to overcome the limitations of FFRCFD, machine learning (ML) methods have been studied. Compared with the CFD method, ML can perform calculations in few minutes using lesser computational resources. Researchers from various medical fields are adopting ML for diagnosis and disease prediction. For example, Tripathy et al. performed a study on classification of breast cancer using cellular images with ML algorithm.7 Moreover, Khanmohammadi et al. attempted to apply ML algorithm for diagnosing basal cell carcinoma via blood sample.8
Certain studies related to cell rheology such as the study by Kihm et al. used ML to classify cell types in blood.9 Furthermore, attempts have been made to apply ML to estimate FFR. Kim et al. trained an ML model using intravascular ultrasound (IVUS) images to predict FFR and achieved an accuracy of 81%.10 The limitations of their study were that the process was tedious and the segmentation of the IVUS image step was manual, which made it difficult to further increase the input data for the ML training. Another approach to address the lack of ML training data is to use a synthetic model. For example, Itu et al. generated a synthetic model of the circulatory system for ML training;11 the model was generated by randomly extracting the characteristics of patient data. Then, CFD was used to calculate the FFR from these composite models. Compared with patient data, synthetic models can be infinitely amplified. Furthermore, because the features can be easily controlled, the uniformity of the data can be enhanced. Consequently, the ML model could estimate the FFR with the same accuracy as FFRCFD; however, this indicates that the accuracy of ML FFR is limited to that of FFRCFD, which is 83% at maximum.
Tesche et al. and Hu et al. attempted to use synthetic models with other ML models to achieve an accuracy similar to that of the FFRCFD.12,13 Using ML-based FFR to increase the computational speed with accuracy constraints is an ineffective approach. The advantage of ML is the possibility of considering various features and determining their relationships. By maximizing the quality and quantity of the input features, the accuracy of ML-based FFR could surpass that of FFRCFD.
In this study, a two-step ML algorithm for estimating both FFR and decision (DEC) is introduced. The primary purpose of this model is to suggest the possibility of ML-based FFR to be more accurate than FFRCFD. For this purpose, a two-step ML algorithm that considers flow characteristics and biometric features as input features of ML is designed. Flow characteristics are the primary cause of pressure drop; thus, FFR is affected by both stenosis severity and flow characteristics. The relationship between the geometric features and FFR has been analyzed based on flow characteristics such as vorticity or turbulence intensity.14,15 By providing flow characteristics as input parameters, the ML algorithm can have more information for increasing its accuracy.
Furthermore, regardless of the geometric features, biometric features can affect FFR. The limitation of CFD is the absence of a method that considers biometric features. Various attempts have been made to reflect biometric features, such as age or body mass index (BMI), in CFD;16–18 however, these models are based on various assumptions and empirical equations that result in low accuracy. If these features can be analyzed using ML, the accuracy of ML-based FFR could surpass that of FFRCFD. In this study, a two-step ML algorithm was developed to efficiently handle the flow characteristics and biometric features.
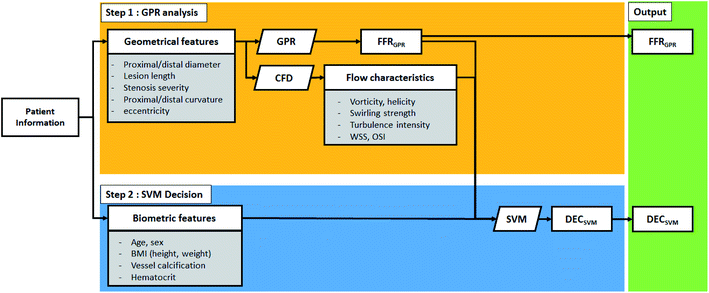
The summary of the algorithm process is shown in Fig. 1. This algorithm separately provides both estimated FFR and DEC. In the first step, the Gaussian progress regression (GPR) model is used to calculate FFRGPR. In the second step, support vector machine (SVM) is used to calculate DECSVM.19 The GPR model is trained from the CFD results of the synthetic model; therefore, the target accuracy of the FFRGPR is the same as that of the FFRCFD. However, the SVM model is trained by both FFRGPR and flow characteristics and biometric features; therefore, the target accuracy of DECSVM should be higher than those of FFRGPR or FFRCFD.
This study focuses on categorizing and analyzing the mismatched cases of the two-step ML algorithm. Mismatch is defined as the wrong estimation of either FFR or DEC compared to FFREXP or DECEXP. To prove the need for the additional features, the flow characteristics and biometric features are analyzed for these mismatched cases.
Numerical methods
Lattice Boltzmann method
The lattice Boltzmann method is extensively used to solve microfluidics-related problems.20–23 The Bhatnagar–Gross–Krook model with a single relaxation time is used to solve an incompressible fluid.24 The governing equation with the forcing term can be written as follows:
 | (1) |
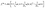 | (2) |
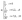 | (3) |
 | (4) |
In eqn (1), the density distribution function fi(x,t) indicates the proportion of particles moving with the i-th lattice velocity at lattice site x and time t; Δt is the time step; τ is the particle relaxation time; ei is the discrete microscopic velocity; fi is the local equilibrium distribution function; and  is the speed of sound with c = (Δx/Δt). The fluid density ρ and velocity u can be calculated using the following formula:
is the speed of sound with c = (Δx/Δt). The fluid density ρ and velocity u can be calculated using the following formula:
 | (5) |
The kinematic viscosity of plasma is given as follows:
 | (6) |
Moreover, the local shear stress and local dynamic viscosity can be calculated as follows:
 | (7) |
 | (8) |
The inlet boundary condition of the simulation was given as the pulsatile pressure inlet, with a maximum pressure and minimum pressure were obtained from the patient information. Also, for the outlet boundary condition, the Windkessel model was used to reflect the compliance of the blood vessel, which was estimated from the height, BMI, and age of the patients. Note that for the synthetic models, the inlet and outlet parameters are randomized.
Biometric data and OCT-CT fusion image
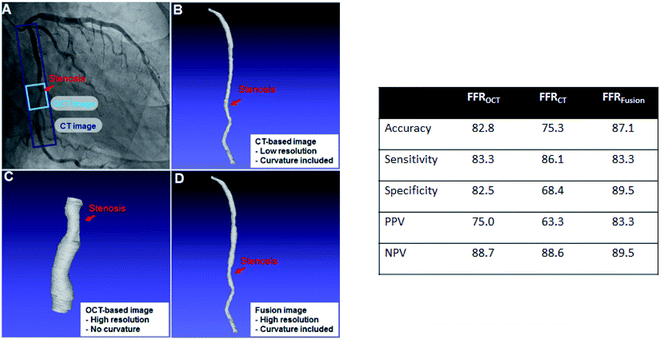
The 3D image of the vessel for each patient can be obtained by reconstructing OCT and CT images. As reference, the FFREXP of a patient is measured using a pressure wire. Moreover, DECEXP is defined to have the value of 1 when stent surgery is required (FFR < 0.8) and 0 when it is not required (FFR ≥ 0.8). Furthermore, various biometric features, such as age, BMI, calcium score, and hematocrit, are collected along with the vessel geometry and FFREXP. The selection of the base 3D image for CFD analysis is important as geometric characteristics, such as resolution or curvature, can affect the FFR.25,26 Both the OCT and CT images are merged to obtain an OCT-CT fusion image, as shown in Fig. 2. While OCT can obtain a high-resolution image of the lumen, the curvature of the vessels cannot be measured by this method. By fusing two images, more reliable information about coronary stenosis can be obtained by the contribution of the delicate vessel curvature of the coronary CT image and the precise lumen contour of the OCT image.For ML training, geometric features are extracted from the OCT-CT fusion image. The extracted features are diameter; length; the curvatures of the proximal, central, and distal segments of the lumen; and the cross section eccentricity. Table 1 lists the geometric features and their average, minimum, and maximum values.
| Average | Minimum | Maximum | |
|---|---|---|---|
| Total length (mm) | 3.8 | 1.7 | 7.3 |
| Proximal area (mm2) | 0.81 | 0.54 | 0.94 |
| Center area (mm2) | 0.73 | 0.48 | 0.97 |
| Distal area (mm2) | 0.76 | 0.53 | 0.94 |
| Total curvature (degree) | 21 | 0 | 90 |
| Cross section eccentricity (%) | 31 | 4 | 78 |
Also, the synthetic vessel model is generated to amplify the quantity of data required for training the ML algorithm. The synthetic model is generated using the same geometric features extracted from the OCT-CT fusion image. Each value was randomized within a range of maximum/minimum values from patient data. Moreover, the biometric values used in fluid or boundary conditions were randomized. Table 1 lists the exact range of values of each parameter. The synthetic models are used to train the first step of our two-step algorithm.
Two-step ML algorithm training process
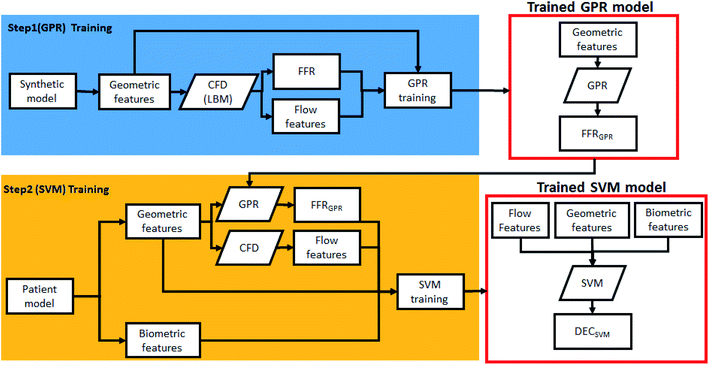
Fig. 3 shows the overall method of training the two-step ML algorithm. In summary, the first step is to train the GPR model using the synthetic model, while the second step is to train the SVM model with patient data. Each models are selected by considering the quality of input data (distance of data and outliers), along with model tests.GPR is able to statistically model and predict an arbitrary smooth function even with small number of observations.27–30 A Gaussian progress (GP) is a set of random variables which have a joint Gaussian distribution for any finite number of them. If {f(x), x ∈ Rd} is a GP, then given n observations x1, x2,…,xn, the joint distribution of the random variables f(x1), f(x2),…, f(xn) is Gaussian. A GP is defined by its mean function m(x) and covariance function k(x,x′), which becomes:
| E(f(x)) = m(x) | (9) |
| E[{f(x) − m(x)}{f(x′) − m(x′)}] = k(x,x′) | (10) |
From the model h(x)Tβ + f(x), where f(x) are from a zero mean GP with covariance function, or f(x) ∼ GP(0,k(x,x′)). h(x) are a set of basis functions that transform the original feature vector x in Rd into a new feature vector h(x) in Rp. β is a p-by-1 vector of basis function coefficients. This model represents a GPR model. An instance of response y can be modeled as
| P(yi|f(xi),xi) ∼ N(yi|h(xi)Tβ + f(xi), σ2 | (11) |
SVM is a widely used classifier that uses supervised machine learning methods.31,32 The purpose of the SVM is to construct an optimal hyperplane that separates the sample into its maximum margins. The SVM handles the classification of nonlinear data by nonlinear mapping the input space to the higher dimensional feature space using the appropriate kernel.33
The major advantage of SVM is that it guarantees the global optimality.34 Let there be N data points  where
where  is the ith feature vector, and yi ∈ {−1, +1} is ith class label. Then, the hyperplane decision function f(x) = sgn((wTx) + b), where w is a weight vector and b is a bias, can be expressed as
is the ith feature vector, and yi ∈ {−1, +1} is ith class label. Then, the hyperplane decision function f(x) = sgn((wTx) + b), where w is a weight vector and b is a bias, can be expressed as
 | (12) |
 | (13) |
Features used in this study consist of biometric features including age, BMI, vessel calcification, etc. and dynamic features related to flow characteristics including vorticity, helicity, OSI, etc. Each flow characteristic has 11 points along the direction of the length of the vessel. Using these points, dynamic features were made by considering raw data, max/min value, max/min index, differences between points, derivatives, max/min value/index of derivatives, and area under the curve. A set of 94 features is extracted from each of the six flow characteristics and 14 demographic features are added to create a total of 580 features.
Also, before training SVM model, feature selection is performed. Feature selection is an essential technique in machine learning. Highly correlated, irrelevant features increase operation time and computational load and have a negative impact on performance. Feature selection techniques can be used to prevent overfitting and to improve model performance with minimizing variance and maximizing model the generalizability of the model. In this paper, Boruta is employed as the feature selection method. Boruta is an all-relevant feature selection method and one of the wrapper algorithms on the Random Forest.35 It works through the following procedure:
(1) Add copies of all features to data set and shuffle them (which are called shadow features.)
(2) Train the Random forest classifier for extended data set and gather the feature importance scores that are Z scores.
(3) Check the importance of real features by comparing the Z scores of real features to the maximum Z score of the shadow feature and remove real features with lower Z scores.
(4) Repeat the process until the importance is assigned to all features, or until the algorithm reaches a specifically set limit for the Random forest runs.
The result of the Boruta algorithm is to divide the features into confirmed and rejected.
Results
ML result
Twenty patient cases were used to test the trained two-step algorithm. Table 2 presents the ML result. As seen in the table, the result cases are categorized into four types for further analysis: category 1 comprises the matched cases between experimental results and the algorithm for both FFRGPR and DECSVM; category 2 comprises the cases that FFRGPR mismatched but DECSVM matched; category 3 comprises cases where FFRGPR is matched but DECSVM is mismatched; and category 4 is the case where both that FFRGPR and DECSVM are mismatched. In terms of the two-step algorithm, category 2 is the most important one because it indicates that the two-step algorithm could determine an error in the CFD method, indicating the possibility of ML having a higher accuracy. However, category 3 includes cases where the algorithm had errors that should be fixed. Because the number of cases in category 2 (four cases) exceeded that in category 3 (two cases), it can be confirmed that DECSVM can provide more information than FFRGPR. Table 3 lists the accuracy, sensitivity, positive predictive value (PPV), and negative predictive value (NPV) for 20 cases. Accuracy is defined as the percentage of correctly guessed cases, for both positive and negative results by FFR ≥ 0.8. Sensitivity is defined as correctly guessed cases among FFREXP ≥ 0.8 cases, while specificity is defined as correctly guessed cases among FFREXP < 0.8 cases. Also, PPV is defined as correctly guessed cases among FFRGPR ≥ 0.8 or DECSVM = 0 cases, while NPV is defined as correctly guessed cases among FFRGPR < 0.8 or DECSVM = 1 cases.| Number | Patient ID | FFREXP | DECEXP | FFRCFD | FFRGPR | DECSVM | Category |
|---|---|---|---|---|---|---|---|
| 1 | F155 | 0.38 | 1 | 0.722 | 0.723 | 1 | 1 (matched) |
| 2 | F187 | 0.53 | 1 | 0.624 | 0.622 | 1 | |
| 3 | F172 | 0.71 | 1 | 0.767 | 0.773 | 1 | |
| 4 | F200 | 0.78 | 1 | 0.696 | 0.701 | 1 | |
| 5 | F134 | 0.79 | 1 | 0.704 | 0.698 | 1 | |
| 6 | F194 | 0.85 | 0 | 0.842 | 0.838 | 0 | |
| 7 | F87 | 0.86 | 0 | 0.904 | 0.906 | 0 | |
| 8 | F133 | 0.87 | 0 | 0.823 | 0.819 | 0 | |
| 9 | F18 | 0.9 | 0 | 0.901 | 0.901 | 0 | |
| 10 | F176 | 0.91 | 0 | 0.847 | 0.844 | 0 | |
| 11 | F201 | 0.94 | 0 | 0.926 | 0.928 | 0 | |
| 12 | F152 | 0.88 | 0 | 0.752 | 0.745 | 0 | 2 (only SVM matched) |
| 13 | F188 | 0.88 | 0 | 0.782 | 0.784 | 0 | |
| 14 | F159 | 0.90 | 0 | 0.759 | 0.763 | 0 | |
| 15 | F198 | 0.77 | 1 | 0.789 | 0.8140 | 1 | |
| 16 | F178 | 0.79 | 1 | 0.799 | 0.7942 | 0 | 3 (only GPR matched) |
| 17 | F163 | 0.78 | 1 | 0.799 | 0.7920 | 0 | |
| 18 | F136 | 0.6 | 1 | 0.86 | 0.8537 | 0 | 4 (mismatched) |
| 19 | F116 | 0.77 | 1 | 0.829 | 0.8291 | 0 | |
| 20 | F168 | 0.94 | 0 | 0.760 | 0.7512 | 1 |
| FFRCFD | FFRGPR | DECSVM | |
|---|---|---|---|
| Accuracy | 65 | 65 | 75 |
| Sensitivity | 70 | 70 | 50 |
| Specificity | 60 | 60 | 80 |
| PPV | 75 | 75 | 83 |
| NPV | 25 | 25 | 64 |
The performance of FFRGPR was not very different from that of FFRCFD. However, the accuracy of DECSVM was slightly higher than that of FFRGPR with higher specificity but lower sensitivity. Furthermore, both the PPV and NPV of DECSVM were higher than those of FFRGPR.
Fig. 4 shows the error percentage with data index aligned by FFRGPR. The error value was calculated by the difference between FFREXP and FFRGPR. The average error percentage was 27.46% when FFREXP < 0.75 (4 cases), 3.80% when 0.75 ≤ FFREXP < 0.85 (6 cases), and 12.70% when FFREXP ≥ 0.85 (10 cases).
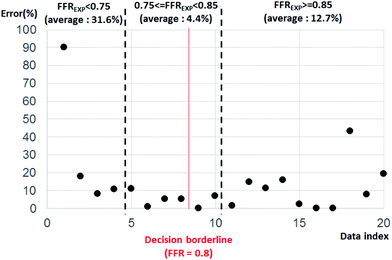 | ||
| Fig. 4 Error percentage by data index aligned by FFREXP. The average error percentage was 27.46% when FFREXP < 0.75, 3.80% when 0.75 ≤ FFREXP < 0.85, and 12.70% when FFREXP ≥ 0.85. | ||
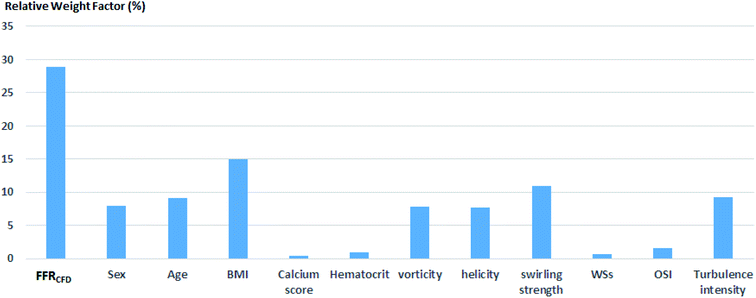
Because the decision borderline, or where DECEXP value changes, was at FFREXP = 0.8, the most important region was when 0.75 ≤ FFREXP < 0.85. Note that the error percentage was the lowest in this region. Fig. 5 shows the relative weight factor of each features when the SVM model was trained. A higher weight factor indicates that the DECSVM is more affected by that feature.
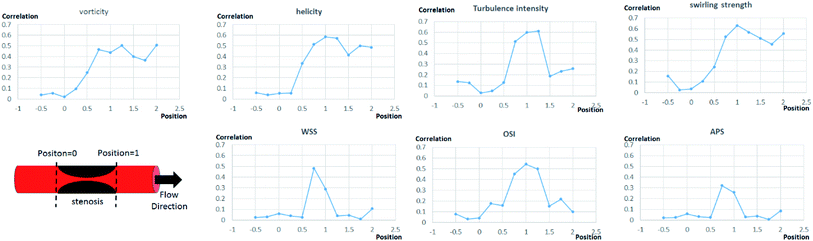
Flow characteristics analysis
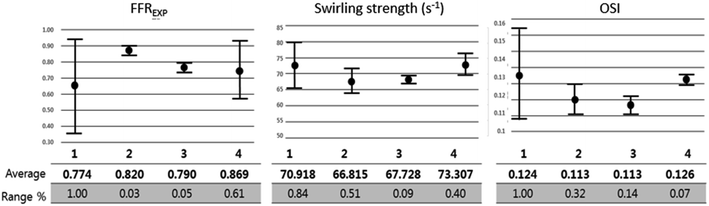
Further analysis of each category was performed in terms of the flow characteristics, and we analyzed two types of flow characteristics. The first type is related to secondary flow, which includes vorticity, helicity, swirling strength, and turbulence intensity; however, the second type is related to the wall shear, including wall shear stress (WSS), oscillatory shear index (OSI), and axial plaque stress (APS). Fig. 6 shows the correlation between flow features and FFREXP. The position between −1 and 0 is the proximal lumen, that between 0 and 1 is the center lumen, and that between 1 and 2.5 is the distal lumen. Most of the features had the highest correlation when the distance was near 1.0. The wall shear features had an overall lower correlation compared with the secondary flow features, and the swirling strength showed the highest correlation among other features. This confirms that flow energy loss by secondary flow was dominant compared with other wall shear features.Fig. 7 shows pressure, vorticity, and WSS of 20 cases separated by four categories. Moreover, it shows the contours of pressure, vorticity, and WSS with sample cases from each category. In Fig. 7, it is important to note the range of values and not only the average value. If the range of a feature in category 2 or 3 is similar to that in categories 1 and 4, it indicates that the feature does not contribute to the mismatch. However, if this range is smaller in category 2 or 3, it indicates that the feature might be related to the mismatch and additional investigation is required. Fig. 8 shows that the FFREXP, vorticity, and OSI showed a smaller range in categories 2 and 3 compared with category 1.
Biometric parameter analysis
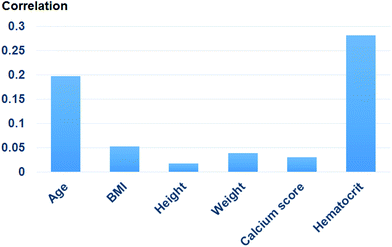
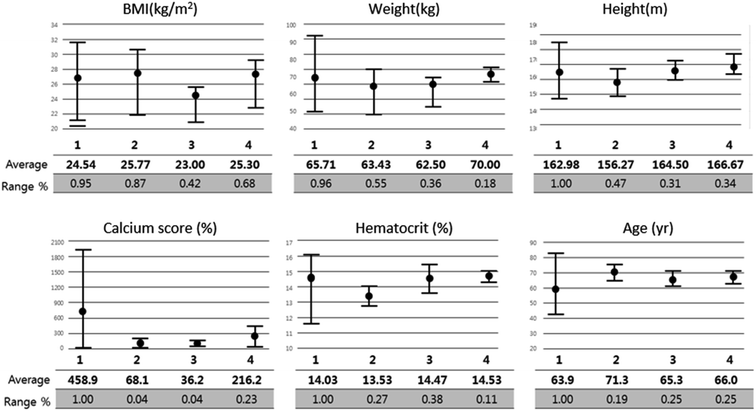
Fig. 9 shows the correlation between biometric features such as age, BMI, calcium score, and hematocrit. Fig. 10 shows each biometric feature of the 20 cases separated into four categories. As in the case of Fig. 7, the range difference in each category should be noted. Among all the features, hematocrit showed the highest correlation, followed by age. Note that the correlation of BMI was higher than that of height and weight. If the effects of height and weight were independent of each other, their correlation should have been higher than that of BMI because BMI is a function of height and weight. However, the higher correlation of BMI indicates that height and weight are dependent and should be merged with BMI for better analysis.Conclusions
In this study, a two-step ML algorithm is introduced to estimate FFR and obtain DEC. By training the model with both a synthetic model and a patient model with the help of CFD, flow characteristics and biometric features could be used. Consequently, DECSVM was higher than FFRCFD or FFRGPR, which confirmed the potential of this algorithm to overcome the accuracy limitation compared with FFRCFD.There are still a few limitations that should be further studied to achieve a better model. The most critical limitation is that the quality and quantity of biometric features might not be enough. For example, while age or calcification is used to represent vessel stiffness, the exact vessel stiffness cannot be obtained unless it is measured directly. However, it is almost impossible to measure every FFR-related feature from every patient. Even the synthetic models used for amplifying the cases are not helpful for solving this problem because the features estimable by synthetic models are limited to CFD.
Also, the category 3 cases in the performance test result should be further analyzed and be eliminated. Category 3 means that DECSVM has poorly guessed even after the correct estimation of FFRGPR. The cause of these errors are probably due to the overfitting problem of the SVM algorithm, but the cases used for performance test are yet not enough to fully analyze and correct this error. In future works, solving this problem and reducing category 3 cases is going to be the main objectives to improve the algorithm.
Regardless of these limitations, it was confirmed that the accuracy of the ML algorithm can surpass that of CFD. The ultimate goal of ML-based FFR should not only be a reduced calculation time but also obtaining a sufficiently high accuracy and practicality so as to replace the FFREXP.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work of Yong Woo Kim, Jung-Sun Kim, Jinyong Ha, and Joon Sang Lee was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (NRF-2017M3A9E9073371). Also, The work of Hee-Jin Yu and Jongeun Choi was supported in part by the National Research Foundation of Korea (NRF) under Grant 2018R1A4A1025986 funded by the Korea government (MSIT). Young Woo Kim and Hee-Jin Yu contributed equally to this work as first authors. Also, Jongeun Choi and Joon Sang Lee contributed equally to this work as corresponding authors.Notes and references
- B. D. Bruyne and J. Sarma, Heart, 2008, 94, 949–959 CrossRef PubMed.
- P. A. Tonino, W. F. Fearon, B. De Bruyne, K. G. Oldroyd, M. A. Leesar, P. N. Ver Lee, P. A. MacCarthy, V. Marcel and N. H. Pijls, J. Am. Coll. Cardiol., 2010, 55, 2816–2821 CrossRef.
- M. A. Mamas, S. Honer, E. Welch, A. Ashworth, S. Millington, D. Fraser, F. Fath-Ordoudabadi, L. Neyses and M. El-Omar, J. Invasive Cardiol., 2010, 22, 260–265 Search PubMed.
- G. Casella, M. Leibig, T. M. Scheile, R. Schrepf, V. Seeling, H. Stempfle, P. Erdin, J. Rieber, A. Konig, U. Siebert and V. Klauss, Am. Heart J., 2004, 148, 590–595 CrossRef CAS.
- A. Coenen, M. M. Lubbers, A. Kono, A. Dedic, R. G. Chelu, M. L. Dijkshoorn, F. J. Gijsen, M. Ouhlous, R. M. van Geuns and K. Nieman, Radiology, 2014, 274, 674–683 CrossRef.
- C. A. Taylor, A. F. Timothy and K. M. James, J. Am. Coll. Cardiol., 2013, 61, 2233–2241 CrossRef.
- R. K. Tripathy, S. Mahanta and S. Paul, RSC Adv., 2014, 4, 9349–9355 RSC.
- M. Khanmohammadi, K. Ghasemi and A. B. Garmarudi, RSC Adv., 2014, 4, 41484–41490 RSC.
- A. Kihm, L. Kaestener, C. Wagner and S. Quint, PLoS Comput. Biol., 2018, 14, e1006278 CrossRef.
- G. Kim, J. G. Lee, S. J. Kang, P. NNguen, D. Y. Kang, P. H. Leem J. M. Ahn, D. W. Park, S. W. Lee, Y. H. Kim, C. W. Lee, S. W. Park, and S. J. Park, Intravascular Imaging and Computer Assisted Stenting and Large-Scale Annotation of Biomedical Data and Expert Label Synthesis, 2018, pp. 73–81 Search PubMed.
- L. Itu, S. Rapaka, T. Passerini, B. Georgescu, C. Schwemmer, M. Schoebinger, T. Flohr, P. Sharma and D. Comaniciu, J. Appl. Physiol., 2016, 121, 42–52 CrossRef.
- C. Tesche, C. N. Cecco, S. Baumann, M. Renker, T. W. McLaurin, T. M. Duguay, R. R. Bayer, D. H. Steinberg, K. L. Grant, C. Canstein, C. Schwemmer, M. Schobinger, L. M. Itu, S. Rapaka, P. Sharma and U. J. Schoepf, Radiology, 2018, 288, 64–72 CrossRef PubMed.
- X. Hu, M. Yang, L. Han and Y. Du, Int. J. Cardiovasc. Imaging, 2018, 34, 1987–1996 CrossRef PubMed.
- M. Chu, C. Birgelen, Y. Li, J. Westra, J. Yang, N. R. Holm, J. H. Reiber, W. Wijns and S. Tu, Atherosclerosis, 2018, 273, 136–144 CrossRef CAS PubMed.
- S. S. Varghese and H. F. Steven, J. Biomech. Eng., 2003, 125, 445–460 CrossRef PubMed.
- H. S. Lim, P. A. Tonino, B. De Bruyne, A. S. Yong, B. K. Lee, N. H. Pijls and W. F. Fearon, Int. J. Cardiol., 2014, 177, 66–70 CrossRef.
- S. Li, X. Tang, L. Peng, Y. Luo, R. Dong and J. Liu, Clin. Radiol., 2015, 70, 476–486 CrossRef CAS.
- M. Renker, U. J. Schoepf, R. Wang, F. G. Meinel, J. D. Rier, R. R. Bayer, H. Mollmann, C. W. Hamm, D. H. Steinberg and S. Baumman, Am. J. Cardiol., 2014, 114, 1303–1308 CrossRef.
- A. Asfaram, M. Ghaedi, M. H. Ahmadi Azqhandi, A. Goudarzi and M. Dastkhoon, RSC Adv., 2016, 6, 40502–40516 RSC.
- Q. Li, Y. Yu, P. Zhou and H. J. Yan, RSC Adv., 2017, 7, 14701–14708 RSC.
- Q. Mei, X. Wei, W. Sun, X. Zhang, W. Li and L. Ma, RSC Adv., 2019, 9, 12846–12853 RSC.
- Y. L. Chen, RSC Adv., 2014, 4, 17908–17916 RSC.
- J. Y. Moon, S. B. Choi, J. S. Lee, R. I. Tanner and J. S. Lee, Phys. Rev. E, 2019, 99, 022607 CrossRef CAS PubMed.
- A. Purqon, J. Phys.: Conf. Ser., 2017, 877, 012035 CrossRef.
- D. Y. Kang, J. M. Ahn, Y. W. Kim, J. Y. Moon, J. S. Lee, B. K. Koo, P. H. Lee, D. W. Park, S. J. Kang, S. W. Lee, Y. H. Kim, S. W. Park and S. J. Park, Circ. Cardiovasc. Imaging, 2018, 11, 007087 Search PubMed.
- K. Govindaraju, G. N. Viswanathan, I. A. Badruddin, S. Kamangar, N. J. Salman and A. A. Al-Rashed, Comput. Methods Biomech. Biomed. Eng., 2016, 19, 1541–1549 CrossRef.
- L. Zhang, Z. Jiang, J. Choi, C. Y. Lim, T. Maiti and S. Baek, IEEE J. Biomed. Health, 2019, 23, 2537–2550 Search PubMed.
- H. N. Do, A. Ijaz, H. Gharahi, B. Zambrano, J. Choi, W. Lee and S. Baek, IEEE Trans. Biomed. Eng., 2018, 66, 609–622 Search PubMed.
- G. W. Colopy, S. J. Roberts and D. A. Clifton, IEEE J. Biomed. Health, 2018, 22, 301–310 Search PubMed.
- S. I. Lee, B. Mortazavi, H. A. Hoffmann, D. S. Lu, C. Li, B. H. Paak, J. H. Garst, M. Razaghy, M. Espinal, E. Park, D. C. Lu and M. Sarrafzadeh, IEEE J. Biomed. Health, 2014, 20, 91–99 Search PubMed.
- E. Byvatov and S. Gisbert, Appl. Bioinf., 2003, 2, 67–77 Search PubMed.
- T. T. Yao, J. L. Cheng, B. R. Xu, M. Z. Zhang, Y. Z. Hu, Ji. H. Zhao and X. W. Dong, RSC Adv., 2015, 61, 49195–49203 RSC.
- S. Hanneke and K. Aryeh, Theor. Comput. Sci., 2019, 796, 99–113 CrossRef.
- J. Chen and Y. Jieping, Proceedings of the 25th international conference on Machine learning., 2008, pp. 136–143 Search PubMed.
- M. B. Kursa and W. R. Rudnicki, J. Stat. Softw., 2010, 36, 1–13 Search PubMed.
| This journal is © The Royal Society of Chemistry 2020 |