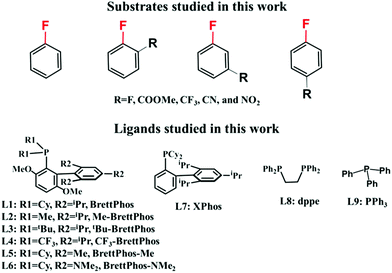
C–F bond arylation of fluoroarenes catalyzed by Pd0 phosphine complexes: theoretical insight into regioselectivity, reactivity, and prediction of ligands†
Rong-Lin
Zhong

Laboratory of Theoretical and Computational Chemistry, Institute of Theoretical Chemistry, College of Chemistry, Jilin University, Changchun, 130023, P. R. China. E-mail: zhongrl898@jlu.edu.cn
First published on 5th November 2019
Abstract
Palladium-catalyzed C–F bond arylation of pentafluorobenzene was theoretically investigated as an example of aryl–F bond functionalization. DFT computations show that C3-regioselective arylation of pentafluorobenzene occurs more favorably than C1 and C2-ones as reported experimentally, through oxidative addition of the C–F bond to Pd0 species, transmetalation and reductive elimination of the C–C bond. Oxidative addition of the C–F bond is the rate-determining and regioselectivity-determining step. The lower energy transition state of the oxidative addition of the C3–F bond (TS-C3) arises from a larger stabilization energy between Pd0(BrettPhos) and distorted pentafluorobenzene moieties in TS-C3 than those in TS-C1 and TS-C2. The larger stabilization energy is a result of a lower σ* orbital energy of the distorted C3–F bond than those of C1–F and C2–F bonds, which leads to a larger charge transfer from the Pd dπ orbital to the σ* orbital of the C3–F bond. The results suggest that both σ* orbital energy and bond dissociation energy are important factors for determining the reactivity of the C–F bond. Also, the activation barriers of the C–F bond with different substitution groups follow the order: NO2 < COOMe < CN ∼ CF3 < F, which is approximately consistent with the order of electron-withdrawing ability of these groups. It is theoretically predicted here that NMe2-substituted BrettPhos is better for C–F bond cleavage than BrettPhos, where three NMe2 groups are introduced to BrettPhos instead of the isopropyl groups.
Introduction
The Pd-catalyzed Suzuki–Miyaura cross-coupling reaction is one of the most efficient and versatile methods for constructing carbon–carbon bonds in biaryls.1–4 Aryl halides (Ar–X, X = Cl, Br and I) have been employed as electrophilic coupling reagents in this reaction.5–8 To broaden its application scope, a large number of efforts have been made to use alternative compounds such as aryl ethers,9 aryl esters,10,11 arenols12 and nitroarenes.13,14 However, the use of aryl fluorides is much less common and much more challenging because the C–F bond is thermodynamically very strong and the cleavage of the C–F bond is difficult.15–18 As shown in Scheme 1, the bond dissociation energy (BDE) of the C–F bond in fluorobenzene is 125.6 kcal mol−1, which is significantly larger than those (65.0–95.5 kcal mol−1) of the C–X (X = Cl, Br and I) bond in the other three analogues.19 It is therefore of fundamental interest to gain a profound understanding of the mechanisms of C–F activation in order to design new metal complexes showing activity toward the functionalization of fluoroarenes and other fluorocarbons. To date, C–F activation and functionalization catalyzed by nickel(0) complexes have been reported by several groups.20–24 However, the catalysts based on nickel(0) systems are air sensitive and difficult to use in conventional organic synthesis.25 In this regard, we are interested in a series of palladium-catalyzed C–F bond functionalization of tetrafluoroethylene,26 fluorobenzene derivatives,27,28 and polyfluoroarenes,25,29,30 because these efforts provided a new perspective for the functionalization of the sp2 C–F bond.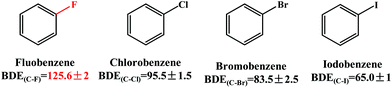 | ||
| Scheme 1 Bond dissociation energy (BDE, kcal mol−1) of the C–X (X = F, Cl, Br, and I) bond in halidebenzenes. | ||
Among these investigations, palladium-catalyzed cross-coupling of pentafluorobenzene with phenylboronic acid reported by the Zhang group30 should be noted because this reaction occurred in a regioselective manner at the C3–F bond, as shown in Scheme 2. Several interesting experimental findings are summarized as below: (1) the arylation of the C3–F bond succeeded and that of C1–F and C2–F bonds rarely occurred despite the difference in the BDE among these three bonds being tiny. (2) High yields of fluoroarene derivatives with electron-withdrawing groups, for example, nitro, cyan, trifluoromethyl, and ester, were obtained in the C–F bond arylation. (3) A special biaryl monophosphine ligand proposed by the Buchwald group, BrettPhos31 as shown in Scheme 3, was used for the successful arylation of pentafluorobenzene but the usual monodentate and bidentate phosphines and even other similar biaryl monophosphines were not useful for this reaction. From these results, we address the following open questions: (i) What is the origin of the interesting C3–F regioselectivity of pentafluorobenzene? (ii) Why does the presence of electron-withdrawing groups in fluoroarenes enhance the reactivity of C–F bonds? (iii) Why is BrettPhos better than Xphos for this reaction while several other similar biaryl monophosphines were not useful? (iv) How can the C–F bond cleavage be accelerated by effective ligand improvement based on BrettPhos? Though the C–F bond cleavage of some fluoroarenes catalyzed by nickel(0) complexes has been discussed in computational studies,32–34 the regioselective arylation of the C–F bonds of polyfluoroarenes catalyzed by palladium(0) complexes is rare, and the origin of the selectivity is still not clear. We need fundamental answers to the above-mentioned questions and to find new ideas for performing more efficiently the regioselective functionalization of the nonreactive sp2 C–F bond.
 | ||
| Scheme 2 The regioselective cross-coupling reaction of pentafluorobenzene and phenylboronic acid catalyzed by the Pd0(BrettPhos) complex.30 | ||
In this work, we theoretically investigated the C–F bond arylation of pentafluorobenzene, fluorobenzene, and various fluorobenzene derivatives with substitution groups such as fluorine, trifluoromethyl, ester, cyan, and nitro as shown in Scheme 3, catalyzed by Pd0(BrettPhos) complexes to elucidate the characteristic features of this reaction and provide clear answers to the above-mentioned questions. We selected these substrates to reveal the relationship between the reactivity of the substrates and substitution groups. Also, ligand effects were investigated by using BrettPhos (L1) and its substituted analogues (L2–L7), bidentate 1,2-bis(diphenylphosphino)ethane, dppe (L8) and monodentate triphenyl phosphine, PPh3 (L9). Through these examinations, we wish to obtain a comprehensive understanding of C–F bond arylation catalyzed by Pd0 phosphine complexes and predict better ligands.
Computational details
All geometry optimizations were performed using the ωB97XD functional35 in the gas phase, using the Stuttgart–Dresden–Bonn basis set36 for Pd with effective core potentials for its core electrons and 6-31G(d) basis sets for other atoms; this basis set system is named BS-I. The combination of functional and BS-I reproduces the crystal structure well; see Table S1 in the ESI† for the functional test. Single-point calculations were performed using the ωB97XD functional together with a larger basis set system (BS-II) to provide a better potential energy. In BS-II, two f polarization functions37 were added to Pd; for Cs, one d polarization function was added and 6-311G(d) basis sets were used for other atoms,38,39 where a set of diffuse functions was added to anionic N, O, and F atoms;40 see Table S2 in the ESI† for the quality of this computational method. The solvation effect was evaluated with the polarizable continuum model (PCM),41–44 where geometries optimized in the gas phase were employed.In this work, discussion is presented based on the Gibbs energy. Thermal correction and entropy contribution to the Gibbs energy were evaluated at 298.15 K and 1 atm, where the translation entropy in solution was corrected using the method of Whitesides et al.45 The Gibbs activation energy (ΔG°‡) is defined as the difference in the Gibbs energy between the transition state (TS) and the most stable intermediate before the TS. The Gibbs reaction energy (ΔG°) is defined as the difference in the Gibbs energy between the product and the most stable intermediate before the TS. All these calculations were carried out using the Gaussian09 program.46 All the geometries were displayed using CYLview software.47
Results and discussion
Firstly, the reaction mechanism, energy profile of the full catalytic cycle, and rate-determining step will be discussed by taking the palladium-catalyzed arylation of pentafluorobenzene as an example. Then, the origin of C3-selectivity will be elucidated because regioselectivity is an important issue. Next, a comparison of the reactivity among various substrates will be done and the determining factors of the reactivity will be discussed to obtain a comprehensive understanding of palladium-catalyzed C–F bond activation and functionalization, which is still a challenging issue in organic chemistry. In the end, the theoretical prediction of better ligands for the palladium catalyst will be presented on the basis of computational results.Overview of the catalytic cycle
According to the experimental results30 and previous investigations,25 the reaction mechanism of the arylation of pentafluorobenzene has been proposed, as shown in Scheme 4. This reaction occurs through the Pd(0)/Pd(II) catalytic cycle; the first step is the oxidative addition of the C–F bond to the Pd(0) complex affording an intermediate, PdII(BrettPhos)(C6F4H)(F); the second step is transmetalation from PdII(BrettPhos)(C6F4H)(F) reacting with the (PhB(OH)2)·(CsF) complex to afford an intermediate, PdII(BrettPhos)(C6F4H)(Ph), and a byproduct, (FB(OH)2)·(CsF); the third step is reductive elimination to afford the biphenyl product, 2,3,5,6-tetrafluoro-biphenyl and regenerate Pd0(BrettPhos). This catalytic cycle is essentially the same as those of other Suzuki–Miyaura cross-coupling reactions catalyzed by the Pd(0) complex.5,6 The Gibbs energy profile of the full catalytic cycle is shown in Fig. 1.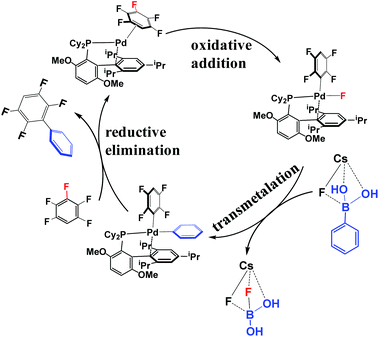 | ||
| Scheme 4 Proposed reaction mechanism of the cross-coupling between pentafluorobenzene and phenylboronic acid. | ||
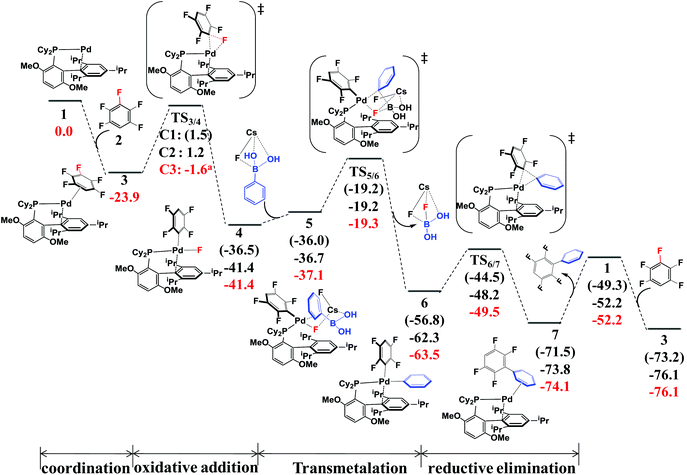 | ||
| Fig. 1 The Gibbs energy profile (in kcal mol−1) of Suzuki–Miyaura cross-coupling of pentafluorobenzene catalyzed by the Pd0(BrettPhos) complex. | ||
Pd0(BrettPhos), 1 is a coordinately unsaturated 16-electrons complex. The C–C double bonds of pentafluorobenzene, 2 should coordinate to the Pd0 center to form η2-adducts. We calculated these adducts as shown in Fig. S3 in the ESI† and results suggest that Pd0(BrettPhos) (pentafluorobenzene), 3 is the most stable one. The coordination distance between Pd and pentafluorobenzene in 3 is 2.125–2.154 Å, in which the C1–C6 bond coordinates with the Pd atom as shown in Fig. 2. Starting from 3, the oxidative addition of the C3–F bond occurs through a three-center transition state TS3/4-C3 to afford PdII(BrettPhos)(C6F4H)(F), 4-C3. TS3/4-C3 is a typical TS of concerted oxidative addition,32 in which the C3–F distance increases to 1.509 Å and the Pd–C3 and Pd–F distances decrease to 2.090 Å and 2.241 Å, respectively. In 4-C3, Pd–C3 and Pd–F distances further decrease to 1.991 Å and 1.976 Å, respectively, suggesting that 4-C3 is a four-coordinated Pd(II) complex. The activation barrier (ΔG°‡) is 22.3 kcal mol−1 and the reaction energy (ΔG°) is −17.5 kcal mol−1 relative to 3.
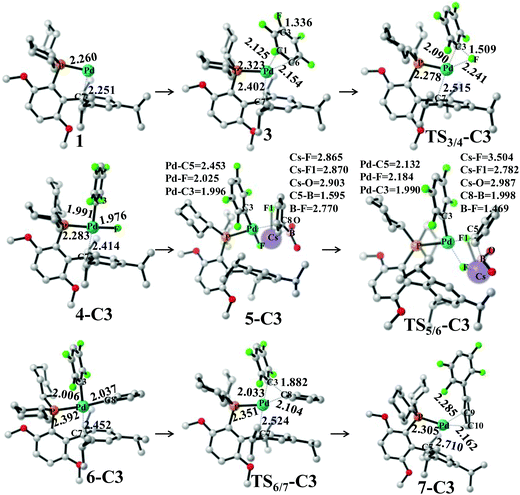 | ||
| Fig. 2 Geometry changes in Suzuki–Miyaura cross-coupling of pentafluorobenzene catalyzed by the Pd0(BrettPhos) complex. Bond distances are in angstroms. | ||
As we know, bases play important roles in the transmetalation step of Suzuki–Miyaura cross-coupling reactions.48,49 Here, CsF was employed as a base instead of Cs2CO3 for calculations because CsF was also effective for this reaction.30,50 According to our previous investigations, phenylboronic acid, PhB(OH)2, should firstly react with CsF to form a stable complex, (PhB(OH)2)·(CsF), under such conditions.13 After that, (PhB(OH)2)·(CsF) reacts with 4-C3 to afford an intermediate, PdII(BrettPhos)(C6F4H)(F)(PhB(OH)2·(CsF)) 5-C3, in which the Cs–F bond distance is 2.865 Å, suggesting that Cs+ plays a crucial role in accepting the F− of 4-C3 by electrostatic interaction. The transmetalation reaction occurs through TS5/6-C3 to afford a four-coordinated intermediate PdII(BrettPhos) (C6F4H)(Ph), 6-C3 and byproduct (CsF)·(FB(OH)2) with the ΔG°‡ value of 22.1 kcal mol−1. In TS5/6-C3, the B–C8 bond distance increases to 1.998 Å and the B–F bond distance decreases to 1.469 Å. Similar to our previous investigation,13 CsF can activate the Ph–B bond by the interaction with the B atom forming a strong B–F bond, which is an important interaction in transmetalation; details are shown in Fig. S5 in the ESI.† Therefore, it should be concluded that CsF plays crucial roles in the transmetalation step by Cs⋯F interaction with 4 and B⋯F interaction with PhB(OH)2.
The reductive elimination of the biphenyl product occurs through TS6/7-C3 to regenerate the Pd(0) complex Pd0(BrettPhos) (2,3,5,6-tetrafluoro-biphenyl), 7-C3 with a moderate ΔG°‡ value (14.0 kcal mol−1). TS6/7-C3 is a typical three-center TS, in which the Pd–C3 and Pd–C8 distances increase to 2.033 Å and 2.104 Å, respectively; and the C3–C8 distance decreases to 1.882 Å. In 7-C3, the coordination distance between Pd and 2,3,5,6-tetrafluoro-biphenyl is 2.162–2.285 Å, which is the usual η2-coordinated distance similar to that found in 3. This reductive elimination is essentially the same as that for Suzuki–Miyaura cross-coupling reactions catalyzed by the Pd0 complex.6 After that, dissociation of 2,3,5,6-tetrafluoro-biphenyl from the Pd(0) center occurs and another pentafluorobenzene coordinates to Pd(0) starting a new cycle. The concerted oxidative addition of the C3–F bond is the rate-determining step and pentafluorobenzene π-complex 3 is the resting state. The cross-couplings through the cleavage of C1–F and C2–F bonds occur through the same catalytic cycle, while the energy differs moderately; the ΔG°‡ values (25.4 and 25.1 kcal mol−1, respectively) for the oxidative addition of C1–F and C2–F bonds are moderately higher than those for the C3–F bond by 3.1 and 2.8 kcal mol−1, respectively. These results clearly show that the cross-coupling reaction through the C3–F bond cleavage occurs kinetically more favorably than through C1–F and C2–F bonds, which is consistent with experimentally observed C3-regioselectivity.30 It should be concluded that the C3-regioselectivity of pentafluorobenzene is determined at the oxidative addition step.
Origin of C3-regioselectivity of pentafluorobenzene
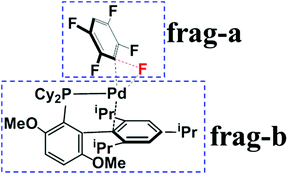
To understand the origin of C3-regioselectivity, we separated the transition states into pentafluorobenzene (frag-a) and Pd0(BrettPhos) (frag-b) moieties to perform deformation/interaction analysis,51–53 as shown in Scheme 5. In order to show this analysis clearly, we compared these three transition states at almost the same position on the reaction coordinate because the comparison between the late and early transition states does not show a clear difference; for instance, deformation energy and interaction energy are larger in the late transition state than in the early one. Here, we took the C–F bond distance (1.600 Å) as an approximate reaction coordinate and obtained such an approximate transition state geometry by IRC calculation, because this is used for the analysis of the oxidative addition of the C–F bond; details are described in Page S9 of the ESI.† As listed in Table 1, the increasing order of the activation barrier (Ea) is 21.8 (C3–F) < 25.1 (C2–F) < 26.3 (C1–F) kcal mol−1, where Ea is the potential energy difference between the TS and the resting state, 3. This order is the same as that of ΔG°‡, suggesting that the analysis of Ea provides reason(s) as to why did the C3-regioselectivity of pentafluorobenzene occur. Because the sum of EDef-a and EDef-b is slightly larger in TS3/4-C3 than in TS3/4-C1 and TS3/4-C2, the two terms are not responsible for the lower energy of TS3/4-C3. However, the increasing order of Eint is −54.8 (TS3/4-C3) < −49.3 (TS3/4-C2) < −47.9 (TS3/4-C1) kcal mol−1, which is consistent with Ea, indicating that this term is responsible for the smaller Ea of C3–F bond cleavage than C2–F and C1–F ones.| Pentafluorobenzene | Fluorobenzene | |||
|---|---|---|---|---|
| TS3/4-C1 | TS3/4-C2 | TS3/4-C3 | TS3/4 | |
| ΔG°‡ | 25.4 | 25.1 | 22.2 | 29.7 |
| E a | 26.3 | 25.1 | 21.8 | 30.6 |
| ΔG°(TS) | 1.5 | 1.2 | −1.6 | 9.8 |
| ΔE(TS) | −5.0 | −7.0 | −10.3 | 4.6 |
| E Def-a | 39.3 | 38.7 | 40.6 | 35.5 |
| E Def-b | 3.5 | 3.7 | 3.8 | 4.1 |
| E int | −47.9 | −49.3 | −54.8 | −34.4 |
| BDE | 123.4 | 122.2 | 122.1 | 126.9 |
| ε HOMO-b | −5.62 | −5.61 | −5.59 | −5.72 |
| ε LUMO-a | −1.42 | −1.54 | −1.78 | 0.09 |
| HOMO-b (occ) | 1.361e | 1.347e | 1.295e | 1.582e |
| LUMO-a (occ) | 0.721e | 0.737e | 0.792e | 0.557e |
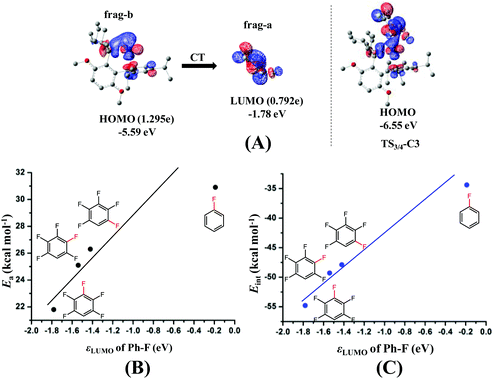
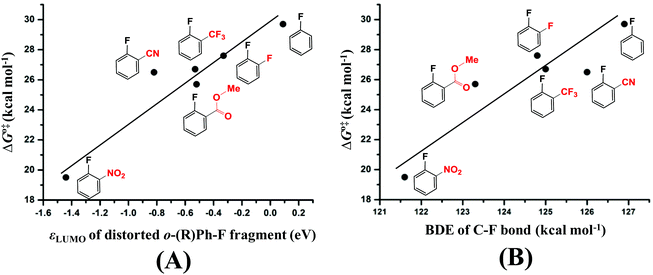
The next question is why the Eint is more negative in TS3/4-C3 than in TS3/4-C1 and TS3/4-C2. According to previous investigations,54–56 charge transfer (CT) from the metal moiety to the substrate plays an important role in oxidative addition reactions, which contributes to the Eint value. In TS3/4-C3, CT occurs from the HOMO (ϕPd-HOMO) of Pd to the LUMO of distorted pentafluorobenzene, as shown in Fig. 3(A). The HOMO of Pd0(BrettPhos) consists of the Pd dπ orbital and the LUMO consists of the σ* orbital of the C3–F bond mixing with the π* orbital of C6F4H. As a result of CT from the HOMO of Pd0(BrettPhos) to the LUMO of the distorted C6F4H-F moiety, the LUMO has 0.792e electron population, where these populations were evaluated using the linear combination of fragment MOs. It is worth noting that the increasing order of electron populations of the σ* orbital of the C–F bond is 0.721e (C1–F) < 0.737e (C2–F) < 0.792e (C3–F), which is consistent with the decreasing order of σ* orbital energy, −1.42 (C1–F) > −1.54 (C2–F) > −1.78 (C3–F) eV. As we know, the lower the LUMO energy, the larger the CT. This CT plays crucially important roles in the oxidative addition, because it leads to weakening of the σ-bond and formation of negatively charged Ph and F groups (atom). Therefore, the more negative Eint in TS3/4-C3 arises from the lower σ* orbital energy of the distorted C3–F bond, as shown Fig. 3(C). It should be concluded that the C3–F bond is more reactive than C1–F and C2–F bonds because the σ* orbital of the C3–F bond is at a lower energy than those of C1–F and C2–F bonds in distorted pentafluorobenzene. We also checked the C–F bond dissociation energy (BDE) because the activation barrier of a weaker bond is generally lower than that of a stronger bond. However, the difference among the BDE of the three C–F bonds is tiny as listed in Table 1. Therefore, the σ* orbital energy of the C–F bond is a crucially important factor for determining the C3-regioselectivity of pentafluorobenzene as shown in Fig. 3(B).
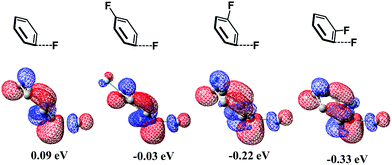
It is interesting that the σ* orbital energy of the distorted C3–F bond is lower than those of C1–F and C2–F bonds despite the distortion and BDEs of the three bonds being almost the same. This feature likely arises from the different substitution effect of the F atom at the ortho (o)-, meta (m)- and para (p)-position of the C–F bond.30 In order to quantitatively evaluate the effect of substitution of the F atom at the o-, m- and p-position of the C–F bond, we calculated the σ* orbital of the C–F bond in distorted fluorobenzene and difluorobenzene, in which the distortion of the C–F bond is the same (details are shown in Page S10 of the ESI†). As shown in Scheme 6, the increasing order of the LUMO energy is −0.33 (o-difluorobenzene) < −0.22 (m-difluorobenzene) < −0.03 (p-difluorobenzene) < 0.09 eV (fluorobenzene). These results suggest that the σ* orbital of the distorted C–F bond is decreased by the substitution of another F atom in the following order: 0.42 (o-substitution) > 0.31 (m-substitution) > 0.12 eV (p-substitution). Hence, the σ* orbital energy of C3–F in distorted pentafluorobenzene is lower than those of C1–F and C2–F because o- and m-substitution of the F atom decrease the σ* orbital energy more than does p-substitution; the σ* orbital energy of the C2–F bond is lower than that of C1–F because o-substitution of F atoms decreases the σ* orbital energy more than does m-substitution (details are shown in Page S11 of the ESI†). It should be concluded that the σ* orbital energy of the C–F bond is decreased by the substitution of another F atom in the following order: o-substitution > m-substitution > p-substitution, which is the origin of the C3-regioselectivity of pentafluorobenzene.
C–F bond reactivity of various substrates
According to the experimental findings on the C–F bond arylation of polyfluoroarenes, the substitution of electron-withdrawing groups on the substrates accelerated the reactions.30 To broaden the C–F bond functionalization by a transition metal catalyst, we need fundamental knowledge of the reactivity of different C–F bonds in various substrates. For this purpose, we investigated the oxidative addition of the C–F bond of fluorobenzene derivatives with substitution groups such as F, CF3, COOMe, CN and NO2 as shown in Scheme 3. The results suggest that o-substitution is more effective than m-substitution and p-substitution for enhancing the reactivity of the C–F bond, because the ΔG°‡ values with the o-substitution become smaller than those with m- and p-substitution as listed in Table 2. For o-substitution, the ΔG°‡ values of C–F bond oxidative addition with different groups follow the order: NO2 < COOMe < CN ∼ CF3 < F, which is approximately consistent with the relative order of the electron-withdrawing ability of these substitution groups.| R | o | m | p | |
|---|---|---|---|---|
| a o represents the R group (atom) which is at the ortho-position of the C–F bond; m represents the R group (atom) which is at the meta-position of the C–F bond; p represents the R group (atom) which is at the para-position of the C–F bond. | ||||
| H | ΔG°‡ | 29.7a | 29.7 | 29.7 |
| ε LUMO | 0.09 | 0.09 | 0.09 | |
| BDE | 126.9 | 126.9 | 126.9 | |
| F | ΔG°‡ | 27.6 | 29.4 | 30.5 |
| ε LUMO | −0.33 | −0.22 | −0.03 | |
| BDE | 124.8 | 126.4 | 126.6 | |
| CF3 | ΔG°‡ | 26.7 | 28.6 | 27.6 |
| ε LUMO | −0.53 | −0.38 | −0.51 | |
| BDE | 125.0 | 126.4 | 126.8 | |
| COOMe | ΔG°‡ | 25.7 | 30.1 | 29.2 |
| LUMO | −0.52 | −0.29 | −0.65 | |
| BDE | 123.3 | 127.3 | 127.1 | |
| CN | ΔG°‡ | 26.5 | 29.5 | 26.7 |
| ε LUMO | −0.82 | −0.6 | −0.91 | |
| BDE | 126.0 | 126.1 | 126.7 | |
| NO2 | ΔG°‡ | 19.5 | 29.3 | 26.7 |
| ε LUMO | −1.44 | −0.54 | −1.56 | |
| BDE | 121.6 | 126.1 | 126.9 | |
As discussed in the above section, the activation barrier of the C–F bond is significantly relative to the CT from the dπ orbital of Pd to the σ* orbital of the distorted C–F bond.57 We calculated the σ* orbital (LUMO) energy (εLUMO, eV) of the distorted substrate moieties as listed in Table 2. From these results, we can easily understand that the activation barrier becomes lower when the LUMO of the distorted substrate is at a lower energy, because CT from Pd to the substrate is larger which stabilizes the TS more. We plotted ΔG°‡ against εLUMO, as shown in Fig. 4(A). Almost a linear relationship is found with only one moderate deviation when R is the CN group; The LUMO energy of 2-fluorobenzonitrile is at a lower energy than that of methyl 2-fluorobenzoate but the activation barrier of 2-fluorobenzonitrile is moderately higher than that of methyl 2-fluorobenzoate. This result suggests that other factor(s) might also be responsible for the activation barrier of C–F bond activation in addition to the σ* orbital energy. It is likely that another factor arises from the BDE of C–F because the activation barrier of a weaker bond is generally lower than that of a stronger bond. We plotted ΔG°‡ against the BDE as shown in Fig. 4(B) and another approximately linear relationship is found. We can understand from Fig. 4(B) that the activation barrier of the C–F bond of 2-fluorobenzonitrile is moderately higher than that of methyl 2-fluorobenzoate mainly because the C–F bond of 2-fluorobenzonitrile is stronger than that of methyl 2-fluorobenzoate (the reasons are provided in Page S12 of the ESI†). Therefore, these results lead us to the conclusion that both the σ* orbital energy and the BDE of the C–F bond are important factors for determining the reactivity of the C–F bond.
Ligand effects
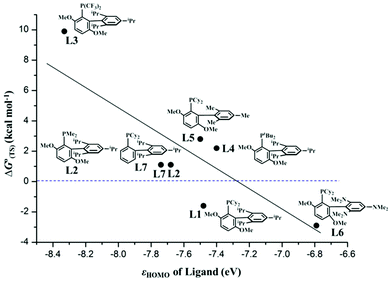
According to the experimental results on the palladium-catalyzed arylation of pentafluorobenzene, BrettPhos is better than XPhos while other similar biaryl monophosphine and the usual monodentate and bidentate phosphine ligands were not useful.30 BrettPhos is a biaryl monophosphine ligand proposed by the Buchwald group, in which the presence of the 2,4,6-tris(isopropyl)phenyl group is crucially important because its π orbital overlaps with the Pd dπ orbital to raise the dπ orbital energy.14 To understand this ligand effect and to predict a better ligand for Pd0 catalyst, we investigated the oxidative addition of the C3–F bond of pentafluorobenzene by employing nine ligands as shown in Scheme 3, because this is the rate-determining step. As shown in Fig. 5, the ΔG°(TS) value of the oxidative addition decreases almost linearly with the lone pair orbital energy of biaryl monophosphine ligands, showing that the electron-donating ligand is suitable for the catalyst, which is consistent with the previous hypothesis proposed by the Zhang group.30 This is reasonable because the high energy lone pair orbital of the ligand raises the Pd dπ orbital energy to increase the CT from the Pd0(L) complex to pentafluorobenzene, which further increases the stabilization energy of the TS and decreases the activation barrier.Among these ligands, BrettPhos–NMe2 is the best for complexing with Pd0 for catalyzing the C–F bond cleavage because the ΔG°‡ value is the smallest and the ΔG°(TS) value relative to the sum of the reactants is the most negative as listed in Table 3. These features arise from the high energy HOMO (ϕPd-HOMO) of Pd0(BrettPhos–NMe2), which is contributed by the high energy HOMO (ϕL-HOMO) of BrettPhos–NMe2. The next is BrettPhos, because the ΔG°(TS) value is the next smallest despite the slightly larger ΔG°‡ value than those of some other biaryl monophosphine ligands. For Me–BrettPhos and XPhos, the ΔG°(TS) value is positive and somewhat large, indicating that the two ligands might be useful for the C–F bond oxidative addition of pentafluorobenzene but less effective because these two ligands have ϕL-HOMO at a lower energy than BrettPhos. For tBu–BrettPhos and BrettPhos–Me, the ΔG°(TS) value is much more positive, indicating that these two ligands might be much less useful for C–F bond oxidative addition of pentafluorobenzene. The larger steric effect of the tBu group might be responsible for this positive ΔG°(TS) value despite ϕL-HOMO of tBu–BrettPhos being at a higher energy than that of BrettPhos.14 For CF3–BrettPhos, the ΔG°(TS) value is 9.9 kcal mol−1 much higher than those of other analogues, indicating that CF3–BrettPhos is not useful because the ϕL-HOMO energies of CF3–BrettPhos are much lower than those of BrettPhos. For PPh3 and dppe, ΔG°(TS) values are 17.1 and 7.6 kcal mol−1, respectively; these values are also much positive, indicating that the pentafluorobenzene tends to dissociate from the Pd center in Pd0(PPh3)2(pentafluorobenzene) and Pd0(dppe) (pentafluorobenzene) rather than the two adducts pass through the transition states for oxidative addition reaction.14 On the other hand, the ΔG°‡ values of the two ligands are also higher than that of BrettPhos. Therefore, it is concluded that the oxidative addition of pentafluorobenzene to the Pd0 complex of these two ligands should not occur. This is consistent with the experimental results that the Suzuki–Miyaura reaction of pentafluorobenzene was not successful using the usual monodentate phosphines such as triphenylphsophine and tricyclohexylphosphine, and bidentate phosphines such as dppe, BINAP, and so on.30
| Ligand | ϕ L-HOMO | ϕ Pd-HOMO | ΔG° | ΔG°‡ | ΔG°(D) | ΔG°(TS) | |
|---|---|---|---|---|---|---|---|
| L1 | BrettPhos | −7.48 | −5.82 | −17.6 | 22.2 | 23.9 | −1.7 |
| L2 | Me–BrettPhos | −7.68 | −5.88 | −21.7 | 21.8 | 20.7 | 1.1 |
| L3 | t Bu–BrettPhos | −7.40 | −5.77 | −10.1 | 23.7 | 21.6 | 2.1 |
| L4 | CF3–BrettPhos | −8.33 | −6.62 | −10.7 | 25.4 | 15.5 | 9.9 |
| L5 | BrettPhos–Me | −7.50 | −6.03 | −17.9 | 20.9 | 18.0 | 2.9 |
| L6 | BrettPhos–NMe2 | −6.79 | −5.65 | −25.8 | 19.6 | 22.5 | −2.9 |
| L7 | XPhos | −7.74 | −6.22 | −18.6 | 20.5 | 19.4 | 1.1 |
| L8 | dppe | −7.61 | −6.17 | −29.7 | 24.6 | 17.0 | 7.6 |
| L9 | PPh3 | −8.01 | −7.94 | −12.8 | 24.4 | 7.3 | 17.1 |
Conclusions
In this work, C–F bond arylation of pentafluorobenzene catalyzed by the Pd0 phosphine complex was investigated by DFT calculations. The catalytic cycle consists of C–F cleavage through oxidative addition of the C–F bond to Pd0(BrettPhos), transmetalation from PdII(BrettPhos)(C6F4H)(F) reacting with the (PhB(OH)2)·(CsF) complex, and the reductive elimination between C6F4H and Ph groups. The reaction mechanism is essentially the same as that proposed for the usual Pd-catalyzed Suzuki–Miyaura cross-coupling reaction. Oxidative addition of the C–F bond is the rate-determining step and C3-regioselectivity is also determined at this step. Oxidative addition occurs through TS-C3, which is more favorable than through TS-C1 and TS-C2 because of the more negative Eint between Pd0(BrettPhos) and distorted pentafluorobenzene moieties in TS-C3. The more negative Eint in the TS-C3 arises from the larger CT from the dπ orbital of Pd0 to the σ* orbital of the C3–F bond than to that of C1–F and C2–F bonds, because the σ* orbital of the C3–F bond is at a lower energy than C1–F and C2–F bonds. This feature essentially arises from the different substitution effect of the F atoms at the ortho-, meta- and para-position of the C–F bond. The C–F σ* orbital energy is decreased by the substitution of the F atom in the order: o-substitution > m-substitution > p-substitution. In other words, C3-regioselectivity is determined by the electronic factor and the substitution effect of the F atom at different positions of the C–F bond plays a crucially important role for determining the regioselectivity.The oxidative additions of the C–F bond of various fluorobenzene derivatives with substitution groups such as fluorine, trifluoromethyl, ester, cyan, and nitro were investigated. The results show that the ΔG°‡ values of C–F bond oxidative addition follow the order: NO2 < COOMe < CN ∼ CF3 < F, which is almost consistent with the order of the electron-withdrawing ability of the substitution groups. The plot of ΔG°‡ for the oxidative addition against the σ* orbital of the C–F bond exhibits an approximately linear relationship. On the other hand, the plot of ΔG°‡ for the oxidative addition against the BDE of the C–F bond exhibits another approximately linear relationship. These suggest that both the σ* orbital energy and BDE of the C–F bond are important factors for determining the reactivity of the C–F bond.
Ligand effects were investigated by using various biaryl monophosphine and monodentate and bidentate phosphine ligands and the results show that the electron-donating ligand is suitable for the catalyst. This is reasonable because the high energy lone pair orbital of the ligand raises the Pd dπ orbital energy to increase the CT from the Pd0(L) complex to pentafluorobenzene, which further increases the stabilization energy of the TS and decreases the activation barrier. Among these ligands, BrettPhos–NMe2 is the best for C–F bond oxidative addition.
These findings provide us with new ideas on how to perform arylation and similar transformations of the sp2 C–F bond; (i) the use of electron-donating ligands such as BrettPhos–NMe2 is recommended, which is consistent with the previous hypothesis proposed by the Zhang group;30 (ii) the reactivity of the C–F bond is determined by the σ* orbital energy and BDE of the C–F bond; and (iii) the substitution of the electron-withdrawing groups effectively enhances the reactivity of fluoroarenes for C–F functionalization.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge financial support from the National Natural Science Foundation of China (NSFC) (21603082 and 21673092).Notes and references
- N. Miyaura, T. Yanagi and A. Suzuki, Synth. Commun., 1981, 11, 513–519 CrossRef CAS.
- A. Suzuki, J. Organomet. Chem., 1999, 576, 147–168 CrossRef CAS.
- N. Miyaura, Cross-Coupling Reactions: A Practical Guide, Springer, Berlin, 2002 Search PubMed.
- N. Miyaura, Bull. Chem. Soc. Jpn., 2008, 81, 1535–1553 CrossRef CAS.
- A. Suzuki, Angew. Chem., Int. Ed., 2011, 50, 6722–6737 CrossRef CAS.
- R. Martin and S. L. Buchwald, Acc. Chem. Res., 2008, 41, 1461–1473 CrossRef CAS PubMed.
- L. Xue and Z. Lin, Chem. Soc. Rev., 2010, 39, 1692–1705 RSC.
- X. F. Wu, P. Anbarasan, H. Neumann and M. Beller, Angew. Chem., Int. Ed., 2010, 49, 9047–9050 CrossRef CAS PubMed.
- M. Tobisu, T. Shimasaki and N. Chatani, Angew. Chem., Int. Ed., 2008, 47, 4866–4869 CrossRef CAS.
- B.-T. Guan, Y. Wang, B.-J. Li, D.-G. Yu and Z.-J. Shi, J. Am. Chem. Soc., 2008, 130, 14468–14470 CrossRef CAS PubMed.
- K. Muto, J. Yamaguchi, D. G. Musaev and K. Itami, Nat. Commun., 2015, 6, 7508 CrossRef PubMed.
- D.-G. Yu and Z.-J. Shi, Angew. Chem., Int. Ed., 2011, 50, 7097–7100 CrossRef CAS.
- M. R. Yadav, M. Nagaoka, M. Kashihara, R.-L. Zhong, T. Miyazaki, S. Sakaki and Y. Nakao, J. Am. Chem. Soc., 2017, 139, 9423–9426 CrossRef CAS.
- R.-L. Zhong, M. Nagaoka, Y. Nakao and S. Sakaki, Organometallics, 2018, 37, 3480–3487 CrossRef CAS.
- H. Amii and K. Uneyama, Chem. Rev., 2009, 109, 2119–2183 CrossRef CAS PubMed.
- E. Clot, O. Eisenstein, N. Jasim, S. A. Macgregor, J. E. McGrady and R. N. Perutz, Acc. Chem. Res., 2011, 44, 333–348 CrossRef CAS PubMed.
- T. Ahrens, J. Kohlmann, M. Ahrens and T. Braun, Chem. Rev., 2015, 115, 931–972 CrossRef CAS.
- O. Eisenstein, J. Milani and R. N. Perutz, Chem. Rev., 2017, 117, 8710–8753 CrossRef CAS.
- Y.-R. Luo, Handbook of Bond Dissociation Energies in Organic Compounds, CRC Press, Boca Raton, FL, 2003 Search PubMed.
- T. Braun, R. N. Perutz and M. I. Sladek, Chem. Commun., 2001, 2254–2255 RSC.
- A. Steffen, M. I. Sladek, T. Braun, B. Neumann and H.-G. Stammler, Organometallics, 2005, 24, 4057–4064 CrossRef CAS.
- N. Yoshikai, H. Mashima and E. Nakamura, J. Am. Chem. Soc., 2005, 127, 17978–17979 CrossRef CAS PubMed.
- T. Schaub, M. Backes and U. Radius, J. Am. Chem. Soc., 2006, 128, 15964–15965 CrossRef CAS.
- Y. Nakamura, N. Yoshikai, L. Ilies and E. Nakamura, Org. Lett., 2012, 14, 3316–3319 CrossRef CAS.
- M. R. Cargill, G. Sandford, A. J. Tadeusiak, D. S. Yufit, J. A. K. Howard, P. Kilickiran and G. Nelles, J. Org. Chem., 2010, 75, 5860–5866 CrossRef CAS.
- M. Ohashi, H. Saijo, M. Shibata and S. Ogoshi, Eur. J. Org. Chem., 2013, 443–447 CrossRef CAS.
- Y. M. Kim and S. Yu, J. Am. Chem. Soc., 2003, 125, 1696–1697 CrossRef CAS.
- D. A. Widdowson and R. Wilhelm, Chem. Commun., 2003, 578–579 CAS.
- M. Ohashi, R. Doi and S. Ogoshi, Chem. – Eur. J., 2014, 20, 2040–2048 CrossRef CAS.
- Z.-J. Luo, H.-Y. Zhao and X. Zhang, Org. Lett., 2018, 20, 2543–2546 CrossRef CAS.
- B. P. Fors, D. A. Watson, M. R. Biscoe and S. L. Buchwald, J. Am. Chem. Soc., 2008, 130, 13552–13554 CrossRef CAS PubMed.
- T. Schaub, P. Fischer, A. Steffen, T. Braun, U. Radius and A. Mix, J. Am. Chem. Soc., 2008, 130, 9304–9317 CrossRef CAS.
- Ò. Torres, N. Pfister, T. Braun and P. Wittwer, Dalton Trans., 2019, 48, 6153–6161 RSC.
- W.-J. Chen, R.-N. Xu, W. Lin, X. Sun, B. Wang, Q.-H. Wu and X. Huang, Front. Chem., 2018, 6, 319 CrossRef.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1991, 78, 247–266 CrossRef CAS.
- J. M. L. Martin and A. Sundermann, J. Chem. Phys., 2001, 114, 3408–3420 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS.
- B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 106, 5151–5158 CrossRef CAS.
- E. Cancès, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041 CrossRef.
- M. Cossi, V. Barone, B. Mennucci and J. Tomasi, Chem. Phys. Lett., 1998, 286, 253–260 CrossRef CAS.
- J. Tomasi and M. Persico, Chem. Rev., 1994, 94, 2027–2094 CrossRef CAS.
- M. Mammen, E. I. Shakhnovich, J. M. Deutch and G. M. Whitesides, J. Org. Chem., 1998, 63, 3821–3830 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013.
- C. Y. Legault, CYLview, 1.0b, Université de Sherbrooke, http://www.cylview.org, 2009 Search PubMed.
- C. Amatore, A. Jutand and G. Le Duc, Chem. – Eur. J., 2011, 17, 2492–2503 CrossRef CAS.
- C. Amatore, A. Jutand and G. Le Duc, Angew. Chem., Int. Ed., 2012, 51, 1379–1382 CrossRef CAS.
- T. Torigoe, T. Ohmura and M. Suginome, J. Org. Chem., 2017, 82, 2943–2956 CrossRef CAS.
- D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2007, 129, 10646–10647 CrossRef CAS.
- D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 10187–10198 CrossRef CAS.
- B. J. Levandowski and K. N. Houk, J. Am. Chem. Soc., 2016, 138, 16731–16736 CrossRef CAS.
- S. Sakaki and M. Ieki, J. Am. Chem. Soc., 1993, 115, 2373–2381 CrossRef CAS.
- N. Ochi, Y. Nakao, H. Sato and S. Sakaki, J. Am. Chem. Soc., 2007, 129, 8615–8624 CrossRef CAS.
- W. Guan, F. B. Sayyed, G. Zeng and S. Sakaki, Inorg. Chem., 2014, 53, 6444–6457 CrossRef CAS.
- G. Li, D. Leow, L. Wan and J. Q. Yu, Angew. Chem., Int. Ed., 2013, 52, 1245–1247 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Benchmark calculations to select DFT functionals and basis sets for geometry optimization and to select DFT functionals and basis sets for energy evaluation and NBO population analysis, proposed reaction mechanism of the cross-coupling between pentafluorobenzene and phenylboronic acid, isomers of Pd0(BrettPhos)(pentafluorobenzene), three transition states for oxidative addition of pentafluorobenzene to the Pd0(BrettPhos) complex, effect of CsF, details about deformation/interaction analysis, and bond dissociation energy of the C–F bond in 2-fluorobenzonitrile (PDF). Cartesian coordinates (TXT). See DOI: 10.1039/c9qo01095e |
| This journal is © the Partner Organisations 2020 |