Electronic, vibrational, and charge-transport properties of benzothienobenzothiophene–TCNQ co-crystals†‡
Ajith
Ashokan
 a,
Caitlin
Hanson§
a,
Caitlin
Hanson§
 a,
Nathan
Corbin¶
a,
Nathan
Corbin¶
 a,
Jean-Luc
Brédas
a,
Jean-Luc
Brédas
 *ab and
Veaceslav
Coropceanu
*ab and
Veaceslav
Coropceanu
 *ab
*ab
aSchool of Chemistry and Biochemistry & Center for Organic Photonics and Electronics (COPE), Georgia Institute of Technology, Atlanta, Georgia 30332-0400, USA
bDepartment of Chemistry and Biochemistry, The University of Arizona, Tucson, Arizona 85721-0088, USA. E-mail: jlbredas@arizona.edu; coropceanu@arizona.edu
First published on 5th August 2020
Abstract
The electronic, vibrational, and charge-transport properties of a series of benzothieno-benzothiophene (BTBT)–FmTCNQ (m = 0, 2, 4) and diCnBTBT–FmTCNQ (n = 8, 12; m = 0, 4) donor–acceptor (DA) co-crystals have been investigated by means of density functional theory calculations. The electronic-structure calculations predict wide conduction bands and small effective masses for electrons along the DA stacking directions. The results indicate that the increase in the number of F atoms on the acceptor molecules results in an increase of superexchange couplings along the DA stacks, while the addition of the alkyl side chains results in a decrease of through-space transfer integrals between neighboring stacks. Time-dependent density functional theory calculations of the optical properties describe the lowest two optical transitions as having a charge-transfer character and being related to the two electronic coupling pathways that contribute to the superexchange couplings. The results also indicate that the ionicity parameter in the diCnBTBT–FmTCNQ cocrystals is somewhat larger than in the BTBT analogues. Overall, we find that DFT calculations based on periodic boundary conditions are a reliable tool to estimate the ionicity parameter in DA cocrystals.
1. Introduction
Over the last two decades, π-conjugated organic materials have attracted considerable attention for potential applications in various optoelectronic devices1–5 with organic donor–acceptor (DA) co-crystals being considered as promising materials for OFET (organic field-effect transistor) applications.6–20 In the case of binary molecular systems, the latter consist of a regular arrangement of D and A molecular moieties with a defined stoichiometry. Usually, DA co-crystals display a ground-state charge transfer (CT) configuration (Dρ+–Aρ−) with a partial ionicity. The ionicity parameter (ρ) plays a critical role in defining the optical, electronic, and electrical properties of co-crystals, with ρ strongly correlated to the crystal packing motif. In binary crystals with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry, two types of molecular stacking patterns are typically found: (i) segregated stacks, in which the D and A moieties align in separate, well-ordered stacks, –D–D–D– and –A–A–A–; and (ii) mixed stacks, in which the D and A moieties alternate along the stacking directions.7 Segregated co-crystals are characterized by ρ values around 0.5 and predominantly exhibit metallic-like electrical properties; mixed-type co-crystals are usually semiconductors when ρ < 0.5 or insulators when ρ ∼ 1.6–9
1 stoichiometry, two types of molecular stacking patterns are typically found: (i) segregated stacks, in which the D and A moieties align in separate, well-ordered stacks, –D–D–D– and –A–A–A–; and (ii) mixed stacks, in which the D and A moieties alternate along the stacking directions.7 Segregated co-crystals are characterized by ρ values around 0.5 and predominantly exhibit metallic-like electrical properties; mixed-type co-crystals are usually semiconductors when ρ < 0.5 or insulators when ρ ∼ 1.6–9
In recent years, benzothieno[3,2-b][1]benzothiophene (BTBT, see Fig. 1) and its alkylated derivatives have found wide applications as p-type semiconducting materials for OFET devices. In their pristine form, BTBT crystals show a high degree of layered crystallinity which facilitates hole transport and leads to mobilities up to 10 cm2 V−1 s−1.21–23 Recently, it was found that BTBT and its derivatives can form DA cocrystals with 7,7,8,8-tetracyanoquinodimethane (TCNQ) and its fluorinated derivatives.24–29 Interestingly, in contrast to the p-channel transport found in the BTBT crystals, the BTBT-based DA cocrystals mostly exhibit n-channel characteristics.25–29
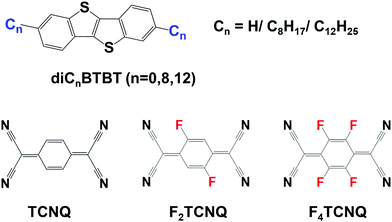 | ||
Fig. 1 Chemical structures of the BTBT (n = 0, Cn![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) H), diC8BTBT (C8 H), diC8BTBT (C8![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C8H17), and diC12BTBT (C12 C8H17), and diC12BTBT (C12![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C12H25) donors as well as the TCNQ, F2TCNQ, and F4TCNQ acceptor molecules. C12H25) donors as well as the TCNQ, F2TCNQ, and F4TCNQ acceptor molecules. | ||
A few theoretical studies have been reported on BTBT–TCNQ co-crystals.24,25,29–31 However, the calculations of the electronic-structure properties had so far been limited to the evaluation of the electronic couplings. Here, we greatly expand on these initial investigations and perform a detailed study of the electronic, optical, vibrational, and charge-transport properties of a series of BTBT–FmTCNQ (m = 0, 2, 4) and diCnBTBT–FmTCNQ (n = 8, 12; m = 0, 4) co-crystals, see Fig. 1 (we note that the diC8BTBT–F2TCNQ and diC12BTBT–F2TCNQ crystals are not considered here due to the positional disorder of the F atoms in their experimental crystal structures).
2. Methodology
The geometry optimizations and calculations of the individual molecular energies of BTBT, diCnBTBT (n = 8, 12), and FmTCNQ (m = 0, 2, 4) were performed at the density functional theory (DFT) B3LYP/6-31G(d,p) level. Time-dependent density functional theory (TDDFT) was then used with the same functional and basis set to calculate the electronic excitations from the ground state. A natural transition orbital (NTO) analysis was applied to characterize the electronic excitations.32 All these calculations were performed with the Gaussian 09-D01 package.33The geometry optimizations of the DA co-crystals were also conducted at the DFT B3LYP/6-31G(d,p) level. In the course of the optimizations, the cell parameters were kept fixed at their experimental values while the atomic positions were allowed to relax. Harmonic vibrational frequencies were calculated at the Γ point of the co-crystals. The coupled perturbed Hartree–Fock/Kohn–Sham (CPHF/CPKS) approach34 was used for the calculation of the vibrational spectra and the determination of the IR and Raman intensities. These calculations were carried out with the CRYSTAL 17 package.35
DFT B3LYP/6-31G(d,p) electronic band structures and densities of states (DOS) were calculated with the CRYSTAL 14 package.36 In order to compare our results with previous studies, the electronic-structure calculations of the co-crystals were performed as well using the experimental crystal structures.37 Uniform 8 × 8 × 8 or 8 × 8 × 4 Monkhorst–Pack k-point meshes were employed for the BTBT–FmTCNQ (m = 0, 2, 4) and diCnBTBT–FmTCNQ (n = 8, 12 and m = 0, 4) co-crystals, respectively.
The electronic couplings between nearest-neighbor pairs of donor–donor, donor–acceptor, and acceptor–acceptor components were evaluated with a fragment orbital approach in combination with a basis set orthogonalization procedure.38 The electronic couplings between D molecules [or A molecules] along the stacking directions were also estimated via an energy-splitting approach by considering the energy levels of a D–A–D [or A–D–A] triad:8
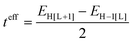 | (1) |
We recall that the inverse effective mass tensor of a crystal, mji−1, is defined as:39
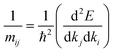 | (2) |
3. Results and discussion
3.1. Electronic structure
The crystal structures of BTBT–FmTCNQ and diCnBTBT–FmTCNQ were taken from the Cambridge Structural Database (the unit-cell parameters are collected in Table S1 in the ESI‡).25,28 BTBT–TCNQ, BTBT–F2TCNQ, and diCnBTBT–FmTCNQ (n = 8, 12; m = 0, 4) co-crystals belong to the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , while the BTBT–F4TCNQ co-crystal belongs to the monoclinic P21/c space group. All co-crystals considered in this work are characterized by a 1
, while the BTBT–F4TCNQ co-crystal belongs to the monoclinic P21/c space group. All co-crystals considered in this work are characterized by a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry and crystallize as mixed stacks. The DA stacks in BTBT–TCNQ, BTBT–F2TCNQ, and diCnBTBT–FmTCNQ co-crystals are located along the a crystallographic axis while those in BTBT–F4TCNQ are along the b axis (see Fig. S1, ESI‡). In all systems, the donor and acceptor molecules are equidistant from each other along the stacking directions.
1 stoichiometry and crystallize as mixed stacks. The DA stacks in BTBT–TCNQ, BTBT–F2TCNQ, and diCnBTBT–FmTCNQ co-crystals are located along the a crystallographic axis while those in BTBT–F4TCNQ are along the b axis (see Fig. S1, ESI‡). In all systems, the donor and acceptor molecules are equidistant from each other along the stacking directions.
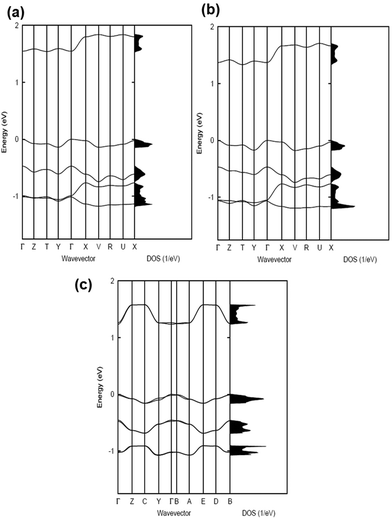
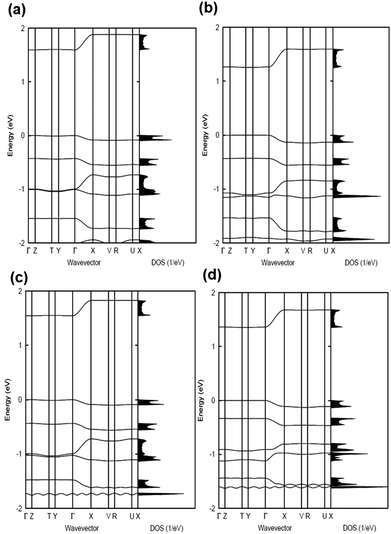
The electronic band structures and the densities of states of the co-crystals are given in Fig. 2 and 3, while Table 1 collects the widths of the conduction bands (CB) and valence bands (VB) along with the effective masses for each co-crystal (see also Table S2, ESI‡ for additional details). The CB widths are found to be significant, in the range of 280–380 meV, and are comparable to those already reported in the literature for co-crystals based on TCNQ and F4TCNQ acceptors.8,37 The largest values among the CB widths are estimated for the BTBT–F2TCNQ, BTBT–F4TCNQ, diC8BTBT–F4TCNQ, and di-C12BTBT–F4TCNQ co-crystals; this is due to the large effective (superexchange) transfer integral (∼60–80 meV) present along the stacking directions (see Table 2).
| Co-crystals | Bandwidth (in meV) | Effective mass | ||||
|---|---|---|---|---|---|---|
| CB | VB | Electrons | Holes | |||
| m 1/m0 | m 2/m0 | m 1/m0 | m 2/m0 | |||
| BTBT–TCNQ | 299 (250) | 139 (23) | 1.0 | 3.2 | 1.3 | 4.7 |
| BTBT–F2TCNQ | 372 (288) | 177 (28) | 0.8 | 1.5 | 1.0 | 3.4 |
| BTBT–F4TCNQ | 345 (340) | 157 (77) | 0.8 | 3.6 | 2.1 | 2.3 |
| diC8BTBT–TCNQ | 286 (280) | 89 (82) | 1.0 | >10 | 3.1 | >10 |
| diC8BTBT–F4TCNQ | 340 (329) | 132 (128) | 0.7 | >10 | 1.5 | >10 |
| diC12BTBT–TCNQ | 283 (280) | 100 (88) | 1.2 | 7.5 | 3.9 | >10 |
| diC12BTBT–F4TCNQ | 324 (316) | 128 (110) | 1.1 | 6.0 | 3.6 | >10 |
| Co-crystals | t A–A | t D–D | t effe | t effh |
|---|---|---|---|---|
| BTBT–TCNQ | 1.9 | 14.2 | 56.3 | 3.6 |
| BTBT–F2TCNQ | 7.2 | 17.6 | 63.2 | 5.3 |
| BTBT–F4TCNQ | 2.7 | 13.9 | 66.5 | 16.5 |
| diC8BTBT–TCNQ | 0.7 | 4.7 | 67.2 | 17.6 |
| diC8BTBT–F4TCNQ | 3.3 | 1.1 | 78.1 | 34.7 |
| diC12BTBT–TCNQ | 0.6 | 5.3 | 66.2 | 18.7 |
| diC12BTBT–F4TCNQ | 2.7 | 1.9 | 74.5 | 29.5 |
The VB widths fall in the range of 80–180 meV. In all investigated systems, the width of the VB is narrower than that of the CB. The largest band dispersions for the VB in BTBT–FmTCNQ co-crystals are observed along directions perpendicular to the DA stacks. In contrast, in the co-crystals based on the diCnBTBT donors, the largest VB band dispersions are observed along the stacking directions. The calculations show that, in BTBT–TCNQ and BTBT–F2TCNQ co-crystals, the direct through-space electronic couplings (tD–D) related to hole transfer between BTBT molecules residing on adjacent DA stacks are much larger than the superexchange couplings (teffh) along the stacking directions. In BTBT–F4TCNQ, the tD–D and teffh couplings are comparable and contribute nearly equally to the VB width. Overall, the calculations show that in all co-crystals the superexchange couplings for the electrons (teffe) are much larger than those (teffh) for the holes. As seen from Table 2, the values of both teffe and teffh in the co-crystals systematically increase with the increase in the number of F atoms on the acceptor molecule. This is due to the decrease in the D–A distances along the stacking directions in the co-crystals where the FmTCNQ molecules have a larger number of fluorine atoms, see the crystallographic data in Table S2 (ESI‡).25 We note that the dependence of the D–A distances on the number of fluorine atoms can be attributed to the variations in halogen bonding; a strong impact of halogen bonding on crystal packing has been reported in DA co-crystals based on substituted benzoquinone acceptors.14 The crystallographic data25,28,29 also show that upon addition of the alkyl side chains (Cn), there occurs an increase in the separation distance between DA stacks. As a result, in contrast to the BTBT–FmTCNQ co-crystals, the direct through-space transfer integrals for both holes and electrons in diCnBTBT–FmTCNQ co-crystals are significantly smaller than the corresponding superexchange couplings (see Table 2).
The smallest effective masses for electrons in all co-crystals are found along the stacking directions, which is consistent with the band structure and electronic-coupling results. Very small effective-mass values of 0.8m0, 0.8m0, and 0.7m0 (where m0 is the rest mass of electrons in vacuum) are calculated for electrons along the mixed-stack directions in BTBT–F2TCNQ, BTBT–F4TCNQ, and diC8BTBT–F4TCNQ, respectively. The effective mass values for electrons in the other co-crystals are in the range of 1.0–1.2m0. The effective masses for holes are larger than for electrons; however, in the BTBT–TCNQ, BTBT–F2TCNQ, and diC8BTBT–F4TCNQ cases, the hole effective masses are still relatively small, falling in the range of 1.0–1.5m0. We note that the smallest component of the effective mass for holes in the BTBT–FmTCNQ (m = 0, 2, 4) co-crystals is oriented perpendicular to the stacking direction (see Table 1 and Table S2, ESI‡) while they are oriented along the mixed-stack directions in the diCnBTBT–FmTCNQ (n = 8, 12; m = 0, 4) co-crystals. These results imply that in BTBT–FmTCNQ hole transport along the DA stacks is less effective than along other directions, a feature similar to that we recently found for co-crystals based on the 1,3,4,5,7,8-hexafluoro-11,11,12,12-tetracyanonaphtho-2,6-quinodimethane acceptor.11
Experimentally, based on OFET device measurements, Sato et al.28 have found n-channel charge transport along the mixed-stack direction in the BTBT–FmTCNQ (m = 0, 2, 4) single crystals, with the largest mobility of about 0.2 cm2 V−1 s−1 observed in the case of BTBT–F4TCNQ. Tsutsumi et al.25 have also found predominately n-channel charge transport in OFET devices based on diC8BTBT–FmTCNQ (m = 0, 2, 4) co-crystals, with the largest electron mobility 0.4 cm2 V−1 s−1, measured along the DA stacks in diC8BTBT–F2TCNQ.25 Our electronic-structure calculations are consistent with the experimental findings as they predict anisotropic electron transport properties (along the DA stacks) for all investigated systems. Our calculations suggest that in addition to electron transport along the DA stacks, hole transport could be operational in the BTBT–TCNQ and BTBT–F2TCNQ co-crystals along directions perpendicular to the DA stacks, and in the diC8BTBT–F4TCNQ co-crystal along the DA stacks. However, in OFET devices, hole mobilities were observed only in the case of the diC8BTBT–TCNQ co-crystal and were measured to be very small.25 We note that OFET mobilities depend on many other factors (disorder, domain boundaries, etc.) that should be considered for a detailed comparison between experiment and theory. For instance, in contrast to single-crystal results, the measurements performed on thin-film based devices show that all diC8BTBT–FmTCNQ systems display similar electron mobilities. In addition, we recall that our theoretical evaluations are based only on electronic-structure results and the role of electron–phonon interactions on charge mobility remains to be investigated.
3.2. Electron–hole asymmetry
A characteristic feature of many DA co-crystals is the “mirror symmetry” between the VBs and CBs in their band structures.8 However, in the co-crystals considered here, the mirror symmetry between VB and CB is absent. A rationalization of why the electron–hole symmetry is observed in some co-crystals but is absent in others can be obtained by treating superexchange coupling in the perturbation limit. The superexchange couplings for holes and electrons in this limit are given as: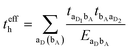 | (3) |
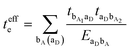 | (4) |
When only the transfer integral from the HOMO (HD) of the donor to the LUMO (LA) of the acceptor contributes to the superexchange couplings, we obtain the well-established expression:
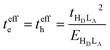 | (5) |
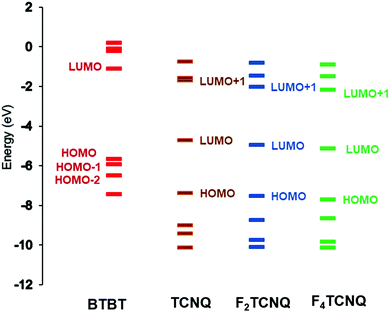 | ||
| Fig. 4 Energy levels of the BTBT, TCNQ, F2TCNQ, and F4TCNQ molecules, as calculated at the B3LYP/6-31G(d,p) level. | ||
| Co-crystals | t HD–LA (meV) | t (H−1)D–LA (meV) |
|---|---|---|
| BTBT–TCNQ | 160.3 | 348.1 |
| BTBT–F2TCNQ | 226.7 | 329.5 |
| BTBT–F4TCNQ | 252.4 | 331.9 |
| diC8BTBT–TCNQ | 271.3 | 298.3 |
| diC8BTBT–F4TCNQ | 334.8 | 267.1 |
| diC12BTBT–TCNQ | 271.2 | 289.3 |
| diC12BTBT–F4TCNQ | 327.1 | 266.7 |
3.3. Charge-transfer optical transitions
As a result of donor–acceptor interactions, the DA systems usually exhibit charge-transfer (CT) excited states that are located below the donor and acceptor local excitations. The characteristics of the optical CT bands are directly related to the electronic couplings tDA between the D and A frontier orbitals (and thus to the degree of ground-state ionicity). According to the Mulliken–Hush model,41–43 the transition dipole moment (dCT) of a CT band that peaks at ECT is proportional to the ratio tDA/ECT. The diC8BTBT–FmTCNQ co-crystals exhibit two low-energy optical transitions with dipole moments parallel to the DA stacking direction, which were assigned as CT transitions related to HOMOD ⇒ LUMOA and HOMO−1D ⇒ LUMOA coupling channels.25 Our excited-state calculations fully support this assignment, as the NTO analyses show that the first two optical transitions have a nearly 100% CT character (see Fig. S2, ESI‡). Our calculations indicate that two separate CT transitions should be observed in all the co-crystals considered here (see Table 4). The difference of 0.5–0.6 eV observed experimentally between the two CT transitions in the diC8BTBT–FmTCNQ co-crystals25 is well reproduced by our calculations. In line with the experimental findings25 our results also show that the CT transitions (see Table 4) exhibit a systematic redshift with the increase in the number of F atoms on the acceptor; this can be attributed to a corresponding decrease in the acceptor LUMO energy with the number of fluorine atoms (see Fig. 4). Taken together, our excited-state calculations and the experimental optical data provide strong support for the existence of comparable HOMOD ⇒ LUMOA and HOMO−1D ⇒ LUMOA contributions to the superexchange coupling in diCnBTBT–FmTCNQ co-crystals.| Co-crystals | S1 (f) | S2 (f) |
|---|---|---|
| BTBT–TCNQ | 1.19 (0.0061) | 1.78 (0.0620) |
| BTBT–F2TCNQ | 1.10 (0.0106) | 1.65 (0.0616) |
| BTBT–F4TCNQ | 1.06 (0.0107) | 1.61 (0.0666) |
| di-C8BTBT–TCNQ | 1.16 (0.0164) | 1.63 (0.0570) |
| di-C8BTBT–F4TCNQ | 1.01 (0.0198) | 1.43 (0.0634) |
| di-C12BTBT–TCNQ | 1.13 (0.0171) | 1.59 (0.0555) |
| di-C12BTBT–F4TCNQ | 1.05 (0.0143) | 1.42 (0.0641) |
3.4. Ground-state ionicity
It is also of interest to quantify the ground-state ionicity (degree of charge transfer), ρ, in the current set of co-crystals. Vibrational spectroscopy is a commonly used tool to characterize ρ. In the case of the BTBT–FmTCNQ co-crystals, Sato et al.28 and Castagnetti et al.29 used the IR C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N and C
N and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching modes of the acceptor respectively, to estimate ρ. Here, in order to provide additional insight on the ground-state ionicity, we computed the IR spectra, Raman spectra, and Mulliken molecular charges of the investigated co-crystals. The IR and Raman spectra are displayed in Fig. S3 and S4 (ESI‡), respectively. We estimated the ground-state ionicity parameter from the vibrational properties on the basis of two widely used approaches in the literature. The first approach is based on the formula:44
C stretching modes of the acceptor respectively, to estimate ρ. Here, in order to provide additional insight on the ground-state ionicity, we computed the IR spectra, Raman spectra, and Mulliken molecular charges of the investigated co-crystals. The IR and Raman spectra are displayed in Fig. S3 and S4 (ESI‡), respectively. We estimated the ground-state ionicity parameter from the vibrational properties on the basis of two widely used approaches in the literature. The first approach is based on the formula:44 | (6) |
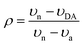 | (7) |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching modes are located at 1524 cm−1 and 1567 cm−1 in neutral F2TCNQ, 1444 cm−1 and 1502 cm−1 in the radical-anion state of F2TCNQ, and 1520 cm−1 and 1560 cm−1 in the BTBT–F2TCNQ co-crystal. By substituting the average frequency values of the two modes in either eqn (6) or eqn (7), we obtain the same ρ value of 0.08, which agrees very well with the value of 0.09 reported by Castagnetti et al.29 on the basis of the experimental IR spectra. We note, however, that the Dushinsky matrix46 calculations (see ESI,‡ Table S4) show that the normal modes of the neutral and radical-anion states are highly intermixed; the high-frequency 1567 cm−1 mode of the neutral F2TCNQ is found to have a larger projection coefficient on the 1444 cm−1 mode of the radical-anion state than on its 1502 cm−1 mode. If we consider 1567 cm−1, 1444 cm−1, and 1560 cm−1 as the values for υn, υa, and υDA respectively, the linear scaling approach yields ρ = 0.05. In the case of the C
C stretching modes are located at 1524 cm−1 and 1567 cm−1 in neutral F2TCNQ, 1444 cm−1 and 1502 cm−1 in the radical-anion state of F2TCNQ, and 1520 cm−1 and 1560 cm−1 in the BTBT–F2TCNQ co-crystal. By substituting the average frequency values of the two modes in either eqn (6) or eqn (7), we obtain the same ρ value of 0.08, which agrees very well with the value of 0.09 reported by Castagnetti et al.29 on the basis of the experimental IR spectra. We note, however, that the Dushinsky matrix46 calculations (see ESI,‡ Table S4) show that the normal modes of the neutral and radical-anion states are highly intermixed; the high-frequency 1567 cm−1 mode of the neutral F2TCNQ is found to have a larger projection coefficient on the 1444 cm−1 mode of the radical-anion state than on its 1502 cm−1 mode. If we consider 1567 cm−1, 1444 cm−1, and 1560 cm−1 as the values for υn, υa, and υDA respectively, the linear scaling approach yields ρ = 0.05. In the case of the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N vibrations in the IR spectra, the two IR active modes are observed at 2226 cm−1 and 2240 cm−1 in the co-crystal, at 2233 cm−1 and 2251 cm−1 in neutral F2TCNQ, and at 2176 cm−1 and 2208 cm−1 in the radical-anion state of F2TCNQ. The use of eqn (6) and (7) yields ρ values of 0.19 and 0.18, respectively, which are slightly larger than the value of 0.16 derived by Sato et al.28 from the experimental C
N vibrations in the IR spectra, the two IR active modes are observed at 2226 cm−1 and 2240 cm−1 in the co-crystal, at 2233 cm−1 and 2251 cm−1 in neutral F2TCNQ, and at 2176 cm−1 and 2208 cm−1 in the radical-anion state of F2TCNQ. The use of eqn (6) and (7) yields ρ values of 0.19 and 0.18, respectively, which are slightly larger than the value of 0.16 derived by Sato et al.28 from the experimental C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N IR data. The ρ value estimated from the C
N IR data. The ρ value estimated from the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N modes is thus larger than that estimated from the C
N modes is thus larger than that estimated from the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching modes, which is not unexpected since it was suggested earlier that the approach based on C
C stretching modes, which is not unexpected since it was suggested earlier that the approach based on C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N modes systematically overestimates ρ.28 The ρ values derived from DFT and experimental IR data for BTBT–F2TCNQ are collected in Table 5, along with those for BTBT–TCNQ and BTBT–F4TCNQ. The results indicate that the three systems share a similar ionicity parameter.
N modes systematically overestimates ρ.28 The ρ values derived from DFT and experimental IR data for BTBT–F2TCNQ are collected in Table 5, along with those for BTBT–TCNQ and BTBT–F4TCNQ. The results indicate that the three systems share a similar ionicity parameter.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C mode (ρC
C mode (ρC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) and C
C) and C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N mode (ρC
N mode (ρC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N) analyses
N) analyses
| Co-crystal | ρ |
ρ
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C
|
ρ
C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N N
|
||
|---|---|---|---|---|---|
| a Current work based on eqn (7). b From ref. 28. c From ref. 29. | |||||
| BTBT–TCNQ | 0.04 | 0.08a | 0.10b | 0.19a | 0.20c |
| BTBT–F2TCNQ | 0.04 | 0.08a | 0.09b | 0.18a | 0.16c |
| BTBT–F4TCNQ | 0.04 | 0.09a | 0.12b | 0.13a | 0.11c |
| diC8BTBT–TCNQ | 0.07 | — | — | — | — |
| diC8BTBT–F4TCNQ | 0.07 | — | — | — | — |
| diC12BTBT–TCNQ | 0.06 | — | — | — | — |
| diC12BTBT–F4TCNQ | 0.05 | — | — | — | — |
The ρ values estimated on the basis of Mulliken charges are also given in Table 5. In line with the results derived from the frequency-shift approach, similar ρ values are obtained for the co-crystals based on unsubstituted BTBT. However, the Mulliken charge approach yields values that are about 60% smaller than the ones estimated from the vibrational frequency shifts. The co-crystals where BTBT has alkyl-chain substitutions display overall higher ρ values. The largest ρ value is calculated for the diC8BTBT–F4TCNQ system, which also shows one of the largest transfer integrals and conduction bandwidths along the stacking direction as well as one of the smallest effective masses for electrons. Moreover, diC8BTBT–F4TCNQ shows the largest OFET mobility values among the co-crystals in single-crystal based devices.25 Finally, we note that the underestimation of ρ in the present calculations could be related to the use of the B3LYP functional. While we have previously shown that in DA co-crystals the super-exchange electronic couplings, the band structures, and the effective masses are not strongly affected by the choice of the DFT functional,47 this might not be the case for the estimations of the ionicity parameter. Therefore, the implementation of range-separated hybrid functionals that are known to provide a reliable description of CT excitations48,49 is desirable in order to obtain a better characterization of the co-crystal electronic properties in the context of periodic-boundary condition calculations.
4. Conclusions
We have investigated the electronic structure, vibrational properties, and charge-transport properties of co-crystals based on BTBT and di-CnBTBT (n = 8, 12) donors and FmTCNQ (m = 0, 2, 4) acceptors. The DFT calculations predict large conduction bandwidths and small effective masses for electrons in all co-crystals, which points to efficient electron transport in these systems. Large values of the valence bandwidths and small effective masses for holes are also observed for the BTBT–FmTCNQ (m = 0, 2, 4) co-crystals, which suggests ambipolar transport characteristics in these systems.Our calculations indicate that the superexchange electronic couplings systematically increase with the increase in the number of fluorine atoms on the acceptor molecules. This can be attributed to the decrease in D–A distances along the stacking directions as a result of an increase in halogen bonding.14 These results suggest that halogen coupling could have a much stronger effect on the structure–property relations in DA co-crystals than usually expected from a simple picture based on the modification of the molecular electron affinity by halogenation. The addition of the alkyl side chains (Cn) results in an increase in the distance separating the DA stacks. As a consequence, the direct through-space transfer integrals for both holes and electrons between neighboring stacks is significantly reduced upon substitution of BTBT with a di-CnBTBT donor.
We have also evaluated the ground-state ionicity parameter of the co-crystals on the basis of the DFT-derived crystal and molecular IR spectra as well as the Mulliken charges. The estimated values of ρ based on Mulliken charges are about 60% smaller than those based on IR vibration mode frequency shifts, with the latter in very good agreement with those based on experimental vibrational data. This indicates that DFT calculations relying on periodic boundary conditions can be used to obtain reliable estimates of ρ in addition to or in the absence of experimental data.
Finally, our calculations indicate that accounting for vibrational-mode mixing (Dushinsky effect) in the frequency-shift based approaches can increase accuracy in the derivation of the ionicity parameters. Consequently, such calculations can provide a better description of the electronic properties of DA co-crystals.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the National Science Foundation (under Awards No. DMR-1708147 and DMR-2023497) and the University of Arizona.References
- M. Bendikov, F. Wudl and D. F. Perepichka, Tetrathiafulvalenes, oligoacenenes, and their buckminsterfullerene derivatives: The brick and mortar of organic electronics, Chem. Rev., 2004, 104, 4891 CrossRef CAS PubMed.
- J. E. Anthony, The Larger Acenes: Versatile Organic Semiconductors, Angew. Chem., Int. Ed., 2008, 47, 452 CrossRef CAS PubMed.
- C. Wang, H. Dong, L. Jiang and W. Hu, Organic semiconductor crystals, Chem. Soc. Rev., 2018, 47, 422 RSC.
- H. Oberhofer, K. Reuter and J. Blumberger, Charge Transport in Molecular Materials: An Assessment of Computational Methods, Chem. Rev., 2017, 117, 10319 CrossRef CAS PubMed.
- M. Ball, B. Zhang, Y. Zhong, B. Fowler, S. Xiao, F. Ng, M. Steigerwald and C. Nuckolls, Conjugated Macrocycles in Organic Electronics, Acc. Chem. Res., 2019, 52, 1068 CrossRef CAS PubMed.
- T. Hasegawa and J. Takeya, Organic field-effect transistors using single crystals, Sci. Technol. Adv. Mater., 2009, 10, 024314 CrossRef PubMed.
- T. Mori and T. Kawamoto, Organic conductors—from fundamentals to nonlinear conductivity, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2007, 103, 134 RSC.
- L. Zhu, Y. Yi, Y. Li, E.-G. Kim, V. Coropceanu and J.-L. Brédas, Prediction of Remarkable Ambipolar Charge-Transport Characteristics in Organic Mixed-Stack Charge-Transfer Crystals, J. Am. Chem. Soc., 2012, 134, 2340 CrossRef CAS PubMed.
- K. P. Goetz, D. Vermeulen, M. E. Payne, C. Kloc, L. E. McNeil and O. D. Jurchescu, Charge-transfer complexes: new perspectives on an old class of compounds, J. Mater. Chem. C, 2014, 2, 3065 RSC.
- L. J. Sun, F. X. Yang, X. T. Zhang and W. P. Hu, Stimuli-responsive behaviors of organic charge transfer cocrystals: recent advances and perspectives, Mater. Chem. Front., 2020, 4, 715 RSC.
- R. R. Dasari, X. Wang, R. A. Wiscons, H. F. Haneef, A. Ashokan, Y. Zhang, M. S. Fonari, S. Barlow, V. Coropceanu, T. V. Timofeeva, O. D. Jurchescu, J.-L. Brédas, A. J. Matzger and S. R. Marder, Charge-Transport Properties of F6TNAP-Based Charge-Transfer Cocrystals, Adv. Funct. Mater., 2019, 29, 1904858 CrossRef CAS.
- R. A. Wiscons, V. Coropceanu and A. J. Matzger, Quaternary Charge-Transfer Solid Solutions: Electronic Tunability through Stoichiometry, Chem. Mater., 2019, 31, 6598 CrossRef CAS.
- N. R. Goud, X. P. Zhang, J. L. Bredas, V. Coropceanu and A. J. Matzger, Discovery of Non-linear Optical Materials by Function-Based Screening of Multi-component Solids, Chem, 2018, 4, 150 CAS.
- R. K. Behera, N. R. Goud, A. J. Matzger, J.-L. Brédas and V. Coropceanu, Electronic Properties of 1,5-Diaminonaphthalene:Tetrahalo-1,4-benzoquinone Donor–Acceptor Cocrystals, J. Phys. Chem. C, 2017, 121, 23633 CrossRef CAS.
- N. Castagnetti, M. Masino, C. Rizzoli, A. Girlando and C. Rovira, Mixed stack charge transfer crystals: Crossing the neutral-ionic borderline by chemical substitution, Phys. Rev. Mater., 2018, 2, 024602 CrossRef CAS.
- Y. K. Qin, J. Zhang, X. Y. Zheng, H. Geng, G. Y. Zhao, W. Xu, W. P. Hu, Z. G. Shuai and D. B. Zhu, Charge-Transfer Complex Crystal Based on Extended--Conjugated Acceptor and Sulfur-Bridged Annulene: Charge-Transfer Interaction and Remarkable High Ambipolar Transport Characteristics, Adv. Mater., 2014, 26, 4093 CrossRef CAS PubMed.
- K. P. Goetz, A. Fonari, D. Vermeulen, P. Hu, H. Jiang, P. J. Diemer, J. W. Ward, M. E. Payne, C. S. Day, C. Kloc, V. Coropceanu, L. E. McNeil and O. D. Jurchescu, Freezing-in orientational disorder induces crossover from thermally-activated to temperature-independent transport in organic semiconductors, Nat. Commun., 2014, 5, 5642 CrossRef CAS PubMed.
- H. Geng, X. Zheng, Z. Shuai, L. Zhu and Y. Yi, Understanding the Charge Transport and Polarities in Organic Donor–Acceptor Mixed-Stack Crystals: Molecular Insights from the Super-Exchange Couplings, Adv. Mater., 2015, 27, 1443 CrossRef CAS PubMed.
- J. Zhang, W. Xu, P. Sheng, G. Zhao and D. Zhu, Organic Donor–Acceptor Complexes as Novel Organic Semiconductors, Acc. Chem. Res., 2017, 50, 1654 CrossRef CAS PubMed.
- H. Geng, L. Y. Zhu, Y. P. Yi, D. B. Zhu and Z. G. Shuai, Superexchange Induced Charge Transport in Organic Donor-Acceptor Cocrystals and Copolymers: A Theoretical Perspective, Chem. Mater., 2019, 31, 6424 CrossRef CAS.
- H. Ebata, T. Izawa, E. Miyazaki, K. Takimiya, M. Ikeda, H. Kuwabara and T. Yui, Highly Soluble [1]Benzothieno[3,2-b]benzothiophene (BTBT) Derivatives for High-Performance, Solution-Processed Organic Field-Effect Transistors, J. Am. Chem. Soc., 2007, 129, 15732 CrossRef CAS PubMed.
- H. Minemawari, T. Yamada, H. Matsui, J. y. Tsutsumi, S. Haas, R. Chiba, R. Kumai and T. Hasegawa, Inkjet printing of single-crystal films, Nature, 2011, 475, 364 CrossRef CAS PubMed.
- K. Nakayama, Y. Hirose, J. Soeda, M. Yoshizumi, T. Uemura, M. Uno, W. Li, M. J. Kang, M. Yamagishi, Y. Okada, E. Miyazaki, Y. Nakazawa, A. Nakao, K. Takimiya and J. Takeya, Patternable Solution-Crystallized Organic Transistors with High Charge Carrier Mobility, Adv. Mater., 2011, 23, 1626 CrossRef CAS PubMed.
- H. Méndez, G. Heimel, A. Opitz, K. Sauer, P. Barkowski, M. Oehzelt, J. Soeda, T. Okamoto, J. Takeya, J.-B. Arlin, J.-Y. Balandier, Y. Geerts, N. Koch and I. Salzmann, Doping of Organic Semiconductors: Impact of Dopant Strength and Electronic Coupling, Angew. Chem., Int. Ed., 2013, 52, 7751 CrossRef PubMed.
- J. Tsutsumi, S. Matsuoka, S. Inoue, H. Minemawari, T. Yamada and T. Hasegawa, N-type field-effect transistors based on layered crystalline donor–acceptor semiconductors with dialkylated benzothienobenzothiophenes as electron donors, J. Mater. Chem. C, 2015, 3, 1976 RSC.
- Y. Shibata, J. Tsutsumi, S. Matsuoka, K. Matsubara, Y. Yoshida, M. Chikamatsu and T. Hasegawa, Uniaxially oriented polycrystalline thin films and air-stable n-type transistors based on donor-acceptor semiconductor (diC8BTBT)(FnTCNQ) [n = 0, 2, 4], Appl. Phys. Lett., 2015, 106, 143303 CrossRef.
- T. Higashino, M. Dogishi, T. Kadoya, R. Sato, T. Kawamoto and T. Mori, Air-stable n-channel organic field-effect transistors based on charge-transfer complexes including dimethoxybenzothienobenzothiophene and tetracyanoquinodimethane derivatives, J. Mater. Chem. C, 2016, 4, 5981 RSC.
- R. Sato, M. Dogishi, T. Higashino, T. Kadoya, T. Kawamoto and T. Mori, Charge-Transfer Complexes of Benzothienobenzothiophene with Tetracyanoquinodimethane and the n-Channel Organic Field-Effect Transistors, J. Phys. Chem. C, 2017, 121, 6561 CrossRef CAS.
- N. Castagnetti, A. Girlando, M. Masino, C. Rizzoli and C. Rovira, Mixed Stack Organic Semiconductors: The Anomalous Case of the BTBT-TCNQFx Series, Cryst. Growth Des., 2017, 17, 6255 CrossRef CAS.
- Z. P. Zhang, L. Jiang, C. L. Cheng, Y. G. Zhen, G. Y. Zhao, H. Geng, Y. P. Yi, L. Q. Li, H. L. Dong, Z. G. Shuai and W. P. Hu, The Impact of Interlayer Electronic Coupling on Charge Transport in Organic Semiconductors: A Case Study on Titanylphthalocyanine Single Crystals, Angew. Chem., Int. Ed., 2016, 55, 5206 CrossRef CAS PubMed.
- R. Sato, T. Kawamoto and T. Mori, Asymmetrical hole/electron transport in donor-acceptor mixed-stack cocrystals, J. Mater. Chem. C, 2019, 7, 567 RSC.
- R. L. Martin, Natural transition orbitals, J. Chem. Phys., 2003, 118, 4775 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D. 01, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- M. Rérat, L. Maschio, B. Kirtman, B. Civalleri and R. Dovesi, Computation of Second Harmonic Generation for Crystalline Urea and KDP. An ab Initio Approach through the Coupled Perturbed Hartree–Fock/Kohn–Sham Scheme, J. Chem. Theory Comput., 2016, 12, 107 CrossRef PubMed.
- R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Quantum-mechanical condensed matter simulations with CRYSTAL, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360 Search PubMed.
- R. Dovesi, R. Orlando, A. Erba, C. M. Zicovich-Wilson, B. Civalleri, S. Casassa, L. Maschio, M. Ferrabone, M. De La Pierre, P. D'Arco, Y. Noël, M. Causà, M. Rérat and B. Kirtman, CRYSTAL14: A program for the ab initio investigation of crystalline solids, Int. J. Quantum Chem., 2014, 114, 1287 CrossRef CAS.
- L. Zhu, Y. Yi, A. Fonari, N. S. Corbin, V. Coropceanu and J.-L. Brédas, Electronic Properties of Mixed-Stack Organic Charge-Transfer Crystals, J. Phys. Chem. C, 2014, 118, 14150 CrossRef CAS.
- V. Coropceanu, J. Cornil, D. A. da Silva Filho, Y. Olivier, R. Silbey and J.-L. Brédas, Charge Transport in Organic Semiconductors, Chem. Rev., 2007, 107, 926 CrossRef CAS PubMed.
- K. Seeger, Semiconductor physics: an introduction, Berlin: Springer, Berlin, 9th edn, 2010 Search PubMed.
- L. Zhu, H. Geng, Y. Yi and Z. Wei, Charge transport in organic donor–acceptor mixed-stack crystals: the role of nonlocal electron–phonon couplings, Phys. Chem. Chem. Phys., 2017, 19, 4418 RSC.
- R. S. Mulliken, Molecular Compounds and their Spectra. II, J. Am. Chem. Soc., 1952, 74, 811 CrossRef CAS.
- N. S. Hush, Homogeneous and heterogeneous optical and thermal electron transfer, Electrochim. Acta, 1968, 13, 1005 CrossRef CAS.
- V. Coropceanu, X.-K. Chen, T. Wang, Z. Zheng and J.-L. Brédas, Charge-transfer electronic states in organic solar cells, Nat. Rev. Mater., 2019, 4, 689 CrossRef.
- E. Kampar and O. Neilands, Degree of Charge Transfer in Donor–Acceptor Systems of the π–π Type, Russ. Chem. Rev., 1986, 55, 334 CrossRef.
- D. Vermeulen, L. Y. Zhu, K. P. Goetz, P. Hu, H. Jiang, C. S. Day, O. D. Jurchescu, V. Coropceanu, C. Kloc and L. E. McNeil, Charge Transport Properties of Perylene–TCNQ Crystals: The Effect of Stoichiometry, J. Phys. Chem. C, 2014, 118, 24688 CrossRef CAS.
- J. R. Reimers, A practical method for the use of curvilinear coordinates in calculations of normal-mode-projected displacements and Duschinsky rotation matrices for large molecules, J. Chem. Phys., 2001, 115, 9103 CrossRef CAS.
- A. Fonari, C. Sutton, J.-L. Brédas and V. Coropceanu, Impact of exact exchange in the description of the electronic structure of organic charge-transfer molecular crystals, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 165205 CrossRef.
- L. Kronik and S. Kümmel, Dielectric Screening Meets Optimally Tuned Density Functionals, Adv. Mater., 2018, 30, 1706560 CrossRef PubMed.
- Z. Zheng, D. A. Egger, J.-L. Brédas, L. Kronik and V. Coropceanu, Effect of Solid-State Polarization on Charge-Transfer Excitations and Transport Levels at Organic Interfaces from a Screened Range-Separated Hybrid Functional, J. Phys. Chem. Lett., 2017, 8, 3277 CrossRef CAS PubMed.
Footnotes |
| † This article is dedicated to our mentor and friend Professor Fred Wudl, who has been at the forefront of design and synthesis of organic semiconducting and metallic materials for the past fifty years. |
| ‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/d0qm00420k |
| § Department of Chemistry and Biochemistry, The University of Alabama, Tuscaloosa, Alabama 35487, USA. |
| ¶ Department of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, Massachusetts 02142, USA. |
| This journal is © the Partner Organisations 2020 |