Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
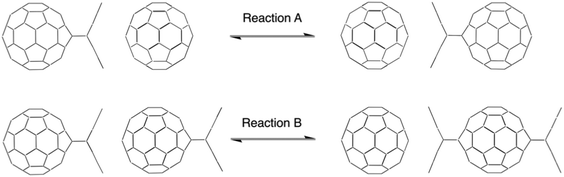
The intermolecular anthracene-transfer in a regiospecific antipodal C60 difunctionalization†
Radu A.
Talmazan
 a,
Klaus R.
Liedl
a,
Klaus R.
Liedl
 a,
Bernhard
Kräutler
a,
Bernhard
Kräutler
 b and
Maren
Podewitz
b and
Maren
Podewitz
 *a
*a
aInstitute of General, Inorganic and Theoretical Chemistry, and Centre of Molecular Biosciences, University of Innsbruck, Innrain 80/82, 6020 Innsbruck, Austria. E-mail: maren.podewitz@uibk.ac.at
bInstitute of Organic Chemistry, and Centre of Molecular Biosciences, University of Innsbruck, Innrain 80/82, 6020 Innsbruck, Austria
First published on 19th May 2020
Abstract
Ever since the discovery of fullerenes, their mono- and multi-functionalization by exohedral addition chemistry has been a fundamental topic. A few years ago, a topochemically controlled regiospecific difunctionalization of C60 fullerene by anthracene in the solid state was discovered. In the present work, we analyse the mechanism of this unique reaction, where an anthracene molecule is transferred from one C60 mono-adduct to another one, under exclusive formation of equal amounts of C60 and of the difficult to make, highly useful, antipodal C60 bis-adduct. Our herein disclosed dispersion corrected DFT studies show the anthracene transfer to take place in a synchronous retro Diels–Alder/Diels–Alder reaction: an anthracene molecule dissociates from one fullerene under formation of an intermediate, while undergoing stabilizing interactions with both neighbouring fullerene molecules, facilitating the reaction kinetically. In the intermediate, a planar anthracene molecule is sandwiched between two neighbouring fullerenes and forms equally strong ‘double-decker’ type π–π stacking interactions with both of these fullerenes. Analysis with the distortion interaction model shows that the anthracene unit of the intermediate is almost planar with minimal distortion. This analysis highlights the existence of simultaneous noncovalent interactions engaging both faces of a planar polyunsaturated ring and two convex fullerene surfaces in an unprecedented ‘inverted sandwich’ structure. Hence, it sheds light on new strategies to design functional fullerene based materials.
Introduction
Fullerenes, the spherical molecular carbon allotropes first discovered in mass-spectrometric experiments in 1985,1–3 open up exciting fields of chemical research.4–7 The unique properties of the icosahedral C60 molecules have particularly inspired a multitude of studies concerning the functionalization of this polyunsaturated carbon compound by the means of addition reactions.2,5,8 Early on, a range of cyclopropanations4,8,9 and pyrrolidine forming reactions8,10 as well as other formal cycloaddition reactions8 were used very effectively. The synthetic interest in the chemistry of C60 was further boosted by its pronounced and theoretically rationalized selectivity for cycloaddition reactions at its so called [6,6]-bonds.6,8,11–13 Indeed, the thermally reversible [4 + 2]-cycloaddition (Diels–Alder, DA) reaction has become a most versatile methodology for the creation of exohedrally functionalized fullerene derivatives.8,14–17 Polycyclic aromatic hydrocarbons, such as anthracene,8,17–21 other acenes,22–25 and derivatives thereof,26 were found to represent surprisingly suitable diene-components for functionalization of C60 by [4 + 2] cycloaddition reactions. The experimental work on the fullerene functionalization has been accompanied and guided by insightful theoretical studies.27–30 Suitably functionalized fullerenes have been widely applied as key components,31–34 in photovoltaic devices,35–39 in artificial photosynthesis,40,41 drug delivery,32,42 bio- and nanomedicine,41,42 in material science,31,43–48 and as self-healing polymers.49,50The molecular features of the fullerenes as polyunsaturated spherical carbon compounds have drawn particular attention to the synthesis of di- and multi-functionalized derivatives with high regio- and stereo-control.8,51–57 Sequential addition reactions to create multi-adducts with exceptional architectures were presented,57–63 including reactions between C60 and anthracenes, where mono-,16–18,21,26,64 bis-,19,64–68 and specific tris-adducts were reported.63,69 The kinetic and thermodynamic driving forces for the formation of specific bis- and tris-adducts has become a much discussed issue.8 Thermolysis of the crystalline mono-adduct of C60 and anthracene has provided a strikingly efficient means for achieving regiospecific antipodal bis-addition.65 The exquisite selectivity in this process was proposed to result from topochemical control in the solid state,20,65 because the alternative solution chemistry led to a mixture of anthracene adducts, among them the antipodal bis-adduct as only a minor component.19,70
The (thermal) DA reaction has become a fundamental synthetic method for the stereo-controlled formation of two new C–C bonds in a 6-memberd ring structure, and a mechanistic textbook topic of (orbital and state) symmetry control,71–74 thoroughly investigated in experimental and theoretical studies.75–78 For typical hydrocarbons, the two new C–C bonds formed by the DA reaction are made in a concerted and thermally reversible process.79–84 Quantum chemical studies have fully verified these ‘basic rules’ of the thermal [4 + 2]-cycloaddition chemistry.85–90 The spherical architecture of the fullerenes induces pyramidalisation of the unsaturated carbon centers,91 rendering the C60 electrophilic and specifically dienophilic – an early recognized factor for further enhancing reactivity in exohedral addition reactions,8,28,92,93 decreasing the activation barrier in DA reactions.94 Aromatic hydrocarbons first associate with C60 to form a non-covalently bound intermediate complex.95 Recent studies at the example of benzene and C60 shed light on the interaction of a planar aromatic compound and a curved fullerene surface,74 which was shown to be different in nature from π–π stacking interactions between two planes.
Regioselectivity of the DA cycloaddition with C60 has also been computationally investigated,57,66,96–99 for example, revealing the preference of additions to the [6,6]-bond over the [5,6]-position to be attributed to more favourable interactions between the reactants in the transition state.12 A finding later confirmed by decomposition of the electron activity13 and also put forward by Garcia-Rodeja et al. to rationalize the regio-selectivity of bis-cycloaddition reactions to fullerenes.11
The regiospecific formation of the antipodal bis-adduct from the crystalline mono-adduct of C60 and anthracene in the solid state suggested a topochemical control.65 Potentially, the anthracene transfer between two pre-aligned mono-adducts, takes place in a synchronous fashion. However, the detailed reaction mechanism of this anthracene transfer was not established. Formally, this reaction could be achieved by a complete dissociation of the anthracene moiety from one mono-adduct by a retro-DA reaction, followed by the highly regio-selective DA-cycloaddition at another one. Alternatively, the anthracene transfer could proceed via a direct one-step reaction, where the transition state would represent a planar anthracene molecule interacting similarly with both fullerenes. A third variant could be via a synchronous two-step reaction, where in a retro-DA step an intermediate is first formed that is stabilized by two neighbouring fullerene moieties, followed by an addition at the back of the mono-adduct to generate the antipodal bis-adduct. Unravelling this reaction mechanism is of significant interest, as it implies a correlated defunctionalisation of one mono-adduct molecule, coupled with functionalization of a neighbouring mono-adduct molecule. Hence, a thorough computational analysis of this anthracene transfer between two fullerenes was carried out, in order to gain insights into the simultaneous interaction of two spherical and one planar poly-unsaturated carbon molecules.
We investigated the topochemically controlled regiospecific anthracene transfer by two model reactions: reaction A describes the transfer of one anthracene molecule from one C60 fullerene mono-adduct to a 2nd C60 fullerene (Scheme 1, upper panel), while reaction B describes the transfer of one anthracene from one C60 fullerene mono-adduct to another C60 fullerene–anthracene mono-adduct, resulting in the antipodal bis-adduct (Scheme 1, lower panel). Density Functional Theory (DFT) calculations were performed to elucidate the reaction mechanism and to shed light on the interactions occurring at the unique reaction intermediate, where a planar anthracene is sandwiched between two fullerenes.
Computational methodology
As no high resolution X-ray crystal structures were available, the initial structures for the C60 fullerene and C60:anthracene mono-adduct were set-up using Gaussview 4.1.2.100 All subsequent structure optimizations and harmonic frequency calculations were performed using Turbomole 7.3101 and were done in C1 symmetry. Structure optimizations have been carried out with Density Functional Theory (DFT) utilizing the GGA density functional BP86102–105 in combination with the def2-SVP basis set.106 As shown in previous studies, empirical dispersion corrections, that are not intrinsically dealt with in DFT, are essential to obtain reliable structures in such extended π-systems and to localize reaction intermediates.95 Therefore, Grimme's empirical dispersion corrections with Becke–Johnson damping of the DFT-D3107 type were employed in all calculations. Selected structures were re-optimised with BP86/def2-TZVP108/D3 but structural differences were found to be small. Reported electronic energies were calculated as single points BP86/def2-TZVP/D3 on the BP86/def2-SVP/D3 optimized structures. An even larger def2-QZVP109 basis set yielded very similar single point energies with differences less than 2 kJ mol−1 compared to def2-TZVP. Hence, the triple-zeta def2-TZVP basis set was considered to be accurate enough. To test the effect of the density functional, single point calculations with B3LYP102,105,110,111/def2-TZVP/D3 were computed on the BP86/def2-SVP/D3 optimized structures too. To validate our chosen methodology (density functional/basis set), we compared structural parameters with known experimental data. As to our knowledge, currently no crystal structure of the C60:anthracene mono-adduct exists, we compared our calculated structures to the available experimental C60:antracene bis-adducts (“edge” and “trans-4”) structures.67 Through the comparison with the aforementioned C60:anthracene bis-adducts, it is shown that the methods chosen offer accurate structures, as the bond lengths deviate less than 0.01 Å from their crystal counterparts, while the angles and dihedrals are within 0.1°.To further test our methodology, we also calculated the formation of the C60:anthracene mono-adduct (see also Tables S6 and S7 in the ESI†), for which experimental data is available. In their 2004 paper, Sarova et al.24 reported an activation enthalpy of ΔH‡ = 57 kJ mol−1 and a Gibbs energy of ΔG‡ = 93 kJ mol−1 in toluene. While this enthalpy is very close to our BP86 calculated value of ΔH‡ = 59.4 kJ mol−1, the Gibbs energy was with ΔG‡ = 72.6 kJ mol−1 a bit underestimated. B3LYP values, however, overestimated the reaction barrier compared to experiment, ΔH‡B3LYP = 86.2 kJ mol−1 and ΔG‡B3LYP = 114.6 kJ mol−1. The experimental reaction energy was found to be ΔH = −81 kJ mol−1 and ΔG = −23 kJ mol−1. BP86 underestimated these values (ΔH = −54.5 kJ mol−1 and ΔG = 7.4 kJ mol−1) and the trend got worse for B3LYP (ΔH = −31.4 kJ mol−1 and ΔG = 31.7 kJ mol−1). Full optimisations and calculation of thermodynamic corrections at the BP86/D3/def2-TZVP level alleviated these shortcomings to some extend and correctly predicted the reaction to be exergonic with ΔG = −5.2 kJ mol−1 (see also Table S7†), but are not feasible given the size of the investigated structures. In our view, BP86 yielded a better overall performance although barriers are likely to be underestimated.
As the initial reaction is in solid-state, involving no charged species, no long-range interactions were expected. Indeed, taking the effect of the crystal environment into account by a dielectric constant, we chose ε = 4 here,112 in agreement with previous studies, had little effect on the resulting energies. As can be seen from Table S5 in the ESI,† the electronic energies decreased by less than 2 kJ mol−1. Thus, modelling the reaction in gas phase is adequate.
The correct stationary points were identified through harmonic frequency calculations, by examining the eigenvalues of the Hessian corresponding to each structure. Minima show only positive eigenvalues, while a transition state shows exactly one imaginary eigenvalue and its associated eigenvector corresponds to the reaction coordinate.
To obtain Gibbs energies, zero-point energies and thermal corrections at 298.15 K were calculated via approximation of the partition function by the standard rigid rotator and harmonic oscillator model using Turbomole's “freeh” tool. Obtained harmonic frequencies were scaled with a factor of 0.9914113 to increase the accuracy. These corrections were calculated with BP86/def2-SVP/D3 and added to the BP86/def2-TZVP/D3 electronic energies.
Assuming (hindered) rotation of the nonfunctionalized C60 fullerene in INTBis, TS(INTBis-3) and 3, results in additional contributions to the rotational entropy. To approximately account for these stabilizing effects, the structures were split up into two moieties – a C60 fullerene and a bis-adduct-like structure – and the rotational entropy was calculated for each moiety separately. The resulting contributions were summed up and replaced the rotational entropy contributions of the full complex in the Gibbs energy calculation, thereby, taking additional stabilizing effects due to the (hindered) rotation of the nonfunctionalized fullerene into account.
The 2D potential energy surfaces (PES) scans were obtained by modifying the structure along the chosen degrees of freedom, then subsequently calculating single point energies of each resulting structure. The resulting PES is visualized with Origin 2018b.114
To highlight the non-covalent interactions, NCIPLOT was used,115 where the second eigenvalue of the electron-density Hessian matrix, sign(λ2)ρ, is depicted on an isosurface of the reduced gradient s.116 Areas with (weak) non-covalent interactions are characterized with a low (reduced) electron density gradient and a sign(λ2)ρ close to zero (depicted in green). Large negative values of sign(λ2)ρ are indicative of attractive interactions (depicted in blue), whereas large positive values of sign(λ2)ρ indicate non-bonding repulsive interactions (depicted in red).
All structures were visualized using PyMol,117 except for those depicting non-covalent interactions, which were displayed with VMD.118
Results
Mechanism of the topochemically controlled regiospecific C60 fullerene–anthracene transfer reaction
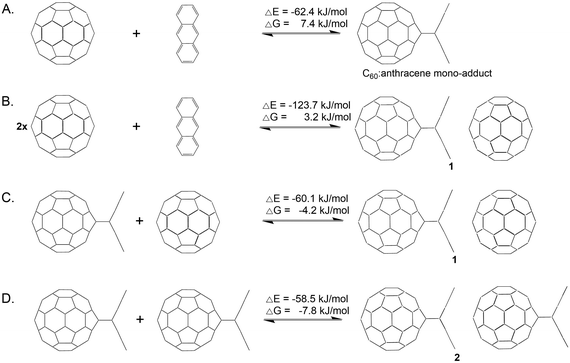
Prior to investigating the C60 fullerene–anthracene transfer reaction, we evaluated the reaction energies associated with the formation of an isolated C60:anthracene mono-adduct, see Scheme 2 (panel A), for which we found a stabilizing energy of ΔE = −62.4 kJ mol−1 and ΔG = 7.4 kJ mol−1. Comparing this value to the experimentally found one of ΔG = −23 kJ mol−1,24 we see that the Gibbs energy is underestimated in our calculations (see also Computational methodology). However, the reaction is correctly predicted to be exergonic (ΔG = −5.2 kJ mol−1), when structures and thermodynamic corrections were calculated with a larger basis set (see also Table S7 in the ESI†). The formation of the complex 1 from the constituents yields an energy gain of ΔE = −123.7 kJ mol−1 and ΔG = 3.2 kJ mol−1 (see panel B). The coordination of a 2nd C60 fullerene to the C60:anthracene mono-adduct to form 1, exerts a stabilizing effect of ΔE = −60.1 kJ mol−1 and a Gibbs reaction energy of ΔG = −4.2 kJ mol−1 (panel C). Similarly, aligning two C60:anthracene mono-adducts, to form the complex 2, also results in a stabilization of ΔE = −58.5 kJ mol−1 and ΔG = −7.8 kJ mol−1. It is noteworthy here that the stabilization energy of the second reaction partner to form the stable complexes 1 and 2, is roughly the same as the formation energy of the C60:mono-adduct, −60.1/−58.5 kJ mol−1vs. −62.4 kJ mol−1.The proposed reaction pathway for the anthracene transfer as modelled by reaction A (see Scheme 1) is shown in Fig. 1, depicting educts, products, intermediates as well as transition states. Relative electronic energies (BP86/def2-TZVP/D3//BP86/def2-SVP/D3) are given in red and reaction Gibbs energies in green. For the sake of comparison, B3LYP/def2-TZVP/D3//BP86/def2-SVP/D3 are listed in blue.
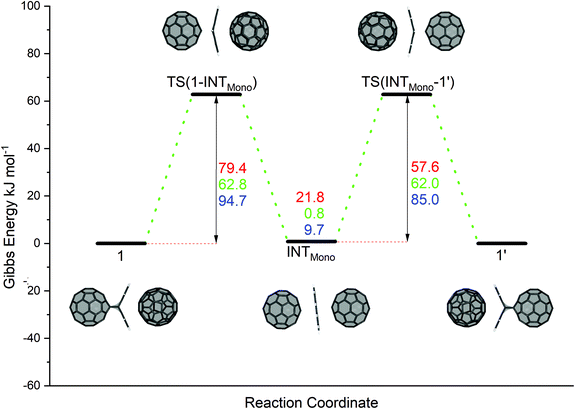 | ||
| Fig. 1 Reaction mechanism of the anthracene transfer (reaction A in Scheme 1) from the C60:anthracene mono-adduct (see complex 1) to a neighbouring C60 fullerene (see complex 1′) in a two-step synchronous Retro Diels–Alder and Diels–Alder reaction via an inverted sandwich intermediate (INTMono). Red values denote BP86/def2-TZVP/D3//BP86/def2-SVP/D3 relative electronic energies, green values denote reaction Gibbs energies and blue values denote relative electronic energies computed with B3LYP/def2-TZVP/D3//BP86/def2-SVP/D3. All values are in kJ mol−1. | ||
While the formation of complex 1, from two fullerenes and an anthracene molecule is energetically favoured, the most stable conformation of 1 was determined by a potential energy scan of the rotation of the 2nd fullerene as depicted in the ESI in Fig. S12.†
In the initial reaction step, complex 1 undergoes a Retro-Diels–Alder type process, in which the anthracene separates from the fullerene moiety, while still being trapped between and stabilized by the two fullerene species. The transition state TS(1-INTMono) for this reaction step has a barrier of ΔE‡ = 79.4 kJ mol−1, ΔG‡ = 62.8 kJ mol−1 and ΔE‡B3LYP = 94.7 kJ mol−1. The reaction then proceeds to reach a stable intermediate structure (INTMono). This energy minimum structure is less stable than the educt, 1, by ΔE = 21.8 kJ mol−1 (ΔG = 0.8 kJ mol−1, and ΔEB3LYP = 9.7 kJ mol−1). Remarkably, the anthracene molecule lies completely flat between the two fullerenes, experiencing interactions with both sides. The reaction then continues in a mirrored fashion, with a [4 + 2] cycloaddition step. The second transition state, TS(INTMono-1′), lies above the intermediate state, with ΔE‡ = 57.6 kJ mol−1, ΔG‡ = 62.0 kJ mol−1, and ΔE‡B3LYP = 85.0 kJ mol−1, exhibiting energy values identical to the reversed reaction to TS(1-INTMono). The product compound (1′) is chemically identical to the educt 1 (ΔE = 0.0 kJ mol−1). Compared to BP86, for B3LYP somewhat higher electronic energies were found. Nevertheless, both are in good agreement with each other.
In model reaction B (see Scheme 2), structure 2, where two C60:anthracene mono-adducts are aligned, reacts exclusively to the antipodal trans–bis-adduct in complex with C60 (denoted as 3) undergoing a proposed mechanism as depicted in Fig. 2.
 | ||
| Fig. 2 Reaction pathway of the anthracene transfer between two mono-adducts (reaction B in Scheme 1). Electronic and the Gibbs energies of the reaction calculated with BP86/def2-TZVP/D3//BP86/def2-SVP/D3 are depicted in red and green, respectively. Energies calculated with B3LYP/def2-TZVP/D3//BP86/def2-SVP/D3 are shown in blue. The grey lines represent the Gibbs energy when additional rotational entropy of the C60 is taken into account too (see Computational methodology for details). All values are in kJ mol−1. | ||
Similar as in reaction A, the mechanism starts with a retro Diels Alder step to yield the stable intermediate INTBis, where the anthracene is trapped between two fullerenes. For this reaction step, an energy barrier of ΔE‡ = 76.8 kJ mol−1 (ΔG‡ = 64.5 kJ mol−1 and ΔE‡B3LYP = 94.3 kJ mol−1) was found, being very similar to the corresponding energy barrier in reaction A. The intermediate (INTBis) has a relative electronic energy ΔE = 19.1 kJ mol−1 (ΔEB3LYP = 9.5 kJ mol−1) and a Gibbs energy of ΔG = 2.8 kJ mol−1, indicating the stabilizing effect of the neighbouring fullerenes on the anthracene. INTBis then reaches a 2nd transition state TS(INTBis-3) with a relative energy of ΔE‡ = 84.7 kJ mol−1, a relative Gibbs energy of ΔG‡ = 72.0 kJ mol−1 (ΔE‡B3LYP = 110.0 kJ mol−1) before forming the antipodal bis-adduct in complex with C60, denoted as 3. The 2nd transition state is energetically less favourable than TS(2-INTBis), but the barrier is with ΔE‡ = 65.6 kJ mol−1 (ΔG‡ = 69.2 kJ mol−1, ΔE‡B3LYP = 100.4 kJ mol−1) slightly lower due to the higher energy of INTBis. In the initial calculations, the formed antipodal C60:anthracenes bis-adduct in complex with C60 (3) is with a relative electronic energy of 7.9 kJ mol−1 (ΔG = 7.2 kJ mol−1 and ΔEB3LYP = 7.6 kJ mol−1) thermodynamically slightly less favoured than 2. However, as shown by low barrier to rotation of the C60 moiety in complex 1 (see Fig. S12†), a hindered rotation of C60 in INTBis, TS(INTBis-3) and 3 could be anticipated resulting in additional rotational entropy. This contribution lowers the total Gibbs energy of 3 by about 39 kJ mol−1, whereas a smaller stabilising effect is expected for INTBis and TS(INTBis-3) due to more pronounced rotational hindrance.
To further analyse the reaction, we used the distortion interaction model/activation strain model independently developed by Houk and Bickelhaupt93,119,120 to characterise all stationary points in the reaction including intermediates and product/educt structures. As results are expected to be similar, we restrict our analyses to reaction A only.
We intended to quantify the effects of the deformations exerted by the weak, non-covalent interactions and to characterise the planar anthracene molecule in the intermediate structure. In our distortion interaction analysis along the reaction coordinate, the interactions on both sides of the anthracene were considered by taking the unperturbed fullerene and anthracene molecule as reference structures.
The deformation and interaction energies, ΔEDef. and ΔEInt., can be computed using the following equations,
| ΔEElectronic = ∑ΔEDef. + ∑ΔEInt. | (1) |
| ΔEDef. = EDefomed − EOptimized | (2) |
By summing up the deformation energies ΔEDef. and subtracting them from the electronic energy ΔEElectronic, we obtain the total interaction energy as
| ∑ΔEInt. = ΔEElectronic − ∑ΔEDef. | (3) |
When looking at the deformation energies ΔEElectronic for the C60 fullerene along the reaction coordinate of reaction A as listed in Table 1, a maximum of ΔEC60 Def. = 174.3 kJ mol−1 was found in 1 and 1′, decreasing to 48.4 kJ mol−1 in the transition states and reaching a minimum in the intermediate INTMono. A mere deformation of ΔEC60 Def. = 18.5 kJ mol−1 indicate that the structure is close to that of an unperturbed C60 fullerene. The same trend was observed for the deformation of anthracene. Of course, the strong deformations of bound anthracene are alleviated upon reaching the TS. However remarkably, INTMono has a very small anthracene deformation energy of only ΔEAnthracene Def. = 3.2 kJ mol−1, indicating that the anthracene is stabilized almost at its ideal gas phase geometry. The total deformation energy is, therefore, by far the smallest in INTMono (ΔETotal Def. = 21.7 kJ mol−1). The interplay of distortion and interaction results in a striking stabilization of INTMono in unprecedented ‘inverted sandwich’ structure with ΔEElectronic = −80.7 kJ mol−1, when assembled from two fullerenes and an anthracene.
| Structure | 1 | TS(1-INTMono) | INTMono | TS(INTMono-1′) | 1′ |
|---|---|---|---|---|---|
| ΔEC60 Def. | 174.3 | 48.4 | 18.5 | 48.4 | 174.3 |
| ΔEAnthracene Def. | 306.8 | 86.0 | 3.2 | 86.0 | 306.8 |
| ΔETotal Def. | 481.1 | 134.4 | 21.7 | 134.4 | 481.1 |
| ΔETotal Int. | −583.6 | −157.6 | −102.4 | −157.6 | −583.6 |
| ΔEElectronic | −102.5 | −23.1 | −80.7 | −23.1 | −102.5 |
Structure and electronic properties of the intermediate INTMono
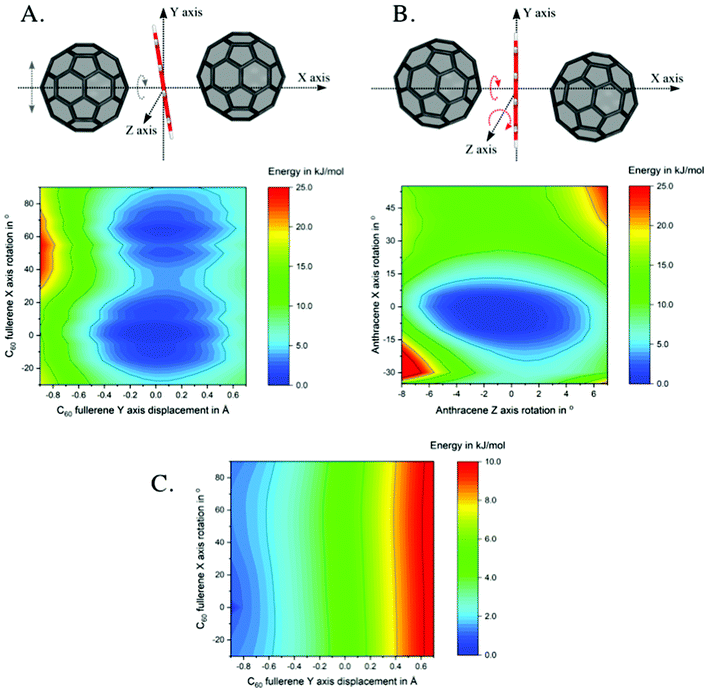
To shed light on the nature of the unprecedented intermediates, INTMono and INTBis, where the anthracene lies almost perfectly planar between the two curved fullerenes, potential energy surfaces as well as non-covalent interactions were investigated.Two 2D potential energy surface (PES) scans were performed at the example of INTMono, see Fig. 3. On the left-hand side (A), the PES for the displacement of the left C60 fullerene along the y-axis and its rotation around the x-axis is depicted. On the right-hand side (B), the rotation of the anthracene around the x-axis and its tilt, i.e., its rotation around the z-axis is shown. As evident from the plot, the PES is rather flat allowing for a wide range of motion of the anthracene and fullerene without significant increase in energy. The energy minimum, as verified by analysis of the harmonic frequencies, was determined for a conformation, where – compared to an idealized C2v symmetric complex – the anthracene is rotated by 32.5° around the x-axis and rotated around the z-axis by 8° resulting in a tilt. Last, the two fullerenes are oriented with their centre of mass above and below the xz-plane (see Fig. 3). Consequently, this anthracene orientation maximizes attractive interactions with the neighbouring fullerenes. While the dispersion corrections become more favourable when the anthracene–fullerene distance is minimized (see x-axis in the dispersion energy surface shown in Fig. 3C), it can also be seen that these interactions depend on the rotation of the fullerene (see y-axis in Fig. 3C).
We also tested replacement of anthracene by smaller rings, such as naphthalene and benzene, in INTMono. Both naphthalene and benzene assume positions very close to that of the anthracene, being tilted by 8° (rotated by 8° around the z-axis) and rotated by 32.5° around the x-axis, even though the arrangement of the acene over the ring slightly differs (see Fig. S15 ESI†).
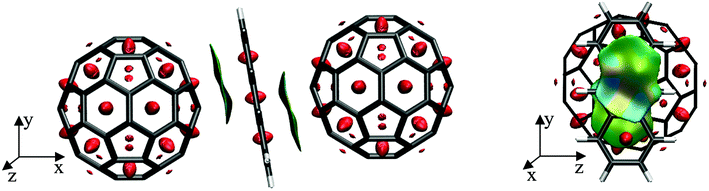
To further elucidate the interactions between the anthracene and their two neighbouring fullerenes, the non-covalent interactions were visualized using NCIPLOT115,116 as depicted in Fig. 4. Here, the electronic density is examined as a function of an isosurface of the reduced gradient, thus allowing for a quantitative assessment of these interactions. Red areas in Fig. 4 denote strong repulsive interaction, whereas green denote weakly attractive regions, typical for dispersive interactions. These are found between the upper and middle C6-ring of anthracene and the closest C6-ring of the left fullerene as well as between the middle and lower C6-ring of anthracene and the closest C6-ring of the right fullerene, showing symmetric π–π double decker interactions in this ‘inverted sandwich’ structure.
Characterization of transition states
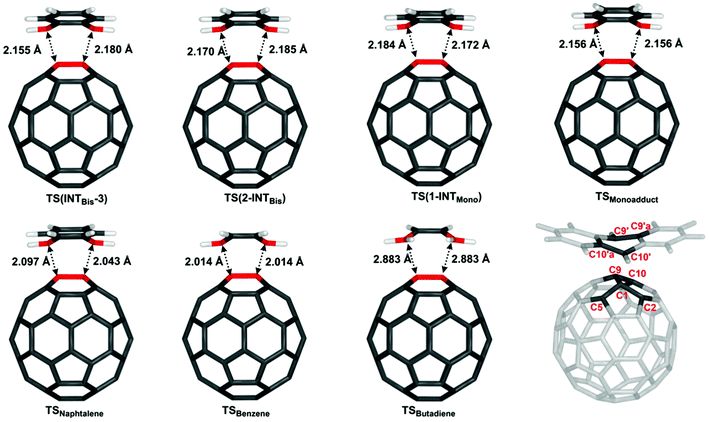
To evaluate the effect of a second fullerene or C60:anthracene on the transition state for the cycloaddition or cycloreversion, we analysed the structural and electronic effects in the obtained transition states TS(INTBis-3), TS(2-INTBis), and TS(1-INTMono) and compared them to a number of C60:arene transition states as well as the C60:butadiene transition state (Table 2).| Structure | TS(INTBis-3) | TS(2-INTBis) | TS(1-INTMono) | TSMonoadduct | TSNaphtalene | TSBenzene | TSButadiene |
|---|---|---|---|---|---|---|---|
| Bond lengths | |||||||
| C1–C10′ | 2.180 | 2.185 | 2.184 | 2.156 | 2.097 | 2.014 | 2.883 |
| C9–C9′ | 2.155 | 2.170 | 2.172 | 2.156 | 2.043 | 2.014 | 2.884 |
| C1–C5 | 1.485 | 1.483 | 1.484 | 1.485 | 1.493 | 1.497 | 1.479 |
| C1–C9 | 1.480 | 1.482 | 1.482 | 1.483 | 1.482 | 1.481 | 1.480 |
| Angles | |||||||
| C5–C1–C2 | 104.5 | 104.7 | 104.7 | 104.5 | 103.7 | 103.4 | 105.3 |
| C5–C1–C9 | 117.6 | 117.8 | 117.7 | 117.6 | 116.8 | 117.0 | 118.3 |
| Dihedral angles | |||||||
| C5–C1–C9–C10 | 126.8 | 126.8 | 126.9 | 126.2 | 124.5 | 123.4 | 129.0 |
| C10′a–C10′–C9′–C9′a | 147.8 | 147.8 | 148.4 | 148.6 | 144.9 | 143.0 | — |
| ΔE ‡ Barrier | 65.6 | 57.7 | 57.6 | 62.4 | 100.9 | 128.1 | 30.5 |
Most notable differences in the transition states can be seen in the C1–C10′ and C9–C9′ bond lengths. With TSButadiene being a somewhat different case due to the absence of an aromatic ring, it can be seen the C1–C10′ and the C9–C9′ bond lengths increase with increasing ring size and further increases in the presence of a 2nd fullerene. In addition, the transition states become more asymmetric in TS(1-INTMono), TS(2-INTBis) and TS(INTBis-3). As the TS of the mono-adduct and of the antipodal bis-adduct (see ESI Fig. S7†) are almost perfectly symmetric, the asymmetry likely arises due to interaction with the 2nd fullerene, which is aligned slightly off axis.
Considering the energy barriers, when the non-covalently bound intermediate is taken as a reference (see Fig. S16† for structures), it can be seen that TS(1-INTMono) and TS(2-INTBis) not only have very similar barrier heights but also the lowest energy barriers for this set of structures (57.6 and 57.7 kJ mol−1). The formation of the bis-adduct in TS(INTBis-3) has a higher energy barrier with ΔE‡Barrier = 65.6 kJ mol−1 as expected, which is very similar to that of the antipodal bis-adduct (67.2 kJ mol−1, see ESI Table S2†), slightly surpassing the activation energy necessitated by the formation of the C60:anthracene mono-adduct at ΔE‡Barrier = 62.4 kJ mol−1. The energy barrier for the formation of mono-adducts increases as the diene gets smaller, ΔE‡Barrier = 100.9 kJ mol−1 for TSNaphtalene, ΔE‡Barrier = 128.1 kJ mol−1 for TSBenzene, with the notable exception of TSButadiene, where the energy is the lowest out of all investigated transition states, at only 30.5 kJ mol−1.
We also performed a distortion–interaction analysis93,119,120 on the transition states depicted in Fig. 5, for details see illustration in Fig. S13 in the ESI.† It can be seen from Table 3, that the total deformation energies are smallest, 115.9 and 113.6 kJ mol−1, for the two transition states TS(2-INTBis) and TS(1-INTMono), where a C60:anthracene mono-adduct is formed in the presence of a second fullerene. The deformation energy increases slightly when we look at the mono-adduct, at 119.2 kJ mol−1 as well as when reducing the size of the added molecule. Thus, it reaches 159.2 kJ mol−1 for naphthalene and 186.6 kJ mol−1 for benzene. Butadiene, requires a minimal amount of deformation energy compared to the other transition states, with a total of 67.7 kJ mol−1. The interaction energy of the transfer reactions is consistent with all transition states involving aromatic hydrocarbons showing little variation. TS(INTBis-3) has the least favourable energy, −52.4 kJ mol−1, and TS(2-INTBis) the most favourable one, at −58.3 kJ mol−1. The deformation energy largely correlates with the barrier height with the exception of TS(INTBis-3), where the less favourable interaction energy and higher C60 deformation energy can be considered the cause for the high transition-state energy.
| Structure | TS(INTBis-3) | TS(2-INTBis) | TS(1-INTMono) | TSMonoadduct | TSNaphtalene | TSBenzene | TSButadiene |
|---|---|---|---|---|---|---|---|
| ΔEC60 Def. | 32.8 | 32.5 | 30.8 | 34.9 | 45.2 | 53.3 | 17.6 |
| ΔEDiene Def. | 85.2 | 83.5 | 82.8 | 84.3 | 114.0 | 133.4 | 50.1 |
| ΔETotal Def. | 118.0 | 115.9 | 113.6 | 119.2 | 159.2 | 186.6 | 67.7 |
| ΔETotal Int. | −52.4 | −58.3 | −56.0 | −56.8 | −58.3 | −58.3 | −37.2 |
| ΔE‡Barrier | 65.6 | 57.7 | 57.6 | 62.4 | 100.9 | 128.3 | 30.5 |
Discussion
Reaction mechanism
Both investigated reaction A and B (see Scheme 1) follow a synchronous two-step retro DA/DA sequence, where the anthracene dissociates while still being trapped between two fullerenes during the entire reaction to yield a regiospecific difunctionalization.The starting point of reaction A is represented by a stabilized complex, 1, consisting of a C60 fullerene and a C60:anthracene mono-adduct. The interactions between the mono-adduct and the fullerene, while being favourable, allow for a large rotational movement of the C60 fullerene as the potential energy surface is very shallow (see Fig. S12†). This indicates that a pre-alignment in the first reaction step is not immanent to the structures, but facilitated due to the confined arrangement of molecules in the solid state.
By comparing the transition states of reactions A and B, with several transition states for C60:arene-mono-adduct formation a systematic trend becomes apparent: in the series from benzene, to naphthalene, to anthracene, to TS(1-INTMono), to TS(2-INTBis), and to, TS(INTBis-3) the C1–C10′ and C9–C9′ bonds elongate, which relates well to the Hammond postulate. The cycloaddition becomes more exothermic (compare Table S9†), making the TS more intermediate like (earlier TS for cycloaddition/later TS for cycloreversion). Moreover, the 2nd fullerene induced a difference in the two bond lengths resulting in more asymmetric transition states, which likely arises because the 2nd fullerene is located off centre the anthracene–fullerene axis, but whether this is a result of the gas phase calculation and whether this also pertains the solid state remains speculative. Still, the presence of the 2nd fullerene decreases the transition-barrier height mostly by minimizing deformation.
The reaction rate for the elementary cycloreversion step and the according half-life can be calculated using the Eyring equation,
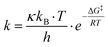 | (4) |
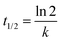 | (5) |
At room temperature, for reaction A reaction rate of 6.2 × 101 s−1 is obtained for the cycloreversion (t1/2 = 1.1 × 10−5 s), while heated up to 180 °C the reaction rate increases to k = 5.4 × 105 s−1 (t1/2 = 1.3 × 10−9 s). Similar values are found for reaction B, k = 4.8 s−1 (t1/2 = 1.5 × 10−1 s) at room temperature and k = 1.0 × 105 s−1 (t1/2 = 6.9 × 10−9 s) at 180 °C. This agrees with the experimentally observed fast reaction at elevated temperatures and shows that the reaction model is indeed plausible.65 It should be kept in mind, however, that reported calculated values for the energy barriers might be underestimated by several kJ mol−1 (see also Computational methodology and Tables S5–S7 in the ESI†).
Concerning reaction B, our initial calculations showed structure 3 is slightly less table than the educts. However, thermodynamic corrections are calculated with the standard rigid rotator model/harmonic oscillator model of the entire complex 3. In this model, the rotational entropy is calculated for the whole complex not allowing for individual rotation of the C60 fullerene.
If we assume the nonfunctionalized C60 fullerene to be rotating, the additional rotational entropy lowers ΔG of INTBis, TS(INTBis-3), and 3. In the limit of a freely rotating C60, the Gibbs energy of 3 is lowered by approximately 39 kJ mol−1 making it the thermodynamically favoured species. The gain in rotational entropy for INTBis and TS(INTBis-3) can be expected to be smaller as the C60 rotation is potentially more hindered there, hence, we have not assigned any number in Fig. 2, but just indicated the stabilising effect. In any case, this correction to the standard model makes 3 the thermodynamically favoured product of reaction B and entropic effects are likely to be the driving force for this reaction.65 Of course, this also holds for reaction A, but the effect is symmetric and does not affect the relative energy difference between the structures.
The planar intermediate INTMono with double decker π–π stacking interactions
INTMono represents an unprecedented case of non-covalent π–π-stacking interactions between a planar and two curved surfaces.Being exposed to a convex surface, planar structures such as anthracene tend to deform and adapt to the convex shape to maximize attractive dispersive interactions as indicated by the slight bend in the anthracene when forming a noncovalently bound intermediate with C60 as depicted in Fig. S17.† The deformation of the anthracene can be characterized by the bowl depth – calculated according to ref. 124, which amounts to 0.14 Å for the C60 and anthracene intermediate. Such a deformation is also observed for other acenes.95 In the presence of a 2nd C60 fullerene as in INTMono and INTBis, the anthracene is almost perfectly planar with minimal distortion from the gas phase geometry. This finding is supported by the distortion–interaction analysis, where for INTMono a minimal distortion of anthracene was found (3.2 kJ mol−1). Thus, an alignment with the two fullerenes stabilizes a planar structure and counteracts the tendency of a large aromatic hydrocarbons to slightly bend towards C60 surfaces.
Further analysing the interactions between the C60:anthracene and the 2nd fullerene (1, TS(1-INTMono), INTMono), we see that the calculated the bowl depth124 of anthracene correlates with the stabilization energy: INTMono (anthracene is planar) has the smallest stabilization energy (−51.9 kJ mol−1) but it gets more favourable for TS(1-INTMono), with a bowl depths of anthracene of 0.88 Å and an interaction energy of −57.8 kJ mol−1. The stabilization energy is with −60.1 kJ mol−1 most pronounced in 1, where a bowl depth of 1.63 Å was determined. This finding is in line with previous studies, where the bowl depth of hexabenzocorones was found to correlate with the C60 interaction strength, reaching an optimum at 1.5 Å.124
Concerning the position of the anthracene relative to the two fullerenes, a rotation around the x-axis by 32.5° and a rotation around the z-axis by 8° with respect to an idealized C2v symmetric molecule maximizes favourable interactions. This orientation is very different from the position an anthracene molecule adopts when interacting with a single C60 fullerene, where it is aligned directly on top of the bond-to-be-formed, along the common edge formed by two C6 rings on the fullerene.95,125 When a second fullerene is added, the simultaneous double decker π–π stacking interactions induce a rearranging of the anthracene to stack the 6-membered carbon ring of one C60 on its upper ring and of the other C60 fullerene on the lower ring. In contrast, if two benzene molecules are stacked in parallel, the two rings are slightly shifted so that one carbon atom stands over the centre of the second benzene molecule.126 In addition, the presented intermediate INTMono shows with 3.06 Å shorter π–π stacking distances between anthracene and each fullerene (compare also with ref. 127) than found in planar π–π stacking structures. For example, in benzene dimers the distance between the two faces is 3.8 Å.126
Conclusion
Our quantum chemical investigations revealed the anthracene-transfer in the experimentally observed regiospecific C60:anthracene difunctionalization to proceeds via a synchronous two-step retro Diels–Alder/Diels Alder type process. The central species is a low lying intermediate, where a planar anthracene molecule is non-covalently bound to two fullerene moieties. The rate determining step in this reaction is the initial cycloreversion to form anthracene sandwiched intermediates, either in the form of INTMono or as INTBis. The presence of the second fullerene lowers the activation energies and stabilizes intermediates with planar anthracene species. The potential driving force for experimentally observed antipodal bis-adduct is the gain in rotational entropy upon formation of complex 3.Given that in experiment only the formation of C60 and the antipodal bis-adduct occurs, despite the latter being the thermodynamically least stable of all C60:anthracene bis-adducts, strongly suggests that crystal packing pre-aligns the structures to control the regiospecific reaction. These findings encourage new approaches of topochemically steered C60 multi-functionalization.
The intermediate structures INTMono and INTBis present a central point of interest, as they are to the best of our knowledge an unprecedented case of a perfectly planar molecule, trapped between equal and opposing π–π stacking interactions with ‘curved’ fullerenes. Our studies shed more light on the nature of π–π stacking interactions between a planar and (two) curved surfaces, as we report the first example of a double decker type of π–π stacking in an ‘inverted sandwich’ arrangement. These findings could open up new possibilities in designing functional fullerene based materials.
Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
The authors declare no conflict of interest.Funding sources
FWF (M-2005).Acknowledgements
The computational results presented in this work have been achieved using the HPC infrastructure of the University of Innsbruck (leo3e) and the Vienna Scientific Cluster VSC3. M. P. would like to thank the Austrian Science Fund (FWF) for a generous Lise Meitner Fellowship (M-2005).Notes and references
- H. W. Kroto, J. R. Heath, S. C. Obrien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163 CrossRef CAS.
- H. W. Kroto, Angew. Chem., Int. Ed. Engl., 1992, 31, 111–129 CrossRef.
- W. Krätschmer, L. D. Lamb, K. Fostiropoulos and D. R. Huffman, Nature, 1990, 347, 354–358 CrossRef.
- F. Wudl, Acc. Chem. Res., 1992, 25, 157–161 CrossRef CAS.
- F. Diederich and C. Thilgen, Science, 1996, 271, 317–323 CrossRef CAS.
- J. M. Hawkins, Acc. Chem. Res., 1992, 25, 150–160 CrossRef CAS.
- H. Schwarz, Angew. Chem., Int. Ed. Engl., 1992, 31, 293–298 CrossRef.
- A. Hirsch and M. Brettreich, Fullerenes, Wiley-VCH, Weinheim, 2005 Search PubMed.
- C. Bingel, Chem. Ber., 1993, 126, 1957–1959 CrossRef CAS.
- M. Prato and M. Maggini, Acc. Chem. Res., 1998, 31, 519–526 CrossRef CAS.
- Y. Garcia-Rodeja, M. Sola and I. Fernandez, J. Org. Chem., 2018, 83, 3285–3292 CrossRef CAS PubMed.
- I. Fernandez, M. Sola and F. M. Bickelhaupt, Chem. – Eur. J., 2013, 19, 7416–7422 CrossRef CAS PubMed.
- N. Villegas-Escobar, A. Poater, M. Sola, H. F. Schaefer and A. Toro-Labbe, Phys. Chem. Chem. Phys., 2019, 21, 5039–5048 RSC.
- P. Belik, A. Gügel, J. Spickermann and K. Müllen, Angew. Chem., Int. Ed. Engl., 1993, 32, 78–80 CrossRef.
- F. Diederich, U. Jonas, V. Gramlich, A. Herrmann, H. Ringsdorf and C. Thilgen, Helv. Chim. Acta, 1993, 76, 2445–2453 CrossRef CAS.
- B. Kräutler and M. Puchberger, Helv. Chim. Acta, 1993, 76, 1626–1631 CrossRef.
- M. Tsuda, T. Ishida, T. Nogami, S. Kurono and M. Ohashi, J. Chem. Soc., Chem. Commun., 1993, 1296–1298 RSC.
- J. A. Schlüter, J. M. Seaman, S. Taha, H. Cohen, K. R. Lykke, H. H. Wang and J. M. Williams, J. Chem. Soc., Chem. Commun., 1993, 972–974 RSC.
- A. Duarte-Ruiz, T. Müller, K. Wurst and B. Kräutler, Tetrahedron, 2001, 57, 3709–3714 CrossRef CAS.
- A. Duarte-Ruiz, K. Wurst and B. Kräutler, Helv. Chim. Acta, 2001, 84, 2167–2177 CrossRef CAS.
- B. Kräutler, T. Müller and A. Duarte-Ruiz, Chem. – Eur. J., 2001, 7, 3223–3235 CrossRef.
- F. Cataldo, D. A. Garcia-Hernandez and A. Manchado, Fullerenes, Nanotubes, Carbon Nanostruct., 2015, 23, 760–768 CrossRef CAS.
- F. Cataldo, D. A. Garcia-Hernandez and A. Manchado, Fullerenes, Nanotubes, Carbon Nanostruct., 2015, 23, 818–823 CrossRef CAS.
- G. H. Sarova and M. N. Berberan-Santos, Chem. Phys. Lett., 2004, 397, 402–407 CrossRef CAS.
- W. T. Su, M. Watanabe, Y. J. Chang, P. T. Chou, A. Ghosh and T. J. Chow, Tetrahedron Lett., 2015, 56, 1092–1095 CrossRef CAS.
- G.-W. Wang, Z.-X. Chen, Y. Murata and K. Komatsu, Tetrahedron, 2005, 61, 4851–4856 CrossRef CAS.
- M. Sola, M. Duran and J. Mestres, J. Am. Chem. Soc., 1996, 118, 8920–8924 CrossRef CAS.
- S. Osuna and K. N. Houk, Chem. – Eur. J., 2009, 15, 13219–13231 CrossRef CAS PubMed.
- A. Chikama, H. Fueno and H. Fujimoto, J. Phys. Chem., 1995, 99, 8541–8549 CrossRef CAS.
- A. A. Peyghan and S. Yourdkhani, Struct. Chem., 2014, 25, 785–791 CrossRef CAS.
- M. Prato, J. Mater. Chem., 1997, 7, 1097–1109 RSC.
- H. Wang, Q. W. Chen and S. Q. Zhou, Chem. Soc. Rev., 2018, 47, 4198–4232 RSC.
- R. Macovez, Front. Mater., 2018, 4, 46 CrossRef.
- C. C. Wang, Z. X. Guo, S. K. Fu, W. Wu and D. B. Zhu, Prog. Polym. Sci., 2004, 29, 1079–1141 CrossRef CAS.
- S. Collavini and J. L. Delgado, Sustainable Energy Fuels, 2018, 2, 2480–2493 RSC.
- C. J. Brabec, S. Gowrisanker, J. J. M. Halls, D. Laird, S. J. Jia and S. P. Williams, Adv. Mater., 2010, 22, 3839–3856 CrossRef CAS PubMed.
- G. V. Dubacheva, C. K. Liang and D. M. Bassani, Coord. Chem. Rev., 2012, 256, 2628–2639 CrossRef CAS.
- M. A. Faist, S. Shoaee, S. Tuladhar, G. F. A. Dibb, S. Foster, W. Gong, T. Kirchartz, D. D. C. Bradley, J. R. Durrant and J. Nelson, Adv. Energy Mater., 2013, 3, 744–752 CrossRef CAS.
- A. P. Proudian, M. B. Jaskot, C. Lyiza, D. R. Diercks, B. P. Gorman and J. D. Zimmerman, Nano Lett., 2016, 16, 6086–6091 CrossRef CAS PubMed.
- M. Rudolf, S. V. Kirner and D. M. Guldi, Chem. Soc. Rev., 2016, 45, 612–630 RSC.
- I. Rasovic, Mater. Sci. Technol., 2017, 33, 777–794 CrossRef CAS.
- R. Bakry, R. M. Vallant, M. Najam-Ul-Haq, M. Rainer, Z. Szabo, C. W. Huck and G. K. Bonn, Int. J. Nanomed., 2007, 2, 639–649 CAS.
- J. Lee, S. Mahendra and P. J. J. Alvarez, ACS Nano, 2010, 4, 3580–3590 CrossRef CAS PubMed.
- A. M. Lopez, A. Mateo-Alonso and M. Prato, J. Mater. Chem., 2011, 21, 1305–1318 RSC.
- D. Jariwala, V. K. Sangwan, L. J. Lauhon, T. J. Marks and M. C. Hersam, Chem. Soc. Rev., 2013, 42, 2824–2860 RSC.
- L. K. Shrestha, Q. M. Ji, T. Mori, K. Miyazawa, Y. Yamauchi, J. P. Hill and K. Ariga, Chem. – Asian J., 2013, 8, 1662–1679 CrossRef CAS PubMed.
- V. Biju, Chem. Soc. Rev., 2014, 43, 744–764 RSC.
- W. B. Yan, S. M. Seifermann, P. Pierrat and S. Brase, Org. Biomol. Chem., 2015, 13, 25–54 RSC.
- J. Kotteritzsch, R. Geitner, J. Ahner, M. Abend, S. Zechel, J. Vitz, S. Hoeppener, B. Dietzek, M. Schmitt, J. Popp, U. S. Schubert and M. D. Hager, J. Appl. Polym. Sci., 2018, 135, 45916 CrossRef.
- R. Geitner, J. Kotteritzsch, M. Siegmann, R. Fritzsch, T. W. Bocklitz, M. D. Hager, U. S. Schubert, S. Grafe, B. Dietzek, M. Schmitt and J. Popp, Phys. Chem. Chem. Phys., 2016, 18, 17973–17982 RSC.
- A. Hirsch, I. Lamparth and H. R. Karfunkel, Angew. Chem., Int. Ed. Engl., 1994, 33, 437–438 CrossRef.
- F. Djojo, A. Herzog, I. Lamparth, F. Hampel and A. Hirsch, Chem. – Eur. J., 1996, 2, 1537–1547 CrossRef CAS.
- J. F. Nierengarten, V. Gramlich, F. Cardullo and F. Diederich, Angew. Chem., Int. Ed. Engl., 1996, 35, 2101–2103 CrossRef CAS.
- A. Kraszewska, P. Rivera-Fuentes, G. Rapenne, J. Crassous, A. G. Petrovic, J. L. Alonso-Gomez, E. Huerta, F. Diederich and C. Thilgen, Eur. J. Org. Chem., 2010, 4402–4411 CAS.
- W. Y. Qian and Y. Rubin, Angew. Chem., Int. Ed., 1999, 38, 2356–2360 CrossRef CAS PubMed.
- W. Qian and Y. Rubin, J. Am. Chem. Soc., 2000, 122, 9564–9565 CrossRef CAS.
- R. Schwenninger, T. Müller and B. Kräutler, J. Am. Chem. Soc., 1997, 119, 9317–9318 CrossRef CAS.
- I. Lamparth, C. Maichle-Mössmer and A. Hirsch, Angew. Chem., Int. Ed. Engl., 1995, 34, 1607–1609 CrossRef CAS.
- A. Hirsch, I. Lamparth, T. Grösser and H. R. Karfunkel, J. Am. Chem. Soc., 1994, 116, 9385–9386 CrossRef CAS.
- F. Cardullo, L. Isaacs, F. Diederich, J. P. Gisselbrecht, C. Boudon and M. Gross, Chem. Commun., 1996, 797–799 RSC.
- G. Schick, M. Levitus, L. Kvetko, B. A. Johnson, I. Lamparth, R. Lunkwitz, B. Ma, S. I. Khan, M. A. Garcia-Garibay and Y. Rubin, J. Am. Chem. Soc., 1999, 121, 3246–3247 CrossRef.
- B. Kräutler and J. Maynollo, Angew. Chem., Int. Ed. Engl., 1995, 34, 87–88 CrossRef.
- A. Duarte-Ruiz, K. Wurst and B. Kräutler, Helv. Chim. Acta, 2008, 91, 1401–1408 CrossRef CAS.
- F. Cataldo, D. A. Garcia-Hernandez and A. Manchado, Fullerenes, Nanotubes, Carbon Nanostruct., 2014, 22, 565–574 CrossRef CAS.
- B. Kräutler, T. Müller, J. Maynollo, K. Gruber, C. Kratky, P. Ochsenbein, D. Schwarzenbach and H. B. Burgi, Angew. Chem., Int. Ed. Engl., 1996, 35, 1204–1206 CrossRef.
- A. Duarte-Ruiz, K. Wurst and B. Kräutler, Helv. Chim. Acta, 2001, 84, 2167–2177 CrossRef CAS.
- A. Duarte-Ruiz, T. Müller, K. Wurst and B. Kräutler, Tetrahedron, 2001, 57, 3709–3714 CrossRef CAS.
- W. Jia and G. P. Miller, Fullerenes, Nanotubes, Carbon Nanostruct., 2008, 16, 58–65 CrossRef CAS.
- A. Duarte-Ruiz, L. Echegoyen, A. Aya and F. Gomez-Baquero, J. Mex. Chem. Soc., 2009, 53, 169–173 CAS.
- D. S. Sabirov, A. O. Terentyev and F. Cataldo, Comput. Theor. Chem., 2016, 1081, 44–48 CrossRef CAS.
- I. Fleming, in Molecular Orbitals and Organic Chemical Reactions, John Wiley & Sons Chichester, UK, 2010, pp. 253–368, DOI:10.1002/9780470689493.ch6.
- A. H. Streitwieser, C. Heathcock and E. M. Kosower, Introduction to organic chemistry, Macmillan, New York, 1992 Search PubMed.
- T. H. Lowry and K. S. Richardson, Mechanism and Theory in Organic Chemistry, Harper & Row, New York, 1976 Search PubMed.
- R. B. Woodward and R. Hoffmann, Angew. Chem., Int. Ed. Engl., 1969, 8, 781–853 CrossRef CAS.
- J. Sauer and R. Sustmann, Angew. Chem., Int. Ed., 1980, 19, 779–807 CrossRef.
- M. B. Smith and J. March, March's Advanced Organic Chemistry, Wiley-Interscience, Hoboken New Jersey, 6th edn, 2007 Search PubMed.
- K. N. Houk, J. Am. Chem. Soc., 1973, 95, 4092–4094 CrossRef CAS.
- K. N. Houk, Y. Li and J. D. Evanseck, Angew. Chem., Int. Ed. Engl., 1992, 31, 682–708 CrossRef.
- S. Osuna, M. Swart and M. Sola, Phys. Chem. Chem. Phys., 2011, 13, 3585–3603 RSC.
- I. Lamparth, C. Maichlemossmer and A. Hirsch, Angew. Chem., Int. Ed. Engl., 1995, 34, 1607–1609 CrossRef CAS.
- G. W. Wang, M. Saunders and R. J. Cross, J. Am. Chem. Soc., 2001, 123, 256–259 CrossRef CAS PubMed.
- G. W. Wang, Z. X. Chen, Y. Murata and K. Komatsu, Tetrahedron, 2005, 61, 4851–4856 CrossRef CAS.
- M. A. Herranz, N. Martin, J. Ramey and D. M. Guldi, Chem. Commun., 2002, 2968–2969 RSC.
- Y. Takaguchi, T. Tajima, K. Ohta, J. Motoyoshiya, H. Aoyama, T. Wakahara, T. Akasaka, M. Fujitsuka and O. Ito, Angew. Chem., Int. Ed., 2002, 41, 817–819 CrossRef CAS PubMed.
- K. N. Houk, Y. T. Lin and F. K. Brown, J. Am. Chem. Soc., 1986, 108, 554–556 CrossRef CAS PubMed.
- H. J. Jiao and P. V. Schleyer, J. Phys. Org. Chem., 1998, 11, 655–662 CrossRef CAS.
- E. Goldstein, B. Beno and K. N. Houk, J. Am. Chem. Soc., 1996, 118, 6036–6043 CrossRef CAS.
- K. N. Houk, J. Gonzalez and Y. Li, Acc. Chem. Res., 1995, 28, 81–90 CrossRef CAS.
- Y. Li and K. N. Houk, J. Am. Chem. Soc., 1993, 115, 7478–7485 CrossRef CAS.
- K. N. Houk, Acc. Chem. Res., 1975, 8, 361–369 CrossRef CAS.
- R. C. Haddon, J. Am. Chem. Soc., 1997, 119, 1797–1798 CrossRef CAS.
- R. C. Haddon, Science, 1993, 261, 1545–1550 CrossRef CAS PubMed.
- F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070–10086 CrossRef CAS PubMed.
- B. Willocq, V. Lemaur, M. El Garah, A. Ciesielski, P. Samori, J. M. Raquez, P. Dubois and J. Cornil, Chem. Commun., 2016, 52, 7608–7611 RSC.
- S. Osuna, M. Swart and M. Sola, J. Phys. Chem. A, 2011, 115, 3491–3496 CrossRef CAS PubMed.
- F. Diederich and R. Kessinger, Acc. Chem. Res., 1999, 32, 537–545 CrossRef CAS.
- Y. Nakamura, K. O-kawa and J. Nishimura, Bull. Chem. Soc. Jpn., 2003, 76, 865–882 CrossRef CAS.
- L. Chaker, A. B. Yongye, A. Nefzi and K. Martinez-Mayorga, J. Phys. Org. Chem., 2012, 25, 894–901 CrossRef CAS.
- M. Garcia-Borras, S. Osuna, M. Swart, J. M. Luis and M. Sola, Chem. Commun., 2013, 49, 1220–1222 RSC.
- T. K. Roy Dennington and J. Millam, GaussView 4.1.2, Semichem Inc., Shawnee Mission, KS, 2009 Search PubMed.
- TURBOMOLE V7.3 2018, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com.
- J. C. Slater, Phys. Rev., 1951, 81, 385–390 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. C. Eklund, A. M. Rao, Y. Wang, P. Zhou, K. A. Wang, J. M. Holden, M. S. Dresselhaus and G. Dresselhaus, Thin Solid Films, 1995, 257, 211–232 CrossRef CAS.
- A. P. Scott and L. Radom, J. Phys. Chem., 1996, 100, 16502–16513 CrossRef CAS.
- OriginPro, OriginLab Corporation, Version 2018b, 2018.
- J. Contreras-Garcia, E. R. Johnson, S. Keinan, R. Chaudret, J. P. Piquemal, D. N. Beratan and W. T. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef CAS PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. T. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- The PyMOL Molecular Graphics System, Version 1.8, Schrödinger, LLC, 2018 Search PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics Modell., 1996, 14, 33–38 CrossRef CAS.
- L. P. Wolters and F. M. Bickelhaupt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 324–343 CAS.
- D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2007, 129, 10646–10647 CrossRef CAS PubMed.
- S. E. Zhu, F. Li and G. W. Wang, Chem. Soc. Rev., 2013, 42, 7535–7570 RSC.
- V. Neti, M. R. Ceron, A. Duarte-Ruiz, M. M. Olmstead, A. L. Balch and L. Echegoyen, Chem. Commun., 2014, 50, 10584–10587 RSC.
- M. R. Ceron and L. Echegoyen, J. Phys. Org. Chem., 2016, 29, 613–619 CrossRef CAS.
- D. Sepulveda, Y. F. Guan, U. Rangel and S. E. Wheeler, Org. Biomol. Chem., 2017, 15, 6042–6049 RSC.
- M. M. Li, Y. B. Wang, Y. Zhang and W. Wang, J. Phys. Chem. A, 2016, 120, 5766–5772 CrossRef CAS PubMed.
- R. G. Huber, M. A. Margreiter, J. E. Fuchs, S. von Grafenstein, C. S. Tautermann, K. R. Liedl and T. Fox, J. Chem. Inf. Model., 2014, 54, 1371–1379 CrossRef CAS PubMed.
- J. W. Li, Y. Y. Liu, Y. Qian, L. Li, L. H. Xie, J. Z. Shang, T. Yu, M. D. Yi and W. Huang, Phys. Chem. Chem. Phys., 2013, 15, 12694–12701 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed information about bis-adduct structures and energetics, comparison with experimental data, details on the distortion–interaction analyses, detailed energy decomposition analyses, structures of intermediates with smaller acenes, as well as xyz structure coordinates of all investigated species, their total energies and thermodynamic corrections. See DOI: 10.1039/d0ob00520g |
| This journal is © The Royal Society of Chemistry 2020 |