Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Entropic factors and structural motifs of triblock-terpolymer-based patchy nanoparticles†
Nicolas
Moreno‡
 *,
Burhannudin
Sutisna
*,
Burhannudin
Sutisna
 and
Eliot
Fried
and
Eliot
Fried
 *
*
Mathematics, Mechanics, and Materials Unit. Okinawa Institute of Science and Technology Graduate University, 1919-1 Tancha, Onna-son, Kunigami-gun, Okinawa, 904-0495, Japan. E-mail: nicolas.morenoch@gmail.com; eliot.fried@oist.jp
First published on 6th October 2020
Abstract
A prevalent strategy for synthesizing patchy nanoparticles is through the self-assembly of triblock terpolymers in selective solvents. Since the thermodynamic and kinetic factors that govern the morphology of the particles produced in this way are not fully understood, this strategy usually demands trial-and-error methodologies. We investigate the fundamental mechanisms that produce multiple types of patchy nanoparticles and identify the conditions needed to program the shapes of the nanoparticles and predict their assembly. Our findings demonstrate that particle morphology can be described in a generic fashion by accounting for the energetic balance between the conformation of the polymer coils and the formation of interfaces. This allows us to forecast the synthesis of patchy nanoparticles for systems with different triblock terpolymers and solvents. Since the shape, size, and distribution of the patches influence the growth of larger microscale structures, we construct a library of elemental nanoparticles, or building blocks, suitable for the study of hierarchically larger self-assembled aggregates and useful for streamlining the design of functional materials. Our results provide new insights into the intriguing mechanisms that determine the morphology of soft nanoscale objects, whether synthetic or naturally occurring.
Introduction
The hierarchical self-assembly of ABC triblock terpolymers in solution is a successful bottom-up methodology for constructing functional materials with nanoscale resolution, including decorated nanoparticles with precisely tailored structural motifs.1–3 In this methodology, the self-assembly process is mediated by polymer–solvent phase separation, which induces the formation of nanoscopic aggregates such as micelles. Due to the connectivity of the blocks and the presence of the solvent, phase separation takes place within nanoparticles, giving rise to decorating patches. The nanoparticle motifs reported in the literature evidence a ubiquitous range of morphologies independent of the chemistry of the system. This suggests the existence of ground states that determine the morphology of the nanoparticles. An understanding of the critical balance between the thermodynamic and kinetic factors that must be achieved to control the size, shape, and distribution of the particle patches has not yet been achieved. Kinetic control is, in particular, indispensable for reaching metastable ground states.1,4,5The design of patterned nanoparticles currently hinges on iterative processes for identifying the experimental parameters which suffice to produce any desired pattern. Predicting the synthetic pathway sufficient to achieve any particular morphology for different solvents, molecular weights of the constituent polymer blocks, and ambient conditions is problematic. Strategies based on trial and error are cumbersome because of the limited understanding of how the mechanisms underlying patch transitions are influenced by compositional variations.6 A rational correspondence between the shapes and patch distribution of the nanoparticles and their dependence on composition has rarely been tackled in experimental investigations.4,7–9 Free energy considerations and scaling arguments have been used to interpret experimentally observed morphological transitions of nanoparticles for different proportions of the polymer blocks.4,8,9
We find that the balance between the coil conformations and interface formation dictates the morphology of the nanoparticles. This balance provides a basis for classifying the variety of nanoparticle motifs that are attainable for various systems independent of their detailed chemistry. These conclusions are based on systematic numerical studies of patchy nanoparticle formation and validated through experimental synthesis of nanoparticles using different triblock terpolymers. We also construct and make freely available a computational library of the stable nanoparticles, that are characterized in terms of their conformational and interfacial features. Elements of this library can be used to further investigate kinetic mechanisms of patchy nanoparticles aggregation, on the upstream stages of the hierarchical aggregation of patchy nanoparticles into supracolloidal structures for nanoparticles with given fixed morphologies and numbers of patches.10,11 Furthermore, we demonstrate that elements of our library can be mapped to experimental counterparts and directly associated with actual physical systems.
Self-assembly of triblock terpolymers in solution
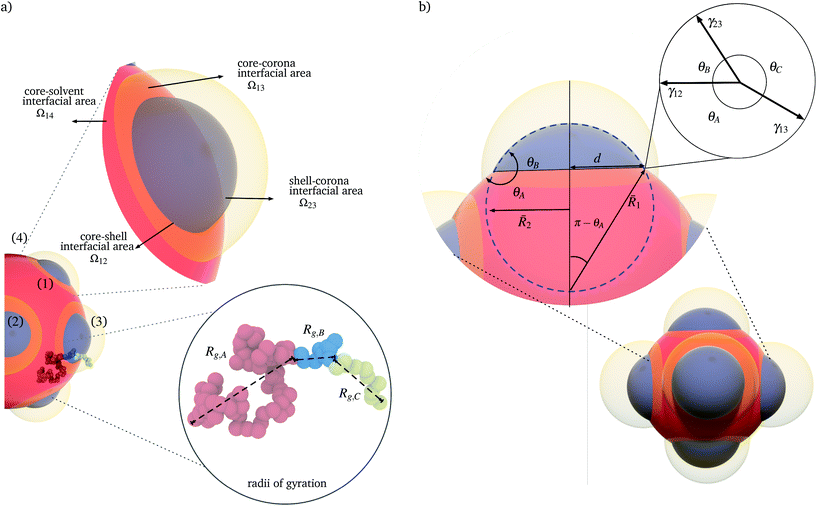
We consider a polymeric solution of volume V, containing z polymer chains of an ABC triblock terpolymer, in a solvent, S. We represent the triblock terpolymer chains as a set of N = NA + NB + NC segments of volume vseg. When appearing as subscripts, A, B, and C designate quantities associated with the individual block and S designates quantities associated with the solvent. The volume vseg of the segment is a characteristic reference measure and can be chosen for convenience in various ways without loss of generality; for example, vseg can be associated with the statistical segment size of one of the species, or the solvent. The solvent concentration is given by ϕS = 1 − zNvseg/V.We consider nanoparticles comprised by core, shell, and corona regions, as depicted in Fig. 1. For simplicity we use the subscripts 1, 2, 3 and 4, to indicate the core, shell, corona, and surrounding solvent, respectively. In a triblock terpolymer, the balance of the polymer–polymer and polymer–solvent interactions determine any tendency of the blocks to phase separate. Multiple interaction strengths for which the phases segregate to minimize the energy of the patchy nanoparticles can be identified. Decorated nanoparticles typically assemble if one of the blocks is soluble, there is a tendency for the remaining blocks to phase separate, and the polymer concentrations are dilute.4,8,9,12 We therefore consider polymer–solvent interactions consistent with these conditions and estipulate that the polymer concentration is dilute in the sense that (zNvseg)/V ≪ 1.
An equilibrium configuration of a nanoparticle must correspond to a local minimum of its total free-energy 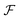 . It is convenient to decompose
. It is convenient to decompose 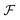 into a sum consisting of a mixing term of Flory–Huggins type, a term which penalizes the formation of interfaces between the constituent blocks, and a term which penalizes changes in the conformation of the polymer coils.13 We thus take
into a sum consisting of a mixing term of Flory–Huggins type, a term which penalizes the formation of interfaces between the constituent blocks, and a term which penalizes changes in the conformation of the polymer coils.13 We thus take 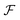 to be of the form
to be of the form 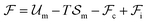 , where
, where 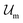 and
and 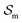 are the enthalpic and entropic contributions to the mixing energy, T is the absolute temperature, and
are the enthalpic and entropic contributions to the mixing energy, T is the absolute temperature, and 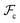 and
and 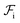 are the free energies associated with conformational changes and interface formation, respectively. Due to the competition between these contributions, the energy landscape associated with the formation of nanoparticles may be complex, corresponding to various kinetically-controlled metastable morphologies.
are the free energies associated with conformational changes and interface formation, respectively. Due to the competition between these contributions, the energy landscape associated with the formation of nanoparticles may be complex, corresponding to various kinetically-controlled metastable morphologies.
Mixing free energy
Introducing Flory–Huggins pair interaction parameters χAB, χBC, χAC, χAS, χBS, and χCS between blocks and the solvent, we assume that the enthalpic contribution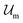 to the free-energy of a nanoparticle consisting of z polymer chains is given by
to the free-energy of a nanoparticle consisting of z polymer chains is given by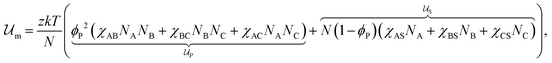 | (1) |
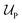 corresponds to the enthalpic interactions between the polymer blocks,
corresponds to the enthalpic interactions between the polymer blocks, 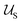 account for polymer–solvent interactions. The entropy of mixing can be expressed as
account for polymer–solvent interactions. The entropy of mixing can be expressed as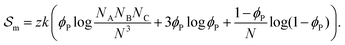 | (2) |
Conformational free energy
Considering a nanoparticle formed by z polymer coils of blocks A, B, and C with corresponding ensemble-averaged radii of gyration 〈Rg,A〉, 〈Rg,B〉, and 〈Rg,C〉, we take the conformational free energy to be of the form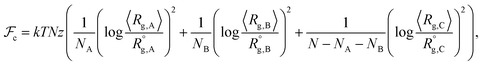 | (3) |
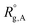 ,
, 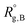 , and
, and 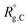 are the unperturbed (or theta) radii. The free energy
are the unperturbed (or theta) radii. The free energy 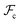 is essentially entropic, and penalizes the stretching of the polymer coil away from its unperturbed condition.
is essentially entropic, and penalizes the stretching of the polymer coil away from its unperturbed condition.
Interfacial free energy
We take the contribution to the free energy associated with the formation of interfaces to be of the form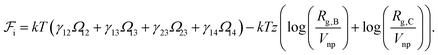 | (4) |
Although 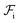 can be considered as entropic, it originates from both enthalpic and entropic components. The first term of (4) is largely connected to the enthalpic interactions between the blocks and the solvent. Therein, γ12, γ13, γ14, and γ23 are the dimensionless energy of formation for core–shell, core–corona, core–solvent, and shell–corona interfaces, respectively. Additionally, Ω12, Ω13, Ω14, and Ω23 denote the total area fractions of the corresponding interfaces. The second term of (4) is purely entropic and can be thought as the constrained localization of the joints linking blocks A with B, and B with C in the interfacial regions. This entropic loss can be expressed in terms of their configurational volume, defined as the ratio between the volume available to the joints in the core–shell (and shell–corona) interfaces and the total volume of the nanoparticle Vnp.
can be considered as entropic, it originates from both enthalpic and entropic components. The first term of (4) is largely connected to the enthalpic interactions between the blocks and the solvent. Therein, γ12, γ13, γ14, and γ23 are the dimensionless energy of formation for core–shell, core–corona, core–solvent, and shell–corona interfaces, respectively. Additionally, Ω12, Ω13, Ω14, and Ω23 denote the total area fractions of the corresponding interfaces. The second term of (4) is purely entropic and can be thought as the constrained localization of the joints linking blocks A with B, and B with C in the interfacial regions. This entropic loss can be expressed in terms of their configurational volume, defined as the ratio between the volume available to the joints in the core–shell (and shell–corona) interfaces and the total volume of the nanoparticle Vnp.
Multistage solubilization
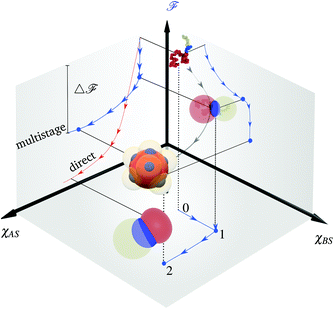
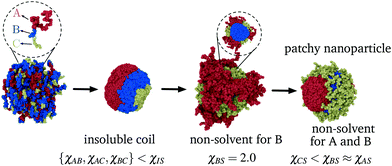
Typically the formation of the patchy nanoparticles involves a multistage solubilization approach, where the selectivity of the solvent is changed to guide the system towards local energy minima.4 In Fig. 2, we present a schematic of two-stage solubilization, where the solubility of block B is decreased in the first stage, followed by a decrease in the solubility of block A in the second stage. Without loss of generality, we choose the final stage blocks A and B to be insoluble and block C to be soluble. With these choices, blocks A and B form the core and shell of a nanoparticle while the swollen block C and surrounding solvent molecules form the corona. We assume that the shell region consists of locally phase-separated patches of block B and we use p to denote the total number of such patches. Considering that during the solubilization stages the composition of the blocks and the solvent are given and that T is fixed, changes in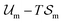 should occur only due to enthalpic interactions
should occur only due to enthalpic interactions 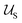 between the polymer blocks and the solvent at each stage. The equilibrium configurations we obtain therefore reflect a competition between
between the polymer blocks and the solvent at each stage. The equilibrium configurations we obtain therefore reflect a competition between 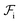 and
and 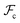 and is accomplished by minimizing the free energy
and is accomplished by minimizing the free energy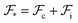 | (5) |
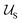 .
.
Since the blocks A and B form the majority of the core and shell regions and since the corona is constituted by block C and interstitial solvent (see Fig. 1), the free energy of interface formation can be expressed as
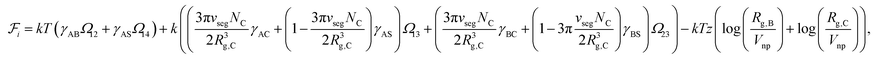 | (6) |
Whereas the conformational free energy 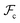 defined in (3) depends explicitly on the radius of gyration of each block, the interfacial free energy
defined in (3) depends explicitly on the radius of gyration of each block, the interfacial free energy 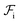 defined in (6) varies with the interfacial area fractions and the local compositions between the different regions. To estimate how the total free energy
defined in (6) varies with the interfacial area fractions and the local compositions between the different regions. To estimate how the total free energy 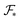 varies with composition, it is therefore necessary to understand how the radii of gyration and the interfacial areas vary with composition. Since there is no general expression that accounts explicitly for such dependencies, we approximate the variations of the radii of gyration and interfacial areas numerically while accounting for the balance between conformational and interfacial effects.
varies with composition, it is therefore necessary to understand how the radii of gyration and the interfacial areas vary with composition. Since there is no general expression that accounts explicitly for such dependencies, we approximate the variations of the radii of gyration and interfacial areas numerically while accounting for the balance between conformational and interfacial effects.
Approach
To capture length and time scales associated with the motion and assembly of the polymer coils while incorporating, to reasonable approximation, effects associated with the chemical affinities, we model nanoparticle formation at the mesoscale. Since our primary interest is in the different structural motifs that arise during the phase separation, we consider a system involving a single isolated nanoparticle constituted by triblock terpolymer chains and solvent molecules. Thus, we model aggregation in solution and then identify the morphology of the nanoparticles. We use dissipative particle dynamics (DPD) to simulate nanoparticle formation, as described in the methods section and the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15–17 In addition to our numerical investigation, we adopt a methodology due to Löbling et al.9 to synthesize nanoparticles for various molecular weights, solubilities, and affinities of the blocks out of the range explored computationally.
15–17 In addition to our numerical investigation, we adopt a methodology due to Löbling et al.9 to synthesize nanoparticles for various molecular weights, solubilities, and affinities of the blocks out of the range explored computationally.
To examine the influence of composition on the conformational and interfacial free energy of the assembled nanoparticles, it is necessary to determine the radii of gyration and the end-to-end distances of the different blocks in the polymer coil and the interfacial areas between the core, shell, corona, and surrounding solvent. This involves varying N, the block terpolymer compositions NA/N and NB/N, and the number z of polymer chains or, equivalently, the polymer concentration zNvseg/V, as described in the ESI.† In our synthesis efforts, we work with three different triblock terpolymers, poly(styrene-b-butadiene-b-methyl methacrylate) (SBM), poly(styrene-b-isoprene-b-methyl methacrylate) (SIM), and poly(styrene-b-isoprene-b-2-vinyl pyridine) (SIV). To characterize the nanoparticles morphologies and number of patches we use transmission electron microscopy (TEM). We use Dynamic light scattering (DLS) to estimate the hydrodynamic radii and morphologies of the nanoparticles. A description of the experimental conditions is included in the ESI,† and the characteristics of the polymers are provided in Tables 1 and 2.† The range of parameters we consider significantly exceeds the corresponding range of experimental and computational conditions reported to date (see ESI Fig. 1†).4,9
Methods
Poly(styrene-b-butadiene(1,2)-b-methyl methacrylate) (PS-b-PBd-b-PMMA), poly(styrene-b-isoprene(1,4)-b-methyl methacrylate) (PS-b-PIP-b-PMMA), and poly(styrene-b-isoprene(1,4)-b-2-vinyl pyridine) (PS-b-PIP-b-P2VP) triblock terpolymers were purchased from Polymer Source Inc., Canada. Dimethylacetamide (DMAc) (SAJ special grade), osmium tetroxide (OsO4, 4 wt% in H2O), isopropanol (JIS special grade, ≥99.5%), and acetone (JIS special grade, ≥99.5%) were purchased from Sigma-Aldrich and used as received.Preparation of patchy nanoparticles
Patchy nanoparticles were fabricated using a previously reported stepwise procedure.4 The terpolymer was first dissolved in DMAc at a concentration of 1 g l−1. The solution was stirred overnight at 70 °C before dialysis. Regenerated cellulose (Spectrum Laboratories, Inc., Spectra/Por) with a molecular weight cut-off of 12–14 kDa was used as the dialysis membrane. The membrane was first immersed in water for ≈10 min, and was then washed with DMAc. Around 4–5 ml of the terpolymer solution in DMAc was dialyzed against 500 ml acetone/isopropanol mixture for 30 h. The dialysate (acetone/isopropanol mixture) was changed with a fresh mixture twice: ≈5 h after starting the experiment, and ≈5 h before completion. To characterize the nanoparticles, we used transmission electron microscopy (TEM) and dynamic light scattering (DLS). See the ESI† for further details.Nanoparticle self-assembly
To construct the library, we conducted simulations for different interaction parameters and block compositions NI/N for I = A,B, and C, with N between 25 to 100 beads per chain. We checked the nanoparticle morphology at different polymer compositions by changing the total number of chains in the computational box leading to aggregation numbers z ranging from 100 to 500 chains. We carried out each simulation in three stages (see Fig. 3) to obtain equilibrated patchy nanoparticles. Although the patchy nanoparticle morphologies obtained at each stage correspond to equilibrated structures, the kinetics of nanoparticle fabrication are incorporated by following this stepwise approach. The morphologies at each stage account for memory effects at the previous stage and are consistent with metastable structures, that cannot be obtained from direct solubilization of the triblock copolymer, as we show in Fig. 7 of the ESI.†Numerical method and setup
To model the assembly of triblock terpolymer nanoparticles, we used the dissipative particle dynamics (DPD),15,18 a particle-based mesoscale method that has been widely used to study self-assembly in diverse polymer systems. In the framework of DPD, we considered dimensionless quantities for the length r* = r/r0, mass m* = m/m0 and energy ε* = ε/ε0, and the time t* = (m*r*2/ε*)1/2, where r0 = vref1/3 is the characteristic segment size, m0 is the mass of the segment, and ε0 = kT. All simulations were conducted using LAMMPS19 with r* = 1, m* = 1, and ε* = 1. The particle density used the simulation was ρ = 3 particles per r*3. To keep temperature fluctuations below 2%, we used a time step of Δt* = 0.03. Each simulation was run for three million dimensionless time steps. The cutoff radius rc for the interaction force between particles was taken to be rc = 1r* and the equilibrium distance between connected particles was taken to be rspring = 0.80r*. Simulations were conducted in a cubic box with edge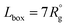 , where
, where 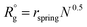 , and the prefactor indicates the size of the patchy nanoparticles that commensurate with the simulation box while avoiding spurious size effects due to periodicity. To characterize the simulated nanoparticles we measure the radius of gyrations of the polymer chains, the number of patches, and the interfacial areas as described in ESI.† We use the clustering and surface reconstruction algorithms of the software OVITO20 to compute the interfacial area, number of patches, and to perform nanoparticle visualization.
, and the prefactor indicates the size of the patchy nanoparticles that commensurate with the simulation box while avoiding spurious size effects due to periodicity. To characterize the simulated nanoparticles we measure the radius of gyrations of the polymer chains, the number of patches, and the interfacial areas as described in ESI.† We use the clustering and surface reconstruction algorithms of the software OVITO20 to compute the interfacial area, number of patches, and to perform nanoparticle visualization.
To construct the library, we conducted simulations for ABC chains with N between 25 to 100 beads and with aggregation numbers z ranging from 100 to 500. The solvent was modeled as particles which fill the computational box. The DPD interaction parameters aIJ (with I = A,B,C, and S) and the number of beads per block were varied depending on the phase space evaluated for each system. To map the reduced Flory–Huggins parameters to DPD, we used effective interaction parameters 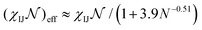 , where
, where 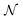 corresponds to the number of monomers per block of the actual polymer, where N denotes the number of particles we used to construct the polymer chain. The details of parameters calculation is included in the ESI.† Because the solvent is modeled a single bead, localization effects that may be present in solvent mixtures are not captured by our current approach. Specifically, we model the solvent mixture implicitly as a single effective solvent with molecular weight dependent properties. Further improvement of this approach using more than one type of particle is feasible but will necessarily entail additional computational challenges.
corresponds to the number of monomers per block of the actual polymer, where N denotes the number of particles we used to construct the polymer chain. The details of parameters calculation is included in the ESI.† Because the solvent is modeled a single bead, localization effects that may be present in solvent mixtures are not captured by our current approach. Specifically, we model the solvent mixture implicitly as a single effective solvent with molecular weight dependent properties. Further improvement of this approach using more than one type of particle is feasible but will necessarily entail additional computational challenges.
Results and discussion
Structural motifs
Granted that the volumes of the core, shell, and corona regions are proportional to the radii of gyration of their constituent blocks, those volumes should correlate with the corresponding coil conformations. The ratio between the volume of the core and the volume of the corona has been used to characterize the morphology of micellar systems such as surfactants,21 diblock copolymers,22 and triblock terpolymers.9 Here, we characterize the sizes of the core, shell, and corona regions by computing the radii of gyration of the blocks and account for the difference in conformation through the ratios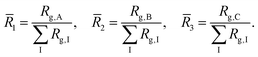 | (7) |
The previous scalings stem from mean-field approximations to the radii of gyration of the blocks, an approximation that holds adequately under the range of surface tensions explored for the different combinations of blocks. The radius of gyration of a polymer block with NI segments, I = A,B,C, can be expressed as 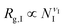 , where the exponent νI depends on the strength of the bonding interactions within the block and the interactions with the surrounding molecules.23 Typically for homopolymer segments the magnitude of νI is determined by its affinity with the solvent.23 For example, for poor solvents νI = 1/3, whereas for good solvents νI = 3/5. Here, due to the connectivity between the blocks and the interfacial tensions, the coils are forced to pack within the nanoparticle and therefore typically exhibit conformational frustration. This conformational penalty is reflected in the contribution (3) to the free energy. Consistent with this approximation data fits yield:
, where the exponent νI depends on the strength of the bonding interactions within the block and the interactions with the surrounding molecules.23 Typically for homopolymer segments the magnitude of νI is determined by its affinity with the solvent.23 For example, for poor solvents νI = 1/3, whereas for good solvents νI = 3/5. Here, due to the connectivity between the blocks and the interfacial tensions, the coils are forced to pack within the nanoparticle and therefore typically exhibit conformational frustration. This conformational penalty is reflected in the contribution (3) to the free energy. Consistent with this approximation data fits yield:
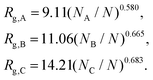 | (8) |
A phase diagram for nanoparticle assembly provided in Fig. 4 depicts a diverse spectrum of morphologies obtained in terms of the size ratios ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 1,
1, ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2, and
2, and ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 3 of the core, shell, and corona. This diagram was constructed by varying the compositions NA/N, NB/N, and NC/N, the ratios γAB/γAC and γBC/γAC, and the polymer concentration zNvseg/V. A database with the different morphologies obtained and is available on https://bitbucket.org/nmorenoc/patchy-nanoparticles/src/master/ as LAMMPS data files. During nanoparticle formation, we computed the ensemble average of (7) in terms of the number z of polymer chains.
3 of the core, shell, and corona. This diagram was constructed by varying the compositions NA/N, NB/N, and NC/N, the ratios γAB/γAC and γBC/γAC, and the polymer concentration zNvseg/V. A database with the different morphologies obtained and is available on https://bitbucket.org/nmorenoc/patchy-nanoparticles/src/master/ as LAMMPS data files. During nanoparticle formation, we computed the ensemble average of (7) in terms of the number z of polymer chains.
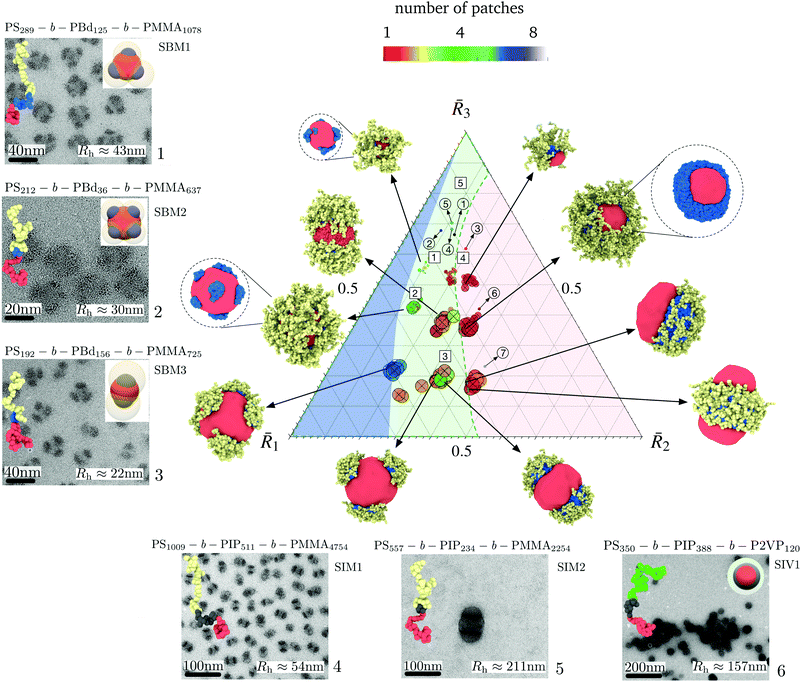 | ||
| Fig. 4 Phase diagram of patchy nanoparticle formation. The morphologies correspond to NC/N = 0.1, NC/N = 0.3, and NC/N = 0.5, with the ratio NB/(NA + NB) of the insoluble blocks equal to 0.1, 0.3, and 0.5. Also, γAB/γAC and γBC/γAC ranges from 0.5 to 1.5 and two polymer compositions, 0.05 and 0.1, are considered. The effective block size ratio determines the size of a nanoparticle and its number of patches. Polymer–solvent interactions strongly influence transitions in patch shape and arrangement. The three regions indicate the degree of patchiness or number p of B domains. Blue: highly patchy nanoparticles (p > 4), Green: medium patchy nanoparticles (p > 1), and Red: Janus-like nanoparticles. We locate in the predicted diagram the patchy nanoparticles obtained experimentally for different SBM, SIM, and SIV samples. Whereas circular markers correspond to the ratios computed from (8), square markers are derived from TEM and DLS results. The sample number 7 corresponds to conditions under which self-assembled larger bicontinuous aggregates emerge and is included in ESI Fig. 2† along with an equivalent simulation aggregate in the same regime. The name of the triblock and the number of effective repetitive units appear at the top of each figure. | ||
From Fig. 4, we identify three dominant degrees of patchiness (or the number p of patches) for the nanoparticles: (i) Janus-like nanoparticles with p = 1; (ii) intermediate patchy nanoparticles with 1 < p ≤ 4; and (iii) highly patchy nanoparticles with p > 4. As noted previously, the conformational energy imposes geometrical constraints and strongly determines the size and the number of patches of each particular aggregate. Nevertheless, the interfacial energy allows for the coexistence of patches with different topologies and shapes in each region of the phase diagram. Consistent with intuitive expectations, we see from Fig. 4 that a larger number of patches can be allocated on the surface of the core for smaller sizes ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2 of the shell region and, thus, smaller patch sizes. Consequently, as
2 of the shell region and, thus, smaller patch sizes. Consequently, as ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2 increases, merging of the patches occurs and Janus-like nanoparticles become more stable.
2 increases, merging of the patches occurs and Janus-like nanoparticles become more stable.
Experimentally, the effects of ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2 were also identified. In Fig. 4 we locate in the predicted diagram the patchy nanoparticles obtained experimentally for different samples of triblock terpolymers SBM, SIM, and SIV. Additionally, we include the TEM images and hydrodynamic radius of the nanoparticles. From the variation in the number p of patches for samples 1, 2, and 3, it is evident that sample 2 exhibits the larger number of patches with p > 5 due to its overall smaller value of
2 were also identified. In Fig. 4 we locate in the predicted diagram the patchy nanoparticles obtained experimentally for different samples of triblock terpolymers SBM, SIM, and SIV. Additionally, we include the TEM images and hydrodynamic radius of the nanoparticles. From the variation in the number p of patches for samples 1, 2, and 3, it is evident that sample 2 exhibits the larger number of patches with p > 5 due to its overall smaller value of ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2. Samples 6 and 7, with a larger
2. Samples 6 and 7, with a larger ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2 lie on the extreme of the diagram favoring the formation of a fully fused shell with p = 1, corresponding to self-assembled larger bicontinuous aggregates. In Fig. 4, we also locate in the phase diagram samples 1 to 5 for
2 lie on the extreme of the diagram favoring the formation of a fully fused shell with p = 1, corresponding to self-assembled larger bicontinuous aggregates. In Fig. 4, we also locate in the phase diagram samples 1 to 5 for ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 1 and
1 and ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 3, as derived from TEM and DLS results. TEM is used to deduce the apparent size of the core and patches and the hydrodynamic radii obtained by DLS (see ESI Table 4†). Compared to the values given by (8), the location for samples 1, 2, and 3 shift to lower values of
3, as derived from TEM and DLS results. TEM is used to deduce the apparent size of the core and patches and the hydrodynamic radii obtained by DLS (see ESI Table 4†). Compared to the values given by (8), the location for samples 1, 2, and 3 shift to lower values of ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 3 in the diagram. However, our prediction in the number of patches remains valid.
3 in the diagram. However, our prediction in the number of patches remains valid.
The variety of possible nanoparticle morphologies is also consistent with previously reported experimental results and theoretical explanations.4,8,12 However, we identify a richer spectrum of conditions for which a given morphology can be produced depending on the balance between the conformational and interfacial energy. In the following sections, we elucidate the existence of the various patch density regimes as the energetic balance varies.
Patch distribution
The patch distribution should satisfy geometrical restrictions that reflect the balance between the conformational and interfacial entropies. For instance, the number of patches a nanoparticle can accommodate is limited by its radius. We show in the ESI† that the number p of spherical caps of radius![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2 on a spherical core of radius
2 on a spherical core of radius ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 1 is given by
1 is given by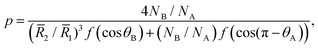 | (9) |
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2/
2/![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 1 and NB/NA but also depends implicitly on γAB/γAC. Motivated by this finding, we explore the extent to which
1 and NB/NA but also depends implicitly on γAB/γAC. Motivated by this finding, we explore the extent to which ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2/
2/![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 1, NB/NA, and γAB/γAC can be used to describe the variety of nanoparticles for the patch and core shapes determined numerically. The ratio
1, NB/NA, and γAB/γAC can be used to describe the variety of nanoparticles for the patch and core shapes determined numerically. The ratio ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2/
2/![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 1 account conformational entropy effects on the distribution of patches, whereas γAB/γAC account for the interfacial contributions.
1 account conformational entropy effects on the distribution of patches, whereas γAB/γAC account for the interfacial contributions.
From data fits, we find that
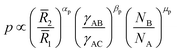 | (10) |
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2/
2/![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 1 decreases because a larger number of phase separated B patches can be accommodated by a larger A core. However the scaling for this case is smaller than the idealization (9), where αp = 3, because the patches may arrange in other morphologies such as cylinders or dense films of lower dimensionality. Although the number of patches may vary with the size of block C and the interaction of the patches with the corona γBC/γAC, these effects do not exhibit a clear trend for the proposed fitting. In Fig. 5a we use the color of the markers to indicate
1 decreases because a larger number of phase separated B patches can be accommodated by a larger A core. However the scaling for this case is smaller than the idealization (9), where αp = 3, because the patches may arrange in other morphologies such as cylinders or dense films of lower dimensionality. Although the number of patches may vary with the size of block C and the interaction of the patches with the corona γBC/γAC, these effects do not exhibit a clear trend for the proposed fitting. In Fig. 5a we use the color of the markers to indicate ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 3, and the size of the markers correspond to the ratio γBC/γAC. This evidences that the number of patches can be predicted up to a good approximation using only terms of (10). This fitting concisely reproduces the variation in the number of patches for a large range of experimental and numerical evidence, while incorporating the effects of both conformational change and interface formation. In Fig. 5b, we present the predicted variation of the patches with
3, and the size of the markers correspond to the ratio γBC/γAC. This evidences that the number of patches can be predicted up to a good approximation using only terms of (10). This fitting concisely reproduces the variation in the number of patches for a large range of experimental and numerical evidence, while incorporating the effects of both conformational change and interface formation. In Fig. 5b, we present the predicted variation of the patches with ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2/
2/![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 1 and γAB/γAC for three different choices of NB/NA.
1 and γAB/γAC for three different choices of NB/NA.
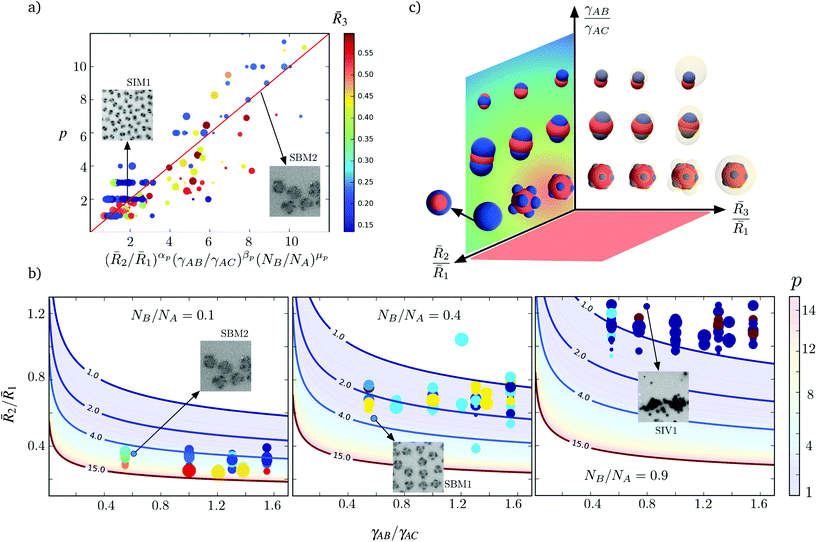 | ||
Fig. 5 (a) Predicted scaling of the number p of patches with ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2/ 2/![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 1, γAB/γAC, and NB/NA. The solid line correspond to the fit (10), with αp = −2.36, βp = −0.56, and μp = 0.44, with a coefficient of correlation R = 0.9. TEM images for two different triblock terpolymers are included. While the size of the markers reflects the magnitude of the ratio γBC/γAC, their color is determined by 1, γAB/γAC, and NB/NA. The solid line correspond to the fit (10), with αp = −2.36, βp = −0.56, and μp = 0.44, with a coefficient of correlation R = 0.9. TEM images for two different triblock terpolymers are included. While the size of the markers reflects the magnitude of the ratio γBC/γAC, their color is determined by ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 3. The proposed fitting is therefore independent of those parameters. (b) Comparison between the number p of patches measured with respect to the predicted by (10) for different choices of NB/NA. The measured values of p from different simulations are included with the circular markers. The colors indicate the number of patches and the patch size derives from 3. The proposed fitting is therefore independent of those parameters. (b) Comparison between the number p of patches measured with respect to the predicted by (10) for different choices of NB/NA. The measured values of p from different simulations are included with the circular markers. The colors indicate the number of patches and the patch size derives from ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 3. TEM images for three different samples are included. (c) Schematic representation of the various patchy nanoparticles obtained for different conditions. 3. TEM images for three different samples are included. (c) Schematic representation of the various patchy nanoparticles obtained for different conditions. | ||
In Table 1, we compare (10) with the number of patches of the nanoparticles that we synthesize and previously reported evidence,4 leading to the conclusion that (10) provides a good approximation for the variation in p in actual systems. For the nanoparticles that we synthesize the approximation (10) tend to overestimate the number of patches for the nanoparticles with p > 6. This occurs due to the combined effect of smaller ratios ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2/
2/![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 1 and larger
1 and larger ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 3, where the force balance and minimum interfacial area at the patch-core contact line are largely affected by the covalent bonding between blocks A and B. Thus, (10) forecasts patches with smaller areas that those imposed by the connectivity of the blocks. In the ESI,† we determine the parameters used in (10) for the polymers and solvents considered.
3, where the force balance and minimum interfacial area at the patch-core contact line are largely affected by the covalent bonding between blocks A and B. Thus, (10) forecasts patches with smaller areas that those imposed by the connectivity of the blocks. In the ESI,† we determine the parameters used in (10) for the polymers and solvents considered.
| Sample name | Observed | Predicted |
|---|---|---|
| SBM1 | 3 | 3 |
| SBM2 | >5 | 9 |
| SBM3 | 3 | 2 |
| SIM1 | 2 | 2 |
| SIM2 | 1 | 2 |
| SIV1 | (Contiguous shell) 1 | 1 |
| SIV2 | (Contiguous shell) 1 | 1 |
| SBM1* | >8 | 9 |
| SBM2* | >6 | 7 |
| SBM3* | 3 | 3 |
| SBM4* | 4 | 3 |
| SBM5* | >6 | 3 |
| SBM6* | 2 | 3 |
| SBM7* | 4 | 2 |
| SBM9* | 2 | 2 |
Patch morphology
The morphologies of the shell and decorating patches differ significantly depending upon whether conformational or interfacial effects dominate. Consistent with the reported experimental evidence,4,8,9,12,24–28 we observe sphere-to-rod morphological transitions of the B patches. Conformationally-driven transitions from spheres to rod occur as the ratio![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2/
2/![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 1 increases. However, we also identify the conditions where interfacial interactions induce such transitions even if
1 increases. However, we also identify the conditions where interfacial interactions induce such transitions even if ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2/
2/![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 1 is fixed. In Fig. 6, we present TEM images of the patchy nanoparticles obtained for poly(styrene-b-butadiene-b-methyl methacrylate) with fixed molecular weights (sample SIM1, see ESI Table 1†) in solvent mixtures of acetone–isopropanol in three different ratios. In these images, the shape of the patches changes from spherical for solvent mixtures acetone/isopropanol 60/40 to wormlike for 40/60 mixtures. The larger amount of isopropanol makes the solvent less favorable for block A and, thereby, increases γAS. The merging of the patches therefore reduces the interfacial area Ω14 between the core and solvent. Similar interfacial effects are responsible for other morphological helix-to-film transitions of the shell,9 where the formation of a homogeneous B shell around the A core requires an exchange between A–B, B–S, and A–S interactions.
1 is fixed. In Fig. 6, we present TEM images of the patchy nanoparticles obtained for poly(styrene-b-butadiene-b-methyl methacrylate) with fixed molecular weights (sample SIM1, see ESI Table 1†) in solvent mixtures of acetone–isopropanol in three different ratios. In these images, the shape of the patches changes from spherical for solvent mixtures acetone/isopropanol 60/40 to wormlike for 40/60 mixtures. The larger amount of isopropanol makes the solvent less favorable for block A and, thereby, increases γAS. The merging of the patches therefore reduces the interfacial area Ω14 between the core and solvent. Similar interfacial effects are responsible for other morphological helix-to-film transitions of the shell,9 where the formation of a homogeneous B shell around the A core requires an exchange between A–B, B–S, and A–S interactions.
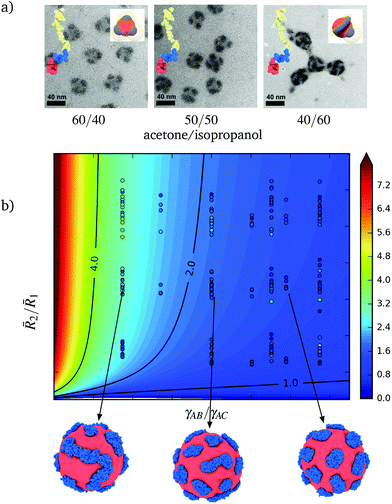 | ||
Fig. 6 (a) TEM images of poly(styrene-b-butadiene-b-methyl methacrylate) in different acetone/isopropanol mixtures. A transitions from spheres to rod-like patches is induced due to changes in the interfacial interactions between the core and corona. (b) Influence of ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2/ 2/![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 1 and γAB/γAC on the interfacial area ratio Ω12/pΩ0, signaling the morphological transition from spherical to elongates patches. The circular markers indicate the measured ratios and points evaluated in our simulations. The contours correspond to the fit (11). Three different simulated nanoparticle are obtained by varying γAB/γAC. Block C is omitted from the images for clarity. 1 and γAB/γAC on the interfacial area ratio Ω12/pΩ0, signaling the morphological transition from spherical to elongates patches. The circular markers indicate the measured ratios and points evaluated in our simulations. The contours correspond to the fit (11). Three different simulated nanoparticle are obtained by varying γAB/γAC. Block C is omitted from the images for clarity. | ||
To explain these morphological transitions of the patches in terms of the conformational and interfacial contributions to the free energy, we consider the ratio Ω12/pΩ0, where Ω0 = 2πRg,B2 corresponds to the interfacial area of one spherical patch of size Rg,B. Whereas ratios close to unity correspond to the existence of patches shaped like spherical caps, larger values indicate cylindrical patches or that the shell is contiguous. In Fig. 6, we present the values Ω12/pΩ0 measured for different choices of ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2/
2/![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 1 and γAB/γAC. We find that the variation of Ω12/pΩ0 in terms of the conformational and interfacial contributions is well approximated by
1 and γAB/γAC. We find that the variation of Ω12/pΩ0 in terms of the conformational and interfacial contributions is well approximated by
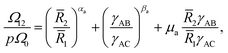 | (11) |
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2 of the patches is preserved. However,
2 of the patches is preserved. However, ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2 increases during conformationally driven transitions. The first term on the right-hand side of (11) accounts for the change in only one dimension of the characteristic patch size. The second term on the right-hand side of (11) accounts the stronger effect of the interfacial contributions and, thus, is associated with changes in the net area of the patches. The third term on the right-hand side of (11) incorporates coupling between conformational and interfacial effects.
2 increases during conformationally driven transitions. The first term on the right-hand side of (11) accounts for the change in only one dimension of the characteristic patch size. The second term on the right-hand side of (11) accounts the stronger effect of the interfacial contributions and, thus, is associated with changes in the net area of the patches. The third term on the right-hand side of (11) incorporates coupling between conformational and interfacial effects.
Influence of corona size
The stabilization of patches in our nanoparticles is greatly favored by the presence of block C. We find that the size![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 3 of the corona controls the growth of the nanoparticles and the distribution of the decorating domains via steric hindrance. Steric effects differ substantially depending on whether
3 of the corona controls the growth of the nanoparticles and the distribution of the decorating domains via steric hindrance. Steric effects differ substantially depending on whether ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 1 +
1 + ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2 <
2 < ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 3 or
3 or ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 1 +
1 + ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2 >
2 > ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 3.
3.
If ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 1 +
1 + ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2 <
2 < ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 3, then the number of polymer chains per aggregate reduces, leading to smaller nanoparticles. For the idealized case of spherical caps on a sphere, we know from (9) that smaller nanoparticles decreases have fewer patches. More generally, as we see from Fig. 4, as
3, then the number of polymer chains per aggregate reduces, leading to smaller nanoparticles. For the idealized case of spherical caps on a sphere, we know from (9) that smaller nanoparticles decreases have fewer patches. More generally, as we see from Fig. 4, as ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 3 increases the occurrence of nanoparticles with large number of patches decreases, as does the nanoparticle size. For
3 increases the occurrence of nanoparticles with large number of patches decreases, as does the nanoparticle size. For ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 1 +
1 + ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2 <
2 < ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 3, the phase separation of the short nonsoluble A and B blocks and the large swollen C block is conformationally costly, with the consequence nanoparticles with smaller aggregation number z are favored. This steric effect of the corona was identified in the samples 4 and 5, which have larger corona-forming blocks. If we compare the size of the core and shell for samples 1 and 4 (see ESI Table 4† and Fig. 4), we find they nearly the same, despite of the fewer repetitive units of sample 1, NA + NB = 412, compared to sample 4, NA + NB = 1520. The similarity on the size of the patchy nanoparticles arises from a disparity in the aggregation number z. In sample 4, the longer C block constrains the aggregation of the polymer leading to fewer chains, that are closely packed.
3, the phase separation of the short nonsoluble A and B blocks and the large swollen C block is conformationally costly, with the consequence nanoparticles with smaller aggregation number z are favored. This steric effect of the corona was identified in the samples 4 and 5, which have larger corona-forming blocks. If we compare the size of the core and shell for samples 1 and 4 (see ESI Table 4† and Fig. 4), we find they nearly the same, despite of the fewer repetitive units of sample 1, NA + NB = 412, compared to sample 4, NA + NB = 1520. The similarity on the size of the patchy nanoparticles arises from a disparity in the aggregation number z. In sample 4, the longer C block constrains the aggregation of the polymer leading to fewer chains, that are closely packed.
If ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 1 +
1 + ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2 >
2 > ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 3, then the C blocks of neighboring patches overlap. Due to the swelling of the corona, the C blocks tend to repel one another and to favor interaction with the solvent. Thus, the C blocks screen the patches prevent the merging of the patches on the core surface. This condition can be identified for samples 1 and 3 (see ESI Table 4† and Fig. 4) where the reduction in the corona-block facilitate the merging of the patches leading to nanoparticles with lower p. This effect has also been experimentally reported for PS-PB-PT triblock terpolymers,9 which form spherical nanoparticles when the soluble blocks of PT are sufficiently large but undergo a transition to larger nanoparticles with cylindrical and lamellar shapes if the PT blocks are sufficiently short.
3, then the C blocks of neighboring patches overlap. Due to the swelling of the corona, the C blocks tend to repel one another and to favor interaction with the solvent. Thus, the C blocks screen the patches prevent the merging of the patches on the core surface. This condition can be identified for samples 1 and 3 (see ESI Table 4† and Fig. 4) where the reduction in the corona-block facilitate the merging of the patches leading to nanoparticles with lower p. This effect has also been experimentally reported for PS-PB-PT triblock terpolymers,9 which form spherical nanoparticles when the soluble blocks of PT are sufficiently large but undergo a transition to larger nanoparticles with cylindrical and lamellar shapes if the PT blocks are sufficiently short.
In addition to the steric effects of the corona at the nanoparticle level, we also observe experimentally, that steric interactions play a relevant role on the hierarchical aggregation of the nanoparticles at larger scales. Patchy nanoparticles with larger coronas showed to be monodisperse in size, and more stable against the formation of larger lumps; see ESI Fig. 7.† This is important in the fabrication of homogeneously dispersed nanoparticles.
Conclusions
We have constructed a generalized library of self-assembled patchy triblock terpolymer nanoparticles, including some newly discovered morphologies. Our results shed light on the set of conditions required to produce nanoparticles with prescribed patch densities. We found that similar morphologies and patch distributions can be produced under disparate conditions. The database of the different stabilized morphologies is available on https://bitbucket.org/nmorenoc/patchy-nanoparticles/src/master/ in LAMMPS data file format.We showed that the changes in core–shell interfacial area and patch density of the nanoparticles can be expressed in terms of their scaling with the dimensionless parameters ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2/
2/![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 1, γAB/γAC, and NB/NA. For the idealized case of a sphere decorated by spherical caps, these parameters emerge as natural geometrical descriptors. Whereas conformational entropic effects are encompassed by the ratio between the respective sizes
1, γAB/γAC, and NB/NA. For the idealized case of a sphere decorated by spherical caps, these parameters emerge as natural geometrical descriptors. Whereas conformational entropic effects are encompassed by the ratio between the respective sizes ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 1 and
1 and ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2 of the core and shell, interfacial effects enter through the relative affinities between the core-forming block A with the shell-forming block B and the corona-forming mixture C and solvent. The interfacial term associated with γAB/γAC dominates the morphology of the decorating patches and mediates the merging of the patches. In contrast, the conformational contribution is largely responsible for the number of patches. The most important impact of the size
2 of the core and shell, interfacial effects enter through the relative affinities between the core-forming block A with the shell-forming block B and the corona-forming mixture C and solvent. The interfacial term associated with γAB/γAC dominates the morphology of the decorating patches and mediates the merging of the patches. In contrast, the conformational contribution is largely responsible for the number of patches. The most important impact of the size ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 3 of the corona is through steric interactions that control the aggregation number of the nanoparticles and determine their number p of patches. For smaller corona sizes, larger nanoparticles which can accommodate more patches are favored. Additionally, those patches must be more closely packed for smaller coronas. We showed that the morphological transition from spherical patches to rod-like patches has a distinct physical foundation arising from geometrical constraints and that the underlying mechanism can be traced variations in the interfacial area. Apart from the identification of the dominant contributions that control the distribution and shape of the patches, we provided expressions that allow us predict the emergence of different structural motifs. The predictions agree both with previous experimental observations and with our experimental results.
3 of the corona is through steric interactions that control the aggregation number of the nanoparticles and determine their number p of patches. For smaller corona sizes, larger nanoparticles which can accommodate more patches are favored. Additionally, those patches must be more closely packed for smaller coronas. We showed that the morphological transition from spherical patches to rod-like patches has a distinct physical foundation arising from geometrical constraints and that the underlying mechanism can be traced variations in the interfacial area. Apart from the identification of the dominant contributions that control the distribution and shape of the patches, we provided expressions that allow us predict the emergence of different structural motifs. The predictions agree both with previous experimental observations and with our experimental results.
Since the characteristic shapes, sizes, and distributions of the decorating patches are crucial to gaining control over the growth of microscale superstructures, the identification and classification of nanoparticles that we present in our library provide a platform for studying the hierarchical assembly of mesostructures in terms of the nanoparticle morphology rather than the pair interactions and compositions of the individual blocks. The set of LAMMPS data files we provide can be used to streamline studies of aggregation of soft patchy colloids at larger scales. This opens new avenues for investigating the kinetic mechanisms of soft patchy nanoparticle aggregation.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Okinawa Institute of Science and Technology Graduate University with subsidy funding from the Cabinet Office, Government of Japan. The authors thank Dr Atsushi Matsumoto for initial assistance on the dialysis experiment and dynamic light scattering and Dr Toshio Sasaki for support on the TEM measurements.References
- H. Cui, Z. Chen, S. Zhong, K. L. Wooley and D. J. Pochan, Block copolymer assembly via kinetic control, Science, 2007, 317(5838), 647–650 CrossRef CAS.
- S. Kubowicz, J.-F. Baussard, J.-F. Lutz, A. F. Thünemann, H. von Berlepsch and A. Laschewsky, Multicompartment micelles formed by self-assembly of linear ABC triblock copolymers in aqueous medium, Angew. Chem., Int. Ed., 2005, 44(33), 5262–5265 CrossRef CAS.
- D. J. Lunn, J. R. Finnegan and I. Manners, Self-assembly of “patchy” nanoparticles: A versatile approach to functional hierarchical materials, Chem. Sci., 2015, 6(7), 3663–3673 RSC.
- A. H. Gröschel, F. H. Schacher, H. Schmalz, O. V. Borisov, E. B. Zhulina, A. Walther and A. H. E. Müller, Precise hierarchical self-assembly of multicompartment micelles, Nat. Commun., 2012, 3(1), 710 CrossRef.
- A. H. Gröschel and A. H. Müller, Self-assembly concepts for multicompartment nanostructures, Nanoscale, 2015, 7(28), 11841–11876 RSC.
- A. Walther and A. H. E. Müller, Janus particles: Synthesis, self-Assembly, physical properties, and applications, Chem. Rev., 2013, 113(7), 5194–5261 CrossRef CAS.
- L. Zhang and A. Eisenberg, Multiple morphologies and characteristics of “crew-cut” mcelle-like aggregates of polystyrene-b-poly(acrylic acid) diblock copolymers in aqueous solutions, J. Am. Chem. Soc., 1996, 118(13), 3168–3181 CrossRef CAS.
- A. H. Gröschel, A. Walther, T. I. Löbling, F. H. Schacher, H. Schmalz and A. H. E. Müller, Guided hierarchical co-assembly of soft patchy nanoparticles, Nature, 2013, 503(7475), 247–251 CrossRef.
- T. I. Löbling, O. Borisov, J. S. Haataja, O. Ikkala, A. H. Gröschel and A. H. E. Müller, Rational design of ABC triblock terpolymer solution nanostructures with controlled patch morphology, Nat. Commun., 2016, 7(1), 12097 CrossRef.
- X. Ma, Y. Zhou, L. Zhang, J. Lin and X. Tian, Polymerization-like kinetics of the self-assembly of colloidal nanoparticles into supracolloidal polymers, Nanoscale, 2018, 10(35), 16873–16880 RSC.
- X. Ma, M. Gu, L. Zhang, J. Lin and X. Tian, Sequence-regulated supracolloidal copolymers via copolymerization-like coassembly of binary mixtures of patchy nanoparticles, ACS Nano, 2019, 13(2), 1968–1976 CAS.
- A. H. Gröschel, A. Walther, T. I. Löbling, J. Schmelz, A. Hanisch, H. Schmalz and A. H. E. Müller, Facile, Solution-based synthesis of soft, nanoscale Janus particles with tunable Janus balance, J. Am. Chem. Soc., 2012, 134(33), 13850–13860 CrossRef.
- L. Leibler, H. Orland and J. C. Wheeler, Theory of critical micelle concentration for solutions of block copolymers, J. Chem. Phys., 1983, 79(7), 3550–3557 CrossRef CAS.
- R. Nagarajan, “Non-equilibrium” block copolymer micelles with glassy cores: A predictive approach based on theory of equilibrium micelles, J. Colloid Interface Sci., 2014, 449, 416–427 CrossRef.
- P. J. Hoogerbrugge and J. M. V. A. Koelman, Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics, Europhys. Lett., 1992, 19(3), 155–160 CrossRef.
- P. Español and P. B. Warren, Statistical mechanics of dissipative particle dynamics, Europhys. Lett., 1995, 30(4), 191–196 CrossRef.
- R. D. Groot and P. B. Warren, Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation, J. Chem. Phys., 1997, 107(11), 4423–4435 CrossRef CAS.
- P. Español, Hydrodynamics from dissipative particle dynamics, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1995, 52(2), 1734–1742 CrossRef.
- S. Plimpton, Fast parallel algorithms for short-Range molecular dynamics, J. Comput. Phys., 1995, 117(1), 1–19 CrossRef CAS.
- A. Stukowski, Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool, Modell. Simul. Mater. Sci. Eng., 2010, 18(1), 015012 CrossRef.
- J. N. Israelachvili, D. J. Mitchell and B. W. Ninham, Theory of self-assembly of lipid bilayers and vesicles, Biochim. Biophys. Acta, Biomembr., 1977, 470(2), 185–201 CrossRef CAS.
- E. B. Zhulina, M. Adam, I. LaRue, S. S. Sheiko and M. Rubinstein, Diblock Copolymer Micelles in a Dilute Solution, Macromolecules, 2005, 38(12), 5330–5351 CrossRef CAS.
- P. G. de Gennes, Molecular individualism, Science, 1997, 276(5321), 1999–2000 CrossRef CAS.
- T. I. Löbling, O. Ikkala, A. H. Gröschel and A. H. E. Müller, Controlling multicompartment morphologies using solvent conditions and chemical modification, ACS Macro Lett., 2016, 5(9), 1044–1048 CrossRef.
- C. H. Evers, J. A. Luiken, P. G. Bolhuis and W. K. Kegel, Self-Assembly of microcapsules via colloidal bond hybridization and anisotropy, Nature, 2016, 534(7607), 364–368 CrossRef.
- T.-L. Nghiem, T. Löbling and A. H. Gröschel, Supracolloidal Chains of Patchy Micelles in Water, Polym. Chem., 2017, 9(13), 1583–1592 RSC.
- A. Walther, C. Barner-Kowollik and A. H. E. Müller, Mixed, multicompartment, or Janus micelles? A systematic study of thermoresponsive bis-hydrophilic block terpolymers, Langmuir, 2010, 26(14), 12237–12246 CrossRef CAS.
- B. Fang, A. Walther, A. Wolf, Y. Xu, J. Yuan and A. Müller, Undulated multicompartment cylinders by the controlled and directed stacking of polymer micelles with a compartmentalized corona, Angew. Chem., Int. Ed., 2009, 48(6), 2877–2880 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/D0NR06192A |
| ‡ Present address: Basque Center for Applied Mathematics, Bilbao, Spain. |
| This journal is © The Royal Society of Chemistry 2020 |