Open Access Article
Open Access ArticleTuning exciton diffusion, mobility and emission line width in CdSe nanoplatelets via lateral size†
Alexander W.
Achtstein‡
 *a,
Sabrine
Ayari‡
*b,
Sophia
Helmrich
a,
Michael T.
Quick
a,
Nina
Owschimikow
a,
Sihem
Jaziri
bc and
Ulrike
Woggon
a
*a,
Sabrine
Ayari‡
*b,
Sophia
Helmrich
a,
Michael T.
Quick
a,
Nina
Owschimikow
a,
Sihem
Jaziri
bc and
Ulrike
Woggon
a
aInstitute of Optics and Atomic Physics, Technische Universität Berlin, Strasse des 17. Juni 135, 10623 Berlin, Germany. E-mail: achtstein@tu-berlin.de
bLaboratoire de Physique des Materiaux, Faculte des Sciences de Bizerte, Universite de Carthage, Jarzouna 7021, Tunisia
cLaboratoire de Physique de la Matiere Condensee, Departement de Physique, Faculte des Sciences de Tunis, Campus Universitaire, 1060 Tunis, Tunisia
First published on 2nd November 2020
Abstract
We investigate the lateral size tunability of the exciton diffusion coefficient and mobility in colloidal quantum wells by means of line width analysis and theoretical modeling. We show that the exciton diffusion coefficient and mobility in laterally finite 2D systems like CdSe nanoplatelets can be tuned via the lateral size and aspect ratio. The coupling to acoustic and optical phonons can be altered via the lateral size and aspect ratio of the platelets. Subsequently the exciton diffusion and mobility become tunable since these phonon scattering processes determine and limit the mobility. At 4 K the exciton mobility increases from ∼ 4 × 103 cm2 V−1 s−1 to more than 1.4 × 104 cm2 V−1 s−1 for large platelets, while there are weaker changes with size and the mobility is around 8 × 101 cm2 V−1 s−1 for large platelets at room temperature. In turn at 4 K the exciton diffusion coefficient increases with the lateral size from ∼ 1.3 cm2 s−1 to ∼ 5 cm2 s−1, while it is around half the value for large platelets at room temperature. Our experimental results are in good agreement with theoretical modeling, showing a lateral size and aspect ratio dependence. The findings open up the possibility for materials with tunable exciton mobility, diffusion or emission line width, but quasi constant transition energy. High exciton mobility is desirable e.g. for solar cells and allows efficient excitation harvesting and extraction.
1. Introduction
CdSe nanoplatelets1,2 (NPLs) are colloidal analogues to both conventional 2D quantum wells, produced via molecular beam epitaxy (MBE), and monolayers of van der Waals semiconductors like transition metal dichalcogenides (TMDCs). While graphene exhibits high (carrier) mobilities3,4 and diffusion coefficients, it is a gap less material, which makes its application in optoelectronics more complicated. Novel ultrathin 2D semiconductor materials combine high mobility, strong light matter interaction and short radiative lifetimes resulting in high quantum efficiencies.2,5–11 CdSe NPLs are set apart from laterally infinite quantum wells as they exhibit a finite lateral size and weak lateral confinement12,13 resulting in size tunable exciton-phonon interaction12 or giant two photon absorption.7,14–17 Furthermore, their directed emission18 and emission polarization19 as well as their high, well-width dependent dark-bright splitting20,21 of 3–6 meV are of great interest. Robust excitons even at room temperature with high exciton binding energies (of ∼200 meV) have been found.2,22–24 The low temperature double peak emission of CdSe NPLs has been attributed to exciton and additional trion states,21,25,26 where the latter exhibit a fine structure due to shakeup lines27 that originate from the quantized nature of electron states in the laterally weakly confined system.Inspired by a phenomenological correlation between the exciton mobility and emission line width in ref. 28, we investigate in this paper the exciton (quasiparticle) diffusion constant, exciton mobility and scattering rate using temperature dependent photoluminescence (PL) spectroscopy and theoretical modeling for CdSe nanoplatelets, a model system for 2D semiconductors of finite lateral size. Unlike charge carrier mobility determination by classical transport measurements with contact or contact-less THz and microwave conductivity measurements,29,30 we determine the diffusion coefficient and mobility of neutral excitons by connecting the temperature dependent emission line width of the considered colloidal CdSe quantum wells to the microscopic scattering rates and subsequently to the (exciton) diffusivity. We demonstrate that our method shows good agreement with theoretical modeling and other methods, e.g. with dephasing data. The exciton diffusion and emission line width are linked, as scattering events (with e.g. phonons) do not only result in diffusion, but also randomize the PL emitter phase of the excitons, causing dephasing and line width broadening. We show in the following that the acoustic and optical phonon limited scattering rates, exciton mobility and diffusion in CdSe nanoplatelets can be tuned by their lateral size and aspect ratio.
2. Results and discussion
4.5 monolayer (ML) zinc blende (ZB) CdSe nanoplatelets with different lateral sizes of 17 × 6 nm2 to 41 × 13 nm2 (17 × 6 nm2, 19 × 7 nm2, 17 × 11 nm2, 29 × 8 nm2, 30 × 15 nm2, 41 × 13 nm2) and corresponding platelet areas (rounded) of 102, 134, 187, 232, 450 and 533 nm2 were synthesized according to ref.1 and 31, analyzed by transmission electron microscopy (TEM) and embedded into a polymer layer (see the Methods section). Fig. 1 shows temperature dependent PL emission spectra of exemplary sizes at 4 and 200 K under off-resonant 2.95 eV (420 nm) excitation. Clearly a double emission is observed, which has been attributed to trion (lower energy emission T−) and exciton (upper energy emission X)21,25–27 PL. We remark that due to the low coupling to LO-phonons in the CdSe platelets, e.g. confirmed by Raman32,33 or pump–probe spectroscopy,34 no relevant LO-phonon replicas of the exciton emission are present in the PL spectra.35The lateral size tunable trion binding energy and oscillator strength in CdSe nanoplatelets have been studied systematically in ref. 26. We focus in this paper on the exciton emission line and exciton–phonon coupling. Therefore we fit the double emission by two Voigt functions accounting for the homogeneous (Lorentzian) and inhomogeneous (Gaussian) contributions to each emission peak (see also the Methods section). They are related to the natural line width (the former) and lateral size dispersion altering the weak lateral confinement12 of the nanoplatelets (the latter). The inhomogeneous contribution is temperature independent, and hence kept as a constant parameter for each platelet size for all temperatures in the fit, see also the Methods section for a discussion. In line with ref. 12 we obtain the temperature dependent homogeneous line width, which can be fitted according to:
 | (1) |
Δ
0 is the zero temperature homogeneous line width, while  and
and  describe the line width broadening due to scattering with acoustic phonons or optical-phonons of energy ELO. We use ELO = 25.6 meV from Raman results in ref. 32. Exemplary fits to this equation are shown in Fig. 1(c) for our nanoplatelets of different sizes, resulting in the coupling coefficients displayed in Fig. 2 (orange points).
describe the line width broadening due to scattering with acoustic phonons or optical-phonons of energy ELO. We use ELO = 25.6 meV from Raman results in ref. 32. Exemplary fits to this equation are shown in Fig. 1(c) for our nanoplatelets of different sizes, resulting in the coupling coefficients displayed in Fig. 2 (orange points).
In Fig. 2(a) we observe a decrease of the coupling to acoustic modes with increasing platelet size,12 while by trend the coupling strength of excitons to optical-phonons in (b) increases. Since both  and
and  can be tuned by the size of the platelets, the exciton–phonon interaction becomes size dependent, so that also the associated microscopic scattering rates ΓAC,Opt become tunable. The larger data scatter for the optical-phonons among the samples may be related to the fact that optical-phonon scattering is more susceptible to alterations by (charged) defects as well as strain fields in the NPLs, which can be a result of NPL quality distribution.
can be tuned by the size of the platelets, the exciton–phonon interaction becomes size dependent, so that also the associated microscopic scattering rates ΓAC,Opt become tunable. The larger data scatter for the optical-phonons among the samples may be related to the fact that optical-phonon scattering is more susceptible to alterations by (charged) defects as well as strain fields in the NPLs, which can be a result of NPL quality distribution.
To analyze the underlying trends in detail, Fig. 2 contains the results of theoretical modeling of the exciton–phonon interaction in these 2D quantum wells, which depends on the NPL area and lateral aspect ratio. The lateral aspect ratio R = Lx/Ly, defined as the ratio of the platelet extent in the long and short in-plane directions, is varied from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 4
1 to 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. In our theoretical calculation, we take into account all relevant couplings to acoustic (AC) and optical (Opt) phonons in CdSe nanoplatelets. This includes (i) scattering by acoustic phonons (AC) via deformation potential (DA) and piezoelectric interaction (PA) and (ii) scattering by optical phonons (Opt) via the Fröhlich interaction (LO, Fr) and nonpolar (optical) deformation-potential (NP, Def). For the acoustic phonon, while the deformation potential primarily yields interactions with longitudinal acoustics phonons, the piezoelectric scattering couples the electronic system to both longitudinal LA and transversal TA acoustics phonons36,37 (for more details, see the Methods section). To build up our theory, we at first relate the microscopic scattering rates with phonons (Γλ=AC,Opt) to the coupling parameters
1. In our theoretical calculation, we take into account all relevant couplings to acoustic (AC) and optical (Opt) phonons in CdSe nanoplatelets. This includes (i) scattering by acoustic phonons (AC) via deformation potential (DA) and piezoelectric interaction (PA) and (ii) scattering by optical phonons (Opt) via the Fröhlich interaction (LO, Fr) and nonpolar (optical) deformation-potential (NP, Def). For the acoustic phonon, while the deformation potential primarily yields interactions with longitudinal acoustics phonons, the piezoelectric scattering couples the electronic system to both longitudinal LA and transversal TA acoustics phonons36,37 (for more details, see the Methods section). To build up our theory, we at first relate the microscopic scattering rates with phonons (Γλ=AC,Opt) to the coupling parameters  in Fig. 2. Acoustic phonon scattering results in an emission linewidth contribution of38,39
in Fig. 2. Acoustic phonon scattering results in an emission linewidth contribution of38,39
 | (2) |
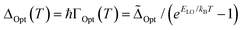 | (3) |
 | (4) |
 is given by a Bose distribution. The sum in eqn (4) extends over all possible phonon wave vectors q and final exciton states f. The matrix element of the exciton–phonon interaction involved in the transition is given by
is given by a Bose distribution. The sum in eqn (4) extends over all possible phonon wave vectors q and final exciton states f. The matrix element of the exciton–phonon interaction involved in the transition is given by![[Doublestruck G]](https://www.rsc.org/images/entities/char_e16a.gif) λ,f(q) = 〈ΨfX| λ,f(q) = 〈ΨfX|![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) λX–ph|ΨiX〉 λX–ph|ΨiX〉 | (5) |
![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) X–ph = (Veλ(q)e−iq·re − Vhλ(q)e−iq·rh) + c.c is the exciton–phonon interaction Hamiltonian, with re(ρe,ze) and rh(ρh,zh) the electron and hole spatial coordinates. c.c. stands for the complex conjugate. Vλe(h)(q) is the electron (hole) coupling element. (See also the Methods section with a detailed description of the theory and a list of all used material constants.) The modeling results for the acoustic and the optical coupling are depicted in Fig. 2 for varying lateral aspect ratios as well as for the exact sizes and lateral aspect ratios of the platelets (see the Methods section) used in experiments. In the ESI† the contributions of different coupling mechanisms (via DA, PA, LO-Fr and NP-Def couplings) to optical and acoustic phonon scattering are shown. Overall, we find that the acoustic deformation potential interaction and the Fröhlich interaction dominate the coupling to acoustic and optical phonon, respectively. The piezoelectric interaction and the nonpolar (optical) deformation-potential coupling are weak and their role is negligible in the coupling to acoustic and optical phonons; however it is taken into account in our calculations.
X–ph = (Veλ(q)e−iq·re − Vhλ(q)e−iq·rh) + c.c is the exciton–phonon interaction Hamiltonian, with re(ρe,ze) and rh(ρh,zh) the electron and hole spatial coordinates. c.c. stands for the complex conjugate. Vλe(h)(q) is the electron (hole) coupling element. (See also the Methods section with a detailed description of the theory and a list of all used material constants.) The modeling results for the acoustic and the optical coupling are depicted in Fig. 2 for varying lateral aspect ratios as well as for the exact sizes and lateral aspect ratios of the platelets (see the Methods section) used in experiments. In the ESI† the contributions of different coupling mechanisms (via DA, PA, LO-Fr and NP-Def couplings) to optical and acoustic phonon scattering are shown. Overall, we find that the acoustic deformation potential interaction and the Fröhlich interaction dominate the coupling to acoustic and optical phonon, respectively. The piezoelectric interaction and the nonpolar (optical) deformation-potential coupling are weak and their role is negligible in the coupling to acoustic and optical phonons; however it is taken into account in our calculations.
Our theory in Fig. 2 shows – in line with the experimental results – that the coupling to acoustic phonons decreases with the platelet area and lateral aspect ratio, while the coupling to optical-phonons increases with the platelet area and decreasing aspect ratio. The demonstrated area and lateral aspect ratio dependence of the acoustic and optical phonon scattering rates and subsequently the coupling constants (Fig. 2) arises from the effects of lateral confinement on the exciton–phonon wave function overlap as well as from the q dependence of the coupling matrix elements. Inserting the expression for the optical and acoustic matrix element in exciton basis, converting the sum over q into an integral and evaluating the δ-function, leads to the following dependency: for the acoustic scattering rate we obtain the scaling  , while for optical phonon scattering ΓOpt ≃ CLO,Fr2
, while for optical phonon scattering ΓOpt ≃ CLO,Fr2![[Doublestruck F]](https://www.rsc.org/images/entities/char_e169.gif) LO,Fr(qx,qy,qz)A (see the ESI† and Methods section). This explains the observed trend of a decrease of acoustic and an increase of the optical phonon coupling with the lateral platelet area. Here, CLO,Fr and CDA are material constants and A the platelet area. The matrix element
LO,Fr(qx,qy,qz)A (see the ESI† and Methods section). This explains the observed trend of a decrease of acoustic and an increase of the optical phonon coupling with the lateral platelet area. Here, CLO,Fr and CDA are material constants and A the platelet area. The matrix element ![[Doublestruck F]](https://www.rsc.org/images/entities/char_e169.gif) λ(qx,qy,qz) imposes an additional alteration, depending on lateral size Lx and Ly. Therefore the coupling constants (Fig. 2(a) and (b)) are a function of the lateral aspect ratio
λ(qx,qy,qz) imposes an additional alteration, depending on lateral size Lx and Ly. Therefore the coupling constants (Fig. 2(a) and (b)) are a function of the lateral aspect ratio  for fixed area A. Hence the phonon coupling in CdSe NPLs can be tuned by the platelet area and lateral aspect ratio. This directly impacts the emitter line width, as reflected in eqn (1)–(3), so that it becomes tunable too.
for fixed area A. Hence the phonon coupling in CdSe NPLs can be tuned by the platelet area and lateral aspect ratio. This directly impacts the emitter line width, as reflected in eqn (1)–(3), so that it becomes tunable too.
We compare the results for optical phonon coupling with published Raman data yielding a Huang–Rhys factor of S = 0.08 for 156 nm2 NPLs with a lateral aspect ratio of 4.3.33 Using S = (ΔOpt/ELO)2/2 (ref. 41) we calculate a 10 meV coupling strength. This is in agreement with the trend of the R = 4 theory line in Fig. 2(b) and the general trend of a reduction of the coupling strength with reduced size. Comparing the acoustic coupling in Fig. 2(a) with the literature is less straight forward. Dong et al.34 reported dimensionless displacements 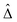 for in-plane and out-of-plane direction for acoustic phonons in CdSe NPLs by pump–probe spectroscopy. They relate via
for in-plane and out-of-plane direction for acoustic phonons in CdSe NPLs by pump–probe spectroscopy. They relate via to the Huang–Rhys factor S. It is related to the exciton–phonon coupling strength aACvia S = (1/2)(aAC/EAC)2, with EAC the acoustic phonon energy. The acoustic line width contribution in eqn (1) relates to the coupling strength via ΔACT = kBaAC/EAC, so that
to the Huang–Rhys factor S. It is related to the exciton–phonon coupling strength aACvia S = (1/2)(aAC/EAC)2, with EAC the acoustic phonon energy. The acoustic line width contribution in eqn (1) relates to the coupling strength via ΔACT = kBaAC/EAC, so that  . Summing this over the in- and out of plane results of ref. 34 results in 4.2 × 10–5 eV K−1. The platelet area used here is 203 nm2 and the lateral aspect ratio R = 4.1. The obtained value is in good agreement with the R = 4 line of our simulations in Fig. 2(a), substantiating our results.
. Summing this over the in- and out of plane results of ref. 34 results in 4.2 × 10–5 eV K−1. The platelet area used here is 203 nm2 and the lateral aspect ratio R = 4.1. The obtained value is in good agreement with the R = 4 line of our simulations in Fig. 2(a), substantiating our results.
An increasing deviation of our experimental results from the theory for the polar LO–phonon coupling is observed in Fig. 2(b) for the smallest considered platelet (17 × 6 nm2), which is already in an intermediate to strong (lateral) confinement, as the short direction approaches the bulk exciton Bohr radius of CdSe. We therefore indicate in the figure also the strong confinement theory limit of the phonon coupling, which agrees well with the experimental result. In general, a continuous theory ranging from strong to weak lateral confinement regimes is very difficult, as the confinement in the unequal lateral x and y dimensions can be in different regimes for (lateral) aspect ratios R bigger than one. Nevertheless we can conclude that our theory reproduces the observed trends in the phonon couplings well.
The mentioned scattering events with phonons (eqn (1)–(3)) do not only result in line broadening, but also impact the exciton mobility and diffusion constant. According to the relaxation time approximation the scattering time τ = 1/Γ, with Γ, the scattering rate, is related to the diffusion coefficient D via42,43
 | (6) |
| D = μkBT | (7) |
 | (8) |
 | (9) |
 | ||
| Fig. 3 Temperature dependent (scaled) CdSe platelet exciton mobility (μqe) (a) and diffusion coefficient (b) as well as scattering rate and line width (c), as obtained from the experimental results in Fig. 2, for two exemplary platelet sizes.(two darker lines) Corresponding theory results for weak lateral confinement (pale lines) for the same sizes. Additional reference data points from the literature (including methods) of Tomar et al. (ref. 29, area = 326 nm2 CdSe NPLs, THz time-domain spectroscopy), Li et al. (ref. 45, CdS NPLs, pump–probe spectroscopy (PP)), Wu et al. (ref. 46, CdS rods, PP), Erland et al. (ref. 43, wurtzite CdSe in c-direction, four wave mixing (FWM)). CdSe NPLs: Cassette et al. (ref. 47, 380 nm2 NPLs, FWM), Tessier et al. (ref. 35, 280 nm2 NPLs, single particle PL), and Naeem et al. (ref. 8, range of values for NPLs of different sizes, from 100 to 350 nm2, FWM). | ||
As a general trend, Fig. 3 shows that larger platelets have lower coupling to acoustic phonons, so that the 533 nm2 platelets exhibit higher mobilities (diffusion coefficients), especially at low temperatures, as compared to the smaller samples. This also results in a lower emission line width (Fig. 3(c)). At low temperature, the exciton mobility in CdSe nanoplatelets can reach more than 104 cm2 V−1 s−1, a considerably high value. At room temperature, the (experimental) mobilities are with 36 cm2 V−1 s−1 and 82 cm2 V−1 s−1 lower due to the increasing contribution of optical phonon scattering. Fig. 3 also shows reference values from other methods, namely THz pump–probe spectroscopy, four wave mixing dephasing and line-width measurements, which nicely agree with our results, as reflected in the shown values for the mobility, diffusion constant and scattering rate. Our measured exciton mobilities are also comparable in order of magnitude with electron mobilities for TMDC materials like MoS2, which has 400 cm2 V−1 s−1 at 300 K and ∼ 104 cm2 V−1 s−1 at low temperature.48,49 The abovementioned exciton mobility values for CdSe nanoplatelets translate viaeqn (7) into exciton diffusion constants of 1.3 cm2 s−1 (134 nm2) and 4.9 cm2 s−1 (533 nm2) at 4 K, as well as 1.0 cm2 s−1 and 2.1 cm2 s−1 at 300 K (see also later Fig. 4). These values are comparable to measured exciton diffusion constants of 2.2 cm2 s−1 in CdS platelets45 or 2.3 cm2 s−1 in CdS rods.46 Further reference values are indicated in Fig. 3(b) for comparison and show good agreement with our results. The mentioned diffusion constant values, shown in (b), are slightly lower than typical values for bulk wurtzite CdSe in ref. 43, reflecting the known decrease in phonon coupling strength with a reduced quantum well width.38,39
 | ||
Fig. 4 Dots: Experimental, lateral size (area) dependent exciton diffusion constant D and mobility μ·qe at 4 K (green) and 300 K (blue) for the six considered platelet sizes obtained from Fig. 2 using eqn. (8) and (9). Continuous lines result from our weak lateral confinement theory for different lateral aspect ratios from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 4 1 to 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Two axes are drawn for D on the right side due to the temperature dependent scaling factor kBT between μ and D in eqn (7). 1. Two axes are drawn for D on the right side due to the temperature dependent scaling factor kBT between μ and D in eqn (7). | ||
A comparison of subfigure (a) and (b) together with eqn (7) shows that the main part of the temperature dependence of the exciton mobility is related to the 1/kBT prefactor of the mobility in μ = D/kBT, while the direct temperature dependence of D is smaller. Furthermore, we can state from the data in Fig. 3(c) that exciton diffusion is the dominant transport mechanism in 2D nanoplatelets, so that the exciton movement is not radiatively (or lifetime) limited by population decay or trapping. This can be seen from the fact that the scattering rates in Fig. 3(c) exceed the radiative rates (inverse lifetimes) in CdSe nanoplatelets well. The latter are of the order of ∼1 − 5 × 1010 s−1 at 4 K (ref. 6 and 50) and even lower at elevated temperatures, due to the increase of exciton lifetime with temperature caused by the giant oscillator strength effect51,52 in 2D. A further important feature is that the exciton mobility and exciton–phonon scattering rate in CdSe NPLs can be tuned by the lateral size at low temperatures, as seen in Fig. 3(a) and (c).
Fig. 4 shows the nanoplatelet lateral size (area) dependence of the exciton diffusion constant and mobility at 4 K and 300 K, as obtained from the experiment and theory displayed in Fig. 2 and using eqn (7)–(9). Again, both quantities are higher at low temperature, with a larger variation at low temperature (see double ordinate) and an overall increase with the lateral size and aspect ratio. The first perception is due to the temperature dependence of the scattering rates, while the latter two are related to the size-dependent coupling coefficients (Fig. 2). For 300 K Fig. 4 shows a weaker (lateral) size dependence as compared to 4 K, as the (lateral size) trends of acoustic and optical phonon contributions (Fig. 2) partially compensate each other at higher temperatures, where not only acoustic phonons contribute like at 4 K. As a general trend the coupling to acoustic phonons and with it the scattering rate increases with decreasing well thickness39 (from bulk to a narrow 2D system), which is in principle an effect of the increasing (exciton) wave function amplitude (or normalization pre-factor) upon stronger z-confinement. Hence, the mobility and diffusion coefficient for (ZB) CdSe NPLs (Fig. 4), e.g. at 4 K, is a bit lower than that for bulk (WZ) CdSe,43 having 14 cm2 s−1. Data on ZB bulk do not exist, as it is not a stable bulk modification. Since optical-phonon scattering dominates at elevated temperatures (e.g. at 300 K) and adds to the acoustic scattering rate, eqn (6) and (7) translate this to a reduced mobility. This results in lower exciton diffusion constants and mobility at 300 K, as seen in Fig. 4. Increasing the lateral platelet area results in an increase of the mobility and diffusion constant for small platelets, while a saturation behavior is observed for large NPLs, which is the result of the saturation behaviors of the coupling constants observed in Fig. 2. With increasing lateral size (Lx, Ly), the lateral confinement becomes weaker and the exciton is increasingly delocalized; i.e. the exciton center of mass (CM) motion is (quasi) free and can be described by the plane wave function  . Hence the CM matrix element reduces to the conservation of the crystal momentum δKXi−KXf, Q in the free directions. This case is analogous to ideal 2D quantum wells and TMDC materials. There, (i) the scattering rate and subsequently the mobility μ and the diffusion coefficient D are independent of the area. Furthermore, (ii) the deformation-potential interaction weakens due to the decreasing phonon wave vector q and becomes constant for large wells. Additionally, (iii) the Fröhlich interaction saturates and becomes sensitive to the dielectric environment. For (iii) screening will be relevant in the phonon-momentum dependency of the polar-optical coupling.53,54 Due to (i)–(iii) it is not surprising that e.g. the room temperature mobility remains at a constant, area independent value for large platelets. This corresponds to a bulk like limit for the two weakly confined lateral dimensions.
. Hence the CM matrix element reduces to the conservation of the crystal momentum δKXi−KXf, Q in the free directions. This case is analogous to ideal 2D quantum wells and TMDC materials. There, (i) the scattering rate and subsequently the mobility μ and the diffusion coefficient D are independent of the area. Furthermore, (ii) the deformation-potential interaction weakens due to the decreasing phonon wave vector q and becomes constant for large wells. Additionally, (iii) the Fröhlich interaction saturates and becomes sensitive to the dielectric environment. For (iii) screening will be relevant in the phonon-momentum dependency of the polar-optical coupling.53,54 Due to (i)–(iii) it is not surprising that e.g. the room temperature mobility remains at a constant, area independent value for large platelets. This corresponds to a bulk like limit for the two weakly confined lateral dimensions.
A brief note relates to the contributions of the nonpolar (optical) deformation-potential coupling and piezoelectric (acoustic) interaction on the total diffusion coefficient and mobility. They are considerably weaker than the Fröhlich and the acoustic deformation potential interaction and have a very minor effect on the total mobility. We demonstrate and discuss this in section S1A and B of the ESI† by further calculations. Additionally Table S1† shows a comparison of their impact on the total mobility. The acoustic deformation potential and the Fröhlich interaction dominate the total mobility, while the piezoelectric interaction results in only a slight reduction of the total mobility. The optical deformation potential has a vanishing contribution with respect to the other interactions as Matthiessens’ rule for the total mobility is applied.
Summing up, our results in Fig. 3 and 4 show that there is an opportunity to tune the exciton mobility and diffusion constant in our CdSe nanoplatelets via lateral platelet size and aspect ratio as well as the sample temperature, especially for smaller NPLs. This is based on the lateral size and aspect ratio dependencies of the acoustic and Fröhlich coupling.
Finally we remark that a similar analysis of the trion diffusion coefficient and mobility, based on the T− peak in Fig. 1, like performed for the excitons in this paper, is not possible. This is due to the fact that the trion line width does not only depend on the mentioned scattering processes, but is also influenced by the energy, density of states and occupation probability of final states for the residual electron transferred to a continuum state upon radiative trion decay. This energy and momentum transfer to the electron alters the trion emission line width, both with the platelet size and temperature, and is beyond the scope of this investigation.
3. Conclusions
In summary we have shown that the exciton diffusion coefficient and mobility in CdSe nanoplatelets can be tuned via the lateral extent and aspect ratio. The coupling to acoustic and optical phonons can be engineered via the lateral size of the platelets. As these phonon scattering processes determine and limit the exciton diffusion and mobility, both can be tuned via the lateral size and aspect ratio. At 4 K the exciton mobility increases with the lateral size from ∼4 × 103 cm2 V−1 s−1 to more than 1.4 × 104 cm2 V−1 s−1, while it is about 8 × 101 cm2 V−1 s−1 for large platelets at room temperature. In turn, at 4 K the exciton diffusion coefficient increases with the lateral size from ∼1.3 cm2 s−1 to ∼5 cm2 s−1, while it is around half the value for large platelets at room temperature. We have shown good agreement between our theory predictions and experimental results as well as with other experimental methods like four wave mixing, THz conductivity and mobility measurements. Our theoretical modeling shows that the exciton diffusion coefficient and mobility in the 2D nanoplatelets are tunable by the platelet area and lateral aspect ratio as well as the sample temperature.Our findings open up the possibility for materials with e.g. engineerable (exciton) diffusion, mobility and PL line width. Especially important is that this tuneability via lateral size and aspect ratio is quasi independent from the optical transition energy, which is given by the strong, but constant z-confinement in our colloidal quantum wells and only minorly by the weak lateral confinement (Scott et al.12) in NPLs, which is of the order of <30 meV. The presented findings will strongly impact further studies, as the demonstrated lateral size tuneability of the exciton mobility can improve e.g. excitation or charge extraction efficiencies of solar cells, solar hydrogen generation, or conversely light emission efficiencies of LEDs or lasers. Tuning e.g. exciton diffusion might be interesting for instance for investigations about biexciton formation upon exciton fusion, as it determines the encounter probability of the two particles. Our results provide a toolbox for the design of photonic materials with engineered properties, that is directly transferable to other 2D materials of current interest, like Perovskite (Weidman et al.55) and TMDC materials, which can be grown also with finite lateral size.
4. Methods
4.1. Samples and setup
4.5 monolayer (ML) zinc blende (ZB) CdSe nanoplatelet samples with the first exciton absorption band around 512 nm and different average lateral sizes of 17 × 6 nm2 to 41 × 13 nm2 were synthesized according to ref.1 and 31 and characterized by transmission electron microscopy (TEM). The corresponding lateral aspect ratios R are: 2.8 (17 × 6 nm2), 2.7 (19 × 7 nm2), 1.5 (17 × 11 nm2), 3.6 (29 × 8 nm2), 2.0 (30 × 15 nm2) and 3.2 (41 × 13 nm2).The samples were embedded in PMAO polymer on fused silica substrates. The volume fraction in the polymer was kept below 1% to avoid any aggregation or FRET effects.56 We remark that the TEM images in Fig. 1 are made by a different coating process for the TEM grids without any (host) polymer. The samples were mounted in a CryoVac Micro cryostat. The second harmonic of a 150 fs, 75.4 MHz repetition rate Ti:Sa laser (Coherent Mira 900HP) at 420 nm was used for confocal excitation with an 0.4 NA objective (≈0.2 W cm−2 CW equivalent excitation density). The moderate excitation density leads to <0.1 percent of the platelets being excited within one laser pulse (average number of excitons per platelet per pulse below 10–3, estimated viaref. 57 and the measured continuum absorption). This low density excludes multiexcitonic processes. Time integrated PL detection was realized using a Horiba IHR550 spectrometer with an attached LN2 cooled CCD (Roper Spec 10).
The emission line width fits in Fig. 1 result in the following Gaussian inhomogeneous contributions, which depend on the platelet size and lateral aspect ratio (17 × 6 nm2, 7.5 meV; 19 × 7 nm2, 12.9 meV; 17 × 11 nm2, 10 meV; 29 × 8 nm2, 10.1 meV; 30 × 15 nm2, 15 meV; 41 × 13 nm2, 10.4 meV). They are temperature independent and reflect the lateral size dispersion of CdSe NPLs. The inhomogeneous contribution is not relevant for the determination of  and
and 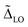 as the quantities do not relate to any offset in Fig. 2. We remark that the order of magnitude of the inhomogeneous lateral center of mass confinement (inhomogeneous Gaussian component of the fits mentioned above) can be reasoned by simply considering the lateral confinement energy of the exciton center of mass motion and relating it to the lateral size dispersion of the samples. Adapting the infinitely deep well expression for a quantum box and its confinement energies ΔE = (1/2μ)(nzπħ/Lz)2 + (π2ħ2/2M)(nx2/Lx2 + ny2 + Ly2)12 for our NPLs, the first term reflects the strong z-confinement in the well, while the second term the weak center of mass confinement in x and y direction. μ is the reduced exciton mass and M is the total exciton mass, and ni is the quantized state quantum numbers in i = x,y,z direction. We consider the lowest states ni = 1. A fluctuation propagation calculation is analogous to conventional error propagation to the following expression for the inhomogeneous broadening of the emission energies due to lateral (and transversal) size distribution: Δ00 = (π2ħ2/Mx,y)(δLx + Lx3 + δLy/Ly3) + (π2ħ2/μz)(δLz/Lz3), with δLi the standard deviation of an approximately Gaussian size distribution from TEM characterization in direction i.
as the quantities do not relate to any offset in Fig. 2. We remark that the order of magnitude of the inhomogeneous lateral center of mass confinement (inhomogeneous Gaussian component of the fits mentioned above) can be reasoned by simply considering the lateral confinement energy of the exciton center of mass motion and relating it to the lateral size dispersion of the samples. Adapting the infinitely deep well expression for a quantum box and its confinement energies ΔE = (1/2μ)(nzπħ/Lz)2 + (π2ħ2/2M)(nx2/Lx2 + ny2 + Ly2)12 for our NPLs, the first term reflects the strong z-confinement in the well, while the second term the weak center of mass confinement in x and y direction. μ is the reduced exciton mass and M is the total exciton mass, and ni is the quantized state quantum numbers in i = x,y,z direction. We consider the lowest states ni = 1. A fluctuation propagation calculation is analogous to conventional error propagation to the following expression for the inhomogeneous broadening of the emission energies due to lateral (and transversal) size distribution: Δ00 = (π2ħ2/Mx,y)(δLx + Lx3 + δLy/Ly3) + (π2ħ2/μz)(δLz/Lz3), with δLi the standard deviation of an approximately Gaussian size distribution from TEM characterization in direction i.
Since nanoplatelets are atomically smooth quantum wells, we neglect at first the last contribution in z and assume a ∼20% size dispersion in x- and y-directions, as obtained from TEM for the 17 × 6 nm2 sample. Using effective masses from ref. 23 we obtain an ∼7 meV predicted inhomogeneous contribution, in good agreement with our experimental result (7.5 meV) above, substantiating our findings and the magnitude of the inhomogeneous contribution. For increasingly larger platelets additional effects occur, which impact the transverse confinement. It is known that extended NPLs tend to bend, which causes inhomogeneous strain in the platelet due to the distortion of the zinc blende lattice.58 This translates to small well width variations from platelet to platelet and within the platelet. The effect increases by trend for larger platelets as there is stronger bending, which could explain an additional and increasing contribution to the inhomogeneous broadening for larger platelets. The bending directly impacts the third contribution in the equation above by altering the z-confinement.
4.2. Theoretical formulation of the exciton–phonon coupling matrix element
The exciton phonon matrix element reads:![[Doublestruck G]](https://www.rsc.org/images/entities/char_e16a.gif) λ,f(q) = 〈ΨfX|Veλ(q)e−iq·re − Vhλ(q)e−iq·rh)|ΨiX〉 λ,f(q) = 〈ΨfX|Veλ(q)e−iq·re − Vhλ(q)e−iq·rh)|ΨiX〉 | (10) |
For a zinc blende crystal structure, the coupling to acoustic phonons is a sum of deformation potential (DA) and piezoelectric (PA) interactions. In such a structure, only the longitudinal acoustic-phonon modes (LA) are connected with the deformation potential while the piezoelectric scattering couples the electronic system to both λ = LA and TA phonons.36,37 The coupling of electrons (holes) to longitudinal-acoustic (LA) phonons by means of a deformation potential D is described by:36,48,59,60
 | (11) |
In non-centrosymmetric crystals such as II–VI polar semiconductors, a strain associated with acoustic phonons can induce a macroscopic electric polarization in the crystal, which is known as the piezoelectric effect. The piezoelectric interaction is given by:36,37,61
 | (12) |
The piezoelectric constant ekij is a third rank tensor, and the subscripts l,j or k are for (x,y,z). In a zinc blende structure semiconductor such as CdSe, there is only one nonzero independent piezoelectric constant e14 = e25 = e36. ξl(λ,q) is the unit polarisation vector, εs is the static dielectric constant, ε0 denotes the vacuum susceptibility, while e represents the elementary charge. Notably, the piezoelectric coupling would lead to an anisotropy that is, however, usually neglected. Instead, an effective isotropic model is constructed that is obtained by averaging over the angles.36,37 In the calculation of the acoustic scattering rate, we have assumed that Eλ(q) ≪ KBT, so that we have  .
.
The coupling to optical phonons has contributions from both the longitudinal optical (LO) polar-Fröhlich interaction and the nonpolar optical interaction through a zero order optical deformation potential. The contribution of polar transverse optical (TO) phonons in polar crystals (e.g. II–VI semiconductors) to the Fröhlich interaction can in general be ignored, because TO phonons produce negligible electric fields, whereas longitudinal optical (LO) phonons produce sizeable electric fields along the direction of phonon propagation.36,37 The interaction with the polar LO phonon, which originates from the macroscopic electric field set up by its lattice vibration, is described by the Fröhlich interaction. For bulk three-dimensional systems, the amplitude of the long-range 3D Fröhlich interaction is given by (the same for electrons and holes):36,48
 | (13) |
 | (14) |
The inclusion of the complementary error function  , where σ is the effective width of the electronic Bloch states (see the ESI†), reflects the constrained interaction of LO phonons with charge carriers in two-dimensional materials. Since Fermi's Golden Rule requires an energy continuum, the LO phonon energy is approximated by13,40
, where σ is the effective width of the electronic Bloch states (see the ESI†), reflects the constrained interaction of LO phonons with charge carriers in two-dimensional materials. Since Fermi's Golden Rule requires an energy continuum, the LO phonon energy is approximated by13,40
 | (15) |
In the narrow thickness platelets, and due to the fact that there is no common frequency domain for optical modes with the vibration modes of the organic ligands and host polymer, in which the platelets are embedded, we assume that 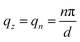 , where d = 4.5 ML. This is not the case for the acoustic phonon for which we take into account propagating phonon modes in the z-direction (thickness direction). Here βLO is the LO-phonon dispersion parameter and ħωBulk,LO is given by:13,40
, where d = 4.5 ML. This is not the case for the acoustic phonon for which we take into account propagating phonon modes in the z-direction (thickness direction). Here βLO is the LO-phonon dispersion parameter and ħωBulk,LO is given by:13,40
 | (16) |
Here  and
and  and hence En,LO(q) can be rewritten as:
and hence En,LO(q) can be rewritten as:
 | (17) |
In a semiconductor in principle phonon scattering can also occur by a zero-order optical deformation potential Dopt. The interaction of the exciton with nonpolar optical phonons (LO and TO) can be described by48,61
 | (18) |
| β LO = 2.97 × 103 ms−1 (ref. 40) | ω ΓLO = 0.038 fs−1 (ref. 72) |
| ω XLO = 0.0396 fs−1 (ref. 72) | m e = 0.22m0 (ref. 23) |
| C LA = 3.63 km s−1 (ref. 73) | C TA = 1.56 km s−1 (ref. 37) |
| m h = 0.41m0 (ref. 23) | D c = −6 eV (ref. 74 and 75) |
| ρ d = 5.82 g cm−3 (ref. 13) | D v = −3 eV (ref. 74 and 75) |
| ε ∞ = 7.9 (ref. 6) | ε s = 9.4 (ref. 6) |
| D opt = 1 × 109 eV cm−1 (ref. 64 and 65) | σ = 4.45 Å (ref. 13) |
| e 14 = 0.16 C m−2 (ref. 76) |
For phonon scattering processes, the matrix elements are evaluated with the corresponding wave functions. In the expressions of the scattering rate (eqn (4)+(5)), the exciton wavefunctions Ψi(f)X and the energies Ei(f)X are the solutions of the following Schrödinger equation:
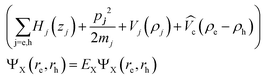 | (19) |
Here Hj(zj) is the single electron (hole) Hamiltonian in the z direction (perpendicular to the layers of the NPLs), pj = −iħ∇pj are the in plane momentum operators, mj is the in-plane mass of carrier j, and Vj(ρj) are the confinement potentials of the electron and hole.  is the nonlocally screened electron–hole interaction originating from the change in the dielectric environment, given by a Rytova–Keldysh potential.13,68–71 For the calculation of the matrix element, we factorize the wave function of the exciton into an in-plane part ξp(ρe, ρh) and z-confinement related functions χe(ze) and χh(zh), the solutions of the single electron (hole) Hamiltonian for the lowest electron and heavy-hole sublevel. The solutions of the single electron (hole) Hamiltonian in the z-direction are:
is the nonlocally screened electron–hole interaction originating from the change in the dielectric environment, given by a Rytova–Keldysh potential.13,68–71 For the calculation of the matrix element, we factorize the wave function of the exciton into an in-plane part ξp(ρe, ρh) and z-confinement related functions χe(ze) and χh(zh), the solutions of the single electron (hole) Hamiltonian for the lowest electron and heavy-hole sublevel. The solutions of the single electron (hole) Hamiltonian in the z-direction are:
| ΨX(re, rh) = χe(ze)χh(zh)ξp(ρe, ρh) |
Furthermore, using the relative ρ = ρe − ρh and center of mass coordinates  we separate the center of mass and the relative motion of the exciton (weak confinement limit), i.e. assuming that the NPLs are more quantum well like, as this paper aims for larger platelets (for more details see ref. 13 and 68). Hence the in-plane exciton wave function can be written as the product of the exciton center of mass and the relative wave function
we separate the center of mass and the relative motion of the exciton (weak confinement limit), i.e. assuming that the NPLs are more quantum well like, as this paper aims for larger platelets (for more details see ref. 13 and 68). Hence the in-plane exciton wave function can be written as the product of the exciton center of mass and the relative wave function  . Here, the relative wave function
. Here, the relative wave function 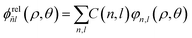 is the solution of the relative Hamiltonian and can be expanded in terms of 2D hydrogenic states φn,l(ρ, θ). ñ,l (n∈
is the solution of the relative Hamiltonian and can be expanded in terms of 2D hydrogenic states φn,l(ρ, θ). ñ,l (n∈![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) *) represents the quasi hydrogenic series obtained for the exciton using a Rytova–Keldysh potential. Using the exciton wave function above and expressing the in-plane position vectors of the electrons and holes as a function of the center of mass RX and relative coordinates ρ, the resulting matrix element in eqn (10) can be rewritten as
*) represents the quasi hydrogenic series obtained for the exciton using a Rytova–Keldysh potential. Using the exciton wave function above and expressing the in-plane position vectors of the electrons and holes as a function of the center of mass RX and relative coordinates ρ, the resulting matrix element in eqn (10) can be rewritten as
 | (20) |
 | (21) |
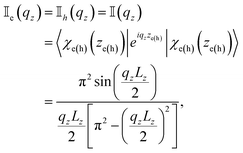 | (22) |
This expression shows that the squared matrix element decreases strongly for  . This reflects a general feature of electron (hole)–phonon interaction: the coupling is weak when along a given direction the phonon wavelength is small compared to the spatial variation of the electron (hole)wave function. The center of the mass matrix element is given by:
. This reflects a general feature of electron (hole)–phonon interaction: the coupling is weak when along a given direction the phonon wavelength is small compared to the spatial variation of the electron (hole)wave function. The center of the mass matrix element is given by:
 | (23) |
In the case of infinite confinement potential, the center of the mass matrix element is given by ![[Doublestruck M]](https://www.rsc.org/images/entities/char_e170.gif) CM(qx,qy) =
CM(qx,qy) = ![[Doublestruck M]](https://www.rsc.org/images/entities/char_e170.gif) CM(qx)
CM(qx)![[Doublestruck M]](https://www.rsc.org/images/entities/char_e170.gif) CM(qy), where
CM(qy), where ![[Doublestruck M]](https://www.rsc.org/images/entities/char_e170.gif) CM(qx(y)) is defined by the following expression:
CM(qx(y)) is defined by the following expression:
 | (24) |
For the case of laterally unconfined wells (for example laterally infinite TMDCs), the center of the mass matrix element reduces to the conservation of the crystal momentum  , where Ki(f)X is the initial (final) in-plane free center of the mass wave vector.
, where Ki(f)X is the initial (final) in-plane free center of the mass wave vector.
Finally, Table 1 shows the material parameters used in the calculations.
Author contributions
A.W.A. designed and performed measurements, analyzed data, and carried out calculations. A.W.A and S.A. wrote the paper. S.A. and S.J. did theoretical modeling. A.W.A. contributed to modeling. S.H., M.T.Q., N.O., and U.W. contributed to discussion and interpretation of results.Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. W. A. acknowledges R. Scott for support and funding by DFG projects AC290/2-1 and AC290/2-2. We thank I. Moreels, M. Artemyev and their groups for providing samples.References
- S. Ithurria and B. Dubertret, J. Am. Chem. Soc., 2008, 130, 16504–16505 CrossRef CAS.
- A. W. Achtstein, A. Schliwa, A. Prudnikau, M. Hardzei, M. V. Artemyev, C. Thomsen and U. Woggon, Nano Lett., 2012, 12, 3151–3157 CrossRef CAS.
- K. Bolotin, K. Sikes, Z. Jiang, M. Klima, G. Fudenberg, J. Hone, P. Kim and H. Stormer, Solid State Commun., 2008, 146, 351 CrossRef CAS.
- S. Bruzzone and G. Fiori, Appl. Phys. Lett., 2011, 99, 222108 CrossRef.
- S. Ithurria, M. D. Tessier, B. Mahler, R. P. S. M. Lobo, B. Dubertret and A. L. Efros, Nat. Mater., 2011, 10, 936–941 CrossRef CAS.
- A. W. Achtstein, R. Scott, S. Kickhöfel, S. T. Jagsch, S. Christodoulou, G. H. Bertrand, A. V. Prudnikau, A. Antanovich, M. Artemyev, I. Moreels, A. Schliwa and U. Woggon, Phys. Rev. Lett., 2016, 116, 116802 CrossRef.
- J. Planelles, A. W. Achtstein, R. Scott, N. Owschimikow, U. Woggon and J. I. Climente, ACS Photonics, 2018, 5, 3680–3688 CrossRef CAS.
- A. Naeem, F. Masia, S. Christodoulou, I. Moreels, P. Borri and W. Langbein, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 121302 CrossRef.
- A. Polovitsyn, Z. Dang, J. L. Movilla, B. Martín-García, A. H. Khan, G. H. V. Bertrand, R. Brescia and I. Moreels, Chem. Mater., 2017, 29, 5671–5680 CrossRef CAS.
- A. W. Achtstein, O. Marquardt, R. Scott, M. Ibrahim, T. Riedl, A. V. Prudnikau, A. Antanovich, N. Owschimikow, J. K. N. Lindner, M. Artemyev and U. Woggon, ACS Nano, 2018, 12, 9476–9483 CrossRef CAS.
- W. Zhang, Z. Huang, W. Zhang and Y. Li, Nano Res., 2014, 7, 1731 CrossRef CAS.
- R. Scott, A. V. Prudnikau, A. Antanovich, S. Christodoulou, T. Riedl, G. H. V. Bertrand, N. Owschimikow, J. K. N. Lindner, Z. Hens, I. Moreels, M. Artemyev, U. Woggon and A. W. Achtstein, Nanoscale, 2019, 11, 3958–3967 RSC.
- J. F. Specht, R. Scott, M. C. Castro, S. Christodoulou, G. H. Bertrand, A. Prudnikau, A. Antanovich, L. Siebbeles, N. Owschimikow and I. Moreels, et al. , Nanoscale, 2019, 11, 12230–12241 RSC.
- R. Scott, A. W. Achtstein, A. Prudnikau, A. Antanovich, S. Christodoulou, I. Moreels, M. Artemyev and U. Woggon, Nano Lett., 2015, 15, 4985–4992 CrossRef CAS.
- J. Heckmann, R. Scott, A. V. Prudnikau, A. Antanovich, N. Owschimikow, M. Artemyev, J. I. Climente, U. Woggon, N. B. Grosse and A. W. Achtstein, Nano Lett., 2017, 17, 6321–6329 CrossRef CAS.
- M. Li, M. Zhi, H. Zhu, W.-Y. Wu, Q.-H. Xu, M. H. Jhon and Y. Chan, Nat. Commun., 2015, 6, 8513 CrossRef CAS.
- M. T. Quick, N. Owschimikow, A. H. Khan, A. Polovitsyn, I. Moreels, U. Woggon and A. W. Achtstein, Nanoscale, 2019, 11, 17293–17300 RSC.
- R. Scott, J. Heckmann, A. V. Prudnikau, A. Antanovich, A. Mikhailov, N. Owschimikow, M. Artemyev, J. I. Climente, U. Woggon, N. B. Grosse and A. W. Achtstein, Nat. Nanotechnol., 2017, 1155–1160 CrossRef CAS.
- D.-E. Yoon, W. D. Kim, D. Kim, D. Lee, S. Koh, W. K. Bae and D. C. Lee, J. Phys. Chem. C, 2017, 121, 24837–24844 CrossRef CAS.
- L. Biadala, F. Liu, M. D. Tessier, D. R. Yakovlev, B. Dubertret and M. Bayer, Nano Lett., 2014, 14, 1134–1139 CrossRef CAS.
- E. V. Shornikova, L. Biadala, D. R. Yakovlev, V. F. Sapega, Y. G. Kusrayev, A. A. Mitioglu, M. V. Ballottin, P. C. M. Christianen, V. V. Belykh, M. V. Kochiev, N. N. Sibeldin, A. A. Golovatenko, A. V. Rodina, N. A. Gippius, A. Kuntzmann, Y. Jiang, M. Nasilowski, B. Dubertret and M. Bayer, Nanoscale, 2018, 10, 646–656 RSC.
- R. Scott, A. W. Achtstein, A. V. Prudnikau, A. Antanovich, L. D. A. Siebbeles, M. Artemyev and U. Woggon, Nano Lett., 2016, 16, 6576–6583 CrossRef CAS.
- R. Benchamekh, N. A. Gippius, J. Even, M. O. Nestoklon, J.-M. Jancu, S. Ithurria, B. Dubertret, A. L. Efros and P. Voisin, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 035307 CrossRef.
- J. Q. Grim, S. Christodoulou, F. Di Stasio, R. Krahne, R. Cingolani, L. Manna and I. Moreels, Nat. Nanotechnol., 2014, 9, 891–895 CrossRef CAS.
- E. V. Shornikova, L. Biadala, D. R. Yakovlev, D. Feng, V. F. Sapega, N. Flipo, A. A. Golovatenko, M. A. Semina, A. V. Rodina, A. A. Mitioglu, M. V. Ballottin, P. C. M. Christianen, Y. G. Kusrayev, M. Nasilowski, B. Dubertret and M. Bayer, Nano Lett., 2018, 18, 373–380 CrossRef CAS.
- S. Ayari, M. T. Quick, N. Owschimikow, S. Christodoulou, G. H. V. Bertrand, M. Artemyev, I. Moreels, U. Woggon, S. Jaziri and A. W. Achtstein, Nanoscale, 2020, 12, 14448–14458 RSC.
- F. V. Antolinez, F. T. Rabouw, A. A. Rossinelli, J. Cui and D. J. Norris, Nano Lett., 2019, 19, 8495–8502 CrossRef CAS.
- G. Bacher, H. Schweizer, J. Kovac, H. Nickel, W. Schlapp and R. Lösch, Appl. Phys. Lett., 1992, 61, 702–704 CrossRef CAS.
- R. Tomar, A. Kulkarni, K. Chen, S. Singh, D. van Thourhout, J. M. Hodgkiss, L. D. Siebbeles, Z. Hens and P. Geiregat, J. Phys. Chem. C, 2019, 123, 9640–9650 CrossRef CAS.
- L. T. Kunneman, J. M. Schins, S. Pedetti, H. Heuclin, F. C. Grozema, A. J. Houtepen, B. Dubertret and L. D. A. Siebbeles, Nano Lett., 2014, 14, 7039–7045 CrossRef CAS.
- G. H. V. Bertrand, A. Polovitsyn, S. Christodoulou, A. H. Khan and I. Moreels, Chem. Commun., 2016, 52, 11975–11978 RSC.
- S. A. Cherevkov, M. V. Artemyev, A. V. Prudnikau and A. V. Baranov, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 041303 CrossRef.
- C. J. A. Maddux, D. F. Kelley and A. M. Kelley, J. Phys. Chem. C, 2018, 122, 27100–27106 CrossRef CAS.
- S. Dong, J. Lian, M. H. Jhon, Y. Chan and Z.-H. Loh, Nano Lett., 2017, 17, 3312–3319 CrossRef CAS.
- M. D. Tessier, C. Javaux, I. Maksimovic, V. Loriette and B. Dubertret, ACS Nano, 2012, 6, 6751–6758 CrossRef CAS.
- G. D. Mahan, Many-particle physics, Springer Science & Business Media, 2013 Search PubMed.
- G. D. Mahan, in Polarons in Ionic Crystals and Polar Semiconductors, ed. J. T. Devreese, North-Holland, Amsterdam, 1972, p. 533 Search PubMed.
- P. K. Basu, Theory of Optical Processes in Semiconductors, Oxford Science Publications, 1997 Search PubMed.
- C. Hamaguchi, Basic Semiconductor Physics, Springer, 2017, vol. 3 Search PubMed.
- D. O. Sigle, J. T. Hugall, S. Ithurria, B. Dubertret and J. J. Baumberg, Phys. Rev. Lett., 2014, 113, 087402 CrossRef.
- A. P. Shreve, E. H. Haroz, S. M. Bachilo, R. B. Weisman, S. Tretiak, S. Kilina and S. K. Doorn, Phys. Rev. Lett., 2007, 98, 037405 CrossRef.
- F. Cadiz, C. Robert, E. Courtade, M. Manca, L. Martinelli, T. Taniguchi, K. Watanabe, T. Amand, A. C. H. Rowe, D. Paget, B. Urbaszek and X. Marie, Appl. Phys. Lett., 2018, 112, 152106 CrossRef.
- J. Erland, B. S. Razbirin, K.-H. Pantke, V. G. Lyssenko and J. M. Hvam, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 3582–3587 CrossRef CAS.
- R. P. Feynman, The Feynman Lectures on Physics, Basic Books, 2005, vol. 1 Search PubMed.
- Q. Li, K. Wu, J. Chen, Z. Chen, J. R. McBride and T. Lian, ACS Nano, 2016, 10, 3843–3851 CrossRef CAS.
- K. Wu, L. J. Hill, J. Chen, J. R. McBride, N. G. Pavlopolous, N. E. Richey, J. Pyun and T. Lian, ACS Nano, 2015, 9, 4591–4599 CrossRef CAS.
- E. Cassette, R. D. Pensack, B. Mahler and G. D. Scholes, Nat. Commun., 2015, 6, 6086 CrossRef CAS.
- K. Kaasbjerg, K. S. Thygesen and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 115317 CrossRef.
- K. Kaasbjerg, K. S. Thygesen and A.-P. Jauho, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 235312 CrossRef.
- R. Scott, S. Kickhofel, O. Schoeps, A. Antanovich, A. Prudnikau, A. Chuvilin, U. Woggon, M. Artemyev and A. W. Achtstein, Phys. Chem. Chem. Phys., 2016, 18, 3197–3203 RSC.
- H. Akiyama, S. Koshiba, T. Someya, K. Wada, H. Noge, Y. Nakamura, T. Inoshita, A. Shimizu and H. Sakaki, Phys. Rev. Lett., 1994, 72, 924–927 CrossRef CAS.
- J. Feldmann, G. Peter, E. Göbel, P. Dawson, K. Moore, C. Foxon and R. Elliott, Phys. Rev. Lett., 1987, 59, 2337 CrossRef CAS.
- T. Sohier, M. Calandra and F. Mauri, Phys. Rev. B, 2016, 94, 085415 CrossRef.
- S. Shree, M. Semina, C. Robert, B. Han, T. Amand, A. Balocchi, M. Manca, E. Courtade, X. Marie and T. Taniguchi, et al. , Phys. Rev. B, 2018, 98, 035302 CrossRef CAS.
- M. C. Weidman, M. Seitz, S. D. Stranks and W. A. Tisdale, ACS Nano, 2016, 10, 7830–7839 CrossRef CAS.
- B. Guzelturk, O. Erdem, M. Olutas, Y. Kelestemur and H. V. Demir, ACS Nano, 2014, 8, 12524–12533 CrossRef CAS.
- A. W. Achtstein, A. Antanovich, A. Prudnikau, R. Scott, U. Woggon and M. Artemyev, J. Phys. Chem. C, 2015, 119, 20156–20161 CrossRef CAS.
- E. M. Hutter, E. Bladt, B. Goris, F. Pietra, J. C. van der Bok, M. P. Boneschanscher, C. de Mello Donegá, S. Bals and D. Vanmaekelbergh, Nano Lett., 2014, 14, 6257–6262 CrossRef CAS.
- T. Takagahara, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 6552 CrossRef CAS.
- P. Zhao and D. L. Woolard, Phys. Lett. A, 2008, 372, 1666–1670 CrossRef CAS.
- M. Pugnet, J. Collet and A. Cornet, Solid State Commun., 1981, 38, 531–536 CrossRef CAS.
- Z.-W. Wang, R.-Z. Li, X.-Y. Dong, Y. Xiao and Z.-Q. Li, Front. Phys., 2018, 13, 137305 CrossRef.
- A. Thilagam, J. Appl. Phys., 2016, 120, 124306 CrossRef.
- M. Pugnet, J. Collet and A. Cornet, Solid State Commun., 1981, 38, 531–536 CrossRef CAS.
- M. R. Junnarkar and R. Alfano, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 7045 CrossRef CAS.
- W. Pötz and P. Vogl, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 24, 2025 CrossRef.
- A. Blacha, H. Presting and M. Cardona, Phys. Status Solidi B, 1984, 126, 11–36 CrossRef CAS.
- M. Richter, Phys. Rev. Mater., 2017, 1, 016001 CrossRef.
- A. Hichri, I. B. Amara, S. Ayari and S. Jaziri, J. Phys.: Condens. Matter, 2017, 29, 435305 CrossRef CAS.
- L. Keldysh, JETP. Lett., 1979, 29, 658 Search PubMed.
- A. Chernikov, T. C. Berkelbach, H. M. Hill, A. Rigosi, Y. Li, O. B. Aslan, D. R. Reichman, M. S. Hybertsen and T. F. Heinz, Phys. Rev. Lett., 2014, 113, 076802 CrossRef.
- R. Parsons, W. Wardzynski and A. Yoffe, Proc. R. Soc. London, Ser. A, 1961, 262, 120–131 CAS.
- C. F. Cline, H. L. Dunegan and G. W. Henderson, J. Appl. Phys., 1967, 38, 1944–1948 CrossRef CAS.
- A. Antanovich, A. Achtstein, A. Matsukovich, A. Prudnikau, P. Bhaskar, V. Gurin, M. Molinari and M. Artemyev, Nanoscale, 2017, 9, 18042–18053 RSC.
- J. Li and L.-W. Wang, Appl. Phys. Lett., 2004, 85, 2929–2931 CrossRef CAS.
- J. Xin, Y. Zheng and E. Shi, Appl. Phys. Lett., 2007, 91, 112902 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Details on the relevance of individual phonon scattering process contribution to the mobility as well as the σ parameter. See DOI: 10.1039/D0NR04745G |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2020 |