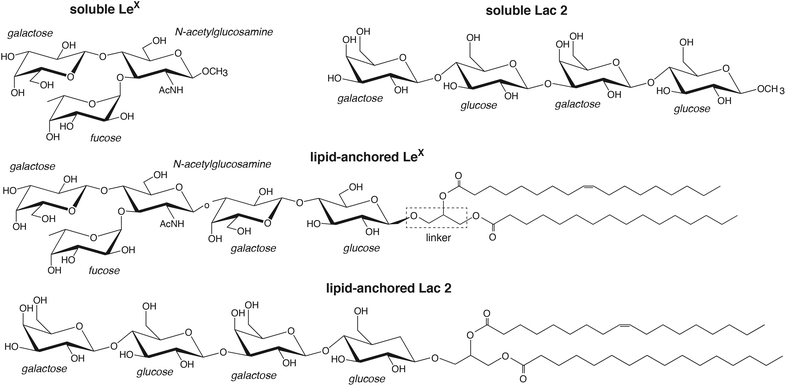
Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Weak carbohydrate–carbohydrate interactions in membrane adhesion are fuzzy and generic
Batuhan
Kav
 a,
Andrea
Grafmüller
a,
Andrea
Grafmüller
 a,
Emanuel
Schneck
a,
Emanuel
Schneck
 bc and
Thomas R.
Weikl
bc and
Thomas R.
Weikl
 *a
*a
aMax Planck Institute of Colloids and Interfaces, Department of Theory and Bio-Systems, Am Mühlenberg 1, 14476 Potsdam, Germany. E-mail: thomas.weikl@mpikg.mpg.de
bMax Planck Institute of Colloids and Interfaces, Department of Biomaterials, Am Mühlenberg 1, 14476 Potsdam, Germany
cTechnische Universität Darmstadt, Physics Department, Hochschulstraße 8, 64289 Darmstadt, Germany
First published on 4th August 2020
Abstract
Carbohydrates such as the trisaccharide motif LeX are key constituents of cell surfaces. Despite intense research, the interactions between carbohydrates of apposing cells or membranes are not well understood. In this article, we investigate carbohydrate–carbohydrate interactions in membrane adhesion as well as in solution with extensive atomistic molecular dynamics simulations that exceed the simulation times of previous studies by orders of magnitude. For LeX, we obtain association constants of soluble carbohydrates, adhesion energies of lipid-anchored carbohydrates, and maximally sustained forces of carbohydrate complexes in membrane adhesion that are in good agreement with experimental results in the literature. Our simulations thus appear to provide a realistic, detailed picture of LeX–LeX interactions in solution and during membrane adhesion. In this picture, the LeX–LeX interactions are fuzzy, i.e. LeX pairs interact in a large variety of short-lived, bound conformations. For the synthetic tetrasaccharide Lac 2, which is composed of two lactose units, we observe similarly fuzzy interactions and obtain association constants of both soluble and lipid-anchored variants that are comparable to the corresponding association constants of LeX. The fuzzy, weak carbohydrate–carbohydrate interactions quantified in our simulations thus appear to be a generic feature of small, neutral carbohydrates such as LeX and Lac 2.
Introduction
Carbohydrates are omnipresent at cell surfaces as constituents of glycolipids and glycoproteins.1–3 During cell adhesion, these carbohydrates come into contact with proteins and carbohydrates on apposing cell surfaces. While specific interactions between carbohydrates and proteins are known to play important roles in cell adhesion events, the role of carbohydrate–carbohydrate interactions in these events is less clear.4–8 About three decades ago, homophilic carbohydrate–carbohydrate interactions of the trisaccharide LewisX (LeX) have been reported to be involved in embryonal cell compaction and aggregation,9–11 and interactions between long carbohydrate chains have been linked to the species-specific aggregation of marine sponges.12 In the following decades, carbohydrate–carbohydrate interactions in adhesion have been investigated in a variety of reconstituted or synthetic systems including nanoparticles and surfaces functionalized with carbohydrates,13–15 atomic force microscopy setups,16–19 and reconstituted vesicles20,21 or membranes22–24 containing glycolipids. While some carbohydrate–carbohydrate interactions have been reported to be strong,17,25,26 interactions of small, neutral carbohydrates are typically considered to be weak.27,28 However, the binding association constants, in particular at membrane interfaces, and the structural binding mechanisms are often not known.In this article, we present detailed results from atomistic molecular dynamics simulations of carbohydrate–carbohydrate interactions in membrane adhesion and in solution for LeX and the synthetic saccharide Lac 2, which is composed of two lactose units29 (see Fig. 1). Our simulations employ a recent carbohydrate force field30 that allows a more faithful representation of carbohydrate–carbohydrate interactions30–32 and exceed the times and system sizes in previous simulation studies of carbohydrate–carbohydrate interactions in solution33–35 by orders of magnitude. LeX has been investigated extensively as a model system for carbohydrate–carbohydrate interactions,13,14,16,19–21,23 and experimental data available from these investigations are central to corroborate our simulation results. In our LeX glycolipids, the LeX trisaccharide is connected via a lactose disaccharide and a glycerol linker to lipids tails (see Fig. 1). In our Lac 2 glycolipids, the LeX trisaccharide is replaced by another lactose disaccharide, which allows to compare the carbohydrate–carbohydrate interactions of LeX to those of the common saccharide lactose. From simulations of soluble pairs of LeX and Lac 2, we obtain association constants Ka of the order of 10 M−1, which agrees with a Ka value of LeX derived from weak affinity chromatography experiments.16,36 From simulations of pairs of LeX and Lac 2 glycolipids at apposing membrane surfaces, we obtain comparable association constants Ktrans for the LeX and Lac 2 glycolipids that strongly decrease with increasing membrane separation. For the membrane separation and thermal roughness of membrane multilayers with 10 mol% LeX glycolipids measured in neutron scattering experiments,23 we determine an adhesion energy per area of the order of 10 μJ m−2 from our Ktrans values, in agreement with the adhesion energy per area reported for vesicles that contain 10 mol% of LeX glycolipids.20 The average force on bound LeX glycolipid complexes determined in our simulations increases with increasing membrane separation up to a maximum value of about 20 pN, which agrees with the LeX–LeX unbinding force obtained from atomic force microscopy experiments.16 The agreement with experimental results indicates that our simulations provide a realistic, detailed picture of weak carbohydrate–carbohydrate interactions in solution as well as in membrane adhesion. A striking feature is that the carbohydrate–carbohydrate interactions are fuzzy, i.e. both soluble and lipid-anchored variants of LeX and Lac 2 interact in our simulations via a large variety of diverse, bound conformations.
Results
Interactions of soluble carbohydrates
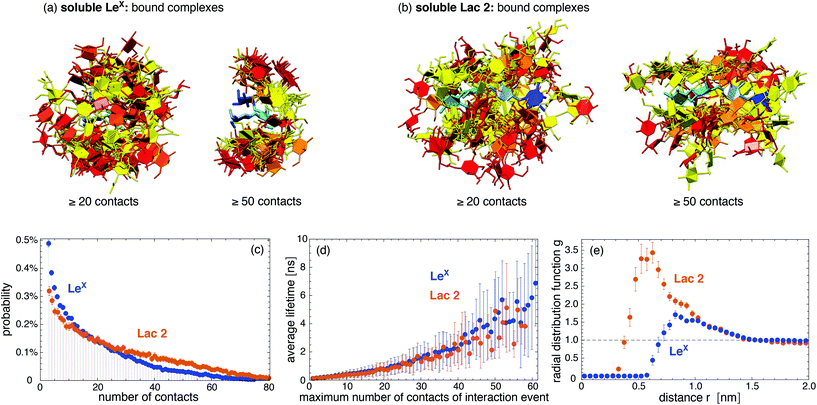
We first consider the interaction of two LeX trisaccharides in solution and compare this LeX–LeX pair interaction to the interaction of two Lac 2 tetrasaccharides, which are composed of two lactose units29 (see Fig. 1). Standard carbohydrate force fields lead to osmotic pressures for solutions of neutral carbohydrates that are systematically too low compared to experimental values. This underestimation of the osmotic pressure of the carbohydrate solutions results from an overestimation of attractive carbohydrate–carbohydrate interactions.30,31 To avoid unrealistically attractive carbohydrate–carbohydrate interactions, we have used the GLYCAM06TIP5POSMOr14 force field, in which the van der Waals parameters for saccharide–saccharide interactions of the standard force field GLYCAM06 have been reparametrized to correctly reproduce experimentally measured osmotic pressures.30 The GLYCAM06TIP5POSMOr14 force field employs the TIP5P water model because this water model leads to more reliable carbohydrate–carbohydrate interactions in GLYCAM06, compared to the standard TIP3P water model.32,37 Using graphics processing units (GPUs) and the software AMBER GPU,38,39 we have generated 50 simulation trajectories with a length of 2.0 μs for two LeX molecules in a periodic simulation box of volume V = 131.5 nm3, and 40 trajectories with a length of 1 μs or close to 1 μs for two Lac 2 molecules in a simulation box of volume V = 260.5 nm3, at the simulation temperature 30 °C. Our total simulation times are 100 μs for the LeX pair and 39.5 μs for the Lac 2 pair, which greatly exceed the total simulation times up to 40 ns in previous simulation studies of LeX–LeX pair interactions in solution33,34 and the total simulation time of a few ns for pair interactions of trisaccharide epitopes from marine sponges.35In our simulations, we observe thousands of interaction events in which the two LeX molecules or the two Lac 2 molecules are in contact. These interaction events are separated by longer or shorter trajectory parts in which the two molecules are not in contact. Fig. 2(a) and (b) display pair conformations of LeX and Lac 2 in which the two molecules exhibit at least 20 or 50 contacts of non-hydrogen atoms, respectively. The shown pair conformations are randomly selected from the simulation frames of our trajectories. One of the carbohydrate molecules is aligned in the pair conformations and represented in blue colors, while the other molecule is represented in red/yellow colors. The clouds of red/yellow molecules around the aligned blue molecules in these conformations illustrate that the carbohydrate–carbohydrate interactions are ‘fuzzy’,40,41i.e. the two molecules interact in broad ensembles of conformations, rather than via a single binding conformation. For both LeX and Lac 2, the ensembles of conformations with at least 50 contacts are narrower than the ensembles of conformations with at least 20 contacts. In conformations with at least 50 contacts, the two LeX molecules tend to stack above each other in different orientations, and the two Lac 2 molecules tend to align parallel or anti-parallel. However, the probability distributions of contact numbers in Fig. 2(c) illustrate that pair conformations with 50 or more contacts of non-hydrogen atoms are rather rare and not typical. The probability distributions decrease monotonously with increasing number of contacts.
The interaction events of the two LeX molecules or the two Lac 2 molecules can be characterized by their lifetime and by the maximum number of contacts of the events. These interaction events are obtained from our simulation trajectories as consecutive stretches of frames at intervals of 0.1 ns with nonzero contacts of the two molecules. Fig. 2(d) shows that the average lifetime of the interaction events increases with the maximum number of contacts observed during the event. With average lifetimes in the nanoseconds range, the interactions of the two LeX or the two Lac 2 molecules are rather short-lived. Nonetheless, the radial distribution functions in Fig. 2(e) indicate that the interactions are attractive. The maxima of the radial distribution functions at center-of-mass distances of about 0.8 nm for LeX and 0.6 nm for Lac 2 are significantly larger than the value 1 for a non-interacting ideal solution.
Quantifying the attractive interactions of the two LeX or two Lac 2 molecules requires distinguishing bound and unbound states. This distinction is somewhat arbitrary because of the fuzzy interactions of the carbohydrates. The probability distributions of carboyhydrate–carbohydrate contact numbers in Fig. 2(c) are monotonously decreasing and, thus, not bimodal as required for a clear distinction of two states. Table 1 presents association constants of two LeX or two Lac 2 molecules calculated for different cutoffs nc of the maximum number of contacts of interaction events. In these calculations, only interaction events with a maximum number of contacts larger or equal to the cutoff nc are taken to be binding events. The probability Pb that the two LeX or two Lac 2 molecules are bound has been determined from the total duration of the binding events, and the association constants from Ka = VPb/Pu where Pu = 1 − Pb is the probability that the molecules are unbound, and V is the volume of the simulation box. The Ka values in Table 1 slightly decrease with increasing contact cutoff nc for binding events. For LeX, a Ka value of 10 M−1 has been obtained from weak affinity chromatography experiments,36 which is of the same order of magnitude as the values derived from our simulations.
| n c = 5 | n c = 10 | n c = 20 | |
|---|---|---|---|
| LeX | 6.4 ± 0.3 | 5.7 ± 0.3 | 4.5 ± 0.3 |
| Lac 2 | 13.2 ± 1.0 | 12.3 ± 1.0 | 10.7 ± 0.9 |
Interactions of lipid-anchored carbohydrates
To investigate the interactions of two lipid-anchored LeX or two lipid-anchored Lac 2 molecules, we have performed simulations of LeX and Lac 2 glycolipids embedded in POPC lipid membranes. Our LeX and Lac 2 glycolipids have the same lipid tails as POPC, and carbohydrate tips that are connected to these lipid tails by a glycerol linker group (see Fig. 1). The carbohydrate tip of the LeX glycolipid consists of the LeX trisaccharide and an additional lactose disaccharide as spacer between LeX and the glycerol linker. The Lac 2 glycolipid has the linear Lac 2 tetrasaccharide as carbohydrate tip. The force field of our simulations combines the GLYCAM06TIP5POSMOr14 carbohydrate force field30,42 for the TIP5P water model with the AMBER Lipid14 force field43 for lipid membranes. Because simulations of AMBER Lipid14 POPC membranes in TIP5P water lead to an unreasonably small area per lipid, we have rescaled the Lennard-Jones interactions between the TIP5P water molecules and the lipid headgroup atoms to obtain the same area per lipid as in standard AMBER Lipid14 simulations with the TIP3P water model (see Methods).We quantify the interactions of two LeX or two Lac 2 glycolipids at apposing membrane surfaces in a system that consists of a single lipid bilayer with one glycolipid anchored in each monolayer (see Fig. 3). In this system, the two glycolipids in the different monolayers interact due to the periodic boundary conditions of the simulation box, and the separation of the membrane monolayers can be adjusted by varying the number of water molecules in the simulation box. The values for the membrane separation l given in Fig. 3 correspond to the separation from membrane midplane to membrane midplane and, thus, to the height of the simulation box. At each membrane separation, we have generated 10 trajectories with a length of 3 μs for the LeX system and a length of 1 μs for the Lac 2 system at the temperature 30 °C. The total simulation times at each membrane separation thus are 30 μs and 10 μs for the LeX and Lac 2 systems, respectively. The membranes contain in each monolayer 35 lipids besides the single glycolipid and have an area A of 23.3 nm2. The height of the simulation box l increases with the number of water molecules nw as l ≃ 3.8 nm + 0.013nw nm. The thickness of the water layer in the simulations thus is about l − 3.8 nm.
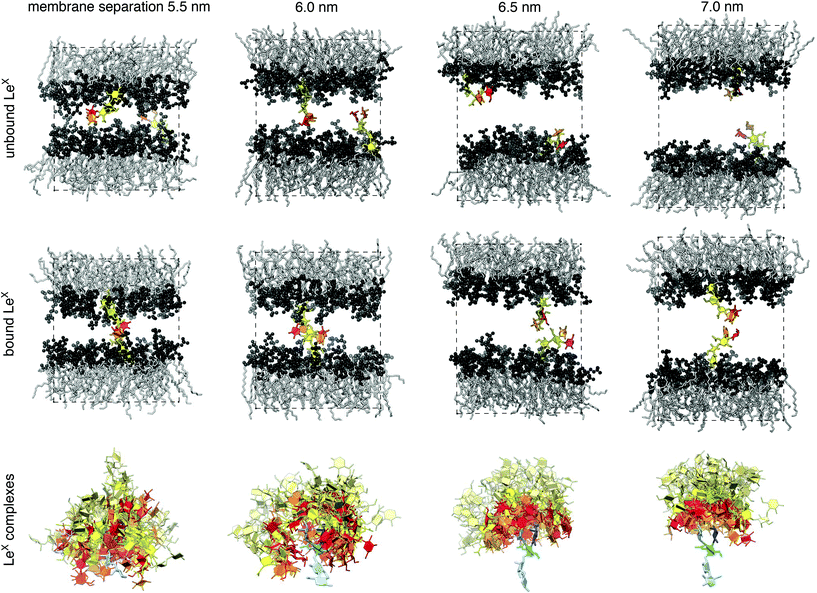 | ||
| Fig. 3 (Top) Membrane conformations with two unbound or bound LeX glycolipids. The LeX glycolipids are anchored in the different monolayers of the membrane and interact because of the periodic boundary conditions of the simulation box. The height of the simulation box corresponds to the membrane separation from bilayer midplane to midplane. Each membrane monolayer contains 35 POPC lipids, which have the same lipid tails as the LeX glycolipids. The fucose and galactose at the branched tip of the LeX glycolipids are represented in red and orange, and the remaining three monosaccharide units in yellow. (Bottom) 50 randomly selected complexes of the carboyhydrate tips of the LeX glycolipids at different membrane separations. The selected complexes exhibit at least 10 contacts between non-hydrogen atoms of the two carbohydate tips. The carbohydrate tip of the lower LeX glycolipid is aligned in the 50 complexes and represented in blue colors, while the carbohydrate tip of the upper glycolipid is represented in red/yellow colors. The LeX motif of the carbohydrate tips are represented in the same colors as in Fig. 2(a). The lactose disaccharides of the carbohydrate tips, which are located between the LeX trisaccharide and the linker group of the glycolipid, are represented in light blue and light yellow, respectively. | ||
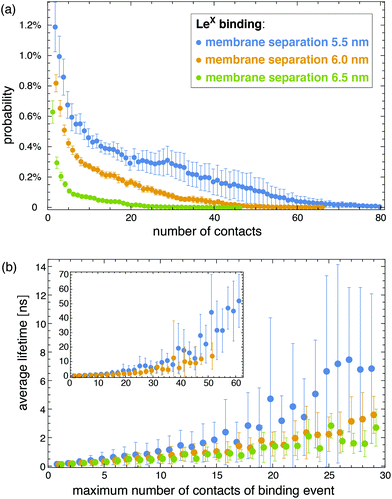
The interactions of the glycolipids strongly depend on the membrane separation. For the membrane separations l = 5.5, 6.0, 6.5, and 7.0 nm, 50 randomly selected complexes of the LeX glycolipid tips with at least 10 contacts of non-hydrogen atoms are displayed at the bottom of Fig. 3. The carbohydrate tip of the lower LeX glycolipid is aligned in the 50 complexes and represented in blue colors, while the carbohydrate tip of the upper glycolipid is represented in red/yellow colors. The clouds of red/yellow carbohydrates illustrate that the interactions of lipid-anchored LeX are fuzzy, similar to soluble LeX and Lac 2 (see Fig. 2). The overlap of the cloud of the upper, red/yellow carbohydrates with the lower, blue carbohydrate decreases with increasing membrane separation. At the membrane separation 5.5 nm, the LeX glycolipids interact via their entire carbohydrate tips. At the separation 6.0 nm, the interactions are limited to the LeX trisaccharide of the glycolipid tip, and at the membrane separations 6.5 nm and 7.0 nm, the interactions are further restricted to the galactose and fucose monosaccharides at the branched end of the LeX glycolipid. The decrease of interactions with increasing separation is also reflected in the probability distributions of contact numbers shown in Fig. 4(a) and in the average lifetime of the interaction events for different maximum numbers of contacts in Fig. 4(b). At the smallest membrane separation 5.5 nm, complexes of LeX glycolipids can exhibit up to 60 and more contacts of non-hydrogen atoms (see Fig. 4(a)), and average lifetimes up to 50 ns for interaction events with a maximum number of 60 contacts (see inset of Fig. 4(b)), which are about one order of magnitude larger than the average lifetimes for interaction events of soluble LeX molecules with the same maximum number of contacts. At the membrane separations 6.0 and 6.5 nm, the overall contact numbers and lifetimes of interaction events are significantly smaller.
Analogous to soluble carbohydrates, the binding association constants Ktrans = APb/(1 − Pb) of the glycolipids in the different membrane monolayers can be determined from the probability Pb that the two LeX or two Lac 2 glycolipids are bound. The binding constants shown in Fig. 5 are calculated for binding events with a maximum number of at least nc = 5 contacts of non-hydrogen atoms. For the larger binding cutoff nc = 10, the Ktrans values of the two LeX glycolipids are about 10% smaller than the values in Fig. 5 at the membrane separations 5.5 and 6.0 nm, and the values of the Lac 2 glycolipids are about 15% smaller at these separations. The Ktrans values decrease with increasing membrane separation. For membrane separations larger than about 7.5 nm, the glycolipids cannot form contacts.
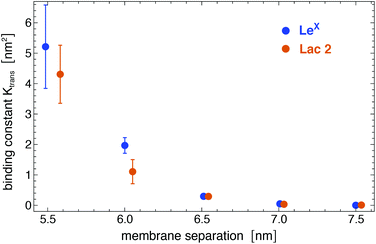 | ||
| Fig. 5 Binding constant Ktrans of two LeX and two Lac 2 glycolipids versus membrane separation, calculated for binding events with a maximum number of at least nc = 5 contacts of non-hydrogen atoms. | ||
The binding constant Ktrans can be related to membrane adhesion energies, which have been measured for membrane vesicles that contain 10 mol% of LeX glycolipids.20,27 For two apposing, large membrane surfaces of area A that contain a total number of Nt glycolipids, the free energy difference for forming the nth bond of the glycolipids is (see Methods)
ΔGn = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln[Ktrans(Nt − n + 1)2/nA] ln[Ktrans(Nt − n + 1)2/nA] | (1) |
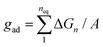 | (2) |
Forces on lipid-anchored carbohydrates in trans-direction
The binding of glycolipids in our simulations is associated with deviations of the glycolipids relative to the surrounding lipids. These deviations in the trans-direction perpendicular to the membrane surface result from forces on bound glycolipid complexes. Fig. 6(a) illustrates distributions of trans-deviations between the center of mass of the linker group of a LeX glycolipid (see Fig. 1) and the center of mass of all lipid head groups in the same monolayer as the glycolipid. The trans-deviations d are calculated from the simulation frames of our trajectories at intervals of 0.1 ns. We obtain two values of d per simulation frame for the two glycolipids relative to the monolayer in which they are embedded. An increase in d indicates glycolipid motion away from the membrane midplane. With increasing membrane separation, the distributions for bound LeX glycolipids deviate more and more from the distribution for unbound LeX, which reflects increasing forces. The distribution of trans-deviations d of unbound LeX glycolipids shown in Fig. 6(a) is calculated from our simulation trajectories at the membrane separation 8.0 nm, at which LeX bonds do not occur, and can be approximated by a Gaussian distribution exp[−V(d)/kBT] with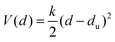 . The trans-deviations d of unbound LeX glycolipids thus can be described by a harmonic potential V(d) with force constant k and mean extension du, which can be determined from the standard deviation σ and mean
. The trans-deviations d of unbound LeX glycolipids thus can be described by a harmonic potential V(d) with force constant k and mean extension du, which can be determined from the standard deviation σ and mean ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) of the Gaussian as k = kBT/σ2 = 94 ± 4 pN nm−1 and du =
of the Gaussian as k = kBT/σ2 = 94 ± 4 pN nm−1 and du = ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) = −0.31 ± 0.10 nm. The distributions of trans-deviations of bound LeX glycolipids in Fig. 6(a) are calculated from our simulation trajectories at the membrane separations 5.5, 6.0, 6.5, and 7.0 nm, for binding events with a maximum number of at least nc = 5 contacts of non-hydrogen atoms. The average force f = k(db − du) on bound LeX glycolipids at the membrane separations l = 5.5, 6.0, 6.5, and 7.0 nm then can be calculated from the difference between the mean trans-deviations db = −0.26 ± 0.01, −0.22 ± 0.01, −0.16 ± 0.01, and −0.08 ± 0.02 nm of the bound glycolipids at these membrane separations and the mean trans-deviation du of the unbound glycolipids. The force f on bound LeX glycolipids increases with increasing membrane separation up to a value of 21.7 ± 2.4 pN at the separation 7.0 nm (see Fig. 6(b)). This maximal force value agrees with the unbinding force 20 ± 4 pN of two LeX molecules obtained from atomic force microscopy experiments.16 For bound Lac 2 glycolipids, we obtain a maximal force of 14.7 ± 3.5 pN at the separation 7.0 nm, which is about of the same magnitude as the maximal force sustained by the LeX complexes.
= −0.31 ± 0.10 nm. The distributions of trans-deviations of bound LeX glycolipids in Fig. 6(a) are calculated from our simulation trajectories at the membrane separations 5.5, 6.0, 6.5, and 7.0 nm, for binding events with a maximum number of at least nc = 5 contacts of non-hydrogen atoms. The average force f = k(db − du) on bound LeX glycolipids at the membrane separations l = 5.5, 6.0, 6.5, and 7.0 nm then can be calculated from the difference between the mean trans-deviations db = −0.26 ± 0.01, −0.22 ± 0.01, −0.16 ± 0.01, and −0.08 ± 0.02 nm of the bound glycolipids at these membrane separations and the mean trans-deviation du of the unbound glycolipids. The force f on bound LeX glycolipids increases with increasing membrane separation up to a value of 21.7 ± 2.4 pN at the separation 7.0 nm (see Fig. 6(b)). This maximal force value agrees with the unbinding force 20 ± 4 pN of two LeX molecules obtained from atomic force microscopy experiments.16 For bound Lac 2 glycolipids, we obtain a maximal force of 14.7 ± 3.5 pN at the separation 7.0 nm, which is about of the same magnitude as the maximal force sustained by the LeX complexes.
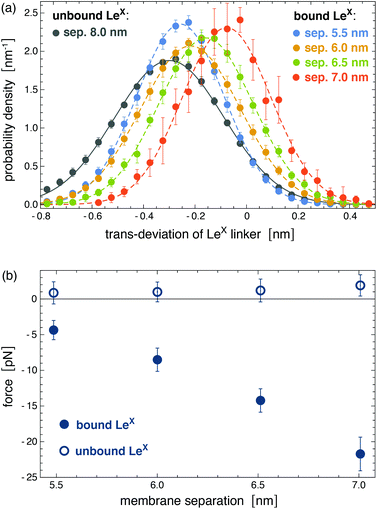 | ||
| Fig. 6 (a) Distributions of trans-deviations of LeX linker groups relative to the surrounding lipids. The trans-deviations are calculated as the difference between the center of mass of the LeX glycolipid linker group (see Fig. 1) and the center of mass of all lipid head groups in the same monolayer as the glycolipid. These trans-deviations of LeX in the direction perpendicular to the membrane plane are determined from the simulation trajectories of the system illustrated in Fig. 3. (b) Forces on bound and unbound LeX glycolipids at the different membrane separations. The trans-deviations and forces of bound glycolipids are obtained from the simulation frames of binding events with a maximum number of at least nc = 5 contacts of non-hydrogen atoms. Deviations to force values obtained for the cutoff nc = 10 are smaller than the error bars. Forces an unbound glycolipids are calculated from simulation frames with zero contacts between the glycolipids. | ||
The forces on bound LeX glycolipids lead to an adhesion pressure between the membranes. Fig. 7 illustrates the adhesion pressure p of membranes that contain 10 mol% of LeX glycolipids as a function of the membrane separation. The adhesion pressure is estimated as p = Pb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f/A where Pb is the probability that a LeX glycolipid is bound at the concentration 10 mol%, f is the average force on the bound glycolipid, and A ≃ 6.5 nm2 is the average membrane area of membrane patch with a single glycolipid at this concentration (see above). The negative pressure values for membrane separations l of 7.0 nm and smaller, at which the glycolipids can bind, indicate membrane attraction. From integration of the pressure profile along the dashed interpolation line shown in Fig. 7, we obtain adhesion energies
f/A where Pb is the probability that a LeX glycolipid is bound at the concentration 10 mol%, f is the average force on the bound glycolipid, and A ≃ 6.5 nm2 is the average membrane area of membrane patch with a single glycolipid at this concentration (see above). The negative pressure values for membrane separations l of 7.0 nm and smaller, at which the glycolipids can bind, indicate membrane attraction. From integration of the pressure profile along the dashed interpolation line shown in Fig. 7, we obtain adhesion energies 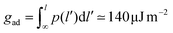 for l = 6.0 nm and gad ≃ 30 μJ m−2 for l = 6.5 nm. These adhesion energies per area agree with values gad = 150 ± 20 μJ m−2 and 28 ± 5 μJ m−2 obtained directly from the binding constants Ktrans at the membrane separations l = 6.0 and 6.5 nm (see above), which indicates that average forces f on bound LeX glycolipids of Fig. 6(b) are consistent with the binding constants Ktrans shown in Fig. 5.
for l = 6.0 nm and gad ≃ 30 μJ m−2 for l = 6.5 nm. These adhesion energies per area agree with values gad = 150 ± 20 μJ m−2 and 28 ± 5 μJ m−2 obtained directly from the binding constants Ktrans at the membrane separations l = 6.0 and 6.5 nm (see above), which indicates that average forces f on bound LeX glycolipids of Fig. 6(b) are consistent with the binding constants Ktrans shown in Fig. 5.
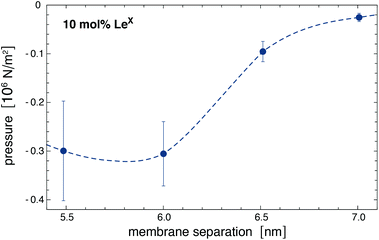 | ||
| Fig. 7 Adhesion pressure p of membranes with 10 mol% of LeX glycolipids obtained for the force values f on bound LeX of Fig. 6(b). The dashed interpolation line is added as a guide for the eye and used to estimate adhesion energies via integration (see text). In this integration, the pressure p is taken to be zero at separations l ≥ 7.5 nm. | ||
Discussion and conclusions
The membranes in our simulation systems are essentially planar because of the small size of the membranes, and because the glycolipid in one monolayer interacts with the glycolipid in the other monolayer across the periodic boundary of the simulation box. In larger, experimental systems, in contrast, the membranes exhibit thermally excited shape fluctuations, which lead to a steric repulsion between adjacent membranes.44 During membrane adhesion, this steric repulsion needs to be overcome by attractive interactions.45 The average separation and thermal roughness of the adhering membranes is determined by the interplay of the attractive interactions and the steric repulsion.46 From neutron scattering experiments of DPPC membrane multilayers that contain 10 mol% of LeX glycolipids,23 an average membrane separation of![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) = 7.7 ± 0.1 nm and a relative membrane roughness of ξ⊥ = 0.73 ± 0.03 nm has been obtained.† Because of the periodicity of the membrane multilayers, the distribution of the local membrane separations l between adjacent membranes can be approximated by the symmetric Gaussian distribution
= 7.7 ± 0.1 nm and a relative membrane roughness of ξ⊥ = 0.73 ± 0.03 nm has been obtained.† Because of the periodicity of the membrane multilayers, the distribution of the local membrane separations l between adjacent membranes can be approximated by the symmetric Gaussian distribution 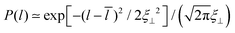 with mean
with mean ![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) and standard deviation ξ⊥. The average membrane separation
and standard deviation ξ⊥. The average membrane separation ![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) obtained from neutron scattering is larger than the membrane separations at which the LeX glycolipids interact in our simulations. Trans-binding of the glycolipids therefore requires local membrane separations of the fluctuating membranes that are smaller than the average separation of the membranes. The average adhesion energy per area of adjacent membranes can be estimated as
obtained from neutron scattering is larger than the membrane separations at which the LeX glycolipids interact in our simulations. Trans-binding of the glycolipids therefore requires local membrane separations of the fluctuating membranes that are smaller than the average separation of the membranes. The average adhesion energy per area of adjacent membranes can be estimated as 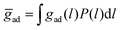 , where gad(l) is the adhesion energy as a function of the local membrane separation l. From the four values of gad(l) at the membrane separations l = 5.5, 6.0, 6.5, and 7.0 nm determined in the section “Interactions of lipid-anchored carbohydrates”, we obtain the estimate ḡad = 7 ± 3 μJ m−2 for the average separation
, where gad(l) is the adhesion energy as a function of the local membrane separation l. From the four values of gad(l) at the membrane separations l = 5.5, 6.0, 6.5, and 7.0 nm determined in the section “Interactions of lipid-anchored carbohydrates”, we obtain the estimate ḡad = 7 ± 3 μJ m−2 for the average separation ![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) and relative membrane roughness ξ⊥ of the neutron scattering experiments. This estimate of the average adhesion energy per area is comparable in magnitude to the adhesion free energy per area of 27 ± 2 μJ m−2 reported for adhering membrane vesicles that contain 10 mol% of LeX glycolipids.20 The LeX glycolipids embedded in the vesicles have the same carbohydrate tip as the LeX glycolipids of the neutron scattering experiments and of our simulations. However, the carbohydrate tip of the vesicle system is connected to a ceramide, which contains a different linker between the carbohydrate tip and the lipid tails. Another difference is that the neutron scattering experiments have been performed at the temperature 60 °C to ensure that the DPPC membranes in these experiments are fluid.23 The LeX glycolipids of our simulations differ from those of the neutron scattering experiments only in the lipid tails. We have focused on POPC membranes and corresponding glycolipid tails to be able to run simulations of fluid membranes at the temperature 30 °C, which is close to the calibration temperature of the force fields. In principle, membrane tension suppresses shape fluctuations of the membranes and can lead to stronger adhesion. However, the suppression of fluctuations occurs only on lateral length scales larger than the characteristic length
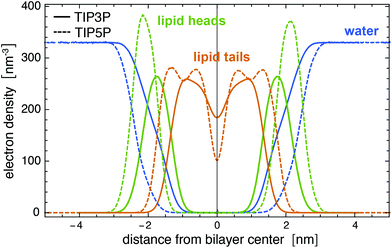
and relative membrane roughness ξ⊥ of the neutron scattering experiments. This estimate of the average adhesion energy per area is comparable in magnitude to the adhesion free energy per area of 27 ± 2 μJ m−2 reported for adhering membrane vesicles that contain 10 mol% of LeX glycolipids.20 The LeX glycolipids embedded in the vesicles have the same carbohydrate tip as the LeX glycolipids of the neutron scattering experiments and of our simulations. However, the carbohydrate tip of the vesicle system is connected to a ceramide, which contains a different linker between the carbohydrate tip and the lipid tails. Another difference is that the neutron scattering experiments have been performed at the temperature 60 °C to ensure that the DPPC membranes in these experiments are fluid.23 The LeX glycolipids of our simulations differ from those of the neutron scattering experiments only in the lipid tails. We have focused on POPC membranes and corresponding glycolipid tails to be able to run simulations of fluid membranes at the temperature 30 °C, which is close to the calibration temperature of the force fields. In principle, membrane tension suppresses shape fluctuations of the membranes and can lead to stronger adhesion. However, the suppression of fluctuations occurs only on lateral length scales larger than the characteristic length 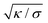 ,47 which adopts values between 100 and 400 nm for typical membrane tensions σ of a few μN m−1 (ref. 48–50) and typical membrane bending rigidities κ between 10 and 40kBT.51,52 These values are significantly larger than the lateral correlation length ξ∥ of membranes adhering via LeX glycolipids, which is only a few nanometers for a relative membrane roughness ξ⊥ of about 0.7 nm.53 On these small length scales, the membrane shape fluctuations are dominated by the bending energy of the membranes and the adhesion energies of the glycolipids, and are not affected by membrane tension.
,47 which adopts values between 100 and 400 nm for typical membrane tensions σ of a few μN m−1 (ref. 48–50) and typical membrane bending rigidities κ between 10 and 40kBT.51,52 These values are significantly larger than the lateral correlation length ξ∥ of membranes adhering via LeX glycolipids, which is only a few nanometers for a relative membrane roughness ξ⊥ of about 0.7 nm.53 On these small length scales, the membrane shape fluctuations are dominated by the bending energy of the membranes and the adhesion energies of the glycolipids, and are not affected by membrane tension.
The fuzzy interactions and comparable magnitude of the association constants of LeX and Lac 2 obtained in our simulations indicate that the interactions of small, neutral carbohydrates such as LeX and Lac 2 are rather generic and not dependent on specific, structural aspects of the carbohydrates. The good agreement to experimental results for the association constant of soluble LeX,36 adhesion energies of membranes with LeX glycolipids,20 and maximally sustained forces of LeX complexes16 suggests that our simulations provide a realistic, detailed picture of weak carbohydrate–carbohydrate interactions in solution as well as in membrane adhesion. The fuzzy binding reduces the loss of rotational and translational entropy of the molecules during binding,40 because binding can occur for a large variety of different relative orientations of the saccharides, in contrast to e.g. binding via specific hydrogen-bond patterns as suggested previously for LeX based on simulations on short timescales up to 40 ns.33,34 The fuzzy binding results from a subtle interplay between the rotational and translational entropy of the saccharides and the van der Waals, hydrogen bond, and hydrophobic interactions of the saccharides in the various binding conformations.
We have investigated the binding of LeX in the absence of Ca2+. Several groups have reported that LeX binding depends on Ca2+,13,14,19–21,54,55 whereas other groups have observed no dependence on Ca2+.16,23 As pointed out by Kunze et al.,21 the Ca2+ concentrations used by most groups are of the order of 10 mM and, thus, greatly beyond physiological Ca2+ concentrations. In vesicle adhesion experiments, Kunze et al.21 observed a rather small increase of the number of bound vesicles for a physiological Ca2+ concentration of 0.9 mM, compared to experiments in the absence of Ca2+. However, a strong increase of the number of bound vesicles in the experiments occurred for a Ca2+ concentration of 10 mM. In atomic force microscopy experiments of LeX unbinding,16 in contrast, the same unbinding force of about 20 ± 4 pN has been obtained both in the absence of Ca2+ and for a Ca2+ concentration of 10 mM. Overall, these experimental results suggest that the binding of LeX is not strongly affected at least by physiological concentrations of Ca2+.
Methods
Simulations of soluble carbohydrates
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 integration time steps of 2 fs with temperature control by a Langevin thermostat57 with collision frequency γ = 1.0 ps−1.
000 integration time steps of 2 fs with temperature control by a Langevin thermostat57 with collision frequency γ = 1.0 ps−1.
Simulations of lipid-anchored saccharides
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MD integration steps of length 2 fs with temperature control by a Langevin thermostat with a collision frequency of 5.0 ps−1.
000 MD integration steps of length 2 fs with temperature control by a Langevin thermostat with a collision frequency of 5.0 ps−1.
 | ||
| Fig. 8 Area per lipid for a Lipid14 POPC membrane in TIP5P water as a function of the scaling factor α for well-depth of the Lennard-Jones interactions between TIP5P water molecule and the lipid head group atoms. The dashed horizontal lines represent the area per lipid values of POPC membranes for Lipid14 in TIP3P water and from experiments.64 The dashed line through the data points is a guide for the eye. Errors or the simulation data are smaller than the point sizes. The error of the experimental value is indicated by they shaded region. The temperature of the simulations and experiments is 30 °C. | ||
 | ||
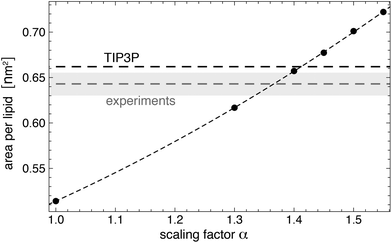
| Fig. 9 Electron density profiles for a Lipid14 POPC membrane in TIP3P and TIP5P water at the temperature 303 K. The membrane is composed of 128 lipids. | ||
Fig. 8 illustrates simulation results for the area per lipid as a function of the scaling factor α. The membranes in these simulations consists of 128 POPC lipids, and the number of water molecules is 6400. For each value of α, we have generated 10 independent trajectories of length 150 ns with semi-isotropic pressure coupling at a membrane tension of zero and a temperature of 303 K using the same barostat and thermostat settings as in the last heating step of the system setup (see above). We have determined the area per lipid from the last 100 ns of these trajectories, with errors calculated as error of the mean of the values for the individual trajectories. The value α = 1.4 leads to an area per lipid in TIP5P simulations that is close to the area per lipid both in TIP3P simulations and in experiments (see Fig. 8). We have therefore used α = 1.4 in our simulations of lipid-anchored saccharides. For this value of α, the density profile of AMBER Lipid14 POPC membranes in TIP5P water (not shown) is practically identical to density profile in TIP3P water, and the membrane thickness dm and lateral diffusion coefficient D of the lipids are identical within errors or close to the values obtained in TIP3P simulations (see Table 2). We have determined the bilayer thickness as the distance between the electron density peaks of the lipid head groups, and the lateral diffusion constant from the relation D = MSD(t)/(4t) where MSD(t) is the mean-squared-displacement of a lipid molecule at time t. To obtain MSD(t), we have first removed the center of mass motion of each leaflet to eliminate the ‘caterpillar effect’67 and have divided our trajectories into 20 ns fragments. We have then calculated MSD(t) from the MSD profiles of single lipids by averaging over all lipids and all trajectory fragments. The diffusion coefficients in Table 2 are calculated from linear fits in the time intervals from t = 10 ns to 20 ns in which MSD(t) approaches a constant slope.
To ensure independence from the initial conformation of the trajectories, we have discarded the first 10% of each trajectory in our calculations of the binding probablity Pb of the two molecules. In analogy to soluble carbohydrates, we have determined Pb and its error as mean and error of the mean of the values for the 10 trajectories at a given membrane separation. The binding constant then follows as Ktrans = APb/(1 − Pb) where A is the membrane area.63 We have calculated the errors of the probability distributions in Fig. 4(a) and 6(a) and of the forces in Fig. 6(b) as error of the mean of the corresponding quantities for the individual trajectories.
Calculation of adhesion free energies from trans-binding constants of membrane-anchored molecules
The binding constant Ktrans of molecules anchored to two apposing membrane surfaces 1 and 2 of area A is related to the on- and off-rate constants of these molecules via| Ktrans = kon/koff | (3) |
| k+ = kon(N1 − n + 1)(N2 − n + 1)/A | (4) |
| k− = nkoff | (5) |
| Pn−1k+ = k−Pn | (6) |
| exp[−ΔGnkBT] = Pn/Pn−1 | (7) |
 | (8) |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support of the International Max Planck Research School (IMPRS) on Multiscale Bio-Systems and by the German Research Foundation (DFG) via Emmy Noether grant SCHN 1396/1 is gratefully acknowledged. We would like to thank Mark Santer for helpful discussions. Open Access funding provided by the Max Planck SocietyReferences
- B. Alberts, A. Johnson, J. Lewis, D. Morgan, M. Raff, K. Roberts, P. Walter, J. Wilson and T. Hunt, Molecular Biology of the Cell, Garland Science, New York, 6th edn, 2014 Search PubMed.
- A. Varki, Nature, 2007, 446, 1023–1029 CrossRef CAS PubMed.
- J. W. Dennis, I. R. Nabi and M. Demetriou, Cell, 2009, 139, 1229–1241 CrossRef PubMed.
- R. L. Schnaar, Arch. Biochem. Biophys., 2004, 426, 163–172 CrossRef CAS PubMed.
- F. T. Liu and G. A. Rabinovich, Nat. Rev. Cancer, 2005, 5, 29–41 CrossRef CAS PubMed.
- J. Arnaud, A. Audfray and A. Imberty, Chem. Soc. Rev., 2013, 42, 4798–4813 RSC.
- A. Varki, Glycobiology, 2017, 27, 3–49 CrossRef CAS PubMed.
- J. Poole, C. J. Day, M. von Itzstein, J. C. Paton and M. P. Jennings, Nat. Rev. Microbiol., 2018, 16, 440–452 CrossRef CAS PubMed.
- I. Eggens, B. Fenderson, T. Toyokuni, B. Dean, M. Stroud and S. Hakomori, J. Biol. Chem., 1989, 264, 9476–9484 CAS.
- N. Kojima, B. A. Fenderson, M. R. Stroud, R. I. Goldberg, R. Habermann, T. Toyokuni and S.-I. Hakomori, Glycoconjugate J., 1994, 11, 238–248 CrossRef CAS PubMed.
- K. Handa, T. Takatani-Nakase, L. Larue, M. P. Stemmler, R. Kemler and S.-I. Hakomori, Biochem. Biophys. Res. Commun., 2007, 358, 247–252 CrossRef CAS PubMed.
- G. N. Misevic, J. Finne and M. M. Burger, J. Biol. Chem., 1987, 262, 5870–5877 CAS.
- J. M. de la Fuente, A. G. Barrientos, T. C. Rojas, J. Rojo, J. Cañada, A. Fernández and S. Penadés, Angew. Chem., Int. Ed., 2001, 40, 2257–2261 CrossRef PubMed.
- M. J. Hernaiz, J. M. de la Fuente, A. G. Barrientos and S. Penades, Angew. Chem., Int. Ed., 2002, 41, 1554–1557 CrossRef CAS PubMed.
- J. M. de la Fuente, P. Eaton, A. G. Barrientos, M. Menendez and S. Penades, J. Am. Chem. Soc., 2005, 127, 6192–6197 CrossRef CAS PubMed.
- C. Tromas, J. Rojo, J. M. de la Fuente, A. G. Barrientos, R. Garcia and S. Penades, Angew. Chem., Int. Ed., 2001, 40, 3052–3055 CrossRef CAS PubMed.
- I. Bucior, S. Scheuring, A. Engel and M. M. Burger, J. Cell Biol., 2004, 165, 529–537 CrossRef CAS PubMed.
- B. Lorenz, L. Álvarez de Cienfuegos, M. Oelkers, E. Kriemen, C. Brand, M. Stephan, E. Sunnick, D. Yüksel, V. Kalsani, K. Kumar, D. B. Werz and A. Janshoff, J. Am. Chem. Soc., 2012, 134, 3326–3329 CrossRef CAS PubMed.
- H. Witt, F. Savic, M. Oelkers, S. I. Awan, D. B. Werz, B. Geil and A. Janshoff, Biophys. J., 2016, 110, 1582–1592 CrossRef CAS PubMed.
- C. Gourier, F. Pincet, E. Perez, Y. M. Zhang, Z. Y. Zhu, J. M. Mallet and P. Sinay, Angew. Chem., Int. Ed., 2005, 44, 1683–1687 CrossRef CAS PubMed.
- A. Kunze, M. Bally, F. Höök and G. Larson, Sci. Rep., 2013, 3, 1452 CrossRef PubMed.
- Z. W. Yu, T. L. Calvert and D. Leckband, Biochemistry, 1998, 37, 1540–1550 CrossRef CAS PubMed.
- E. Schneck, B. Deme, C. Gege and M. Tanaka, Biophys. J., 2011, 100, 2151–2159 CrossRef CAS PubMed.
- V. M. Latza, B. Deme and E. Schneck, Biophys. J., 2020, 118, 1602–1611 CrossRef CAS PubMed.
- C. J. Day, E. N. Tran, E. A. Semchenko, G. Tram, L. E. Hartley-Tassell, P. S. K. Ng, R. M. King, R. Ulanovsky, S. McAtamney, M. A. Apicella, J. Tiralongo, R. Morona, V. Korolik and M. P. Jennings, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E7266–E7275 CrossRef CAS PubMed.
- Y. Yu, T. Tyrikos-Ergas, Y. Zhu, G. Fittolani, V. Bordoni, A. Singhal, R. J. Fair, A. Grafmueller, P. H. Seeberger and M. Delbianco, Angew. Chem., Int. Ed., 2019, 58, 13127–13132 CrossRef CAS PubMed.
- F. Pincet, T. Le Bouar, Y. M. Zhang, J. Esnault, J. M. Mallet, E. Perez and P. Sinay, Biophys. J., 2001, 80, 1354–1358 CrossRef CAS PubMed.
- T. R. Patel, S. E. Harding, A. Ebringerova, M. Deszczynski, Z. Hromadkova, A. Togola, B. S. Paulsen, G. A. Morris and A. J. Rowe, Biophys. J., 2007, 93, 741–749 CrossRef CAS PubMed.
- M. F. Schneider, G. Mathe, M. Tanaka, C. Gege and R. R. Schmidt, J. Phys. Chem. B, 2001, 105, 5178–5185 CrossRef CAS.
- J. Sauter and A. Grafmüller, J. Chem. Theory Comput., 2016, 12, 4375–4384 CrossRef CAS PubMed.
- W. K. Lay, M. S. Miller and A. H. Elcock, J. Chem. Theory Comput., 2016, 12, 1401–1407 CrossRef CAS PubMed.
- R. J. Woods, Chem. Rev., 2018, 118, 8005–8024 CrossRef CAS PubMed.
- C. Gourmala, Y. Luo, F. Barbault, Y. Zhang, S. Ghalem, F. Maurel and B. Fan, J. Mol. Struct.: THEOCHEM, 2007, 821, 22–29 CrossRef CAS.
- Y. Luo, F. Barbault, C. Gourmala, Y. Zhang, F. Maurel, Y. Hu and B. T. Fan, J. Mol. Model., 2008, 14, 901–910 CrossRef CAS PubMed.
- J. I. Santos, A. Carvalho de Souza, F. J. Cañada, S. Martín-Santamaría, J. P. Kamerling and J. Jiménez-Barbero, ChemBioChem, 2009, 10, 511–519 CrossRef CAS PubMed.
- J. M. de la Fuente and S. Penades, Glycoconjugate J., 2004, 21, 149–163 CrossRef CAS PubMed.
- J. Sauter and A. Grafmüller, J. Chem. Theory Comput., 2015, 11, 1765–1774 CrossRef CAS PubMed.
- R. Salomon-Ferrer, A. W. Goetz, D. Poole, S. Le Grand and R. C. Walker, J. Chem. Theory Comput., 2013, 9, 3878–3888 CrossRef CAS PubMed.
- S. Le Grand, A. W. Goetz and R. C. Walker, Comput. Phys. Commun., 2013, 184, 374–380 CrossRef CAS.
- P. Tompa and M. Fuxreiter, Trends Biochem. Sci., 2008, 33, 2–8 CrossRef CAS PubMed.
- V. N. Uversky and A. K. Dunker, Anal. Chem., 2012, 84, 2096–2104 CrossRef CAS PubMed.
- K. N. Kirschner, A. B. Yongye, S. M. Tschampel, J. Gonzalez-Outeirino, C. R. Daniels, B. L. Foley and R. J. Woods, J. Comput. Chem., 2008, 29, 622–655 CrossRef CAS PubMed.
- C. J. Dickson, B. D. Madej, A. A. Skjevik, R. M. Betz, K. Teigen, I. R. Gould and R. C. Walker, J. Chem. Theory Comput., 2014, 10, 865–879 CrossRef CAS PubMed.
- W. Helfrich, Z. Naturforsch., A: Phys., Phys. Chem., Kosmophys., 1978, 33, 305–315 Search PubMed.
- R. Lipowsky and S. Leibler, Phys. Rev. Lett., 1986, 56, 2541–2544 CrossRef CAS PubMed.
- J. Steinkühler, B. Rozycki, C. Alvey, R. Lipowsky, T. R. Weikl, R. Dimova and D. E. Discher, J. Cell Sci., 2019, 132, jcs216770 CrossRef PubMed.
- T. R. Weikl, Annu. Rev. Phys. Chem., 2018, 69, 521–539 CrossRef CAS PubMed.
- R. Simson, E. Wallraff, J. Faix, J. Niewohner, G. Gerisch and E. Sackmann, Biophys. J., 1998, 74, 514–522 CrossRef CAS.
- G. Popescu, T. Ikeda, K. Goda, C. A. Best-Popescu, M. Laposata, S. Manley, R. R. Dasari, K. Badizadegan and M. S. Feld, Phys. Rev. Lett., 2006, 97, 218101 CrossRef PubMed.
- T. Betz, M. Lenz, J.-F. Joanny and C. Sykes, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15320–15325 CrossRef CAS PubMed.
- J. F. Nagle, Faraday Discuss., 2013, 161, 11–29 RSC.
- R. Dimova, Adv. Colloid Interface Sci., 2014, 208, 225–234 CrossRef CAS PubMed.
- G.-K. Xu, J. Hu, R. Lipowsky and T. R. Weikl, J. Chem. Phys., 2015, 143, 243136 CrossRef PubMed.
- A. Geyer, C. Gege and R. R. Schmidt, Angew. Chem., Int. Ed., 2000, 39, 3246 CrossRef CAS.
- G. Nodet, L. Poggi, D. Abergel, C. Gourmala, D. Dong, Y. Zhang, J.-M. Mallet and G. Bodenhausen, J. Am. Chem. Soc., 2007, 129, 9080–9085 CrossRef CAS PubMed.
- Woods Group, GLYCAM Web, Complex Carbohydrate Research Center, University of Georgia, Athens, GA, 2005–2020, http://glycam.org.
- R. Salomon-Ferrer, D. A. Case and R. C. Walker, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 198–210 CAS.
- M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Oxford University Press, 2017 Search PubMed.
- S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962 CrossRef CAS.
- J.-P. Ryckaert, G. Ciccotti and H. J. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- J. Hu, R. Lipowsky and T. R. Weikl, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15283–15288 CrossRef CAS PubMed.
- N. Kucerka, M.-P. Nieh and J. Katsaras, Biochim. Biophys. Acta, Biomembr., 2011, 1808, 2761–2771 CrossRef CAS PubMed.
- S. Jo, T. Kim, V. G. Iyer and W. Im, J. Comput. Chem., 2008, 29, 1859–1865 CrossRef CAS PubMed.
- H. J. Berendsen, J. v. Postma, W. F. van Gunsteren, A. DiNola and J. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- C. Anezo, A. H. de Vries, H. D. Holtje, D. P. Tieleman and S. J. Marrink, J. Phys. Chem. B, 2003, 107, 9424–9433 CrossRef CAS.
- N. Kucerka, S. Tristram-Nagle and J. F. Nagle, J. Membr. Biol., 2005, 208, 193–202 CrossRef CAS PubMed.
- A. Filippov, G. Oradd and G. Lindblom, Langmuir, 2003, 19, 6397–6400 CrossRef CAS.
- T. Morishita, J. Chem. Phys., 2000, 113, 2976–2982 CrossRef CAS.
Footnote |
† The relative membrane roughness follows from eqn (2) of ref. 23 as 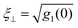 with parameter values given in Table 2. Here, g1(r) is the membrane displacement correlation function of adjacent membranes in the multilayer. with parameter values given in Table 2. Here, g1(r) is the membrane displacement correlation function of adjacent membranes in the multilayer. |
| This journal is © The Royal Society of Chemistry 2020 |