Dynamic single-molecule counting for the quantification and optimization of nanoparticle functionalization protocols

Abstract

Applications of colloidal particles in the fields of i.e. biosensors, molecular targeting, or drug-delivery require their functionalization with biologically active and specific molecular ligands. Functionalization protocols often result in a heterogeneous population of particles with a varying density, spatial distribution and orientation of the functional groups on the particle surface. A lack of methods to directly resolve these molecular properties of the particle's surface hampers optimization of functionalization protocols and applications. Here quantitative single-molecule interaction kinetics is used to count the number of ligands on the surface of hundreds of individual nanoparticles simultaneously. By analyzing the waiting-time between single-molecule binding events we quantify the particle functionalization both accurately and precisely for a large range of ligand densities. We observe significant particle-to-particle differences in functionalization which are dominated by the particle-size distribution for high molecular densities, but are substantially broadened for sparsely functionalized particles. From time-dependent studies we find that ligand reorganization on long timescales drastically reduces this heterogeneity, a process that has remained hidden up to now in ensemble-averaged studies. The quantitative single-molecule counting therefore provides a direct route to quantification and optimization of coupling protocols towards molecularly controlled colloidal interfaces.

---

Introduction

Nano- and micro-sized particles proved themselves as versatile probes in bioscience enabling targeting and visualization of specific cellular structures,¹ drug delivery,² or even single-molecule sensing.³ Particularly plasmonic nanoparticles receive attention due to their tunable optical properties,⁴ the ability to photothermally heat the particle and release e.g. DNA,^5,6 and their biocompatibility upon functionalization.⁷ The kinetic response and specificity in these applications is governed by the functionalization of the particle surface with specific biomolecules. In a typical coupling protocol the particles are mixed with the bio-active molecules at specific chemical conditions.^8,9 It is however statistically unlikely that such chemical conjugation protocols result in a homogeneous population of particles each with the same number or density of functional groups (Fig. 1a). In addition to the variation in the number of functional groups expected from Poisson statistics, additional heterogeneity may be present due to limitations in the functionalization protocol. These particle-to-particle variations may impair the performance of the functionalized particles, wherein e.g. the affinity of a particle for a membrane or the kinetic response of a biosensor depend sensitively on the number of receptors on the particle surface.

Fig. 1 (a) Functionalization of nanoparticles leads to a distribution of bio-active molecules on the surface of the particle, each particle exhibiting a different number of functional groups. (b) After functionalization the particles are immobilized to allow for quantitative single-molecule counting using DNA-hybridization kinetics. Herein a fluorescently labelled imager strand reversibly binds to the docking strands on the particle. (c) Using a wide-field fluorescence microscope, each single-molecule hybridization event causes a fluorescent burst. Temporal analysis of the bursts reveals the number of functional groups on each individual particle.

Common methods to characterize particle-functionalization, however, have relied on ensemble averaged results, where underlying particle-to-particle heterogeneities remain hidden. The kinetics of ligand functionalization and corresponding ligand density are routinely characterized using i.e. differential centrifugal sedimentation,^10,11 mass spectrometry,¹² dynamic-light scattering,^10,13,14 and fluorescence assays.^15–18 The charge of the interfacial layer on the other hand has been determined using zeta-potential measurements^10,13 whereas XPS provides compositional information.^14,19–21 These ensemble techniques have proven extremely useful to get insight into biomolecular functionalization processes for numerous particle sizes, shapes and materials. However, emerging single-particle applications desire a detailed description and control of the biomolecular layer on the surface of particles. To gain access to particle-to-particle differences the sample needs to be analyzed at the single-particle level²² while studying many particles simultaneously is crucial to obtain statistics.

Characterization of biomolecular functionalization at the single particle level has been reported using electron microscopy^23,24 due to its high spatial-resolution. Electron microscopy however suffers from a low contrast when imaging biomolecules²⁵ unless they are labeled using e.g. metallic particles.²³ Recently, Eller et al.²⁶ directly determined the ligand loading on individual gold nanoparticles using a secondary ion mass spectroscopy, and found that the relative DNA loading depends on the particle geometry. Our previous study²⁷ probed plasmon shifts in response to particle functionalization and highlighted the importance of particle-to-particle differences in the kinetics of ssDNA binding to gold nanoparticles. The mentioned methods however either rely on complex instrumentation, do not enable in situ characterization, or provide relative loading densities instead of an absolute count of the number of ligands.

Quantitative counting of individual molecules was accomplished by fluorescent labeling and subsequent monitoring of single-molecule photobleaching steps directly after the laser illumination had been applied.^28,29 The method is however limited to particles with a low number of functional groups because single-molecule photobleaching steps should exceed the shotnoise on the total fluorescence signal. Stochastic optical reconstruction microscopy (STORM) localizes fluorescence bursts from single molecules that get activated and then bleach, and has been used to study the spatial distribution,^30,31 and density³² of ligands. The localization precision of ∼10 nm however puts a limit on the maximum density of ligands, and as a result localization microscopy is also limited to low molecular densities. The dynamic range can be extended up to several hundreds of ligands by counting the frequency of blinking events,^33,34 but this is difficult to quantitate and easily results in overcounting (due to multiple blinks from the same molecule) or undercounting (due to rapid photobleaching). Quantitative single-molecule counting on the other hand has been pioneered by Jungmann who used it to count the number of binding sites on DNA origami structures,³⁵ and was later applied to count the number of sites on large polystyrene beads.³⁶

Here we use such quantitative single-molecule counting to guide functionalization protocols of nanometer size plasmonic particles at the single-particle and single-molecule level (Fig. 1b and c). This method is accurate for a large range of functionalization densities and does not suffer from blinking and bleaching.³⁷ We use a stochastic model to predict the precision and accuracy of counting, and demonstrate the method by counting the number of DNA strands on single gold nanoparticles across several orders of magnitude. Although we use gold colloidal nanoparticles, the method proposed here can be in principle applied on particles of any size, shape or material. Since the recorded signal relies on the transient re-binding of a fluorescently labelled ligand, the only requirement is that the particles can be functionalized with a receptor that exhibits a reversible interaction with its ligand. We compare particle-to-particle variations in the number of functional groups for different functionalization conditions, and we find that protocols reported in literature yield fast functionalization but with larger than expected particle-to-particle differences. Ligand reorganization over timescales of several hours is needed to reach a state in which particle-to-particle variations are limited by Poisson statistics. The method we present provides a quantitative measure of the number and heterogeneity of functional groups and is a promising avenue to optimize particle-functionalization protocols at the single-particle and single-molecule level.

Methods

The method is based on quantitative PAINT (qPAINT), which was originally developed to count the number of docking strands on DNA origami structures.³⁵ We apply this method to DNA-functionalized single crystalline gold nanoparticles because they are extensively used for biosensing^3,38,39 and drug delivery.⁴⁰ We first spin-coat the particles onto a thiolated glass coverslip at low surface coverage, see Fig. 1b, and insert the sample in a flow cell. Subsequently we functionalize the particles with thiolated ssDNA docking strands of 30 nucleotides using a protocol at low pH.^16,17 The docking strands are mixed with short 10 nt antifouling ssDNA strands at varying fractions to provide control over the average number of docking strands per particle. The flow cell is then inserted into an inverted wide-field optical microscope (Nikon Ti) equipped with an oil-immersive objective (Nikon Apo TIRF 100× Oil DIC N2). We excite the sample using objective-type total internal reflection, collect the emitted light with the same objective, and send the wide-field image to an EMCCD camera (Andor DU-888 X-9414). A typical field of view is shown in Fig. 2a where individual diffraction limited spots correspond to either single particles or clusters.

Fig. 2 (a) Typical field of view where each diffraction limited spot corresponds to one-photon luminescence from individual nanoparticles or clusters. Scalebar is 30 μm. (b) Scattering spectra of a typical nanoparticle measured using hyperspectral microscopy. The solid line shows a fit with a single Lorentzian corresponding to a single nanorod. (c) Fluorescence intensity timetrace of the blue square ROI indicated in (a). (d) Bursts above a threshold level (dashed line) are detected, taking into account intermittent dark frames due to blinking. The red arrows indicate examples of two events that ire identified. (e) Individual events are localized, allowing us to identify events that occurred on the particle and events that occurred on the coverslip away from the particle. (f) The dark-time between events is extracted from the timetrace (events away from the particle are discarded). The distribution of dark-times is fitted with a single-exponential yielding the mean dark-time for each particle in the field of view.

To distinguish single nanoparticles from clusters we record scattering spectra of the nanoparticles using hyperspectral microscopy.^27,41 We illuminate the particles through the objective with a white-light beam (Energetiq) and record wide-field images of the scattered intensity for a set of band-pass filters. Fig. 2b shows an example of such a scattering spectrum for a single nanoparticle. Clusters are identified based on their non-Lorentzian lineshape and broad linewidth, and they are subsequently discarded from further analysis.

After identification of the single particles in the field of view we introduce the imager strand (9 nt complementarity, in PBS with additional 500 mM NaCl) in the flow cell using a syringe pump and excite the ATTO647N label using a 637 nm fiber-coupled laser (intensity in the focal plane ∼ 1900 W cm⁻²). The emission spectrum of ATTO647N (see ESI†) is detuned by nearly 100 nm to the blue of the longitudinal plasmon of the used gold nanorods to reduce plasmon–fluorophore coupling and minimize the ensuing mislocalization.^42–45 We record movies at 20 fps for at least 40 minutes. Transient hybridization of the imager strand to the docking strand on the particle results in bursts of fluorescence, a typical timetrace is shown in Fig. 2c.

To identify binding events we threshold the timetrace (see Fig. 2d). In a small fraction of events the detected intensity fluctuates during an event, possibly due to blinking or reorientation of the fluorophore in the polarized excitation beam. These phenomena are corrected for (see ESI†) to ensure such cases are treated as a single event. We then localize each event (see ESI†) to identify whether it occurred near the particle, or on the substrate away from the particle (see Fig. 2e). To achieve this we first subtract the one-photon luminescence (1PL) background originating from the particle and fit the resulting point-spread-function with a 2D Gaussian using the maximum likelihood estimation method.⁴⁶ The obtained localizations are drift corrected using fiducial markers (particles with a strong 1PL signal), allowing for reconstruction of the particle geometry and identification of events that occurred away from the particle that were discarded from further analysis. Note that this filtering of events based on localization is only possible because we employ a fluorophore with an emission that is blue-shifted from the plasmon resonance, resulting in minimal mislocalization.^43,47–50

After this process we have obtained a list of events with different start- and bright-times (τ_b). The number of hybridizations per unit time scales with the number of docking strands per particle, and this can be quantified in two ways, namely (1) by statistically analyzing the total number of detected fluorescence bursts, or (2) by analyzing the distribution of dark times between the bursts. Which approach is most accurate is not a-priori clear, so we performed stochastic simulations to choose the optimum experimental parameters and quantification method. We simulated the binding and unbinding of the imager strand as a random sequential process in which the waiting time until binding (the dark time, or τ_d) and unbinding (the bright time, or τ_b) are both governed by Poisson statistics and thus exponentially distributed. This allows us to generate a timetrace for each docking strand present on a particle, and the response of the particle as a whole then follows from the sum of all N (independent) docking strands.

To investigate the degree of quantification we introduce the concept of counting precision and counting accuracy. If the number of binding sites on a single particle is estimated n times by independent experiments, the counting precision describes the spread of these estimates around its mean value N̄, commonly expressed in terms of a standard deviation σ_N. The counting precision is then essentially determined by the number of events detected on a particle, so for method (1) the number of detected fluorescence bursts, and for method (2) the number of detected dark times.

The counting accuracy describes to what degree the mean estimated number of sites N̄ deviates from the true number of sites N. These deviations mainly arise when binding events overlap in time, resulting in undercounting. These counting inaccuracies are given by ΔN = N̄ − N. We analyze the counting precision and accuracy as a function of the ratio between mean dark- and bright times τ_d/τ_b, which can be expressed in the experimental parameters as

where k_off, k_on, and c_img are the imager strand's dissociation rate, association rate, and concentration, respectively. This ratio between dark- and bright times can be experimentally tuned by simply changing the imager strand concentration.

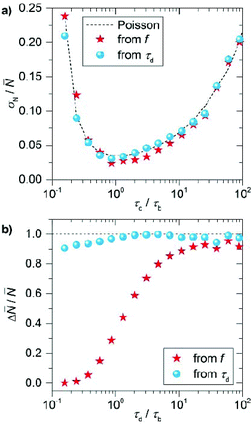
In Fig. 3a we plot the normalized counting precision (coefficient of variation), where we observe a low precision for low and high τ_d/τ_b ratios with an optimum at τ_d/τ_b ∼ 1. For large ratios the number of events per timetrace is limited (e.g. due to a low c_img), resulting in unprecise counting. For small ratios on the other hand, the large binding frequency results in a fraction of events overlapping in time. This cannot be identified reliably in an experiment, resulting in missed events and thus a reduced total number of events per timetrace for decreasing ratios. The normalized counting precision scales nearly identically for both quantification methods, confirming that the precision is indeed dominated by the (Poissonian) counting statistics. These results indicate that a measurement time of 40 minutes results in a maximum counting precision of σ_N/N̄ = 0.04, which can evidently be further improved by increasing the measurement time.

Fig. 3 Simulated normalized precision (a) and accuracy (b) extracted from stochastic simulations of timetraces with a duration of 45 minutes, a camera framerate of 20 Hz, association rate k_on = 2.3 × 10⁶ M⁻¹ s⁻¹ and dissociation rate k_off = 1.6 s⁻¹. The precision and accuracy are extracted from 100 simulations performed using these input parameters.

For the counting accuracy however we find a large difference between the two methods. Quantification by the frequency of events produces consistent undercounting because each double event affects this frequency. The probability of double events is low (but not zero) at high τ_d/τ_b ratios, producing less than 10% deviation in the number of counted sites, but the accuracy substantially decreases for τ_d/τ_b < 10 due to the increased probability of double events. When the mean dark time is considered the counting accuracy is substantially higher over a larger range of τ_d/τ_b because double events reduce the number of detected dark times (as captured by σ_N) but do not affect their mean. So although the counting precision reduces when a substantial number of events overlap, the counting accuracy is robust against double events. The deviation of this behavior for τ_d/τ_b < 1 observed in Fig. 3b is caused by the finite camera frame rate (20 fps), which results in overestimation of the dark time and thus undercounting for short dark times.

These stochastic simulations provide guidelines on for the experimental design, and will allow us to quantify the effects of the (intrinsically limited) number of events on the counting precision and accuracy. Based on these simulations we performed the experiments at an imager concentration c_img that leads to τ_d/τ_b ∼ 20 (for our imager k_on ∼ 2.3 × 10⁶ M⁻¹ s⁻¹ and k_off ∼ 1.6 s⁻¹).³⁷ This corresponds to imager strand concentrations ranging from 50 pM to 3 nM depending on the expected mean number of docking strands. Although the counting precision could be further improved by working at lower ratios (Fig. 3a), we will see below that the particle-to-particle variations are dominated by other factors.

From the experimental data in Fig. 2 we then finally construct a histogram of all dark times between individual binding events for each single nanoparticle, and fit the histogram with an exponential distribution (Fig. 2f). The mean dark-time can then be related to the number of docking strands on the particle using eqn (1).

Results

Efficient suppression of non-specific interactions with both the particle and the nearby substrate are crucial to achieve accurate counting. The results in Fig. 2e illustrate that imager strands bind dominantly to the functionalized nanorods with minimal non-specific binding to the glass coverslip. To ensure that the fluorescent bursts we observe are due to specific hybridization between the docking and the imager strands (rather than non-specific binding of the imager strand with the particle) we performed control experiments on nanoparticles functionalized with a mismatched docking strand. Only very few molecular events are detected corresponding that are mostly localized away from the particle and are thus caused by non-specific binding to the coverslip (see ESI†). To further conclude if the signals in Fig. 2c are due to specific interactions we determined the dissociation rate of the DNA hybridization (see ESI†) and we find a mean bright time of τ_b = 0.6 ± 0.3 s corresponding to the mean dissociation rate of k_off = 2.2 ± 1.0 s⁻¹ matching well with the literature for this sequence.³⁷ These observations indicate that interference from non-specific interactions after localization filtering is minimal.

We then measured the number of docking strands per particle after functionalization with a low pH protocol reported in literature.^16,17 This protocol was reported to yield near-instantaneous and quantitative conjugation of DNA. We varied the time of incubation of a 5 μM solution of 30 nt thiolated docking strand in citric acid buffer, and afterward we back-filled the DNA coating using a 5 μM solution of 10 nt thiolated strands (Fig. 1b). Histograms of the distribution of the number of docking strands per particle are shown as histograms on a log–log scale in Fig. 4 (see ESI for reproducibility studies†). For short incubation times of a few seconds we find very heterogeneous functionalization, where the number of docking strands ranges from zero to two hundred per particle. However, as the ssDNA functionalization progresses by an extension of the incubation time we find only a slight increase in the maximum number of binding sites but a significant reduction in the heterogeneity.

Fig. 4 (a) Suppression of heterogeneity in particle functionalization by prolonging the incubation time. The grey shaded areas are the expected distributions based on the contributions due to the particle size-distribution, and the random nature of the ssDNA functionalization. In (b) these two contributions are disentangled, showing that at low numbers of sites the contribution due to the Poisson distributed number of strands for equally sized particles dominates, whereas for larger mean numbers of strands the heterogeneity is dominated by the particle-size distribution.

This suggests that individual particles undergo a vastly different rate of functionalization, but that the number of ssDNA converges at timescales of a few hundred seconds. This is in agreement with our previous study where we probed plasmon shifts to study the kinetics of ssDNA coating, where we indeed found a large range of initial functionalization rates.²⁷ For longer incubation times the protocol reaches a plateau at 180 ± 77 binding sites per particle with strongly reduced particle-to-particle differences.

Prior to the discovery of the “low pH” method dense coatings of thiolated ssDNA on gold nanoparticles were conventionally achieved using the so-called salt-aging method,^15,51,52 in which the electrostatic repulsion due to the negative charges on the gold particles and the ssDNA is gradually reduced by stepwise addition of salt over 1 or 2 days. In the ESI (Section S7†) we investigated the number of binding sites on individual nanorods coupled by the salt-aging protocol. We find a similar mean docking density, however the heterogeneity of the salt-aging functionalization increased by a factor 2 compared to the low pH coupling.

The single particle approach gives crucial information on the particle-to-particle differences in the number of docking strands. The underlying sources of heterogeneity can be quantified by the total variance of a measured distribution σ_tot², which can be rewritten as a sum of individual contributions as σ_tot² = σ_parts² + σ_Poisson² + σ_counting², where σ_parts² represents a variance due to the underlying size distribution of the particles, σ_Poisson² stands for the intrinsic variation due to the randomized number of strands per particle following Poisson statistics. The factor σ_counting² represents the counting error due to a finite number of detected events, which we neglect in this analysis because under our optimized conditions it is substantially smaller than the other contributions. Assuming normally distributed variables is a convenient approximation although we note that e.g. the Poissonian contribution only approximates a normal one for large values of N. The particle size distribution is well approximated by a normal distribution, whereas the residual heterogeneity can in principle have any distribution function. Nevertheless, this approximation allows us to conveniently disentangle the different contributions to the heterogeneity, and any heterogeneity beyond the expected σ_tot is due to sub-optimal functionalization protocols.

The contributions from σ_pcles² and σ_Poisson² can be estimated a-priori. The latter can be expressed as σ_Poisson² = N, and is dominant over σ_pcles² for low values of N. For high values of N the term σ_pcles² dominates, which we estimate by assuming a ssDNA docking strand footprint of ∼16 nm² using a conical representation of the ligand¹⁵ (see ESI†). Further we measured the exact dimensions of the nanorods using TEM (see ESI†), to obtain the maximum number of docking strands per particle and its standard deviation of N_max = 338 ± 85(N ± σ). For one hour of incubation we find in our experiments that N_max = 180 ± 77 and find that our particles load approximately to half of the theoretical prediction. This moderate mismatch is possibly caused by steric effects and electrostatic repulsion between randomly absorbed ssDNA strands hindering close-packed functionalization. Comparing the estimated spread to the experimental results (Fig. 4) we find a drastically broadened distribution compared to our expectations for short incubation times. For the 3 seconds incubation time the spread in the number of binding sites is ∼5 fold higher than expected. We attribute this, in concert with our previous study, to a heterogeneous binding rate²⁷ caused by particle-to-particle differences in the zeta-potential,⁵³ or possible remaining CTAB residuals.

Many applications will benefit from precise control over the number of receptors on the particles because the kinetics of a particle-based sensor depends on the number of functional groups,^54,55 and in nanomedicine applications the specificity and efficiency of delivery relies on matching the receptor density on the particle with the one on the cell membrane. Controlling the number of receptors is often done by mixing in a second ligand that functions as a spacer, where it is assumed that the number of receptors on each particle is proportional to the mixing fraction. To verify this simple extrapolation for DNA-functionalized particles we varied the density of docking strands by employing a mixture with a short antifouling strand at varying fractions. We then count the number of docking strands on each individual particle after 1 hour of functionalization. The results are shown in Fig. 5a, where we observe that for a high fraction of docking strands the number of receptors per particle indeed follows the expected linear trend. However for low fractions of docking strand we find a significant broadening of the distribution, and a deviation from the linear scaling. Moreover, the particle-to-particle differences are amplified at low fractions of docking strand.

Fig. 5 (a) Controlling the number of functionalized docking strands. The black solid line corresponds to a slope of 1. (b) Incubation series using 1% docking solution. The black arrow corresponds to the theoretical prediction based on our model.

To rule out a possible contribution of non-specific interactions in the experiments with a low fraction of docking strand, we also performed a control measurement in which we functionalize the nanoparticles with only 10 nt antifouling strands without any docking strands. Non-specific interactions contribute a mean of 0.4 docking strands per particle, with the majority of particles showing nearly no events at all, see Fig. 5a (the contribution of non-specific events is marked by the shaded area).

To identify the origin of this non-linearity we incubated the samples with a 1% fraction of docking strand and vary the incubation time (Fig. 5b). The data for very short incubation time of 10 seconds shows a very broad distribution, mainly due to the contribution of non-specific interactions indicated by the shaded area. A general trend can be observed in Fig. 5b where the maximum number of docking strands is reached in approximately one hour (N̄ = 20), when the functionalization is also most heterogeneous. A further increase in the incubation time surprisingly reveals a slow decrease in the mean number of binding sites while also the heterogeneity decreases. For the longest measured incubation time of five days we find an almost 4× reduction in the mean number of binding sites to N̄ = 5, and a nearly 10-fold reduction in the heterogeneity compared to 1 hour of incubation. Interestingly, for these long incubation times the counted number of binding sites approaches a plateau that is very close to the theoretically predicted number of sites based on the average particle dimensions and DNA footprint (marked by the black arrow in Fig. 5b).

We hypothesize that three mechanisms might be at play that cause the observed trends in Fig. 5: (i) DNA release from the particle, (ii) ligand exchange of 30 nt docking strand with 10 nt strands, or (iii) ligand reorganization. The first contributor can be ruled out based on the timescale of our incubation because earlier studies concerning release of thiolated ssDNA from the surface of gold nanospheres reported unbinding of only ∼1.5% of ssDNA at room temperature per day.⁵⁶ We observe a substantially greater reduction, ruling out the thiol release as the main mechanism to the gradual reduction in the number of counted docking strands.

To check mechanism (ii) the ligand exchange we incubated the samples with 1% docking strand for one hour, subsequently washed them to remove the residual unbound DNA and left particles in pure citric acid buffer for two days. In Fig. 6a we show the obtained results (green distribution) and compare them directly to samples incubated for 1 hour (pink) and two continuous days (cyan). In agreement with Fig. 5 we again observe a decrease in the mean number of binding sites compared to a 1 hour incubation. The results for a 2 day incubation in the DNA, and a 1 hour incubation in DNA followed by a 2 day incubation in buffer show similarly heterogeneous distributions. This allows us to conclude that ligand exchange is not the dominant effect because the sample aged in the pure citric acid buffer for two days has negligible residual ligands present in the pure buffer solution. This is further confirmed by results for 100% docking strand functionalization (see ESI†), where we observe the same trends in the measured data.

Fig. 6 (a) Ligand reorganization evidenced by the incubation of samples in DNA solutions with 1% docking strand for 2 days, and in DNA solution for 1 hour followed by incubation in buffer for 2 days. (b) Cartoon showing the emerging picture of ligand reorganization that follows from quantitative single-molecule counting.

Ligand reorganization is therefore the dominant factor, where we hypothesize that desorption of non-specifically bound docking strand combined with rearrangement of thiol-bound docking strand are at play, illustrated in Fig. 6b. The timescales on which this behavior is observed is in good agreement with the timescales involved in formation of self-assembled monolayers on metals, where slow diffusion and rearrangement of thiol-bound ligands leads to reorganization of molecular layers.¹⁹ The rearrangement may therefore include such diffusion of interface Au atoms with a ssDNA attached to it, but may also involve changes in accessibility of the docking strand for hybridization with imager strands. We note that ligand reorganization was observed before on gold nanorods,³¹ but these experiments were performed in air resulting in initial collapse and thermally induced regeneration of the particle coating. The current experiments provide a direct quantification in aqueous media that is often used in biomedical devices, and thus provides a method to optimize the number of ligands per particle for applications such as sensing and drug-delivery.

The future combination with super-resolution localization microscopy is attractive because it will provide insight into the distribution of receptors on the surface of the particle, and may facilitate the development of functionalization protocols that provide control over receptor location. Such localization microscopy has already been applied to large (micron-sized) polystyrene spheres³⁶ and has revealed that e.g. microswimmers are propelled due to an anisotropic distribution of enzymes on their surface,³⁴ and heterogeneous protein absorption over-time leads to largely different protein coronas compositions between individual particles related to the surface chemistry and degradability of the studied particles.³³ For nano-sized particles, and particularly plasmonic ones, the use of localization microscopy will require further development of the technology to correct for mislocalizations induced by plasmon–fluorophore coupling. Although for fluorophores that are blue-shifted by >100 nm from the plasmon resonance the mislocalization is limited to ∼5 nm,^43,47–50 a general approach to resolve functional groups on metallic particles will require a refined method to correct for mislocalization that accounts for the spectral properties of dye and particle, and their relative position. Although complex, this will provide the attractive opportunity to obtain the true location of the functional group and characterize the molecular composition of particle coatings at the single-molecule level, and may even enable the tracking of single functional groups during the slow ligand reorganization that we observed.

Conclusions

We directly counted the number of binding sites on individual single nanoparticles in aqueous solution using stochastic single-molecule interactions. For a typical measurement time of 40 minutes the method exhibits a counting precision better than 5% with a near-unity counting accuracy for a large range of functionalization densities. Statistical analysis of the interaction kinetics indicated that the particle-to-particle differences we observe are dominated by the particle-size distribution for large particle sizes, but are substantially broadened for short incubation times and for low fractions of functional groups in a mixed monolayer coating. The residual contribution to the heterogeneity was minimized by extending the incubation time. The underlying mechanism points toward ligand reorganization over timescales of several hours to days before the coating reaches a state in which the particle-to-particle variations are limited by Poisson statistics. The methodology presented here enables quantification and optimization of coupling protocols in solution, and opens the window to obtaining molecular control over functionalization protocols for particle-based biosensors and drug-delivery vehicles.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

P.Z. acknowledges financial support from The Netherlands Organisation for Scientific Research (NWO VIDI). This work is part of the research programme of the Foundation for Fundamental Research on Matter (FOM) which is financially supported by The Netherlands Organisation for Scientific Research (NWO).

Notes and references

1. D. Van Der Zwaag, N. Vanparijs, S. Wijnands, R. De Rycke, B. G. De Geest and L. Albertazzi, ACS Appl. Mater. Interfaces, 2016, 8, 6391–6399.
2. R. Singh and J. W. Lillard, Exp. Mol. Pathol., 2009, 86, 215–223.
3. P. Zijlstra, P. M. R. Paulo and M. Orrit, Nat. Nanotechnol., 2012, 7, 379–382.
4. P. Zijlstra and M. Orrit, Rep. Prog. Phys., 2011, 74, 106401.
5. R. Huschka, J. Zuloaga, M. W. Knight, L. V. Brown, P. Nordlander and N. J. Halas, J. Am. Chem. Soc., 2011, 133, 12247–12255.
6. A. M. Goodman, N. J. Hogan, S. Gottheim, C. Li, S. E. Clare and N. J. Halas, ACS Nano, 2017, 11, 171–179.
7. H. Wang, T. B. Huff, D. A. Zweifel, W. He, P. S. Low, A. Wei and J. X. Cheng, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 15752–15756.
8. K. E. Sapsford, W. R. Algar, L. Berti, K. B. Gemmill, B. J. Casey, E. Oh, M. H. Stewart and I. L. Medintz, Chem. Rev., 2013, 113, 1904–2074.
9. R. A. Sperling and W. J. Parak, Philos. Trans. R. Soc., A, 2010, 368, 1333–1383.
10. M. P. Monopoli, D. Walczyk, A. Campbell, G. Elia, I. Lynch, F. Baldelli Bombelli and K. A. Dawson, J. Am. Chem. Soc., 2011, 133, 2525–2534.
11. R. Oliveira-Silva, M. Sousa-Jerónimo, D. Botequim, N. J. O. Silva, D. M. F. Prazeres and P. M. R. Paulo, Nanomaterials, 2019, 9, 893.
12. S. Ritz, S. Schöttler, N. Kotman, G. Baier, A. Musyanovych, J. Kuharev, K. Landfester, H. Schild, O. Jahn, S. Tenzer and V. Mailänder, Biomacromolecules, 2015, 16, 1311–1321.
13. A. M. Clemments, P. Botella and C. C. Landry, ACS Appl. Mater. Interfaces, 2015, 7, 21682–21689.
14. N. A. Belsey, A. G. Shard and C. Minelli, Biointerphases, 2015, 10, 019012.
15. H. D. Hill, J. E. Millstone, M. J. Banholzer and C. a. Mirkin, ACS Nano, 2009, 3, 418–424.
16. X. Zhang, M. R. Servos and J. Liu, J. Am. Chem. Soc., 2012, 134, 7266–7269.
17. X. Zhang, T. Gouriye, K. Göeken, M. R. Servos, R. Gill and J. Liu, J. Phys. Chem. C, 2013, 117, 15677–15684.
18. D. H. M. Dam, H. Lee, R. C. Lee, K. H. Kim, N. L. Kelleher and T. W. Odom, Bioconjugate Chem., 2015, 26, 279–285.
19. C. Y. Lee, P. Gong, G. M. Harbers, D. W. Grainger, D. G. Castner and L. J. Gamble, Anal. Chem., 2006, 78, 3316–3325.
20. M. D. Torelli, R. A. Putans, Y. Tan, S. E. Lohse, C. J. Murphy and R. J. Hamers, ACS Appl. Mater. Interfaces, 2015, 7, 1720–1725.
21. A. Rafati, A. G. Shard and D. G. Castner, Biointerphases, 2016, 11, 04B304.
22. J. M. Rabanel, V. Adibnia, S. F. Tehrani, S. Sanche, P. Hildgen, X. Banquy and C. Ramassamy, Nanoscale, 2019, 11, 383–406.
23. P. M. Kelly, C. Åberg, E. Polo, A. O'Connell, J. Cookman, J. Fallon, Ž. Krpetić and K. A. Dawson, Nat. Nanotechnol., 2015, 10, 472–479.
24. H. Hinterwirth, S. Kappel, T. Waitz, T. Prohaska, W. Lindner and M. Lämmerhofer, ACS Nano, 2013, 7, 1129–1136.
25. M. Choěl, K. Deboudt, J. Osán, P. Flament and R. Van Grisken, Anal. Chem., 2005, 77, 5686–5692.
26. M. J. Eller, K. Chandra, E. E. Coughlin, T. W. Odom and E. A. Schweikert, Anal. Chem., 2019, 91, 5566–5572.
27. M. Horáček, R. E. Armstrong and P. Zijlstra, Langmuir, 2018, 34, 131–138.
28. L. Belfiore, L. M. Spenkelink, M. Ranson, A. M. van Oijen and K. L. Vine, J. Controlled Release, 2018, 278, 80–86.
29. S. Dominguez-Medina, L. Kisley, L. J. Tauzin, A. Hoggard, B. Shuang, A. S. D. S. Indrasekara, S. Chen, L. Wang, P. J. Derry, A. Liopo, E. R. Zubarev, C. F. Landes and S. Link, ACS Nano, 2016, 10, 2103–2112.
30. A. M. Clemments, P. Botella and C. C. Landry, J. Am. Chem. Soc., 2017, 139, 3978–3981.
31. X. Cheng, T. P. Anthony, C. A. West, Z. Hu, V. Sundaresan, A. J. McLeod, D. J. Masiello and K. A. Willets, J. Phys. Chem. Lett., 2019, 10, 1394–1401.
32. K. L. Blythe, E. J. Titus and K. A. Willets, J. Phys. Chem. C, 2015, 119, 28099–28110.
33. N. Feiner-Gracia, M. Beck, S. Pujals, S. Tosi, T. Mandal, C. Buske, M. Linden and L. Albertazzi, Small, 2017, 13, 1–11.
34. T. Patiño, N. Feiner-Gracia, X. Arqué, A. Miguel-López, A. Jannasch, T. Stumpp, E. Schäffer, L. Albertazzi and S. Sánchez, J. Am. Chem. Soc., 2018, 140, 7896–7903.
35. R. Jungmann, M. S. Avendaño, M. Dai, J. B. Woehrstein, S. S. Agasti, Z. Feiger, A. Rodal and P. Yin, Nat. Methods, 2016, 13, 439–442.
36. P. Delcanale, B. Miret-Ontiveros, M. Arista-Romero, S. Pujals and L. Albertazzi, ACS Nano, 2018, 12, 7629–7637.
37. R. Jungmann, C. Steinhauer, M. Scheible, A. Kuzyk, P. Tinnefeld and F. C. Simmel, Nano Lett., 2010, 10, 4756–4761.
38. I. Ament, J. Prasad, A. Henkel, S. Schmachtel and C. Sönnichsen, Nano Lett., 2012, 12, 1092–1095.
39. M. A. Beuwer, M. W. J. Prins and P. Zijlstra, Nano Lett., 2015, 15, 3507–3511.
40. D. H. M. Dam, J. H. Lee, P. N. Sisco, D. T. Co, M. Zhang, M. R. Wasielewski and T. W. Odom, ACS Nano, 2012, 6, 3318–3326.
41. S. M. E. Peters, M. W. J. Prins and P. Zijlstra, Nanotechnology, 2015, 27, 24001.
42. E. Wertz, B. P. Isaacoff, J. D. Flynn and J. S. Biteen, Nano Lett., 2015, 15, 2662–2670.
43. K. L. Blythe and K. A. Willets, J. Phys. Chem. C, 2016, 120, 803–815.
44. B. Fu, B. P. Isaacoff and J. S. Biteen, ACS Nano, 2017, 11, 8978–8987.
45. M. Raab, C. Vietz, F. D. Stefani, G. P. Acuna and P. Tinnefeld, Nat. Commun., 2017, 8, 1–6.
46. K. I. Mortensen, L. S. Churchman, J. A. Spudich and H. Flyvbjerg, Nat. Methods, 2010, 7, 377–381.
47. D. L. Mack, E. Cortés, V. Giannini, P. Török, T. Roschuk and S. A. Maier, Nat. Commun., 2017, 8, 1–10.
48. A. S. De Silva Indrasekara, B. Shuang, F. Hollenhorst, B. S. Hoener, A. Hoggard, S. Chen, E. Villarreal, Y. Y. Cai, L. Kisley, P. J. Derry, W. S. Chang, E. R. Zubarev, E. Ringe, S. Link and C. F. Landes, J. Phys. Chem. Lett., 2017, 8, 299–306.
49. A. Taylor, R. Verhoef, M. Beuwer, Y. Wang and P. Zijlstra, J. Phys. Chem. C, 2018, 122, 2336–2342.
50. L. Saemisch, M. Liebel and N. van Hulst, 2019, arXiv:1904.08883.
51. S. J. Hurst, A. K. R. Lytton-Jean and C. a Mirkin, Anal. Chem., 2006, 78, 8313–8.
52. L. M. Demers, C. A. Mirkin, R. C. Mucic, R. A. Reynolds, R. L. Letsinger, R. Elghanian and G. Viswanadham, Anal. Chem., 2000, 72, 5535–5541.
53. N. Arjmandi, W. Van Roy, L. Lagae and G. Borghs, Anal. Chem., 2012, 84, 8490–8496.
54. B. Pérez-López and A. Merkoçi, Anal. Bioanal. Chem., 2011, 399, 1577–1590.
55. A. B. Taylor and P. Zijlstra, ACS Sens., 2017, 2, 1103–1122.
56. F. Li, H. Zhang, B. Dever, X. F. Li and X. C. Le, Bioconjugate Chem., 2013, 24, 1790–1797.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9nr10218c

---