Plasmene nanosheets as optical skin strain sensors†
Runfang
Fu
a,
Tharindu
Warnakula
 b,
Qianqian
Shi
a,
Lim Wei
Yap
b,
Qianqian
Shi
a,
Lim Wei
Yap
 a,
Dashen
Dong
a,
Dashen
Dong
 a,
Yiyi
Liu
a,
Malin
Premaratne
a,
Yiyi
Liu
a,
Malin
Premaratne
 b and
Wenlong
Cheng
b and
Wenlong
Cheng
 *a
*a
aDepartment of Chemical Engineering, Faculty of Engineering, Monash University, Clayton 3800, Victoria, Australia. E-mail: wenlong.cheng@monash.edu
bAdvanced Computing and Simulation Laboratory (AχL), Department of Electrical and Computer Systems Engineering, Faculty of Engineering, Monash University, Clayton 3800, Victoria, Australia
First published on 19th August 2020
Abstract
Skin-like optoelectronic sensors can have a wide range of technical applications ranging from wearable/implantable biodiagnostics, human–machine interfaces, and soft robotics to artificial intelligence. The previous focus has been on electrical signal transduction, whether resistive, capacitive, or piezoelectric. Here, we report on “optical skin” strain sensors based on elastomer-supported, highly ordered, and closely packed plasmonic nanocrystal arrays (plasmene). Using gold nanocubes (AuNCs) as a model system, we find that the types of polymeric ligands, interparticle spacing, and AuNC sizes play vital roles in strain-induced plasmonic responses. In particular, brush-forming polystyrene (PS) is a “good” ligand for forming elastic plasmenes which display strain-induced blue shift of high-energy plasmonic peaks with high reversibility upon strain release. Further experimental and simulation studies reveal the transition from isotropic uniform plasmon coupling at a non-strained state to anisotropic plasmon coupling at strained states, due to the AuNC alignment perpendicular to the straining direction. The two-term plasmonic ruler model may predict the primary high-energy peak location. Using the relative shift of the averaged high-energy peak to the coupling peak before straining, a plasmene nanosheet may be used as a strain sensor with the sensitivity depending on its internal structures, such as the constituent AuNC size or inter-particle spacing.
New conceptsWe propose and demonstrate a new “optical skins” concept with elastomer-supported, 2D highly-ordered and closely-packed gold nanocube (AuNC) arrays (plasmenes). Different from the previous elastomer-supported plasmonic nanostructures that are typically well-spaced with weak plasmon coupling or no coupling, our plasmenes show strong plasmonic coupling effects. Both experimental and simulation studies demonstrate that the isotropic uniform plasmon coupling in the non-strained state would transform to anisotropic plasmon coupling at strained states, due to the uniaxial strain-induced alignment of AuNCs. We found that the sensitivity of plasmonic skin strain sensors is influenced by the type of polymeric ligands, interparticle spacing, and size of the building blocks. This work not only establishes the design principle of plasmene-based strain sensors but also offers a new insight into the future design of “skin-like” plasmonic optics for applications in soft wearable electronics, soft robotics and artificial intelligence. |
Introduction
It is expected that electronics will evolve from current rigid electronics to flexible electronics to ultimately stretchable electronics (i.e. elastronics).1 Past decades have witnessed intensive research efforts to design soft, ultrathin, skin-conformal electronics for a range of technical applications including wearable electronics,2–5 soft robotics6,7 and prosthetic skins.8,9 One of the key parameters is to detect strains that have implications in motion tracking, ankle movement, sports, etc.10 These skin-like sensors are predominantly based on an electrical signal transduction strategy, which may be resistive,2,11–13 capacitance,14,15 piezoelectric,16–18 or triboelectric.19,20 Note that skin is the largest organ in humans. To map the specific strain distribution throughout the human body, millions of pixels are required. With the electrical signal transduction method, numerous wire connections are needed to address specific pixels.The wiring issue may be potentially circumvented if optical signal transduction is introduced. Recently, novel mechanochromic skins have been reported by using force-responsive polymers21 and hydrogels.22 In contrast to these organic mechanophores, inorganic colorimetric materials may offer high durability against oxidation under ambient conditions. In particular, plasmonic nanoparticles are novel optical materials because of their distinct scattering, absorbance, and coupling properties different from their bulk counterparts. Previously, plasmonic nanostructures have been fabricated on elastomeric substrates, which are typically well-spaced with weak plasmon coupling or no coupling.23–26 Enhanced plasmon coupling was observed upon external strains applied due to decreased inter-element spacing, leading to the typical red-shifts in resonance peaks. Unlike these reported plasmonic nanostructures, our group has recently successfully developed a general and powerful drying-mediated self-assembly strategy to fabricate two-dimensional (2D) monolayered and closely packed plasmonic nanocrystal arrays (termed as plasmene nanosheets) out of more than 15 different constituent building blocks.27 We have demonstrated novel applications of plasmene materials in surface-enhanced Raman scattering,28,29 anti-counterfeit,30 ionic gating,31 and flat lens.32 For these applications, plasmene nanosheets were either supported by a rigid substrate or a holey grid.
Here, we extend the previous fabrication of plasmene nanosheets to elastomeric substrates to reveal how plasmonic coupling responds to external strains. Unlike previous nanorod-incorporated elastomers where nanoparticles are sparsely distributed without plasmonic coupling,33–35 plasmonic building blocks in our plasmene nanosheets are closely packed with strong plasmonic coupling effects. Using polystyrene-capped gold nanocubes (AuNCs) as model building blocks, we show that the coupling strength among AuNCs will be substantially weakened along the straining direction when a strain is applied but the coupling strength in the perpendicular direction enhances simultaneously. This led to the blue shift of the primary high-energy resonance peak relative to the strong plasmon coupling peak under non-strain state. This shift can be well predicted by the two-term plasmonic ruler model, demonstrating the tendency of AuNC alignment under external strains. The level of blue shift depends on the strain level, with the sensitivity tunable by adjusting internal structures of plasmenes (e.g. AuNC sizes and/or edge-to-edge spacing). We also found that thiolated polystyrene (PS) ligands play a crucial role in the strain-controlled plasmonic coupling, which offers the nanoscale elasticity enabling reversible interparticle switching. In contrast, polyvinylpyrrolidone (PVP)-based AuNC arrays exhibit red shift upon straining due to enhanced plasmonic coupling induced by the film crack. Our results demonstrate the significance of surface-capping ligands in strain-induced plasmonic responses. Both our experimental and theoretical studies revealed the nature of a strain-induced directional decoupling profile of closely spaced nanoparticle arrays upon the stretching direction, which can well explain the unusual blue-shifting phenomenon observed for a PS–ligand system. The degree of shift could be well predicted by the two-term plasmonic ruler model.
Results and discussion
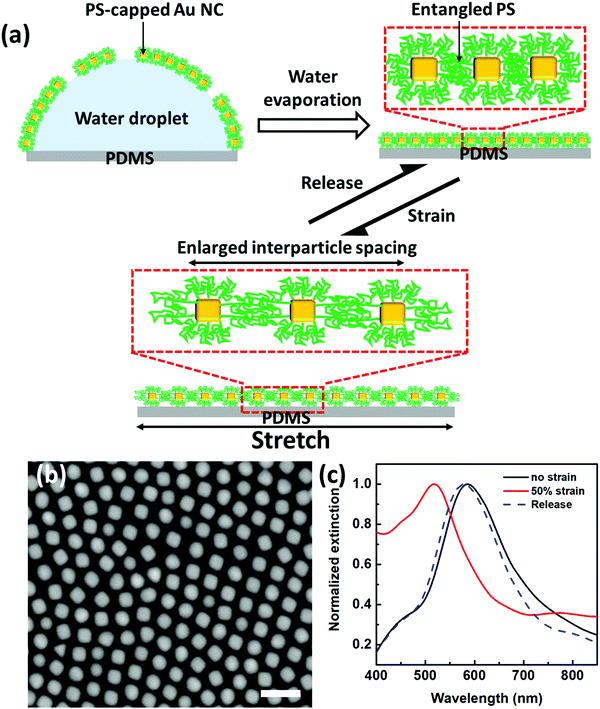
We extend our recently developed two-step drying-mediated self-assembly27 of PS-capped plasmonic nanoparticles to an elastomeric polydimethylsiloxane (PDMS) substrate for the construction of soft strain gauge sensors. AuNCs were used as model building blocks, which were synthesized by a seed-mediated method according to the literature.36 Fig. S1 (ESI†) shows the transmission electron microscope (TEM) image of the as-obtained AuNCs demonstrating high monodispersity. By using stronger binding SH-PS ligands, the pristine hexadecyltrimethylammonium bromide (CTAB) could be replaced to render the AuNCs transferred into an organic phase such as chloroform.37 Further drop-casting the suspension of PS-capped AuNCs onto a sessile droplet sitting on PDMS (Fig. 1a) could lead to the formation of highly ordered, closely packed, and one-particle thick nanosheets (i.e. plasmene) upon sequential chloroform and water evaporation (Fig. 1b).In the absence of strain, the AuNC plasmene displayed a characteristic plasmonic resonance peak at the wavelength of ∼586 nm (Fig. 1c), which is attributed to the coupling effect between adjacent AuNCs. In contrast, the resonance peak blue shifted to ∼517 nm upon applying 50% strain. This indicates weakened plasmonic coupling among AuNCs, which may be due to strain-induced dominant enlargement of interparticle spacing along the stretching direction. This observation is consistent with our previous 1-dodecanethiol (DDT) ligand-based plasmonic nanoassemblies.38
Remarkably, the plasmonic coupling peak shift was reversible, which could shift back to the original wavelength (586 nm) upon strain release (Fig. 1c). The reversible plasmonic switching indicates elastic deformation of PS capping ligands, which may experience spring-like chain configurational changes during the stretch–release cycle. It is well-known that particle-to-particle van der Waals (vdW) attraction is very strong. Once nanoparticles are in vdW contacts forming aggregates, it is very difficult to separate them with mechanical or other means.39 In this context, firm Au–S covalent bonding enabled the formation of a self-assembled monolayer of PS ligands with a brush-like configuration in solution.40 In the dried state, PS collapsed but remained to provide effective protection of AuNCs from direct particle-to-particle vdW contact. Therefore, the PS-based plasmene nanosheets were compliant with PDMS substrate deformation (Fig. 1a). This is the key to the reversible plasmonic switching behavior we observed.
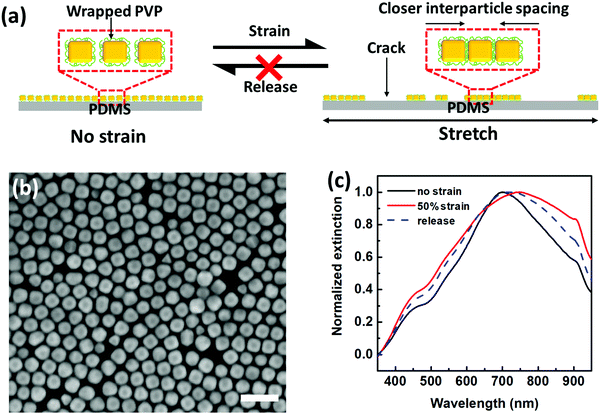
To further demonstrate and elucidate this argument, we undertook control experiments with PVP as ligands. Following a similar procedure, we fabricated PVP-based AuNC plasmene by using PVP with similar molecular weight as PS. Unlike PS ligands with only a terminal thiol group binding to AuNCs, PVP ligands have random gold-binding pyrrolidone groups throughout the chain. Therefore, PVP ligands will wrap around the AuNCs (Fig. 2a) rather than forming a standing brush-like configuration. This offered inadequate protection of AuNCs, leading to much more closely packed nanoassemblies. This can be proved from SEM characterization (Fig. 2b), in which the edge-to-edge spacing is 7.0 ± 4.2 nm (Fig. S2a, ESI†) for the PVP-based plasmene, whereas, for the PS-based plasmene, the edge-to-edge spacing is 14.2 ± 3.6 nm (Fig. S2b, ESI†). Consistent with this, PS-based plasmene displayed a characteristic coupling resonance peak at 586 nm (Fig. 1c), but PVP-based plasmene showed a characteristic coupling resonance peak at 701 nm (Fig. 2c).
The strong vdW forces for PVP-based plasmene rendered it difficult to separate AuNCs under mechanical strains. Instead, the stress caused even “closer” edge-to-edge spacing due to the dominant crack/delamination under strain (Fig. 2a). In other words, PVP-based plasmene was relatively rigid and not compliant to PDMS substrate deformation. This is in agreement with coupling the plasmonic spectral shift. Unlike PS-based plasmene, red shift was observed for the PVP-based system under strain. Under 50% strain, the coupling peak shifted from 701 nm to 749 nm (Fig. 2c) with simultaneous peak broadening, which indicated stronger plasmonic coupling.
A systematic comparison of the plasmonic peak shift of PS-based and PVP-based sensors further showed different shift trends with increased strains. A good linear relationship was found from 0% to 90% strain for the PVP-based sensor with a positive slope of 98 and an R2 value of 0.97 (Fig. S3a, ESI†), but the PS-based sensor displayed a linear regime (with a slope of −141 and a R2 value of 0.90) up to ∼40% strain after which a plateau was observed (Fig. S3b, ESI†). Nonetheless, the PS-based sensor showed much better reversibility than the PVP-based sensor when the sensor was released after straining. The plasmonic peak of the PS-based sensor reversed back to 574 ± 6.4 nm after releasing, giving a 99.1% recovery (Fig. S3b, ESI†). However, the PVP-based sensor showed only 97.6% recovery (Fig. S3a, ESI†).
We further investigate how the level of strain influences plasmonic coupling and how PS ligand length influences such strain-induced plasmonic profiles. We first tuned the edge-to-edge interparticle spacing with our PS ligand-based strategy by using two different methods: (1) utilize PS ligands with different molecular weights and (2) sacrificial Ag etching. For the first method, AuNCs with the size of about 36 nm were used as building blocks to fabricate the plasmene sheets. PS with Mn = 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 (12k) and Mn = 50
000 g mol−1 (12k) and Mn = 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 (50k) were chosen to fabricate plasmene. As expected, smaller edge-to-edge spacing was for 12k PS (Fig. S4, ESI†) in comparison to 50k PS ligands (Fig. 1b). For the second method, Ag-coated AuNC plasmene was first fabricated, followed by an Ag shell removal process to introduce a larger inter-particle spacing. In this method, Ag-coated AuNC nanoparticles were synthesized and characterized with a 36 nm AuNC core (Fig. S5, ESI†), and assembled into plasmenes using a 50k PS ligand (Fig. S6a, ESI†). After that, the Ag shell was selectively etched away to obtain plasmene with a large edge-to-edge spacing (Fig. S6b, ESI†). Such a large spacing (∼40 nm) was not possible to achieve with the PS-based method alone.
000 g mol−1 (50k) were chosen to fabricate plasmene. As expected, smaller edge-to-edge spacing was for 12k PS (Fig. S4, ESI†) in comparison to 50k PS ligands (Fig. 1b). For the second method, Ag-coated AuNC plasmene was first fabricated, followed by an Ag shell removal process to introduce a larger inter-particle spacing. In this method, Ag-coated AuNC nanoparticles were synthesized and characterized with a 36 nm AuNC core (Fig. S5, ESI†), and assembled into plasmenes using a 50k PS ligand (Fig. S6a, ESI†). After that, the Ag shell was selectively etched away to obtain plasmene with a large edge-to-edge spacing (Fig. S6b, ESI†). Such a large spacing (∼40 nm) was not possible to achieve with the PS-based method alone.
Detailed structural analysis of the as-fabricated three plasmenes shows that the edge-to-edge spacings were ∼8, ∼14 and ∼40 nm for the 12k-PS, 50k-PS and etched method, respectively (Fig. S7, ESI†). For convenience purposes, they are termed ss-plasmene, ms-plasmene and ls-plasmene, respectively. In comparison to discrete AuNCs in solution, all three plasmenes display red-shifted and broadened resonance peaks (Fig. S8, ESI†), demonstrating the strong plasmonic coupling. The degree of plasmonic coupling correlates very well with the expected edge-to-edge interparticle spacing (Fig. S7, ESI†).
A series of strains from 10% to 90% were tuned to investigate the strain-induced evolution of plasmon coupling (Fig. S9, ESI†). When at a relatively low strain (e.g. 10%), we observed a peak splitting phenomenon which is more predominant for closely spaced ss-plasmene (Fig. 3a). Typically, one peak located at a relatively high energy range (λT) and another located at the low energy range (λL), in comparison to the plasmon coupling peak at non-strained states (λC). This kind of phenomenon was also observed for ms-plasmene and ls-plasmene (Fig. S10, ESI†), albeit sometimes only a small shoulder peak for λL. We also noticed that the peak splitting at low strain was location-specific, especially for ss-plasmene (Fig. 3a and Fig. S11a, ESI†). This may indicate the heterogeneity of the lattice orientations to the straining direction (Fig. 3c and f), which is responsible for variances in the spectra (Red and green lines in Fig. 3a and Fig. S11a, ESI†). Nevertheless, the high-energy peak λT tends to unify with much less location dependence as the strain level is increased (Fig. S11b and c, ESI†). At 90% strain, location-dependent drifting is almost gone (Fig. S11c, ESI†).
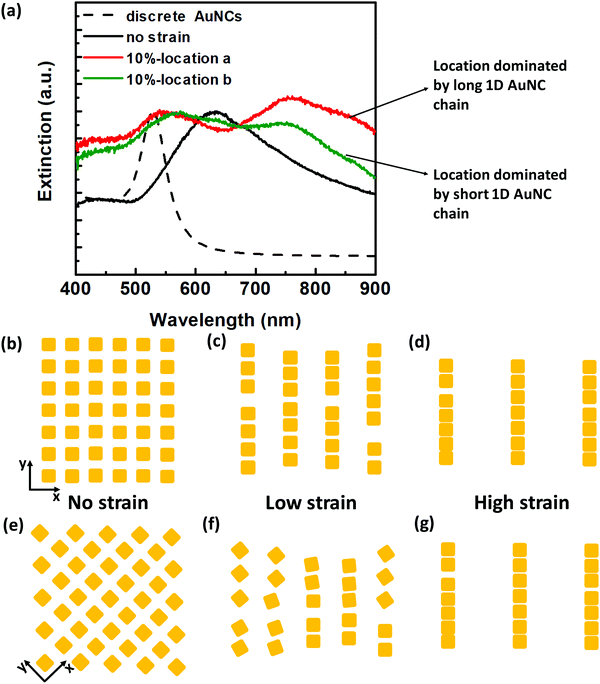 | ||
| Fig. 3 Strain-induced plasmonic peak evolution at different strain levels. (a) Representative extinction spectra of the ss-plasmene under 10% strain: green and red colored spectra were from different locations within one plasmene. (b–d) Schematic of possible AuNC packing orders with increasing strains along the x-direction. (e–g) Schematic of possible AuNC packing orders with increasing strains along the diagonal direction. Although the stochastic square lattice stretching direction may differ from location to location, uniform alignment prevails at a high strain level as evidenced from unified spectra at 90% strain shown in Fig. S11c (ESI†). | ||
These studies indicate that AuNCs tend to align under external mechanical strains, consistent with our previous free-standing DNA-capped nanosphere nanosheets.34 Hence, the high energy peak might correspond to resonance at the transverse direction of AuNC chain assemblies, and the low energy peak was due to resonance at the longitudinal direction of the assemblies. At the small strains, plasmenes may fragment into heterogonous 1D AuNC assemblies depending on specific lattice orientations to the stretching direction (Fig. 3c and f), which displayed bi-modal resonance peaks that have been observed experimentally (Fig. 3a). The low-energy peak can be well predicted theoretically by modelling resonance along the 1D chain-like assemblies (Fig. S12, ESI†). With further enhanced strain levels, fragmented 1D oligomer assemblies gradually evolved into uniform, much longer 1D chain-like configurations under high strain levels (Fig. 3d and g), hence displaying consistent plasmonic profiles (Fig. S11c, ESI†). The low-energy longitudinal modes for these long 1D chain assemblies will be in the near-infrared region depending on the length. Theoretical modelling shows the transverse-mode high-energy peak (Fig. S13, ESI†) can be even higher than the non-coupling discrete AuNCs (Fig. S12b, ESI†), consistent with experimental observation (Fig. S9, ESI†).
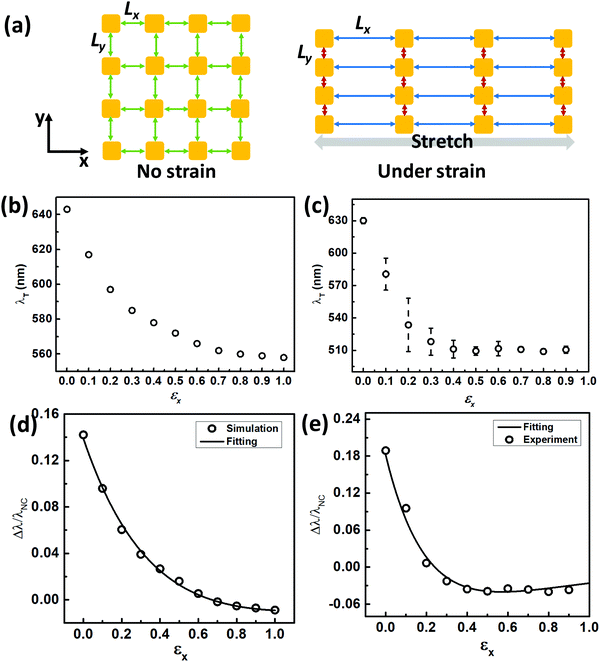
The strain-induced alignment tendency may be well explained by the known Poisson effect of elastomeric sheets, in which AuNCs are being pulled apart along the straining direction but compressed under the normal direction. This can result in alignment of AuNCs. To further prove strain-induced AuNC alignment in the vertical direction, we simulated by assuming an ideal square lattice with uniform edge-to-edge spacing at a non-strained state (Fig. 4a). Under the strained state, AuNCs align vertically, leading to the change in the edge-to-edge spacing (Fig. 4a). With a Poisson ratio of PDMS (∼0.5), this means that every increase (ΔLx) in the edge-to-edge spacing (Lx) in the stretching direction will accompany a decrease of 1/2ΔLx in the perpendicular edge-to-edge spacing (Ly). By applying a linear tensile strain step of ΔLx = 4 nm (Fig. S14, circular, ESI†), we could then predict the corresponding Ly values, which predicted a compression limit of ∼2 nm at 40% strain (Fig. S14, triangle, ESI†). With those spacing values of Lx and Ly, we calculated the corresponding plasmonic peak position for stretched plasmene sheets (Fig. 4b). The resulting peak-shifting trend (Fig. 4b) matched well with our experimental results (Fig. 4c).
The above modelling results revealed that the blue-shifting trend observed for PS–AuNC plasmene sheets under uniaxial strain was a result of reduced plasmonic coupling along the stretching direction with simultaneously enhanced plasmonic coupling within the AuNC chains. The degree of the blue shift was a trade-off of two competing factors. In both experimental and theoretical studies, the blue-shifting trend could reach the plateau stage at a strain level of about 50%. It might mean that Lx was so large that plasmonic coupling became insignificant in the stretching direction. Yet simultaneously Ly reached the minimum corresponding to the strongest plasmonic coupling in the vertical direction. Surprisingly, this plateau plasmonic resonance energy could be even higher than the coupling-free resonance energy for discrete AuNCs (e.g. ∼511 nm vs. ∼530 nm in one of our experimental studies shown in Fig. S9, blue line, ESI†). While it might appear counter-intuitive, this observation was theoretically supported by our modelling of one-dimensionally packed AuNCs. By using polarized light (Fig. S13a, ESI†), the transverse-mode energy was calculated, which predicted a resonance peak at ∼530 nm (Fig. S13b, ESI†) in contrast to ∼560 nm calculated for discrete AuNCs (Fig. S12b, ESI†). This in turn supported extremely strong plasmon coupling in the perpendicular direction due to the smallest possible edge-to-edge inter-particle spacing Ly (Fig. 4a), leading to nanorod-like plasmonic properties.
We further attempted to quantify the blue-shifting trend by applying the well-established plasmonic ruler equation.41,42 Considering the weakening coupling along the stretching direction and strengthening coupling in the vertical direction when a tensile uniaxial strain is applied, we used two different terms for fitting to reflect the respective contributions. Note that interparticle spacing was not measurable on a non-conducting elastomeric PDMS substrate, so we replaced the commonly used normalized spacing with tensile strain. The following equation may predict the fractional plasmonic shift as a function of strain:
| Δλ/λNC = a·exp(−εx/τx) − b·exp(−εy/τy) | (1) |
Besides the edge-to-edge spacing, particle size is another factor that influences the optical properties of plasmene. To investigate the size-dependency, we further fabricate the plasmenes on PDMS from AuNCs with varying sizes that were synthesized by tuning the concentration of Au seeds. Fig. S16 (ESI†) shows the size distributions of AuNCs, which indicates a small size of 36 ± 1.6 nm (defined as S-AuNCs), a medium size of 41 ± 2.8 nm (defined as M-AuNCs) and a large size of 56 ± 3.2 nm (defined as L-AuNCs). The morphology of the obtained plasmenes was investigated under SEM (Fig. 1b and Fig. S17a, b, ESI†), showing a closely packed and highly ordered packing for all of the samples. We have further carried out the two-term non-linear least squares fit on the plasmonic coupling peak shift of S-AuNCs, M-AuNCs, and L-AuNCs plasmene by using eqn (1). Reasonable fitting results with a high goodness of fit (95.6% for S-AuNCs, 96.0% for M-AuNCs and 98.5% for L-AuNCs) were achieved, which further confirmed the generality of our two-term fitting model (Fig. S18, ESI†). Multiple factors including non-ideal packing orders might influence the variation in values of the fitting parameters (Table S1, ESI†).
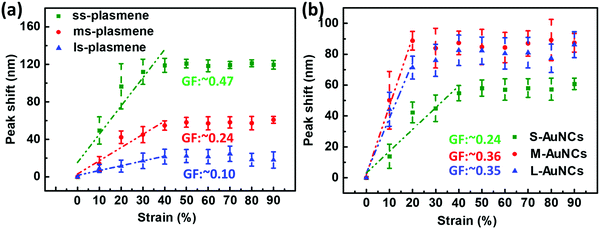
The blue-shifting λT was found to be dependent on uniaxial tensile strain, roughly following a linear relationship within a certain strain regime. The plasmonic properties of ss-, ms- and ls-plasmenes were compared under sequential straining up to 90% with 10% increment. Their peak-shifting trends were plotted (Fig. 5a). Note that the blue-shifting trend followed by a plateau was observed for all these samples. It appeared that the blue-shifting trends might be described roughly by a linear function with strain, for which we may compare their sensitivity by defining a gauge factor (GF) with the following equation:
| GF = Δλ/(λCε) | (2) |
Fig. 5b shows the plasmonic shift of different-sized AuNC plasmene-based sensors as a function of strain from 0% to 90%. The plateaued stage of the small AuNC-based sensor was observed at the strain of around 40% while that of the medium and large AuNC-based ones appeared at a lower strain (∼20%). The strain sensitivity, GF of these sensors was calculated using eqn (2). These results indicated that the GF of the plasmonic strain sensor in the 0% to 40% range increases with increasing particle size up to 41 nm and the further increment of particle size would not lead to an improved sensitivity. Simulated results further confirmed the size-dependence of the sensitivity of our plasmene strain sensors (Fig. S20, ESI†). Unlike the previously reported graphene-based optical strain sensor, which could only detect small strains (lower than 0.3%),43 our plasmonic strain sensors are sensitive to large strains from 10% to 40%. Besides, the sensitivity of our plasmonic strain sensor is tunable by tuning the inter-particle spacing and particle size, which allows the custom design of plasmonic strain sensors for the desired sensing performance.
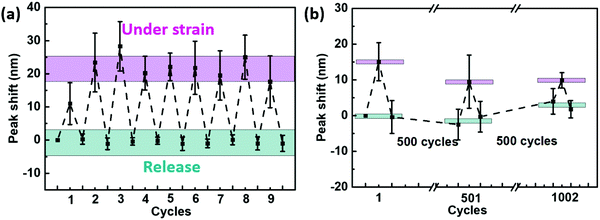
To evaluate the reversibility and durability of the plasmonic strain sensor, a cyclic stretch–release test was carried out (Fig. 6a). The plasmonic strain sensor showed an average peak shift of 21 ± 4.9 nm under 10% strain and almost recovered to its original state after releasing, which demonstrates the good reversibility of the sensor. The durability test was carried out for 1000 cycles under the stretching and releasing test at a rate of 2 mm s−1. As shown in Fig. 5b, the plasmonic sensor showed a response to the strain even after 500 cycles of stretching, releasing, and almost fully recovered after release. However, the plasmonic sensor couldn’t recover entirely after another 500 cycles of cyclic stretching test, which might be due to the de-bonding between neighboring AuNCs and/or orientational changes in lattice directions to the straining directions under repeated straining cycles.
Conclusions
In this study, we have demonstrated new “optical skin” strain sensors based on 2D highly ordered and closely packed AuNC arrays (i.e. plasmene nanosheets). We further found that a “good” ligand (i.e. PS in this work) is crucial for adequate protection of plasmonic nanoparticles from strong vdW contact and endows the plasmene with nanoscale elasticity enabling reversible strain-induced plasmonic coupling switching. Both experimental and theoretical studies show that the uniaxial strain induces the gradual formation of aligned AuNCs, leading to substantial plasmonic decoupling along the strain direction yet with simultaneously enhanced coupling in the vertical direction due to the Poisson effect. This explains well the peak splitting phenomena and the typical blue shifts in transverse mode λT as well as their particle size- and edge-to-edge spacing-dependent sensitivity. The simplicity of our fabricating method makes the skin-like plasmonic strain sensor a promising candidate for future applications in wearable/implantable devices, soft robotics, and artificial intelligence.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the Australian Research Council Discovery Projects DP170102208 and DP200100624. The authors also gratefully acknowledge the use of facilities at the Monash Centre for Electron Microscopy and the Melbourne Centre for Nanofabrication (MCN) in the Victorian Node of the Australian National Fabrication Facility (ANFF).Notes and references
- B. Zhu, S. Gong and W. Cheng, Chem. Soc. Rev., 2019, 48, 1668–1711 RSC.
- S. Gong, W. Schwalb, Y. Wang, Y. Chen, Y. Tang, J. Si, B. Shirinzadeh and W. Cheng, Nat. Commun., 2014, 5, 3132 CrossRef.
- J. Choi, R. Ghaffari, L. B. Baker and J. A. Rogers, Sci. Adv., 2018, 4, eaar3921 CrossRef.
- M. Kaltenbrunner, T. Sekitani, J. Reeder, T. Yokota, K. Kuribara, T. Tokuhara, M. Drack, R. Schwödiauer, I. Graz, S. Bauer-Gogonea, S. Bauer and T. Someya, Nature, 2013, 499, 458–463 CrossRef CAS.
- D. Son, J. Kang, O. Vardoulis, Y. Kim, N. Matsuhisa, J. Y. Oh, J. W. F. To, J. Mun, T. Katsumata, Y. Liu, A. F. McGuire, M. Krason, F. Molina-Lopez, J. Ham, U. Kraft, Y. Lee, Y. Yun, J. B. H. Tok and Z. Bao, Nat. Nanotechnol., 2018, 13, 1057–1065 CrossRef CAS.
- S. I. Rich, R. J. Wood and C. Majidi, Nat. Electron., 2018, 1, 102–112 CrossRef.
- D. Rus and M. T. Tolley, Nature, 2015, 521, 467–475 CrossRef CAS.
- A. Chortos, J. Liu and Z. Bao, Nat. Mater., 2016, 15, 937–950 CrossRef CAS.
- A. P. Gerratt, H. O. Michaud and S. P. Lacour, Adv. Funct. Mater., 2015, 25, 2287–2295 CrossRef CAS.
- Y. Wang, S. Gong, S. J. Wang, G. P. Simon and W. Cheng, Mater. Horiz., 2016, 3, 208–213 RSC.
- S. Gong, Y. Wang, L. W. Yap, Y. Ling, Y. Zhao, D. Dong, Q. Shi, Y. Liu, H. Uddin and W. Cheng, Nanoscale Horiz., 2018, 3, 640–647 RSC.
- S. Gong, D. T. Lai, B. Su, K. J. Si, Z. Ma, L. W. Yap, P. Guo and W. Cheng, Adv. Electron. Mater., 2015, 1, 1400063 CrossRef.
- N. N. Jason, M. D. Ho and W. Cheng, J. Mater. Chem. C, 2017, 5, 5845–5866 RSC.
- D. J. Lipomi, M. Vosgueritchian, B. C. K. Tee, S. L. Hellstrom, J. A. Lee, C. H. Fox and Z. Bao, Nat. Nanotechnol., 2011, 6, 788–792 CrossRef CAS.
- D. P. Cotton, I. M. Graz and S. P. Lacour, IEEE Sens. J., 2009, 9, 2008–2009 Search PubMed.
- J. M. Wu, C.-Y. Chen, Y. Zhang, K.-H. Chen, Y. Yang, Y. Hu, J.-H. He and Z. L. Wang, ACS Nano, 2012, 6, 4369–4374 CrossRef CAS.
- C. Dagdeviren, P. Joe, O. L. Tuzman, K.-I. Park, K. J. Lee, Y. Shi, Y. Huang and J. A. Rogers, Extreme Mech. Lett., 2016, 9, 269–281 CrossRef.
- J. Park, M. Kim, Y. Lee, H. S. Lee and H. Ko, Sci. Adv., 2015, 1, e1500661 CrossRef.
- X. Pu, M. Liu, X. Chen, J. Sun, C. Du, Y. Zhang, J. Zhai, W. Hu and Z. L. Wang, Sci. Adv., 2017, 3, e1700015 CrossRef.
- C. Garcia and I. Trendafilova, Nano Energy, 2019, 60, 527–535 CrossRef CAS.
- J. Park, Y. Lee, M. H. Barbee, S. Cho, S. Cho, R. Shanker, J. Kim, J. Myoung, M. P. Kim and C. Baig, Adv. Mater., 2019, 31, 1808148 CrossRef.
- H. Chen, F. Yang, Q. Chen and J. Zheng, Adv. Mater., 2017, 29, 1606900 CrossRef.
- J.-E. Lee, C. Park, K. Chung, J. W. Lim, F. Marques Mota, U. Jeong and D. H. Kim, Nanoscale, 2018, 10, 4105–4112 RSC.
- J. Wen, H. Zhang, H. Chen, W. Zhang and J. Chen, J. Opt., 2015, 17, 114015 CrossRef.
- X. Zhu, L. Shi, X. Liu, J. Zi and Z. Wang, Nano Res., 2010, 3, 807–812 CrossRef CAS.
- M. L. Tseng, J. Yang, M. Semmlinger, C. Zhang, P. Nordlander and N. J. Halas, Nano Lett., 2017, 17, 6034–6039 CrossRef CAS.
- D. Dong, R. Fu, Q. Shi and W. Cheng, Nat. Protoc., 2019, 14, 2691–2706 CrossRef CAS.
- K. J. Si, P. Guo, Q. Shi and W. Cheng, Anal. Chem., 2015, 87, 5263–5269 CrossRef CAS.
- Q. Shi, K. J. Si, D. Sikdar, L. W. Yap, M. Premaratne and W. Cheng, ACS Nano, 2016, 10, 967–976 CrossRef CAS.
- K. J. Si, D. Sikdar, L. W. Yap, J. K. K. Foo, P. Guo, Q. Shi, M. Premaratne and W. Cheng, Adv. Opt. Mater., 2015, 3, 1710–1717 CrossRef CAS.
- S. Rao, K. J. Si, L. W. Yap, Y. Xiang and W. Cheng, ACS Nano, 2015, 9, 11218–11224 CrossRef CAS.
- K. J. Si, D. Dong, Q. Shi, W. Zhu, M. Premaratne and W. Cheng, Mater. Today, 2019, 23, 9–15 CrossRef CAS.
- J. Li, S. Liu, Y. Liu, F. Zhou and Z.-Y. Li, Appl. Phys. Lett., 2010, 96, 263103 CrossRef.
- H. Pletsch, M. Tebbe, M. Dulle, B. Förster, A. Fery, S. Förster, A. Greiner and S. Agarwal, Polymer, 2015, 66, 167–172 CrossRef CAS.
- L. Fu, Y. Liu, W. Wang, M. Wang, Y. Bai, E. L. Chronister, L. Zhen and Y. Yin, Nanoscale, 2015, 7, 14483–14488 RSC.
- T. K. Sau and C. J. Murphy, J. Am. Chem. Soc., 2004, 126, 8648–8649 CrossRef CAS.
- K. J. Si, D. Sikdar, Y. Chen, F. Eftekhari, Z. Xu, Y. Tang, W. Xiong, P. Guo, S. Zhang, Y. Lu, Q. Bao, W. Zhu, M. Premaratne and W. Cheng, ACS Nano, 2014, 8, 11086–11093 CrossRef CAS.
- P. Guo, D. Sikdar, X. Huang, K. J. Si, B. Su, Y. Chen, W. Xiong, L. W. Yap, M. Premaratne and W. Cheng, J. Phys. Chem. C, 2014, 118, 26816–26824 CrossRef CAS.
- K. J. Si, Y. Chen, Q. Shi and W. Cheng, Adv. Sci., 2018, 5, 1700179 CrossRef.
- Q. Shi, D. Dong, K. J. Si, D. Sikdar, L. W. Yap, M. Premaratne and W. Cheng, ACS Nano, 2018, 12, 1014–1022 CrossRef CAS.
- W. Cheng, M. J. Campolongo, J. J. Cha, S. J. Tan, C. C. Umbach, D. A. Muller and D. Luo, Nat. Mater., 2009, 8, 519–525 CrossRef CAS.
- N. Hooshmand and M. A. El-Sayed, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 19299–19304 CrossRef CAS.
- A. P. A. Raju, A. Lewis, B. Derby, R. J. Young, I. A. Kinloch, R. Zan and K. S. Novoselov, Adv. Funct. Mater., 2014, 24, 2865–2874 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental section, supplementary figures (Fig. S1–S20) and supplementary table (Table S1). See DOI: 10.1039/d0nh00393j |
| This journal is © The Royal Society of Chemistry 2020 |