Integration of graphene and two-dimensional ferroelectrics: properties and related functional devices†
Xin
Jin
a,
Yu-Yang
Zhang
 *ab,
Sokrates T.
Pantelides
*ab,
Sokrates T.
Pantelides
 ac and
Shixuan
Du
ac and
Shixuan
Du
 *abd
*abd
aInstitute of Physics & University of Chinese Academy of Sciences, Chinese Academy of Sciences, Beijing 100190, China. E-mail: zhangyuyang@ucas.ac.cn; sxdu@iphy.ac.cn
bCAS Centre for Excellence in Topological Quantum Computation, Beijing 100190, P. R. China
cDepartment of Physics and Astronomy and Department of Electrical Engineering and Computer Science, Vanderbilt University, Nashville, TN 37235, USA
dSongshan Lake Materials Laboratory, Dongguan 523808, China
First published on 2nd July 2020
Abstract
Ferroelectric (FE) thin films have been investigated for many years due to their broad applications in electronic devices. It was recently demonstrated that FE functionality persists in ultrathin films, possibly even in monolayers of two-dimensional (2D) FEs. However, the feasibility of 2D-based FE functional devices remains an open challenge. Here, we employ density-functional-theory calculations to propose and document the possible integration of graphene with 2D FE materials on metal substrates in the form of functional FE devices. We show that monolayers of proposed M2O3 (M = Al, Y) in the quintuple layer (QL) In2Se3 struCture are stable 2D FE materials and that QL-M2O3 is a functional tunnel barrier in a graphene/QL-M2O3/Ru heterostructure. The QL-M2O3 barrier width can be modulated by its polarization direction, whereby the heterostructure can function as a prototype ferroelectric tunnel junction. Moreover, alternating the polarization of QL-M2O3 modulates the doping type of graphene, enabling the fabrication of graphene p–n junctions. By design, the proposed heterostructures can in principle be fabricated by intercalation, which is known to produce high-quality, large-scale 2D-based heterostructures.
New conceptsFerroelectric (FE) devices based on vertical monolayer heterostructures have been hampered by difficulties in fabricating known layered FE materials in monolayer (ML) form. Here, motivated by recent demonstrations of the fabrication of high-quality graphene-ML heterostructures on metal substrates by first growing epitaxial graphene and subsequently growing MLs or multilayers by intercalation, we employ density-functional theory calculations and predict new, stable, ML FE materials, QL-M2O3, where M = Al or Y, in the QL-In2Se3 structure, and that metal/QL-M2O3/graphene structures can function as prototype monolayer-based FE tunnel junctions or potentially graphene p–n junctions. These findings provide new perspectives on the integration of graphene and monolayer FEs, as well as related functional devices. |
Introduction
Ferroelectric (FE) materials, which possess an electrically switchable spontaneous polarization, generate broad interest because of potential applications in nonvolatile memory, field-effect transistors, and photovoltaics.1–4 Motivated by the miniaturization of electronic devices, extensive research has been pursued on the fabrication of ferroelectric films that are only a few nanometers thick or even a monolayer. Recently, several two-dimensional (2D) FE materials were discovered.5–10 For example, SnTe, which is not a layered material, was discovered to maintain stable in-plane polarization when its thickness is reduced to one unit cell (0.63 nm).6 On the other hand, for FE materials with out-of-plane polarization, thickness reduction is generally limited by the depolarization field.11–13 Nevertheless, BiFeO3 has been demonstrated to possess an out-of-plane polarization when its thickness is reduced to ∼1 nm (two unit cells),10 while the layered materials CuInP2S6 and In2Se3 have been shown to maintain an out-of-plane polarization when their thickness is 4 nm (∼5 layers) and 2–6 nm (∼2 to 6 layers) respectively.5,8,9,14 Moreover, it has been theoretically predicted that robust ferroelectricity persists in monolayer In2Se3, which is usually referred to as In2Se3 quintuple layer (QL-In2Se3) because each In2Se3 layer contains five planes of atoms.7 This robust ferroelectricity has been explained in terms of dipole locking that is enabled by the unique atomic arrangements of QL-In2Se3.9Integration of 2D materials, such as graphene, with nanoscale-thickness or bulk FE materials has been shown to enable fabrication of functional devices. For example, a Au/In2Se3/graphene heterostructure with 6 nm of In2Se3 (∼6 QLs) has been fabricated.14 In this structure, Au and graphene serve as top and bottom electrodes, respectively, while the 6 nm In2Se3 works as a tunnel barrier. The heterostructure shows resistive switching behavior driven by polarization reversal, by which the heterostructure can work as a ferroresistive memory device. Until now, there are no theoretical investigations about this heterostructure. Another case is the integration of graphene with FE bulk LiNbO3.15 Graphene was transferred onto bulk single-domain LiNbO3 that is poled periodically, i.e., it possesses stripes of opposite polarization vectors, by which the doping level of graphene on top of each stripe is modulated. This integration provides a method to fabricate a graphene p–n junction, which is the core part of graphene-based photodetectors.16,17
Despite the above successes, so far there have not been any investigations of functional FE devices based on monolayer FEs with out-of-plane polarization, integrated with other monolayers such as graphene into vertical heterostructures. Such increased miniaturization is always desirable as it improves performance.1 The main difficulty has been the inability so far to fabricate monolayer FEs starting with known layered FEs in bulk or thin-film form or grow them directly by chemical vapor deposition or other methods. The main motivation for the present paper is the existence of an experimental technique that, not only produces large-scale, high-quality monolayers, but does it by naturally integrating them into high-quality heterostructures with graphene monolayers on a metal substrate. It has been demonstrated that large-scale, high-quality graphene can be grown epitaxially on transition-metal substrates such as Ru(0001)18,19 and, subsequently, monolayers or multilayers of other materials can be grown by intercalation in the graphene–metal interface.20–24 This process eliminates the need for a transfer process that can induce defects and contamination. Recently, bilayer SiO2 with similar thickness as QL-In2Se3 was fabricated in this fashion and proved to be crystalline and weakly bonded to the Ru metal substrate.20,25,26 QL-In2Se3 has not been grown in this fashion yet, but there may be other possibilities as well. Considering that O and Se are same-group elements and the robust ferroelectricity of QL-In2Se3 is enabled by its unique atomic arrangements,9 oxides that adopt the structure of QL-In2Se3 might also be stable monolayer FEs, providing new perspective about the possible integration of graphene and monolayer FEs, as well as related functional devices.
In this paper, we employ density-functional-theory (DFT) calculations and explore theoretically if a single QL of In2Se3 or other 2D materials that may also exhibit out-of-plane ferroelectricity can be integrated with graphene on a metal substrate, e.g., Ru (0001), which would enable the fabrication of functional FE devices. We find that QL-In2Se3 bonds strongly to the Ru substrate, which destroys its FE properties. We predict, however, that two 2D oxides of the form M2O3 (M = Al, Y) in the QL-In2Se3 structure, fulfill all the necessary requirements. More specifically, these materials indeed form In2Se3-like, energetically stable, QL structures. We then investigate the properties of graphene/QL-M2O3/Ru(0001) heterostructures. We find that the QL-M2O3 layer works as a ferroelectric tunnel barrier. The barrier width can be modulated by reversing the polarization of the QL-M2O3, which leads to a resistance switching behavior, whereby the graphene/QL-M2O3/Ru(0001) heterostructure can work as a prototype ferroelectric tunnel junction (FTJ). Moreover, we show that the doping type of graphene (n- or p-type doping) can also be modulated in principle by alternating the polarization of the QL-M2O3, which provides a method to fabricate a graphene p–n junction.15 These results show the possibility of achieving 2D-materials-based non-volatile memory devices and graphene-based optoelectronics through the integration of graphene and monolayer ferroelectrics.
Computational methods
We performed DFT calculations using the Vienna ab initio simulation package (VASP)27–29 with the projected augmented wave (PAW)30 method. The generalized gradient approximation of Perdew–Burke–Ernzerhof (PBE)31 was used to describe the exchange–correlation potential of electrons. The plane-wave cutoff was set at 500 eV for all calculations and Γ-centered (24 × 24 × 1) and (18 × 18 × 1) k-meshes were used for freestanding Al2O3 and Y2O3 quintuple layers, respectively. The supercell sizes were 7 × 7 and 5 × 5, respectively. The phonon dispersion calculations for freestanding Al2O3 and Y2O3 quintuple layers were done by the finite-displacement method as implemented in the PHONOPY package.32–34To decrease the lattice mismatch of graphene and the intercalated M2O3 (M = Al, Y), two kinds of supercells, 6 × 6 graphene/5 × 5 Al2O3/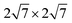 Ru(0001) and 3 × 3 graphene/2 × 2 Y2O3/
Ru(0001) and 3 × 3 graphene/2 × 2 Y2O3/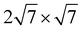 Ru(0001) were constructed. For both supercells, the graphene was compressed by 3.6% while the lattice constant of Ru(0001) was set to the experimentally measured value (2.696 Å). The intercalated Al2O3 and Y2O3 quintuple layers in the corresponding supercells were compressed by 3.0% and 1.1% respectively. We also performed calculations to illustrate that these artificial strains do not have a significant effect on the properties of the heterostructure, as shown in Fig. S8 (ESI†). Vacuum layers more than 15 Å were introduced in both supercells to decrease the interaction between periodic images. Γ-Centered (3 × 3 × 1) and (9 × 9 × 1) k-meshes were applied to supercells containing Al2O3 and Y2O3 respectively. The atoms in all supercells were fully relaxed by a conjugate gradient method until the interaction force between atoms was less than 0.01 eV Å−1, while the bottom two layers of Ru(0001) substrate were fixed to describe the interaction with bulk Ru. The DFT-D3 approach35 was employed to include van der Waals interactions.
Ru(0001) were constructed. For both supercells, the graphene was compressed by 3.6% while the lattice constant of Ru(0001) was set to the experimentally measured value (2.696 Å). The intercalated Al2O3 and Y2O3 quintuple layers in the corresponding supercells were compressed by 3.0% and 1.1% respectively. We also performed calculations to illustrate that these artificial strains do not have a significant effect on the properties of the heterostructure, as shown in Fig. S8 (ESI†). Vacuum layers more than 15 Å were introduced in both supercells to decrease the interaction between periodic images. Γ-Centered (3 × 3 × 1) and (9 × 9 × 1) k-meshes were applied to supercells containing Al2O3 and Y2O3 respectively. The atoms in all supercells were fully relaxed by a conjugate gradient method until the interaction force between atoms was less than 0.01 eV Å−1, while the bottom two layers of Ru(0001) substrate were fixed to describe the interaction with bulk Ru. The DFT-D3 approach35 was employed to include van der Waals interactions.
Results and discussion
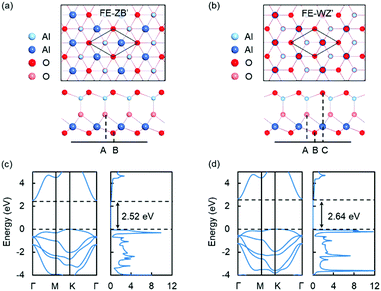
The theoretical results obtained by DFT calculations for graphene/QL-In2Se3/Ru(0001) heterostructures are displayed in Fig. S1 (ESI†), showing that the QL-In2Se3 bonds strongly to the Ru substrate and loses its FE properties. Clearly, the Ru substrate is not suitable for QL-In2Se3, unlike a Au substrate, which has been demonstrated experimentally to preserve the FE properties of 6QL-In2Se3.14 We performed calculations for a QL-In2Se3/Au(111) and indeed found weak bonding, which is a necessary condition for the preservation of FE properties (Fig. S2, ESI†). The result is expected to hold for 6QL-In2Se3/Au(111), in accord with observations. Nevertheless, we pursued investigations of QL-M2O3/Ru(111) expecting that, like bilayer SiO2,25,26 they also bond weakly to Ru(0001). Turning to 2D QL-M2O3 (M = Al, Y), we first investigated the atomic configurations and properties of freestanding QL's. As mentioned above, starting from QL-In2Se3, we replace the Se atoms by O atoms, anticipating that oxides in a QL-In2Se3 structure may be stable monolayer ferroelectrics. The In atoms are replaced by M (M = Al, Y) atoms as both Al2O3 and Y2O3 layers are expected to be insulating, which can work as a tunnel barrier. Here, we show the results of QL-Al2O3, while the results of QL-Y2O3, which are quite similar, are shown in ESI.†The predicted atomic configurations of freestanding QL-Al2O3 are shown in Fig. 1. QL-Al2O3 possesses two phases that are nearly energetically degenerate. The two side views reveal that each phase is noncentrosymmetric with a nonzero polarization. Given that the polarization of QL-In2Se3 has been shown to be reversible by a lateral shift of the middle Se layer,7 the reversal of the polarization of QL-Al2O3 should also be achievable by lateral displacement of the middle O layer, resulting in an identical structure with reverse polarization, i.e., like QL-In2Se3, the two QL-Al2O3 phases are 2D ferroelectrics with out-of-plane polarization. We adopt a terminology introduced for In2Se3 structures7 and label the two phases as FE-ZB′ and FE-WZ′. The lattice constants of both FE-ZB′ and FE-WZ′ QL-Al2O3 are 2.94 Å. In FE-ZB′ and FE-WZ′ QL-Al2O3, the O atoms are stacked in A–B and A–B–C sequences respectively, as shown in Fig. 1(a) and (b). For Al atoms in QL-Al2O3, there are two different types of coordination, tetrahedral and octahedral, which is common in several bulk Al2O3 polymorphs.37
We then calculated the phonon dispersions of freestanding QL-Al2O3 and QL-Y2O3 to check their stability, and the results are shown in Fig. S5 (ESI†). The absence of imaginary-frequency modes indicates that both QL-Al2O3 and QL-Y2O3 are dynamically stable. To demonstrate the likely feasibility of synthesizing QL-Al2O3, we compare the energy of α-Al2O3 with that of layered bulk Al2O3 comprising a stack of Al2O3 QLs, as well as the energy of freestanding Al2O3 layer in different configurations. Other bulk-alumina polymorphs, e.g., γ-Al2O3, are not considered in the calculations since α-Al2O3 is the most stable bulk alumina polymorph and can be truncated into a 2D form with the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 stoichiometry. The calculated energies are shown in Table 1, while the configurations employed in calculations are shown in Fig. S3 (ESI†). We note that the energy of layered bulk Al2O3 is only slightly higher (91 meV per f.u.) than that of α-Al2O3. However, in 2D form, the QL-Al2O3 is energetically favored over α-Al2O3 (0001) layer or Al2O3 ML. These results indicate that it may be possible to fabricate stable 2D M2O3 in the prototype structure of QL-In2Se3. We note in particular that the bilayer SiO2 that has been fabricated by intercalation in a graphene-on-Ru(0001) structure also is not known to correspond to a bulk SiO2 polymorph.
3 stoichiometry. The calculated energies are shown in Table 1, while the configurations employed in calculations are shown in Fig. S3 (ESI†). We note that the energy of layered bulk Al2O3 is only slightly higher (91 meV per f.u.) than that of α-Al2O3. However, in 2D form, the QL-Al2O3 is energetically favored over α-Al2O3 (0001) layer or Al2O3 ML. These results indicate that it may be possible to fabricate stable 2D M2O3 in the prototype structure of QL-In2Se3. We note in particular that the bilayer SiO2 that has been fabricated by intercalation in a graphene-on-Ru(0001) structure also is not known to correspond to a bulk SiO2 polymorph.
| Bulk | Freestanding layer | ||||||
|---|---|---|---|---|---|---|---|
| α-Al2O3 | α-2H Al2O3 | α-3R Al2O3 | α-Al2O3 (0001) | ML Al2O3 | FE-ZB′ QL-Al2O3 | FE-WZ′ QL-Al2O3 | |
| Relative energy (eV per f.u.) | 0 | 0.091 | 0.114 | 0.153 | 2.326 | 0 | 0.007 |
We further investigated the electronic properties of QL-Al2O3 and QL-Y2O3 and show the results of QL-Al2O3 in Fig. 1(c) and (d). The PBE-calculated band structure and DOS show that the two phases of QL-Al2O3 possess indirect band gaps of 2.52 eV and 2.64 eV, respectively. Similar results for QL-Y2O3 are shown in Fig. S4 (ESI†). PBE-based calculations are known to underestimate band gaps by about a factor 2, whereby the gaps of these materials are substantially larger, perhaps of order 5 eV, which would be very practical for tunnel barriers. All the results so far indicate that the fabrication of QL-M2O3 (M = Al, Y) is possible and that the two materials could serve as a tunnel barrier in graphene/QL-M2O3/metal heterostructures.
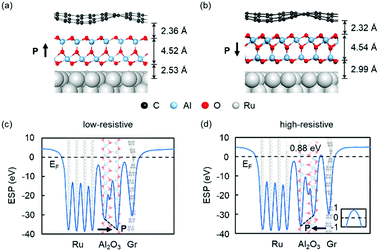
We now examine the properties of graphene/QL-M2O3/Ru heterostructures (M = Al, Y). Here, we report results for graphene/QL-Al2O3/Ru(0001), while the results for QL-Y2O3 are shown in ESI.† We used the FE-ZB′ phase of QL-Al2O3 to construct the heterostructure because it is energetically favored, as shown in Table 1. As QL-Al2O3 possesses out-of-plane polarization, there are two possible configurations for graphene/QL-Al2O3/Ru(0001) heterostructures, in which the polarization points towards or away from graphene [see Fig. 2(a) and (b)]. After relaxation, graphene in the heterostructure becomes corrugated, which is likely to result from the small compressive strain in graphene in the heterostructure,38 which we imposed to enable practical computations. As shown in Fig. 2(a) and (b), the vertical distance between the bottom surface of the QL-Al2O3 and Ru(0001), 2.53 and 2.99 Å for up and down polarization, respectively, is much larger than the typical Ru–O bond length, 1.94–1.98 Å,39 which indicates that QL-Al2O3 and Ru(0001) are bonded through van der Waals interactions. Graphene and QL-Al2O3 are also bonded through van der Waals interactions.
We further calculated the plane-averaged electrostatic potential (ESP) for the two heterostructures. The results are shown in Fig. 2(c) and (d). An electrostatic potential drop is present across the QL-Al2O3 in the polarization direction, shown as a sloped dashed line, which indicates that the out-of-plane polarization of the QL-Al2O3 is preserved in Gr/QL-Al2O3/Ru heterostructures. When the polarization points to graphene, as shown in Fig. 2(c), there are no potential barriers above the Fermi energy. However, when the polarization is reversed, as shown in Fig. 2(d), a barrier of 0.88 eV above the Fermi energy is present. These results indicate the emergence of two different states in Gr/QL-Al2O3/Ru heterostructure with the reversal of the polarization.
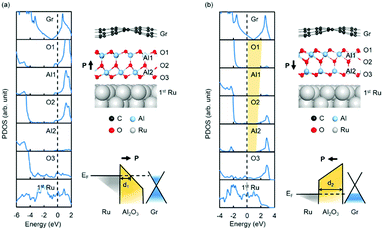
The influence of the polarization direction of QL-Al2O3 is further investigated by calculating the electronic structure of a graphene/QL-Al2O3/Ru(0001) heterostructure. The layer-resolved PDOS in Fig. 3(a) shows that, when the polarization points towards graphene, a metallic region near the graphene/QL-Al2O3 interface forms, whereby the whole system is conductive. The mechanism for this feature is shown schematically in the band diagram: the polarization-induced potential drop causes the barrier's CBM near the graphene/QL-Al2O3 interface drop below the Fermi level, which reduces the barrier width dramatically. However, when the polarization is reversed, as shown in Fig. 3(b), a tunnel barrier between graphene and Ru(0001) forms, which is shown by the yellow region in the layer-resolved PDOS. When a bias voltage is applied between graphene and Ru, the heterostructure shown in Fig. 3a exhibits a relatively low-resistive state comparing with that in Fig. 3b. This “reversible barrier metallization” mechanism, which was first reported in SrRuO3/BaTiO3/n-SrTiO340 and Co/PbTiO3/La0.7Sr0.3MnO3 heterostructures41 FTJs, induces a large tunnelling electroresistance (TER) effect. Thus, we expect that the graphene/QL-Al2O3/Ru(0001) heterostructure can work as a prototype FTJ.
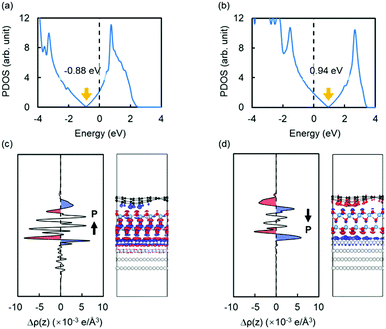
We also found that the doping type of graphene changes by reversing the polarization of the QL-Al2O3. As shown in Fig. 4(a) and 4(b), graphene is doped n- or p-type when the polarization points towards or away from graphene, respectively. For n- and p-type doped graphene, the Fermi level locates 0.88 eV above and 0.94 eV below the Dirac point of graphene, respectively. The doping of graphene can be understood by calculating the plane-averaged electron-density difference. The results, calculated using the formula Δρ = ρ(graphene/QL − Al2O3/Ru(0001)) − ρ(graphene) − ρ(QL-Al2O3) − ρ(Ru(0001)), are shown in Fig. 4(c) and (d). It is clear that the doping of graphene originates from the effect of polarization charge. For example, in Fig. 4(d), when the polarization points away from graphene, negative polarization charge accumulates at the top surface of QL-Al2O3, which induces positive charge in graphene, making graphene to be p-doped.
On the basis of the properties we presented above, we propose two kinds of model devices based on graphene/QL-Al2O3/Ru(0001) heterostructures. First, a ferroelectric tunnel junction (FTJ), a kind of non-volatile memory device. As shown in Fig. 5(a), we demonstrated that the graphene/QL-Al2O3/Ru(0001) heterostructure is in low-resistive or high-resistive state when polarization points towards or away from graphene, corresponding to the ON and OFF state of the FTJ. The polarization of QL-Al2O3 can be reversed by applying an electric field between graphene and Ru. Second, a graphene p–n junction, which is the core component of a graphene-based photodetector. As we presented above, the doping type of graphene can be modulated by reversing the polarization of QL-Al2O3. If an experimental way can be found to pole adjacent regions of the FE layer in opposite directions, a graphene p–n junction and even a graphene p–n junction array can in principle be fabricated, as shown in Fig. 5(b). Here we note that a clean graphene-FE interface is crucial for the modulation of graphene's doping by ferroelectric polarization.15 Thus, it is useful to consider how such structures might be fabricated and how a clean interface can be assured in the fabrication process.
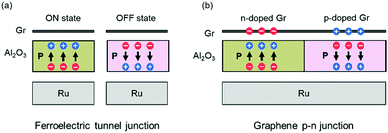 | ||
| Fig. 5 Schematic of devices based on graphene/QL-Al2O3/Ru(0001) heterostructures. (a) Ferroelectric tunnel junction. (b) Graphene p–n junction. | ||
Motivated by the fact that Gr/SiO2/Ru and Gr/Al2O3/Ni3Al heterostructures have been achieved experimentally by the intercalation method,20,24 intercalation of the QL-FEs under monolayer graphene grown epitaxially on Ru(0001) appears most promising for the following reasons: (i) graphene epitaxially grown on Ru(0001) substrates has been demonstrated to be large-scale, single-crystal and high-quality,18,19 which is necessary for high-quality graphene/monolayer-ferroelectrics heterostructures. (ii) By using the intercalation method, a clean graphene-ferroelectric interface can be assured22,23 and the degradation of monolayer ferroelectrics, which may be induced during the electrode evaporation process,42 can be avoided. (iii) It has been demonstrated that graphene/silicene/Ru(0001) heterostructures fabricated by intercalation method show good air stability for up to two weeks,22 the heterostructures proposed here should exhibit the same robustness in air, i.e., we do not expect O2 and water contaminants to passivate the ferroelectric surface charge43 or oxidize the Ru substrate. Long-term protection can be achieved by proper encapsulation of the device.
Conclusions
In this work, we investigated the effects of intercalating 2D ferroelectric materials into a graphene/metal-substrate interface. We demonstrated that freestanding monolayer M2O3 (M = Al, Y) are in principle stable in the prototype structure of QL-In2Se3. We found that graphene/QL-M2O3/Ru(0001) heterostructures exhibit reversible resistive/non-resistive switching behavior by reversing the polarization of intercalated QL-M2O3, whereby such heterostructures work as prototype ferroelectric tunnel junctions. Moreover, we found that the doping type of graphene can be changed by reversing the polarization of the intercalated QL-M2O3, potentially providing a way to fabricate graphene-based p–n junctions for photovoltaic applications. Finally we propose that intercalation is likely to be an effective method to achieve the integration of graphene and 2D FE materials, as well as corresponding device fabrication.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Work in China is supported by the National Natural Science Foundation of China (Grants No. 51922011 and 61888102), the National Key Research & Development Projects Program of China (No. 2016YFA0202300, 2018YFA0305800, and 2019YFA0308500), K. C. Wong Education Foundation, the Strategic Priority Research Program of Chinese Academy of Sciences (No. XDB30000000). A portion of the research was performed in CAS Key Laboratory of Vacuum Physics. Work at Vanderbilt was supported in part by the McMinn Endowment.References
- V. Garcia and M. Bibes, Nat. Commun., 2014, 5, 4289 CrossRef CAS PubMed.
- S. Yuan, Z. Yang, C. Xie, F. Yan, J. Dai, S. P. Lau, H. L. W. Chan and J. Hao, Adv. Mater., 2016, 28, 10048–10054 CrossRef CAS PubMed.
- M. Si, P.-Y. Liao, G. Qiu, Y. Duan and P. D. Ye, ACS Nano, 2018, 12, 6700–6705 CrossRef CAS PubMed.
- C. Paillard, X. Bai, I. C. Infante, M. Guennou, G. Geneste, M. Alexe, J. Kreisel and B. Dkhil, Adv. Mater., 2016, 28, 5153–5168 CrossRef CAS PubMed.
- F. Liu, L. You, K. L. Seyler, X. Li, P. Yu, J. Lin, X. Wang, J. Zhou, H. Wang, H. He, S. T. Pantelides, W. Zhou, P. Sharma, X. Xu, P. M. Ajayan, J. Wang and Z. Liu, Nat. Commun., 2016, 7, 12357 CrossRef CAS PubMed.
- K. Chang, J. Liu, H. Lin, N. Wang, K. Zhao, A. Zhang, F. Jin, Y. Zhong, X. Hu, W. Duan, Q. Zhang, L. Fu, Q.-K. Xue, X. Chen and S.-H. Ji, Science, 2016, 353, 274–278 CrossRef CAS PubMed.
- W. Ding, J. Zhu, Z. Wang, Y. Gao, D. Xiao, Y. Gu, Z. Zhang and W. Zhu, Nat. Commun., 2017, 8, 14956 CrossRef CAS PubMed.
- C. Cui, W.-J. Hu, X. Yan, C. Addiego, W. Gao, Y. Wang, Z. Wang, L. Li, Y. Cheng, P. Li, X. Zhang, H. N. Alshareef, T. Wu, W. Zhu, X. Pan and L.-J. Li, Nano Lett., 2018, 18, 1253–1258 CrossRef CAS PubMed.
- J. Xiao, H. Zhu, Y. Wang, W. Feng, Y. Hu, A. Dasgupta, Y. Han, Y. Wang, D. A. Muller, L. W. Martin, P. Hu and X. Zhang, Phys. Rev. Lett., 2018, 120, 227601 CrossRef CAS PubMed.
- D. Ji, S. Cai, T. R. Paudel, H. Sun, C. Zhang, L. Han, Y. Wei, Y. Zang, M. Gu, Y. Zhang, W. Gao, H. Huyan, W. Guo, D. Wu, Z. Gu, E. Y. Tsymbal, P. Wang, Y. Nie and X. Pan, Nature, 2019, 570, 87–90 CrossRef CAS PubMed.
- R. R. Mehta, B. D. Silverman and J. T. Jacobs, J. Appl. Phys., 1973, 44, 3379–3385 CrossRef CAS.
- J. Junquera and P. Ghosez, Nature, 2003, 422, 506–509 CrossRef CAS PubMed.
- C. H. Ahn, K. M. Rabe and J.-M. Triscone, Science, 2004, 303, 488–491 CrossRef CAS PubMed.
- S. M. Poh, S. J. R. Tan, H. Wang, P. Song, I. H. Abidi, X. Zhao, J. Dan, J. Chen, Z. Luo, S. J. Pennycook, A. H. Castro Neto and K. P. Loh, Nano Lett., 2018, 18, 6340–6346 CrossRef CAS PubMed.
- C. Baeumer, D. Saldana-Greco, J. M. P. Martirez, A. M. Rappe, M. Shim and L. W. Martin, Nat. Commun., 2015, 6, 6136 CrossRef CAS PubMed.
- F. H. L. Koppens, T. Mueller, P. Avouris, A. C. Ferrari, M. S. Vitiello and M. Polini, Nat. Nanotechnol., 2014, 9, 780 CrossRef CAS PubMed.
- G. Wang, M. Zhang, D. Chen, Q. Guo, X. Feng, T. Niu, X. Liu, A. Li, J. Lai, D. Sun, Z. Liao, Y. Wang, P. K. Chu, G. Ding, X. Xie, Z. Di and X. Wang, Nat. Commun., 2018, 9, 5168 CrossRef PubMed.
- Y. Pan, H. Zhang, D. Shi, J. Sun, S. Du, F. Liu and H.-J. Gao, Adv. Mater., 2009, 21, 2777–2780 CrossRef CAS.
- H. Guo, X. Wang, H. Lu, L. Bao, H. Peng, K. Qian, J. Ma, G. Li, L. Huang, X. Lin, Y.-Y. Zhang, S. Du, S. T. Pantelides and H.-J. Gao, 2D Mater., 2019, 6, 045044 CrossRef CAS.
- S. Lizzit, R. Larciprete, P. Lacovig, M. Dalmiglio, F. Orlando, A. Baraldi, L. Gammelgaard, L. Barreto, M. Bianchi, E. Perkins and P. Hofmann, Nano Lett., 2012, 12, 4503–4507 CrossRef CAS PubMed.
- Z. Y. Al Balushi, K. Wang, R. K. Ghosh, R. A. Vilá, S. M. Eichfeld, J. D. Caldwell, X. Qin, Y.-C. Lin, P. A. DeSario, G. Stone, S. Subramanian, D. F. Paul, R. M. Wallace, S. Datta, J. M. Redwing and J. A. Robinson, Nat. Mater., 2016, 15, 1166 CrossRef CAS PubMed.
- G. Li, L. Zhang, W. Xu, J. Pan, S. Song, Y. Zhang, H. Zhou, Y. Wang, L. Bao, Y.-Y. Zhang, S. Du, M. Ouyang, S. T. Pantelides and H.-J. Gao, Adv. Mater., 2018, 30, 1804650 CrossRef PubMed.
- J. Mao, L. Huang, Y. Pan, M. Gao, J. He, H. Zhou, H. Guo, Y. Tian, Q. Zou, L. Zhang, H. Zhang, Y. Wang, S. Du, X. Zhou, A. H. C. Neto and H.-J. Gao, Appl. Phys. Lett., 2012, 100, 093101 CrossRef.
- L. Omiciuolo, E. R. Hernández, E. Miniussi, F. Orlando, P. Lacovig, S. Lizzit, T. O. Menteş, A. Locatelli, R. Larciprete, M. Bianchi, S. Ulstrup, P. Hofmann, D. Alfè and A. Baraldi, Nat. Commun., 2014, 5, 5062 CrossRef CAS PubMed.
- B. Yang, W. E. Kaden, X. Yu, J. A. Boscoboinik, Y. Martynova, L. Lichtenstein, M. Heyde, M. Sterrer, R. Włodarczyk, M. Sierka, J. Sauer, S. Shaikhutdinov and H.-J. Freund, Phys. Chem. Chem. Phys., 2012, 14, 11344–11351 RSC.
- D. Löffler, J. J. Uhlrich, M. Baron, B. Yang, X. Yu, L. Lichtenstein, L. Heinke, C. Büchner, M. Heyde, S. Shaikhutdinov, H. J. Freund, R. Włodarczyk, M. Sierka and J. Sauer, Phys. Rev. Lett., 2010, 105, 146104 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115–13118 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- K. Parlinski, Z. Q. Li and Y. Kawazoe, Phys. Rev. Lett., 1997, 78, 4063–4066 CrossRef CAS.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- T. T. Song, M. Yang, J. W. Chai, M. Callsen, J. Zhou, T. Yang, Z. Zhang, J. S. Pan, D. Z. Chi, Y. P. Feng and S. J. Wang, Sci. Rep., 2016, 6, 29221 CrossRef CAS PubMed.
- K. Sohlberg, S. J. Pennycook and S. T. Pantelides, J. Am. Chem. Soc., 1999, 121, 7493–7499 CrossRef CAS.
- Y. Zhang and F. Liu, Appl. Phys. Lett., 2011, 99, 241908 CrossRef.
- A. A. Bolzan, C. Fong, B. J. Kennedy and C. J. Howard, Acta Crystallogr., Sect. B: Struct. Sci., 1997, 53, 373–380 CrossRef.
- X. Liu, J. D. Burton and E. Y. Tsymbal, Phys. Rev. Lett., 2016, 116, 197602 CrossRef PubMed.
- A. Quindeau, V. Borisov, I. Fina, S. Ostanin, E. Pippel, I. Mertig, D. Hesse and M. Alexe, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 035130 CrossRef.
- Y. Liu, J. Guo, E. Zhu, L. Liao, S.-J. Lee, M. Ding, I. Shakir, V. Gambin, Y. Huang and X. Duan, Nature, 2018, 557, 696–700 CrossRef CAS PubMed.
- A. Kakekhani and S. Ismail-Beigi, J. Mater. Chem. A, 2016, 4, 5235–5246 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0nh00255k |
| This journal is © The Royal Society of Chemistry 2020 |