Ferroelastic domains drive charge separation and suppress electron–hole recombination in all-inorganic halide perovskites: time-domain ab initio analysis

Abstract

All-inorganic perovskites have great potential in photovoltaic applications and their performance is subject to phonon-assisted charge recombination dynamics. Local microstructures, such as ferroelastic domains, are considered to have a significant influence on the charge carrier lifetime in the CsPbBr₃ perovskite. Employing a combination of time-domain density functional theory and nonadiabatic (NA) molecular dynamics simulations, we demonstrate that the formation of ferroelastic domains weakens the NA coupling and suppresses the non-radiative electron–hole recombination. This effect originates from the ferroelastic domains separating electron and hole wave functions spatially and decreasing the NA coupling by a factor of 2.4 compared to pristine CsPbBr₃, delaying electron–hole recombination by a factor of 4.2. We also show that symmetry breaking enhances electronic–vibrational interactions, activating more phonon modes and accelerating quantum decoherence by 1 fs or so, which further slows recombination. Both factors compete successfully with the slightly reduced bandgap of about 0.2 eV and prolong the charge carrier lifetime to several nanoseconds. Our study advances the understanding of the atomistic mechanism for inhibited recombination in the CsPbBr₃ perovskite in the presence of ferroelastic domains, providing an effective route to design high-performance all-inorganic halide perovskites.

---

New concepts

The mechanism of suppressed electron–hole recombination in the all-inorganic perovskite CsPbBr₃ in the presence of ferroelastic domains arises due to the antiphase contortion of the [PbBr₆]⁴⁻ octahedrons separating positive and negative charges spatially. Phonon-assisted electron–hole recombination in pristine CsPbBr₃ and CsPbBr₃ containing ferroelastic domains is governed by low-frequency vibrational modes. The design of special domain structures in ferroics, including ferroelastics, ferroelectrics, and ferromagnets, provides a promising route to engineer the electronic structure and excited-state properties of materials. The reported results have been obtained by state-of-the-art simulations combining non-adiabatic molecular dynamics simulations and the time-domain density functional theory.

Hybrid organic–inorganic halide perovskite (HOIP) solar cells have shown competitive power conversion efficiency (PCE) as compared to the traditional silicon solar cells. The great breakthrough of the increase in PCE to 25.2%¹ from 3.81%² in only ten years is due to their excellent optoelectronic properties including larger light absorption cross-sections,³ tunable bandgaps by mixing cations/anions,^4–6 long excited-state lifetimes and long charge carrier diffusion lengths,^7,8 and beneficial defect tolerance.⁹ However, the HOIP materials, such as the most widely studied methylammonium lead iodide (MAPbI₃), can undergo rapid degradation by exposure to an ambient environment or light irradiation due to the presence of A-site organic cations.^10,11 Inorganic Cs cations similar to the organic counterparts enter the perovskites and form all-inorganic cesium-based halide perovskites CsPbX₃ (X = Cl⁻, Br⁻ and I⁻), which enhances their stability¹² and results in competitive advantages with those of HOIPs, such as efficient photoluminescence,¹³ narrow emission line widths¹⁴ and low threshold lasing.¹⁵ These promising merits enable all-inorganic halide perovskites to be used in a broad range of areas similar to HOIPs,^16–23 such as solar cells,^16,17 photodetectors,^18,19 light-emitting diodes,²⁰ lasers,²¹ sensors,²² and thermoelectric devices.²³

The bandgap of the MAPbI₃ perovskites in the tetragonal phase is 1.65 eV,²⁴ which was recently tuned to be closer to the ideal bandgap of single-junction solar cells²⁵ by mixing with tin, resulting in 24.8% PCE.²⁶ The all-inorganic perovskite CsPbI₃ has a similar bandgap of 1.73 eV,²⁷ and it tends to easily undergo phase transition from the cubic to orthorhombic phase under light irradiation,²⁸ losing the remarkable photovoltaic properties. Although the stability of CsPbBr₃ is superior to that of CsPbI₃, the large bandgap of CsPbBr₃ (2.36 eV)²⁷ limits its light-harvesting regime below 525 nm in the solar spectrum. Furthermore, the charge carrier lifetimes of all-inorganic CsPbBr₃ and CsPbI₃ are typically within several hundred picoseconds,^29,30 in which the non-radiative charge and energy losses to heat are substantially faster as compared to those of their HOIP counterparts. Due to the high stability of CsPbBr₃ perovskites, the limited charge carrier lifetime constitutes the major obstacle for optoelectronic and photovoltaic devices.^29,30 Many strategies have been explored, such as passivation with molecules and polymers,^31,32 covering with a buffer layer,³³ and doping with foreign atoms,^20,32,34 to extend the charge carrier lifetime for merging two excellent properties.

In addition to external factors, many intrinsic factors can extend the charge carrier lifetime of CsPbBr₃ by reducing non-radiative electron–hole recombination. For example, Chergui and coauthors showed that the formation of small hole polarons in the CsPbBr₃ perovskite significantly delays charge recombination, as measured by picosecond X-ray absorption spectroscopy.³⁵ Our previous simulations confirmed the experimental observations that reduced recombination arises because the photoinduced distortion of the Pb–Br octahedra localizes holes on Br atoms for decreasing NA coupling.³⁶ Prior to this work, large polaron formation was reported in MAPbI₃ because the rotation of MA cations caused distortion of the Pb–I framework,^37,38 which notably extended the charge carrier lifetime. Furthermore, the ordered alignment of polar MA cations can form ferroelectric phases of MAPbI₃, in which the built-in electric field drives electrons and holes to move in opposite directions to achieve efficient charge separation, leading to the significant deceleration of electron–hole recombination.^39,40 Likewise, the ferroelectric order of the polar C–N bonds was also explored in two-dimensional hybrid perovskites, which decreased non-radiative electron–hole recombination and extended the excited-state charge carrier lifetime by reducing NA coupling.⁴¹ Owing to the lack of reproducible experimental evidence for polarization–electric field hysteresis loops, Fan et al. argued that room-temperature ferroelectricity can be ruled out as the observed amplitude and phase changes are electrochemical phenomena.⁴² Shortly thereafter, Hermes et al. reported the striped ferroelastic twin domains in MAPbI₃ formed due to the released strain during the cubic-tetragonal phase transition,⁴³ which was supported by the selected area electron diffraction patterns⁴⁴ and various spectroscopy techniques.⁴⁵ Ferroelasticity describes the relationship between external stress and internal spontaneous strain, which can form nonpolar twin domains by experiencing a local change in the crystal phase subjected to external mechanical deformation similar to how spontaneous polarization leads to ferroelectricity.⁴⁶

Stimulated by the achievements and debates on the existence of ferroelectricity and ferroelasticity in MAPbI₃ and the nonpolar nature of Cs ions, Jiang et al. provided solid evidence of ferroelastic domains in CsPbBr₃ perovskites for the first time, which enhanced photoluminescence intensity and extended carrier lifetime under remote epitaxy.³³ At the same time, first-principles calculations also suggested the formation of twin ferroelastic domains in CsPbI₃ perovskites with the assistance of charge separation.⁴⁷ However, the photoexcitation charge dynamics, particularly how ferroelastic domains regulate electron–hole recombination in all-inorganic perovskites, are still not fully understood, which is a key parameter affecting the performance of solar cells. The mechanistic understanding of the change in the electronic structure and charge recombination in the presence of ferroelastic domains at the atomistic level will provide detailed information for further engineering material and device performance.

Motivated by the recent experimental³³ and theoretical studies,⁴⁷ we apply a combination of time-dependent density functional theory (TDDFT)^48,49 and nonadiabatic molecular dynamics (NAMD)⁵⁰ to investigate the non-radiative electron–hole recombination in CsPbBr₃ perovskites affected by the formation of ferroelastic domains. Our simulations demonstrate that the formation of twin ferroelastic domains in CsPbBr₃ delays the recombination time scales to several nanoseconds, which takes place on the sub-nanosecond time scale in pristine CsPbBr₃, agreeing well with the experimental data.^29,30 The increased charge carrier lifetime of the ferroelastic system can be attributed to decreased NA coupling between the ground and excited states: about 0.67 versus 1.62 meV. This is because ferroelastic domains separate electron and hole wave functions spatially, while they are uniformly distributed on the Pb and I atoms in pristine CsPbBr₃. At the same time, the ferroelastic domains break the symmetry in the presence of the antiphase contortion of the [PbBr₆]⁴⁻ octahedron and induce strong electronic–vibrational interactions, which accelerate the phonon-induced loss of quantum coherence by about 1 fs and further delay the charge recombination. Both factors compete successfully with the slightly reduced bandgap of about 0.2 eV and lead to a decrease in electron–hole recombination by a factor of 4.2. The atomistic time-domain study rationalizes key factors in the control of the fundamental charge recombination dynamics in ferroelastic perovskites, providing important insights for the design of high-performance perovskite photovoltaic and optoelectronic devices.

In this study, the NAMD simulations are employed with the decoherence-induced surface hopping (DISH) technique⁵¹ and implemented within TDDFT in the Kohn–Sham framework.^48,49 In quantum-classical hybrid dynamics, the lighter and faster electrons are treated quantum mechanically, whereas the heavier and slower nuclei are handled semi-classically.^48,52,53 Decoherence reflects the destruction of superpositions formed between pairs of electronic states via NA coupling. Decoherence time is estimated as the pure dephasing time in the optical-response theory.⁵⁴ The DISH algorithm inherently characterizes nuclear wave function branching during quantum transition, which incorporates decoherence correction into the current NAMD approach.⁵³ It is necessary to consider the decoherence effect during calculations because the decoherence time is significantly shorter than the non-radiative electron–hole recombination time. This approach has been applied to investigate photoexcitation dynamics in a wide range of systems,^55–61 including MAPbI₃ in contact with oxygen molecules,⁵⁵ MAPbI₃ containing grain boundaries,⁵⁶ cation/anion mixing⁵⁷ and temperature influence,⁵⁸ passivating Pb-dimers in CsPbBr₃⁵⁹ and pressure effects,⁶⁰ and two-dimensional Ruddlesden–Popper perovskites.⁶¹

Geometry optimization and adiabatic MD and NA coupling calculations are performed using the Vienna ab initio simulation package,⁶² employing the Perdew–Burke–Ernzerhof functional to treat electronic exchange–correlation interactions⁶³ and the projector-augmented wave (PAW) approach to describe electron–ion interactions.⁶⁴ Geometry optimizations for both pristine CsPbBr₃ and CsPbBr₃ containing twin ferroelastic domains are calculated at the Γ-centered 2 × 2 × 2 Monkhorst–Pack k-point mesh,⁶⁵ with the plane wave energy cutoff of 400 eV. A much denser 2 × 12 × 8 k-point mesh is employed for the density of states calculations to obtain accurate electronic structures. Geometry optimization stops when ion forces are less than 10⁻³ eV Å⁻¹. The Grimme DFT-D3 method with Becke–Johnson damping is used to treat the van der Waals interactions.^66,67 The NA coupling calculations and NAMD simulations for electron–hole recombination are performed at the Γ-point because the fundamental bandgap between the conduction band minimum (CBM) and valence band maximum (VBM) of two systems is located at the Γ-point. After the geometry is relaxed at 0 K, repeated velocity rescaling is applied to heat each system to 300 K lasting for 2 ps. Then, a 6 ps adiabatic MD trajectory is obtained at the Γ-point in the microcanonical ensemble with a 1 fs atomic time step. All the geometries of the adiabatic MD trajectories are chosen as initial configurations and 1000 random numbers are used for sampling the surface hopping probability to simulate the electron–hole recombination dynamics using the PYXAID code.^52,53

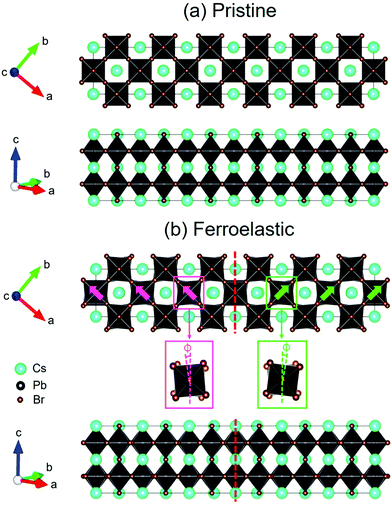
The structure of CsPbBr₃ containing twin ferroelastic domains is constructed by referring to the experimentally observed 90° twin domains with a mirrored orientation in MAPbI₃ during the cubic-to-tetragonal phase transition⁴⁴ and theoretically predicted results of CsPbI₃.⁴⁷ The optimized lattice parameter of the cubic CsPbBr₃ unit cell (space group Pm3m) is 5.898 Å, and it is in accordance with the experimental value of 5.870 Å.⁶⁸ Then, we transformed the unit cell in the cubic phase to the tetragonal phase (space group I4/mcm) by expanding lattice constants to 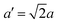, , 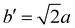and c′ = 2a. After that, we created a 120-atom (6 × 1 × 1) supercell (Cs₂₄Pb₂₄Br₇₂) to represent the pristine system based on the transformed CsPbBr₃ cell (Fig. 1a). The optimized average Pb–Br bond length and Br–Pb–Br angle are 3.022 Å and 90.002°, respectively, and they are in agreement with the experimental values.⁶⁹ Using the same supercell, we rotate the corner-sharing Br atoms of the [PbBr₆]⁴⁻ octahedron in the equatorial plane by about Φ = 5° along the [001] direction to describe the applied antiphase contortion to mirror the octahedron in the ferroelastic response, as shown in Fig. 1b. The mirror-symmetric central axis is denoted by the red dashed lines in Fig. 1b. The calculated total energy of the ferroelastic system is about 7.0 eV higher than that of the pristine system. To evaluate the stability of the ferroelastic system, we plotted the evolution of the total energy (Fig. S1 in the ESI†). The total energy shows convergence during the MD trajectories, suggesting that the geometry is in equilibrium after heating the systems at 300 K for 2 ps.

Fig. 1 Top views (top panel) and side views (bottom panel) of (a) pristine CsPbBr₃ and (b) CsPbBr₃ containing twin ferroelastic domains, in which the Br₆ octahedron antiphase was contorted. The central red dashed line is denoted as the mirror-symmetric central axis, which divides the CsPbBr₃ supercell into two symmetric components (highlighted by pink and green colors) with opposite torsional directions. The zoom-in top views (middle panel) display the chosen octahedron inside the pink and green boxes, in which the pink and green dotted lines are denoted as tetrad axes of the bi-level octahedron. The [PbBr₆]⁴⁻ octahedron maintains corner connectivity and tilts in the antiphase by about Φ = 5° along the [001] direction.

In particular, Fig. 1b shows that the antiphase contortion of the octahedron along the c axis forms the twin ferroelastic domains, mimicking the experimental findings of two overlapping single-crystal diffraction patterns with a mirrored orientation observed by Rothmann et al.⁴⁴ Upon the formation of the ferroelastic domains, the Pb–Br bond length either lengthens (3.272 Å) or shortens (2.771 Å), giving rise to an average bond length of 3.021 Å, approaching that in pristine CsPbBr₃; the average Br–Pb–Br angle decreases to 89.742°. The significant distortions of the inorganic Pb–Br sublattice in the ferroelastic system relative to that in the pristine system may affect the electronic–vibrational interactions and electron–hole recombination because the inorganic sublattice can modulate the electronic structure and NA coupling of perovskites.

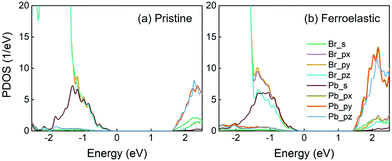
The results for the projected density of states (PDOS) of both the pristine and ferroelastic systems computed using optimized geometry are displayed in Fig. 2. In particular, PDOS can be divided into contributions from the s and p (p_x, p_y, p_z) orbitals of Br and Pb atoms. Fig. 2a shows that the Pb-p orbitals dominate CBM, while the Br-p orbitals contribute primarily to VBM and the Pb-s orbital contributes secondarily. The nature of PDOS remains largely unchanged in the CsPbBr₃-containing ferroelastic domain system (Fig. 2b). The CBM and VBM constitute the initial and final states, respectively, for non-radiative electron–hole recombination in both systems. As a result, the Pb and Br atoms primarily contribute to creating the NA couplings because they are composed of the band edge states. In contrast, the Cs atoms contribute to neither CBM nor VBM. They do not directly generate NA coupling and influence the coupling indirectly via perturbing the inorganic Pb–Br sublattice. The calculated direct bandgap of CsPbBr₃ is 1.85 eV at the Γ-point, which is in excellent agreement with a previous DFT result.⁷⁰ This value shows a 0.51 eV underestimation relative to the experimental bandgap of 2.36 eV²⁷ due to the well-known DFT problem. The calculated bandgap decreases to 1.68 eV in the ferroelastic system because the enhanced hybridization among the p_x, p_y and p_z orbitals moves the CBM downward. In general, the quantum transition rate is linearly proportional to the bandgap.⁷¹ A smaller bandgap generally creates greater NA coupling and favors faster non-radiative electron–hole recombination; however, this is not the case in the present system and this point will be discussed below. The 0.17 eV bandgap reduction allows the ferroelastic system to adsorb longer wavelengths in the solar spectra, while it has a negligible influence on non-radiative electron–hole recombination time scales.

Fig. 2 Projected density of states (PDOS) of (a) pristine CsPbBr₃ and (b) CsPbBr₃ containing ferroelastic domains, calculated using the optimized geometry. The PDOS is split into the contributions to s and p (p_x, p_y, p_z) orbitals of Br and Pb atoms. Zero energy is set to the Fermi level. The CBM is composed primarily of Pb-p orbitals; the VBM arises mainly from Br-p orbitals and secondarily from the Pb-s orbital.

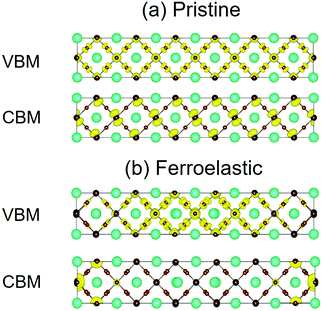
In addition to the bandgap, the strength of NA coupling affects the recombination more significantly, which is directly related to the overlap of electron (CBM) and hole (VBM) wave functions 〈ϕ_CBM|∇_R|ϕ_VBM〉. Fig. 3 presents the charge densities of VBM and CBM for pristine CsPbBr₃ and CsPbBr₃ containing ferroelastic domain systems. Fig. 3a shows that in the pristine system, the VBM is mainly localized on the Br atoms and is slightly localized on the Pb atoms and the CBM is uniformly distributed on the Pb atoms. The formation of ferroelastic domains can break the perfect crystalline symmetry, leading to the VBM charge densities mainly localizing on the Br and Pb atoms belonging to the octahedrons next to the mirror-symmetric central axis (the red dashed line in Fig. 1b), while the CBM charge densities accumulate on the Pb atoms of both the left and right edges of the simulation cell (Fig. 3b). The electron and hole wave functions are located spatially in different positions in the presence of ferroelastic domains, minimizing the overlap of the initial and final state wave functions and reducing NA coupling. At the same time, the photo-created electron–hole pairs immediately dissociate into free electrons and holes, providing another advantage to suppress non-radiative charge recombination. The benign properties can be rationalized by the special structure of twin ferroelastic domains, in which the head-to-head or tail-to-tail orientations of the [PbBr₆]⁴⁻ octahedrons create an opposite built-in electric field that drives the positive and negative charges to move in opposite directions in the formation of charge-separated states. Moreover, the conductive ferroelastic domain walls provide excellent conducting channels for electron and hole transport along different domain walls that potentially reduce charge recombination further and are similar to the parallel polarized walls in ferroelastic twins depicted by Warwick et al.⁴⁷ The difference in the charge densities between the pristine and ferroelastic systems gives rise to a significant change in the averaged NA coupling: 1.62 versus 0.67 meV (Table 1). Smaller NA coupling slows electron–hole recombination. A drop in NA coupling by a factor of 2.4 should notably impact the non-radiative electron–hole recombination dynamics.

Fig. 3 Charge densities of VBM and CBM in (a) pristine CsPbBr₃ and (b) CsPbBr₃ containing ferroelastic domains. Ferroelastic domains break symmetry and drive electron and hole wave functions located spatially in different positions, thus decreasing NA coupling and delaying non-radiative electron–hole recombination.

Table 1 Band gap, average absolute NA coupling, pure-dephasing time, and non-radiative electron–hole recombination time for the pristine and ferroelastic CsPbBr₃ systems

	Band gap (eV)	NA coupling (meV)	Dephasing (fs)	Recombination (ns)
Pristine	2.36	1.62	5.18	0.59
Ferroelastic	2.14	0.67	4.07	2.49

---

Electronic–vibrational interactions create NA coupling and promote non-radiative electron–hole recombination. In order to identify the phonon modes that coupled to the electronic subsystem, we computed the spectral density by performing Fourier transforms (FTs) of the autocorrelation functions for the CBM–VBM bandgap fluctuations. Low-frequency modes dominate the entire spectra in the two systems. Symmetry breaking in the ferroelastic system increased the intensity of the main mode and activated more phonon modes (Fig. 4a). Both FTs exhibited similar features, such as the strongest mode being below 100 cm⁻¹ and a series of modes with low-intensity peaks falling in the range of 100–300 cm⁻¹. According to the experimentally reported Raman spectrum of CsPbBr₃ perovskites,^72–75 the major peak at 72 cm⁻¹ can be assigned to the vibrational modes of the [PbBr₆]⁴⁻ octahedron.⁷² This mode contributes to generating the majority of NA coupling. The small peak at 33 cm⁻¹ is associated with the Br₆ distortion.⁷³ A series of low-intensity modes within the range of 100–200 cm⁻¹ can be assigned to the bending and stretching motions of the Pb–Br bonds,⁷⁵ and the small peak at 310 cm⁻¹ is related to the second-order phonon mode of the [PbBr₆]⁴⁻ octahedron.^72,74 These weak modes contribute secondarily to NA coupling. The peaks located at around 110–120 cm⁻¹ can be attributed to the Cs atomic motions,⁷² which contribute to the NA coupling indirectly by perturbing the Pb–Br backbones. In addition, the higher intensity of the main peak at 72 cm⁻¹ and a broader range of phonon modes presented in the ferroelastic system also accelerate the phonon-induced loss of coherence.

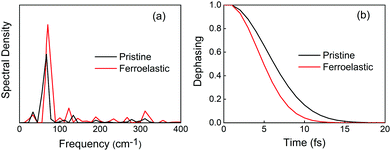Fig. 4 (a) Spectral density obtained from Fourier transforms (FTs) of the autocorrelation functions for the CBM–VBM bandgap fluctuations of the pristine CsPbBr₃ and CsPbBr₃ containing ferroelastic domain systems. The non-radiative electron–hole recombination is primarily driven by low-frequency modes. (b) The corresponding pure-dephasing functions of the two systems. The pure-dephasing times shown in Table 1 are obtained by fitting the functions to a Gaussian. A shorter pure-dephasing time favors longer charge carrier lifetime.

Decoherence constitutes another factor for influencing non-radiative electron–hole recombination. The decoherence time can be estimated as the pure dephasing time in the optical response theory⁵⁴ using the second-order cumulant approximation. In principle, a shorter decoherence time leads to slower quantum dynamics. The quantum transition even stops if the decoherence time approaches an infinitesimal value known as the quantum Zeno effect.⁷⁶ The pure dephasing functions of both systems under investigation are shown in Fig. 4b. Fitting the data to a Gaussian function, 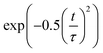, gives the pure dephasing time, τ. The pure dephasing times of about 5 fs in both systems are short because the electronic subsystem interacts with multiple phonon modes. In particular, the antiphase contortion of the octahedron presented in the ferroelastic system further shortens the pure dephasing time to 4.07 fs, which is 5.18 fs in pristine CsPbBr₃. The shortened pure dephasing time can be understood by the higher intensity of the major peak and much broader phonon modes relative to that for the pristine system (Fig. 4a). Since the rapid loss of quantum coherence suppresses charge recombination,⁵⁴ the presence of twin ferroelastic domains is expected to further prolong the excited-state lifetime.

The time evolution population of the first excited state, CBM, can provide the information for non-radiative electron–hole recombination across the fundamental bandgap. Fig. 5 shows the population decay of both pristine CsPbBr₃ and CsPbBr₃ containing ferroelastic domain systems. In order to reasonably mimic the experimental conditions, we scaled the calculated averaged bandgap 2.15 eV of the MD run for pristine CsPbBr₃ to the experimental value of 2.36 eV²⁷ by adding a constant of 0.21 eV for the NAMD simulation of electron–hole recombination. The same constant was added to the averaged bandgap of 1.93 eV for the ferroelastic system and a bandgap of 2.14 eV was obtained by assuming the same PBE functional generating identical underestimations for both systems. Here, thermal fluctuations of the bandgap are in the range of 0.2–0.3 eV and should be taken into account for calculating solar cell efficiency. Fitting the data presented in Fig. 5 using the short-time linear approximation to the exponential decay, 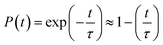, leads to the recombination time, τ (Table 1). The electron–hole recombination in pristine CsPbBr₃ takes 0.59 ns, showing good agreement with the experimentally measured data.^29,30 The formation of ferroelastic domains delays the recombination and extends the charge carrier lifetime to 2.49 ns. An extension by a factor of 4.2 is especially important for solar cell applications because this can significantly minimize charge and energy losses and enhance photocurrent. Although the bandgap of CsPbBr₃ containing ferroelastic domains decreases by 0.22 eV compared to that of the pristine system, the small reduction results in only slight acceleration of the electron–hole recombination. Importantly, ferroelastic domains drive positive and negative charge separation and thus weaken the NA coupling by a factor of 2.4, which significantly suppresses electron–hole recombination. At the same time, symmetry breaking enhances electronic–vibrational interactions and accelerates the loss of coherence, which further decelerates the recombination. However, the approximately 1 fs difference in pure dephasing times cannot explain the large difference in the recombination time scales; therefore, the NA coupling constitutes the major source responsible for the difference in the obtained time scales in both the pristine and ferroelastic systems. The observations demonstrate the importance of ferroelastic domains for reducing non-radiative electron–hole recombination by facilitating charge separation and decreasing NA coupling and provide a mechanistic understanding for the experimentally reported prolonged charge carrier lifetime of CsPbBr₃ perovskites in the presence of ferroelastic domains.³³

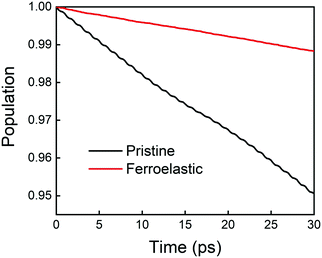Fig. 5 Non-radiative electron–hole recombination dynamics in the pristine CsPbBr₃ and CsPbBr₃ containing ferroelastic domain systems.

By performing a combination of NAMD with ab initio real-time TDDFT simulations, we studied the non-radiative electron–hole recombination in pristine CsPbBr₃ and CsPbBr₃ containing ferroelastic domain systems. The calculated results demonstrate that driven by low-frequency phonon modes below 200 cm⁻¹, CsPbBr₃ containing ferroelastic domains delays electron–hole recombination and extends the charge carrier lifetime to several nanoseconds with an increase by a factor greater than 4 as compared to the pristine system, in which the electron–hole recombination occurs on a sub-nanosecond scale and shows agreement with the experimentally measured several hundred picoseconds.³⁰ Ferroelastic domains drive the electron and hole wave functions located spatially at different positions and reduce NA coupling to 0.67 meV due to the antiphase contortion of the mirrored [PbBr₆]⁴⁻ octahedron. In contrast, the electron and hole wave functions are uniformly supported by the Pb and Br atoms inside the pristine CsPbBr₃ perovskite and achieve 1.62 meV NA coupling. A drop in the NA coupling by a factor of 2.4 in the ferroelastic system plays a dominant role in decreasing electron–hole recombination because the bandgap reduction is small, about 0.2 eV, and the pure dephasing time is slightly shortened to about 1 fs. Our study rationalizes the extended charge carrier lifetime of CsPbBr₃ in the presence of ferroelastic domains, shedding new light on the design of high-performance all-inorganic halide perovskites by ferroelastic engineering.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Science Foundation of China, grant No. 21573022, 51861135101, 21590801, 21520102005 and 21688102. R. L. acknowledges the Fundamental Research Funds for the Central Universities, the Recruitment Program of Global Youth Experts of China, and the Beijing Normal University Startup.

References

1. National Renewable Energy Laboratory (NREL) Best ResearchCell Efficiency Chart, https://www.nrel.gov/pv/cell-efficiency.html, accessed on November 9, 2019.
2. A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051.
3. W. J. Yin, T. Shi and Y. Yan, Adv. Mater., 2014, 26, 4653–4658.
4. J. H. Noh, S. H. Im, J. H. Heo, T. N. Mandal and S. I. Seok, Nano Lett., 2013, 13, 1764–1769.
5. N. Pellet, P. Gao, G. Gregori, T. Y. Yang, M. K. Nazeeruddin, J. Maier and M. Gratzel, Angew. Chem., Int. Ed., 2014, 53, 3151–3157.
6. D. D. Dong, H. Deng, C. Hu, H. B. Song, K. K. Qiao, X. K. Yang, J. Zhang, F. S. Cai, J. Tang and H. S. Song, Nanoscale, 2017, 9, 1567–1574.
7. D. Shi, V. Adinolfi, R. Comin, M. Yuan, E. Alarousu, A. Buin, Y. Chen, S. Hoogland, A. Rothenberger, K. Katsiev, Y. Losovyj, X. Zhang, P. A. Dowben, O. F. Mohammed, E. H. Sargent and O. M. Bakr, Science, 2015, 347, 519–522.
8. S. H. Turren-Cruz, M. Saliba, M. T. Mayer, H. Juarez-Santiesteban, X. Mathew, L. Nienhaus, W. Tress, M. P. Erodici, M. J. Sher, M. G. Bawendi, M. Gratzel, A. Abate, A. Hagfeldt and J. P. Correa-Baena, Energy Environ. Sci., 2018, 11, 78–86.
9. D. Meggiolaro, S. G. Motti, E. Mosconi, A. J. Barker, J. Ball, C. A. R. Perini, F. Deschler, A. Petrozza and F. D. Angelis, Energy Environ. Sci., 2018, 11, 702–713.
10. T. A. Berhe, W.-N. Su, C.-H. Chen, C.-J. Pan, J.-H. Cheng, H.-M. Chen, M.-C. Tsai, L.-Y. Chen, A. A. Dubale and B.-J. Hwang, Energy Environ. Sci., 2016, 9, 323–356.
11. Y. Hou, Z. R. Zhou, T. Y. Wen, H. W. Qiao, Z. Q. Lin, B. Ge and H. G. Yang, Nanoscale Horiz., 2019, 4, 208–213.
12. R. E. Beal, D. J. Slotcavage, T. Leijtens, A. R. Bowring, R. A. Belisle, W. H. Nguyen, G. F. Burkhard, E. T. Hoke and M. D. McGehee, J. Phys. Chem. Lett., 2016, 7, 746–751.
13. A. Swarnkar, R. Chulliyil, V. K. Ravi, M. Irfanullah, A. Chowdhury and A. Nag, Angew. Chem., Int. Ed., 2015, 54, 15424–15428.
14. Q. Liu, Y. Wang, N. Sui, Y. Wang, X. Chi, Q. Wang, Y. Chen, W. Ji, L. Zou and H. Zhang, Sci. Rep., 2016, 6, 29442.
15. Y. Wang, X. Li, X. Zhao, L. Xiao, H. Zeng and H. Sun, Nano Lett., 2015, 16, 448–453.
16. S. S. Xiang, W. P. Li, Y. Wei, J. M. Liu, H. C. Liu, L. Q. Zhu and H. N. Chen, Nanoscale, 2018, 10, 9996–10004.
17. P. Wang, X. Zhang, Y. Zhou, Q. Jiang, Q. Ye, Z. Chu, X. Li, X. Yang, Z. Yin and J. You, Nat. Commun., 2018, 9, 2225.
18. R. Dong, C. Lan, F. Li, S. Yip and J. C. Ho, Nanoscale Horiz., 2019, 4, 1342–1352.
19. Z. Zheng, Q. Hu, H. Zhou, P. Luo, A. Nie, H. Zhu, L. Gan, F. Zhuge, Y. Ma, H. Song and T. Zhai, Nanoscale Horiz., 2019, 4, 1372–1379.
20. Q. Huang, Y. Zou, S. A. Bourelle, T. Zhai, T. Wu, Y. Tan, Y. Li, J. Li, S. Duhm, T. Song, L. Wang, F. Deschler and B. Sun, Nanoscale Horiz., 2019, 4, 924–932.
21. S. W. Eaton, M. Lai, N. A. Gibson, A. B. Wong, L. Dou, J. Ma, L.-W. Wang, S. R. Leone and P. Yang, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 1993–1998.
22. Y. Wang, Y. Zhu, J. Huang, J. Cai, J. Zhu, X. Yang, J. Shen and C. Li, Nanoscale Horiz., 2017, 2, 225–232.
23. P. Wu, Y. Xiong, L. Sun, G. Xie and L. Xu, Org. Electron., 2018, 55, 90–96.
24. M. A. Green, Y. Jiang, A. M. Soufiani and A. Ho-Baillie, J. Phys. Chem. Lett., 2015, 6, 4774–4785.
25. A. Polman, M. Knight, E. C. Garnett, B. Ehrler and W. C. Sinke, Science, 2016, 352, aad4424.
26. R. Lin, K. Xiao, Z. Qin, Q. Han, C. Zhang, M. Wei, M. I. Saidaminov, Y. Gao, J. Xu and M. Xiao, Nat. Energy, 2019, 1–10.
27. J. B. Hoffman, A. L. Schleper and P. V. Kamat, J. Am. Chem. Soc., 2016, 138, 8603–8611.
28. C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2013, 52, 9019–9038.
29. N. Mondal and A. Samanta, Nanoscale, 2017, 9, 1878–1885.
30. N. Soetan, A. Puretzky, K. Reid, A. Boulesbaa, H. F. Zarick, A. Hunt, O. Rose, S. Rosenthal, D. B. Geohegan and R. Bardhan, ACS Photonics, 2018, 5, 3575–3583.
31. B. Li, Y. Zhang, L. Fu, T. Yu, S. Zhou, L. Zhang and L. Yin, Nat. Commun., 2018, 9, 1076.
32. Q. Zeng, X. Zhang, X. Feng, S. Lu, Z. Chen, X. Yong, S. A. T. Redfern, H. Wei, H. Wang, H. Shen, W. Zhang, W. Zheng, H. Zhang, J. S. Tse and B. Yang, Adv. Mater., 2018, 30, 1705393.
33. J. Jiang, X. Sun, X. C. Chen, B. W. Wang, Z. Z. Chen, Y. Hu, Y. W. Guo, L. F. Zhang, Y. Ma, L. Gao, F. S. Zheng, L. Jin, M. Chen, Z. W. Ma, Y. Y. Zhou, N. P. Padture, K. Beach, H. Terrones, Y. F. Shi, D. Gall, T. M. Lu, E. Wertz, J. Feng and J. Shi, Nat. Commun., 2019, 10, 1–12.
34. Y. Hu, F. Bai, X. Liu, Q. Ji, X. Miao, T. Qiu and S. Zhang, ACS Energy Lett., 2017, 2, 2219–2227.
35. F. G. Santomauro, J. Grilj, L. Mewes, G. Nedelcu, S. Yakunin, T. Rossi, G. Capano, A. Al Haddad, J. Budarz, D. Kinschel, D. S. Ferreira, G. Rossi, M. G. Tovar, D. Grolimund, V. Samson, M. Nachtegaal, G. Smolentsev, M. V. Kovalenko and M. Chergui, Struct. Dyn., 2017, 4, 044002.
36. J. He, M. Guo and R. Long, J. Phys. Chem. Lett., 2018, 9, 3021–3028.
37. X.-Y. Zhu and V. Podzorov, J. Phys. Chem. Lett., 2015, 4758–4761.
38. X. Wu, L. Z. Tan, X. Shen, T. Hu, K. Miyata, M. T. Trinh, R. Li, R. Coffee, S. Liu, D. A. Egger, I. Makasyuk, Q. Zheng, A. Fry, J. S. Robinson, M. D. Smith, B. Guzelturk, H. I. Karunadasa, X. Wang, X. Zhu, L. Kronik, A. M. Rappe and A. M. Lindenberg, Sci. Adv., 2017, 3, e1602388.
39. C. Quarti, E. Mosconi and F. De Angelis, Chem. Mater., 2014, 26, 6557–6569.
40. L. M. Garten, D. T. Moore, S. U. Nanayakkara, S. Dwaraknath, P. Schulz, J. Wands, A. Rockett, B. Newell, K. A. Persson, S. Trolier-McKinstry and D. S. Ginley, Sci. Adv., 2019, 5, eaas9311.
41. J. Jankowska and O. V. Prezhdo, J. Phys. Chem. Lett., 2017, 8, 812–818.
42. Z. Fan, J. Xiao, K. Sun, L. Chen, Y. Hu, J. Ouyang, K. P. Ong, K. Zeng and J. Wang, J. Phys. Chem. Lett., 2015, 6, 1155–1161.
43. I. M. Hermes, S. A. Bretschneider, V. W. Bergmann, D. Li, A. Klasen, J. Mars, W. Tremel, F. Laquai, H. J. Butt, M. Mezger, R. Berger, B. J. Rodriguez and S. A. L. Weber, J. Phys. Chem. C, 2016, 120, 5724–5731.
44. M. U. Rothmann, W. Li, Y. Zhu, U. Bach, L. Spiccia, J. Etheridge and Y.-B. Cheng, Nat. Commun., 2017, 8, 14547.
45. Y. Liu, L. Collins, A. Belianinov, S. M. Neumayer, A. V. Ievlev, M. Ahmadi, K. Xiao, S. T. Retterer, S. Jesse, S. V. Kalinin, B. Hu and O. S. Ovchinnikova, Appl. Phys. Lett., 2018, 113, 072102.
46. A. K. Tagantsev, L. E. Cross and J. Fousek, Domains in Ferroic Crystals and Thin Films, Springer, 2010.
47. A. R. Warwick, J. Íñiguez, P. D. Haynes and N. C. Bristowe, J. Phys. Chem. Lett., 2019, 10, 1416–1421.
48. C. F. Craig, W. R. Duncan and O. V. Prezhdo, Phys. Rev. Lett., 2005, 95, 163001.
49. S. A. Fischer, B. F. Habenicht, A. B. Madrid, W. R. Duncan and O. V. Prezhdo, J. Chem. Phys., 2011, 134, 024102.
50. B. J. Schwartz, E. R. Bittner, O. V. Prezhdo and P. J. Rossky, J. Chem. Phys., 1996, 104, 5942–5955.
51. H. M. Jaeger, S. Fischer and O. V. Prezhdo, J. Chem. Phys., 2012, 137, 22A545.
52. A. V. Akimov and O. V. Prezhdo, J. Chem. Theory Comput., 2013, 9, 4959–4972.
53. A. V. Akimov and O. V. Prezhdo, J. Chem. Theory Comput., 2014, 10, 789–804.
54. S. Mukamel, Principles of nonlinear optical spectroscopy, Oxford University Press, New York, 1995.
55. J. He, W.-H. Fang, R. Long and O. V. Prezhdo, J. Am. Chem. Soc., 2019, 141, 5798–5807.
56. Y. Wang, W.-H. Fang, R. Long and O. V. Prezhdo, J. Phys. Chem. Lett., 2019, 10, 1617–1623.
57. Z. Zhang and R. Long, J. Phys. Chem. Lett., 2019, 10, 3433–3439.
58. Y. Wang and R. Long, ACS Appl. Mater. Interfaces, 2019, 11, 32069–32075.
59. L. Qiao, R. Long and W.-H. Fang, J. Phys. Chem. Lett., 2019, 10, 5499–5506.
60. Y. Wang and R. Long, J. Phys. Chem. Lett., 2019, 10, 4354–4361.
61. Z. Zhang, W.-H. Fang, R. Long and O. V. Prezhdo, J. Am. Chem. Soc., 2019, 141, 15557–15566.
62. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
63. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3869.
64. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
65. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5215.
66. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
67. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
68. C. K. Moller, Nature, 1958, 182, 1436.
69. Y. Q. Zhao, Q. R. Ma, B. Liu, Z. L. Yu and M. Q. Cai, Phys. Chem. Chem. Phys., 2018, 20, 14718–14724.
70. L. Protesescu, S. Yakunin, M. I. Bodnarchuk, F. Krieg, R. Caputo, C. H. Hendon, R. X. Yang, A. Walsh and M. V. Kovalenko, Nano Lett., 2015, 15, 3692–3696.
71. R. Englman and J. Jortner, Mol. Phys., 1970, 18, 145–164.
72. J. H. Cha, J. H. Han, W. Yin, C. Park, Y. Park, T. K. Ahn, J. H. Cho and D. Y. Jung, J. Phys. Chem. Lett., 2017, 8, 565–570.
73. O. Yaffe, Y. S. Guo, L. Z. Tan, D. A. Egger, T. Hull, C. C. Stoumpos, F. Zheng, T. F. Heinz, L. Kronik, M. G. Kanatzidis, J. S. Owen, A. M. Rappe, M. A. Pimenta and L. E. Brus, Phys. Rev. Lett., 2017, 118, 13600.
74. D. M. Calistru, L. Mihut, S. Lefrant and I. Baltog, J. Appl. Phys., 1997, 82, 5391–5395.
75. C. C. Stoumpos, C. D. Malliakas, J. A. Peters, Z. Liu, M. Sebastian, J. Im, T. C. Chasapis, A. C. Wibowo, D. Y. Chung and A. J. Freeman, et al. , Cryst. Growth Des., 2013, 13, 2722–2727.
76. S. V. Kilina, A. J. Neukirch, B. F. Habenicht, D. S. Kilin and O. V. Prezhdo, Phys. Rev. Lett., 2013, 110, 180404.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9nh00717b

---